First tutorial on MULTIBINIT¶
Build a harmonic lattice model and run a dynamics¶
This lesson aims at showing how to build a harmonic model by using a second-principles approach for lattice dynamics simulations based on atomic potentials fitted on first-principles calculations.
Before beginning, it is very important to read the reference [Wojdel2013].
With this lesson, you will learn to:
- Compute the model from the DDB
- Generate the XML for the model
- Run a dynamics within MULTIBINIT
In this tutorial, all the knowledge about the Density Functional Theory (DFT) and Density Functional Perturbation Theory (DFPT) should have been already acquired. In addition, the DFPT is a key feature of ABINIT for MULTIBINIT thus, in order to learn how to use the DFPT (producing the related DDB) and the associated code to merge different DDB files, please have a look at the tutorials on Phonon response, strain response and Mrgddb before to continue. After these tutorials you should be able to compute a full DFPT calculation and a complete DDB file. Thereby this tutorial will not provide the inputs for ABINIT, that you can find, however, in the previously cited tutorials.
The AGATE software, used to make the analysis of the results, is also required for this tutorial. You can install it on debian with:
sudo add-apt-repository ppa:piti-diablotin/abiout sudo apt-get update && sudo apt-get install abiout
Note
Supposing you made your own installation of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.
In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:
export ABI_HOME=Replace_with_absolute_path_to_abinit_top_level_dir # Change this line export PATH=$ABI_HOME/src/98_main/:$PATH # Do not change this line: path to executable export ABI_TESTS=$ABI_HOME/tests/ # Do not change this line: path to tests dir export ABI_PSPDIR=$ABI_TESTS/Psps_for_tests/ # Do not change this line: path to pseudos dir
Examples in this tutorial use these shell variables: copy and paste
the code snippets into the terminal (remember to set ABI_HOME first!) or, alternatively,
source the set_abienv.sh script located in the ~abinit directory:
source ~abinit/set_abienv.sh
The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.
To execute the tutorials, create a working directory (Work*) and
copy there the input files of the lesson.
Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel with MPI, see the topic on parallelism.
1 The Harmonic part of the lattice model¶
As described in [Wojdel2013], the construction of a model starts by defining the reference structure (RS) of the system under study:
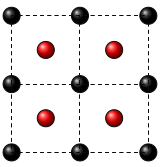
Fig. 1: Example of cubic RS made by two different (black and red) atomic species.
The choice of this RS is fundamental since the model will be based on perturbations acting on it. Once this choice is done, make sure than your system is fully relaxed and perform a single DFT calculation on this system in order to generate a DDB file. In this tutorial, we will take as an example of a material without instabilities, the perovskite CaTiO3 in the Pnma phase.
From the RS, now we consider the perturbations: the set of atomic displacements \boldsymbol{u} and lattice strain \boldsymbol{\eta}:

Fig. 2: Example of lattice perturbations: atomic displacements and strain.
At the harmonic level, we can express the potential energy as a sum of three contributions as a function of the set of perturbations (\boldsymbol{u}, \boldsymbol{\eta}):
This calculation requires:
- the computation of the phonon response (including short range and dipole-dipole interactions):
-
the computation of the strain response: $$\displaystyle E^{harm}(\boldsymbol{\eta}) \Longrightarrow \underbrace{\frac{\partial^2 E}{\partial \boldsymbol{\eta}^2}}_{\text{Elastic constants}} $$
-
the computation of the strain-phonon coupling: $$\displaystyle E^{harm}(\boldsymbol{u},\boldsymbol{\eta}) \Longrightarrow \underbrace{\frac{\partial^2 E}{\partial\boldsymbol{\eta}\partial\boldsymbol{u}}}_{\substack{\text{Internal strain}}} $$
We note that all the needed quantities related to the harmonic part can be computed by using the DFPT method and, once obtained, they are stored in a database (DDB) file. In the case of an insulator, the dipole-dipole interaction will be recomputed directly by MULTIBINIT. Thereby you need to provide into the DDB file the clamped-ion dielectric tensor and the Born effective charges.
Note
Do not forget to include in the final DDB file the DDB obtained from the RS single DFT calculation (you can still use Mrgddb). Indeed, the DDB file is also an output of a DFT calculation and, in order to build of a model, it is important to include it in the DDB file to be used.
In this tutorial, we will take as an example of a material without lattice instabilities: the perovskite CaTiO_3 in its Pnma phase.
Optional exercise \Longrightarrow Compute the phonon band structure with Anaddb. You can download the complete DDB file (resulting from the previous calculations) here:
**** DERIVATIVE DATABASE ****
+DDB, Version number 100401CaTiO3
usepaw 1 natom 20 nkpt 108 nsppol 1 nsym 8 ntypat 3 occopt 3 nband 100 acell 0.10000000000000D+01 0.10000000000000D+01 0.10000000000000D+01 amu 0.40078000000000D+02 0.47880000000000D+02 0.15999400000000D+02dilatmx 0.10000000000000D+01 ecut 0.50000000000000D+02 pawecutdg 0.80000000000000D+02 ecutsm 0.50000000000000D+00 intxc 0 iscf 7 ixc 7 kpt 0.83333333333333D-01 0.83333333333333D-01 0.83333333333333D-01 0.25000000000000D+00 0.83333333333333D-01 0.83333333333333D-01 0.41666666666667D+00 0.83333333333333D-01 0.83333333333333D-01 -0.41666666666667D+00 0.83333333333333D-01 0.83333333333333D-01 -0.25000000000000D+00 0.83333333333333D-01 0.83333333333333D-01 -0.83333333333334D-01 0.83333333333333D-01 0.83333333333333D-01 0.83333333333333D-01 0.25000000000000D+00 0.83333333333333D-01 0.25000000000000D+00 0.25000000000000D+00 0.83333333333333D-01 0.41666666666667D+00 0.25000000000000D+00 0.83333333333333D-01 -0.41666666666667D+00 0.25000000000000D+00 0.83333333333333D-01 -0.25000000000000D+00 0.25000000000000D+00 0.83333333333333D-01 -0.83333333333334D-01 0.25000000000000D+00 0.83333333333333D-01 0.83333333333333D-01 0.41666666666667D+00 0.83333333333333D-01 0.25000000000000D+00 0.41666666666667D+00 0.83333333333333D-01 0.41666666666667D+00 0.41666666666667D+00 0.83333333333333D-01 -0.41666666666667D+00 0.41666666666667D+00 0.83333333333333D-01 -0.25000000000000D+00 0.41666666666667D+00 0.83333333333333D-01 -0.83333333333334D-01 0.41666666666667D+00 0.83333333333333D-01 0.83333333333333D-01 -0.41666666666667D+00 0.83333333333333D-01 0.25000000000000D+00 -0.41666666666667D+00 0.83333333333333D-01 0.41666666666667D+00 -0.41666666666667D+00 0.83333333333333D-01 -0.41666666666667D+00 -0.41666666666667D+00 0.83333333333333D-01 -0.25000000000000D+00 -0.41666666666667D+00 0.83333333333333D-01 -0.83333333333334D-01 -0.41666666666667D+00 0.83333333333333D-01 0.83333333333333D-01 -0.25000000000000D+00 0.83333333333333D-01 0.25000000000000D+00 -0.25000000000000D+00 0.83333333333333D-01 0.41666666666667D+00 -0.25000000000000D+00 0.83333333333333D-01 -0.41666666666667D+00 -0.25000000000000D+00 0.83333333333333D-01 -0.25000000000000D+00 -0.25000000000000D+00 0.83333333333333D-01 -0.83333333333334D-01 -0.25000000000000D+00 0.83333333333333D-01 0.83333333333333D-01 -0.83333333333334D-01 0.83333333333333D-01 0.25000000000000D+00 -0.83333333333334D-01 0.83333333333333D-01 0.41666666666667D+00 -0.83333333333334D-01 0.83333333333333D-01 -0.41666666666667D+00 -0.83333333333334D-01 0.83333333333333D-01 -0.25000000000000D+00 -0.83333333333334D-01 0.83333333333333D-01 -0.83333333333334D-01 -0.83333333333334D-01 0.83333333333333D-01 0.83333333333333D-01 0.83333333333333D-01 0.25000000000000D+00 0.25000000000000D+00 0.83333333333333D-01 0.25000000000000D+00 0.41666666666667D+00 0.83333333333333D-01 0.25000000000000D+00 -0.41666666666667D+00 0.83333333333333D-01 0.25000000000000D+00 -0.25000000000000D+00 0.83333333333333D-01 0.25000000000000D+00 -0.83333333333334D-01 0.83333333333333D-01 0.25000000000000D+00 0.83333333333333D-01 0.25000000000000D+00 0.25000000000000D+00 0.25000000000000D+00 0.25000000000000D+00 0.25000000000000D+00 0.41666666666667D+00 0.25000000000000D+00 0.25000000000000D+00 -0.41666666666667D+00 0.25000000000000D+00 0.25000000000000D+00 -0.25000000000000D+00 0.25000000000000D+00 0.25000000000000D+00 -0.83333333333334D-01 0.25000000000000D+00 0.25000000000000D+00 0.83333333333333D-01 0.41666666666667D+00 0.25000000000000D+00 0.25000000000000D+00 0.41666666666667D+00 0.25000000000000D+00 0.41666666666667D+00 0.41666666666667D+00 0.25000000000000D+00 -0.41666666666667D+00 0.41666666666667D+00 0.25000000000000D+00 -0.25000000000000D+00 0.41666666666667D+00 0.25000000000000D+00 -0.83333333333334D-01 0.41666666666667D+00 0.25000000000000D+00 0.83333333333333D-01 -0.41666666666667D+00 0.25000000000000D+00 0.25000000000000D+00 -0.41666666666667D+00 0.25000000000000D+00 0.41666666666667D+00 -0.41666666666667D+00 0.25000000000000D+00 -0.41666666666667D+00 -0.41666666666667D+00 0.25000000000000D+00 -0.25000000000000D+00 -0.41666666666667D+00 0.25000000000000D+00 -0.83333333333334D-01 -0.41666666666667D+00 0.25000000000000D+00 0.83333333333333D-01 -0.25000000000000D+00 0.25000000000000D+00 0.25000000000000D+00 -0.25000000000000D+00 0.25000000000000D+00 0.41666666666667D+00 -0.25000000000000D+00 0.25000000000000D+00 -0.41666666666667D+00 -0.25000000000000D+00 0.25000000000000D+00 -0.25000000000000D+00 -0.25000000000000D+00 0.25000000000000D+00 -0.83333333333334D-01 -0.25000000000000D+00 0.25000000000000D+00 0.83333333333333D-01 -0.83333333333334D-01 0.25000000000000D+00 0.25000000000000D+00 -0.83333333333334D-01 0.25000000000000D+00 0.41666666666667D+00 -0.83333333333334D-01 0.25000000000000D+00 -0.41666666666667D+00 -0.83333333333334D-01 0.25000000000000D+00 -0.25000000000000D+00 -0.83333333333334D-01 0.25000000000000D+00 -0.83333333333334D-01 -0.83333333333334D-01 0.25000000000000D+00 0.83333333333333D-01 0.83333333333333D-01 0.41666666666667D+00 0.25000000000000D+00 0.83333333333333D-01 0.41666666666667D+00 0.41666666666667D+00 0.83333333333333D-01 0.41666666666667D+00 -0.41666666666667D+00 0.83333333333333D-01 0.41666666666667D+00 -0.25000000000000D+00 0.83333333333333D-01 0.41666666666667D+00 -0.83333333333334D-01 0.83333333333333D-01 0.41666666666667D+00 0.83333333333333D-01 0.25000000000000D+00 0.41666666666667D+00 0.25000000000000D+00 0.25000000000000D+00 0.41666666666667D+00 0.41666666666667D+00 0.25000000000000D+00 0.41666666666667D+00 -0.41666666666667D+00 0.25000000000000D+00 0.41666666666667D+00 -0.25000000000000D+00 0.25000000000000D+00 0.41666666666667D+00 -0.83333333333334D-01 0.25000000000000D+00 0.41666666666667D+00 0.83333333333333D-01 0.41666666666667D+00 0.41666666666667D+00 0.25000000000000D+00 0.41666666666667D+00 0.41666666666667D+00 0.41666666666667D+00 0.41666666666667D+00 0.41666666666667D+00 -0.41666666666667D+00 0.41666666666667D+00 0.41666666666667D+00 -0.25000000000000D+00 0.41666666666667D+00 0.41666666666667D+00 -0.83333333333334D-01 0.41666666666667D+00 0.41666666666667D+00 0.83333333333333D-01 -0.41666666666667D+00 0.41666666666667D+00 0.25000000000000D+00 -0.41666666666667D+00 0.41666666666667D+00 0.41666666666667D+00 -0.41666666666667D+00 0.41666666666667D+00 -0.41666666666667D+00 -0.41666666666667D+00 0.41666666666667D+00 -0.25000000000000D+00 -0.41666666666667D+00 0.41666666666667D+00 -0.83333333333334D-01 -0.41666666666667D+00 0.41666666666667D+00 0.83333333333333D-01 -0.25000000000000D+00 0.41666666666667D+00 0.25000000000000D+00 -0.25000000000000D+00 0.41666666666667D+00 0.41666666666667D+00 -0.25000000000000D+00 0.41666666666667D+00 -0.41666666666667D+00 -0.25000000000000D+00 0.41666666666667D+00 -0.25000000000000D+00 -0.25000000000000D+00 0.41666666666667D+00 -0.83333333333334D-01 -0.25000000000000D+00 0.41666666666667D+00 0.83333333333333D-01 -0.83333333333334D-01 0.41666666666667D+00 0.25000000000000D+00 -0.83333333333334D-01 0.41666666666667D+00 0.41666666666667D+00 -0.83333333333334D-01 0.41666666666667D+00 -0.41666666666667D+00 -0.83333333333334D-01 0.41666666666667D+00 -0.25000000000000D+00 -0.83333333333334D-01 0.41666666666667D+00 -0.83333333333334D-01 -0.83333333333334D-01 0.41666666666667D+00 kptnrm 0.10000000000000D+01 ngfft 64 72 96 nspden 1 nspinor 1 occ 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.20000000000000D+01 0.19999999999999D+01 0.19999999999989D+01 0.19999999999893D+01 0.19999999999682D+01 0.19999999999410D+01 0.39656570915656D-09 0.58583960618032D-10 0.21346736332624D-10 0.13279285888916D-11 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 rprim 0.99768860156182D+01 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.10189033854233D+02 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.14203477974238D+02 sciss 0.00000000000000D+00 spinat 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 symafm 1 1 1 1 1 1 1 1 symrel 1 0 0 0 1 0 0 0 1 -1 0 0 0 -1 0 0 0 -1 -1 0 0 0 1 0 0 0 -1 1 0 0 0 -1 0 0 0 1 -1 0 0 0 -1 0 0 0 1 1 0 0 0 1 0 0 0 -1 1 0 0 0 -1 0 0 0 -1 -1 0 0 0 1 0 0 0 1 tnons 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 -0.11102230246252D-15 0.22204460492503D-15 0.50000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 0.00000000000000D+00 -0.11102230246252D-15 0.50000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 0.22204460492503D-15 0.50000000000000D+00 0.50000000000000D+00 0.00000000000000D+00 tolwfr 0.10000000000000D+01 tphysel 0.00000000000000D+00 tsmear 0.20000000000000D-02 typat 1 1 1 1 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 wtk 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 0.92592592592593D-02 xred -0.10201848807187D-01 0.46692381249475D-01 0.25000000000000D+00 0.10201848807187D-01 0.95330761875053D+00 0.75000000000000D+00 0.51020184880719D+00 0.54669238124948D+00 0.25000000000000D+00 0.48979815119281D+00 0.45330761875053D+00 0.75000000000000D+00 0.00000000000000D+00 0.50000000000000D+00 0.00000000000000D+00 0.00000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 0.50000000000000D+00 -0.41633363423443D-16 0.00000000000000D+00 0.50000000000000D+00 -0.41633363423443D-16 0.50000000000000D+00 0.81552484811706D-01 0.47887988451146D+00 0.25000000000000D+00 0.91844751518829D+00 0.52112011548854D+00 0.75000000000000D+00 0.58155248481171D+00 0.21120115488542D-01 0.75000000000000D+00 0.41844751518829D+00 0.97887988451146D+00 0.25000000000000D+00 0.70722784504830D+00 0.29197152603914D+00 0.42924517110982D-01 0.29277215495170D+00 0.70802847396086D+00 0.95707548288902D+00 0.29277215495170D+00 0.70802847396086D+00 0.54292451711098D+00 0.70722784504830D+00 0.29197152603914D+00 0.45707548288902D+00 0.79277215495170D+00 0.79197152603914D+00 0.42924517110982D-01 0.20722784504830D+00 0.20802847396086D+00 0.95707548288902D+00 0.20722784504830D+00 0.20802847396086D+00 0.54292451711098D+00 0.79277215495170D+00 0.79197152603914D+00 0.45707548288902D+00 znucl 0.20000000000000D+02 0.22000000000000D+02 0.80000000000000D+01 zion 0.10000000000000D+02 0.12000000000000D+02 0.60000000000000D+01
Description of the PAW dataset(s) vrsio8 (for pseudopotentials)=100401 usepaw = 1 Atom type= 1 basis_size= 6 lmn_size= 18 Basis functions= 0 0 1 1 2 2 r_PAW= 1.914 shape_type= 2 r_shape= 1.914 Dij0= (only the 27 values different from zero) i j Dij0 i j Dij0 i j Dij0 i j Dij0 1 1 6.01844E-01 1 2 -1.69136E-01 2 2 5.02568E-02 3 3 2.97024E-01 4 4 2.97024E-01 5 5 2.97024E-01 3 6 -5.76535E-01 6 6 1.05142E+00 4 7 -5.76535E-01 7 7 1.05142E+00 5 8 -5.76535E-01 8 8 1.05142E+00 9 9 3.19950E-01 10 10 3.19950E-01 11 11 3.19950E-01 12 12 3.19950E-01 13 13 3.19950E-01 9 14 -1.75337E+00 14 14 9.40833E+00 10 15 -1.75337E+00 15 15 9.40833E+00 11 16 -1.75337E+00 16 16 9.40833E+00 12 17 -1.75337E+00 17 17 9.40833E+00 13 18 -1.75337E+00 18 18 9.40833E+00 Atom type= 2 basis_size= 6 lmn_size= 18 Basis functions= 0 0 1 1 2 2 r_PAW= 2.300 shape_type= 3 r_shape= 2.026 Dij0= (only the 27 values different from zero) i j Dij0 i j Dij0 i j Dij0 i j Dij0 1 1 2.80756E-01 1 2 -1.76009E-01 2 2 7.78180E-02 3 3 3.10817E-01 4 4 3.10817E-01 5 5 3.10817E-01 3 6 -5.80992E-01 6 6 6.92775E-01 4 7 -5.80992E-01 7 7 6.92775E-01 5 8 -5.80992E-01 8 8 6.92775E-01 9 9 6.68832E-01 10 10 6.68832E-01 11 11 6.68832E-01 12 12 6.68832E-01 13 13 6.68832E-01 9 14 1.11840E+01 14 14 1.86980E+02 10 15 1.11840E+01 15 15 1.86980E+02 11 16 1.11840E+01 16 16 1.86980E+02 12 17 1.11840E+01 17 17 1.86980E+02 13 18 1.11840E+01 18 18 1.86980E+02 Atom type= 3 basis_size= 4 lmn_size= 8 Basis functions= 0 0 1 1 r_PAW= 1.415 shape_type= 2 r_shape= 1.202 Dij0= (only the 12 values different from zero) i j Dij0 i j Dij0 i j Dij0 i j Dij0 1 1 4.26924E-01 1 2 -1.15918E+00 2 2 3.13411E+00 3 3 3.21024E-01 4 4 3.21024E-01 5 5 3.21024E-01 3 6 -2.31575E+00 6 6 1.61464E+01 4 7 -2.31575E+00 7 7 1.61464E+01 5 8 -2.31575E+00 8 8 1.61464E+01
**** Database of total energy derivatives **** Number of data blocks= 10
Total energy - # elements : 1 -0.57854395375878D+03 0.00000000000000D+00
1st derivatives - # elements : 66 1 1 -0.30800054330621D-05 0.00000000000000D+00 2 1 -0.10255014582818D-04 0.00000000000000D+00 3 1 -0.31554436208840D-29 0.00000000000000D+00 1 2 0.30800054330621D-05 0.00000000000000D+00 2 2 0.10255014582818D-04 0.00000000000000D+00 3 2 -0.15777218104420D-29 0.00000000000000D+00 1 3 0.30800054330621D-05 0.00000000000000D+00 2 3 -0.10255014582818D-04 0.00000000000000D+00 3 3 0.00000000000000D+00 0.00000000000000D+00 1 4 -0.30800054330621D-05 0.00000000000000D+00 2 4 0.10255014582818D-04 0.00000000000000D+00 3 4 0.00000000000000D+00 0.00000000000000D+00 1 5 0.00000000000000D+00 0.00000000000000D+00 2 5 0.00000000000000D+00 0.00000000000000D+00 3 5 0.00000000000000D+00 0.00000000000000D+00 1 6 0.00000000000000D+00 0.00000000000000D+00 2 6 0.00000000000000D+00 0.00000000000000D+00 3 6 0.00000000000000D+00 0.00000000000000D+00 1 7 0.00000000000000D+00 0.00000000000000D+00 2 7 0.00000000000000D+00 0.00000000000000D+00 3 7 0.00000000000000D+00 0.00000000000000D+00 1 8 0.00000000000000D+00 0.00000000000000D+00 2 8 0.00000000000000D+00 0.00000000000000D+00 3 8 0.00000000000000D+00 0.00000000000000D+00 1 9 -0.19666635157446D-03 0.00000000000000D+00 2 9 -0.33774783069308D-03 0.00000000000000D+00 3 9 0.00000000000000D+00 0.00000000000000D+00 1 10 0.19666635157446D-03 0.00000000000000D+00 2 10 0.33774783069308D-03 0.00000000000000D+00 3 10 0.00000000000000D+00 0.00000000000000D+00 1 11 -0.19666635157446D-03 0.00000000000000D+00 2 11 0.33774783069308D-03 0.00000000000000D+00 3 11 0.00000000000000D+00 0.00000000000000D+00 1 12 0.19666635157446D-03 0.00000000000000D+00 2 12 -0.33774783069308D-03 0.00000000000000D+00 3 12 0.00000000000000D+00 0.00000000000000D+00 1 13 0.24085510507883D-03 0.00000000000000D+00 2 13 -0.36542027355862D-03 0.00000000000000D+00 3 13 0.13299856666605D-03 0.00000000000000D+00 1 14 -0.24085510507883D-03 0.00000000000000D+00 2 14 0.36542027355862D-03 0.00000000000000D+00 3 14 -0.13299856666605D-03 0.00000000000000D+00 1 15 -0.24085510507883D-03 0.00000000000000D+00 2 15 0.36542027355862D-03 0.00000000000000D+00 3 15 0.13299856666605D-03 0.00000000000000D+00 1 16 0.24085510507883D-03 0.00000000000000D+00 2 16 -0.36542027355862D-03 0.00000000000000D+00 3 16 -0.13299856666605D-03 0.00000000000000D+00 1 17 -0.24085510507883D-03 0.00000000000000D+00 2 17 -0.36542027355862D-03 0.00000000000000D+00 3 17 0.13299856666605D-03 0.00000000000000D+00 1 18 0.24085510507883D-03 0.00000000000000D+00 2 18 0.36542027355862D-03 0.00000000000000D+00 3 18 -0.13299856666605D-03 0.00000000000000D+00 1 19 0.24085510507883D-03 0.00000000000000D+00 2 19 0.36542027355862D-03 0.00000000000000D+00 3 19 0.13299856666605D-03 0.00000000000000D+00 1 20 -0.24085510507883D-03 0.00000000000000D+00 2 20 -0.36542027355862D-03 0.00000000000000D+00 3 20 -0.13299856666605D-03 0.00000000000000D+00 1 23 -0.12767600154201D-06 0.00000000000000D+00 2 23 -0.54202778619616D-08 0.00000000000000D+00 3 23 -0.33397035949234D-07 0.00000000000000D+00 1 24 0.00000000000000D+00 0.00000000000000D+00 2 24 0.00000000000000D+00 0.00000000000000D+00 3 24 0.00000000000000D+00 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 4401 qpt 0.00000000E+00 0.00000000E+00 0.00000000E+00 1.0 1 1 1 1 0.81203128415000D+01 0.00000000000000D+00 2 1 1 1 0.12436704136623D+01 0.00000000000000D+00 3 1 1 1 -0.28051399907497D-13 0.00000000000000D+00 1 2 1 1 0.34987277568363D+00 0.68797925310824D-16 2 2 1 1 0.12115031098928D+00 -0.55810000467929D-16 3 2 1 1 -0.18927487859339D-15 0.63090673737335D-16 1 3 1 1 -0.12246624973114D+01 0.12746263089435D-15 2 3 1 1 0.45714883171459D-01 0.95487418768123D-17 3 3 1 1 -0.42610524337518D-15 0.15591136511187D-15 1 4 1 1 -0.32779267280938D+00 0.15862114244729D-16 2 4 1 1 -0.76625510255641D-02 -0.93263580938444D-17 3 4 1 1 0.66353202062457D-14 0.27028369965889D-17 1 5 1 1 0.18468616774238D+01 0.24787171987873D-15 2 5 1 1 -0.48120751386206D+00 0.20619448816667D-16 3 5 1 1 0.88453624905697D-01 0.57239351219095D-16 1 6 1 1 0.18468616774238D+01 -0.22151723697057D-15 2 6 1 1 -0.48120751386206D+00 -0.20222910069220D-16 3 6 1 1 -0.88453624905700D-01 0.18604088994794D-15 1 7 1 1 -0.34702975859620D+01 0.42995031273227D-15 2 7 1 1 -0.16950473476875D+00 -0.97372952800124D-17 3 7 1 1 0.17733915225121D+00 0.18656514979451D-15 1 8 1 1 -0.34702975859621D+01 -0.41051684855619D-15 2 8 1 1 -0.16950473476875D+00 0.28107041595958D-18 3 8 1 1 -0.17733915225121D+00 0.33906411303125D-15 1 9 1 1 -0.77674382781079D+00 0.18765477395692D-15 2 9 1 1 -0.18749557140930D+00 -0.59060369868399D-16 3 9 1 1 0.75466399839838D-15 -0.11951612243952D-15 1 10 1 1 -0.26914411630483D+00 0.26809669450733D-15 2 10 1 1 0.94460139173844D-01 -0.96692501228189D-16 3 10 1 1 -0.35060350010322D-14 0.49361025532691D-16 1 11 1 1 0.25378428539173D+00 0.75997281559267D-16 2 11 1 1 0.22699110656133D-01 -0.31915466111290D-16 3 11 1 1 0.21338458831932D-15 -0.87636878613530D-16 1 12 1 1 -0.11806024688095D+01 0.19002640044625D-16 2 12 1 1 0.46317205304328D+00 0.69218924749749D-16 3 12 1 1 0.88738087947166D-17 -0.34703608978371D-18 1 13 1 1 -0.14436289574768D+00 -0.29861018016239D-15 2 13 1 1 -0.14973724147436D+00 0.67861230639091D-16 3 13 1 1 0.49053376962295D+00 0.23394384524115D-16 1 14 1 1 0.28264640601233D-01 -0.91052705652805D-15 2 14 1 1 -0.19808731105277D+00 0.71768639374546D-16 3 14 1 1 -0.30078101445077D+00 0.12452365524684D-15 1 15 1 1 0.28264640601224D-01 -0.27459600205042D-15 2 15 1 1 -0.19808731105277D+00 0.10002819600716D-15 3 15 1 1 0.30078101445076D+00 -0.24904211190902D-16 1 16 1 1 -0.14436289574768D+00 -0.86267637938029D-15 2 16 1 1 -0.14973724147438D+00 0.10226724733592D-16 3 16 1 1 -0.49053376962291D+00 -0.92585419668332D-18 1 17 1 1 -0.61006835472897D+00 -0.48496217341254D-15 2 17 1 1 -0.34687872745002D+00 0.13402184812400D-15 3 17 1 1 -0.65187452572500D+00 -0.17628964027527D-17 1 18 1 1 -0.12068954502770D+00 0.54084107214775D-16 2 18 1 1 0.44226102341464D+00 0.81785023902869D-16 3 18 1 1 -0.68182003040278D+00 0.91623939697941D-16 1 19 1 1 -0.12068954502770D+00 -0.66087773300862D-15 2 19 1 1 0.44226102341463D+00 -0.10641944536708D-16 3 19 1 1 0.68182003040279D+00 -0.15146865381197D-15 1 20 1 1 -0.61006835472897D+00 0.35667554013304D-15 2 20 1 1 -0.34687872745002D+00 -0.71243927875379D-16 3 20 1 1 0.65187452572499D+00 -0.27590809359557D-15 1 22 1 1 -0.52688016478444D+02 0.00000000000000D+00 2 22 1 1 0.64693039354347D+00 0.00000000000000D+00 3 22 1 1 0.91942873650490D-07 0.00000000000000D+00 1 1 2 1 0.12436666124788D+01 0.00000000000000D+00 2 1 2 1 0.80127167812916D+01 0.00000000000000D+00 3 1 2 1 -0.27689910128720D-13 0.00000000000000D+00 1 2 2 1 0.12115037615800D+00 -0.55810000467929D-16 2 2 2 1 0.33484108894359D+00 0.46987812523996D-15 3 2 2 1 -0.10624157066503D-14 -0.10205126420286D-15 1 3 2 1 -0.45714883171462D-01 0.95487418768123D-17 2 3 2 1 -0.13327351863997D+01 -0.77929787037515D-18 3 3 2 1 -0.44466032053114D-15 -0.25205532505040D-17 1 4 2 1 0.76625510255635D-02 -0.93263580938444D-17 2 4 2 1 -0.27371212859831D+00 -0.56486491805201D-15 3 4 2 1 0.48788415016848D-14 -0.49068093803254D-15 1 5 2 1 0.10000557330860D+00 0.20619448816667D-16 2 5 2 1 -0.35171355713439D+01 -0.12487128786025D-14 3 5 2 1 0.19095533834566D+01 -0.38013761490726D-15 1 6 2 1 0.10000557330860D+00 -0.20222910069220D-16 2 6 2 1 -0.35171355713439D+01 0.13210115945622D-14 3 6 2 1 -0.19095533834566D+01 0.38730513200384D-16 1 7 2 1 -0.47288082163058D+00 -0.97372952800124D-17 2 7 2 1 0.17955315438035D+01 -0.92788066229945D-15 3 7 2 1 -0.82601941198911D+00 -0.29460170226133D-15 1 8 2 1 -0.47288082163058D+00 0.28107041595958D-18 2 8 2 1 0.17955315438035D+01 -0.96683961735236D-16 3 8 2 1 0.82601941198910D+00 0.77227825202825D-16 1 9 2 1 -0.35482314400285D+00 -0.59060369868399D-16 2 9 2 1 0.95058343600151D-01 0.11716279074583D-15 3 9 2 1 -0.10344144117261D-14 -0.18303200307812D-15 1 10 2 1 -0.41513718820356D-01 -0.96692501228189D-16 2 10 2 1 0.27398820110282D+00 -0.64589147146955D-16 3 10 2 1 0.16530527942191D-14 0.90424073524862D-16 1 11 2 1 0.10273435141376D+00 -0.31915466111290D-16 2 11 2 1 -0.31914217638625D+00 -0.63162171521417D-16 3 11 2 1 0.10113459263781D-14 0.36127648766785D-16 1 12 2 1 0.55667005686751D+00 0.69218924749749D-16 2 12 2 1 -0.70674797946593D+00 0.41012253742538D-16 3 12 2 1 0.24510025725082D-15 -0.72208080639260D-16 1 13 2 1 -0.28804688099402D+00 0.67861230639091D-16 2 13 2 1 -0.45653987193766D+00 -0.13082470335337D-15 3 13 2 1 -0.40599057130751D+00 0.18965561318988D-16 1 14 2 1 -0.38810233286827D-01 0.71768639374546D-16 2 14 2 1 0.30018923206282D+00 -0.44846436349985D-15 3 14 2 1 0.30570828755132D+00 0.18747603182295D-16 1 15 2 1 -0.38810233286827D-01 0.10002819600716D-15 2 15 2 1 0.30018923206281D+00 0.61976825113806D-15 3 15 2 1 -0.30570828755132D+00 0.11595318775828D-15 1 16 2 1 -0.28804688099402D+00 0.10226724733592D-16 2 16 2 1 -0.45653987193765D+00 -0.67496567844563D-15 3 16 2 1 0.40599057130755D+00 0.14033022694346D-16 1 17 2 1 -0.45466061858329D+00 0.13402184812400D-15 2 17 2 1 -0.84809723947373D+00 -0.15678432116134D-16 3 17 2 1 -0.87453604592941D+00 0.32347620798335D-16 1 18 2 1 0.36233757220372D+00 0.81785023902869D-16 2 18 2 1 -0.31551995169718D+00 0.47177814430928D-15 3 18 2 1 -0.52515542902001D+00 -0.22848336129013D-16 1 19 2 1 0.36233757220371D+00 -0.10641944536708D-16 2 19 2 1 -0.31551995169717D+00 0.64619732413977D-15 3 19 2 1 0.52515542902002D+00 -0.63351840100069D-16 1 20 2 1 -0.45466061858329D+00 -0.71243927875379D-16 2 20 2 1 -0.84809723947373D+00 -0.43070691908749D-15 3 20 2 1 0.87453604592941D+00 0.15171250368160D-16 1 22 2 1 0.41434324231002D+00 0.00000000000000D+00 2 22 2 1 -0.52504398906346D+02 0.00000000000000D+00 3 22 2 1 0.11761788120670D-06 0.00000000000000D+00 1 1 3 1 -0.28051399907497D-13 0.00000000000000D+00 2 1 3 1 -0.27689910155189D-13 0.00000000000000D+00 3 1 3 1 0.15326659944323D+02 0.00000000000000D+00 1 2 3 1 -0.18927487858607D-15 0.63090673737335D-16 2 2 3 1 -0.10624157068056D-14 -0.10205126420286D-15 3 2 3 1 -0.39754212280728D+01 0.26944573083175D-15 1 3 3 1 -0.42610524356842D-15 0.15591136511187D-15 2 3 3 1 -0.44466032042966D-15 -0.25205532505040D-17 3 3 3 1 0.24037950696125D+01 -0.40206251324528D-16 1 4 3 1 0.66353202065530D-14 0.27028369965889D-17 2 4 3 1 0.48788415016273D-14 -0.49068093803254D-15 3 4 3 1 -0.20951322426494D+01 0.31364061903847D-16 1 5 3 1 0.58307082393925D+00 0.57239351219095D-16 2 5 3 1 0.15558625568466D+01 -0.38013761490726D-15 3 5 3 1 -0.18192617348357D+01 -0.38466917078643D-14 1 6 3 1 -0.58307082393925D+00 0.18604088994794D-15 2 6 3 1 -0.15558625568466D+01 0.38730513200384D-16 3 6 3 1 -0.18192617348358D+01 0.35228234523366D-14 1 7 3 1 -0.52011443648193D+00 0.18656514979451D-15 2 7 3 1 -0.61335189982914D+00 -0.29460170226133D-15 3 7 3 1 -0.16896824586355D+01 0.37369363115984D-14 1 8 3 1 0.52011443648194D+00 0.33906411303125D-15 2 8 3 1 0.61335189982913D+00 0.77227825202825D-16 3 8 3 1 -0.16896824586355D+01 -0.27887153015553D-14 1 9 3 1 0.75466399839839D-15 -0.11951612243952D-15 2 9 3 1 -0.10344144117261D-14 -0.18303200307812D-15 3 9 3 1 -0.40944405466441D+01 -0.10095439249349D-15 1 10 3 1 -0.35060350011674D-14 0.49361025532691D-16 2 10 3 1 0.16530527939092D-14 0.90424073524862D-16 3 10 3 1 0.27059870734659D+01 0.12649352504901D-16 1 11 3 1 0.21338458841704D-15 -0.87636878613530D-16 2 11 3 1 0.10113459230775D-14 0.36127648766785D-16 3 11 3 1 0.26941601320165D+01 0.22808811993813D-16 1 12 3 1 0.88738093204033D-17 -0.34703608978371D-18 2 12 3 1 0.24510025735415D-15 -0.72208080639260D-16 3 12 3 1 -0.39144574651961D+01 -0.94836035610104D-16 1 13 3 1 0.28620314857711D+00 0.23394384524115D-16 2 13 3 1 -0.35776806400799D+00 0.18965561318988D-16 3 13 3 1 -0.32666358052665D+00 0.95829343298283D-15 1 14 3 1 -0.35192012181659D+00 0.12452365524684D-15 2 14 3 1 0.35485508012215D+00 0.18747603182295D-16 3 14 3 1 0.77323372312265D+00 -0.24327992842462D-14 1 15 3 1 0.35192012181659D+00 -0.24904211190902D-16 2 15 3 1 -0.35485508012216D+00 0.11595318775828D-15 3 15 3 1 0.77323372312267D+00 0.36042142116454D-14 1 16 3 1 -0.28620314857708D+00 -0.92585419668332D-18 2 16 3 1 0.35776806400803D+00 0.14033022694346D-16 3 16 3 1 -0.32666358052664D+00 -0.24443995047951D-14 1 17 3 1 -0.78331374891634D+00 -0.17628964027527D-17 2 17 3 1 -0.83980060330551D+00 0.32347620798335D-16 3 17 3 1 -0.25037435958720D+01 0.13526379567169D-14 1 18 3 1 -0.65718925843967D+00 0.91623939697941D-16 2 18 3 1 -0.50703823584813D+00 -0.22848336129013D-16 3 18 3 1 0.10425035738157D+01 0.11559810105626D-14 1 19 3 1 0.65718925843968D+00 -0.15146865381197D-15 2 19 3 1 0.50703823584813D+00 -0.63351840100069D-16 3 19 3 1 0.10425035738157D+01 -0.22878758314701D-14 1 20 3 1 0.78331374891633D+00 -0.27590809359557D-15 2 20 3 1 0.83980060330548D+00 0.15171250368160D-16 3 20 3 1 -0.25037435958720D+01 -0.10492863082214D-14 1 22 3 1 0.84270752667703D-07 0.00000000000000D+00 2 22 3 1 -0.13489974907705D-06 0.00000000000000D+00 3 22 3 1 -0.52023080182610D+02 0.00000000000000D+00 1 1 1 2 0.34987277568363D+00 -0.68797925310824D-16 2 1 1 2 0.12115031098928D+00 0.55810000467929D-16 3 1 1 2 -0.18927487859339D-15 -0.63090673737335D-16 1 2 1 2 0.81203128415000D+01 0.00000000000000D+00 2 2 1 2 0.12436704136621D+01 0.00000000000000D+00 3 2 1 2 0.14581163080057D-13 0.00000000000000D+00 1 3 1 2 -0.32779267280939D+00 0.15349082765761D-15 2 3 1 2 -0.76625510255625D-02 -0.14552930193627D-16 3 3 1 2 0.20483464712640D-15 0.84043450467676D-17 1 4 1 2 -0.12246624973113D+01 0.45237283912319D-16 2 4 1 2 0.45714883171453D-01 -0.25686170189749D-16 3 4 1 2 0.41453810321600D-15 -0.50788311727545D-19 1 5 1 2 0.18468616774239D+01 -0.62141597054302D-16 2 5 1 2 -0.48120751386207D+00 -0.49798861406667D-17 3 5 1 2 0.88453624905700D-01 -0.19581517367757D-16 1 6 1 2 0.18468616774238D+01 -0.15197635308381D-16 2 6 1 2 -0.48120751386207D+00 -0.23554984201183D-16 3 6 1 2 -0.88453624905696D-01 0.32303636218740D-15 1 7 1 2 -0.34702975859623D+01 -0.92271339110125D-15 2 7 1 2 -0.16950473476875D+00 -0.12599140137640D-17 3 7 1 2 0.17733915225120D+00 -0.15128155190980D-15 1 8 1 2 -0.34702975859620D+01 -0.12176021730230D-14 2 8 1 2 -0.16950473476875D+00 0.10247351816969D-16 3 8 1 2 -0.17733915225119D+00 -0.73159074961550D-16 1 9 1 2 -0.26914411630484D+00 0.24901340642106D-16 2 9 1 2 0.94460139173847D-01 -0.21813514712056D-17 3 9 1 2 -0.10193258925506D-14 0.44518202327703D-18 1 10 1 2 -0.77674382781071D+00 0.16131509069749D-15 2 10 1 2 -0.18749557140934D+00 0.67387848017710D-16 3 10 1 2 0.45366017482106D-14 -0.30023330642231D-15 1 11 1 2 -0.11806024688092D+01 -0.66795033115537D-16 2 11 1 2 0.46317205304344D+00 -0.44751693876427D-17 3 11 1 2 0.10861186043671D-14 -0.84129965349657D-16 1 12 1 2 0.25378428539174D+00 0.52283014009992D-16 2 12 1 2 0.22699110656128D-01 -0.59324865083067D-16 3 12 1 2 0.33067227183038D-14 -0.67172158160343D-16 1 13 1 2 0.28264640601229D-01 -0.60016102963866D-15 2 13 1 2 -0.19808731105278D+00 0.93817065467195D-16 3 13 1 2 -0.30078101445079D+00 -0.10601352680866D-15 1 14 1 2 -0.14436289574778D+00 0.31188295150378D-17 2 14 1 2 -0.14973724147434D+00 0.42973289964874D-16 3 14 1 2 0.49053376962285D+00 0.15035719293683D-15 1 15 1 2 -0.14436289574774D+00 0.67732518763108D-15 2 15 1 2 -0.14973724147439D+00 0.98636640995889D-16 3 15 1 2 -0.49053376962289D+00 -0.17415527749819D-16 1 16 1 2 0.28264640601237D-01 0.93098660074166D-16 2 16 1 2 -0.19808731105279D+00 0.80921478848267D-17 3 16 1 2 0.30078101445080D+00 -0.28303747654153D-16 1 17 1 2 -0.12068954502773D+00 0.21534838163192D-15 2 17 1 2 0.44226102341461D+00 0.23362134733422D-16 3 17 1 2 -0.68182003040262D+00 0.12490572576917D-15 1 18 1 2 -0.61006835472893D+00 -0.10236925639623D-14 2 18 1 2 -0.34687872744998D+00 -0.20417943091574D-15 3 18 1 2 -0.65187452572486D+00 0.16310352555728D-15 1 19 1 2 -0.61006835472892D+00 0.59615727525842D-16 2 19 1 2 -0.34687872744991D+00 -0.67171661048263D-16 3 19 1 2 0.65187452572476D+00 -0.12214438971797D-15 1 20 1 2 -0.12068954502773D+00 -0.46849267652837D-15 2 20 1 2 0.44226102341466D+00 -0.67681305636528D-16 3 20 1 2 0.68182003040271D+00 -0.11652560812199D-15 1 22 1 2 -0.52688016478446D+02 0.00000000000000D+00 2 22 1 2 0.64693039354344D+00 0.00000000000000D+00 3 22 1 2 -0.92156753728201D-07 0.00000000000000D+00 1 1 2 2 0.12115037615800D+00 0.55810000467929D-16 2 1 2 2 0.33484108894359D+00 -0.46987812523996D-15 3 1 2 2 -0.10624157066503D-14 0.10205126420286D-15 1 2 2 2 0.12436666124786D+01 0.00000000000000D+00 2 2 2 2 0.80127167812934D+01 0.00000000000000D+00 3 2 2 2 -0.56111620164676D-13 0.00000000000000D+00 1 3 2 2 0.76625510255651D-02 -0.14552930193627D-16 2 3 2 2 -0.27371212859831D+00 -0.72181221259143D-15 3 3 2 2 0.84860268636297D-14 0.26065458903303D-16 1 4 2 2 -0.45714883171468D-01 -0.25686170189749D-16 2 4 2 2 -0.13327351863997D+01 0.73864159722306D-17 3 4 2 2 -0.48083835236316D-15 -0.11304008752959D-17 1 5 2 2 0.10000557330859D+00 -0.49798861406667D-17 2 5 2 2 -0.35171355713441D+01 0.84649239133767D-15 3 5 2 2 0.19095533834568D+01 0.27749398110747D-15 1 6 2 2 0.10000557330860D+00 -0.23554984201183D-16 2 6 2 2 -0.35171355713439D+01 0.12308647537209D-14 3 6 2 2 -0.19095533834568D+01 0.32865651251824D-15 1 7 2 2 -0.47288082163059D+00 -0.12599140137640D-17 2 7 2 2 0.17955315438036D+01 0.85099435007597D-15 3 7 2 2 -0.82601941198916D+00 -0.13432597322363D-15 1 8 2 2 -0.47288082163059D+00 0.10247351816969D-16 2 8 2 2 0.17955315438035D+01 -0.30716263961466D-15 3 8 2 2 0.82601941198916D+00 -0.53002298061763D-16 1 9 2 2 -0.41513718820353D-01 -0.21813514712056D-17 2 9 2 2 0.27398820110282D+00 -0.85030484140122D-16 3 9 2 2 -0.23773724122462D-15 0.25692426802224D-16 1 10 2 2 -0.35482314400289D+00 0.67387848017710D-16 2 10 2 2 0.95058343599952D-01 -0.85495644390301D-16 3 10 2 2 0.17570978807669D-14 -0.36105814952353D-16 1 11 2 2 0.55667005686767D+00 -0.44751693876427D-17 2 11 2 2 -0.70674797946614D+00 0.23597499099886D-16 3 11 2 2 -0.49159827380636D-15 -0.58959951332332D-16 1 12 2 2 0.10273435141376D+00 -0.59324865083067D-16 2 12 2 2 -0.31914217638626D+00 -0.36147188753843D-16 3 12 2 2 -0.27880379777137D-15 -0.23967938101985D-16 1 13 2 2 -0.38810233286836D-01 0.93817065467195D-16 2 13 2 2 0.30018923206277D+00 0.30835158153276D-15 3 13 2 2 0.30570828755135D+00 -0.57998928721722D-16 1 14 2 2 -0.28804688099400D+00 0.42973289964874D-16 2 14 2 2 -0.45653987193755D+00 -0.72953007428119D-15 3 14 2 2 -0.40599057130755D+00 0.30497195037788D-16 1 15 2 2 -0.28804688099403D+00 0.98636640995889D-16 2 15 2 2 -0.45653987193752D+00 -0.32963550993570D-15 3 15 2 2 0.40599057130756D+00 0.29334178975866D-16 1 16 2 2 -0.38810233286846D-01 0.80921478848267D-17 2 16 2 2 0.30018923206278D+00 -0.18432464797805D-15 3 16 2 2 -0.30570828755138D+00 -0.14595720052580D-15 1 17 2 2 0.36233757220369D+00 0.23362134733422D-16 2 17 2 2 -0.31551995169709D+00 0.63978155291857D-16 3 17 2 2 -0.52515542902000D+00 -0.55596056459081D-15 1 18 2 2 -0.45466061858325D+00 -0.20417943091574D-15 2 18 2 2 -0.84809723947389D+00 -0.14594974336973D-15 3 18 2 2 -0.87453604592931D+00 0.18846178817275D-16 1 19 2 2 -0.45466061858318D+00 -0.67171661048263D-16 2 19 2 2 -0.84809723947382D+00 -0.70741799616829D-15 3 19 2 2 0.87453604592928D+00 -0.28511320779630D-16 1 20 2 2 0.36233757220374D+00 -0.67681305636528D-16 2 20 2 2 -0.31551995169712D+00 -0.95615470997254D-15 3 20 2 2 0.52515542902010D+00 -0.37297502647032D-16 1 22 2 2 0.41434324230921D+00 0.00000000000000D+00 2 22 2 2 -0.52504398906346D+02 0.00000000000000D+00 3 22 2 2 -0.11871925034712D-06 0.00000000000000D+00 1 1 3 2 -0.18927487858241D-15 -0.63090673737335D-16 2 1 3 2 -0.10624157068833D-14 0.10205126420286D-15 3 1 3 2 -0.39754212280728D+01 -0.26944573083175D-15 1 2 3 2 0.14581163080057D-13 0.00000000000000D+00 2 2 3 2 -0.56111620191146D-13 0.00000000000000D+00 3 2 3 2 0.15326659944323D+02 0.00000000000000D+00 1 3 3 2 0.20483464743376D-15 0.84043450467676D-17 2 3 3 2 0.84860268635722D-14 0.26065458903303D-16 3 3 3 2 -0.20951322426494D+01 0.20466084984159D-15 1 4 3 2 0.41453810302276D-15 -0.50788311727545D-19 2 4 3 2 -0.48083835226168D-15 -0.11304008752959D-17 3 4 3 2 0.24037950696126D+01 -0.12588837620424D-16 1 5 3 2 0.58307082393925D+00 -0.19581517367757D-16 2 5 3 2 0.15558625568468D+01 0.27749398110747D-15 3 5 3 2 -0.18192617348355D+01 0.22122630360868D-14 1 6 3 2 -0.58307082393925D+00 0.32303636218740D-15 2 6 3 2 -0.15558625568468D+01 0.32865651251824D-15 3 6 3 2 -0.18192617348356D+01 0.40204499008062D-14 1 7 3 2 -0.52011443648195D+00 -0.15128155190980D-15 2 7 3 2 -0.61335189982919D+00 -0.13432597322363D-15 3 7 3 2 -0.16896824586353D+01 0.49147381416925D-14 1 8 3 2 0.52011443648196D+00 -0.73159074961550D-16 2 8 3 2 0.61335189982919D+00 -0.53002298061763D-16 3 8 3 2 -0.16896824586353D+01 -0.28992645024676D-14 1 9 3 2 -0.10193258926406D-14 0.44518202327703D-18 2 9 3 2 -0.23773724132781D-15 0.25692426802224D-16 3 9 3 2 0.27059870734659D+01 -0.27721670257939D-16 1 10 3 2 0.45366017482106D-14 -0.30023330642231D-15 2 10 3 2 0.17570978807669D-14 -0.36105814952353D-16 3 10 3 2 -0.40944405466440D+01 0.74845233809552D-16 1 11 3 2 0.10861186048928D-14 -0.84129965349657D-16 2 11 3 2 -0.49159827370303D-15 -0.58959951332332D-16 3 11 3 2 -0.39144574651962D+01 -0.13724432429729D-15 1 12 3 2 0.33067227184015D-14 -0.67172158160343D-16 2 12 3 2 -0.27880380107192D-15 -0.23967938101985D-16 3 12 3 2 0.26941601320165D+01 -0.10058712729565D-15 1 13 3 2 -0.35192012181660D+00 -0.10601352680866D-15 2 13 3 2 0.35485508012218D+00 -0.57998928721722D-16 3 13 3 2 0.77323372312273D+00 -0.12515816116668D-14 1 14 3 2 0.28620314857701D+00 0.15035719293683D-15 2 14 3 2 -0.35776806400803D+00 0.30497195037788D-16 3 14 3 2 -0.32666358052665D+00 0.25645623914058D-14 1 15 3 2 -0.28620314857706D+00 -0.17415527749819D-16 2 15 3 2 0.35776806400805D+00 0.29334178975866D-16 3 15 3 2 -0.32666358052679D+00 0.77513430053224D-15 1 16 3 2 0.35192012181663D+00 -0.28303747654153D-16 2 16 3 2 -0.35485508012221D+00 -0.14595720052580D-15 3 16 3 2 0.77323372312269D+00 -0.32327040432076D-14 1 17 3 2 -0.65718925843951D+00 0.12490572576917D-15 2 17 3 2 -0.50703823584813D+00 -0.55596056459081D-15 3 17 3 2 0.10425035738155D+01 -0.10475116862543D-14 1 18 3 2 -0.78331374891620D+00 0.16310352555728D-15 2 18 3 2 -0.83980060330541D+00 0.18846178817275D-16 3 18 3 2 -0.25037435958717D+01 0.98259522029051D-15 1 19 3 2 0.78331374891610D+00 -0.12214438971797D-15 2 19 3 2 0.83980060330535D+00 -0.28511320779630D-16 3 19 3 2 -0.25037435958718D+01 0.19725366670101D-14 1 20 3 2 0.65718925843960D+00 -0.11652560812199D-15 2 20 3 2 0.50703823584821D+00 -0.37297502647032D-16 3 20 3 2 0.10425035738157D+01 0.35016936164096D-14 1 22 3 2 -0.84117587715519D-07 0.00000000000000D+00 2 22 3 2 0.13483339888500D-06 0.00000000000000D+00 3 22 3 2 -0.52023080182610D+02 0.00000000000000D+00 1 1 1 3 -0.12246624973114D+01 -0.12746263089435D-15 2 1 1 3 -0.45714883171462D-01 -0.95487418768123D-17 3 1 1 3 -0.42610524356842D-15 -0.15591136511187D-15 1 2 1 3 -0.32779267280939D+00 -0.15349082765761D-15 2 2 1 3 0.76625510255651D-02 0.14552930193627D-16 3 2 1 3 0.20483464743376D-15 -0.84043450467676D-17 1 3 1 3 0.81203128415000D+01 0.00000000000000D+00 2 3 1 3 -0.12436704136621D+01 0.00000000000000D+00 3 3 1 3 0.37030952290746D-15 0.00000000000000D+00 1 4 1 3 0.34987277568361D+00 0.21771083406871D-16 2 4 1 3 -0.12115031098928D+00 -0.15010847461334D-16 3 4 1 3 0.11378900271103D-15 -0.12009895198425D-17 1 5 1 3 -0.34702975859620D+01 0.18966192978282D-15 2 5 1 3 0.16950473476875D+00 0.10219858736834D-16 3 5 1 3 -0.17733915225121D+00 0.31785556481085D-15 1 6 1 3 -0.34702975859621D+01 0.10478840416482D-16 2 6 1 3 0.16950473476875D+00 0.21839779453621D-16 3 6 1 3 0.17733915225121D+00 -0.30656152974319D-15 1 7 1 3 0.18468616774238D+01 -0.20148658895904D-15 2 7 1 3 0.48120751386207D+00 0.67875815588768D-16 3 7 1 3 -0.88453624905700D-01 0.76133560679038D-17 1 8 1 3 0.18468616774238D+01 -0.76686237307878D-17 2 8 1 3 0.48120751386207D+00 -0.41546930527014D-16 3 8 1 3 0.88453624905708D-01 -0.28780870349550D-15 1 9 1 3 -0.11806024688093D+01 -0.43464288250707D-16 2 9 1 3 -0.46317205304348D+00 0.56154614141852D-16 3 9 1 3 -0.16847763474304D-14 0.33860529175102D-15 1 10 1 3 0.25378428539174D+00 -0.17274635335426D-15 2 10 1 3 -0.22699110656128D-01 -0.73196000643904D-16 3 10 1 3 0.14673267309773D-13 0.95727237079771D-16 1 11 1 3 -0.26914411630483D+00 0.43758720828593D-17 2 11 1 3 -0.94460139173844D-01 -0.29317520446519D-16 3 11 1 3 0.23995090622746D-14 0.30261363663284D-15 1 12 1 3 -0.77674382781071D+00 0.13083865885176D-15 2 12 1 3 0.18749557140940D+00 -0.19131850247837D-16 3 12 1 3 -0.46491474382283D-15 0.23164000584344D-16 1 13 1 3 -0.61006835472895D+00 -0.24963705232483D-15 2 13 1 3 0.34687872744995D+00 -0.12137090493023D-16 3 13 1 3 0.65187452572476D+00 -0.45929669213550D-16 1 14 1 3 -0.12068954502770D+00 0.69882144550665D-15 2 14 1 3 -0.44226102341464D+00 0.20019448137245D-16 3 14 1 3 0.68182003040273D+00 0.57117189227182D-16 1 15 1 3 -0.12068954502770D+00 0.28168679533126D-15 2 15 1 3 -0.44226102341464D+00 0.43745839767755D-16 3 15 1 3 -0.68182003040273D+00 0.26860252750672D-16 1 16 1 3 -0.61006835472895D+00 0.24671377177020D-15 2 16 1 3 0.34687872744995D+00 0.55373434730418D-16 3 16 1 3 -0.65187452572476D+00 0.29132472210128D-15 1 17 1 3 -0.14436289574773D+00 -0.48554282959499D-15 2 17 1 3 0.14973724147436D+00 -0.22596188638715D-16 3 17 1 3 -0.49053376962283D+00 -0.46832350657680D-16 1 18 1 3 0.28264640601247D-01 -0.27619810942560D-15 2 18 1 3 0.19808731105280D+00 -0.73342624519378D-16 3 18 1 3 0.30078101445083D+00 -0.10613423588813D-17 1 19 1 3 0.28264640601238D-01 0.92139029761555D-15 2 19 1 3 0.19808731105280D+00 0.36093801875902D-17 3 19 1 3 -0.30078101445082D+00 0.11600383600813D-15 1 20 1 3 -0.14436289574774D+00 -0.91547922116333D-16 2 20 1 3 0.14973724147436D+00 0.22648612388255D-16 3 20 1 3 0.49053376962282D+00 0.13857127472674D-15 1 22 1 3 -0.52688016478819D+02 0.00000000000000D+00 2 22 1 3 -0.64693039350984D+00 0.00000000000000D+00 3 22 1 3 -0.92396082862836D-07 0.00000000000000D+00 1 1 2 3 0.45714883171459D-01 -0.95487418768123D-17 2 1 2 3 -0.13327351863997D+01 0.77929787037515D-18 3 1 2 3 -0.44466032042966D-15 0.25205532505040D-17 1 2 2 3 -0.76625510255625D-02 0.14552930193627D-16 2 2 2 3 -0.27371212859831D+00 0.72181221259143D-15 3 2 2 3 0.84860268635722D-14 -0.26065458903303D-16 1 3 2 3 -0.12436666124787D+01 0.00000000000000D+00 2 3 2 3 0.80127167812934D+01 0.00000000000000D+00 3 3 2 3 -0.41900764860116D-13 0.00000000000000D+00 1 4 2 3 -0.12115037615800D+00 -0.15010847461334D-16 2 4 2 3 0.33484108894354D+00 0.15453559757894D-15 3 4 2 3 -0.51280995227690D-14 0.21976949390874D-15 1 5 2 3 0.47288082163059D+00 0.10219858736834D-16 2 5 2 3 0.17955315438035D+01 -0.72609183418630D-17 3 5 2 3 -0.82601941198920D+00 0.57444676330042D-15 1 6 2 3 0.47288082163059D+00 0.21839779453621D-16 2 6 2 3 0.17955315438035D+01 0.29473678661381D-15 3 6 2 3 0.82601941198920D+00 -0.36405513651912D-15 1 7 2 3 -0.10000557330859D+00 0.67875815588768D-16 2 7 2 3 -0.35171355713439D+01 -0.11334372837508D-14 3 7 2 3 0.19095533834569D+01 0.14526109019941D-16 1 8 2 3 -0.10000557330859D+00 -0.41546930527014D-16 2 8 2 3 -0.35171355713439D+01 -0.80895203060101D-15 3 8 2 3 -0.19095533834569D+01 -0.17093134727524D-16 1 9 2 3 -0.55667005686769D+00 0.56154614141852D-16 2 9 2 3 -0.70674797946603D+00 -0.29137539933179D-15 3 9 2 3 0.16777392624542D-14 -0.95599111010165D-16 1 10 2 3 -0.10273435141376D+00 -0.73196000643904D-16 2 10 2 3 -0.31914217638626D+00 -0.25014240297281D-16 3 10 2 3 -0.24681499372261D-15 0.27965280341337D-16 1 11 2 3 0.41513718820356D-01 -0.29317520446519D-16 2 11 2 3 0.27398820110282D+00 -0.40344845939824D-16 3 11 2 3 0.18799885770158D-14 0.82578618900279D-16 1 12 2 3 0.35482314400295D+00 -0.19131850247837D-16 2 12 2 3 0.95058343599952D-01 -0.25712106159867D-15 3 12 2 3 0.11705141309623D-14 -0.27102660226077D-15 1 13 2 3 0.45466061858322D+00 -0.12137090493023D-16 2 13 2 3 -0.84809723947390D+00 -0.33702259836239D-15 3 13 2 3 -0.87453604592926D+00 -0.54372177320074D-16 1 14 2 3 -0.36233757220373D+00 0.20019448137245D-16 2 14 2 3 -0.31551995169709D+00 0.48356217833335D-15 3 14 2 3 -0.52515542902004D+00 -0.11206516465743D-15 1 15 2 3 -0.36233757220372D+00 0.43745839767755D-16 2 15 2 3 -0.31551995169710D+00 -0.71924376955525D-15 3 15 2 3 0.52515542902003D+00 -0.12538001139428D-15 1 16 2 3 0.45466061858322D+00 0.55373434730418D-16 2 16 2 3 -0.84809723947391D+00 -0.57715477236046D-15 3 16 2 3 0.87453604592927D+00 0.18391818826022D-15 1 17 2 3 0.28804688099400D+00 -0.22596188638715D-16 2 17 2 3 -0.45653987193755D+00 -0.18582337733352D-17 3 17 2 3 -0.40599057130751D+00 0.31241994899975D-16 1 18 2 3 0.38810233286855D-01 -0.73342624519378D-16 2 18 2 3 0.30018923206277D+00 -0.44000099275409D-16 3 18 2 3 0.30570828755140D+00 -0.16358897290871D-15 1 19 2 3 0.38810233286853D-01 0.36093801875902D-17 2 19 2 3 0.30018923206278D+00 0.66814999564684D-15 3 19 2 3 -0.30570828755138D+00 0.13664787718504D-16 1 20 2 3 0.28804688099402D+00 0.22648612388255D-16 2 20 2 3 -0.45653987193756D+00 -0.28559685901210D-15 3 20 2 3 0.40599057130754D+00 0.10063266012984D-15 1 22 2 3 -0.41434324181281D+00 0.00000000000000D+00 2 22 2 3 -0.52504398906628D+02 0.00000000000000D+00 3 22 2 3 0.11788672758611D-06 0.00000000000000D+00 1 1 3 3 -0.42610524337518D-15 -0.15591136511187D-15 2 1 3 3 -0.44466032053114D-15 0.25205532505040D-17 3 1 3 3 0.24037950696125D+01 0.40206251324528D-16 1 2 3 3 0.20483464712640D-15 -0.84043450467676D-17 2 2 3 3 0.84860268636297D-14 -0.26065458903303D-16 3 2 3 3 -0.20951322426494D+01 -0.20466084984159D-15 1 3 3 3 0.37030952290746D-15 0.00000000000000D+00 2 3 3 3 -0.41900764833646D-13 0.00000000000000D+00 3 3 3 3 0.15326659944323D+02 0.00000000000000D+00 1 4 3 3 0.11378900273321D-15 -0.12009895198425D-17 2 4 3 3 -0.51280995228467D-14 0.21976949390874D-15 3 4 3 3 -0.39754212280728D+01 -0.14427530967751D-16 1 5 3 3 0.52011443648194D+00 0.31785556481085D-15 2 5 3 3 -0.61335189982923D+00 0.57444676330042D-15 3 5 3 3 -0.16896824586355D+01 0.64351816298317D-14 1 6 3 3 -0.52011443648194D+00 -0.30656152974319D-15 2 6 3 3 0.61335189982923D+00 -0.36405513651912D-15 3 6 3 3 -0.16896824586355D+01 -0.48008011913020D-14 1 7 3 3 -0.58307082393925D+00 0.76133560679038D-17 2 7 3 3 0.15558625568469D+01 0.14526109019941D-16 3 7 3 3 -0.18192617348358D+01 -0.68147058782069D-14 1 8 3 3 0.58307082393926D+00 -0.28780870349550D-15 2 8 3 3 -0.15558625568469D+01 -0.17093134727524D-16 3 8 3 3 -0.18192617348358D+01 0.37682968062434D-14 1 9 3 3 -0.16847763472217D-14 0.33860529175102D-15 2 9 3 3 0.16777392652151D-14 -0.95599111010165D-16 3 9 3 3 -0.39144574651960D+01 0.16681971577727D-17 1 10 3 3 0.14673267309157D-13 0.95727237079771D-16 2 10 3 3 -0.24681499634060D-15 0.27965280341337D-16 3 10 3 3 0.26941601320165D+01 -0.22132526263134D-17 1 11 3 3 0.23995090624880D-14 0.30261363663284D-15 2 11 3 3 0.18799885766021D-14 0.82578618900279D-16 3 11 3 3 0.27059870734660D+01 0.33676969966402D-16 1 12 3 3 -0.46491474382283D-15 0.23164000584344D-16 2 12 3 3 0.11705141309623D-14 -0.27102660226077D-15 3 12 3 3 -0.40944405466440D+01 -0.79070967606930D-16 1 13 3 3 0.78331374891610D+00 -0.45929669213550D-16 2 13 3 3 -0.83980060330531D+00 -0.54372177320074D-16 3 13 3 3 -0.25037435958717D+01 -0.45938039071743D-15 1 14 3 3 0.65718925843963D+00 0.57117189227182D-16 2 14 3 3 -0.50703823584815D+00 -0.11206516465743D-15 3 14 3 3 0.10425035738156D+01 0.20303572127197D-14 1 15 3 3 -0.65718925843963D+00 0.26860252750672D-16 2 15 3 3 0.50703823584815D+00 -0.12538001139428D-15 3 15 3 3 0.10425035738156D+01 -0.27003139712984D-14 1 16 3 3 -0.78331374891610D+00 0.29132472210128D-15 2 16 3 3 0.83980060330537D+00 0.18391818826022D-15 3 16 3 3 -0.25037435958716D+01 0.60014021929189D-15 1 17 3 3 -0.28620314857701D+00 -0.46832350657680D-16 2 17 3 3 -0.35776806400799D+00 0.31241994899975D-16 3 17 3 3 -0.32666358052674D+00 -0.19451893524558D-14 1 18 3 3 0.35192012181666D+00 -0.10613423588813D-17 2 18 3 3 0.35485508012224D+00 -0.16358897290871D-15 3 18 3 3 0.77323372312275D+00 -0.35491980046754D-14 1 19 3 3 -0.35192012181663D+00 0.11600383600813D-15 2 19 3 3 -0.35485508012221D+00 0.13664787718504D-16 3 19 3 3 0.77323372312276D+00 -0.14587533752576D-14 1 20 3 3 0.28620314857698D+00 0.13857127472674D-15 2 20 3 3 0.35776806400802D+00 0.10063266012984D-15 3 20 3 3 -0.32666358052671D+00 0.18983213450900D-14 1 22 3 3 -0.83137355873317D-07 0.00000000000000D+00 2 22 3 3 -0.13519319891787D-06 0.00000000000000D+00 3 22 3 3 -0.52023080182461D+02 0.00000000000000D+00 1 1 1 4 -0.32779267280938D+00 -0.15862114244729D-16 2 1 1 4 0.76625510255635D-02 0.93263580938444D-17 3 1 1 4 0.66353202065530D-14 -0.27028369965889D-17 1 2 1 4 -0.12246624973113D+01 -0.45237283912319D-16 2 2 1 4 -0.45714883171468D-01 0.25686170189749D-16 3 2 1 4 0.41453810302276D-15 0.50788311727545D-19 1 3 1 4 0.34987277568361D+00 -0.21771083406871D-16 2 3 1 4 -0.12115031098928D+00 0.15010847461334D-16 3 3 1 4 0.11378900270737D-15 0.12009895198425D-17 1 4 1 4 0.81203128415000D+01 0.00000000000000D+00 2 4 1 4 -0.12436704136623D+01 0.00000000000000D+00 3 4 1 4 -0.35156828423150D-13 0.00000000000000D+00 1 5 1 4 -0.34702975859622D+01 0.11894852267496D-15 2 5 1 4 0.16950473476876D+00 0.46863521517321D-16 3 5 1 4 -0.17733915225113D+00 -0.17382024471058D-15 1 6 1 4 -0.34702975859621D+01 -0.20728620148476D-15 2 6 1 4 0.16950473476877D+00 -0.24500781800549D-16 3 6 1 4 0.17733915225106D+00 -0.26699717254028D-15 1 7 1 4 0.18468616774239D+01 0.76120497290076D-16 2 7 1 4 0.48120751386207D+00 0.54016274074149D-17 3 7 1 4 -0.88453624905719D-01 0.20890725913801D-16 1 8 1 4 0.18468616774238D+01 -0.17727954929827D-15 2 8 1 4 0.48120751386207D+00 -0.85896072045117D-16 3 8 1 4 0.88453624905707D-01 -0.30192185661427D-15 1 9 1 4 0.25378428539176D+00 -0.18324896008692D-15 2 9 1 4 -0.22699110656126D-01 -0.21610306985164D-17 3 9 1 4 0.50598843059140D-14 -0.33169809374639D-15 1 10 1 4 -0.11806024688093D+01 0.29087788968623D-15 2 10 1 4 -0.46317205304336D+00 0.31263631319622D-16 3 10 1 4 -0.28617774773792D-14 0.11028701953239D-15 1 11 1 4 -0.77674382781062D+00 -0.12725674646029D-15 2 11 1 4 0.18749557140956D+00 0.29244300429183D-16 3 11 1 4 -0.12213695914716D-14 0.19961428951696D-15 1 12 1 4 -0.26914411630483D+00 0.16722905976617D-15 2 12 1 4 -0.94460139173846D-01 0.25423889374715D-16 3 12 1 4 0.34899544318860D-15 0.86930755485357D-16 1 13 1 4 -0.12068954502774D+00 0.10547589743398D-15 2 13 1 4 -0.44226102341461D+00 -0.15763060474797D-15 3 13 1 4 0.68182003040262D+00 -0.13575254845204D-17 1 14 1 4 -0.61006835472890D+00 -0.38886541703644D-15 2 14 1 4 0.34687872744998D+00 -0.12091351241704D-15 3 14 1 4 0.65187452572482D+00 0.17177508049973D-15 1 15 1 4 -0.61006835472890D+00 0.15185745422468D-15 2 15 1 4 0.34687872744988D+00 -0.22608802282444D-16 3 15 1 4 -0.65187452572468D+00 -0.11497378207745D-15 1 16 1 4 -0.12068954502774D+00 0.52316819472188D-15 2 16 1 4 -0.44226102341466D+00 -0.12028521197973D-16 3 16 1 4 -0.68182003040271D+00 -0.22489337737880D-16 1 17 1 4 0.28264640601235D-01 0.15135745896296D-15 2 17 1 4 0.19808731105280D+00 -0.29770600454208D-16 3 17 1 4 0.30078101445082D+00 0.96234608353360D-16 1 18 1 4 -0.14436289574776D+00 0.41723740583170D-15 2 18 1 4 0.14973724147432D+00 -0.91723345422732D-16 3 18 1 4 -0.49053376962280D+00 0.36191962949854D-18 1 19 1 4 -0.14436289574772D+00 0.12144307459058D-16 2 19 1 4 0.14973724147434D+00 -0.63963776258785D-16 3 19 1 4 0.49053376962288D+00 -0.53907411914521D-16 1 20 1 4 0.28264640601246D-01 0.11631186902758D-15 2 20 1 4 0.19808731105280D+00 -0.32973602142844D-16 3 20 1 4 -0.30078101445082D+00 0.17471817922494D-16 1 22 1 4 -0.52688016478821D+02 0.00000000000000D+00 2 22 1 4 -0.64693039350879D+00 0.00000000000000D+00 3 22 1 4 0.91703365423870D-07 0.00000000000000D+00 1 1 2 4 -0.76625510255641D-02 0.93263580938444D-17 2 1 2 4 -0.27371212859831D+00 0.56486491805201D-15 3 1 2 4 0.48788415016273D-14 0.49068093803254D-15 1 2 2 4 0.45714883171453D-01 0.25686170189749D-16 2 2 2 4 -0.13327351863997D+01 -0.73864159722306D-17 3 2 2 4 -0.48083835226168D-15 0.11304008752959D-17 1 3 2 4 -0.12115037615800D+00 0.15010847461334D-16 2 3 2 4 0.33484108894354D+00 -0.15453559757894D-15 3 3 2 4 -0.51280995228467D-14 -0.21976949390874D-15 1 4 2 4 -0.12436666124789D+01 0.00000000000000D+00 2 4 2 4 0.80127167812934D+01 0.00000000000000D+00 3 4 2 4 0.11086592273895D-12 0.00000000000000D+00 1 5 2 4 0.47288082163060D+00 0.46863521517321D-16 2 5 2 4 0.17955315438035D+01 -0.45793589902345D-15 3 5 2 4 -0.82601941198918D+00 -0.99944914331783D-16 1 6 2 4 0.47288082163060D+00 -0.24500781800549D-16 2 6 2 4 0.17955315438035D+01 -0.39324266028607D-15 3 6 2 4 0.82601941198917D+00 0.33622053283550D-15 1 7 2 4 -0.10000557330859D+00 0.54016274074149D-17 2 7 2 4 -0.35171355713440D+01 0.53082941391073D-15 3 7 2 4 0.19095533834568D+01 -0.16537307837354D-15 1 8 2 4 -0.10000557330859D+00 -0.85896072045117D-16 2 8 2 4 -0.35171355713440D+01 0.28661294495790D-15 3 8 2 4 -0.19095533834569D+01 -0.15077730851045D-15 1 9 2 4 -0.10273435141376D+00 -0.21610306985164D-17 2 9 2 4 -0.31914217638625D+00 0.70789214890200D-16 3 9 2 4 -0.73901435218925D-15 0.22269248963728D-16 1 10 2 4 -0.55667005686757D+00 0.31263631319622D-16 2 10 2 4 -0.70674797946607D+00 -0.51764384639709D-15 3 10 2 4 -0.14943934473388D-15 0.42591283915866D-16 1 11 2 4 0.35482314400311D+00 0.29244300429183D-16 2 11 2 4 0.95058343599696D-01 0.57001762977131D-15 3 11 2 4 -0.13417178082706D-14 -0.20010205725760D-15 1 12 2 4 0.41513718820354D-01 0.25423889374715D-16 2 12 2 4 0.27398820110282D+00 -0.13408074499374D-15 3 12 2 4 0.51012119127622D-14 -0.55233580828542D-17 1 13 2 4 -0.36233757220370D+00 -0.15763060474797D-15 2 13 2 4 -0.31551995169707D+00 -0.65837744463220D-15 3 13 2 4 -0.52515542902002D+00 0.14337894034546D-15 1 14 2 4 0.45466061858325D+00 -0.12091351241704D-15 2 14 2 4 -0.84809723947398D+00 0.59175834564771D-17 3 14 2 4 -0.87453604592934D+00 0.11106029801565D-15 1 15 2 4 0.45466061858315D+00 -0.22608802282444D-16 2 15 2 4 -0.84809723947393D+00 0.54530872388555D-15 3 15 2 4 0.87453604592923D+00 -0.18995671379650D-15 1 16 2 4 -0.36233757220374D+00 -0.12028521197973D-16 2 16 2 4 -0.31551995169711D+00 -0.75077652016686D-15 3 16 2 4 0.52515542902009D+00 0.85576045505394D-16 1 17 2 4 0.38810233286859D-01 -0.29770600454208D-16 2 17 2 4 0.30018923206275D+00 -0.17606837694407D-15 3 17 2 4 0.30570828755140D+00 -0.41186214675138D-16 1 18 2 4 0.28804688099397D+00 -0.91723345422732D-16 2 18 2 4 -0.45653987193756D+00 -0.30848578535435D-15 3 18 2 4 -0.40599057130749D+00 -0.11583759015259D-15 1 19 2 4 0.28804688099399D+00 -0.63963776258785D-16 2 19 2 4 -0.45653987193754D+00 -0.51247508478580D-15 3 19 2 4 0.40599057130748D+00 -0.43406200721385D-16 1 20 2 4 0.38810233286857D-01 -0.32973602142844D-16 2 20 2 4 0.30018923206278D+00 -0.15418773570593D-15 3 20 2 4 -0.30570828755139D+00 0.17422367807414D-15 1 22 2 4 -0.41434324181169D+00 0.00000000000000D+00 2 22 2 4 -0.52504398906627D+02 0.00000000000000D+00 3 22 2 4 -0.11845062831950D-06 0.00000000000000D+00 1 1 3 4 0.66353202062457D-14 -0.27028369965889D-17 2 1 3 4 0.48788415016848D-14 0.49068093803254D-15 3 1 3 4 -0.20951322426494D+01 -0.31364061903847D-16 1 2 3 4 0.41453810321600D-15 0.50788311727545D-19 2 2 3 4 -0.48083835236316D-15 0.11304008752959D-17 3 2 3 4 0.24037950696126D+01 0.12588837620424D-16 1 3 3 4 0.11378900273688D-15 0.12009895198425D-17 2 3 3 4 -0.51280995231826D-14 -0.21976949390874D-15 3 3 3 4 -0.39754212280728D+01 0.14427530967751D-16 1 4 3 4 -0.35156828423150D-13 0.00000000000000D+00 2 4 3 4 0.11086592276542D-12 0.00000000000000D+00 3 4 3 4 0.15326659944323D+02 0.00000000000000D+00 1 5 3 4 0.52011443648202D+00 -0.17382024471058D-15 2 5 3 4 -0.61335189982921D+00 -0.99944914331783D-16 3 5 3 4 -0.16896824586353D+01 0.62887757924279D-14 1 6 3 4 -0.52011443648209D+00 -0.26699717254028D-15 2 6 3 4 0.61335189982920D+00 0.33622053283550D-15 3 6 3 4 -0.16896824586353D+01 -0.30673194027317D-14 1 7 3 4 -0.58307082393927D+00 0.20890725913801D-16 2 7 3 4 0.15558625568468D+01 -0.16537307837354D-15 3 7 3 4 -0.18192617348355D+01 -0.80083183275338D-15 1 8 3 4 0.58307082393926D+00 -0.30192185661427D-15 2 8 3 4 -0.15558625568469D+01 -0.15077730851045D-15 3 8 3 4 -0.18192617348357D+01 0.19575320588394D-14 1 9 3 4 0.50598843052982D-14 -0.33169809374639D-15 2 9 3 4 -0.73901435480724D-15 0.22269248963728D-16 3 9 3 4 0.26941601320165D+01 -0.23698957991494D-16 1 10 3 4 -0.28617774771706D-14 0.11028701953239D-15 2 10 3 4 -0.14943934197293D-15 0.42591283915866D-16 3 10 3 4 -0.39144574651961D+01 -0.58777050406292D-16 1 11 3 4 -0.12213695914716D-14 0.19961428951696D-15 2 11 3 4 -0.13417178082706D-14 -0.20010205725760D-15 3 11 3 4 -0.40944405466437D+01 -0.12137066939274D-15 1 12 3 4 0.34899544321474D-15 0.86930755485357D-16 2 12 3 4 0.51012119126771D-14 -0.55233580828542D-17 3 12 3 4 0.27059870734659D+01 0.34199150270015D-16 1 13 3 4 0.65718925843951D+00 -0.13575254845204D-17 2 13 3 4 -0.50703823584813D+00 0.14337894034546D-15 3 13 3 4 0.10425035738155D+01 -0.94265247396232D-15 1 14 3 4 0.78331374891616D+00 0.17177508049973D-15 2 14 3 4 -0.83980060330540D+00 0.11106029801565D-15 3 14 3 4 -0.25037435958717D+01 -0.56684358694504D-16 1 15 3 4 -0.78331374891602D+00 -0.11497378207745D-15 2 15 3 4 0.83980060330532D+00 -0.18995671379650D-15 3 15 3 4 -0.25037435958718D+01 0.25953673345151D-14 1 16 3 4 -0.65718925843960D+00 -0.22489337737880D-16 2 16 3 4 0.50703823584821D+00 0.85576045505394D-16 3 16 3 4 0.10425035738157D+01 -0.64678579107844D-15 1 17 3 4 0.35192012181664D+00 0.96234608353360D-16 2 17 3 4 0.35485508012224D+00 -0.41186214675138D-16 3 17 3 4 0.77323372312279D+00 -0.35391700461409D-15 1 18 3 4 -0.28620314857698D+00 0.36191962949854D-18 2 18 3 4 -0.35776806400798D+00 -0.11583759015259D-15 3 18 3 4 -0.32666358052669D+00 -0.25347535973515D-15 1 19 3 4 0.28620314857704D+00 -0.53907411914521D-16 2 19 3 4 0.35776806400796D+00 -0.43406200721385D-16 3 19 3 4 -0.32666358052682D+00 0.11874318266631D-14 1 20 3 4 -0.35192012181664D+00 0.17471817922494D-16 2 20 3 4 -0.35485508012223D+00 0.17422367807414D-15 3 20 3 4 0.77323372312275D+00 0.30975462066112D-14 1 22 3 4 0.85250601935833D-07 0.00000000000000D+00 2 22 3 4 0.13454019410055D-06 0.00000000000000D+00 3 22 3 4 -0.52023080182461D+02 0.00000000000000D+00 1 1 1 5 0.18468616062556D+01 -0.24787171987873D-15 2 1 1 5 0.10000454035179D+00 -0.20619448816667D-16 3 1 1 5 0.58307128988747D+00 -0.57239351219095D-16 1 2 1 5 0.18468616062556D+01 0.62141597054302D-16 2 2 1 5 0.10000454035179D+00 0.49798861406667D-17 3 2 1 5 0.58307128988748D+00 0.19581517367757D-16 1 3 1 5 -0.34702975859620D+01 -0.18966192978282D-15 2 3 1 5 0.47288082163059D+00 -0.10219858736834D-16 3 3 1 5 0.52011443648194D+00 -0.31785556481085D-15 1 4 1 5 -0.34702975859622D+01 -0.11894852267496D-15 2 4 1 5 0.47288082163060D+00 -0.46863521517321D-16 3 4 1 5 0.52011443648202D+00 0.17382024471058D-15 1 5 1 5 0.17662550828636D+02 0.00000000000000D+00 2 5 1 5 0.46163742265035D+00 0.00000000000000D+00 3 5 1 5 -0.72684139393893D+00 0.00000000000000D+00 1 6 1 5 0.10582222744076D+01 0.00000000000000D+00 2 6 1 5 -0.14989449594138D+00 0.00000000000000D+00 3 6 1 5 -0.42173512680128D+01 0.00000000000000D+00 1 7 1 5 -0.13669505028554D+02 0.00000000000000D+00 2 7 1 5 -0.47212921920618D+01 0.00000000000000D+00 3 7 1 5 -0.48524629094079D+01 0.00000000000000D+00 1 8 1 5 -0.32956689542690D+00 0.00000000000000D+00 2 8 1 5 -0.81588147068491D-01 0.00000000000000D+00 3 8 1 5 0.32385070169896D+00 0.00000000000000D+00 1 9 1 5 -0.15725316985842D+01 -0.54325641826435D-15 2 9 1 5 -0.88530873634906D-01 -0.33236873731901D-17 3 9 1 5 0.51032796555911D+00 0.91014423190876D-16 1 10 1 5 -0.15725316985839D+01 -0.12528183832509D-14 2 10 1 5 -0.88530873634891D-01 -0.43807353085505D-16 3 10 1 5 0.51032796555911D+00 0.40218535164441D-16 1 11 1 5 0.12597052197366D+01 -0.13189128600793D-15 2 11 1 5 0.37871643932605D+00 0.59052550880210D-16 3 11 1 5 0.55913866598669D+00 -0.10914708572143D-15 1 12 1 5 0.12597052197366D+01 0.27797139080262D-16 2 12 1 5 0.37871643932608D+00 -0.45352092317229D-16 3 12 1 5 0.55913866598670D+00 -0.88563926901218D-17 1 13 1 5 -0.47205630832728D+00 0.34172112609615D-15 2 13 1 5 0.80829208278334D+00 -0.43723574251308D-16 3 13 1 5 0.12067628732447D+01 -0.12105974288004D-15 1 14 1 5 -0.47205630832703D+00 -0.55605901675018D-15 2 14 1 5 0.80829208278341D+00 0.50938376677407D-16 3 14 1 5 0.12067628732443D+01 0.25847212148978D-15 1 15 1 5 -0.37877129705309D-01 0.43994838456847D-15 2 15 1 5 0.13310522665979D-01 0.42069481764430D-16 3 15 1 5 0.83818842403369D-02 0.81230446742012D-16 1 16 1 5 -0.37877129705308D-01 -0.46888651093540D-16 2 16 1 5 0.13310522665981D-01 0.13563707818804D-16 3 16 1 5 0.83818842403218D-02 -0.19443713283607D-15 1 17 1 5 0.14572086039215D+00 -0.20359724274569D-15 2 17 1 5 0.57907236680427D+00 0.11868506827686D-15 3 17 1 5 0.12614849187089D+01 -0.83663155464845D-16 1 18 1 5 0.14572086039211D+00 -0.12253514312844D-15 2 18 1 5 0.57907236680447D+00 0.84111649352257D-17 3 18 1 5 0.12614849187088D+01 0.11641248338691D-15 1 19 1 5 -0.61748566762754D-01 0.33129667180942D-15 2 19 1 5 -0.20804343225725D-01 0.14885976625228D-16 3 19 1 5 0.10357201143747D+00 0.22547608697163D-15 1 20 1 5 -0.61748566762772D-01 0.32475389971199D-15 2 20 1 5 -0.20804343225729D-01 0.55575491183039D-17 3 20 1 5 0.10357201143744D+00 0.14956530333043D-15 1 22 1 5 -0.31238332545780D+02 0.00000000000000D+00 2 22 1 5 0.31236553853961D+01 0.00000000000000D+00 3 22 1 5 0.32507934447167D+01 0.00000000000000D+00 1 1 2 5 -0.48120495601929D+00 -0.20619448816667D-16 2 1 2 5 -0.35171325566685D+01 0.12487128786025D-14 3 1 2 5 0.15558599906723D+01 0.38013761490726D-15 1 2 2 5 -0.48120495601930D+00 0.49798861406667D-17 2 2 2 5 -0.35171325566687D+01 -0.84649239133767D-15 3 2 2 5 0.15558599906724D+01 -0.27749398110747D-15 1 3 2 5 0.16950473476875D+00 -0.10219858736834D-16 2 3 2 5 0.17955315438035D+01 0.72609183418630D-17 3 3 2 5 -0.61335189982923D+00 -0.57444676330042D-15 1 4 2 5 0.16950473476876D+00 -0.46863521517321D-16 2 4 2 5 0.17955315438035D+01 0.45793589902345D-15 3 4 2 5 -0.61335189982921D+00 0.99944914331783D-16 1 5 2 5 0.46164627652384D+00 0.00000000000000D+00 2 5 2 5 0.18517916435199D+02 0.00000000000000D+00 3 5 2 5 -0.26871123781975D+01 0.00000000000000D+00 1 6 2 5 -0.14989449594138D+00 0.00000000000000D+00 2 6 2 5 0.34119604620910D+00 0.00000000000000D+00 3 6 2 5 0.10651445201029D+01 0.00000000000000D+00 1 7 2 5 0.47212921920618D+01 0.00000000000000D+00 2 7 2 5 -0.14761187001991D+02 0.00000000000000D+00 3 7 2 5 0.66258235879515D+00 0.00000000000000D+00 1 8 2 5 0.81587278202461D-01 0.00000000000000D+00 2 8 2 5 -0.29611934821259D+00 0.00000000000000D+00 3 8 2 5 -0.16943728555954D+00 0.00000000000000D+00 1 9 2 5 -0.38630898660346D-01 -0.33236873731901D-17 2 9 2 5 -0.15112161379035D+01 -0.26454865155168D-16 3 9 2 5 -0.17494069864047D+00 -0.19690436477292D-15 1 10 2 5 -0.38630898660331D-01 -0.43807353085505D-16 2 10 2 5 -0.15112161379033D+01 0.17704537914414D-15 3 10 2 5 -0.17494069864029D+00 0.11663140305761D-15 1 11 2 5 -0.48952263584242D+00 0.59052550880210D-16 2 11 2 5 0.13991458022464D+01 -0.37491604998636D-15 3 11 2 5 0.90232092760050D-01 -0.23755913597423D-15 1 12 2 5 -0.48952263584240D+00 -0.45352092317229D-16 2 12 2 5 0.13991458022464D+01 0.76580497854578D-15 3 12 2 5 0.90232092760128D-01 -0.23798329398505D-15 1 13 2 5 -0.75348532218759D+00 -0.43723574251308D-16 2 13 2 5 -0.33013812894421D-01 -0.10829575390688D-14 3 13 2 5 0.68650510820900D+00 0.20747296785272D-15 1 14 2 5 -0.75348532218753D+00 0.50938376677407D-16 2 14 2 5 -0.33013812894591D-01 0.31335327493156D-15 3 14 2 5 0.68650510820879D+00 -0.66639036394084D-15 1 15 2 5 0.80228829136540D-01 0.42069481764430D-16 2 15 2 5 0.15082554883129D-01 0.33851249531504D-15 3 15 2 5 -0.31484626762450D+00 0.24570481253401D-15 1 16 2 5 0.80228829136542D-01 0.13563707818804D-16 2 16 2 5 0.15082554883140D-01 -0.48776792340226D-15 3 16 2 5 -0.31484626762451D+00 -0.12119575263231D-15 1 17 2 5 -0.10265494691603D+01 0.11868506827686D-15 2 17 2 5 -0.14418862649160D+00 -0.69046111567954D-15 3 17 2 5 -0.85602264129847D+00 0.29142939781599D-16 1 18 2 5 -0.10265494691601D+01 0.84111649352257D-17 2 18 2 5 -0.14418862649194D+00 -0.55605291914425D-15 3 18 2 5 -0.85602264129840D+00 0.32634939090171D-15 1 19 2 5 -0.12513983423461D-01 0.14885976625228D-16 2 19 2 5 0.94979983044928D-01 0.70394381565020D-15 3 19 2 5 0.17716412881528D+00 0.21330044356876D-15 1 20 2 5 -0.12513983423465D-01 0.55575491183039D-17 2 20 2 5 0.94979983044905D-01 -0.76430568381739D-15 3 20 2 5 0.17716412881531D+00 0.15034087280436D-15 1 22 2 5 -0.43628339344396D+01 0.00000000000000D+00 2 22 2 5 -0.30364777564228D+02 0.00000000000000D+00 3 22 2 5 -0.10078569968865D+01 0.00000000000000D+00 1 1 3 5 0.88451054934886D-01 -0.57239351219095D-16 2 1 3 5 0.19095566550230D+01 0.38013761490726D-15 3 1 3 5 -0.18192611198142D+01 0.38466917078643D-14 1 2 3 5 0.88451054934890D-01 0.19581517367757D-16 2 2 3 5 0.19095566550232D+01 -0.27749398110747D-15 3 2 3 5 -0.18192611198140D+01 -0.22122630360868D-14 1 3 3 5 -0.17733915225121D+00 -0.31785556481085D-15 2 3 3 5 -0.82601941198920D+00 -0.57444676330042D-15 3 3 3 5 -0.16896824586355D+01 -0.64351816298317D-14 1 4 3 5 -0.17733915225113D+00 0.17382024471058D-15 2 4 3 5 -0.82601941198918D+00 0.99944914331783D-16 3 4 3 5 -0.16896824586353D+01 -0.62887757924279D-14 1 5 3 5 -0.72684326483045D+00 0.00000000000000D+00 2 5 3 5 -0.26871132865079D+01 0.00000000000000D+00 3 5 3 5 0.40365309228722D+02 0.00000000000000D+00 1 6 3 5 0.42173512680128D+01 0.00000000000000D+00 2 6 3 5 -0.10651445201029D+01 0.00000000000000D+00 3 6 3 5 -0.31587118157384D+02 0.00000000000000D+00 1 7 3 5 0.48524629094079D+01 0.00000000000000D+00 2 7 3 5 0.66258235879515D+00 0.00000000000000D+00 3 7 3 5 0.40219158030814D+01 0.00000000000000D+00 1 8 3 5 0.32384676004742D+00 0.00000000000000D+00 2 8 3 5 0.16943374795987D+00 0.00000000000000D+00 3 8 3 5 -0.24694185132679D+01 0.00000000000000D+00 1 9 3 5 -0.22974369595196D+01 0.91014423190876D-16 2 9 3 5 0.50892670057623D+00 -0.19690436477292D-15 3 9 3 5 -0.71472199265708D+00 -0.37633528656737D-15 1 10 3 5 -0.22974369595196D+01 0.40218535164441D-16 2 10 3 5 0.50892670057642D+00 0.11663140305761D-15 3 10 3 5 -0.71472199265787D+00 -0.12174209080626D-13 1 11 3 5 0.26222185156986D+00 -0.10914708572143D-15 2 11 3 5 0.12910144566608D+00 -0.23755913597423D-15 3 11 3 5 0.40721974704081D-01 0.45657645423153D-14 1 12 3 5 0.26222185156988D+00 -0.88563926901218D-17 2 12 3 5 0.12910144566616D+00 -0.23798329398505D-15 3 12 3 5 0.40721974703975D-01 0.42757772589734D-14 1 13 3 5 -0.61569309227077D+00 -0.12105974288004D-15 2 13 3 5 -0.14560847115759D+00 0.20747296785272D-15 3 13 3 5 -0.42530796130873D+01 0.54261715492857D-15 1 14 3 5 -0.61569309227112D+00 0.25847212148978D-15 2 14 3 5 -0.14560847115780D+00 -0.66639036394084D-15 3 14 3 5 -0.42530796130874D+01 -0.41046655576347D-15 1 15 3 5 -0.56222819860821D+00 0.81230446742012D-16 2 15 3 5 -0.20478799764695D+00 0.24570481253401D-15 3 15 3 5 0.37080430568573D+01 -0.16845856460024D-14 1 16 3 5 -0.56222819860822D+00 -0.19443713283607D-15 2 16 3 5 -0.20478799764696D+00 -0.12119575263231D-15 3 16 3 5 0.37080430568572D+01 -0.66662507646345D-15 1 17 3 5 -0.55647288619464D+00 -0.83663155464845D-16 2 17 3 5 0.43393246734524D-01 0.29142939781599D-16 3 17 3 5 -0.42317235399666D+01 -0.23066501139534D-14 1 18 3 5 -0.55647288619470D+00 0.11641248338691D-15 2 18 3 5 0.43393246734610D-01 0.32634939090171D-15 3 18 3 5 -0.42317235399663D+01 0.15840054050645D-14 1 19 3 5 -0.49107362204881D+00 0.22547608697163D-15 2 19 3 5 0.58123273249970D-01 0.21330044356876D-15 3 19 3 5 0.37892078791057D+01 0.62792026748863D-15 1 20 3 5 -0.49107362204884D+00 0.14956530333043D-15 2 20 3 5 0.58123273250001D-01 0.15034087280436D-15 3 20 3 5 0.37892078791057D+01 -0.12650309849828D-14 1 22 3 5 -0.81401623241083D+01 0.00000000000000D+00 2 22 3 5 -0.53635834997517D+00 0.00000000000000D+00 3 22 3 5 -0.30508872247900D+02 0.00000000000000D+00 1 1 1 6 0.18468616062556D+01 0.22151723697057D-15 2 1 1 6 0.10000454035179D+00 0.20222910069220D-16 3 1 1 6 -0.58307128988748D+00 -0.18604088994794D-15 1 2 1 6 0.18468616062556D+01 0.15197635308381D-16 2 2 1 6 0.10000454035179D+00 0.23554984201183D-16 3 2 1 6 -0.58307128988747D+00 -0.32303636218740D-15 1 3 1 6 -0.34702975859621D+01 -0.10478840416482D-16 2 3 1 6 0.47288082163059D+00 -0.21839779453621D-16 3 3 1 6 -0.52011443648194D+00 0.30656152974319D-15 1 4 1 6 -0.34702975859621D+01 0.20728620148476D-15 2 4 1 6 0.47288082163060D+00 0.24500781800549D-16 3 4 1 6 -0.52011443648209D+00 0.26699717254028D-15 1 5 1 6 0.10582222744076D+01 0.00000000000000D+00 2 5 1 6 -0.14989449594138D+00 0.00000000000000D+00 3 5 1 6 0.42173512680128D+01 0.00000000000000D+00 1 6 1 6 0.17662550828636D+02 0.00000000000000D+00 2 6 1 6 0.46163742265040D+00 0.00000000000000D+00 3 6 1 6 0.72684139393915D+00 0.00000000000000D+00 1 7 1 6 -0.32956689542690D+00 0.00000000000000D+00 2 7 1 6 -0.81588147068491D-01 0.00000000000000D+00 3 7 1 6 -0.32385070169896D+00 0.00000000000000D+00 1 8 1 6 -0.13669505028554D+02 0.00000000000000D+00 2 8 1 6 -0.47212921920618D+01 0.00000000000000D+00 3 8 1 6 0.48524629094079D+01 0.00000000000000D+00 1 9 1 6 -0.15725316985842D+01 -0.58607812143411D-15 2 9 1 6 -0.88530873634911D-01 0.21771049524438D-16 3 9 1 6 -0.51032796555906D+00 0.27154092229384D-16 1 10 1 6 -0.15725316985840D+01 0.11566073739313D-14 2 10 1 6 -0.88530873634896D-01 0.52887725610409D-16 3 10 1 6 -0.51032796555926D+00 -0.68005055630173D-16 1 11 1 6 0.12597052197366D+01 0.14701821027814D-15 2 11 1 6 0.37871643932606D+00 0.41068492097126D-16 3 11 1 6 -0.55913866598669D+00 -0.22812022337587D-16 1 12 1 6 0.12597052197366D+01 0.21999207357968D-15 2 12 1 6 0.37871643932607D+00 0.11009242497663D-15 3 12 1 6 -0.55913866598670D+00 -0.94266224127532D-16 1 13 1 6 -0.37877129705305D-01 -0.27605271465377D-15 2 13 1 6 0.13310522665981D-01 -0.21758286222931D-17 3 13 1 6 -0.83818842403307D-02 0.72449153967548D-16 1 14 1 6 -0.37877129705306D-01 0.24631109194898D-15 2 14 1 6 0.13310522665981D-01 -0.11846092054587D-16 3 14 1 6 -0.83818842403378D-02 -0.40908679170914D-16 1 15 1 6 -0.47205630832701D+00 -0.37784658389267D-15 2 15 1 6 0.80829208278345D+00 -0.22286037600643D-16 3 15 1 6 -0.12067628732444D+01 0.20383649362297D-15 1 16 1 6 -0.47205630832727D+00 -0.63187820323953D-15 2 16 1 6 0.80829208278332D+00 -0.18478978601061D-16 3 16 1 6 -0.12067628732447D+01 -0.25878335605230D-15 1 17 1 6 -0.61748566762764D-01 0.15538299952659D-16 2 17 1 6 -0.20804343225730D-01 0.44032530477427D-16 3 17 1 6 -0.10357201143745D+00 -0.15624588538953D-15 1 18 1 6 -0.61748566762763D-01 -0.53887403336858D-16 2 18 1 6 -0.20804343225726D-01 0.96421020791729D-17 3 18 1 6 -0.10357201143747D+00 -0.16785307133470D-16 1 19 1 6 0.14572086039210D+00 0.29900401012140D-15 2 19 1 6 0.57907236680454D+00 -0.71422111272566D-17 3 19 1 6 -0.12614849187088D+01 -0.69551867632395D-15 1 20 1 6 0.14572086039215D+00 -0.14541165250011D-15 2 20 1 6 0.57907236680421D+00 0.17222408892574D-16 3 20 1 6 -0.12614849187088D+01 -0.14419647979723D-15 1 22 1 6 -0.31238332545793D+02 0.00000000000000D+00 2 22 1 6 0.31236553854032D+01 0.00000000000000D+00 3 22 1 6 -0.32507934447046D+01 0.00000000000000D+00 1 1 2 6 -0.48120495601929D+00 0.20222910069220D-16 2 1 2 6 -0.35171325566685D+01 -0.13210115945622D-14 3 1 2 6 -0.15558599906723D+01 -0.38730513200384D-16 1 2 2 6 -0.48120495601930D+00 0.23554984201183D-16 2 2 2 6 -0.35171325566685D+01 -0.12308647537209D-14 3 2 2 6 -0.15558599906724D+01 -0.32865651251824D-15 1 3 2 6 0.16950473476875D+00 -0.21839779453621D-16 2 3 2 6 0.17955315438035D+01 -0.29473678661381D-15 3 3 2 6 0.61335189982923D+00 0.36405513651912D-15 1 4 2 6 0.16950473476877D+00 0.24500781800549D-16 2 4 2 6 0.17955315438035D+01 0.39324266028607D-15 3 4 2 6 0.61335189982920D+00 -0.33622053283550D-15 1 5 2 6 -0.14989449594138D+00 0.00000000000000D+00 2 5 2 6 0.34119604620910D+00 0.00000000000000D+00 3 5 2 6 -0.10651445201029D+01 0.00000000000000D+00 1 6 2 6 0.46164627652389D+00 0.00000000000000D+00 2 6 2 6 0.18517916435199D+02 0.00000000000000D+00 3 6 2 6 0.26871123781975D+01 0.00000000000000D+00 1 7 2 6 0.81587278202461D-01 0.00000000000000D+00 2 7 2 6 -0.29611934821259D+00 0.00000000000000D+00 3 7 2 6 0.16943728555954D+00 0.00000000000000D+00 1 8 2 6 0.47212921920618D+01 0.00000000000000D+00 2 8 2 6 -0.14761187001991D+02 0.00000000000000D+00 3 8 2 6 -0.66258235879515D+00 0.00000000000000D+00 1 9 2 6 -0.38630898660351D-01 0.21771049524438D-16 2 9 2 6 -0.15112161379036D+01 0.56425154143929D-15 3 9 2 6 0.17494069864048D+00 0.19412771063156D-15 1 10 2 6 -0.38630898660335D-01 0.52887725610409D-16 2 10 2 6 -0.15112161379034D+01 0.22645365780369D-15 3 10 2 6 0.17494069864031D+00 0.14678168510907D-15 1 11 2 6 -0.48952263584241D+00 0.41068492097126D-16 2 11 2 6 0.13991458022465D+01 -0.85279536816717D-15 3 11 2 6 -0.90232092760047D-01 0.10868889555974D-15 1 12 2 6 -0.48952263584240D+00 0.11009242497663D-15 2 12 2 6 0.13991458022465D+01 -0.63341820160353D-15 3 12 2 6 -0.90232092760132D-01 0.13361364490719D-15 1 13 2 6 0.80228829136542D-01 -0.21758286222931D-17 2 13 2 6 0.15082554883135D-01 -0.36426903951609D-15 3 13 2 6 0.31484626762451D+00 -0.22883874493035D-15 1 14 2 6 0.80228829136542D-01 -0.11846092054587D-16 2 14 2 6 0.15082554883137D-01 0.36590791500490D-15 3 14 2 6 0.31484626762451D+00 0.10281769560199D-15 1 15 2 6 -0.75348532218752D+00 -0.22286037600643D-16 2 15 2 6 -0.33013812894591D-01 0.69545898586668D-15 3 15 2 6 -0.68650510820879D+00 -0.16971420434979D-16 1 16 2 6 -0.75348532218766D+00 -0.18478978601061D-16 2 16 2 6 -0.33013812894414D-01 -0.83030804851145D-15 3 16 2 6 -0.68650510820898D+00 0.48698743050953D-15 1 17 2 6 -0.12513983423466D-01 0.44032530477427D-16 2 17 2 6 0.94979983044915D-01 -0.29878340771667D-16 3 17 2 6 -0.17716412881531D+00 -0.16783772584646D-15 1 18 2 6 -0.12513983423462D-01 0.96421020791729D-17 2 18 2 6 0.94979983044924D-01 -0.81443627259880D-15 3 18 2 6 -0.17716412881529D+00 -0.18612995474725D-15 1 19 2 6 -0.10265494691600D+01 -0.71422111272566D-17 2 19 2 6 -0.14418862649181D+00 0.73868527818751D-15 3 19 2 6 0.85602264129840D+00 0.10918962662141D-15 1 20 2 6 -0.10265494691603D+01 0.17222408892574D-16 2 20 2 6 -0.14418862649171D+00 -0.54922050726066D-15 3 20 2 6 0.85602264129848D+00 -0.22274335597184D-15 1 22 2 6 -0.43628339344369D+01 0.00000000000000D+00 2 22 2 6 -0.30364777564260D+02 0.00000000000000D+00 3 22 2 6 0.10078569969000D+01 0.00000000000000D+00 1 1 3 6 -0.88451054934889D-01 -0.18604088994794D-15 2 1 3 6 -0.19095566550231D+01 -0.38730513200384D-16 3 1 3 6 -0.18192611198142D+01 -0.35228234523366D-14 1 2 3 6 -0.88451054934885D-01 -0.32303636218740D-15 2 2 3 6 -0.19095566550232D+01 -0.32865651251824D-15 3 2 3 6 -0.18192611198141D+01 -0.40204499008062D-14 1 3 3 6 0.17733915225121D+00 0.30656152974319D-15 2 3 3 6 0.82601941198920D+00 0.36405513651912D-15 3 3 3 6 -0.16896824586355D+01 0.48008011913020D-14 1 4 3 6 0.17733915225106D+00 0.26699717254028D-15 2 4 3 6 0.82601941198917D+00 -0.33622053283550D-15 3 4 3 6 -0.16896824586353D+01 0.30673194027317D-14 1 5 3 6 -0.42173512680128D+01 0.00000000000000D+00 2 5 3 6 0.10651445201029D+01 0.00000000000000D+00 3 5 3 6 -0.31587118157384D+02 0.00000000000000D+00 1 6 3 6 0.72684326483067D+00 0.00000000000000D+00 2 6 3 6 0.26871132865079D+01 0.00000000000000D+00 3 6 3 6 0.40365309228722D+02 0.00000000000000D+00 1 7 3 6 -0.32384676004742D+00 0.00000000000000D+00 2 7 3 6 -0.16943374795987D+00 0.00000000000000D+00 3 7 3 6 -0.24694185132679D+01 0.00000000000000D+00 1 8 3 6 -0.48524629094079D+01 0.00000000000000D+00 2 8 3 6 -0.66258235879515D+00 0.00000000000000D+00 3 8 3 6 0.40219158030814D+01 0.00000000000000D+00 1 9 3 6 0.22974369595196D+01 0.27154092229384D-16 2 9 3 6 -0.50892670057622D+00 0.19412771063156D-15 3 9 3 6 -0.71472199265708D+00 -0.16369976067110D-14 1 10 3 6 0.22974369595194D+01 -0.68005055630173D-16 2 10 3 6 -0.50892670057639D+00 0.14678168510907D-15 3 10 3 6 -0.71472199265730D+00 0.35252272472814D-14 1 11 3 6 -0.26222185156987D+00 -0.22812022337587D-16 2 11 3 6 -0.12910144566608D+00 0.10868889555974D-15 3 11 3 6 0.40721974703998D-01 -0.18050972910388D-14 1 12 3 6 -0.26222185156988D+00 -0.94266224127532D-16 2 12 3 6 -0.12910144566616D+00 0.13361364490719D-15 3 12 3 6 0.40721974704003D-01 0.26953536408205D-14 1 13 3 6 0.56222819860821D+00 0.72449153967548D-16 2 13 3 6 0.20478799764696D+00 -0.22883874493035D-15 3 13 3 6 0.37080430568572D+01 0.11133140746810D-14 1 14 3 6 0.56222819860820D+00 -0.40908679170914D-16 2 14 3 6 0.20478799764696D+00 0.10281769560199D-15 3 14 3 6 0.37080430568573D+01 -0.28679367829196D-14 1 15 3 6 0.61569309227111D+00 0.20383649362297D-15 2 15 3 6 0.14560847115780D+00 -0.16971420434979D-16 3 15 3 6 -0.42530796130873D+01 0.10992928429573D-14 1 16 3 6 0.61569309227080D+00 -0.25878335605230D-15 2 16 3 6 0.14560847115761D+00 0.48698743050953D-15 3 16 3 6 -0.42530796130873D+01 -0.15388241034981D-14 1 17 3 6 0.49107362204883D+00 -0.15624588538953D-15 2 17 3 6 -0.58123273250001D-01 -0.16783772584646D-15 3 17 3 6 0.37892078791057D+01 -0.21473411720111D-15 1 18 3 6 0.49107362204881D+00 -0.16785307133470D-16 2 18 3 6 -0.58123273249975D-01 -0.18612995474725D-15 3 18 3 6 0.37892078791057D+01 0.56847087115902D-15 1 19 3 6 0.55647288619470D+00 -0.69551867632395D-15 2 19 3 6 -0.43393246734610D-01 0.10918962662141D-15 3 19 3 6 -0.42317235399663D+01 -0.13184154622993D-14 1 20 3 6 0.55647288619467D+00 -0.14419647979723D-15 2 20 3 6 -0.43393246734524D-01 -0.22274335597184D-15 3 20 3 6 -0.42317235399666D+01 0.49719767334037D-15 1 22 3 6 0.81401623241162D+01 0.00000000000000D+00 2 22 3 6 0.53635834992105D+00 0.00000000000000D+00 3 22 3 6 -0.30508872247915D+02 0.00000000000000D+00 1 1 1 7 -0.34702975859620D+01 -0.42995031273227D-15 2 1 1 7 -0.47288082163058D+00 0.97372952800124D-17 3 1 1 7 -0.52011443648193D+00 -0.18656514979451D-15 1 2 1 7 -0.34702975859623D+01 0.92271339110125D-15 2 2 1 7 -0.47288082163059D+00 0.12599140137640D-17 3 2 1 7 -0.52011443648195D+00 0.15128155190980D-15 1 3 1 7 0.18468616062556D+01 0.20148658895904D-15 2 3 1 7 -0.10000454035179D+00 -0.67875815588768D-16 3 3 1 7 -0.58307128988748D+00 -0.76133560679038D-17 1 4 1 7 0.18468616062556D+01 -0.76120497290076D-16 2 4 1 7 -0.10000454035178D+00 -0.54016274074149D-17 3 4 1 7 -0.58307128988750D+00 -0.20890725913801D-16 1 5 1 7 -0.13669505028554D+02 0.00000000000000D+00 2 5 1 7 0.47212921920618D+01 0.00000000000000D+00 3 5 1 7 0.48524629094079D+01 0.00000000000000D+00 1 6 1 7 -0.32956689542690D+00 0.00000000000000D+00 2 6 1 7 0.81588147068491D-01 0.00000000000000D+00 3 6 1 7 -0.32385070169896D+00 0.00000000000000D+00 1 7 1 7 0.17662550828636D+02 0.00000000000000D+00 2 7 1 7 -0.46163742265021D+00 0.00000000000000D+00 3 7 1 7 0.72684139393935D+00 0.00000000000000D+00 1 8 1 7 0.10582222744076D+01 0.00000000000000D+00 2 8 1 7 0.14989449594138D+00 0.00000000000000D+00 3 8 1 7 0.42173512680128D+01 0.00000000000000D+00 1 9 1 7 0.12597052197366D+01 -0.86527782906872D-15 2 9 1 7 -0.37871643932608D+00 -0.14941607762018D-16 3 9 1 7 -0.55913866598668D+00 -0.67686087701626D-16 1 10 1 7 0.12597052197366D+01 0.90620029894044D-15 2 10 1 7 -0.37871643932607D+00 -0.72662378760190D-16 3 10 1 7 -0.55913866598669D+00 -0.87765868240689D-16 1 11 1 7 -0.15725316985839D+01 -0.53921718454333D-16 2 11 1 7 0.88530873634798D-01 0.11159347634079D-16 3 11 1 7 -0.51032796555911D+00 -0.17897773192048D-15 1 12 1 7 -0.15725316985841D+01 -0.69072423985496D-15 2 12 1 7 0.88530873634939D-01 0.13739043607004D-16 3 12 1 7 -0.51032796555933D+00 -0.22575676175072D-16 1 13 1 7 0.14572086039215D+00 -0.41410424063641D-15 2 13 1 7 -0.57907236680428D+00 0.24274994697052D-17 3 13 1 7 -0.12614849187089D+01 -0.91718406304011D-16 1 14 1 7 0.14572086039204D+00 -0.23366575253436D-15 2 14 1 7 -0.57907236680471D+00 -0.13024815926906D-17 3 14 1 7 -0.12614849187089D+01 -0.85276383441934D-16 1 15 1 7 -0.61748566762758D-01 0.12983485822364D-15 2 15 1 7 0.20804343225724D-01 -0.83255369944119D-16 3 15 1 7 -0.10357201143747D+00 0.26756594591716D-15 1 16 1 7 -0.61748566762763D-01 -0.94692055402952D-15 2 16 1 7 0.20804343225729D-01 -0.42713968559539D-16 3 16 1 7 -0.10357201143744D+00 -0.13321421487572D-15 1 17 1 7 -0.47205630832742D+00 0.27268009676361D-16 2 17 1 7 -0.80829208278338D+00 0.35102586327187D-16 3 17 1 7 -0.12067628732447D+01 -0.76266544192944D-15 1 18 1 7 -0.47205630832714D+00 0.52926796385336D-15 2 18 1 7 -0.80829208278328D+00 -0.10102680085072D-15 3 18 1 7 -0.12067628732444D+01 -0.40853371866791D-15 1 19 1 7 -0.37877129705314D-01 -0.82181504605089D-15 2 19 1 7 -0.13310522665981D-01 0.35820505499466D-16 3 19 1 7 -0.83818842403360D-02 0.32669725761954D-15 1 20 1 7 -0.37877129705300D-01 -0.11550174301002D-15 2 20 1 7 -0.13310522665982D-01 0.34764633724451D-16 3 20 1 7 -0.83818842403147D-02 -0.16676507451688D-16 1 22 1 7 -0.31238332545772D+02 0.00000000000000D+00 2 22 1 7 -0.31236553854113D+01 0.00000000000000D+00 3 22 1 7 -0.32507934447174D+01 0.00000000000000D+00 1 1 2 7 -0.16950473476875D+00 0.97372952800124D-17 2 1 2 7 0.17955315438035D+01 0.92788066229945D-15 3 1 2 7 -0.61335189982914D+00 0.29460170226133D-15 1 2 2 7 -0.16950473476875D+00 0.12599140137640D-17 2 2 2 7 0.17955315438036D+01 -0.85099435007597D-15 3 2 2 7 -0.61335189982919D+00 0.13432597322363D-15 1 3 2 7 0.48120495601930D+00 -0.67875815588768D-16 2 3 2 7 -0.35171325566684D+01 0.11334372837508D-14 3 3 2 7 0.15558599906726D+01 -0.14526109019941D-16 1 4 2 7 0.48120495601930D+00 -0.54016274074149D-17 2 4 2 7 -0.35171325566686D+01 -0.53082941391073D-15 3 4 2 7 0.15558599906725D+01 0.16537307837354D-15 1 5 2 7 -0.47212921920618D+01 0.00000000000000D+00 2 5 2 7 -0.14761187001991D+02 0.00000000000000D+00 3 5 2 7 0.66258235879515D+00 0.00000000000000D+00 1 6 2 7 -0.81587278202460D-01 0.00000000000000D+00 2 6 2 7 -0.29611934821259D+00 0.00000000000000D+00 3 6 2 7 -0.16943728555954D+00 0.00000000000000D+00 1 7 2 7 -0.46164627652370D+00 0.00000000000000D+00 2 7 2 7 0.18517916435197D+02 0.00000000000000D+00 3 7 2 7 -0.26871123781984D+01 0.00000000000000D+00 1 8 2 7 0.14989449594138D+00 0.00000000000000D+00 2 8 2 7 0.34119604620910D+00 0.00000000000000D+00 3 8 2 7 0.10651445201029D+01 0.00000000000000D+00 1 9 2 7 0.48952263584239D+00 -0.14941607762018D-16 2 9 2 7 0.13991458022464D+01 -0.53113123275583D-16 3 9 2 7 0.90232092760124D-01 -0.41045688335342D-16 1 10 2 7 0.48952263584240D+00 -0.72662378760190D-16 2 10 2 7 0.13991458022464D+01 0.49880290937264D-16 3 10 2 7 0.90232092760105D-01 -0.10310037186314D-15 1 11 2 7 0.38630898660238D-01 0.11159347634079D-16 2 11 2 7 -0.15112161379034D+01 -0.21241828223538D-15 3 11 2 7 -0.17494069863969D+00 0.29811403909872D-16 1 12 2 7 0.38630898660378D-01 0.13739043607004D-16 2 12 2 7 -0.15112161379034D+01 -0.39099735368517D-15 3 12 2 7 -0.17494069864061D+00 -0.82218172909340D-16 1 13 2 7 0.10265494691603D+01 0.24274994697052D-17 2 13 2 7 -0.14418862649161D+00 0.83848347189426D-15 3 13 2 7 -0.85602264129848D+00 0.44231040064958D-15 1 14 2 7 0.10265494691599D+01 -0.13024815926906D-17 2 14 2 7 -0.14418862649194D+00 -0.39544215873847D-15 3 14 2 7 -0.85602264129849D+00 0.30702137696635D-15 1 15 2 7 0.12513983423461D-01 -0.83255369944119D-16 2 15 2 7 0.94979983044930D-01 -0.22728795483601D-15 3 15 2 7 0.17716412881529D+00 -0.81056512587239D-15 1 16 2 7 0.12513983423466D-01 -0.42713968559539D-16 2 16 2 7 0.94979983044916D-01 -0.28864600227788D-15 3 16 2 7 0.17716412881531D+00 -0.49982922431843D-15 1 17 2 7 0.75348532218759D+00 0.35102586327187D-16 2 17 2 7 -0.33013812894296D-01 0.15411815824534D-16 3 17 2 7 0.68650510820900D+00 0.52423292880201D-15 1 18 2 7 0.75348532218766D+00 -0.10102680085072D-15 2 18 2 7 -0.33013812894499D-01 0.52807820190861D-15 3 18 2 7 0.68650510820881D+00 0.42635480740120D-15 1 19 2 7 -0.80228829136542D-01 0.35820505499466D-16 2 19 2 7 0.15082554883131D-01 -0.23398341548826D-15 3 19 2 7 -0.31484626762451D+00 -0.79397770159796D-15 1 20 2 7 -0.80228829136543D-01 0.34764633724451D-16 2 20 2 7 0.15082554883153D-01 -0.52223469469468D-15 3 20 2 7 -0.31484626762451D+00 -0.12328977431911D-15 1 22 2 7 0.43628339344430D+01 0.00000000000000D+00 2 22 2 7 -0.30364777564239D+02 0.00000000000000D+00 3 22 2 7 -0.10078569968913D+01 0.00000000000000D+00 1 1 3 7 0.17733915225121D+00 -0.18656514979451D-15 2 1 3 7 -0.82601941198911D+00 0.29460170226133D-15 3 1 3 7 -0.16896824586355D+01 -0.37369363115984D-14 1 2 3 7 0.17733915225120D+00 0.15128155190980D-15 2 2 3 7 -0.82601941198916D+00 0.13432597322363D-15 3 2 3 7 -0.16896824586353D+01 -0.49147381416925D-14 1 3 3 7 -0.88451054934890D-01 -0.76133560679038D-17 2 3 3 7 0.19095566550233D+01 -0.14526109019941D-16 3 3 3 7 -0.18192611198142D+01 0.68147058782069D-14 1 4 3 7 -0.88451054934908D-01 -0.20890725913801D-16 2 4 3 7 0.19095566550232D+01 0.16537307837354D-15 3 4 3 7 -0.18192611198139D+01 0.80083183275338D-15 1 5 3 7 -0.48524629094079D+01 0.00000000000000D+00 2 5 3 7 0.66258235879515D+00 0.00000000000000D+00 3 5 3 7 0.40219158030814D+01 0.00000000000000D+00 1 6 3 7 -0.32384676004742D+00 0.00000000000000D+00 2 6 3 7 0.16943374795987D+00 0.00000000000000D+00 3 6 3 7 -0.24694185132679D+01 0.00000000000000D+00 1 7 3 7 0.72684326483086D+00 0.00000000000000D+00 2 7 3 7 -0.26871132865088D+01 0.00000000000000D+00 3 7 3 7 0.40365309228724D+02 0.00000000000000D+00 1 8 3 7 -0.42173512680128D+01 0.00000000000000D+00 2 8 3 7 -0.10651445201029D+01 0.00000000000000D+00 3 8 3 7 -0.31587118157385D+02 0.00000000000000D+00 1 9 3 7 -0.26222185156986D+00 -0.67686087701626D-16 2 9 3 7 0.12910144566615D+00 -0.41045688335342D-16 3 9 3 7 0.40721974703973D-01 -0.11379652604697D-13 1 10 3 7 -0.26222185156987D+00 -0.87765868240689D-16 2 10 3 7 0.12910144566613D+00 -0.10310037186314D-15 3 10 3 7 0.40721974704080D-01 0.99952108863478D-15 1 11 3 7 0.22974369595195D+01 -0.17897773192048D-15 2 11 3 7 0.50892670057702D+00 0.29811403909872D-16 3 11 3 7 -0.71472199265753D+00 0.81921031028180D-15 1 12 3 7 0.22974369595193D+01 -0.22575676175072D-16 2 12 3 7 0.50892670057610D+00 -0.82218172909340D-16 3 12 3 7 -0.71472199265730D+00 0.19496962490765D-14 1 13 3 7 0.55647288619464D+00 -0.91718406304011D-16 2 13 3 7 0.43393246734531D-01 0.44231040064958D-15 3 13 3 7 -0.42317235399665D+01 -0.14214531025879D-14 1 14 3 7 0.55647288619460D+00 -0.85276383441934D-16 2 14 3 7 0.43393246734510D-01 0.30702137696635D-15 3 14 3 7 -0.42317235399659D+01 0.14677749939344D-14 1 15 3 7 0.49107362204881D+00 0.26756594591716D-15 2 15 3 7 0.58123273249975D-01 -0.81056512587239D-15 3 15 3 7 0.37892078791057D+01 0.86025090347640D-15 1 16 3 7 0.49107362204883D+00 -0.13321421487572D-15 2 16 3 7 0.58123273250001D-01 -0.49982922431843D-15 3 16 3 7 0.37892078791058D+01 0.13470641901223D-14 1 17 3 7 0.61569309227071D+00 -0.76266544192944D-15 2 17 3 7 -0.14560847115758D+00 0.52423292880201D-15 3 17 3 7 -0.42530796130870D+01 0.21031063752071D-14 1 18 3 7 0.61569309227105D+00 -0.40853371866791D-15 2 18 3 7 -0.14560847115779D+00 0.42635480740120D-15 3 18 3 7 -0.42530796130873D+01 0.43141778514763D-15 1 19 3 7 0.56222819860821D+00 0.32669725761954D-15 2 19 3 7 -0.20478799764695D+00 -0.79397770159796D-15 3 19 3 7 0.37080430568572D+01 -0.98979301282431D-15 1 20 3 7 0.56222819860823D+00 -0.16676507451688D-16 2 20 3 7 -0.20478799764696D+00 -0.12328977431911D-15 3 20 3 7 0.37080430568572D+01 0.14331886448797D-15 1 22 3 7 0.81401623241014D+01 0.00000000000000D+00 2 22 3 7 -0.53635835000200D+00 0.00000000000000D+00 3 22 3 7 -0.30508872247914D+02 0.00000000000000D+00 1 1 1 8 -0.34702975859621D+01 0.41051684855619D-15 2 1 1 8 -0.47288082163058D+00 -0.28107041595958D-18 3 1 1 8 0.52011443648194D+00 -0.33906411303125D-15 1 2 1 8 -0.34702975859620D+01 0.12176021730230D-14 2 2 1 8 -0.47288082163059D+00 -0.10247351816969D-16 3 2 1 8 0.52011443648196D+00 0.73159074961550D-16 1 3 1 8 0.18468616062556D+01 0.76686237307878D-17 2 3 1 8 -0.10000454035179D+00 0.41546930527014D-16 3 3 1 8 0.58307128988748D+00 0.28780870349550D-15 1 4 1 8 0.18468616062556D+01 0.17727954929827D-15 2 4 1 8 -0.10000454035178D+00 0.85896072045117D-16 3 4 1 8 0.58307128988748D+00 0.30192185661427D-15 1 5 1 8 -0.32956689542690D+00 0.00000000000000D+00 2 5 1 8 0.81588147068491D-01 0.00000000000000D+00 3 5 1 8 0.32385070169896D+00 0.00000000000000D+00 1 6 1 8 -0.13669505028554D+02 0.00000000000000D+00 2 6 1 8 0.47212921920618D+01 0.00000000000000D+00 3 6 1 8 -0.48524629094079D+01 0.00000000000000D+00 1 7 1 8 0.10582222744076D+01 0.00000000000000D+00 2 7 1 8 0.14989449594138D+00 0.00000000000000D+00 3 7 1 8 -0.42173512680128D+01 0.00000000000000D+00 1 8 1 8 0.17662550828636D+02 0.00000000000000D+00 2 8 1 8 -0.46163742265023D+00 0.00000000000000D+00 3 8 1 8 -0.72684139393953D+00 0.00000000000000D+00 1 9 1 8 0.12597052197366D+01 0.77886781369037D-16 2 9 1 8 -0.37871643932608D+00 0.32843180755853D-16 3 9 1 8 0.55913866598668D+00 0.83593037925214D-16 1 10 1 8 0.12597052197366D+01 -0.53909826188096D-16 2 10 1 8 -0.37871643932608D+00 0.27539691154932D-16 3 10 1 8 0.55913866598671D+00 -0.12246648678206D-15 1 11 1 8 -0.15725316985840D+01 -0.17474917604691D-14 2 11 1 8 0.88530873634804D-01 -0.11437015366959D-15 3 11 1 8 0.51032796555930D+00 -0.93384049218024D-16 1 12 1 8 -0.15725316985841D+01 0.79123312580195D-15 2 12 1 8 0.88530873634943D-01 0.59798465605054D-17 3 12 1 8 0.51032796555930D+00 0.13340376108810D-15 1 13 1 8 -0.61748566762759D-01 0.11655069286161D-15 2 13 1 8 0.20804343225729D-01 0.17300958049914D-16 3 13 1 8 0.10357201143745D+00 -0.26243127215854D-15 1 14 1 8 -0.61748566762766D-01 -0.12235593823214D-16 2 14 1 8 0.20804343225723D-01 0.15809326418405D-16 3 14 1 8 0.10357201143747D+00 0.19540201021788D-15 1 15 1 8 0.14572086039204D+00 0.68009360038994D-16 2 15 1 8 -0.57907236680472D+00 -0.19658044115020D-16 3 15 1 8 0.12614849187089D+01 -0.18061251572041D-15 1 16 1 8 0.14572086039215D+00 0.29997298684941D-15 2 16 1 8 -0.57907236680421D+00 -0.23246688123530D-16 3 16 1 8 0.12614849187089D+01 0.22825356575423D-15 1 17 1 8 -0.37877129705300D-01 -0.60131990229548D-15 2 17 1 8 -0.13310522665981D-01 -0.53669141322980D-17 3 17 1 8 0.83818842403272D-02 -0.21851319746119D-15 1 18 1 8 -0.37877129705308D-01 -0.39501576237930D-15 2 18 1 8 -0.13310522665983D-01 -0.17593371570744D-16 3 18 1 8 0.83818842403325D-02 -0.43830015049284D-17 1 19 1 8 -0.47205630832707D+00 0.26402514900267D-15 2 19 1 8 -0.80829208278335D+00 -0.10519299950177D-16 3 19 1 8 0.12067628732444D+01 -0.88281887182369D-16 1 20 1 8 -0.47205630832742D+00 -0.10815507284838D-14 2 20 1 8 -0.80829208278325D+00 -0.22780231527695D-16 3 20 1 8 0.12067628732447D+01 -0.10186532904639D-15 1 22 1 8 -0.31238332545786D+02 0.00000000000000D+00 2 22 1 8 -0.31236553854185D+01 0.00000000000000D+00 3 22 1 8 0.32507934447073D+01 0.00000000000000D+00 1 1 2 8 -0.16950473476875D+00 -0.28107041595958D-18 2 1 2 8 0.17955315438035D+01 0.96683961735236D-16 3 1 2 8 0.61335189982913D+00 -0.77227825202825D-16 1 2 2 8 -0.16950473476875D+00 -0.10247351816969D-16 2 2 2 8 0.17955315438035D+01 0.30716263961466D-15 3 2 2 8 0.61335189982919D+00 0.53002298061763D-16 1 3 2 8 0.48120495601930D+00 0.41546930527014D-16 2 3 2 8 -0.35171325566685D+01 0.80895203060101D-15 3 3 2 8 -0.15558599906726D+01 0.17093134727524D-16 1 4 2 8 0.48120495601930D+00 0.85896072045117D-16 2 4 2 8 -0.35171325566685D+01 -0.28661294495790D-15 3 4 2 8 -0.15558599906725D+01 0.15077730851045D-15 1 5 2 8 -0.81587278202460D-01 0.00000000000000D+00 2 5 2 8 -0.29611934821259D+00 0.00000000000000D+00 3 5 2 8 0.16943728555954D+00 0.00000000000000D+00 1 6 2 8 -0.47212921920618D+01 0.00000000000000D+00 2 6 2 8 -0.14761187001991D+02 0.00000000000000D+00 3 6 2 8 -0.66258235879515D+00 0.00000000000000D+00 1 7 2 8 0.14989449594138D+00 0.00000000000000D+00 2 7 2 8 0.34119604620910D+00 0.00000000000000D+00 3 7 2 8 -0.10651445201029D+01 0.00000000000000D+00 1 8 2 8 -0.46164627652372D+00 0.00000000000000D+00 2 8 2 8 0.18517916435197D+02 0.00000000000000D+00 3 8 2 8 0.26871123781985D+01 0.00000000000000D+00 1 9 2 8 0.48952263584239D+00 0.32843180755853D-16 2 9 2 8 0.13991458022464D+01 0.54206332629101D-15 3 9 2 8 -0.90232092760124D-01 0.79310517023191D-16 1 10 2 8 0.48952263584240D+00 0.27539691154932D-16 2 10 2 8 0.13991458022464D+01 -0.32081199231052D-16 3 10 2 8 -0.90232092760112D-01 0.28085912804530D-16 1 11 2 8 0.38630898660243D-01 -0.11437015366959D-15 2 11 2 8 -0.15112161379035D+01 -0.36801425467374D-15 3 11 2 8 0.17494069863973D+00 0.19346577839494D-15 1 12 2 8 0.38630898660382D-01 0.59798465605054D-17 2 12 2 8 -0.15112161379035D+01 -0.20813241494730D-15 3 12 2 8 0.17494069864060D+00 -0.17943907470964D-15 1 13 2 8 0.12513983423466D-01 0.17300958049914D-16 2 13 2 8 0.94979983044916D-01 0.14573865007108D-14 3 13 2 8 -0.17716412881532D+00 0.40832477724953D-15 1 14 2 8 0.12513983423459D-01 0.15809326418405D-16 2 14 2 8 0.94979983044925D-01 -0.98586429822789D-15 3 14 2 8 -0.17716412881529D+00 -0.16637372928033D-15 1 15 2 8 0.10265494691598D+01 -0.19658044115020D-16 2 15 2 8 -0.14418862649183D+00 -0.55007564954403D-15 3 15 2 8 0.85602264129848D+00 -0.27951600820470D-15 1 16 2 8 0.10265494691604D+01 -0.23246688123530D-16 2 16 2 8 -0.14418862649168D+00 -0.36127464996021D-15 3 16 2 8 0.85602264129847D+00 0.49571804948562D-16 1 17 2 8 -0.80228829136542D-01 -0.53669141322980D-17 2 17 2 8 0.15082554883153D-01 -0.74981354706492D-15 3 17 2 8 0.31484626762452D+00 0.78850411075697D-16 1 18 2 8 -0.80228829136544D-01 -0.17593371570744D-16 2 18 2 8 0.15082554883125D-01 0.36072982252709D-15 3 18 2 8 0.31484626762450D+00 0.22429230002051D-15 1 19 2 8 0.75348532218760D+00 -0.10519299950177D-16 2 19 2 8 -0.33013812894499D-01 -0.95436963017721D-15 3 19 2 8 -0.68650510820881D+00 -0.29521547028390D-15 1 20 2 8 0.75348532218767D+00 -0.22780231527695D-16 2 20 2 8 -0.33013812894293D-01 -0.67977509708218D-15 3 20 2 8 -0.68650510820900D+00 -0.43062313554390D-15 1 22 2 8 0.43628339344443D+01 0.00000000000000D+00 2 22 2 8 -0.30364777564263D+02 0.00000000000000D+00 3 22 2 8 0.10078569969046D+01 0.00000000000000D+00 1 1 3 8 -0.17733915225121D+00 -0.33906411303125D-15 2 1 3 8 0.82601941198910D+00 -0.77227825202825D-16 3 1 3 8 -0.16896824586355D+01 0.27887153015553D-14 1 2 3 8 -0.17733915225119D+00 0.73159074961550D-16 2 2 3 8 0.82601941198916D+00 0.53002298061763D-16 3 2 3 8 -0.16896824586353D+01 0.28992645024676D-14 1 3 3 8 0.88451054934898D-01 0.28780870349550D-15 2 3 3 8 -0.19095566550233D+01 0.17093134727524D-16 3 3 3 8 -0.18192611198142D+01 -0.37682968062434D-14 1 4 3 8 0.88451054934896D-01 0.30192185661427D-15 2 4 3 8 -0.19095566550233D+01 0.15077730851045D-15 3 4 3 8 -0.18192611198141D+01 -0.19575320588394D-14 1 5 3 8 0.32384676004742D+00 0.00000000000000D+00 2 5 3 8 -0.16943374795987D+00 0.00000000000000D+00 3 5 3 8 -0.24694185132679D+01 0.00000000000000D+00 1 6 3 8 0.48524629094079D+01 0.00000000000000D+00 2 6 3 8 -0.66258235879515D+00 0.00000000000000D+00 3 6 3 8 0.40219158030814D+01 0.00000000000000D+00 1 7 3 8 0.42173512680128D+01 0.00000000000000D+00 2 7 3 8 0.10651445201029D+01 0.00000000000000D+00 3 7 3 8 -0.31587118157385D+02 0.00000000000000D+00 1 8 3 8 -0.72684326483105D+00 0.00000000000000D+00 2 8 3 8 0.26871132865089D+01 0.00000000000000D+00 3 8 3 8 0.40365309228723D+02 0.00000000000000D+00 1 9 3 8 0.26222185156986D+00 0.83593037925214D-16 2 9 3 8 -0.12910144566615D+00 0.79310517023191D-16 3 9 3 8 0.40721974703996D-01 0.14222901213860D-14 1 10 3 8 0.26222185156989D+00 -0.12246648678206D-15 2 10 3 8 -0.12910144566614D+00 0.28085912804530D-16 3 10 3 8 0.40721974704003D-01 0.27532822069340D-14 1 11 3 8 -0.22974369595194D+01 -0.93384049218024D-16 2 11 3 8 -0.50892670057697D+00 0.19346577839494D-15 3 11 3 8 -0.71472199265713D+00 0.16884935230041D-14 1 12 3 8 -0.22974369595194D+01 0.13340376108810D-15 2 12 3 8 -0.50892670057610D+00 -0.17943907470964D-15 3 12 3 8 -0.71472199265725D+00 -0.34849366233042D-14 1 13 3 8 -0.49107362204882D+00 -0.26243127215854D-15 2 13 3 8 -0.58123273250002D-01 0.40832477724953D-15 3 13 3 8 0.37892078791057D+01 -0.45926449324351D-15 1 14 3 8 -0.49107362204881D+00 0.19540201021788D-15 2 14 3 8 -0.58123273249980D-01 -0.16637372928033D-15 3 14 3 8 0.37892078791056D+01 0.14207451667541D-14 1 15 3 8 -0.55647288619460D+00 -0.18061251572041D-15 2 15 3 8 -0.43393246734531D-01 -0.27951600820470D-15 3 15 3 8 -0.42317235399660D+01 -0.61597355164384D-15 1 16 3 8 -0.55647288619467D+00 0.22825356575423D-15 2 16 3 8 -0.43393246734524D-01 0.49571804948562D-16 3 16 3 8 -0.42317235399666D+01 0.66993639263482D-15 1 17 3 8 -0.56222819860821D+00 -0.21851319746119D-15 2 17 3 8 0.20478799764697D+00 0.78850411075697D-16 3 17 3 8 0.37080430568572D+01 0.11718056840419D-14 1 18 3 8 -0.56222819860821D+00 -0.43830015049284D-17 2 18 3 8 0.20478799764695D+00 0.22429230002051D-15 3 18 3 8 0.37080430568573D+01 -0.74503359127828D-15 1 19 3 8 -0.61569309227104D+00 -0.88281887182369D-16 2 19 3 8 0.14560847115778D+00 -0.29521547028390D-15 3 19 3 8 -0.42530796130872D+01 0.97098469663920D-15 1 20 3 8 -0.61569309227074D+00 -0.10186532904639D-15 2 20 3 8 0.14560847115758D+00 -0.43062313554390D-15 3 20 3 8 -0.42530796130871D+01 0.57398472112883D-15 1 22 3 8 -0.81401623240986D+01 0.00000000000000D+00 2 22 3 8 0.53635834995297D+00 0.00000000000000D+00 3 22 3 8 -0.30508872247907D+02 0.00000000000000D+00 1 1 1 9 -0.77674026578997D+00 -0.18765477395692D-15 2 1 1 9 -0.35482760536318D+00 0.59060369868399D-16 3 1 1 9 0.75466399839839D-15 0.11951612243952D-15 1 2 1 9 -0.26914411630484D+00 -0.24901340642106D-16 2 2 1 9 -0.41513718820353D-01 0.21813514712056D-17 3 2 1 9 -0.10193258926406D-14 -0.44518202327703D-18 1 3 1 9 -0.11806024688093D+01 0.43464288250707D-16 2 3 1 9 -0.55667005686769D+00 -0.56154614141852D-16 3 3 1 9 -0.16847763472217D-14 -0.33860529175102D-15 1 4 1 9 0.25378428539176D+00 0.18324896008692D-15 2 4 1 9 -0.10273435141376D+00 0.21610306985164D-17 3 4 1 9 0.50598843052982D-14 0.33169809374639D-15 1 5 1 9 -0.15725308190996D+01 0.54325641826435D-15 2 5 1 9 -0.38631272565727D-01 0.33236873731901D-17 3 5 1 9 -0.22974382401126D+01 -0.91014423190876D-16 1 6 1 9 -0.15725308190996D+01 0.58607812143411D-15 2 6 1 9 -0.38631272565732D-01 -0.21771049524438D-16 3 6 1 9 0.22974382401126D+01 -0.27154092229384D-16 1 7 1 9 0.12597052197366D+01 0.86527782906872D-15 2 7 1 9 0.48952263584239D+00 0.14941607762018D-16 3 7 1 9 -0.26222185156986D+00 0.67686087701626D-16 1 8 1 9 0.12597052197366D+01 -0.77886781369037D-16 2 8 1 9 0.48952263584239D+00 -0.32843180755853D-16 3 8 1 9 0.26222185156986D+00 -0.83593037925214D-16 1 9 1 9 0.89321756364254D+01 0.00000000000000D+00 2 9 1 9 0.88165383765920D+00 0.00000000000000D+00 3 9 1 9 0.13331142824669D-15 0.00000000000000D+00 1 10 1 9 -0.54280982931804D+00 0.11856946799100D-15 2 10 1 9 0.97802463006024D-01 -0.86919824068046D-16 3 10 1 9 -0.89552542333382D-14 -0.61290509397053D-16 1 11 1 9 -0.30966719072401D+00 0.75478659562199D-17 2 11 1 9 -0.13242363477408D+00 -0.90815368488121D-17 3 11 1 9 -0.10632617385381D-14 0.19241073790641D-17 1 12 1 9 -0.47983244073403D+00 -0.32605608932010D-15 2 12 1 9 -0.18888540485287D+00 -0.47008828524763D-16 3 12 1 9 -0.87463635111544D-15 0.18031700655367D-15 1 13 1 9 -0.16229324914597D+01 -0.13352933963559D-15 2 13 1 9 -0.92467015456394D+00 -0.24016746196710D-16 3 13 1 9 -0.12638908832994D+01 0.57900063890766D-17 1 14 1 9 -0.14317925744116D+00 0.27669861433540D-15 2 14 1 9 -0.56907947121471D+00 -0.46191645595028D-16 3 14 1 9 0.12101428216917D+01 0.59991077733021D-16 1 15 1 9 -0.14317925744116D+00 -0.46952256259113D-15 2 15 1 9 -0.56907947121471D+00 -0.40569499855467D-16 3 15 1 9 -0.12101428216917D+01 -0.97603064886574D-16 1 16 1 9 -0.16229324914597D+01 0.28119232079819D-16 2 16 1 9 -0.92467015456394D+00 -0.36950254083440D-16 3 16 1 9 0.12638908832994D+01 -0.72296488730082D-16 1 17 1 9 -0.76437194269629D+00 -0.17110538624872D-15 2 17 1 9 0.83180397548949D+00 0.12494044870930D-16 3 17 1 9 -0.71982304519630D+00 -0.17812744810089D-15 1 18 1 9 0.14662361543804D-01 0.39560657329009D-16 2 18 1 9 0.39800972332159D+00 0.17338779929251D-16 3 18 1 9 0.95995998170724D+00 0.10331803632508D-15 1 19 1 9 0.14662361543806D-01 0.49829878855886D-16 2 19 1 9 0.39800972332158D+00 -0.19008388597320D-16 3 19 1 9 -0.95995998170723D+00 0.22964023772571D-16 1 20 1 9 -0.76437194269629D+00 -0.57129991600930D-15 2 20 1 9 0.83180397548950D+00 -0.20297752014962D-16 3 20 1 9 0.71982304519629D+00 0.97548571315746D-16 1 22 1 9 -0.50694735321022D+02 0.00000000000000D+00 2 22 1 9 -0.10166764588906D+01 0.00000000000000D+00 3 22 1 9 0.11916407100714D-07 0.00000000000000D+00 1 1 2 9 -0.18749496673953D+00 0.59060369868399D-16 2 1 2 9 0.95061656595128D-01 -0.11716279074583D-15 3 1 2 9 -0.10344144117261D-14 0.18303200307812D-15 1 2 2 9 0.94460139173847D-01 0.21813514712056D-17 2 2 2 9 0.27398820110282D+00 0.85030484140122D-16 3 2 2 9 -0.23773724132781D-15 -0.25692426802224D-16 1 3 2 9 -0.46317205304348D+00 -0.56154614141852D-16 2 3 2 9 -0.70674797946603D+00 0.29137539933179D-15 3 3 2 9 0.16777392652151D-14 0.95599111010165D-16 1 4 2 9 -0.22699110656126D-01 0.21610306985164D-17 2 4 2 9 -0.31914217638625D+00 -0.70789214890200D-16 3 4 2 9 -0.73901435480724D-15 -0.22269248963728D-16 1 5 2 9 -0.88531738131752D-01 0.33236873731901D-17 2 5 2 9 -0.15112151868031D+01 0.26454865155168D-16 3 5 2 9 0.50892527373058D+00 0.19690436477292D-15 1 6 2 9 -0.88531738131757D-01 -0.21771049524438D-16 2 6 2 9 -0.15112151868031D+01 -0.56425154143929D-15 3 6 2 9 -0.50892527373056D+00 -0.19412771063156D-15 1 7 2 9 -0.37871643932608D+00 0.14941607762018D-16 2 7 2 9 0.13991458022464D+01 0.53113123275583D-16 3 7 2 9 0.12910144566615D+00 0.41045688335342D-16 1 8 2 9 -0.37871643932608D+00 -0.32843180755853D-16 2 8 2 9 0.13991458022464D+01 -0.54206332629101D-15 3 8 2 9 -0.12910144566615D+00 -0.79310517023191D-16 1 9 2 9 0.88165303322747D+00 0.00000000000000D+00 2 9 2 9 0.67435912251497D+01 0.00000000000000D+00 3 9 2 9 -0.31710975366428D-13 0.00000000000000D+00 1 10 2 9 0.97803668276649D-01 -0.86919824068046D-16 2 10 2 9 -0.40029413208334D+00 -0.15813617261163D-15 3 10 2 9 0.12829169951538D-14 0.12284919875523D-16 1 11 2 9 0.13242363477408D+00 -0.90815368488121D-17 2 11 2 9 -0.36925578762328D+00 -0.10802693103274D-15 3 11 2 9 -0.95869410084659D-15 -0.31974334550126D-16 1 12 2 9 0.18888540485288D+00 -0.47008828524763D-16 2 12 2 9 -0.64595616152771D+00 0.35381348378586D-16 3 12 2 9 0.15680736546244D-15 0.49089031850199D-17 1 13 2 9 -0.84607573532564D+00 -0.24016746196710D-16 2 13 2 9 -0.19340110479078D+00 0.30056193207541D-15 3 13 2 9 -0.99484570033542D+00 0.65892584310335D-17 1 14 2 9 -0.54965814863808D+00 -0.46191645595028D-16 2 14 2 9 -0.42505814539472D+00 -0.57732361523111D-17 3 14 2 9 0.12123996215333D+01 0.55125797749755D-17 1 15 2 9 -0.54965814863808D+00 -0.40569499855467D-16 2 15 2 9 -0.42505814539472D+00 0.23062249562743D-15 3 15 2 9 -0.12123996215332D+01 -0.20073509105999D-16 1 16 2 9 -0.84607573532564D+00 -0.36950254083440D-16 2 16 2 9 -0.19340110479078D+00 0.20401731510457D-15 3 16 2 9 0.99484570033541D+00 -0.24635292836497D-16 1 17 2 9 0.99208058970531D+00 0.12494044870930D-16 2 17 2 9 -0.10989501560636D+01 0.50944025789981D-15 3 17 2 9 0.97924848375816D+00 0.18602331528573D-15 1 18 2 9 0.49896941366673D+00 0.17338779929251D-16 2 18 2 9 -0.60432485105596D+00 -0.45132700251673D-15 3 18 2 9 -0.16447879168192D+01 -0.72636099432468D-16 1 19 2 9 0.49896941366672D+00 -0.19008388597320D-16 2 19 2 9 -0.60432485105596D+00 -0.20909014145487D-16 3 19 2 9 0.16447879168192D+01 -0.10940473580340D-15 1 20 2 9 0.99208058970532D+00 -0.20297752014962D-16 2 20 2 9 -0.10989501560636D+01 0.11467926428737D-15 3 20 2 9 -0.97924848375814D+00 0.94314770134959D-16 1 22 2 9 0.14337321829397D+00 0.00000000000000D+00 2 22 2 9 -0.49372714613399D+02 0.00000000000000D+00 3 22 2 9 -0.26756897835616D-08 0.00000000000000D+00 1 1 3 9 0.75466399839839D-15 0.11951612243952D-15 2 1 3 9 -0.10344144117261D-14 0.18303200307812D-15 3 1 3 9 -0.40944540762400D+01 0.10095439249349D-15 1 2 3 9 -0.10193258925506D-14 -0.44518202327703D-18 2 2 3 9 -0.23773724122462D-15 -0.25692426802224D-16 3 2 3 9 0.27059870734659D+01 0.27721670257939D-16 1 3 3 9 -0.16847763474304D-14 -0.33860529175102D-15 2 3 3 9 0.16777392624542D-14 0.95599111010165D-16 3 3 3 9 -0.39144574651960D+01 -0.16681971577727D-17 1 4 3 9 0.50598843059140D-14 0.33169809374639D-15 2 4 3 9 -0.73901435218925D-15 -0.22269248963728D-16 3 4 3 9 0.26941601320165D+01 0.23698957991494D-16 1 5 3 9 0.51032670899728D+00 -0.91014423190876D-16 2 5 3 9 -0.17494065514001D+00 0.19690436477292D-15 3 5 3 9 -0.71471835466605D+00 0.37633528656737D-15 1 6 3 9 -0.51032670899721D+00 -0.27154092229384D-16 2 6 3 9 0.17494065514002D+00 -0.19412771063156D-15 3 6 3 9 -0.71471835466599D+00 0.16369976067110D-14 1 7 3 9 -0.55913866598668D+00 0.67686087701626D-16 2 7 3 9 0.90232092760124D-01 0.41045688335342D-16 3 7 3 9 0.40721974703973D-01 0.11379652604697D-13 1 8 3 9 0.55913866598668D+00 -0.83593037925214D-16 2 8 3 9 -0.90232092760124D-01 -0.79310517023191D-16 3 8 3 9 0.40721974703996D-01 -0.14222901213860D-14 1 9 3 9 0.13331142824668D-15 0.00000000000000D+00 2 9 3 9 -0.31710975373046D-13 0.00000000000000D+00 3 9 3 9 0.42417012588669D+02 0.00000000000000D+00 1 10 3 9 -0.89552542305596D-14 -0.61290509397053D-16 2 10 3 9 0.12829169973023D-14 0.12284919875523D-16 3 10 3 9 -0.16605257951220D+02 -0.51615693184140D-16 1 11 3 9 -0.10632617368015D-14 0.19241073790641D-17 2 11 3 9 -0.95869410192844D-15 -0.31974334550126D-16 3 11 3 9 -0.46472005771747D+01 -0.79304921307325D-16 1 12 3 9 -0.87463636404559D-15 0.18031700655367D-15 2 12 3 9 0.15680736562752D-15 0.49089031850199D-17 3 12 3 9 0.37088588450965D+01 0.46525100126681D-16 1 13 3 9 -0.26868099307663D+01 0.57900063890766D-17 2 13 3 9 -0.16574385092918D+01 0.65892584310335D-17 3 13 3 9 -0.14182477210594D+01 -0.95511775535031D-15 1 14 3 9 0.19107812646497D+01 0.59991077733021D-16 2 14 3 9 0.20255749808160D+01 0.55125797749755D-17 3 14 3 9 -0.36637370184662D+01 0.68120040244950D-15 1 15 3 9 -0.19107812646497D+01 -0.97603064886574D-16 2 15 3 9 -0.20255749808160D+01 -0.20073509105999D-16 3 15 3 9 -0.36637370184662D+01 -0.18830076916523D-14 1 16 3 9 0.26868099307663D+01 -0.72296488730082D-16 2 16 3 9 0.16574385092918D+01 -0.24635292836497D-16 3 16 3 9 -0.14182477210594D+01 0.10021630571555D-14 1 17 3 9 -0.18293426717494D+01 -0.17812744810089D-15 2 17 3 9 0.21454480474469D+01 0.18602331528573D-15 3 17 3 9 -0.11154366465566D+01 -0.61169140296512D-15 1 18 3 9 0.14254744662861D+01 0.10331803632508D-15 2 18 3 9 -0.27804859619070D+01 -0.72636099432468D-16 3 18 3 9 -0.41520018439910D+01 0.22233975789265D-14 1 19 3 9 -0.14254744662861D+01 0.22964023772571D-16 2 19 3 9 0.27804859619070D+01 -0.10940473580340D-15 3 19 3 9 -0.41520018439911D+01 0.15780982317576D-14 1 20 3 9 0.18293426717494D+01 0.97548571315746D-16 2 20 3 9 -0.21454480474469D+01 0.94314770134959D-16 3 20 3 9 -0.11154366465566D+01 0.80666316901717D-15 1 22 3 9 0.98435275136597D-08 0.00000000000000D+00 2 22 3 9 -0.36340630140547D-08 0.00000000000000D+00 3 22 3 9 -0.70652545895957D+02 0.00000000000000D+00 1 1 1 10 -0.26914411630483D+00 -0.26809669450733D-15 2 1 1 10 -0.41513718820356D-01 0.96692501228189D-16 3 1 1 10 -0.35060350011674D-14 -0.49361025532691D-16 1 2 1 10 -0.77674026578988D+00 -0.16131509069749D-15 2 2 1 10 -0.35482760536322D+00 -0.67387848017710D-16 3 2 1 10 0.45366017482106D-14 0.30023330642231D-15 1 3 1 10 0.25378428539174D+00 0.17274635335426D-15 2 3 1 10 -0.10273435141376D+00 0.73196000643904D-16 3 3 1 10 0.14673267309157D-13 -0.95727237079771D-16 1 4 1 10 -0.11806024688093D+01 -0.29087788968623D-15 2 4 1 10 -0.55667005686757D+00 -0.31263631319622D-16 3 4 1 10 -0.28617774771705D-14 -0.11028701953239D-15 1 5 1 10 -0.15725308190992D+01 0.12528183832509D-14 2 5 1 10 -0.38631272565712D-01 0.43807353085505D-16 3 5 1 10 -0.22974382401126D+01 -0.40218535164441D-16 1 6 1 10 -0.15725308190993D+01 -0.11566073739313D-14 2 6 1 10 -0.38631272565716D-01 -0.52887725610409D-16 3 6 1 10 0.22974382401124D+01 0.68005055630173D-16 1 7 1 10 0.12597052197366D+01 -0.90620029894044D-15 2 7 1 10 0.48952263584240D+00 0.72662378760190D-16 3 7 1 10 -0.26222185156987D+00 0.87765868240689D-16 1 8 1 10 0.12597052197366D+01 0.53909826188096D-16 2 8 1 10 0.48952263584240D+00 -0.27539691154932D-16 3 8 1 10 0.26222185156989D+00 0.12246648678206D-15 1 9 1 10 -0.54280982931804D+00 -0.11856946799100D-15 2 9 1 10 0.97802463006024D-01 0.86919824068046D-16 3 9 1 10 -0.89552542324120D-14 0.61290509397053D-16 1 10 1 10 0.89321756364247D+01 0.00000000000000D+00 2 10 1 10 0.88165383765916D+00 0.00000000000000D+00 3 10 1 10 0.14579457184217D-12 0.00000000000000D+00 1 11 1 10 -0.47983244073407D+00 0.86636575261189D-16 2 11 1 10 -0.18888540485294D+00 -0.14239094580776D-17 3 11 1 10 0.28389897631242D-15 -0.28447088844605D-15 1 12 1 10 -0.30966719072401D+00 0.46809472450690D-17 2 12 1 10 -0.13242363477408D+00 0.23137850306168D-18 3 12 1 10 0.42713517778952D-16 -0.24431730562261D-17 1 13 1 10 -0.14317925744119D+00 -0.11859674763976D-15 2 13 1 10 -0.56907947121473D+00 -0.22381715659138D-16 3 13 1 10 0.12101428216918D+01 0.63643634965606D-16 1 14 1 10 -0.16229324914597D+01 0.28579787141909D-18 2 14 1 10 -0.92467015456399D+00 0.26238721665069D-16 3 14 1 10 -0.12638908832994D+01 0.55090998514186D-16 1 15 1 10 -0.16229324914597D+01 -0.23429308062606D-15 2 15 1 10 -0.92467015456397D+00 0.41471580557652D-16 3 15 1 10 0.12638908832994D+01 0.43025566532898D-17 1 16 1 10 -0.14317925744119D+00 0.98223936114535D-16 2 16 1 10 -0.56907947121472D+00 0.13624276407728D-16 3 16 1 10 -0.12101428216917D+01 0.57775327349178D-16 1 17 1 10 0.14662361543774D-01 0.35135156467848D-15 2 17 1 10 0.39800972332159D+00 -0.92468437971919D-16 3 17 1 10 0.95995998170726D+00 0.41416353054515D-16 1 18 1 10 -0.76437194269626D+00 0.13097399870699D-15 2 18 1 10 0.83180397548953D+00 0.72226688769405D-17 3 18 1 10 -0.71982304519634D+00 -0.69244886197431D-16 1 19 1 10 -0.76437194269625D+00 0.77465756276236D-16 2 19 1 10 0.83180397548951D+00 0.89066538616191D-16 3 19 1 10 0.71982304519633D+00 -0.64446227512283D-17 1 20 1 10 0.14662361543761D-01 0.26223307929542D-15 2 20 1 10 0.39800972332159D+00 -0.52061873364443D-16 3 20 1 10 -0.95995998170726D+00 -0.86363443445111D-17 1 22 1 10 -0.50694735321022D+02 0.00000000000000D+00 2 22 1 10 -0.10166764588906D+01 0.00000000000000D+00 3 22 1 10 -0.11927026073591D-07 0.00000000000000D+00 1 1 2 10 0.94460139173844D-01 0.96692501228189D-16 2 1 2 10 0.27398820110282D+00 0.64589147146955D-16 3 1 2 10 0.16530527939092D-14 -0.90424073524862D-16 1 2 2 10 -0.18749496673957D+00 -0.67387848017710D-16 2 2 2 10 0.95061656594929D-01 0.85495644390301D-16 3 2 2 10 0.17570978807669D-14 0.36105814952353D-16 1 3 2 10 -0.22699110656128D-01 0.73196000643904D-16 2 3 2 10 -0.31914217638626D+00 0.25014240297281D-16 3 3 2 10 -0.24681499634060D-15 -0.27965280341337D-16 1 4 2 10 -0.46317205304336D+00 -0.31263631319622D-16 2 4 2 10 -0.70674797946607D+00 0.51764384639709D-15 3 4 2 10 -0.14943934197293D-15 -0.42591283915866D-16 1 5 2 10 -0.88531738131737D-01 0.43807353085505D-16 2 5 2 10 -0.15112151868028D+01 -0.17704537914414D-15 3 5 2 10 0.50892527373076D+00 -0.11663140305761D-15 1 6 2 10 -0.88531738131742D-01 -0.52887725610409D-16 2 6 2 10 -0.15112151868029D+01 -0.22645365780369D-15 3 6 2 10 -0.50892527373074D+00 -0.14678168510907D-15 1 7 2 10 -0.37871643932607D+00 0.72662378760190D-16 2 7 2 10 0.13991458022464D+01 -0.49880290937264D-16 3 7 2 10 0.12910144566613D+00 0.10310037186314D-15 1 8 2 10 -0.37871643932608D+00 -0.27539691154932D-16 2 8 2 10 0.13991458022464D+01 0.32081199231052D-16 3 8 2 10 -0.12910144566614D+00 -0.28085912804530D-16 1 9 2 10 0.97803668276649D-01 0.86919824068046D-16 2 9 2 10 -0.40029413208334D+00 0.15813617261163D-15 3 9 2 10 0.12829169953185D-14 -0.12284919875523D-16 1 10 2 10 0.88165303322743D+00 0.00000000000000D+00 2 10 2 10 0.67435912251494D+01 0.00000000000000D+00 3 10 2 10 -0.21052834542195D-13 0.00000000000000D+00 1 11 2 10 0.18888540485281D+00 -0.14239094580776D-17 2 11 2 10 -0.64595616152766D+00 0.24173279445839D-16 3 11 2 10 0.34775705466472D-16 -0.67483478266361D-17 1 12 2 10 0.13242363477408D+00 0.23137850306168D-18 2 12 2 10 -0.36925578762328D+00 0.13892434125075D-15 3 12 2 10 -0.29448921173663D-14 -0.31113507444794D-16 1 13 2 10 -0.54965814863809D+00 -0.22381715659138D-16 2 13 2 10 -0.42505814539470D+00 -0.54109281960968D-15 3 13 2 10 0.12123996215333D+01 0.34822859780792D-16 1 14 2 10 -0.84607573532569D+00 0.26238721665069D-16 2 14 2 10 -0.19340110479079D+00 -0.15417793340086D-15 3 14 2 10 -0.99484570033546D+00 0.54009579256822D-17 1 15 2 10 -0.84607573532566D+00 0.41471580557652D-16 2 15 2 10 -0.19340110479079D+00 0.10198912644821D-16 3 15 2 10 0.99484570033546D+00 -0.17062902546319D-16 1 16 2 10 -0.54965814863808D+00 0.13624276407728D-16 2 16 2 10 -0.42505814539470D+00 0.11796689292581D-15 3 16 2 10 -0.12123996215332D+01 -0.31260300163030D-16 1 17 2 10 0.49896941366673D+00 -0.92468437971919D-16 2 17 2 10 -0.60432485105597D+00 -0.22534938902494D-15 3 17 2 10 -0.16447879168192D+01 0.58075563264886D-16 1 18 2 10 0.99208058970535D+00 0.72226688769405D-17 2 18 2 10 -0.10989501560636D+01 0.68848125699366D-15 3 18 2 10 0.97924848375820D+00 0.70291559555350D-16 1 19 2 10 0.99208058970534D+00 0.89066538616191D-16 2 19 2 10 -0.10989501560636D+01 -0.24653766747314D-15 3 19 2 10 -0.97924848375820D+00 0.94539367790957D-16 1 20 2 10 0.49896941366673D+00 -0.52061873364443D-16 2 20 2 10 -0.60432485105597D+00 0.13551739176166D-15 3 20 2 10 0.16447879168191D+01 0.11280830607539D-15 1 22 2 10 0.14337321829396D+00 0.00000000000000D+00 2 22 2 10 -0.49372714613399D+02 0.00000000000000D+00 3 22 2 10 0.27017824423027D-08 0.00000000000000D+00 1 1 3 10 -0.35060350010322D-14 -0.49361025532691D-16 2 1 3 10 0.16530527942191D-14 -0.90424073524862D-16 3 1 3 10 0.27059870734659D+01 -0.12649352504901D-16 1 2 3 10 0.45366017482106D-14 0.30023330642231D-15 2 2 3 10 0.17570978807669D-14 0.36105814952353D-16 3 2 3 10 -0.40944540762399D+01 -0.74845233809552D-16 1 3 3 10 0.14673267309773D-13 -0.95727237079771D-16 2 3 3 10 -0.24681499372261D-15 -0.27965280341337D-16 3 3 3 10 0.26941601320165D+01 0.22132526263134D-17 1 4 3 10 -0.28617774773792D-14 -0.11028701953239D-15 2 4 3 10 -0.14943934473388D-15 -0.42591283915866D-16 3 4 3 10 -0.39144574651961D+01 0.58777050406292D-16 1 5 3 10 0.51032670899728D+00 -0.40218535164441D-16 2 5 3 10 -0.17494065513983D+00 -0.11663140305761D-15 3 5 3 10 -0.71471835466684D+00 0.12174209080626D-13 1 6 3 10 -0.51032670899741D+00 0.68005055630173D-16 2 6 3 10 0.17494065513985D+00 -0.14678168510907D-15 3 6 3 10 -0.71471835466622D+00 -0.35252272472814D-14 1 7 3 10 -0.55913866598669D+00 0.87765868240689D-16 2 7 3 10 0.90232092760105D-01 0.10310037186314D-15 3 7 3 10 0.40721974704080D-01 -0.99952108863478D-15 1 8 3 10 0.55913866598671D+00 0.12246648678206D-15 2 8 3 10 -0.90232092760112D-01 -0.28085912804530D-16 3 8 3 10 0.40721974704003D-01 -0.27532822069340D-14 1 9 3 10 -0.89552542371770D-14 0.61290509397053D-16 2 9 3 10 0.12829169956479D-14 -0.12284919875523D-16 3 9 3 10 -0.16605257951220D+02 0.51615693184140D-16 1 10 3 10 0.14579457184217D-12 0.00000000000000D+00 2 10 3 10 -0.21052834548813D-13 0.00000000000000D+00 3 10 3 10 0.42417012588670D+02 0.00000000000000D+00 1 11 3 10 0.28389896338228D-15 -0.28447088844605D-15 2 11 3 10 0.34775705631552D-16 -0.67483478266361D-17 3 11 3 10 0.37088588450965D+01 -0.24756856800234D-16 1 12 3 10 0.42713519515528D-16 -0.24431730562261D-17 2 12 3 10 -0.29448921184481D-14 -0.31113507444794D-16 3 12 3 10 -0.46472005771747D+01 -0.11009833728368D-16 1 13 3 10 0.19107812646498D+01 0.63643634965606D-16 2 13 3 10 0.20255749808160D+01 0.34822859780792D-16 3 13 3 10 -0.36637370184662D+01 -0.66141168204448D-15 1 14 3 10 -0.26868099307664D+01 0.55090998514186D-16 2 14 3 10 -0.16574385092919D+01 0.54009579256822D-17 3 14 3 10 -0.14182477210594D+01 0.14429905293441D-14 1 15 3 10 0.26868099307664D+01 0.43025566532898D-17 2 15 3 10 0.16574385092919D+01 -0.17062902546319D-16 3 15 3 10 -0.14182477210595D+01 0.83743289278678D-15 1 16 3 10 -0.19107812646497D+01 0.57775327349178D-16 2 16 3 10 -0.20255749808160D+01 -0.31260300163030D-16 3 16 3 10 -0.36637370184662D+01 0.19875773319800D-15 1 17 3 10 0.14254744662861D+01 0.41416353054515D-16 2 17 3 10 -0.27804859619070D+01 0.58075563264886D-16 3 17 3 10 -0.41520018439910D+01 0.15593316676586D-14 1 18 3 10 -0.18293426717494D+01 -0.69244886197431D-16 2 18 3 10 0.21454480474470D+01 0.70291559555350D-16 3 18 3 10 -0.11154366465567D+01 0.84142186755541D-15 1 19 3 10 0.18293426717494D+01 -0.64446227512283D-17 2 19 3 10 -0.21454480474470D+01 0.94539367790957D-16 3 19 3 10 -0.11154366465567D+01 0.32262139865755D-15 1 20 3 10 -0.14254744662861D+01 -0.86363443445111D-17 2 20 3 10 0.27804859619069D+01 0.11280830607539D-15 3 20 3 10 -0.41520018439910D+01 0.11934110409213D-14 1 22 3 10 -0.98506745650566D-08 0.00000000000000D+00 2 22 3 10 0.36284942782610D-08 0.00000000000000D+00 3 22 3 10 -0.70652545895957D+02 0.00000000000000D+00 1 1 1 11 0.25378428539173D+00 -0.75997281559267D-16 2 1 1 11 0.10273435141376D+00 0.31915466111290D-16 3 1 1 11 0.21338458841704D-15 0.87636878613530D-16 1 2 1 11 -0.11806024688092D+01 0.66795033115537D-16 2 2 1 11 0.55667005686767D+00 0.44751693876427D-17 3 2 1 11 0.10861186048928D-14 0.84129965349657D-16 1 3 1 11 -0.26914411630483D+00 -0.43758720828593D-17 2 3 1 11 0.41513718820356D-01 0.29317520446519D-16 3 3 1 11 0.23995090624880D-14 -0.30261363663284D-15 1 4 1 11 -0.77674026578980D+00 0.12725674646029D-15 2 4 1 11 0.35482760536344D+00 -0.29244300429183D-16 3 4 1 11 -0.12213695914716D-14 -0.19961428951696D-15 1 5 1 11 0.12597052197366D+01 0.13189128600793D-15 2 5 1 11 -0.48952263584242D+00 -0.59052550880210D-16 3 5 1 11 0.26222185156986D+00 0.10914708572143D-15 1 6 1 11 0.12597052197366D+01 -0.14701821027814D-15 2 6 1 11 -0.48952263584241D+00 -0.41068492097126D-16 3 6 1 11 -0.26222185156987D+00 0.22812022337587D-16 1 7 1 11 -0.15725308190993D+01 0.53921718454333D-16 2 7 1 11 0.38631272565619D-01 -0.11159347634079D-16 3 7 1 11 0.22974382401126D+01 0.17897773192048D-15 1 8 1 11 -0.15725308190994D+01 0.17474917604691D-14 2 8 1 11 0.38631272565625D-01 0.11437015366959D-15 3 8 1 11 -0.22974382401124D+01 0.93384049218024D-16 1 9 1 11 -0.30966719072401D+00 -0.75478659562199D-17 2 9 1 11 0.13242363477408D+00 0.90815368488121D-17 3 9 1 11 -0.10632617368015D-14 -0.19241073790641D-17 1 10 1 11 -0.47983244073407D+00 -0.86636575261189D-16 2 10 1 11 0.18888540485281D+00 0.14239094580776D-17 3 10 1 11 0.28389896338228D-15 0.28447088844605D-15 1 11 1 11 0.89321756364243D+01 0.00000000000000D+00 2 11 1 11 -0.88165383765909D+00 0.00000000000000D+00 3 11 1 11 -0.13486980878307D-12 0.00000000000000D+00 1 12 1 11 -0.54280982931803D+00 -0.12565052151974D-15 2 12 1 11 -0.97802463006026D-01 0.33898293851935D-16 3 12 1 11 0.67562269915801D-14 -0.35145588661660D-16 1 13 1 11 0.14662361543804D-01 0.34562495883931D-15 2 13 1 11 -0.39800972332160D+00 0.34586468557984D-16 3 13 1 11 -0.95995998170731D+00 0.65313851526555D-18 1 14 1 11 -0.76437194269624D+00 0.27679561902243D-16 2 14 1 11 -0.83180397548952D+00 0.10638038937330D-16 3 14 1 11 0.71982304519631D+00 -0.35086705600393D-16 1 15 1 11 -0.76437194269623D+00 -0.56344078803869D-16 2 15 1 11 -0.83180397548951D+00 -0.57921925445058D-16 3 15 1 11 -0.71982304519633D+00 -0.68998379417752D-16 1 16 1 11 0.14662361543788D-01 0.30380917840224D-15 2 16 1 11 -0.39800972332160D+00 0.12314042359008D-16 3 16 1 11 0.95995998170731D+00 -0.18326012427170D-16 1 17 1 11 -0.14317925744119D+00 -0.46913020348647D-15 2 17 1 11 0.56907947121473D+00 0.35417972771553D-16 3 17 1 11 -0.12101428216917D+01 -0.53385194165472D-16 1 18 1 11 -0.16229324914598D+01 -0.27339750461519D-15 2 18 1 11 0.92467015456397D+00 0.21711654257282D-16 3 18 1 11 0.12638908832995D+01 -0.35694616322445D-16 1 19 1 11 -0.16229324914597D+01 -0.85016978194032D-17 2 19 1 11 0.92467015456396D+00 -0.98788541182014D-16 3 19 1 11 -0.12638908832995D+01 0.86829554039201D-16 1 20 1 11 -0.14317925744119D+00 0.15835511867675D-15 2 20 1 11 0.56907947121470D+00 0.21564750480621D-16 3 20 1 11 0.12101428216917D+01 -0.10989970498616D-15 1 22 1 11 -0.50694735321014D+02 0.00000000000000D+00 2 22 1 11 0.10166764589081D+01 0.00000000000000D+00 3 22 1 11 0.11925501774458D-07 0.00000000000000D+00 1 1 2 11 0.22699110656133D-01 0.31915466111290D-16 2 1 2 11 -0.31914217638625D+00 0.63162171521417D-16 3 1 2 11 0.10113459230775D-14 -0.36127648766785D-16 1 2 2 11 0.46317205304344D+00 0.44751693876427D-17 2 2 2 11 -0.70674797946614D+00 -0.23597499099886D-16 3 2 2 11 -0.49159827370303D-15 0.58959951332332D-16 1 3 2 11 -0.94460139173844D-01 0.29317520446519D-16 2 3 2 11 0.27398820110282D+00 0.40344845939824D-16 3 3 2 11 0.18799885766021D-14 -0.82578618900279D-16 1 4 2 11 0.18749496673979D+00 -0.29244300429183D-16 2 4 2 11 0.95061656594673D-01 -0.57001762977131D-15 3 4 2 11 -0.13417178082706D-14 0.20010205725760D-15 1 5 2 11 0.37871643932605D+00 -0.59052550880210D-16 2 5 2 11 0.13991458022464D+01 0.37491604998636D-15 3 5 2 11 0.12910144566608D+00 0.23755913597423D-15 1 6 2 11 0.37871643932606D+00 -0.41068492097126D-16 2 6 2 11 0.13991458022465D+01 0.85279536816717D-15 3 6 2 11 -0.12910144566608D+00 -0.10868889555974D-15 1 7 2 11 0.88531738131645D-01 -0.11159347634079D-16 2 7 2 11 -0.15112151868029D+01 0.21241828223538D-15 3 7 2 11 0.50892527373136D+00 -0.29811403909872D-16 1 8 2 11 0.88531738131650D-01 0.11437015366959D-15 2 8 2 11 -0.15112151868030D+01 0.36801425467374D-15 3 8 2 11 -0.50892527373131D+00 -0.19346577839494D-15 1 9 2 11 -0.13242363477408D+00 0.90815368488121D-17 2 9 2 11 -0.36925578762328D+00 0.10802693103274D-15 3 9 2 11 -0.95869410192844D-15 0.31974334550126D-16 1 10 2 11 -0.18888540485294D+00 0.14239094580776D-17 2 10 2 11 -0.64595616152766D+00 -0.24173279445839D-16 3 10 2 11 0.34775705631552D-16 0.67483478266361D-17 1 11 2 11 -0.88165303322736D+00 0.00000000000000D+00 2 11 2 11 0.67435912251499D+01 0.00000000000000D+00 3 11 2 11 -0.56579971330203D-13 0.00000000000000D+00 1 12 2 11 -0.97803668276651D-01 0.33898293851935D-16 2 12 2 11 -0.40029413208335D+00 0.71520792907070D-17 3 12 2 11 0.23361614193027D-14 -0.82921732900381D-16 1 13 2 11 -0.49896941366675D+00 0.34586468557984D-16 2 13 2 11 -0.60432485105591D+00 -0.48335974247628D-15 3 13 2 11 -0.16447879168192D+01 -0.36346403842027D-16 1 14 2 11 -0.99208058970535D+00 0.10638038937330D-16 2 14 2 11 -0.10989501560637D+01 0.19308235335107D-15 3 14 2 11 0.97924848375818D+00 -0.24335475890232D-16 1 15 2 11 -0.99208058970533D+00 -0.57921925445058D-16 2 15 2 11 -0.10989501560636D+01 -0.20794934071746D-15 3 15 2 11 -0.97924848375822D+00 -0.10378811886472D-15 1 16 2 11 -0.49896941366674D+00 0.12314042359008D-16 2 16 2 11 -0.60432485105590D+00 -0.24110223587506D-15 3 16 2 11 0.16447879168192D+01 0.10769787579255D-15 1 17 2 11 0.54965814863810D+00 0.35417972771553D-16 2 17 2 11 -0.42505814539475D+00 0.40637964685694D-15 3 17 2 11 0.12123996215333D+01 0.66980750952940D-16 1 18 2 11 0.84607573532567D+00 0.21711654257282D-16 2 18 2 11 -0.19340110479071D+00 -0.55149671519873D-15 3 18 2 11 -0.99484570033544D+00 -0.79519998047840D-17 1 19 2 11 0.84607573532565D+00 -0.98788541182014D-16 2 19 2 11 -0.19340110479072D+00 0.14121108827776D-15 3 19 2 11 0.99484570033544D+00 -0.49552265361454D-16 1 20 2 11 0.54965814863807D+00 0.21564750480621D-16 2 20 2 11 -0.42505814539475D+00 -0.36798320229780D-15 3 20 2 11 -0.12123996215332D+01 0.43791145737077D-16 1 22 2 11 -0.14337321830717D+00 0.00000000000000D+00 2 22 2 11 -0.49372714613398D+02 0.00000000000000D+00 3 22 2 11 0.26951108096553D-08 0.00000000000000D+00 1 1 3 11 0.21338458831932D-15 0.87636878613530D-16 2 1 3 11 0.10113459263781D-14 -0.36127648766785D-16 3 1 3 11 0.26941601320165D+01 -0.22808811993813D-16 1 2 3 11 0.10861186043671D-14 0.84129965349657D-16 2 2 3 11 -0.49159827380636D-15 0.58959951332332D-16 3 2 3 11 -0.39144574651962D+01 0.13724432429729D-15 1 3 3 11 0.23995090622746D-14 -0.30261363663284D-15 2 3 3 11 0.18799885770158D-14 -0.82578618900279D-16 3 3 3 11 0.27059870734660D+01 -0.33676969966402D-16 1 4 3 11 -0.12213695914716D-14 -0.19961428951696D-15 2 4 3 11 -0.13417178082706D-14 0.20010205725760D-15 3 4 3 11 -0.40944540762396D+01 0.12137066939274D-15 1 5 3 11 0.55913866598669D+00 0.10914708572143D-15 2 5 3 11 0.90232092760050D-01 0.23755913597423D-15 3 5 3 11 0.40721974704081D-01 -0.45657645423153D-14 1 6 3 11 -0.55913866598669D+00 0.22812022337587D-16 2 6 3 11 -0.90232092760047D-01 -0.10868889555974D-15 3 6 3 11 0.40721974703998D-01 0.18050972910388D-14 1 7 3 11 -0.51032670899727D+00 0.17897773192048D-15 2 7 3 11 -0.17494065513923D+00 -0.29811403909872D-16 3 7 3 11 -0.71471835466645D+00 -0.81921031028180D-15 1 8 3 11 0.51032670899747D+00 0.93384049218024D-16 2 8 3 11 0.17494065513927D+00 -0.19346577839494D-15 3 8 3 11 -0.71471835466610D+00 -0.16884935230041D-14 1 9 3 11 -0.10632617385381D-14 -0.19241073790641D-17 2 9 3 11 -0.95869410084659D-15 0.31974334550126D-16 3 9 3 11 -0.46472005771747D+01 0.79304921307325D-16 1 10 3 11 0.28389897631242D-15 0.28447088844605D-15 2 10 3 11 0.34775705466472D-16 0.67483478266361D-17 3 10 3 11 0.37088588450965D+01 0.24756856800234D-16 1 11 3 11 -0.13486980878307D-12 0.00000000000000D+00 2 11 3 11 -0.56579971323586D-13 0.00000000000000D+00 3 11 3 11 0.42417012588670D+02 0.00000000000000D+00 1 12 3 11 0.67562269972713D-14 -0.35145588661660D-16 2 12 3 11 0.23361614186402D-14 -0.82921732900381D-16 3 12 3 11 -0.16605257951220D+02 -0.52426656013799D-16 1 13 3 11 -0.14254744662862D+01 0.65313851526555D-18 2 13 3 11 -0.27804859619070D+01 -0.36346403842027D-16 3 13 3 11 -0.41520018439912D+01 0.77093358911792D-15 1 14 3 11 0.18293426717494D+01 -0.35086705600393D-16 2 14 3 11 0.21454480474469D+01 -0.24335475890232D-16 3 14 3 11 -0.11154366465566D+01 0.22927703772459D-14 1 15 3 11 -0.18293426717494D+01 -0.68998379417752D-16 2 15 3 11 -0.21454480474470D+01 -0.10378811886472D-15 3 15 3 11 -0.11154366465567D+01 -0.11193480597698D-14 1 16 3 11 0.14254744662862D+01 -0.18326012427170D-16 2 16 3 11 0.27804859619070D+01 0.10769787579255D-15 3 16 3 11 -0.41520018439912D+01 0.94908030772338D-15 1 17 3 11 -0.19107812646497D+01 -0.53385194165472D-16 2 17 3 11 0.20255749808160D+01 0.66980750952940D-16 3 17 3 11 -0.36637370184662D+01 0.19868946126478D-14 1 18 3 11 0.26868099307664D+01 -0.35694616322445D-16 2 18 3 11 -0.16574385092918D+01 -0.79519998047840D-17 3 18 3 11 -0.14182477210594D+01 -0.17566627675357D-14 1 19 3 11 -0.26868099307664D+01 0.86829554039201D-16 2 19 3 11 0.16574385092918D+01 -0.49552265361454D-16 3 19 3 11 -0.14182477210595D+01 -0.16332022000679D-14 1 20 3 11 0.19107812646497D+01 -0.10989970498616D-15 2 20 3 11 -0.20255749808160D+01 0.43791145737077D-16 3 20 3 11 -0.36637370184661D+01 0.12147159053349D-14 1 22 3 11 0.98396944736004D-08 0.00000000000000D+00 2 22 3 11 0.36239973871203D-08 0.00000000000000D+00 3 22 3 11 -0.70652545895965D+02 0.00000000000000D+00 1 1 1 12 -0.11806024688095D+01 -0.19002640044625D-16 2 1 1 12 0.55667005686751D+00 -0.69218924749749D-16 3 1 1 12 0.88738093204033D-17 0.34703608978371D-18 1 2 1 12 0.25378428539174D+00 -0.52283014009992D-16 2 2 1 12 0.10273435141376D+00 0.59324865083067D-16 3 2 1 12 0.33067227184015D-14 0.67172158160343D-16 1 3 1 12 -0.77674026578989D+00 -0.13083865885176D-15 2 3 1 12 0.35482760536328D+00 0.19131850247837D-16 3 3 1 12 -0.46491474382283D-15 -0.23164000584344D-16 1 4 1 12 -0.26914411630483D+00 -0.16722905976617D-15 2 4 1 12 0.41513718820354D-01 -0.25423889374715D-16 3 4 1 12 0.34899544321474D-15 -0.86930755485357D-16 1 5 1 12 0.12597052197366D+01 -0.27797139080262D-16 2 5 1 12 -0.48952263584240D+00 0.45352092317229D-16 3 5 1 12 0.26222185156988D+00 0.88563926901218D-17 1 6 1 12 0.12597052197366D+01 -0.21999207357968D-15 2 6 1 12 -0.48952263584240D+00 -0.11009242497663D-15 3 6 1 12 -0.26222185156988D+00 0.94266224127532D-16 1 7 1 12 -0.15725308190995D+01 0.69072423985496D-15 2 7 1 12 0.38631272565760D-01 -0.13739043607004D-16 3 7 1 12 0.22974382401124D+01 0.22575676175072D-16 1 8 1 12 -0.15725308190995D+01 -0.79123312580195D-15 2 8 1 12 0.38631272565763D-01 -0.59798465605054D-17 3 8 1 12 -0.22974382401124D+01 -0.13340376108810D-15 1 9 1 12 -0.47983244073403D+00 0.32605608932010D-15 2 9 1 12 0.18888540485288D+00 0.47008828524763D-16 3 9 1 12 -0.87463636404559D-15 -0.18031700655367D-15 1 10 1 12 -0.30966719072401D+00 -0.46809472450690D-17 2 10 1 12 0.13242363477408D+00 -0.23137850306168D-18 3 10 1 12 0.42713519515528D-16 0.24431730562261D-17 1 11 1 12 -0.54280982931803D+00 0.12565052151974D-15 2 11 1 12 -0.97802463006026D-01 -0.33898293851935D-16 3 11 1 12 0.67562269906539D-14 0.35145588661660D-16 1 12 1 12 0.89321756364254D+01 0.00000000000000D+00 2 12 1 12 -0.88165383765912D+00 0.00000000000000D+00 3 12 1 12 0.72387387858477D-14 0.00000000000000D+00 1 13 1 12 -0.76437194269627D+00 -0.28005092236835D-15 2 13 1 12 -0.83180397548953D+00 0.24731351261858D-16 3 13 1 12 0.71982304519634D+00 0.57161800547882D-16 1 14 1 12 0.14662361543784D-01 0.69746434127906D-15 2 14 1 12 -0.39800972332160D+00 0.60757212353765D-17 3 14 1 12 -0.95995998170727D+00 0.46612469914702D-16 1 15 1 12 0.14662361543791D-01 -0.16480675081472D-18 2 15 1 12 -0.39800972332159D+00 0.24161243247857D-16 3 15 1 12 0.95995998170726D+00 -0.10385019719274D-15 1 16 1 12 -0.76437194269627D+00 -0.30876686880828D-15 2 16 1 12 -0.83180397548954D+00 -0.19439492295250D-16 3 16 1 12 -0.71982304519634D+00 0.24679483559795D-16 1 17 1 12 -0.16229324914597D+01 -0.25765184937318D-15 2 17 1 12 0.92467015456396D+00 -0.72749529650571D-17 3 17 1 12 0.12638908832994D+01 -0.67482023856894D-16 1 18 1 12 -0.14317925744119D+00 0.45819623365556D-15 2 18 1 12 0.56907947121471D+00 0.27329282927755D-16 3 18 1 12 -0.12101428216917D+01 0.77203130860038D-16 1 19 1 12 -0.14317925744119D+00 -0.15136555201918D-15 2 19 1 12 0.56907947121471D+00 -0.10742322787073D-16 3 19 1 12 0.12101428216917D+01 -0.14763723795954D-15 1 20 1 12 -0.16229324914597D+01 0.88148798500575D-16 2 20 1 12 0.92467015456397D+00 -0.90438071529908D-16 3 20 1 12 -0.12638908832994D+01 0.27716099514646D-17 1 22 1 12 -0.50694735321014D+02 0.00000000000000D+00 2 22 1 12 0.10166764589081D+01 0.00000000000000D+00 3 22 1 12 -0.11917931272074D-07 0.00000000000000D+00 1 1 2 12 0.46317205304328D+00 -0.69218924749749D-16 2 1 2 12 -0.70674797946593D+00 -0.41012253742538D-16 3 1 2 12 0.24510025735415D-15 0.72208080639260D-16 1 2 2 12 0.22699110656128D-01 0.59324865083067D-16 2 2 2 12 -0.31914217638626D+00 0.36147188753843D-16 3 2 2 12 -0.27880380107192D-15 0.23967938101985D-16 1 3 2 12 0.18749496673963D+00 0.19131850247837D-16 2 3 2 12 0.95061656594929D-01 0.25712106159867D-15 3 3 2 12 0.11705141309623D-14 0.27102660226077D-15 1 4 2 12 -0.94460139173846D-01 -0.25423889374715D-16 2 4 2 12 0.27398820110282D+00 0.13408074499374D-15 3 4 2 12 0.51012119126771D-14 0.55233580828542D-17 1 5 2 12 0.37871643932608D+00 0.45352092317229D-16 2 5 2 12 0.13991458022464D+01 -0.76580497854578D-15 3 5 2 12 0.12910144566616D+00 0.23798329398505D-15 1 6 2 12 0.37871643932607D+00 -0.11009242497663D-15 2 6 2 12 0.13991458022465D+01 0.63341820160353D-15 3 6 2 12 -0.12910144566616D+00 -0.13361364490719D-15 1 7 2 12 0.88531738131785D-01 -0.13739043607004D-16 2 7 2 12 -0.15112151868030D+01 0.39099735368517D-15 3 7 2 12 0.50892527373044D+00 0.82218172909340D-16 1 8 2 12 0.88531738131789D-01 -0.59798465605054D-17 2 8 2 12 -0.15112151868031D+01 0.20813241494730D-15 3 8 2 12 -0.50892527373044D+00 0.17943907470964D-15 1 9 2 12 -0.18888540485287D+00 0.47008828524763D-16 2 9 2 12 -0.64595616152771D+00 -0.35381348378586D-16 3 9 2 12 0.15680736562752D-15 -0.49089031850199D-17 1 10 2 12 -0.13242363477408D+00 -0.23137850306168D-18 2 10 2 12 -0.36925578762328D+00 -0.13892434125075D-15 3 10 2 12 -0.29448921184481D-14 0.31113507444794D-16 1 11 2 12 -0.97803668276651D-01 -0.33898293851935D-16 2 11 2 12 -0.40029413208335D+00 -0.71520792907070D-17 3 11 2 12 0.23361614186402D-14 0.82921732900381D-16 1 12 2 12 -0.88165303322739D+00 0.00000000000000D+00 2 12 2 12 0.67435912251494D+01 0.00000000000000D+00 3 12 2 12 -0.17500120651226D-13 0.00000000000000D+00 1 13 2 12 -0.99208058970535D+00 0.24731351261858D-16 2 13 2 12 -0.10989501560636D+01 0.45383007458203D-15 3 13 2 12 0.97924848375820D+00 -0.30708218458803D-16 1 14 2 12 -0.49896941366674D+00 0.60757212353765D-17 2 14 2 12 -0.60432485105596D+00 0.45447942549197D-15 3 14 2 12 -0.16447879168192D+01 0.13598584478866D-15 1 15 2 12 -0.49896941366673D+00 0.24161243247857D-16 2 15 2 12 -0.60432485105595D+00 0.93777772264511D-16 3 15 2 12 0.16447879168192D+01 -0.37169366891652D-16 1 16 2 12 -0.99208058970536D+00 -0.19439492295250D-16 2 16 2 12 -0.10989501560636D+01 -0.39283675610759D-16 3 16 2 12 -0.97924848375820D+00 -0.45878619058827D-17 1 17 2 12 0.84607573532566D+00 -0.72749529650571D-17 2 17 2 12 -0.19340110479076D+00 0.59852798948281D-15 3 17 2 12 -0.99484570033544D+00 -0.18024723889939D-15 1 18 2 12 0.54965814863808D+00 0.27329282927755D-16 2 18 2 12 -0.42505814539471D+00 0.37314885126610D-15 3 18 2 12 0.12123996215332D+01 -0.46354543545774D-17 1 19 2 12 0.54965814863808D+00 -0.10742322787073D-16 2 19 2 12 -0.42505814539471D+00 0.57539581193427D-16 3 19 2 12 -0.12123996215332D+01 0.52558359731768D-16 1 20 2 12 0.84607573532566D+00 -0.90438071529908D-16 2 20 2 12 -0.19340110479076D+00 0.10770091817007D-15 3 20 2 12 0.99484570033543D+00 -0.25144853571601D-16 1 22 2 12 -0.14337321830719D+00 0.00000000000000D+00 2 22 2 12 -0.49372714613398D+02 0.00000000000000D+00 3 22 2 12 -0.26823613751177D-08 0.00000000000000D+00 1 1 3 12 0.88738087947158D-17 0.34703608978371D-18 2 1 3 12 0.24510025725082D-15 0.72208080639260D-16 3 1 3 12 -0.39144574651961D+01 0.94836035610104D-16 1 2 3 12 0.33067227183038D-14 0.67172158160343D-16 2 2 3 12 -0.27880379777137D-15 0.23967938101985D-16 3 2 3 12 0.26941601320165D+01 0.10058712729565D-15 1 3 3 12 -0.46491474382283D-15 -0.23164000584344D-16 2 3 3 12 0.11705141309623D-14 0.27102660226077D-15 3 3 3 12 -0.40944540762398D+01 0.79070967606930D-16 1 4 3 12 0.34899544318860D-15 -0.86930755485357D-16 2 4 3 12 0.51012119127622D-14 0.55233580828542D-17 3 4 3 12 0.27059870734659D+01 -0.34199150270015D-16 1 5 3 12 0.55913866598670D+00 0.88563926901218D-17 2 5 3 12 0.90232092760128D-01 0.23798329398505D-15 3 5 3 12 0.40721974703975D-01 -0.42757772589734D-14 1 6 3 12 -0.55913866598670D+00 0.94266224127532D-16 2 6 3 12 -0.90232092760132D-01 -0.13361364490719D-15 3 6 3 12 0.40721974704003D-01 -0.26953536408205D-14 1 7 3 12 -0.51032670899747D+00 0.22575676175072D-16 2 7 3 12 -0.17494065514015D+00 0.82218172909340D-16 3 7 3 12 -0.71471835466622D+00 -0.19496962490765D-14 1 8 3 12 0.51032670899747D+00 -0.13340376108810D-15 2 8 3 12 0.17494065514014D+00 0.17943907470964D-15 3 8 3 12 -0.71471835466622D+00 0.34849366233042D-14 1 9 3 12 -0.87463635111544D-15 -0.18031700655367D-15 2 9 3 12 0.15680736546244D-15 -0.49089031850199D-17 3 9 3 12 0.37088588450965D+01 -0.46525100126681D-16 1 10 3 12 0.42713517778953D-16 0.24431730562261D-17 2 10 3 12 -0.29448921173663D-14 0.31113507444794D-16 3 10 3 12 -0.46472005771747D+01 0.11009833728368D-16 1 11 3 12 0.67562269849626D-14 0.35145588661660D-16 2 11 3 12 0.23361614217842D-14 0.82921732900381D-16 3 11 3 12 -0.16605257951220D+02 0.52426656013799D-16 1 12 3 12 0.72387387858477D-14 0.00000000000000D+00 2 12 3 12 -0.17500120644609D-13 0.00000000000000D+00 3 12 3 12 0.42417012588671D+02 0.00000000000000D+00 1 13 3 12 0.18293426717494D+01 0.57161800547882D-16 2 13 3 12 0.21454480474470D+01 -0.30708218458803D-16 3 13 3 12 -0.11154366465567D+01 -0.99460616435630D-15 1 14 3 12 -0.14254744662861D+01 0.46612469914702D-16 2 14 3 12 -0.27804859619070D+01 0.13598584478866D-15 3 14 3 12 -0.41520018439911D+01 -0.94899530125081D-15 1 15 3 12 0.14254744662861D+01 -0.10385019719274D-15 2 15 3 12 0.27804859619070D+01 -0.37169366891652D-16 3 15 3 12 -0.41520018439911D+01 -0.15499069738181D-14 1 16 3 12 -0.18293426717494D+01 0.24679483559795D-16 2 16 3 12 -0.21454480474470D+01 -0.45878619058827D-17 3 16 3 12 -0.11154366465567D+01 0.10503613079330D-15 1 17 3 12 0.26868099307664D+01 -0.67482023856894D-16 2 17 3 12 -0.16574385092918D+01 -0.18024723889939D-15 3 17 3 12 -0.14182477210594D+01 0.64476076403441D-15 1 18 3 12 -0.19107812646497D+01 0.77203130860038D-16 2 18 3 12 0.20255749808160D+01 -0.46354543545774D-17 3 18 3 12 -0.36637370184662D+01 0.13839719374386D-14 1 19 3 12 0.19107812646497D+01 -0.14763723795954D-15 2 19 3 12 -0.20255749808160D+01 0.52558359731768D-16 3 19 3 12 -0.36637370184662D+01 -0.45483895087509D-15 1 20 3 12 -0.26868099307664D+01 0.27716099514646D-17 2 20 3 12 0.16574385092918D+01 -0.25144853571601D-16 3 20 3 12 -0.14182477210594D+01 -0.14069075249509D-14 1 22 3 12 -0.98545066291715D-08 0.00000000000000D+00 2 22 3 12 -0.36385638013843D-08 0.00000000000000D+00 3 22 3 12 -0.70652545895965D+02 0.00000000000000D+00 1 1 1 13 -0.14436323196730D+00 0.29861018016239D-15 2 1 1 13 -0.28804976638800D+00 -0.67861230639091D-16 3 1 1 13 0.28620407326731D+00 -0.23394384524115D-16 1 2 1 13 0.28264640601229D-01 0.60016102963866D-15 2 2 1 13 -0.38810233286836D-01 -0.93817065467195D-16 3 2 1 13 -0.35192012181660D+00 0.10601352680866D-15 1 3 1 13 -0.61006835472895D+00 0.24963705232483D-15 2 3 1 13 0.45466061858322D+00 0.12137090493023D-16 3 3 1 13 0.78331374891610D+00 0.45929669213550D-16 1 4 1 13 -0.12068954502774D+00 -0.10547589743398D-15 2 4 1 13 -0.36233757220370D+00 0.15763060474797D-15 3 4 1 13 0.65718925843951D+00 0.13575254845204D-17 1 5 1 13 -0.47205798319038D+00 -0.34172112609615D-15 2 5 1 13 -0.75348403514224D+00 0.43723574251308D-16 3 5 1 13 -0.61569286033497D+00 0.12105974288004D-15 1 6 1 13 -0.37877129705305D-01 0.27605271465377D-15 2 6 1 13 0.80228829136542D-01 0.21758286222931D-17 3 6 1 13 0.56222819860821D+00 -0.72449153967548D-16 1 7 1 13 0.14572086039215D+00 0.41410424063641D-15 2 7 1 13 0.10265494691603D+01 -0.24274994697052D-17 3 7 1 13 0.55647288619464D+00 0.91718406304011D-16 1 8 1 13 -0.61749241585748D-01 -0.11655069286161D-15 2 8 1 13 0.12514254043905D-01 -0.17300958049914D-16 3 8 1 13 -0.49107434131212D+00 0.26243127215854D-15 1 9 1 13 -0.16229326487588D+01 0.13352933963559D-15 2 9 1 13 -0.84607588494763D+00 0.24016746196710D-16 3 9 1 13 -0.26868171993405D+01 -0.57900063890766D-17 1 10 1 13 -0.14317947827315D+00 0.11859674763976D-15 2 10 1 13 -0.54965799850788D+00 0.22381715659138D-16 3 10 1 13 0.19107834776752D+01 -0.63643634965606D-16 1 11 1 13 0.14662361543804D-01 -0.34562495883931D-15 2 11 1 13 -0.49896941366675D+00 -0.34586468557984D-16 3 11 1 13 -0.14254744662862D+01 -0.65313851526555D-18 1 12 1 13 -0.76437194269627D+00 0.28005092236835D-15 2 12 1 13 -0.99208058970535D+00 -0.24731351261858D-16 3 12 1 13 0.18293426717494D+01 -0.57161800547882D-16 1 13 1 13 0.12535023461133D+02 0.00000000000000D+00 2 13 1 13 0.58392681818053D+01 0.00000000000000D+00 3 13 1 13 -0.12570584673454D+01 0.00000000000000D+00 1 14 1 13 -0.38809165729707D+01 0.15413234273049D-15 2 14 1 13 -0.28593969073651D+01 -0.12251722139796D-16 3 14 1 13 0.16701677051493D+00 0.80671288128210D-17 1 15 1 13 -0.51645554603745D+00 0.11735417874634D-16 2 15 1 13 -0.32470660052582D+00 -0.36079969146012D-16 3 15 1 13 0.33355766451469D-01 0.14885125549015D-16 1 16 1 13 0.39749073702135D+00 0.17862770669410D-15 2 16 1 13 0.16109511908445D+00 -0.69625704796414D-18 3 16 1 13 0.62166479281127D-01 0.42140566266514D-16 1 17 1 13 0.95623294368768D+00 0.15382223784835D-15 2 17 1 13 -0.10710026254495D+01 -0.22985801261784D-16 3 17 1 13 0.35443867941966D-01 0.71220048440833D-17 1 18 1 13 -0.57363572065418D+01 -0.31949286782644D-17 2 18 1 13 0.95469644395251D+00 0.47996136897421D-17 3 18 1 13 -0.57946867444900D-02 -0.48972342025698D-16 1 19 1 13 -0.23324566422979D+00 0.15738512069920D-16 2 19 1 13 0.18233885955754D+00 -0.22346758107772D-17 3 19 1 13 -0.58580035591798D-01 0.25717600636276D-17 1 20 1 13 0.32395655219218D+00 0.10653384055532D-15 2 20 1 13 -0.13518632858762D+00 0.47415433331157D-16 3 20 1 13 -0.16337033535740D-01 -0.28316891254939D-16 1 22 1 13 -0.59666225483022D+02 0.00000000000000D+00 2 22 1 13 -0.10058609980570D+02 0.00000000000000D+00 3 22 1 13 -0.11301434177004D-02 0.00000000000000D+00 1 1 2 13 -0.14974007339002D+00 -0.67861230639091D-16 2 1 2 13 -0.45654092233183D+00 0.13082470335337D-15 3 1 2 13 -0.35777067486429D+00 -0.18965561318988D-16 1 2 2 13 -0.19808731105278D+00 -0.93817065467195D-16 2 2 2 13 0.30018923206277D+00 -0.30835158153276D-15 3 2 2 13 0.35485508012218D+00 0.57998928721722D-16 1 3 2 13 0.34687872744995D+00 0.12137090493023D-16 2 3 2 13 -0.84809723947390D+00 0.33702259836239D-15 3 3 2 13 -0.83980060330531D+00 0.54372177320074D-16 1 4 2 13 -0.44226102341461D+00 0.15763060474797D-15 2 4 2 13 -0.31551995169707D+00 0.65837744463220D-15 3 4 2 13 -0.50703823584813D+00 -0.14337894034546D-15 1 5 2 13 0.80828268218609D+00 0.43723574251308D-16 2 5 2 13 -0.33012601691908D-01 0.10829575390688D-14 3 5 2 13 -0.14560451909207D+00 -0.20747296785272D-15 1 6 2 13 0.13310522665981D-01 0.21758286222931D-17 2 6 2 13 0.15082554883135D-01 0.36426903951609D-15 3 6 2 13 0.20478799764696D+00 0.22883874493035D-15 1 7 2 13 -0.57907236680428D+00 -0.24274994697052D-17 2 7 2 13 -0.14418862649161D+00 -0.83848347189426D-15 3 7 2 13 0.43393246734531D-01 -0.44231040064958D-15 1 8 2 13 0.20803773942922D-01 -0.17300958049914D-16 2 8 2 13 0.94978646232514D-01 -0.14573865007108D-14 3 8 2 13 -0.58124986485174D-01 -0.40832477724953D-15 1 9 2 13 -0.92466905239825D+00 0.24016746196710D-16 2 9 2 13 -0.19339794421721D+00 -0.30056193207541D-15 3 9 2 13 -0.16574450187903D+01 -0.65892584310335D-17 1 10 2 13 -0.56907900921137D+00 0.22381715659138D-16 2 10 2 13 -0.42505835380042D+00 0.54109281960968D-15 3 10 2 13 0.20255772774882D+01 -0.34822859780792D-16 1 11 2 13 -0.39800972332160D+00 -0.34586468557984D-16 2 11 2 13 -0.60432485105591D+00 0.48335974247628D-15 3 11 2 13 -0.27804859619070D+01 0.36346403842027D-16 1 12 2 13 -0.83180397548953D+00 -0.24731351261858D-16 2 12 2 13 -0.10989501560636D+01 -0.45383007458203D-15 3 12 2 13 0.21454480474470D+01 0.30708218458803D-16 1 13 2 13 0.58392724026000D+01 0.00000000000000D+00 2 13 2 13 0.13758076541722D+02 0.00000000000000D+00 3 13 2 13 0.20415598055507D+01 0.00000000000000D+00 1 14 2 13 -0.28593976346434D+01 -0.12251722139796D-16 2 14 2 13 -0.42081897111825D+01 0.34056090223499D-17 3 14 2 13 -0.74906335409628D-01 -0.35563287269791D-16 1 15 2 13 -0.32470660052582D+00 -0.36079969146012D-16 2 15 2 13 -0.61864659889725D+00 -0.11554562480833D-16 3 15 2 13 -0.65672130808356D-01 0.40043248775714D-16 1 16 2 13 0.16109511908445D+00 -0.69625704796414D-18 2 16 2 13 0.44914722360173D+00 0.42450942505814D-16 3 16 2 13 -0.13491471216581D+00 0.25077882469455D-16 1 17 2 13 0.10710026254495D+01 -0.22985801261784D-16 2 17 2 13 -0.64647188952479D+01 0.53594737461675D-18 3 17 2 13 0.14172485951549D+00 -0.34540383757104D-17 1 18 2 13 -0.95469644395250D+00 0.47996136897421D-17 2 18 2 13 0.88565533669038D+00 0.25376227437474D-15 3 18 2 13 -0.30541858565606D+00 -0.99639505199961D-17 1 19 2 13 -0.18233978195846D+00 -0.22346758107772D-17 2 19 2 13 0.29693616356469D+00 0.78105557192795D-16 3 19 2 13 0.11749352448800D-01 0.92410037920463D-16 1 20 2 13 0.13518674534702D+00 0.47415433331157D-16 2 20 2 13 -0.38035239243249D+00 0.19404678200673D-15 3 20 2 13 -0.24048306292478D-01 -0.11427050079996D-16 1 22 2 13 -0.10173324396297D+02 0.00000000000000D+00 2 22 2 13 -0.60532578336764D+02 0.00000000000000D+00 3 22 2 13 -0.45008015991941D+00 0.00000000000000D+00 1 1 3 13 0.49053289124482D+00 -0.23394384524115D-16 2 1 3 13 -0.40598958753678D+00 -0.18965561318988D-16 3 1 3 13 -0.32666255455159D+00 -0.95829343298283D-15 1 2 3 13 -0.30078101445079D+00 0.10601352680866D-15 2 2 3 13 0.30570828755135D+00 0.57998928721722D-16 3 2 3 13 0.77323372312273D+00 0.12515816116668D-14 1 3 3 13 0.65187452572476D+00 0.45929669213550D-16 2 3 3 13 -0.87453604592926D+00 0.54372177320074D-16 3 3 3 13 -0.25037435958717D+01 0.45938039071743D-15 1 4 3 13 0.68182003040262D+00 0.13575254845204D-17 2 4 3 13 -0.52515542902002D+00 -0.14337894034546D-15 3 4 3 13 0.10425035738155D+01 0.94265247396232D-15 1 5 3 13 0.12067545544197D+01 0.12105974288004D-15 2 5 3 13 0.68649872495409D+00 -0.20747296785272D-15 3 5 3 13 -0.42530775815609D+01 -0.54261715492857D-15 1 6 3 13 -0.83818842403307D-02 -0.72449153967548D-16 2 6 3 13 0.31484626762451D+00 0.22883874493035D-15 3 6 3 13 0.37080430568572D+01 -0.11133140746810D-14 1 7 3 13 -0.12614849187089D+01 0.91718406304011D-16 2 7 3 13 -0.85602264129849D+00 -0.44231040064958D-15 3 7 3 13 -0.42317235399665D+01 0.14214531025879D-14 1 8 3 13 0.10357198728728D+00 0.26243127215854D-15 2 8 3 13 -0.17716441144127D+00 -0.40832477724953D-15 3 8 3 13 0.37892032617639D+01 0.45926449324351D-15 1 9 3 13 -0.12638910221798D+01 -0.57900063890766D-17 2 9 3 13 -0.99484767618447D+00 -0.65892584310335D-17 3 9 3 13 -0.14182402230213D+01 0.95511775535031D-15 1 10 3 13 0.12101427438262D+01 -0.63643634965606D-16 2 10 3 13 0.12123977694114D+01 -0.34822859780792D-16 3 10 3 13 -0.36637372330463D+01 0.66141168204448D-15 1 11 3 13 -0.95995998170731D+00 -0.65313851526555D-18 2 11 3 13 -0.16447879168192D+01 0.36346403842027D-16 3 11 3 13 -0.41520018439912D+01 -0.77093358911792D-15 1 12 3 13 0.71982304519634D+00 -0.57161800547882D-16 2 12 3 13 0.97924848375820D+00 0.30708218458803D-16 3 12 3 13 -0.11154366465567D+01 0.99460616435630D-15 1 13 3 13 -0.12570340613318D+01 0.00000000000000D+00 2 13 3 13 0.20415876309584D+01 0.00000000000000D+00 3 13 3 13 0.15296984004430D+02 0.00000000000000D+00 1 14 3 13 0.16701820768249D+00 0.80671288128210D-17 2 14 3 13 -0.74905075827231D-01 -0.35563287269791D-16 3 14 3 13 -0.41887629667903D+00 0.10095546409821D-15 1 15 3 13 -0.33355766451466D-01 0.14885125549015D-16 2 15 3 13 0.65672130808355D-01 0.40043248775714D-16 3 15 3 13 -0.15417956544810D+01 -0.18809912773710D-15 1 16 3 13 -0.62166479281129D-01 0.42140566266514D-16 2 16 3 13 0.13491471216581D+00 0.25077882469455D-16 3 16 3 13 -0.19584409533204D+01 -0.55328945899113D-15 1 17 3 13 -0.35443867941968D-01 0.71220048440833D-17 2 17 3 13 0.14172485951549D+00 -0.34540383757104D-17 3 17 3 13 0.18487674087043D+01 0.17262678163367D-17 1 18 3 13 0.57946867444948D-02 -0.48972342025698D-16 2 18 3 13 -0.30541858565605D+00 -0.99639505199961D-17 3 18 3 13 0.10975158984982D+01 -0.14914383832257D-14 1 19 3 13 -0.58579992336693D-01 0.25717600636276D-17 2 19 3 13 -0.11748407245337D-01 0.92410037920463D-16 3 19 3 13 -0.69776832341433D+00 0.27805862367119D-16 1 20 3 13 -0.16334488264197D-01 -0.28316891254939D-16 2 20 3 13 0.24046912497817D-01 -0.11427050079996D-16 3 20 3 13 -0.88010030951782D+00 0.17705442938939D-15 1 22 3 13 0.19332062709988D-01 0.00000000000000D+00 2 22 3 13 -0.64318482098328D+00 0.00000000000000D+00 3 22 3 13 -0.49879381635699D+02 0.00000000000000D+00 1 1 1 14 0.28264640601233D-01 0.91052705652805D-15 2 1 1 14 -0.38810233286827D-01 -0.71768639374546D-16 3 1 1 14 -0.35192012181659D+00 -0.12452365524684D-15 1 2 1 14 -0.14436323196740D+00 -0.31188295150378D-17 2 2 1 14 -0.28804976638798D+00 -0.42973289964874D-16 3 2 1 14 0.28620407326721D+00 -0.15035719293683D-15 1 3 1 14 -0.12068954502770D+00 -0.69882144550665D-15 2 3 1 14 -0.36233757220373D+00 -0.20019448137245D-16 3 3 1 14 0.65718925843963D+00 -0.57117189227182D-16 1 4 1 14 -0.61006835472890D+00 0.38886541703644D-15 2 4 1 14 0.45466061858325D+00 0.12091351241704D-15 3 4 1 14 0.78331374891616D+00 -0.17177508049973D-15 1 5 1 14 -0.47205798319013D+00 0.55605901675018D-15 2 5 1 14 -0.75348403514218D+00 -0.50938376677407D-16 3 5 1 14 -0.61569286033532D+00 -0.25847212148978D-15 1 6 1 14 -0.37877129705306D-01 -0.24631109194898D-15 2 6 1 14 0.80228829136542D-01 0.11846092054587D-16 3 6 1 14 0.56222819860820D+00 0.40908679170914D-16 1 7 1 14 0.14572086039204D+00 0.23366575253436D-15 2 7 1 14 0.10265494691599D+01 0.13024815926906D-17 3 7 1 14 0.55647288619460D+00 0.85276383441934D-16 1 8 1 14 -0.61749241585755D-01 0.12235593823214D-16 2 8 1 14 0.12514254043899D-01 -0.15809326418405D-16 3 8 1 14 -0.49107434131211D+00 -0.19540201021788D-15 1 9 1 14 -0.14317947827312D+00 -0.27669861433540D-15 2 9 1 14 -0.54965799850786D+00 0.46191645595028D-16 3 9 1 14 0.19107834776752D+01 -0.59991077733021D-16 1 10 1 14 -0.16229326487588D+01 -0.28579787141909D-18 2 10 1 14 -0.84607588494768D+00 -0.26238721665069D-16 3 10 1 14 -0.26868171993405D+01 -0.55090998514186D-16 1 11 1 14 -0.76437194269624D+00 -0.27679561902243D-16 2 11 1 14 -0.99208058970535D+00 -0.10638038937330D-16 3 11 1 14 0.18293426717494D+01 0.35086705600393D-16 1 12 1 14 0.14662361543784D-01 -0.69746434127906D-15 2 12 1 14 -0.49896941366674D+00 -0.60757212353765D-17 3 12 1 14 -0.14254744662861D+01 -0.46612469914702D-16 1 13 1 14 -0.38809165729707D+01 -0.15413234273049D-15 2 13 1 14 -0.28593969073651D+01 0.12251722139796D-16 3 13 1 14 0.16701677051493D+00 -0.80671288128210D-17 1 14 1 14 0.12535023461133D+02 0.00000000000000D+00 2 14 1 14 0.58392681818057D+01 0.00000000000000D+00 3 14 1 14 -0.12570584673451D+01 0.00000000000000D+00 1 15 1 14 0.39749073702135D+00 0.12459146736278D-15 2 15 1 14 0.16109511908445D+00 -0.14863036725918D-17 3 15 1 14 0.62166479281127D-01 0.31791639221042D-16 1 16 1 14 -0.51645554603745D+00 -0.29435161147724D-15 2 16 1 14 -0.32470660052582D+00 -0.15602335702095D-16 3 16 1 14 0.33355766451469D-01 0.44256711309179D-16 1 17 1 14 -0.57363572065418D+01 -0.36633331796015D-15 2 17 1 14 0.95469644395250D+00 -0.59501919736812D-17 3 17 1 14 -0.57946867445042D-02 -0.64063145527620D-16 1 18 1 14 0.95623294368763D+00 -0.49026636430877D-16 2 18 1 14 -0.10710026254495D+01 -0.13007477942092D-16 3 18 1 14 0.35443867941966D-01 -0.26254943514666D-16 1 19 1 14 0.32395655219218D+00 -0.15522778741972D-15 2 19 1 14 -0.13518632858762D+00 -0.48384263711052D-16 3 19 1 14 -0.16337033535742D-01 -0.43014788585804D-16 1 20 1 14 -0.23324566422979D+00 0.71541216741645D-17 2 20 1 14 0.18233885955754D+00 0.12428380002657D-16 3 20 1 14 -0.58580035591795D-01 -0.20065906224653D-17 1 22 1 14 -0.59666225479317D+02 0.00000000000000D+00 2 22 1 14 -0.10058609976028D+02 0.00000000000000D+00 3 22 1 14 -0.11301410235495D-02 0.00000000000000D+00 1 1 2 14 -0.19808731105277D+00 -0.71768639374546D-16 2 1 2 14 0.30018923206282D+00 0.44846436349985D-15 3 1 2 14 0.35485508012215D+00 -0.18747603182295D-16 1 2 2 14 -0.14974007338999D+00 -0.42973289964874D-16 2 2 2 14 -0.45654092233173D+00 0.72953007428119D-15 3 2 2 14 -0.35777067486433D+00 -0.30497195037788D-16 1 3 2 14 -0.44226102341464D+00 -0.20019448137245D-16 2 3 2 14 -0.31551995169709D+00 -0.48356217833335D-15 3 3 2 14 -0.50703823584815D+00 0.11206516465743D-15 1 4 2 14 0.34687872744998D+00 0.12091351241704D-15 2 4 2 14 -0.84809723947398D+00 -0.59175834564771D-17 3 4 2 14 -0.83980060330540D+00 -0.11106029801565D-15 1 5 2 14 0.80828268218615D+00 -0.50938376677407D-16 2 5 2 14 -0.33012601692079D-01 -0.31335327493156D-15 3 5 2 14 -0.14560451909229D+00 0.66639036394084D-15 1 6 2 14 0.13310522665981D-01 0.11846092054587D-16 2 6 2 14 0.15082554883137D-01 -0.36590791500490D-15 3 6 2 14 0.20478799764696D+00 -0.10281769560199D-15 1 7 2 14 -0.57907236680472D+00 0.13024815926906D-17 2 7 2 14 -0.14418862649194D+00 0.39544215873847D-15 3 7 2 14 0.43393246734510D-01 -0.30702137696635D-15 1 8 2 14 0.20803773942916D-01 -0.15809326418405D-16 2 8 2 14 0.94978646232524D-01 0.98586429822789D-15 3 8 2 14 -0.58124986485152D-01 0.16637372928033D-15 1 9 2 14 -0.56907900921136D+00 0.46191645595028D-16 2 9 2 14 -0.42505835380044D+00 0.57732361523111D-17 3 9 2 14 0.20255772774882D+01 -0.55125797749755D-17 1 10 2 14 -0.92466905239830D+00 -0.26238721665069D-16 2 10 2 14 -0.19339794421723D+00 0.15417793340086D-15 3 10 2 14 -0.16574450187903D+01 -0.54009579256822D-17 1 11 2 14 -0.83180397548952D+00 -0.10638038937330D-16 2 11 2 14 -0.10989501560637D+01 -0.19308235335107D-15 3 11 2 14 0.21454480474469D+01 0.24335475890232D-16 1 12 2 14 -0.39800972332160D+00 -0.60757212353765D-17 2 12 2 14 -0.60432485105596D+00 -0.45447942549197D-15 3 12 2 14 -0.27804859619070D+01 -0.13598584478866D-15 1 13 2 14 -0.28593976346434D+01 0.12251722139796D-16 2 13 2 14 -0.42081897111825D+01 -0.34056090223499D-17 3 13 2 14 -0.74906335409628D-01 0.35563287269791D-16 1 14 2 14 0.58392724026004D+01 0.00000000000000D+00 2 14 2 14 0.13758076541723D+02 0.00000000000000D+00 3 14 2 14 0.20415598055511D+01 0.00000000000000D+00 1 15 2 14 0.16109511908445D+00 -0.14863036725918D-17 2 15 2 14 0.44914722360172D+00 0.96594081961594D-16 3 15 2 14 -0.13491471216581D+00 -0.42492190183211D-16 1 16 2 14 -0.32470660052582D+00 -0.15602335702095D-16 2 16 2 14 -0.61864659889725D+00 -0.11405536163640D-15 3 16 2 14 -0.65672130808354D-01 0.48747538203699D-17 1 17 2 14 -0.95469644395251D+00 -0.59501919736812D-17 2 17 2 14 0.88565533669040D+00 -0.33093204096038D-15 3 17 2 14 -0.30541858565604D+00 -0.77459621164225D-16 1 18 2 14 0.10710026254495D+01 -0.13007477942092D-16 2 18 2 14 -0.64647188952477D+01 0.61846435392819D-17 3 18 2 14 0.14172485951549D+00 0.24930288772476D-17 1 19 2 14 0.13518674534702D+00 -0.48384263711052D-16 2 19 2 14 -0.38035239243248D+00 0.21299519097452D-15 3 19 2 14 -0.24048306292477D-01 -0.26013946545291D-16 1 20 2 14 -0.18233978195846D+00 0.12428380002657D-16 2 20 2 14 0.29693616356469D+00 -0.56687844358756D-16 3 20 2 14 0.11749352448800D-01 -0.10664869943237D-16 1 22 2 14 -0.10173324395822D+02 0.00000000000000D+00 2 22 2 14 -0.60532578342678D+02 0.00000000000000D+00 3 22 2 14 -0.45008016226118D+00 0.00000000000000D+00 1 1 3 14 -0.30078101445077D+00 -0.12452365524684D-15 2 1 3 14 0.30570828755132D+00 -0.18747603182295D-16 3 1 3 14 0.77323372312265D+00 0.24327992842462D-14 1 2 3 14 0.49053289124472D+00 -0.15035719293683D-15 2 2 3 14 -0.40598958753682D+00 -0.30497195037788D-16 3 2 3 14 -0.32666255455159D+00 -0.25645623914058D-14 1 3 3 14 0.68182003040273D+00 -0.57117189227182D-16 2 3 3 14 -0.52515542902004D+00 0.11206516465743D-15 3 3 3 14 0.10425035738156D+01 -0.20303572127197D-14 1 4 3 14 0.65187452572482D+00 -0.17177508049973D-15 2 4 3 14 -0.87453604592934D+00 -0.11106029801565D-15 3 4 3 14 -0.25037435958717D+01 0.56684358694504D-16 1 5 3 14 0.12067545544193D+01 -0.25847212148978D-15 2 5 3 14 0.68649872495389D+00 0.66639036394084D-15 3 5 3 14 -0.42530775815610D+01 0.41046655576347D-15 1 6 3 14 -0.83818842403378D-02 0.40908679170914D-16 2 6 3 14 0.31484626762451D+00 -0.10281769560199D-15 3 6 3 14 0.37080430568573D+01 0.28679367829196D-14 1 7 3 14 -0.12614849187089D+01 0.85276383441934D-16 2 7 3 14 -0.85602264129850D+00 -0.30702137696635D-15 3 7 3 14 -0.42317235399659D+01 -0.14677749939344D-14 1 8 3 14 0.10357198728729D+00 -0.19540201021788D-15 2 8 3 14 -0.17716441144124D+00 0.16637372928033D-15 3 8 3 14 0.37892032617637D+01 -0.14207451667541D-14 1 9 3 14 0.12101427438261D+01 -0.59991077733021D-16 2 9 3 14 0.12123977694114D+01 -0.55125797749755D-17 3 9 3 14 -0.36637372330463D+01 -0.68120040244950D-15 1 10 3 14 -0.12638910221798D+01 -0.55090998514186D-16 2 10 3 14 -0.99484767618451D+00 -0.54009579256822D-17 3 10 3 14 -0.14182402230213D+01 -0.14429905293441D-14 1 11 3 14 0.71982304519631D+00 0.35086705600393D-16 2 11 3 14 0.97924848375818D+00 0.24335475890232D-16 3 11 3 14 -0.11154366465566D+01 -0.22927703772459D-14 1 12 3 14 -0.95995998170727D+00 -0.46612469914702D-16 2 12 3 14 -0.16447879168192D+01 -0.13598584478866D-15 3 12 3 14 -0.41520018439911D+01 0.94899530125081D-15 1 13 3 14 0.16701820768249D+00 -0.80671288128210D-17 2 13 3 14 -0.74905075827231D-01 0.35563287269791D-16 3 13 3 14 -0.41887629667903D+00 -0.10095546409821D-15 1 14 3 14 -0.12570340613314D+01 0.00000000000000D+00 2 14 3 14 0.20415876309588D+01 0.00000000000000D+00 3 14 3 14 0.15296984004429D+02 0.00000000000000D+00 1 15 3 14 -0.62166479281129D-01 0.31791639221042D-16 2 15 3 14 0.13491471216581D+00 -0.42492190183211D-16 3 15 3 14 -0.19584409533204D+01 0.71233860868626D-15 1 16 3 14 -0.33355766451466D-01 0.44256711309179D-16 2 16 3 14 0.65672130808357D-01 0.48747538203699D-17 3 16 3 14 -0.15417956544810D+01 0.21817466365640D-16 1 17 3 14 0.57946867444806D-02 -0.64063145527620D-16 2 17 3 14 -0.30541858565604D+00 -0.77459621164225D-16 3 17 3 14 0.10975158984982D+01 0.13588914469357D-14 1 18 3 14 -0.35443867941968D-01 -0.26254943514666D-16 2 18 3 14 0.14172485951549D+00 0.24930288772476D-17 3 18 3 14 0.18487674087042D+01 0.25085691768208D-16 1 19 3 14 -0.16334488264199D-01 -0.43014788585804D-16 2 19 3 14 0.24046912497819D-01 -0.26013946545291D-16 3 19 3 14 -0.88010030951780D+00 -0.25418616135032D-15 1 20 3 14 -0.58579992336690D-01 -0.20065906224653D-17 2 20 3 14 -0.11748407245337D-01 -0.10664869943237D-16 3 20 3 14 -0.69776832341435D+00 0.10996806099496D-17 1 22 3 14 0.19332058641022D-01 0.00000000000000D+00 2 22 3 14 -0.64318482641994D+00 0.00000000000000D+00 3 22 3 14 -0.49879381669004D+02 0.00000000000000D+00 1 1 1 15 0.28264640601224D-01 0.27459600205042D-15 2 1 1 15 -0.38810233286827D-01 -0.10002819600716D-15 3 1 1 15 0.35192012181659D+00 0.24904211190902D-16 1 2 1 15 -0.14436323196735D+00 -0.67732518763108D-15 2 2 1 15 -0.28804976638802D+00 -0.98636640995889D-16 3 2 1 15 -0.28620407326729D+00 0.17415527749819D-16 1 3 1 15 -0.12068954502770D+00 -0.28168679533126D-15 2 3 1 15 -0.36233757220372D+00 -0.43745839767755D-16 3 3 1 15 -0.65718925843963D+00 -0.26860252750672D-16 1 4 1 15 -0.61006835472890D+00 -0.15185745422468D-15 2 4 1 15 0.45466061858315D+00 0.22608802282444D-16 3 4 1 15 -0.78331374891602D+00 0.11497378207745D-15 1 5 1 15 -0.37877129705309D-01 -0.43994838456847D-15 2 5 1 15 0.80228829136540D-01 -0.42069481764430D-16 3 5 1 15 -0.56222819860821D+00 -0.81230446742012D-16 1 6 1 15 -0.47205798319011D+00 0.37784658389267D-15 2 6 1 15 -0.75348403514215D+00 0.22286037600643D-16 3 6 1 15 0.61569286033532D+00 -0.20383649362297D-15 1 7 1 15 -0.61749241585748D-01 -0.12983485822364D-15 2 7 1 15 0.12514254043900D-01 0.83255369944119D-16 3 7 1 15 0.49107434131211D+00 -0.26756594591716D-15 1 8 1 15 0.14572086039204D+00 -0.68009360038994D-16 2 8 1 15 0.10265494691598D+01 0.19658044115020D-16 3 8 1 15 -0.55647288619460D+00 0.18061251572041D-15 1 9 1 15 -0.14317947827312D+00 0.46952256259113D-15 2 9 1 15 -0.54965799850786D+00 0.40569499855467D-16 3 9 1 15 -0.19107834776752D+01 0.97603064886574D-16 1 10 1 15 -0.16229326487587D+01 0.23429308062606D-15 2 10 1 15 -0.84607588494765D+00 -0.41471580557652D-16 3 10 1 15 0.26868171993405D+01 -0.43025566532898D-17 1 11 1 15 -0.76437194269623D+00 0.56344078803869D-16 2 11 1 15 -0.99208058970533D+00 0.57921925445058D-16 3 11 1 15 -0.18293426717494D+01 0.68998379417752D-16 1 12 1 15 0.14662361543791D-01 0.16480675081472D-18 2 12 1 15 -0.49896941366673D+00 -0.24161243247857D-16 3 12 1 15 0.14254744662861D+01 0.10385019719274D-15 1 13 1 15 -0.51645554603745D+00 -0.11735417874634D-16 2 13 1 15 -0.32470660052582D+00 0.36079969146012D-16 3 13 1 15 -0.33355766451466D-01 -0.14885125549015D-16 1 14 1 15 0.39749073702135D+00 -0.12459146736278D-15 2 14 1 15 0.16109511908445D+00 0.14863036725918D-17 3 14 1 15 -0.62166479281129D-01 -0.31791639221042D-16 1 15 1 15 0.12535023461132D+02 0.00000000000000D+00 2 15 1 15 0.58392681818058D+01 0.00000000000000D+00 3 15 1 15 0.12570584673450D+01 0.00000000000000D+00 1 16 1 15 -0.38809165729708D+01 0.49749384880341D-16 2 16 1 15 -0.28593969073651D+01 0.26894619554961D-16 3 16 1 15 -0.16701677051494D+00 0.25761607492749D-16 1 17 1 15 -0.23324566422979D+00 -0.10485151941248D-16 2 17 1 15 0.18233885955754D+00 -0.10403802946448D-16 3 17 1 15 0.58580035591798D-01 0.85435024987617D-18 1 18 1 15 0.32395655219218D+00 0.18456261996323D-15 2 18 1 15 -0.13518632858762D+00 0.34134657833107D-16 3 18 1 15 0.16337033535742D-01 -0.60195052918774D-16 1 19 1 15 0.95623294368764D+00 -0.18227606075629D-15 2 19 1 15 -0.10710026254495D+01 0.18686783949588D-16 3 19 1 15 -0.35443867941966D-01 0.12728027701046D-16 1 20 1 15 -0.57363572065418D+01 -0.15078763200835D-15 2 20 1 15 0.95469644395250D+00 0.21394449077780D-16 3 20 1 15 0.57946867445022D-02 0.50488390160654D-16 1 22 1 15 -0.59666225483013D+02 0.00000000000000D+00 2 22 1 15 -0.10058609980573D+02 0.00000000000000D+00 3 22 1 15 0.11301434239752D-02 0.00000000000000D+00 1 1 2 15 -0.19808731105277D+00 -0.10002819600716D-15 2 1 2 15 0.30018923206281D+00 -0.61976825113806D-15 3 1 2 15 -0.35485508012216D+00 -0.11595318775828D-15 1 2 2 15 -0.14974007339004D+00 -0.98636640995889D-16 2 2 2 15 -0.45654092233170D+00 0.32963550993570D-15 3 2 2 15 0.35777067486435D+00 -0.29334178975866D-16 1 3 2 15 -0.44226102341464D+00 -0.43745839767755D-16 2 3 2 15 -0.31551995169710D+00 0.71924376955525D-15 3 3 2 15 0.50703823584815D+00 0.12538001139428D-15 1 4 2 15 0.34687872744988D+00 0.22608802282444D-16 2 4 2 15 -0.84809723947393D+00 -0.54530872388555D-15 3 4 2 15 0.83980060330532D+00 0.18995671379650D-15 1 5 2 15 0.13310522665979D-01 -0.42069481764430D-16 2 5 2 15 0.15082554883129D-01 -0.33851249531504D-15 3 5 2 15 -0.20478799764695D+00 -0.24570481253401D-15 1 6 2 15 0.80828268218622D+00 0.22286037600643D-16 2 6 2 15 -0.33012601692075D-01 -0.69545898586668D-15 3 6 2 15 0.14560451909229D+00 0.16971420434979D-16 1 7 2 15 0.20803773942918D-01 0.83255369944119D-16 2 7 2 15 0.94978646232529D-01 0.22728795483601D-15 3 7 2 15 0.58124986485146D-01 0.81056512587239D-15 1 8 2 15 -0.57907236680472D+00 0.19658044115020D-16 2 8 2 15 -0.14418862649183D+00 0.55007564954403D-15 3 8 2 15 -0.43393246734524D-01 0.27951600820470D-15 1 9 2 15 -0.56907900921136D+00 0.40569499855467D-16 2 9 2 15 -0.42505835380044D+00 -0.23062249562743D-15 3 9 2 15 -0.20255772774882D+01 0.20073509105999D-16 1 10 2 15 -0.92466905239828D+00 -0.41471580557652D-16 2 10 2 15 -0.19339794421722D+00 -0.10198912644821D-16 3 10 2 15 0.16574450187903D+01 0.17062902546319D-16 1 11 2 15 -0.83180397548951D+00 0.57921925445058D-16 2 11 2 15 -0.10989501560636D+01 0.20794934071746D-15 3 11 2 15 -0.21454480474470D+01 0.10378811886472D-15 1 12 2 15 -0.39800972332159D+00 -0.24161243247857D-16 2 12 2 15 -0.60432485105595D+00 -0.93777772264511D-16 3 12 2 15 0.27804859619070D+01 0.37169366891652D-16 1 13 2 15 -0.32470660052582D+00 0.36079969146012D-16 2 13 2 15 -0.61864659889725D+00 0.11554562480833D-16 3 13 2 15 0.65672130808355D-01 -0.40043248775714D-16 1 14 2 15 0.16109511908445D+00 0.14863036725918D-17 2 14 2 15 0.44914722360172D+00 -0.96594081961594D-16 3 14 2 15 0.13491471216581D+00 0.42492190183211D-16 1 15 2 15 0.58392724026004D+01 0.00000000000000D+00 2 15 2 15 0.13758076541723D+02 0.00000000000000D+00 3 15 2 15 -0.20415598055509D+01 0.00000000000000D+00 1 16 2 15 -0.28593976346434D+01 0.26894619554961D-16 2 16 2 15 -0.42081897111825D+01 0.20501857109104D-15 3 16 2 15 0.74906335409624D-01 0.73478523169447D-17 1 17 2 15 -0.18233978195846D+00 -0.10403802946448D-16 2 17 2 15 0.29693616356469D+00 0.86165234419398D-16 3 17 2 15 -0.11749352448801D-01 0.29684023002332D-16 1 18 2 15 0.13518674534702D+00 0.34134657833107D-16 2 18 2 15 -0.38035239243249D+00 0.12381989190882D-15 3 18 2 15 0.24048306292478D-01 0.22582672214452D-16 1 19 2 15 0.10710026254495D+01 0.18686783949588D-16 2 19 2 15 -0.64647188952478D+01 0.14418365218723D-16 3 19 2 15 -0.14172485951549D+00 0.31656594076235D-17 1 20 2 15 -0.95469644395251D+00 0.21394449077780D-16 2 20 2 15 0.88565533669040D+00 -0.18088225803494D-16 3 20 2 15 0.30541858565605D+00 0.29786596439677D-16 1 22 2 15 -0.10173324396301D+02 0.00000000000000D+00 2 22 2 15 -0.60532578336789D+02 0.00000000000000D+00 3 22 2 15 0.45008015991612D+00 0.00000000000000D+00 1 1 3 15 0.30078101445076D+00 0.24904211190902D-16 2 1 3 15 -0.30570828755132D+00 -0.11595318775828D-15 3 1 3 15 0.77323372312267D+00 -0.36042142116454D-14 1 2 3 15 -0.49053289124477D+00 0.17415527749819D-16 2 2 3 15 0.40598958753683D+00 -0.29334178975866D-16 3 2 3 15 -0.32666255455172D+00 -0.77513430053224D-15 1 3 3 15 -0.68182003040273D+00 -0.26860252750672D-16 2 3 3 15 0.52515542902003D+00 0.12538001139428D-15 3 3 3 15 0.10425035738156D+01 0.27003139712984D-14 1 4 3 15 -0.65187452572468D+00 0.11497378207745D-15 2 4 3 15 0.87453604592923D+00 0.18995671379650D-15 3 4 3 15 -0.25037435958718D+01 -0.25953673345151D-14 1 5 3 15 0.83818842403369D-02 -0.81230446742012D-16 2 5 3 15 -0.31484626762450D+00 -0.24570481253401D-15 3 5 3 15 0.37080430568573D+01 0.16845856460024D-14 1 6 3 15 -0.12067545544193D+01 -0.20383649362297D-15 2 6 3 15 -0.68649872495388D+00 0.16971420434979D-16 3 6 3 15 -0.42530775815610D+01 -0.10992928429573D-14 1 7 3 15 -0.10357198728729D+00 -0.26756594591716D-15 2 7 3 15 0.17716441144124D+00 0.81056512587239D-15 3 7 3 15 0.37892032617638D+01 -0.86025090347640D-15 1 8 3 15 0.12614849187089D+01 0.18061251572041D-15 2 8 3 15 0.85602264129848D+00 0.27951600820470D-15 3 8 3 15 -0.42317235399660D+01 0.61597355164384D-15 1 9 3 15 -0.12101427438261D+01 0.97603064886574D-16 2 9 3 15 -0.12123977694114D+01 0.20073509105999D-16 3 9 3 15 -0.36637372330463D+01 0.18830076916523D-14 1 10 3 15 0.12638910221798D+01 -0.43025566532898D-17 2 10 3 15 0.99484767618450D+00 0.17062902546319D-16 3 10 3 15 -0.14182402230214D+01 -0.83743289278678D-15 1 11 3 15 -0.71982304519633D+00 0.68998379417752D-16 2 11 3 15 -0.97924848375822D+00 0.10378811886472D-15 3 11 3 15 -0.11154366465567D+01 0.11193480597698D-14 1 12 3 15 0.95995998170726D+00 0.10385019719274D-15 2 12 3 15 0.16447879168192D+01 0.37169366891652D-16 3 12 3 15 -0.41520018439911D+01 0.15499069738181D-14 1 13 3 15 0.33355766451469D-01 -0.14885125549015D-16 2 13 3 15 -0.65672130808356D-01 -0.40043248775714D-16 3 13 3 15 -0.15417956544810D+01 0.18809912773710D-15 1 14 3 15 0.62166479281127D-01 -0.31791639221042D-16 2 14 3 15 -0.13491471216581D+00 0.42492190183211D-16 3 14 3 15 -0.19584409533204D+01 -0.71233860868626D-15 1 15 3 15 0.12570340613314D+01 0.00000000000000D+00 2 15 3 15 -0.20415876309587D+01 0.00000000000000D+00 3 15 3 15 0.15296984004430D+02 0.00000000000000D+00 1 16 3 15 -0.16701820768249D+00 0.25761607492749D-16 2 16 3 15 0.74905075827224D-01 0.73478523169447D-17 3 16 3 15 -0.41887629667901D+00 -0.28112376635092D-15 1 17 3 15 0.58579992336693D-01 0.85435024987617D-18 2 17 3 15 0.11748407245336D-01 0.29684023002332D-16 3 17 3 15 -0.69776832341436D+00 -0.15497754740613D-15 1 18 3 15 0.16334488264200D-01 -0.60195052918774D-16 2 18 3 15 -0.24046912497818D-01 0.22582672214452D-16 3 18 3 15 -0.88010030951782D+00 0.73304793746192D-15 1 19 3 15 0.35443867941969D-01 0.12728027701046D-16 2 19 3 15 -0.14172485951549D+00 0.31656594076235D-17 3 19 3 15 0.18487674087042D+01 0.41934120675538D-16 1 20 3 15 -0.57946867444826D-02 0.50488390160654D-16 2 20 3 15 0.30541858565605D+00 0.29786596439677D-16 3 20 3 15 0.10975158984981D+01 0.11250515276125D-14 1 22 3 15 -0.19332062696203D-01 0.00000000000000D+00 2 22 3 15 0.64318482097774D+00 0.00000000000000D+00 3 22 3 15 -0.49879381635677D+02 0.00000000000000D+00 1 1 1 16 -0.14436323196730D+00 0.86267637938029D-15 2 1 1 16 -0.28804976638801D+00 -0.10226724733592D-16 3 1 1 16 -0.28620407326730D+00 0.92585419668332D-18 1 2 1 16 0.28264640601237D-01 -0.93098660074166D-16 2 2 1 16 -0.38810233286847D-01 -0.80921478848267D-17 3 2 1 16 0.35192012181663D+00 0.28303747654153D-16 1 3 1 16 -0.61006835472895D+00 -0.24671377177020D-15 2 3 1 16 0.45466061858322D+00 -0.55373434730418D-16 3 3 1 16 -0.78331374891610D+00 -0.29132472210128D-15 1 4 1 16 -0.12068954502774D+00 -0.52316819472188D-15 2 4 1 16 -0.36233757220374D+00 0.12028521197973D-16 3 4 1 16 -0.65718925843960D+00 0.22489337737880D-16 1 5 1 16 -0.37877129705308D-01 0.46888651093540D-16 2 5 1 16 0.80228829136542D-01 -0.13563707818804D-16 3 5 1 16 -0.56222819860822D+00 0.19443713283607D-15 1 6 1 16 -0.47205798319037D+00 0.63187820323953D-15 2 6 1 16 -0.75348403514229D+00 0.18478978601061D-16 3 6 1 16 0.61569286033500D+00 0.25878335605230D-15 1 7 1 16 -0.61749241585753D-01 0.94692055402952D-15 2 7 1 16 0.12514254043905D-01 0.42713968559539D-16 3 7 1 16 0.49107434131213D+00 0.13321421487572D-15 1 8 1 16 0.14572086039215D+00 -0.29997298684941D-15 2 8 1 16 0.10265494691604D+01 0.23246688123530D-16 3 8 1 16 -0.55647288619467D+00 -0.22825356575423D-15 1 9 1 16 -0.16229326487588D+01 -0.28119232079819D-16 2 9 1 16 -0.84607588494763D+00 0.36950254083440D-16 3 9 1 16 0.26868171993405D+01 0.72296488730082D-16 1 10 1 16 -0.14317947827315D+00 -0.98223936114535D-16 2 10 1 16 -0.54965799850786D+00 -0.13624276407728D-16 3 10 1 16 -0.19107834776752D+01 -0.57775327349178D-16 1 11 1 16 0.14662361543788D-01 -0.30380917840224D-15 2 11 1 16 -0.49896941366674D+00 -0.12314042359008D-16 3 11 1 16 0.14254744662862D+01 0.18326012427170D-16 1 12 1 16 -0.76437194269627D+00 0.30876686880828D-15 2 12 1 16 -0.99208058970536D+00 0.19439492295250D-16 3 12 1 16 -0.18293426717494D+01 -0.24679483559795D-16 1 13 1 16 0.39749073702135D+00 -0.17862770669410D-15 2 13 1 16 0.16109511908445D+00 0.69625704796414D-18 3 13 1 16 -0.62166479281129D-01 -0.42140566266514D-16 1 14 1 16 -0.51645554603745D+00 0.29435161147724D-15 2 14 1 16 -0.32470660052582D+00 0.15602335702095D-16 3 14 1 16 -0.33355766451466D-01 -0.44256711309179D-16 1 15 1 16 -0.38809165729708D+01 -0.49749384880341D-16 2 15 1 16 -0.28593969073651D+01 -0.26894619554961D-16 3 15 1 16 -0.16701677051494D+00 -0.25761607492749D-16 1 16 1 16 0.12535023461132D+02 0.00000000000000D+00 2 16 1 16 0.58392681818054D+01 0.00000000000000D+00 3 16 1 16 0.12570584673455D+01 0.00000000000000D+00 1 17 1 16 0.32395655219218D+00 0.13276348894469D-15 2 17 1 16 -0.13518632858762D+00 0.23348623548077D-16 3 17 1 16 0.16337033535739D-01 -0.37944066980139D-16 1 18 1 16 -0.23324566422979D+00 -0.34749918167928D-16 2 18 1 16 0.18233885955755D+00 0.16975686386136D-16 3 18 1 16 0.58580035591798D-01 0.49172027615982D-18 1 19 1 16 -0.57363572065418D+01 -0.80844221129564D-16 2 19 1 16 0.95469644395251D+00 0.38893303989191D-18 3 19 1 16 0.57946867444920D-02 0.32143669540553D-16 1 20 1 16 0.95623294368768D+00 -0.36634211693696D-16 2 20 1 16 -0.10710026254495D+01 -0.33852178127381D-17 3 20 1 16 -0.35443867941967D-01 0.17725986518913D-16 1 22 1 16 -0.59666225479308D+02 0.00000000000000D+00 2 22 1 16 -0.10058609976031D+02 0.00000000000000D+00 3 22 1 16 0.11301410298273D-02 0.00000000000000D+00 1 1 2 16 -0.14974007339003D+00 -0.10226724733592D-16 2 1 2 16 -0.45654092233183D+00 0.67496567844563D-15 3 1 2 16 0.35777067486433D+00 -0.14033022694346D-16 1 2 2 16 -0.19808731105279D+00 -0.80921478848267D-17 2 2 2 16 0.30018923206278D+00 0.18432464797805D-15 3 2 2 16 -0.35485508012221D+00 0.14595720052580D-15 1 3 2 16 0.34687872744995D+00 -0.55373434730418D-16 2 3 2 16 -0.84809723947391D+00 0.57715477236046D-15 3 3 2 16 0.83980060330537D+00 -0.18391818826022D-15 1 4 2 16 -0.44226102341466D+00 0.12028521197973D-16 2 4 2 16 -0.31551995169711D+00 0.75077652016686D-15 3 4 2 16 0.50703823584821D+00 -0.85576045505394D-16 1 5 2 16 0.13310522665982D-01 -0.13563707818804D-16 2 5 2 16 0.15082554883140D-01 0.48776792340226D-15 3 5 2 16 -0.20478799764696D+00 0.12119575263231D-15 1 6 2 16 0.80828268218607D+00 0.18478978601061D-16 2 6 2 16 -0.33012601691901D-01 0.83030804851145D-15 3 6 2 16 0.14560451909210D+00 -0.48698743050953D-15 1 7 2 16 0.20803773942923D-01 0.42713968559539D-16 2 7 2 16 0.94978646232514D-01 0.28864600227788D-15 3 7 2 16 0.58124986485173D-01 0.49982922431843D-15 1 8 2 16 -0.57907236680421D+00 0.23246688123530D-16 2 8 2 16 -0.14418862649168D+00 0.36127464996021D-15 3 8 2 16 -0.43393246734524D-01 -0.49571804948562D-16 1 9 2 16 -0.92466905239825D+00 0.36950254083440D-16 2 9 2 16 -0.19339794421721D+00 -0.20401731510457D-15 3 9 2 16 0.16574450187903D+01 0.24635292836497D-16 1 10 2 16 -0.56907900921136D+00 -0.13624276407728D-16 2 10 2 16 -0.42505835380042D+00 -0.11796689292581D-15 3 10 2 16 -0.20255772774882D+01 0.31260300163030D-16 1 11 2 16 -0.39800972332160D+00 -0.12314042359008D-16 2 11 2 16 -0.60432485105590D+00 0.24110223587506D-15 3 11 2 16 0.27804859619070D+01 -0.10769787579255D-15 1 12 2 16 -0.83180397548954D+00 0.19439492295250D-16 2 12 2 16 -0.10989501560636D+01 0.39283675610759D-16 3 12 2 16 -0.21454480474470D+01 0.45878619058827D-17 1 13 2 16 0.16109511908445D+00 0.69625704796414D-18 2 13 2 16 0.44914722360173D+00 -0.42450942505814D-16 3 13 2 16 0.13491471216581D+00 -0.25077882469455D-16 1 14 2 16 -0.32470660052582D+00 0.15602335702095D-16 2 14 2 16 -0.61864659889725D+00 0.11405536163640D-15 3 14 2 16 0.65672130808357D-01 -0.48747538203699D-17 1 15 2 16 -0.28593976346434D+01 -0.26894619554961D-16 2 15 2 16 -0.42081897111825D+01 -0.20501857109104D-15 3 15 2 16 0.74906335409624D-01 -0.73478523169447D-17 1 16 2 16 0.58392724026001D+01 0.00000000000000D+00 2 16 2 16 0.13758076541722D+02 0.00000000000000D+00 3 16 2 16 -0.20415598055508D+01 0.00000000000000D+00 1 17 2 16 0.13518674534702D+00 0.23348623548077D-16 2 17 2 16 -0.38035239243249D+00 -0.89119898684153D-16 3 17 2 16 0.24048306292477D-01 -0.55468767765036D-17 1 18 2 16 -0.18233978195846D+00 0.16975686386136D-16 2 18 2 16 0.29693616356470D+00 -0.32832989001387D-15 3 18 2 16 -0.11749352448801D-01 -0.50022989886897D-16 1 19 2 16 -0.95469644395250D+00 0.38893303989191D-18 2 19 2 16 0.88565533669038D+00 -0.20899210254877D-15 3 19 2 16 0.30541858565605D+00 0.30281851765161D-16 1 20 2 16 0.10710026254495D+01 -0.33852178127381D-17 2 20 2 16 -0.64647188952479D+01 0.45037880146693D-17 3 20 2 16 -0.14172485951549D+00 -0.58747333384920D-18 1 22 2 16 -0.10173324395826D+02 0.00000000000000D+00 2 22 2 16 -0.60532578342702D+02 0.00000000000000D+00 3 22 2 16 0.45008016225787D+00 0.00000000000000D+00 1 1 3 16 -0.49053289124479D+00 0.92585419668332D-18 2 1 3 16 0.40598958753682D+00 -0.14033022694346D-16 3 1 3 16 -0.32666255455157D+00 0.24443995047951D-14 1 2 3 16 0.30078101445080D+00 0.28303747654153D-16 2 2 3 16 -0.30570828755138D+00 0.14595720052580D-15 3 2 3 16 0.77323372312269D+00 0.32327040432076D-14 1 3 3 16 -0.65187452572476D+00 -0.29132472210128D-15 2 3 3 16 0.87453604592927D+00 -0.18391818826022D-15 3 3 3 16 -0.25037435958716D+01 -0.60014021929189D-15 1 4 3 16 -0.68182003040271D+00 0.22489337737880D-16 2 4 3 16 0.52515542902009D+00 -0.85576045505394D-16 3 4 3 16 0.10425035738157D+01 0.64678579107844D-15 1 5 3 16 0.83818842403218D-02 0.19443713283607D-15 2 5 3 16 -0.31484626762451D+00 0.12119575263231D-15 3 5 3 16 0.37080430568572D+01 0.66662507646345D-15 1 6 3 16 -0.12067545544196D+01 0.25878335605230D-15 2 6 3 16 -0.68649872495407D+00 -0.48698743050953D-15 3 6 3 16 -0.42530775815610D+01 0.15388241034981D-14 1 7 3 16 -0.10357198728727D+00 0.13321421487572D-15 2 7 3 16 0.17716441144127D+00 0.49982922431843D-15 3 7 3 16 0.37892032617639D+01 -0.13470641901223D-14 1 8 3 16 0.12614849187088D+01 -0.22825356575423D-15 2 8 3 16 0.85602264129849D+00 -0.49571804948562D-16 3 8 3 16 -0.42317235399666D+01 -0.66993639263482D-15 1 9 3 16 0.12638910221798D+01 0.72296488730082D-16 2 9 3 16 0.99484767618446D+00 0.24635292836497D-16 3 9 3 16 -0.14182402230213D+01 -0.10021630571555D-14 1 10 3 16 -0.12101427438262D+01 -0.57775327349178D-16 2 10 3 16 -0.12123977694113D+01 0.31260300163030D-16 3 10 3 16 -0.36637372330463D+01 -0.19875773319800D-15 1 11 3 16 0.95995998170731D+00 0.18326012427170D-16 2 11 3 16 0.16447879168192D+01 -0.10769787579255D-15 3 11 3 16 -0.41520018439912D+01 -0.94908030772338D-15 1 12 3 16 -0.71982304519634D+00 -0.24679483559795D-16 2 12 3 16 -0.97924848375820D+00 0.45878619058827D-17 3 12 3 16 -0.11154366465567D+01 -0.10503613079330D-15 1 13 3 16 0.62166479281127D-01 -0.42140566266514D-16 2 13 3 16 -0.13491471216581D+00 -0.25077882469455D-16 3 13 3 16 -0.19584409533204D+01 0.55328945899113D-15 1 14 3 16 0.33355766451469D-01 -0.44256711309179D-16 2 14 3 16 -0.65672130808354D-01 -0.48747538203699D-17 3 14 3 16 -0.15417956544810D+01 -0.21817466365640D-16 1 15 3 16 -0.16701820768249D+00 -0.25761607492749D-16 2 15 3 16 0.74905075827224D-01 -0.73478523169447D-17 3 15 3 16 -0.41887629667901D+00 0.28112376635092D-15 1 16 3 16 0.12570340613318D+01 0.00000000000000D+00 2 16 3 16 -0.20415876309585D+01 0.00000000000000D+00 3 16 3 16 0.15296984004430D+02 0.00000000000000D+00 1 17 3 16 0.16334488264196D-01 -0.37944066980139D-16 2 17 3 16 -0.24046912497819D-01 -0.55468767765036D-17 3 17 3 16 -0.88010030951784D+00 -0.38314627956217D-15 1 18 3 16 0.58579992336693D-01 0.49172027615982D-18 2 18 3 16 0.11748407245337D-01 -0.50022989886897D-16 3 18 3 16 -0.69776832341433D+00 0.24356716431955D-16 1 19 3 16 -0.57946867444928D-02 0.32143669540553D-16 2 19 3 16 0.30541858565605D+00 0.30281851765161D-16 3 19 3 16 0.10975158984981D+01 -0.39653525669010D-15 1 20 3 16 0.35443867941967D-01 0.17725986518913D-16 2 20 3 16 -0.14172485951549D+00 -0.58747333384920D-18 3 20 3 16 0.18487674087043D+01 0.17784848328192D-17 1 22 3 16 -0.19332058627242D-01 0.00000000000000D+00 2 22 3 16 0.64318482641441D+00 0.00000000000000D+00 3 22 3 16 -0.49879381668982D+02 0.00000000000000D+00 1 1 1 17 -0.61006835472897D+00 0.48496217341254D-15 2 1 1 17 -0.45466061858329D+00 -0.13402184812400D-15 3 1 1 17 -0.78331374891634D+00 0.17628964027527D-17 1 2 1 17 -0.12068954502773D+00 -0.21534838163192D-15 2 2 1 17 0.36233757220369D+00 -0.23362134733422D-16 3 2 1 17 -0.65718925843951D+00 -0.12490572576917D-15 1 3 1 17 -0.14436323196734D+00 0.48554282959499D-15 2 3 1 17 0.28804976638799D+00 0.22596188638715D-16 3 3 1 17 -0.28620407326723D+00 0.46832350657680D-16 1 4 1 17 0.28264640601235D-01 -0.15135745896296D-15 2 4 1 17 0.38810233286859D-01 0.29770600454208D-16 3 4 1 17 0.35192012181664D+00 -0.96234608353360D-16 1 5 1 17 0.14572086039215D+00 0.20359724274569D-15 2 5 1 17 -0.10265494691603D+01 -0.11868506827686D-15 3 5 1 17 -0.55647288619464D+00 0.83663155464845D-16 1 6 1 17 -0.61749241585754D-01 -0.15538299952659D-16 2 6 1 17 -0.12514254043905D-01 -0.44032530477427D-16 3 6 1 17 0.49107434131213D+00 0.15624588538953D-15 1 7 1 17 -0.47205798319052D+00 -0.27268009676361D-16 2 7 1 17 0.75348403514224D+00 -0.35102586327187D-16 3 7 1 17 0.61569286033492D+00 0.76266544192944D-15 1 8 1 17 -0.37877129705300D-01 0.60131990229548D-15 2 8 1 17 -0.80228829136542D-01 0.53669141322980D-17 3 8 1 17 -0.56222819860821D+00 0.21851319746119D-15 1 9 1 17 -0.76437194269629D+00 0.17110538624872D-15 2 9 1 17 0.99208058970531D+00 -0.12494044870930D-16 3 9 1 17 -0.18293426717494D+01 0.17812744810089D-15 1 10 1 17 0.14662361543774D-01 -0.35135156467848D-15 2 10 1 17 0.49896941366673D+00 0.92468437971919D-16 3 10 1 17 0.14254744662861D+01 -0.41416353054515D-16 1 11 1 17 -0.14317947827315D+00 0.46913020348647D-15 2 11 1 17 0.54965799850788D+00 -0.35417972771553D-16 3 11 1 17 -0.19107834776752D+01 0.53385194165472D-16 1 12 1 17 -0.16229326487588D+01 0.25765184937318D-15 2 12 1 17 0.84607588494765D+00 0.72749529650571D-17 3 12 1 17 0.26868171993405D+01 0.67482023856894D-16 1 13 1 17 0.95623294368768D+00 -0.15382223784835D-15 2 13 1 17 0.10710026254495D+01 0.22985801261784D-16 3 13 1 17 -0.35443867941968D-01 -0.71220048440833D-17 1 14 1 17 -0.57363572065418D+01 0.36633331796015D-15 2 14 1 17 -0.95469644395251D+00 0.59501919736812D-17 3 14 1 17 0.57946867444806D-02 0.64063145527620D-16 1 15 1 17 -0.23324566422979D+00 0.10485151941248D-16 2 15 1 17 -0.18233885955755D+00 0.10403802946448D-16 3 15 1 17 0.58580035591798D-01 -0.85435024987617D-18 1 16 1 17 0.32395655219218D+00 -0.13276348894469D-15 2 16 1 17 0.13518632858762D+00 -0.23348623548077D-16 3 16 1 17 0.16337033535739D-01 0.37944066980139D-16 1 17 1 17 0.12535023461133D+02 0.00000000000000D+00 2 17 1 17 -0.58392681818052D+01 0.00000000000000D+00 3 17 1 17 0.12570584673456D+01 0.00000000000000D+00 1 18 1 17 -0.38809165729708D+01 0.23670220047841D-16 2 18 1 17 0.28593969073651D+01 0.84837858405802D-17 3 18 1 17 -0.16701677051493D+00 0.35736039966319D-16 1 19 1 17 -0.51645554603745D+00 0.53604395782106D-16 2 19 1 17 0.32470660052582D+00 0.13640963768916D-16 3 19 1 17 -0.33355766451467D-01 -0.22452441706793D-16 1 20 1 17 0.39749073702135D+00 -0.30014219852255D-16 2 20 1 17 -0.16109511908445D+00 -0.12307454582832D-18 3 20 1 17 -0.62166479281129D-01 -0.18735084312373D-16 1 22 1 17 -0.59666225483003D+02 0.00000000000000D+00 2 22 1 17 0.10058609980567D+02 0.00000000000000D+00 3 22 1 17 0.11301434190783D-02 0.00000000000000D+00 1 1 2 17 -0.34687872745002D+00 -0.13402184812400D-15 2 1 2 17 -0.84809723947373D+00 0.15678432116134D-16 3 1 2 17 -0.83980060330551D+00 -0.32347620798335D-16 1 2 2 17 0.44226102341461D+00 -0.23362134733422D-16 2 2 2 17 -0.31551995169709D+00 -0.63978155291857D-16 3 2 2 17 -0.50703823584813D+00 0.55596056459081D-15 1 3 2 17 0.14974007339001D+00 0.22596188638715D-16 2 3 2 17 -0.45654092233173D+00 0.18582337733352D-17 3 3 2 17 -0.35777067486429D+00 -0.31241994899975D-16 1 4 2 17 0.19808731105280D+00 0.29770600454208D-16 2 4 2 17 0.30018923206275D+00 0.17606837694407D-15 3 4 2 17 0.35485508012224D+00 0.41186214675138D-16 1 5 2 17 0.57907236680427D+00 -0.11868506827686D-15 2 5 2 17 -0.14418862649160D+00 0.69046111567954D-15 3 5 2 17 0.43393246734524D-01 -0.29142939781599D-16 1 6 2 17 -0.20803773942923D-01 -0.44032530477427D-16 2 6 2 17 0.94978646232513D-01 0.29878340771667D-16 3 6 2 17 -0.58124986485173D-01 0.16783772584646D-15 1 7 2 17 -0.80828268218609D+00 -0.35102586327187D-16 2 7 2 17 -0.33012601691780D-01 -0.15411815824534D-16 3 7 2 17 -0.14560451909207D+00 -0.52423292880201D-15 1 8 2 17 -0.13310522665981D-01 0.53669141322980D-17 2 8 2 17 0.15082554883153D-01 0.74981354706492D-15 3 8 2 17 0.20478799764697D+00 -0.78850411075697D-16 1 9 2 17 0.83180397548949D+00 -0.12494044870930D-16 2 9 2 17 -0.10989501560636D+01 -0.50944025789981D-15 3 9 2 17 0.21454480474469D+01 -0.18602331528573D-15 1 10 2 17 0.39800972332159D+00 0.92468437971919D-16 2 10 2 17 -0.60432485105597D+00 0.22534938902494D-15 3 10 2 17 -0.27804859619070D+01 -0.58075563264886D-16 1 11 2 17 0.56907900921138D+00 -0.35417972771553D-16 2 11 2 17 -0.42505835380047D+00 -0.40637964685694D-15 3 11 2 17 0.20255772774882D+01 -0.66980750952940D-16 1 12 2 17 0.92466905239827D+00 0.72749529650571D-17 2 12 2 17 -0.19339794421720D+00 -0.59852798948281D-15 3 12 2 17 -0.16574450187903D+01 0.18024723889939D-15 1 13 2 17 -0.10710026254495D+01 0.22985801261784D-16 2 13 2 17 -0.64647188952479D+01 -0.53594737461675D-18 3 13 2 17 0.14172485951549D+00 0.34540383757104D-17 1 14 2 17 0.95469644395250D+00 0.59501919736812D-17 2 14 2 17 0.88565533669040D+00 0.33093204096038D-15 3 14 2 17 -0.30541858565604D+00 0.77459621164225D-16 1 15 2 17 0.18233978195846D+00 0.10403802946448D-16 2 15 2 17 0.29693616356469D+00 -0.86165234419398D-16 3 15 2 17 0.11749352448801D-01 -0.29684023002332D-16 1 16 2 17 -0.13518674534702D+00 -0.23348623548077D-16 2 16 2 17 -0.38035239243249D+00 0.89119898684153D-16 3 16 2 17 -0.24048306292486D-01 0.55468767765036D-17 1 17 2 17 -0.58392724025999D+01 0.00000000000000D+00 2 17 2 17 0.13758076541722D+02 0.00000000000000D+00 3 17 2 17 0.20415598055508D+01 0.00000000000000D+00 1 18 2 17 0.28593976346433D+01 0.84837858405802D-17 2 18 2 17 -0.42081897111825D+01 0.13406991315059D-15 3 18 2 17 -0.74906335409622D-01 -0.17017959583876D-16 1 19 2 17 0.32470660052582D+00 0.13640963768916D-16 2 19 2 17 -0.61864659889725D+00 0.10980867713107D-15 3 19 2 17 -0.65672130808356D-01 -0.11151299802869D-15 1 20 2 17 -0.16109511908445D+00 -0.12307454582832D-18 2 20 2 17 0.44914722360174D+00 0.59707085872013D-16 3 20 2 17 -0.13491471216581D+00 0.24940022573201D-16 1 22 2 17 0.10173324396286D+02 0.00000000000000D+00 2 22 2 17 -0.60532578336756D+02 0.00000000000000D+00 3 22 2 17 -0.45008015992308D+00 0.00000000000000D+00 1 1 3 17 -0.65187452572500D+00 0.17628964027527D-17 2 1 3 17 -0.87453604592941D+00 -0.32347620798335D-16 3 1 3 17 -0.25037435958720D+01 -0.13526379567169D-14 1 2 3 17 -0.68182003040262D+00 -0.12490572576917D-15 2 2 3 17 -0.52515542902000D+00 0.55596056459081D-15 3 2 3 17 0.10425035738155D+01 0.10475116862543D-14 1 3 3 17 -0.49053289124472D+00 0.46832350657680D-16 2 3 3 17 -0.40598958753678D+00 -0.31241994899975D-16 3 3 3 17 -0.32666255455167D+00 0.19451893524558D-14 1 4 3 17 0.30078101445082D+00 -0.96234608353360D-16 2 4 3 17 0.30570828755140D+00 0.41186214675138D-16 3 4 3 17 0.77323372312279D+00 0.35391700461409D-15 1 5 3 17 0.12614849187089D+01 0.83663155464845D-16 2 5 3 17 -0.85602264129849D+00 -0.29142939781599D-16 3 5 3 17 -0.42317235399666D+01 0.23066501139534D-14 1 6 3 17 -0.10357198728727D+00 0.15624588538953D-15 2 6 3 17 -0.17716441144127D+00 0.16783772584646D-15 3 6 3 17 0.37892032617638D+01 0.21473411720111D-15 1 7 3 17 -0.12067545544197D+01 0.76266544192944D-15 2 7 3 17 0.68649872495410D+00 -0.52423292880201D-15 3 7 3 17 -0.42530775815607D+01 -0.21031063752071D-14 1 8 3 17 0.83818842403272D-02 0.21851319746119D-15 2 8 3 17 0.31484626762452D+00 -0.78850411075697D-16 3 8 3 17 0.37080430568572D+01 -0.11718056840419D-14 1 9 3 17 -0.71982304519630D+00 0.17812744810089D-15 2 9 3 17 0.97924848375816D+00 -0.18602331528573D-15 3 9 3 17 -0.11154366465566D+01 0.61169140296512D-15 1 10 3 17 0.95995998170726D+00 -0.41416353054515D-16 2 10 3 17 -0.16447879168192D+01 -0.58075563264886D-16 3 10 3 17 -0.41520018439910D+01 -0.15593316676586D-14 1 11 3 17 -0.12101427438262D+01 0.53385194165472D-16 2 11 3 17 0.12123977694114D+01 -0.66980750952940D-16 3 11 3 17 -0.36637372330462D+01 -0.19868946126478D-14 1 12 3 17 0.12638910221798D+01 0.67482023856894D-16 2 12 3 17 -0.99484767618448D+00 0.18024723889939D-15 3 12 3 17 -0.14182402230213D+01 -0.64476076403441D-15 1 13 3 17 0.35443867941966D-01 -0.71220048440833D-17 2 13 3 17 0.14172485951549D+00 0.34540383757104D-17 3 13 3 17 0.18487674087043D+01 -0.17262678163367D-17 1 14 3 17 -0.57946867445042D-02 0.64063145527620D-16 2 14 3 17 -0.30541858565604D+00 0.77459621164225D-16 3 14 3 17 0.10975158984982D+01 -0.13588914469357D-14 1 15 3 17 0.58579992336693D-01 -0.85435024987617D-18 2 15 3 17 -0.11748407245336D-01 -0.29684023002332D-16 3 15 3 17 -0.69776832341436D+00 0.15497754740613D-15 1 16 3 17 0.16334488264196D-01 0.37944066980139D-16 2 16 3 17 0.24046912497810D-01 0.55468767765036D-17 3 16 3 17 -0.88010030951784D+00 0.38314627956217D-15 1 17 3 17 0.12570340613319D+01 0.00000000000000D+00 2 17 3 17 0.20415876309585D+01 0.00000000000000D+00 3 17 3 17 0.15296984004430D+02 0.00000000000000D+00 1 18 3 17 -0.16701820768249D+00 0.35736039966319D-16 2 18 3 17 -0.74905075827223D-01 -0.17017959583876D-16 3 18 3 17 -0.41887629667904D+00 -0.10047331583022D-14 1 19 3 17 0.33355766451468D-01 -0.22452441706793D-16 2 19 3 17 0.65672130808356D-01 -0.11151299802869D-15 3 19 3 17 -0.15417956544810D+01 -0.77791672221634D-16 1 20 3 17 0.62166479281126D-01 -0.18735084312373D-16 2 20 3 17 0.13491471216581D+00 0.24940022573201D-16 3 20 3 17 -0.19584409533204D+01 -0.41415806158633D-15 1 22 3 17 -0.19332062723602D-01 0.00000000000000D+00 2 22 3 17 -0.64318482097025D+00 0.00000000000000D+00 3 22 3 17 -0.49879381635685D+02 0.00000000000000D+00 1 1 1 18 -0.12068954502770D+00 -0.54084107214775D-16 2 1 1 18 0.36233757220372D+00 -0.81785023902869D-16 3 1 1 18 -0.65718925843967D+00 -0.91623939697941D-16 1 2 1 18 -0.61006835472893D+00 0.10236925639623D-14 2 2 1 18 -0.45466061858325D+00 0.20417943091574D-15 3 2 1 18 -0.78331374891620D+00 -0.16310352555728D-15 1 3 1 18 0.28264640601247D-01 0.27619810942560D-15 2 3 1 18 0.38810233286855D-01 0.73342624519378D-16 3 3 1 18 0.35192012181666D+00 0.10613423588813D-17 1 4 1 18 -0.14436323196738D+00 -0.41723740583170D-15 2 4 1 18 0.28804976638796D+00 0.91723345422732D-16 3 4 1 18 -0.28620407326721D+00 -0.36191962949854D-18 1 5 1 18 0.14572086039211D+00 0.12253514312844D-15 2 5 1 18 -0.10265494691601D+01 -0.84111649352257D-17 3 5 1 18 -0.55647288619470D+00 -0.11641248338691D-15 1 6 1 18 -0.61749241585753D-01 0.53887403336858D-16 2 6 1 18 -0.12514254043902D-01 -0.96421020791729D-17 3 6 1 18 0.49107434131211D+00 0.16785307133470D-16 1 7 1 18 -0.47205798319024D+00 -0.52926796385336D-15 2 7 1 18 0.75348403514232D+00 0.10102680085072D-15 3 7 1 18 0.61569286033526D+00 0.40853371866791D-15 1 8 1 18 -0.37877129705308D-01 0.39501576237930D-15 2 8 1 18 -0.80228829136544D-01 0.17593371570744D-16 3 8 1 18 -0.56222819860821D+00 0.43830015049284D-17 1 9 1 18 0.14662361543804D-01 -0.39560657329009D-16 2 9 1 18 0.49896941366673D+00 -0.17338779929251D-16 3 9 1 18 0.14254744662861D+01 -0.10331803632508D-15 1 10 1 18 -0.76437194269626D+00 -0.13097399870699D-15 2 10 1 18 0.99208058970535D+00 -0.72226688769405D-17 3 10 1 18 -0.18293426717494D+01 0.69244886197431D-16 1 11 1 18 -0.16229326487588D+01 0.27339750461519D-15 2 11 1 18 0.84607588494766D+00 -0.21711654257282D-16 3 11 1 18 0.26868171993406D+01 0.35694616322445D-16 1 12 1 18 -0.14317947827315D+00 -0.45819623365556D-15 2 12 1 18 0.54965799850786D+00 -0.27329282927755D-16 3 12 1 18 -0.19107834776752D+01 -0.77203130860038D-16 1 13 1 18 -0.57363572065418D+01 0.31949286782644D-17 2 13 1 18 -0.95469644395250D+00 -0.47996136897421D-17 3 13 1 18 0.57946867444948D-02 0.48972342025698D-16 1 14 1 18 0.95623294368763D+00 0.49026636430877D-16 2 14 1 18 0.10710026254495D+01 0.13007477942092D-16 3 14 1 18 -0.35443867941968D-01 0.26254943514666D-16 1 15 1 18 0.32395655219218D+00 -0.18456261996323D-15 2 15 1 18 0.13518632858762D+00 -0.34134657833107D-16 3 15 1 18 0.16337033535742D-01 0.60195052918774D-16 1 16 1 18 -0.23324566422979D+00 0.34749918167928D-16 2 16 1 18 -0.18233885955754D+00 -0.16975686386136D-16 3 16 1 18 0.58580035591798D-01 -0.49172027615982D-18 1 17 1 18 -0.38809165729708D+01 -0.23670220047841D-16 2 17 1 18 0.28593969073651D+01 -0.84837858405802D-17 3 17 1 18 -0.16701677051493D+00 -0.35736039966319D-16 1 18 1 18 0.12535023461132D+02 0.00000000000000D+00 2 18 1 18 -0.58392681818056D+01 0.00000000000000D+00 3 18 1 18 0.12570584673453D+01 0.00000000000000D+00 1 19 1 18 0.39749073702135D+00 0.60455452269144D-16 2 19 1 18 -0.16109511908445D+00 -0.20340759390948D-17 3 19 1 18 -0.62166479281127D-01 0.24169524079203D-16 1 20 1 18 -0.51645554603745D+00 -0.34955046904666D-16 2 20 1 18 0.32470660052582D+00 0.27221202674133D-16 3 20 1 18 -0.33355766451470D-01 0.58238836375886D-16 1 22 1 18 -0.59666225479298D+02 0.00000000000000D+00 2 22 1 18 0.10058609976025D+02 0.00000000000000D+00 3 22 1 18 0.11301410249305D-02 0.00000000000000D+00 1 1 2 18 0.44226102341464D+00 -0.81785023902869D-16 2 1 2 18 -0.31551995169718D+00 -0.47177814430928D-15 3 1 2 18 -0.50703823584813D+00 0.22848336129013D-16 1 2 2 18 -0.34687872744998D+00 0.20417943091574D-15 2 2 2 18 -0.84809723947389D+00 0.14594974336973D-15 3 2 2 18 -0.83980060330541D+00 -0.18846178817275D-16 1 3 2 18 0.19808731105280D+00 0.73342624519378D-16 2 3 2 18 0.30018923206277D+00 0.44000099275409D-16 3 3 2 18 0.35485508012224D+00 0.16358897290871D-15 1 4 2 18 0.14974007338997D+00 0.91723345422732D-16 2 4 2 18 -0.45654092233174D+00 0.30848578535435D-15 3 4 2 18 -0.35777067486428D+00 0.11583759015259D-15 1 5 2 18 0.57907236680447D+00 -0.84111649352257D-17 2 5 2 18 -0.14418862649194D+00 0.55605291914425D-15 3 5 2 18 0.43393246734610D-01 -0.32634939090171D-15 1 6 2 18 -0.20803773942919D-01 -0.96421020791729D-17 2 6 2 18 0.94978646232522D-01 0.81443627259880D-15 3 6 2 18 -0.58124986485146D-01 0.18612995474725D-15 1 7 2 18 -0.80828268218603D+00 0.10102680085072D-15 2 7 2 18 -0.33012601691986D-01 -0.52807820190861D-15 3 7 2 18 -0.14560451909228D+00 -0.42635480740120D-15 1 8 2 18 -0.13310522665983D-01 0.17593371570744D-16 2 8 2 18 0.15082554883125D-01 -0.36072982252709D-15 3 8 2 18 0.20478799764695D+00 -0.22429230002051D-15 1 9 2 18 0.39800972332159D+00 -0.17338779929251D-16 2 9 2 18 -0.60432485105596D+00 0.45132700251673D-15 3 9 2 18 -0.27804859619070D+01 0.72636099432468D-16 1 10 2 18 0.83180397548953D+00 -0.72226688769405D-17 2 10 2 18 -0.10989501560636D+01 -0.68848125699366D-15 3 10 2 18 0.21454480474470D+01 -0.70291559555350D-16 1 11 2 18 0.92466905239828D+00 -0.21711654257282D-16 2 11 2 18 -0.19339794421714D+00 0.55149671519873D-15 3 11 2 18 -0.16574450187903D+01 0.79519998047840D-17 1 12 2 18 0.56907900921136D+00 -0.27329282927755D-16 2 12 2 18 -0.42505835380043D+00 -0.37314885126610D-15 3 12 2 18 0.20255772774882D+01 0.46354543545774D-17 1 13 2 18 0.95469644395251D+00 -0.47996136897421D-17 2 13 2 18 0.88565533669038D+00 -0.25376227437474D-15 3 13 2 18 -0.30541858565605D+00 0.99639505199961D-17 1 14 2 18 -0.10710026254495D+01 0.13007477942092D-16 2 14 2 18 -0.64647188952477D+01 -0.61846435392819D-17 3 14 2 18 0.14172485951549D+00 -0.24930288772476D-17 1 15 2 18 -0.13518674534702D+00 -0.34134657833107D-16 2 15 2 18 -0.38035239243249D+00 -0.12381989190882D-15 3 15 2 18 -0.24048306292485D-01 -0.22582672214452D-16 1 16 2 18 0.18233978195846D+00 -0.16975686386136D-16 2 16 2 18 0.29693616356470D+00 0.32832989001387D-15 3 16 2 18 0.11749352448801D-01 0.50022989886897D-16 1 17 2 18 0.28593976346433D+01 -0.84837858405802D-17 2 17 2 18 -0.42081897111825D+01 -0.13406991315059D-15 3 17 2 18 -0.74906335409622D-01 0.17017959583876D-16 1 18 2 18 -0.58392724026003D+01 0.00000000000000D+00 2 18 2 18 0.13758076541722D+02 0.00000000000000D+00 3 18 2 18 0.20415598055508D+01 0.00000000000000D+00 1 19 2 18 -0.16109511908445D+00 -0.20340759390948D-17 2 19 2 18 0.44914722360172D+00 0.66797074121275D-16 3 19 2 18 -0.13491471216581D+00 0.19625085109604D-16 1 20 2 18 0.32470660052582D+00 0.27221202674133D-16 2 20 2 18 -0.61864659889725D+00 0.60981978865386D-17 3 20 2 18 -0.65672130808356D-01 -0.10423476339560D-15 1 22 2 18 0.10173324395812D+02 0.00000000000000D+00 2 22 2 18 -0.60532578342670D+02 0.00000000000000D+00 3 22 2 18 -0.45008016226484D+00 0.00000000000000D+00 1 1 3 18 -0.68182003040278D+00 -0.91623939697941D-16 2 1 3 18 -0.52515542902001D+00 0.22848336129013D-16 3 1 3 18 0.10425035738157D+01 -0.11559810105626D-14 1 2 3 18 -0.65187452572486D+00 -0.16310352555728D-15 2 2 3 18 -0.87453604592931D+00 -0.18846178817275D-16 3 2 3 18 -0.25037435958717D+01 -0.98259522029051D-15 1 3 3 18 0.30078101445083D+00 0.10613423588813D-17 2 3 3 18 0.30570828755140D+00 0.16358897290871D-15 3 3 3 18 0.77323372312275D+00 0.35491980046754D-14 1 4 3 18 -0.49053289124469D+00 -0.36191962949854D-18 2 4 3 18 -0.40598958753676D+00 0.11583759015259D-15 3 4 3 18 -0.32666255455163D+00 0.25347535973515D-15 1 5 3 18 0.12614849187088D+01 -0.11641248338691D-15 2 5 3 18 -0.85602264129840D+00 -0.32634939090171D-15 3 5 3 18 -0.42317235399663D+01 -0.15840054050645D-14 1 6 3 18 -0.10357198728729D+00 0.16785307133470D-16 2 6 3 18 -0.17716441144124D+00 0.18612995474725D-15 3 6 3 18 0.37892032617638D+01 -0.56847087115902D-15 1 7 3 18 -0.12067545544194D+01 0.40853371866791D-15 2 7 3 18 0.68649872495391D+00 -0.42635480740120D-15 3 7 3 18 -0.42530775815609D+01 -0.43141778514763D-15 1 8 3 18 0.83818842403325D-02 0.43830015049284D-17 2 8 3 18 0.31484626762450D+00 -0.22429230002051D-15 3 8 3 18 0.37080430568573D+01 0.74503359127828D-15 1 9 3 18 0.95995998170724D+00 -0.10331803632508D-15 2 9 3 18 -0.16447879168192D+01 0.72636099432468D-16 3 9 3 18 -0.41520018439910D+01 -0.22233975789265D-14 1 10 3 18 -0.71982304519634D+00 0.69244886197431D-16 2 10 3 18 0.97924848375820D+00 -0.70291559555350D-16 3 10 3 18 -0.11154366465567D+01 -0.84142186755541D-15 1 11 3 18 0.12638910221799D+01 0.35694616322445D-16 2 11 3 18 -0.99484767618448D+00 0.79519998047840D-17 3 11 3 18 -0.14182402230213D+01 0.17566627675357D-14 1 12 3 18 -0.12101427438262D+01 -0.77203130860038D-16 2 12 3 18 0.12123977694114D+01 0.46354543545774D-17 3 12 3 18 -0.36637372330463D+01 -0.13839719374386D-14 1 13 3 18 -0.57946867444900D-02 0.48972342025698D-16 2 13 3 18 -0.30541858565605D+00 0.99639505199961D-17 3 13 3 18 0.10975158984982D+01 0.14914383832257D-14 1 14 3 18 0.35443867941966D-01 0.26254943514666D-16 2 14 3 18 0.14172485951549D+00 -0.24930288772476D-17 3 14 3 18 0.18487674087042D+01 -0.25085691768208D-16 1 15 3 18 0.16334488264199D-01 0.60195052918774D-16 2 15 3 18 0.24046912497811D-01 -0.22582672214452D-16 3 15 3 18 -0.88010030951782D+00 -0.73304793746192D-15 1 16 3 18 0.58579992336693D-01 -0.49172027615982D-18 2 16 3 18 -0.11748407245336D-01 0.50022989886897D-16 3 16 3 18 -0.69776832341433D+00 -0.24356716431955D-16 1 17 3 18 -0.16701820768249D+00 -0.35736039966319D-16 2 17 3 18 -0.74905075827223D-01 0.17017959583876D-16 3 17 3 18 -0.41887629667904D+00 0.10047331583022D-14 1 18 3 18 0.12570340613316D+01 0.00000000000000D+00 2 18 3 18 0.20415876309585D+01 0.00000000000000D+00 3 18 3 18 0.15296984004429D+02 0.00000000000000D+00 1 19 3 18 0.62166479281129D-01 0.24169524079203D-16 2 19 3 18 0.13491471216581D+00 0.19625085109604D-16 3 19 3 18 -0.19584409533204D+01 -0.84901425153141D-15 1 20 3 18 0.33355766451464D-01 0.58238836375886D-16 2 20 3 18 0.65672130808355D-01 -0.10423476339560D-15 3 20 3 18 -0.15417956544810D+01 0.59718662231123D-16 1 22 3 18 -0.19332058654638D-01 0.00000000000000D+00 2 22 3 18 -0.64318482640692D+00 0.00000000000000D+00 3 22 3 18 -0.49879381668990D+02 0.00000000000000D+00 1 1 1 19 -0.12068954502770D+00 0.66087773300862D-15 2 1 1 19 0.36233757220371D+00 0.10641944536708D-16 3 1 1 19 0.65718925843968D+00 0.15146865381197D-15 1 2 1 19 -0.61006835472892D+00 -0.59615727525842D-16 2 2 1 19 -0.45466061858318D+00 0.67171661048263D-16 3 2 1 19 0.78331374891610D+00 0.12214438971797D-15 1 3 1 19 0.28264640601238D-01 -0.92139029761555D-15 2 3 1 19 0.38810233286854D-01 -0.36093801875902D-17 3 3 1 19 -0.35192012181663D+00 -0.11600383600813D-15 1 4 1 19 -0.14436323196733D+00 -0.12144307459058D-16 2 4 1 19 0.28804976638798D+00 0.63963776258785D-16 3 4 1 19 0.28620407326723D+00 0.53907411914521D-16 1 5 1 19 -0.61749241585744D-01 -0.33129667180942D-15 2 5 1 19 -0.12514254043901D-01 -0.14885976625228D-16 3 5 1 19 -0.49107434131211D+00 -0.22547608697163D-15 1 6 1 19 0.14572086039210D+00 -0.29900401012140D-15 2 6 1 19 -0.10265494691600D+01 0.71422111272566D-17 3 6 1 19 0.55647288619470D+00 0.69551867632395D-15 1 7 1 19 -0.37877129705314D-01 0.82181504605089D-15 2 7 1 19 -0.80228829136542D-01 -0.35820505499466D-16 3 7 1 19 0.56222819860821D+00 -0.32669725761954D-15 1 8 1 19 -0.47205798319017D+00 -0.26402514900267D-15 2 8 1 19 0.75348403514224D+00 0.10519299950177D-16 3 8 1 19 -0.61569286033524D+00 0.88281887182369D-16 1 9 1 19 0.14662361543806D-01 -0.49829878855886D-16 2 9 1 19 0.49896941366672D+00 0.19008388597320D-16 3 9 1 19 -0.14254744662861D+01 -0.22964023772571D-16 1 10 1 19 -0.76437194269625D+00 -0.77465756276236D-16 2 10 1 19 0.99208058970534D+00 -0.89066538616191D-16 3 10 1 19 0.18293426717494D+01 0.64446227512283D-17 1 11 1 19 -0.16229326487588D+01 0.85016978194032D-17 2 11 1 19 0.84607588494764D+00 0.98788541182014D-16 3 11 1 19 -0.26868171993406D+01 -0.86829554039201D-16 1 12 1 19 -0.14317947827315D+00 0.15136555201918D-15 2 12 1 19 0.54965799850786D+00 0.10742322787073D-16 3 12 1 19 0.19107834776752D+01 0.14763723795954D-15 1 13 1 19 -0.23324566422979D+00 -0.15738512069920D-16 2 13 1 19 -0.18233885955755D+00 0.22346758107772D-17 3 13 1 19 -0.58580035591798D-01 -0.25717600636276D-17 1 14 1 19 0.32395655219218D+00 0.15522778741972D-15 2 14 1 19 0.13518632858762D+00 0.48384263711052D-16 3 14 1 19 -0.16337033535742D-01 0.43014788585804D-16 1 15 1 19 0.95623294368764D+00 0.18227606075629D-15 2 15 1 19 0.10710026254495D+01 -0.18686783949588D-16 3 15 1 19 0.35443867941969D-01 -0.12728027701046D-16 1 16 1 19 -0.57363572065418D+01 0.80844221129564D-16 2 16 1 19 -0.95469644395250D+00 -0.38893303989191D-18 3 16 1 19 -0.57946867444928D-02 -0.32143669540553D-16 1 17 1 19 -0.51645554603745D+00 -0.53604395782106D-16 2 17 1 19 0.32470660052582D+00 -0.13640963768916D-16 3 17 1 19 0.33355766451468D-01 0.22452441706793D-16 1 18 1 19 0.39749073702135D+00 -0.60455452269144D-16 2 18 1 19 -0.16109511908445D+00 0.20340759390948D-17 3 18 1 19 0.62166479281129D-01 -0.24169524079203D-16 1 19 1 19 0.12535023461132D+02 0.00000000000000D+00 2 19 1 19 -0.58392681818056D+01 0.00000000000000D+00 3 19 1 19 -0.12570584673453D+01 0.00000000000000D+00 1 20 1 19 -0.38809165729708D+01 -0.17512552497357D-15 2 20 1 19 0.28593969073651D+01 -0.86643534986639D-17 3 20 1 19 0.16701677051493D+00 0.26525726885194D-16 1 22 1 19 -0.59666225482995D+02 0.00000000000000D+00 2 22 1 19 0.10058609980572D+02 0.00000000000000D+00 3 22 1 19 -0.11301434246461D-02 0.00000000000000D+00 1 1 2 19 0.44226102341463D+00 0.10641944536708D-16 2 1 2 19 -0.31551995169717D+00 -0.64619732413977D-15 3 1 2 19 0.50703823584813D+00 0.63351840100069D-16 1 2 2 19 -0.34687872744991D+00 0.67171661048263D-16 2 2 2 19 -0.84809723947382D+00 0.70741799616829D-15 3 2 2 19 0.83980060330535D+00 0.28511320779630D-16 1 3 2 19 0.19808731105280D+00 -0.36093801875902D-17 2 3 2 19 0.30018923206278D+00 -0.66814999564684D-15 3 3 2 19 -0.35485508012221D+00 -0.13664787718504D-16 1 4 2 19 0.14974007338999D+00 0.63963776258785D-16 2 4 2 19 -0.45654092233172D+00 0.51247508478580D-15 3 4 2 19 0.35777067486426D+00 0.43406200721385D-16 1 5 2 19 -0.20803773942918D-01 -0.14885976625228D-16 2 5 2 19 0.94978646232526D-01 -0.70394381565020D-15 3 5 2 19 0.58124986485142D-01 -0.21330044356876D-15 1 6 2 19 0.57907236680454D+00 0.71422111272566D-17 2 6 2 19 -0.14418862649181D+00 -0.73868527818751D-15 3 6 2 19 -0.43393246734610D-01 -0.10918962662141D-15 1 7 2 19 -0.13310522665981D-01 -0.35820505499466D-16 2 7 2 19 0.15082554883131D-01 0.23398341548826D-15 3 7 2 19 -0.20478799764695D+00 0.79397770159796D-15 1 8 2 19 -0.80828268218609D+00 0.10519299950177D-16 2 8 2 19 -0.33012601691983D-01 0.95436963017721D-15 3 8 2 19 0.14560451909226D+00 0.29521547028390D-15 1 9 2 19 0.39800972332158D+00 0.19008388597320D-16 2 9 2 19 -0.60432485105596D+00 0.20909014145487D-16 3 9 2 19 0.27804859619070D+01 0.10940473580340D-15 1 10 2 19 0.83180397548951D+00 -0.89066538616191D-16 2 10 2 19 -0.10989501560636D+01 0.24653766747314D-15 3 10 2 19 -0.21454480474470D+01 -0.94539367790957D-16 1 11 2 19 0.92466905239827D+00 0.98788541182014D-16 2 11 2 19 -0.19339794421715D+00 -0.14121108827776D-15 3 11 2 19 0.16574450187903D+01 0.49552265361454D-16 1 12 2 19 0.56907900921136D+00 0.10742322787073D-16 2 12 2 19 -0.42505835380042D+00 -0.57539581193427D-16 3 12 2 19 -0.20255772774882D+01 -0.52558359731768D-16 1 13 2 19 0.18233978195846D+00 0.22346758107772D-17 2 13 2 19 0.29693616356469D+00 -0.78105557192795D-16 3 13 2 19 -0.11749352448802D-01 -0.92410037920463D-16 1 14 2 19 -0.13518674534702D+00 0.48384263711052D-16 2 14 2 19 -0.38035239243248D+00 -0.21299519097452D-15 3 14 2 19 0.24048306292486D-01 0.26013946545291D-16 1 15 2 19 -0.10710026254495D+01 -0.18686783949588D-16 2 15 2 19 -0.64647188952478D+01 -0.14418365218723D-16 3 15 2 19 -0.14172485951549D+00 -0.31656594076235D-17 1 16 2 19 0.95469644395251D+00 -0.38893303989191D-18 2 16 2 19 0.88565533669038D+00 0.20899210254877D-15 3 16 2 19 0.30541858565605D+00 -0.30281851765161D-16 1 17 2 19 0.32470660052582D+00 -0.13640963768916D-16 2 17 2 19 -0.61864659889725D+00 -0.10980867713107D-15 3 17 2 19 0.65672130808356D-01 0.11151299802869D-15 1 18 2 19 -0.16109511908445D+00 0.20340759390948D-17 2 18 2 19 0.44914722360172D+00 -0.66797074121275D-16 3 18 2 19 0.13491471216581D+00 -0.19625085109604D-16 1 19 2 19 -0.58392724026003D+01 0.00000000000000D+00 2 19 2 19 0.13758076541722D+02 0.00000000000000D+00 3 19 2 19 -0.20415598055507D+01 0.00000000000000D+00 1 20 2 19 0.28593976346433D+01 -0.86643534986639D-17 2 20 2 19 -0.42081897111825D+01 0.11289837228609D-15 3 20 2 19 0.74906335409612D-01 0.15818304481903D-16 1 22 2 19 0.10173324396281D+02 0.00000000000000D+00 2 22 2 19 -0.60532578336789D+02 0.00000000000000D+00 3 22 2 19 0.45008015991410D+00 0.00000000000000D+00 1 1 3 19 0.68182003040279D+00 0.15146865381197D-15 2 1 3 19 0.52515542902002D+00 0.63351840100069D-16 3 1 3 19 0.10425035738157D+01 0.22878758314701D-14 1 2 3 19 0.65187452572476D+00 0.12214438971797D-15 2 2 3 19 0.87453604592928D+00 0.28511320779630D-16 3 2 3 19 -0.25037435958718D+01 -0.19725366670101D-14 1 3 3 19 -0.30078101445082D+00 -0.11600383600813D-15 2 3 3 19 -0.30570828755138D+00 -0.13664787718504D-16 3 3 3 19 0.77323372312276D+00 0.14587533752576D-14 1 4 3 19 0.49053289124475D+00 0.53907411914521D-16 2 4 3 19 0.40598958753675D+00 0.43406200721385D-16 3 4 3 19 -0.32666255455176D+00 -0.11874318266631D-14 1 5 3 19 0.10357198728729D+00 -0.22547608697163D-15 2 5 3 19 0.17716441144123D+00 -0.21330044356876D-15 3 5 3 19 0.37892032617639D+01 -0.62792026748863D-15 1 6 3 19 -0.12614849187088D+01 0.69551867632395D-15 2 6 3 19 0.85602264129840D+00 -0.10918962662141D-15 3 6 3 19 -0.42317235399663D+01 0.13184154622993D-14 1 7 3 19 -0.83818842403360D-02 -0.32669725761954D-15 2 7 3 19 -0.31484626762451D+00 0.79397770159796D-15 3 7 3 19 0.37080430568572D+01 0.98979301282431D-15 1 8 3 19 0.12067545544194D+01 0.88281887182369D-16 2 8 3 19 -0.68649872495391D+00 0.29521547028390D-15 3 8 3 19 -0.42530775815608D+01 -0.97098469663920D-15 1 9 3 19 -0.95995998170723D+00 -0.22964023772571D-16 2 9 3 19 0.16447879168192D+01 0.10940473580340D-15 3 9 3 19 -0.41520018439911D+01 -0.15780982317576D-14 1 10 3 19 0.71982304519633D+00 0.64446227512283D-17 2 10 3 19 -0.97924848375820D+00 -0.94539367790957D-16 3 10 3 19 -0.11154366465567D+01 -0.32262139865755D-15 1 11 3 19 -0.12638910221799D+01 -0.86829554039201D-16 2 11 3 19 0.99484767618448D+00 0.49552265361454D-16 3 11 3 19 -0.14182402230214D+01 0.16332022000679D-14 1 12 3 19 0.12101427438262D+01 0.14763723795954D-15 2 12 3 19 -0.12123977694113D+01 -0.52558359731768D-16 3 12 3 19 -0.36637372330463D+01 0.45483895087509D-15 1 13 3 19 -0.58579992336693D-01 -0.25717600636276D-17 2 13 3 19 0.11748407245336D-01 -0.92410037920463D-16 3 13 3 19 -0.69776832341433D+00 -0.27805862367119D-16 1 14 3 19 -0.16334488264200D-01 0.43014788585804D-16 2 14 3 19 -0.24046912497810D-01 0.26013946545291D-16 3 14 3 19 -0.88010030951780D+00 0.25418616135032D-15 1 15 3 19 -0.35443867941966D-01 -0.12728027701046D-16 2 15 3 19 -0.14172485951549D+00 -0.31656594076235D-17 3 15 3 19 0.18487674087042D+01 -0.41934120675538D-16 1 16 3 19 0.57946867444920D-02 -0.32143669540553D-16 2 16 3 19 0.30541858565605D+00 -0.30281851765161D-16 3 16 3 19 0.10975158984981D+01 0.39653525669010D-15 1 17 3 19 -0.33355766451467D-01 0.22452441706793D-16 2 17 3 19 -0.65672130808356D-01 0.11151299802869D-15 3 17 3 19 -0.15417956544810D+01 0.77791672221634D-16 1 18 3 19 -0.62166479281127D-01 -0.24169524079203D-16 2 18 3 19 -0.13491471216581D+00 -0.19625085109604D-16 3 18 3 19 -0.19584409533204D+01 0.84901425153141D-15 1 19 3 19 -0.12570340613316D+01 0.00000000000000D+00 2 19 3 19 -0.20415876309585D+01 0.00000000000000D+00 3 19 3 19 0.15296984004430D+02 0.00000000000000D+00 1 20 3 19 0.16701820768249D+00 0.26525726885194D-16 2 20 3 19 0.74905075827215D-01 0.15818304481903D-16 3 20 3 19 -0.41887629667901D+00 -0.71574815983961D-15 1 22 3 19 0.19332062724477D-01 0.00000000000000D+00 2 22 3 19 0.64318482099464D+00 0.00000000000000D+00 3 22 3 19 -0.49879381635686D+02 0.00000000000000D+00 1 1 1 20 -0.61006835472897D+00 -0.35667554013304D-15 2 1 1 20 -0.45466061858329D+00 0.71243927875379D-16 3 1 1 20 0.78331374891633D+00 0.27590809359557D-15 1 2 1 20 -0.12068954502773D+00 0.46849267652837D-15 2 2 1 20 0.36233757220374D+00 0.67681305636528D-16 3 2 1 20 0.65718925843960D+00 0.11652560812199D-15 1 3 1 20 -0.14436323196735D+00 0.91547922116333D-16 2 3 1 20 0.28804976638800D+00 -0.22648612388255D-16 3 3 1 20 0.28620407326718D+00 -0.13857127472674D-15 1 4 1 20 0.28264640601246D-01 -0.11631186902758D-15 2 4 1 20 0.38810233286857D-01 0.32973602142844D-16 3 4 1 20 -0.35192012181664D+00 -0.17471817922494D-16 1 5 1 20 -0.61749241585761D-01 -0.32475389971199D-15 2 5 1 20 -0.12514254043905D-01 -0.55575491183039D-17 3 5 1 20 -0.49107434131213D+00 -0.14956530333043D-15 1 6 1 20 0.14572086039215D+00 0.14541165250011D-15 2 6 1 20 -0.10265494691603D+01 -0.17222408892574D-16 3 6 1 20 0.55647288619467D+00 0.14419647979723D-15 1 7 1 20 -0.37877129705300D-01 0.11550174301002D-15 2 7 1 20 -0.80228829136543D-01 -0.34764633724451D-16 3 7 1 20 0.56222819860823D+00 0.16676507451688D-16 1 8 1 20 -0.47205798319052D+00 0.10815507284838D-14 2 8 1 20 0.75348403514232D+00 0.22780231527695D-16 3 8 1 20 -0.61569286033494D+00 0.10186532904639D-15 1 9 1 20 -0.76437194269629D+00 0.57129991600930D-15 2 9 1 20 0.99208058970532D+00 0.20297752014962D-16 3 9 1 20 0.18293426717494D+01 -0.97548571315746D-16 1 10 1 20 0.14662361543761D-01 -0.26223307929542D-15 2 10 1 20 0.49896941366673D+00 0.52061873364443D-16 3 10 1 20 -0.14254744662861D+01 0.86363443445111D-17 1 11 1 20 -0.14317947827315D+00 -0.15835511867675D-15 2 11 1 20 0.54965799850785D+00 -0.21564750480621D-16 3 11 1 20 0.19107834776751D+01 0.10989970498616D-15 1 12 1 20 -0.16229326487588D+01 -0.88148798500575D-16 2 12 1 20 0.84607588494765D+00 0.90438071529908D-16 3 12 1 20 -0.26868171993405D+01 -0.27716099514646D-17 1 13 1 20 0.32395655219218D+00 -0.10653384055532D-15 2 13 1 20 0.13518632858762D+00 -0.47415433331157D-16 3 13 1 20 -0.16337033535740D-01 0.28316891254939D-16 1 14 1 20 -0.23324566422979D+00 -0.71541216741645D-17 2 14 1 20 -0.18233885955755D+00 -0.12428380002657D-16 3 14 1 20 -0.58580035591795D-01 0.20065906224653D-17 1 15 1 20 -0.57363572065418D+01 0.15078763200835D-15 2 15 1 20 -0.95469644395251D+00 -0.21394449077780D-16 3 15 1 20 -0.57946867444826D-02 -0.50488390160654D-16 1 16 1 20 0.95623294368768D+00 0.36634211693696D-16 2 16 1 20 0.10710026254495D+01 0.33852178127381D-17 3 16 1 20 0.35443867941967D-01 -0.17725986518913D-16 1 17 1 20 0.39749073702135D+00 0.30014219852255D-16 2 17 1 20 -0.16109511908445D+00 0.12307454582832D-18 3 17 1 20 0.62166479281126D-01 0.18735084312373D-16 1 18 1 20 -0.51645554603745D+00 0.34955046904666D-16 2 18 1 20 0.32470660052582D+00 -0.27221202674133D-16 3 18 1 20 0.33355766451464D-01 -0.58238836375886D-16 1 19 1 20 -0.38809165729708D+01 0.17512552497357D-15 2 19 1 20 0.28593969073651D+01 0.86643534986639D-17 3 19 1 20 0.16701677051493D+00 -0.26525726885194D-16 1 20 1 20 0.12535023461133D+02 0.00000000000000D+00 2 20 1 20 -0.58392681818052D+01 0.00000000000000D+00 3 20 1 20 -0.12570584673456D+01 0.00000000000000D+00 1 22 1 20 -0.59666225479290D+02 0.00000000000000D+00 2 22 1 20 0.10058609976030D+02 0.00000000000000D+00 3 22 1 20 -0.11301410304961D-02 0.00000000000000D+00 1 1 2 20 -0.34687872745002D+00 0.71243927875379D-16 2 1 2 20 -0.84809723947373D+00 0.43070691908749D-15 3 1 2 20 0.83980060330548D+00 -0.15171250368160D-16 1 2 2 20 0.44226102341466D+00 0.67681305636528D-16 2 2 2 20 -0.31551995169712D+00 0.95615470997254D-15 3 2 2 20 0.50703823584821D+00 0.37297502647032D-16 1 3 2 20 0.14974007339002D+00 -0.22648612388255D-16 2 3 2 20 -0.45654092233173D+00 0.28559685901210D-15 3 3 2 20 0.35777067486432D+00 -0.10063266012984D-15 1 4 2 20 0.19808731105280D+00 0.32973602142844D-16 2 4 2 20 0.30018923206278D+00 0.15418773570593D-15 3 4 2 20 -0.35485508012223D+00 -0.17422367807414D-15 1 5 2 20 -0.20803773942923D-01 -0.55575491183039D-17 2 5 2 20 0.94978646232504D-01 0.76430568381739D-15 3 5 2 20 0.58124986485173D-01 -0.15034087280436D-15 1 6 2 20 0.57907236680424D+00 -0.17222408892574D-16 2 6 2 20 -0.14418862649171D+00 0.54922050726066D-15 3 6 2 20 -0.43393246734524D-01 0.22274335597184D-15 1 7 2 20 -0.13310522665982D-01 -0.34764633724451D-16 2 7 2 20 0.15082554883153D-01 0.52223469469468D-15 3 7 2 20 -0.20478799764696D+00 0.12328977431911D-15 1 8 2 20 -0.80828268218600D+00 0.22780231527695D-16 2 8 2 20 -0.33012601691780D-01 0.67977509708218D-15 3 8 2 20 0.14560451909207D+00 0.43062313554390D-15 1 9 2 20 0.83180397548950D+00 0.20297752014962D-16 2 9 2 20 -0.10989501560636D+01 -0.11467926428737D-15 3 9 2 20 -0.21454480474469D+01 -0.94314770134959D-16 1 10 2 20 0.39800972332159D+00 0.52061873364443D-16 2 10 2 20 -0.60432485105597D+00 -0.13551739176166D-15 3 10 2 20 0.27804859619069D+01 -0.11280830607539D-15 1 11 2 20 0.56907900921135D+00 -0.21564750480621D-16 2 11 2 20 -0.42505835380046D+00 0.36798320229780D-15 3 11 2 20 -0.20255772774882D+01 -0.43791145737077D-16 1 12 2 20 0.92466905239827D+00 0.90438071529908D-16 2 12 2 20 -0.19339794421720D+00 -0.10770091817007D-15 3 12 2 20 0.16574450187903D+01 0.25144853571601D-16 1 13 2 20 -0.13518674534702D+00 -0.47415433331157D-16 2 13 2 20 -0.38035239243249D+00 -0.19404678200673D-15 3 13 2 20 0.24048306292484D-01 0.11427050079996D-16 1 14 2 20 0.18233978195846D+00 -0.12428380002657D-16 2 14 2 20 0.29693616356469D+00 0.56687844358756D-16 3 14 2 20 -0.11749352448802D-01 0.10664869943237D-16 1 15 2 20 0.95469644395250D+00 -0.21394449077780D-16 2 15 2 20 0.88565533669040D+00 0.18088225803494D-16 3 15 2 20 0.30541858565605D+00 -0.29786596439677D-16 1 16 2 20 -0.10710026254495D+01 0.33852178127381D-17 2 16 2 20 -0.64647188952479D+01 -0.45037880146693D-17 3 16 2 20 -0.14172485951549D+00 0.58747333384920D-18 1 17 2 20 -0.16109511908445D+00 0.12307454582832D-18 2 17 2 20 0.44914722360174D+00 -0.59707085872013D-16 3 17 2 20 0.13491471216581D+00 -0.24940022573201D-16 1 18 2 20 0.32470660052582D+00 -0.27221202674133D-16 2 18 2 20 -0.61864659889725D+00 -0.60981978865386D-17 3 18 2 20 0.65672130808355D-01 0.10423476339560D-15 1 19 2 20 0.28593976346433D+01 0.86643534986639D-17 2 19 2 20 -0.42081897111825D+01 -0.11289837228609D-15 3 19 2 20 0.74906335409612D-01 -0.15818304481903D-16 1 20 2 20 -0.58392724025999D+01 0.00000000000000D+00 2 20 2 20 0.13758076541722D+02 0.00000000000000D+00 3 20 2 20 -0.20415598055509D+01 0.00000000000000D+00 1 22 2 20 0.10173324395806D+02 0.00000000000000D+00 2 22 2 20 -0.60532578342703D+02 0.00000000000000D+00 3 22 2 20 0.45008016225586D+00 0.00000000000000D+00 1 1 3 20 0.65187452572499D+00 0.27590809359557D-15 2 1 3 20 0.87453604592941D+00 -0.15171250368160D-16 3 1 3 20 -0.25037435958720D+01 0.10492863082214D-14 1 2 3 20 0.68182003040271D+00 0.11652560812199D-15 2 2 3 20 0.52515542902010D+00 0.37297502647032D-16 3 2 3 20 0.10425035738157D+01 -0.35016936164096D-14 1 3 3 20 0.49053289124469D+00 -0.13857127472674D-15 2 3 3 20 0.40598958753681D+00 -0.10063266012984D-15 3 3 3 20 -0.32666255455165D+00 -0.18983213450900D-14 1 4 3 20 -0.30078101445082D+00 -0.17471817922494D-16 2 4 3 20 -0.30570828755139D+00 -0.17422367807414D-15 3 4 3 20 0.77323372312275D+00 -0.30975462066112D-14 1 5 3 20 0.10357198728727D+00 -0.14956530333043D-15 2 5 3 20 0.17716441144126D+00 -0.15034087280436D-15 3 5 3 20 0.37892032617639D+01 0.12650309849828D-14 1 6 3 20 -0.12614849187088D+01 0.14419647979723D-15 2 6 3 20 0.85602264129849D+00 0.22274335597184D-15 3 6 3 20 -0.42317235399666D+01 -0.49719767334037D-15 1 7 3 20 -0.83818842403147D-02 0.16676507451688D-16 2 7 3 20 -0.31484626762451D+00 0.12328977431911D-15 3 7 3 20 0.37080430568572D+01 -0.14331886448797D-15 1 8 3 20 0.12067545544197D+01 0.10186532904639D-15 2 8 3 20 -0.68649872495410D+00 0.43062313554390D-15 3 8 3 20 -0.42530775815608D+01 -0.57398472112883D-15 1 9 3 20 0.71982304519629D+00 -0.97548571315746D-16 2 9 3 20 -0.97924848375814D+00 -0.94314770134959D-16 3 9 3 20 -0.11154366465566D+01 -0.80666316901717D-15 1 10 3 20 -0.95995998170726D+00 0.86363443445111D-17 2 10 3 20 0.16447879168191D+01 -0.11280830607539D-15 3 10 3 20 -0.41520018439910D+01 -0.11934110409213D-14 1 11 3 20 0.12101427438261D+01 0.10989970498616D-15 2 11 3 20 -0.12123977694113D+01 -0.43791145737077D-16 3 11 3 20 -0.36637372330462D+01 -0.12147159053349D-14 1 12 3 20 -0.12638910221798D+01 -0.27716099514646D-17 2 12 3 20 0.99484767618448D+00 0.25144853571601D-16 3 12 3 20 -0.14182402230213D+01 0.14069075249509D-14 1 13 3 20 -0.16334488264198D-01 0.28316891254939D-16 2 13 3 20 -0.24046912497811D-01 0.11427050079996D-16 3 13 3 20 -0.88010030951782D+00 -0.17705442938939D-15 1 14 3 20 -0.58579992336690D-01 0.20065906224653D-17 2 14 3 20 0.11748407245336D-01 0.10664869943237D-16 3 14 3 20 -0.69776832341435D+00 -0.10996806099496D-17 1 15 3 20 0.57946867445022D-02 -0.50488390160654D-16 2 15 3 20 0.30541858565605D+00 -0.29786596439677D-16 3 15 3 20 0.10975158984981D+01 -0.11250515276125D-14 1 16 3 20 -0.35443867941967D-01 -0.17725986518913D-16 2 16 3 20 -0.14172485951549D+00 0.58747333384920D-18 3 16 3 20 0.18487674087043D+01 -0.17784848328192D-17 1 17 3 20 -0.62166479281129D-01 0.18735084312373D-16 2 17 3 20 -0.13491471216581D+00 -0.24940022573201D-16 3 17 3 20 -0.19584409533204D+01 0.41415806158633D-15 1 18 3 20 -0.33355766451470D-01 -0.58238836375886D-16 2 18 3 20 -0.65672130808356D-01 0.10423476339560D-15 3 18 3 20 -0.15417956544810D+01 -0.59718662231123D-16 1 19 3 20 0.16701820768249D+00 -0.26525726885194D-16 2 19 3 20 0.74905075827215D-01 -0.15818304481903D-16 3 19 3 20 -0.41887629667901D+00 0.71574815983961D-15 1 20 3 20 -0.12570340613319D+01 0.00000000000000D+00 2 20 3 20 -0.20415876309586D+01 0.00000000000000D+00 3 20 3 20 0.15296984004430D+02 0.00000000000000D+00 1 22 3 20 0.19332058655515D-01 0.00000000000000D+00 2 22 3 20 0.64318482643131D+00 0.00000000000000D+00 3 22 3 20 -0.49879381668991D+02 0.00000000000000D+00 1 1 1 22 -0.54454847927476D+02 0.00000000000000D+00 2 1 1 22 0.23263412774042D+00 0.00000000000000D+00 3 1 1 22 0.84270752667703D-07 0.00000000000000D+00 1 2 1 22 -0.54454847927478D+02 0.00000000000000D+00 2 2 1 22 0.23263412773961D+00 0.00000000000000D+00 3 2 1 22 -0.84117587715519D-07 0.00000000000000D+00 1 3 1 22 -0.54454847927851D+02 0.00000000000000D+00 2 3 1 22 -0.23263412724320D+00 0.00000000000000D+00 3 3 1 22 -0.83137355873317D-07 0.00000000000000D+00 1 4 1 22 -0.54454847927852D+02 0.00000000000000D+00 2 4 1 22 -0.23263412724209D+00 0.00000000000000D+00 3 4 1 22 0.85250601935833D-07 0.00000000000000D+00 1 5 1 22 -0.30884069492133D+02 0.00000000000000D+00 2 5 1 22 -0.44126101369814D+01 0.00000000000000D+00 3 5 1 22 -0.82101523428068D+01 0.00000000000000D+00 1 6 1 22 -0.30884069492147D+02 0.00000000000000D+00 2 6 1 22 -0.44126101369787D+01 0.00000000000000D+00 3 6 1 22 0.82101523428146D+01 0.00000000000000D+00 1 7 1 22 -0.30884069492125D+02 0.00000000000000D+00 2 7 1 22 0.44126101369848D+01 0.00000000000000D+00 3 7 1 22 0.82101523427999D+01 0.00000000000000D+00 1 8 1 22 -0.30884069492140D+02 0.00000000000000D+00 2 8 1 22 0.44126101369861D+01 0.00000000000000D+00 3 8 1 22 -0.82101523427971D+01 0.00000000000000D+00 1 9 1 22 -0.50637852326132D+02 0.00000000000000D+00 2 9 1 22 0.14168772609254D+00 0.00000000000000D+00 3 9 1 22 0.98435275136598D-08 0.00000000000000D+00 1 10 1 22 -0.50637852326132D+02 0.00000000000000D+00 2 10 1 22 0.14168772609253D+00 0.00000000000000D+00 3 10 1 22 -0.98506745650566D-08 0.00000000000000D+00 1 11 1 22 -0.50637852326124D+02 0.00000000000000D+00 2 11 1 22 -0.14168772610573D+00 0.00000000000000D+00 3 11 1 22 0.98396944736004D-08 0.00000000000000D+00 1 12 1 22 -0.50637852326124D+02 0.00000000000000D+00 2 12 1 22 -0.14168772610575D+00 0.00000000000000D+00 3 12 1 22 -0.98545066291715D-08 0.00000000000000D+00 1 13 1 22 -0.59563277654309D+02 0.00000000000000D+00 2 13 1 22 -0.10100267574302D+02 0.00000000000000D+00 3 13 1 22 0.21202404084605D-01 0.00000000000000D+00 1 14 1 22 -0.59563277650604D+02 0.00000000000000D+00 2 14 1 22 -0.10100267573828D+02 0.00000000000000D+00 3 14 1 22 0.21202400015639D-01 0.00000000000000D+00 1 15 1 22 -0.59563277654300D+02 0.00000000000000D+00 2 15 1 22 -0.10100267574306D+02 0.00000000000000D+00 3 15 1 22 -0.21202404070821D-01 0.00000000000000D+00 1 16 1 22 -0.59563277650595D+02 0.00000000000000D+00 2 16 1 22 -0.10100267573832D+02 0.00000000000000D+00 3 16 1 22 -0.21202400001859D-01 0.00000000000000D+00 1 17 1 22 -0.59563277654290D+02 0.00000000000000D+00 2 17 1 22 0.10100267574292D+02 0.00000000000000D+00 3 17 1 22 -0.21202404098220D-01 0.00000000000000D+00 1 18 1 22 -0.59563277650585D+02 0.00000000000000D+00 2 18 1 22 0.10100267573817D+02 0.00000000000000D+00 3 18 1 22 -0.21202400029256D-01 0.00000000000000D+00 1 19 1 22 -0.59563277654282D+02 0.00000000000000D+00 2 19 1 22 0.10100267574287D+02 0.00000000000000D+00 3 19 1 22 0.21202404099095D-01 0.00000000000000D+00 1 20 1 22 -0.59563277650577D+02 0.00000000000000D+00 2 20 1 22 0.10100267573812D+02 0.00000000000000D+00 3 20 1 22 0.21202400030133D-01 0.00000000000000D+00 1 22 1 22 -0.23698191555863D+03 0.00000000000000D+00 2 22 1 22 0.00000000000000D+00 0.00000000000000D+00 3 22 1 22 0.00000000000000D+00 0.00000000000000D+00 1 23 1 22 -0.26250055792531D-11 0.21024012392123D-10 2 23 1 22 -0.24042907075287D-11 0.59233120144886D-10 3 23 1 22 -0.23577725738118D-11 0.11149059106486D-11 1 24 1 22 0.77024386068610D-12 -0.14492069030274D-10 2 24 1 22 0.28345401077188D-06 0.32847078464977D+00 3 24 1 22 0.30517858666235D-12 0.11788331075180D-09 1 1 2 22 0.49574842436298D+00 0.00000000000000D+00 2 1 2 22 -0.54110329156581D+02 0.00000000000000D+00 3 1 2 22 -0.13489974907705D-06 0.00000000000000D+00 1 2 2 22 0.49574842436294D+00 0.00000000000000D+00 2 2 2 22 -0.54110329156581D+02 0.00000000000000D+00 3 2 2 22 0.13483339888500D-06 0.00000000000000D+00 1 3 2 22 -0.49574842432935D+00 0.00000000000000D+00 2 3 2 22 -0.54110329156863D+02 0.00000000000000D+00 3 3 2 22 -0.13519319891787D-06 0.00000000000000D+00 1 4 2 22 -0.49574842432830D+00 0.00000000000000D+00 2 4 2 22 -0.54110329156862D+02 0.00000000000000D+00 3 4 2 22 0.13454019410055D-06 0.00000000000000D+00 1 5 2 22 0.31461394958542D+01 0.00000000000000D+00 2 5 2 22 -0.29992912830597D+02 0.00000000000000D+00 3 5 2 22 -0.53098562352783D+00 0.00000000000000D+00 1 6 2 22 0.31461394958613D+01 0.00000000000000D+00 2 6 2 22 -0.29992912830629D+02 0.00000000000000D+00 3 6 2 22 0.53098562347370D+00 0.00000000000000D+00 1 7 2 22 -0.31461394958694D+01 0.00000000000000D+00 2 7 2 22 -0.29992912830609D+02 0.00000000000000D+00 3 7 2 22 -0.53098562355466D+00 0.00000000000000D+00 1 8 2 22 -0.31461394958766D+01 0.00000000000000D+00 2 8 2 22 -0.29992912830633D+02 0.00000000000000D+00 3 8 2 22 0.53098562350563D+00 0.00000000000000D+00 1 9 2 22 -0.10147987406137D+01 0.00000000000000D+00 2 9 2 22 -0.49309735555495D+02 0.00000000000000D+00 3 9 2 22 -0.36340630140547D-08 0.00000000000000D+00 1 10 2 22 -0.10147987406137D+01 0.00000000000000D+00 2 10 2 22 -0.49309735555495D+02 0.00000000000000D+00 3 10 2 22 0.36284942782610D-08 0.00000000000000D+00 1 11 2 22 0.10147987406312D+01 0.00000000000000D+00 2 11 2 22 -0.49309735555495D+02 0.00000000000000D+00 3 11 2 22 0.36239973871203D-08 0.00000000000000D+00 1 12 2 22 0.10147987406312D+01 0.00000000000000D+00 2 12 2 22 -0.49309735555495D+02 0.00000000000000D+00 3 12 2 22 -0.36385638013843D-08 0.00000000000000D+00 1 13 2 22 -0.99886251723246D+01 0.00000000000000D+00 2 13 2 22 -0.60423403772081D+02 0.00000000000000D+00 3 13 2 22 -0.64438600129351D+00 0.00000000000000D+00 1 14 2 22 -0.99886251677825D+01 0.00000000000000D+00 2 14 2 22 -0.60423403777995D+02 0.00000000000000D+00 3 14 2 22 -0.64438600673018D+00 0.00000000000000D+00 1 15 2 22 -0.99886251723279D+01 0.00000000000000D+00 2 15 2 22 -0.60423403772105D+02 0.00000000000000D+00 3 15 2 22 0.64438600128798D+00 0.00000000000000D+00 1 16 2 22 -0.99886251677858D+01 0.00000000000000D+00 2 16 2 22 -0.60423403778019D+02 0.00000000000000D+00 3 16 2 22 0.64438600672464D+00 0.00000000000000D+00 1 17 2 22 0.99886251723216D+01 0.00000000000000D+00 2 17 2 22 -0.60423403772073D+02 0.00000000000000D+00 3 17 2 22 -0.64438600128049D+00 0.00000000000000D+00 1 18 2 22 0.99886251677795D+01 0.00000000000000D+00 2 18 2 22 -0.60423403777986D+02 0.00000000000000D+00 3 18 2 22 -0.64438600671716D+00 0.00000000000000D+00 1 19 2 22 0.99886251723268D+01 0.00000000000000D+00 2 19 2 22 -0.60423403772105D+02 0.00000000000000D+00 3 19 2 22 0.64438600130487D+00 0.00000000000000D+00 1 20 2 22 0.99886251677847D+01 0.00000000000000D+00 2 20 2 22 -0.60423403778019D+02 0.00000000000000D+00 3 20 2 22 0.64438600674154D+00 0.00000000000000D+00 1 22 2 22 0.00000000000000D+00 0.00000000000000D+00 2 22 2 22 -0.23187972339883D+03 0.00000000000000D+00 3 22 2 22 0.00000000000000D+00 0.00000000000000D+00 1 23 2 22 -0.86724892676740D-11 -0.35387248686902D-10 2 23 2 22 -0.81880481283574D-11 -0.10048555043607D-09 3 23 2 22 -0.83566768681182D-11 -0.91325620676930D-10 1 24 2 22 0.15301751605404D-06 0.45136741598798D+00 2 24 2 22 -0.38894455277842D-13 -0.52891751444123D-11 3 24 2 22 -0.10861869001314D-12 0.21571946052373D-10 1 1 3 22 0.91942873650490D-07 0.00000000000000D+00 2 1 3 22 0.11761788120670D-06 0.00000000000000D+00 3 1 3 22 -0.53409674788623D+02 0.00000000000000D+00 1 2 3 22 -0.92156753728201D-07 0.00000000000000D+00 2 2 3 22 -0.11871925034712D-06 0.00000000000000D+00 3 2 3 22 -0.53409674788622D+02 0.00000000000000D+00 1 3 3 22 -0.92396082862836D-07 0.00000000000000D+00 2 3 3 22 0.11788672758611D-06 0.00000000000000D+00 3 3 3 22 -0.53409674788473D+02 0.00000000000000D+00 1 4 3 22 0.91703365423870D-07 0.00000000000000D+00 2 4 3 22 -0.11845062831950D-06 0.00000000000000D+00 3 4 3 22 -0.53409674788474D+02 0.00000000000000D+00 1 5 3 22 0.32828521112343D+01 0.00000000000000D+00 2 5 3 22 -0.10134391945157D+01 0.00000000000000D+00 3 5 3 22 -0.30149167823568D+02 0.00000000000000D+00 1 6 3 22 -0.32828521112222D+01 0.00000000000000D+00 2 6 3 22 0.10134391945292D+01 0.00000000000000D+00 3 6 3 22 -0.30149167823583D+02 0.00000000000000D+00 1 7 3 22 -0.32828521112350D+01 0.00000000000000D+00 2 7 3 22 -0.10134391945205D+01 0.00000000000000D+00 3 7 3 22 -0.30149167823583D+02 0.00000000000000D+00 1 8 3 22 0.32828521112249D+01 0.00000000000000D+00 2 8 3 22 0.10134391945338D+01 0.00000000000000D+00 3 8 3 22 -0.30149167823575D+02 0.00000000000000D+00 1 9 3 22 0.11916407100714D-07 0.00000000000000D+00 2 9 3 22 -0.26756897835616D-08 0.00000000000000D+00 3 9 3 22 -0.70303322832917D+02 0.00000000000000D+00 1 10 3 22 -0.11927026073591D-07 0.00000000000000D+00 2 10 3 22 0.27017824423027D-08 0.00000000000000D+00 3 10 3 22 -0.70303322832917D+02 0.00000000000000D+00 1 11 3 22 0.11925501774458D-07 0.00000000000000D+00 2 11 3 22 0.26951108096553D-08 0.00000000000000D+00 3 11 3 22 -0.70303322832925D+02 0.00000000000000D+00 1 12 3 22 -0.11917931272074D-07 0.00000000000000D+00 2 12 3 22 -0.26823613751177D-08 0.00000000000000D+00 3 12 3 22 -0.70303322832925D+02 0.00000000000000D+00 1 13 3 22 -0.89531373054724D-03 0.00000000000000D+00 2 13 3 22 -0.45060660336971D+00 0.00000000000000D+00 3 13 3 22 -0.49849473494041D+02 0.00000000000000D+00 1 14 3 22 -0.89531133639631D-03 0.00000000000000D+00 2 14 3 22 -0.45060660571147D+00 0.00000000000000D+00 3 14 3 22 -0.49849473527346D+02 0.00000000000000D+00 1 15 3 22 0.89531373682204D-03 0.00000000000000D+00 2 15 3 22 0.45060660336642D+00 0.00000000000000D+00 3 15 3 22 -0.49849473494018D+02 0.00000000000000D+00 1 16 3 22 0.89531134267408D-03 0.00000000000000D+00 2 16 3 22 0.45060660570817D+00 0.00000000000000D+00 3 16 3 22 -0.49849473527323D+02 0.00000000000000D+00 1 17 3 22 0.89531373192506D-03 0.00000000000000D+00 2 17 3 22 -0.45060660337337D+00 0.00000000000000D+00 3 17 3 22 -0.49849473494026D+02 0.00000000000000D+00 1 18 3 22 0.89531133777731D-03 0.00000000000000D+00 2 18 3 22 -0.45060660571514D+00 0.00000000000000D+00 3 18 3 22 -0.49849473527331D+02 0.00000000000000D+00 1 19 3 22 -0.89531373749289D-03 0.00000000000000D+00 2 19 3 22 0.45060660336440D+00 0.00000000000000D+00 3 19 3 22 -0.49849473494027D+02 0.00000000000000D+00 1 20 3 22 -0.89531134334294D-03 0.00000000000000D+00 2 20 3 22 0.45060660570615D+00 0.00000000000000D+00 3 20 3 22 -0.49849473527332D+02 0.00000000000000D+00 1 22 3 22 0.00000000000000D+00 0.00000000000000D+00 2 22 3 22 0.00000000000000D+00 0.00000000000000D+00 3 22 3 22 -0.11784399428177D+03 0.00000000000000D+00 1 23 3 22 -0.23692052585817D-06 0.10349343578854D+01 2 23 3 22 -0.30754050207322D-06 0.15078973756408D+01 3 23 3 22 -0.43749500247071D-06 -0.30748160068167D+01 1 24 3 22 0.13540771192324D-12 0.84553501353279D-11 2 24 3 22 -0.13991612040641D-12 -0.92433412811864D-11 3 24 3 22 -0.11882588363637D-13 0.23246166276636D-10 1 1 1 23 -0.93882668726212D+00 0.00000000000000D+00 2 1 1 23 0.84433932489909D+00 0.00000000000000D+00 3 1 1 23 -0.15105451561161D-10 0.00000000000000D+00 1 2 1 23 0.93882668726076D+00 0.00000000000000D+00 2 2 1 23 -0.84433932489660D+00 0.00000000000000D+00 3 2 1 23 -0.14241236734832D-10 0.00000000000000D+00 1 3 1 23 0.93882668726285D+00 0.00000000000000D+00 2 3 1 23 0.84433932490794D+00 0.00000000000000D+00 3 3 1 23 -0.14504626252782D-10 0.00000000000000D+00 1 4 1 23 -0.93882668726302D+00 0.00000000000000D+00 2 4 1 23 -0.84433932489610D+00 0.00000000000000D+00 3 4 1 23 -0.13391718222771D-10 0.00000000000000D+00 1 5 1 23 -0.23130734415799D-13 0.00000000000000D+00 2 5 1 23 -0.10533891547175D-12 0.00000000000000D+00 3 5 1 23 -0.64434927739465D-12 0.00000000000000D+00 1 6 1 23 0.20385125292248D-12 0.00000000000000D+00 2 6 1 23 -0.40155472912226D-13 0.00000000000000D+00 3 6 1 23 -0.10930750052492D-11 0.00000000000000D+00 1 7 1 23 -0.16812389200881D-12 0.00000000000000D+00 2 7 1 23 0.14248837465931D-12 0.00000000000000D+00 3 7 1 23 -0.83137631619005D-12 0.00000000000000D+00 1 8 1 23 -0.49272431095785D-12 0.00000000000000D+00 2 8 1 23 0.85443653313496D-13 0.00000000000000D+00 3 8 1 23 -0.13111894881417D-11 0.00000000000000D+00 1 9 1 23 -0.16492574323798D+00 0.00000000000000D+00 2 9 1 23 -0.91982523218711D-01 0.00000000000000D+00 3 9 1 23 0.52240142915407D-13 0.00000000000000D+00 1 10 1 23 0.16492574323892D+00 0.00000000000000D+00 2 10 1 23 0.91982523219002D-01 0.00000000000000D+00 3 10 1 23 -0.87835245908193D-14 0.00000000000000D+00 1 11 1 23 -0.16492574323912D+00 0.00000000000000D+00 2 11 1 23 0.91982523218800D-01 0.00000000000000D+00 3 11 1 23 -0.50647874663381D-13 0.00000000000000D+00 1 12 1 23 0.16492574323801D+00 0.00000000000000D+00 2 12 1 23 -0.91982523218434D-01 0.00000000000000D+00 3 12 1 23 0.11918342251870D-12 0.00000000000000D+00 1 13 1 23 -0.10345889124117D+01 0.00000000000000D+00 2 13 1 23 -0.24050678197117D-01 0.00000000000000D+00 3 13 1 23 0.51755739415606D+00 0.00000000000000D+00 1 14 1 23 0.10345889124116D+01 0.00000000000000D+00 2 14 1 23 0.24050678197373D-01 0.00000000000000D+00 3 14 1 23 -0.51755739415741D+00 0.00000000000000D+00 1 15 1 23 0.10345889124120D+01 0.00000000000000D+00 2 15 1 23 0.24050678197295D-01 0.00000000000000D+00 3 15 1 23 0.51755739415745D+00 0.00000000000000D+00 1 16 1 23 -0.10345889124115D+01 0.00000000000000D+00 2 16 1 23 -0.24050678197447D-01 0.00000000000000D+00 3 16 1 23 -0.51755739415886D+00 0.00000000000000D+00 1 17 1 23 0.10345889124110D+01 0.00000000000000D+00 2 17 1 23 -0.24050678197021D-01 0.00000000000000D+00 3 17 1 23 0.51755739415586D+00 0.00000000000000D+00 1 18 1 23 -0.10345889124121D+01 0.00000000000000D+00 2 18 1 23 0.24050678197440D-01 0.00000000000000D+00 3 18 1 23 -0.51755739415734D+00 0.00000000000000D+00 1 19 1 23 -0.10345889124124D+01 0.00000000000000D+00 2 19 1 23 0.24050678197362D-01 0.00000000000000D+00 3 19 1 23 0.51755739415742D+00 0.00000000000000D+00 1 20 1 23 0.10345889124106D+01 0.00000000000000D+00 2 20 1 23 -0.24050678197373D-01 0.00000000000000D+00 3 20 1 23 -0.51755739415885D+00 0.00000000000000D+00 1 22 1 23 0.38139257204122D-13 0.00000000000000D+00 2 22 1 23 -0.20732791007193D-12 0.00000000000000D+00 3 22 1 23 0.29976610923277D-07 0.00000000000000D+00 1 23 1 23 0.19205136903904D+02 0.00000000000000D+00 2 23 1 23 0.65570677712094D+01 0.00000000000000D+00 3 23 1 23 0.58580346842832D+01 0.00000000000000D+00 1 24 1 23 -0.72199989299026D-14 0.00000000000000D+00 2 24 1 23 -0.11838344294875D-13 0.00000000000000D+00 3 24 1 23 -0.24170904900604D-13 0.00000000000000D+00 1 1 2 23 0.40776864634338D+00 0.00000000000000D+00 2 1 2 23 -0.14295838445145D+01 0.00000000000000D+00 3 1 2 23 -0.15758458985585D-10 0.00000000000000D+00 1 2 2 23 -0.40776864634402D+00 0.00000000000000D+00 2 2 2 23 0.14295838445199D+01 0.00000000000000D+00 3 2 2 23 -0.14738729146409D-10 0.00000000000000D+00 1 3 2 23 -0.40776864634299D+00 0.00000000000000D+00 2 3 2 23 -0.14295838444970D+01 0.00000000000000D+00 3 3 2 23 -0.15214701786404D-10 0.00000000000000D+00 1 4 2 23 0.40776864634267D+00 0.00000000000000D+00 2 4 2 23 0.14295838445195D+01 0.00000000000000D+00 3 4 2 23 -0.13910984184683D-10 0.00000000000000D+00 1 5 2 23 -0.21905585357460D-12 0.00000000000000D+00 2 5 2 23 -0.54206718405217D-12 0.00000000000000D+00 3 5 2 23 -0.61215141724792D-12 0.00000000000000D+00 1 6 2 23 -0.19463380796439D-12 0.00000000000000D+00 2 6 2 23 -0.72843701485930D-12 0.00000000000000D+00 3 6 2 23 -0.10409743813485D-11 0.00000000000000D+00 1 7 2 23 -0.88896306646898D-13 0.00000000000000D+00 2 7 2 23 -0.47919556132303D-12 0.00000000000000D+00 3 7 2 23 -0.11486549402326D-11 0.00000000000000D+00 1 8 2 23 -0.15803553362964D-12 0.00000000000000D+00 2 8 2 23 -0.55844535814548D-12 0.00000000000000D+00 3 8 2 23 -0.65549748028572D-12 0.00000000000000D+00 1 9 2 23 0.31727747490158D+00 0.00000000000000D+00 2 9 2 23 0.69522579405253D+00 0.00000000000000D+00 3 9 2 23 -0.34888820465214D-12 0.00000000000000D+00 1 10 2 23 -0.31727747490180D+00 0.00000000000000D+00 2 10 2 23 -0.69522579405098D+00 0.00000000000000D+00 3 10 2 23 0.52149748519977D-12 0.00000000000000D+00 1 11 2 23 0.31727747490164D+00 0.00000000000000D+00 2 11 2 23 -0.69522579404970D+00 0.00000000000000D+00 3 11 2 23 -0.55579551759101D-14 0.00000000000000D+00 1 12 2 23 -0.31727747490207D+00 0.00000000000000D+00 2 12 2 23 0.69522579405298D+00 0.00000000000000D+00 3 12 2 23 -0.10589731158867D-12 0.00000000000000D+00 1 13 2 23 -0.28796500350072D-01 0.00000000000000D+00 2 13 2 23 0.65690521241038D+00 0.00000000000000D+00 3 13 2 23 0.42858473760332D+00 0.00000000000000D+00 1 14 2 23 0.28796500350158D-01 0.00000000000000D+00 2 14 2 23 -0.65690521240960D+00 0.00000000000000D+00 3 14 2 23 -0.42858473760495D+00 0.00000000000000D+00 1 15 2 23 0.28796500349909D-01 0.00000000000000D+00 2 15 2 23 -0.65690521240861D+00 0.00000000000000D+00 3 15 2 23 0.42858473760372D+00 0.00000000000000D+00 1 16 2 23 -0.28796500350399D-01 0.00000000000000D+00 2 16 2 23 0.65690521241047D+00 0.00000000000000D+00 3 16 2 23 -0.42858473760546D+00 0.00000000000000D+00 1 17 2 23 0.28796500349866D-01 0.00000000000000D+00 2 17 2 23 0.65690521241102D+00 0.00000000000000D+00 3 17 2 23 0.42858473760321D+00 0.00000000000000D+00 1 18 2 23 -0.28796500350378D-01 0.00000000000000D+00 2 18 2 23 -0.65690521240986D+00 0.00000000000000D+00 3 18 2 23 -0.42858473760499D+00 0.00000000000000D+00 1 19 2 23 -0.28796500350072D-01 0.00000000000000D+00 2 19 2 23 -0.65690521240890D+00 0.00000000000000D+00 3 19 2 23 0.42858473760371D+00 0.00000000000000D+00 1 20 2 23 0.28796500350019D-01 0.00000000000000D+00 2 20 2 23 0.65690521241104D+00 0.00000000000000D+00 3 20 2 23 -0.42858473760523D+00 0.00000000000000D+00 1 22 2 23 0.66208908263845D-13 0.00000000000000D+00 2 22 2 23 -0.25796767944692D-12 0.00000000000000D+00 3 22 2 23 -0.15943426975886D-07 0.00000000000000D+00 1 23 2 23 0.65571448733949D+01 0.00000000000000D+00 2 23 2 23 0.18660182036461D+02 0.00000000000000D+00 3 23 2 23 0.55631036079785D+01 0.00000000000000D+00 1 24 2 23 -0.21180862627442D-13 0.00000000000000D+00 2 24 2 23 0.23856065506862D-13 0.00000000000000D+00 3 24 2 23 -0.18084368384625D-12 0.00000000000000D+00 1 1 3 23 0.53180648503902D+00 0.00000000000000D+00 2 1 3 23 0.25284909623832D+00 0.00000000000000D+00 3 1 3 23 -0.20156047577314D-10 0.00000000000000D+00 1 2 3 23 -0.53180648503851D+00 0.00000000000000D+00 2 2 3 23 -0.25284909623601D+00 0.00000000000000D+00 3 2 3 23 -0.17940527039852D-10 0.00000000000000D+00 1 3 3 23 -0.53180648503819D+00 0.00000000000000D+00 2 3 3 23 0.25284909624665D+00 0.00000000000000D+00 3 3 3 23 -0.18933175568194D-10 0.00000000000000D+00 1 4 3 23 0.53180648503753D+00 0.00000000000000D+00 2 4 3 23 -0.25284909623553D+00 0.00000000000000D+00 3 4 3 23 -0.18416904992249D-10 0.00000000000000D+00 1 5 3 23 -0.31875628374528D-12 0.00000000000000D+00 2 5 3 23 -0.33106210199895D-12 0.00000000000000D+00 3 5 3 23 -0.80360255447026D-12 0.00000000000000D+00 1 6 3 23 -0.39886157427944D-13 0.00000000000000D+00 2 6 3 23 -0.27807960126636D-12 0.00000000000000D+00 3 6 3 23 -0.61192224614750D-12 0.00000000000000D+00 1 7 3 23 0.95914083062590D-13 0.00000000000000D+00 2 7 3 23 -0.14273417296102D-12 0.00000000000000D+00 3 7 3 23 -0.88699668721393D-12 0.00000000000000D+00 1 8 3 23 0.63753593661257D-13 0.00000000000000D+00 2 8 3 23 -0.28640526666965D-12 0.00000000000000D+00 3 8 3 23 -0.10198959319936D-11 0.00000000000000D+00 1 9 3 23 0.12815527866007D+01 0.00000000000000D+00 2 9 3 23 -0.20735311880145D+00 0.00000000000000D+00 3 9 3 23 -0.51484528554686D-12 0.00000000000000D+00 1 10 3 23 -0.12815527866003D+01 0.00000000000000D+00 2 10 3 23 0.20735311880093D+00 0.00000000000000D+00 3 10 3 23 0.12784488870538D-11 0.00000000000000D+00 1 11 3 23 0.12815527866007D+01 0.00000000000000D+00 2 11 3 23 0.20735311880030D+00 0.00000000000000D+00 3 11 3 23 0.54226401477187D-13 0.00000000000000D+00 1 12 3 23 -0.12815527866009D+01 0.00000000000000D+00 2 12 3 23 -0.20735311880152D+00 0.00000000000000D+00 3 12 3 23 0.96882426736059D-12 0.00000000000000D+00 1 13 3 23 0.13253941070523D-01 0.00000000000000D+00 2 13 3 23 -0.33954541262897D-01 0.00000000000000D+00 3 13 3 23 0.34431717005055D+00 0.00000000000000D+00 1 14 3 23 -0.13253941070129D-01 0.00000000000000D+00 2 14 3 23 0.33954541263455D-01 0.00000000000000D+00 3 14 3 23 -0.34431717004587D+00 0.00000000000000D+00 1 15 3 23 -0.13253941070325D-01 0.00000000000000D+00 2 15 3 23 0.33954541263526D-01 0.00000000000000D+00 3 15 3 23 0.34431717004543D+00 0.00000000000000D+00 1 16 3 23 0.13253941070293D-01 0.00000000000000D+00 2 16 3 23 -0.33954541263245D-01 0.00000000000000D+00 3 16 3 23 -0.34431717004635D+00 0.00000000000000D+00 1 17 3 23 -0.13253941070651D-01 0.00000000000000D+00 2 17 3 23 -0.33954541262958D-01 0.00000000000000D+00 3 17 3 23 0.34431717005043D+00 0.00000000000000D+00 1 18 3 23 0.13253941070122D-01 0.00000000000000D+00 2 18 3 23 0.33954541263377D-01 0.00000000000000D+00 3 18 3 23 -0.34431717004557D+00 0.00000000000000D+00 1 19 3 23 0.13253941070406D-01 0.00000000000000D+00 2 19 3 23 0.33954541263501D-01 0.00000000000000D+00 3 19 3 23 0.34431717004547D+00 0.00000000000000D+00 1 20 3 23 -0.13253941070477D-01 0.00000000000000D+00 2 20 3 23 -0.33954541263228D-01 0.00000000000000D+00 3 20 3 23 -0.34431717004650D+00 0.00000000000000D+00 1 22 3 23 0.45804294932066D-13 0.00000000000000D+00 2 22 3 23 -0.24544002772128D-12 0.00000000000000D+00 3 22 3 23 -0.91639410372001D-08 0.00000000000000D+00 1 23 3 23 0.58580806739478D+01 0.00000000000000D+00 2 23 3 23 0.55631531263625D+01 0.00000000000000D+00 3 23 3 23 0.19712406543737D+02 0.00000000000000D+00 1 24 3 23 0.29269889337782D-13 0.00000000000000D+00 2 24 3 23 -0.56383852307916D-13 0.00000000000000D+00 3 24 3 23 -0.92971985534169D-13 0.00000000000000D+00 1 1 1 24 -0.59426427010404D-11 0.00000000000000D+00 2 1 1 24 -0.94425291975876D-11 0.00000000000000D+00 3 1 1 24 0.52299324799845D+00 0.00000000000000D+00 1 2 1 24 0.64218771405501D-11 0.00000000000000D+00 2 2 1 24 0.39438389672381D-11 0.00000000000000D+00 3 2 1 24 -0.52299324799718D+00 0.00000000000000D+00 1 3 1 24 0.59012203165705D-11 0.00000000000000D+00 2 3 1 24 -0.95226089986407D-11 0.00000000000000D+00 3 3 1 24 0.52299324800424D+00 0.00000000000000D+00 1 4 1 24 -0.64685894588328D-11 0.00000000000000D+00 2 4 1 24 0.42336755722304D-11 0.00000000000000D+00 3 4 1 24 -0.52299324799775D+00 0.00000000000000D+00 1 5 1 24 -0.92903730840924D-13 0.00000000000000D+00 2 5 1 24 0.22758016478509D-12 0.00000000000000D+00 3 5 1 24 -0.67424564427884D-12 0.00000000000000D+00 1 6 1 24 0.71296189312222D-13 0.00000000000000D+00 2 6 1 24 -0.11207750102776D-12 0.00000000000000D+00 3 6 1 24 -0.58169701851170D-12 0.00000000000000D+00 1 7 1 24 0.55831342124931D-14 0.00000000000000D+00 2 7 1 24 0.94360134396856D-13 0.00000000000000D+00 3 7 1 24 -0.75236523522560D-12 0.00000000000000D+00 1 8 1 24 -0.98036792444040D-13 0.00000000000000D+00 2 8 1 24 0.59807010771216D-13 0.00000000000000D+00 3 8 1 24 -0.47128267902438D-12 0.00000000000000D+00 1 9 1 24 0.69850307286789D-11 0.00000000000000D+00 2 9 1 24 -0.16340091519841D-11 0.00000000000000D+00 3 9 1 24 -0.47960942147807D+00 0.00000000000000D+00 1 10 1 24 -0.70165507063157D-11 0.00000000000000D+00 2 10 1 24 0.16171561339673D-11 0.00000000000000D+00 3 10 1 24 0.47960942147881D+00 0.00000000000000D+00 1 11 1 24 0.69815369056145D-11 0.00000000000000D+00 2 11 1 24 0.15035506471473D-11 0.00000000000000D+00 3 11 1 24 0.47960942147968D+00 0.00000000000000D+00 1 12 1 24 -0.70564471879500D-11 0.00000000000000D+00 2 12 1 24 -0.17526828538710D-11 0.00000000000000D+00 3 12 1 24 -0.47960942147780D+00 0.00000000000000D+00 1 13 1 24 0.29375184455004D+00 0.00000000000000D+00 2 13 1 24 0.87036196818158D-01 0.00000000000000D+00 3 13 1 24 -0.14835373131396D+00 0.00000000000000D+00 1 14 1 24 -0.29375184454966D+00 0.00000000000000D+00 2 14 1 24 -0.87036196818549D-01 0.00000000000000D+00 3 14 1 24 0.14835373131449D+00 0.00000000000000D+00 1 15 1 24 0.29375184455491D+00 0.00000000000000D+00 2 15 1 24 0.87036196799960D-01 0.00000000000000D+00 3 15 1 24 0.14835373133872D+00 0.00000000000000D+00 1 16 1 24 -0.29375184455472D+00 0.00000000000000D+00 2 16 1 24 -0.87036196800366D-01 0.00000000000000D+00 3 16 1 24 -0.14835373133812D+00 0.00000000000000D+00 1 17 1 24 -0.29375184454992D+00 0.00000000000000D+00 2 17 1 24 0.87036196818066D-01 0.00000000000000D+00 3 17 1 24 -0.14835373131377D+00 0.00000000000000D+00 1 18 1 24 0.29375184454964D+00 0.00000000000000D+00 2 18 1 24 -0.87036196818606D-01 0.00000000000000D+00 3 18 1 24 0.14835373131435D+00 0.00000000000000D+00 1 19 1 24 -0.29375184455494D+00 0.00000000000000D+00 2 19 1 24 0.87036196800348D-01 0.00000000000000D+00 3 19 1 24 0.14835373133851D+00 0.00000000000000D+00 1 20 1 24 0.29375184455469D+00 0.00000000000000D+00 2 20 1 24 -0.87036196800777D-01 0.00000000000000D+00 3 20 1 24 -0.14835373133784D+00 0.00000000000000D+00 1 22 1 24 0.89833786615283D-14 0.00000000000000D+00 2 22 1 24 -0.10059878250018D-07 0.00000000000000D+00 3 22 1 24 -0.60392029383256D-13 0.00000000000000D+00 1 23 1 24 -0.44788721676158D-10 0.00000000000000D+00 2 23 1 24 -0.39225871909643D-10 0.00000000000000D+00 3 23 1 24 -0.44240934996923D-10 0.00000000000000D+00 1 24 1 24 0.63231946133110D+01 0.00000000000000D+00 2 24 1 24 -0.23766921190750D-13 0.00000000000000D+00 3 24 1 24 0.51846461591171D-13 0.00000000000000D+00 1 1 2 24 -0.99604881433598D-08 0.00000000000000D+00 2 1 2 24 -0.90121414658524D-08 0.00000000000000D+00 3 1 2 24 0.10108710330701D+01 0.00000000000000D+00 1 2 2 24 0.99557155018199D-08 0.00000000000000D+00 2 2 2 24 0.90121261512869D-08 0.00000000000000D+00 3 2 2 24 -0.10108710330708D+01 0.00000000000000D+00 1 3 2 24 0.99565624491861D-08 0.00000000000000D+00 2 3 2 24 -0.90120556366812D-08 0.00000000000000D+00 3 3 2 24 -0.10108710330709D+01 0.00000000000000D+00 1 4 2 24 -0.99611337735411D-08 0.00000000000000D+00 2 4 2 24 0.90121751832532D-08 0.00000000000000D+00 3 4 2 24 0.10108710330692D+01 0.00000000000000D+00 1 5 2 24 0.85659752494229D-13 0.00000000000000D+00 2 5 2 24 -0.61600881950129D-13 0.00000000000000D+00 3 5 2 24 -0.22789829890699D-12 0.00000000000000D+00 1 6 2 24 -0.40621222753988D-13 0.00000000000000D+00 2 6 2 24 0.12172471462926D-12 0.00000000000000D+00 3 6 2 24 -0.42989376531550D-13 0.00000000000000D+00 1 7 2 24 0.93998149496356D-13 0.00000000000000D+00 2 7 2 24 0.58649509719035D-13 0.00000000000000D+00 3 7 2 24 0.11526857842402D-12 0.00000000000000D+00 1 8 2 24 -0.10265894896824D-12 0.00000000000000D+00 2 8 2 24 -0.45397003463857D-13 0.00000000000000D+00 3 8 2 24 -0.68927252209158D-13 0.00000000000000D+00 1 9 2 24 0.98524113773883D-08 0.00000000000000D+00 2 9 2 24 -0.30946470967885D-08 0.00000000000000D+00 3 9 2 24 0.10177300063828D+01 0.00000000000000D+00 1 10 2 24 -0.98525597304642D-08 0.00000000000000D+00 2 10 2 24 0.30947007821474D-08 0.00000000000000D+00 3 10 2 24 -0.10177300063831D+01 0.00000000000000D+00 1 11 2 24 0.98524417020050D-08 0.00000000000000D+00 2 11 2 24 0.30946538336887D-08 0.00000000000000D+00 3 11 2 24 0.10177300063822D+01 0.00000000000000D+00 1 12 2 24 -0.98525836631696D-08 0.00000000000000D+00 2 12 2 24 -0.30946413121835D-08 0.00000000000000D+00 3 12 2 24 -0.10177300063832D+01 0.00000000000000D+00 1 13 2 24 0.15951034808252D+00 0.00000000000000D+00 2 13 2 24 0.32516114585313D+00 0.00000000000000D+00 3 13 2 24 -0.67200430847165D-01 0.00000000000000D+00 1 14 2 24 -0.15951034808425D+00 0.00000000000000D+00 2 14 2 24 -0.32516114585296D+00 0.00000000000000D+00 3 14 2 24 0.67200430847437D-01 0.00000000000000D+00 1 15 2 24 0.15951036386480D+00 0.00000000000000D+00 2 15 2 24 0.32516113159319D+00 0.00000000000000D+00 3 15 2 24 0.67200463340772D-01 0.00000000000000D+00 1 16 2 24 -0.15951036386495D+00 0.00000000000000D+00 2 16 2 24 -0.32516113159329D+00 0.00000000000000D+00 3 16 2 24 -0.67200463340655D-01 0.00000000000000D+00 1 17 2 24 0.15951036386438D+00 0.00000000000000D+00 2 17 2 24 -0.32516113159423D+00 0.00000000000000D+00 3 17 2 24 0.67200463340466D-01 0.00000000000000D+00 1 18 2 24 -0.15951036386571D+00 0.00000000000000D+00 2 18 2 24 0.32516113159300D+00 0.00000000000000D+00 3 18 2 24 -0.67200463340845D-01 0.00000000000000D+00 1 19 2 24 0.15951034808167D+00 0.00000000000000D+00 2 19 2 24 -0.32516114585314D+00 0.00000000000000D+00 3 19 2 24 -0.67200430847669D-01 0.00000000000000D+00 1 20 2 24 -0.15951034808212D+00 0.00000000000000D+00 2 20 2 24 0.32516114585285D+00 0.00000000000000D+00 3 20 2 24 0.67200430847206D-01 0.00000000000000D+00 1 22 2 24 -0.21205594871469D-07 0.00000000000000D+00 2 22 2 24 0.18077904761705D-13 0.00000000000000D+00 3 22 2 24 0.13387832022122D-13 0.00000000000000D+00 1 23 2 24 -0.47544544160278D-07 0.00000000000000D+00 2 23 2 24 -0.48414193636712D-07 0.00000000000000D+00 3 23 2 24 -0.46741571949293D-07 0.00000000000000D+00 1 24 2 24 -0.24312724173735D-13 0.00000000000000D+00 2 24 2 24 0.59668255741835D+01 0.00000000000000D+00 3 24 2 24 -0.18465460664459D-13 0.00000000000000D+00 1 1 3 24 0.60819804892238D+00 0.00000000000000D+00 2 1 3 24 0.17300311722603D+00 0.00000000000000D+00 3 1 3 24 0.17688608449387D-12 0.00000000000000D+00 1 2 3 24 -0.60819804892134D+00 0.00000000000000D+00 2 2 3 24 -0.17300311722658D+00 0.00000000000000D+00 3 2 3 24 0.11901803262388D-12 0.00000000000000D+00 1 3 3 24 0.60819804906344D+00 0.00000000000000D+00 2 3 3 24 -0.17300312088766D+00 0.00000000000000D+00 3 3 3 24 -0.61500018411637D-13 0.00000000000000D+00 1 4 3 24 -0.60819804905842D+00 0.00000000000000D+00 2 4 3 24 0.17300312088654D+00 0.00000000000000D+00 3 4 3 24 -0.35930037087410D-13 0.00000000000000D+00 1 5 3 24 -0.35662176137173D-12 0.00000000000000D+00 2 5 3 24 -0.94687408208965D-13 0.00000000000000D+00 3 5 3 24 -0.52237860719958D-13 0.00000000000000D+00 1 6 3 24 -0.30951929157167D-12 0.00000000000000D+00 2 6 3 24 -0.55455764135961D-13 0.00000000000000D+00 3 6 3 24 0.11321091593248D-12 0.00000000000000D+00 1 7 3 24 -0.19331988296659D-12 0.00000000000000D+00 2 7 3 24 0.27830832368540D-13 0.00000000000000D+00 3 7 3 24 0.47657749008735D-13 0.00000000000000D+00 1 8 3 24 -0.18827710836629D-12 0.00000000000000D+00 2 8 3 24 -0.84988614052156D-13 0.00000000000000D+00 3 8 3 24 -0.53461598421280D-13 0.00000000000000D+00 1 9 3 24 -0.27897084919573D-01 0.00000000000000D+00 2 9 3 24 0.40885724701575D+00 0.00000000000000D+00 3 9 3 24 0.38397596914864D-13 0.00000000000000D+00 1 10 3 24 0.27897084920044D-01 0.00000000000000D+00 2 10 3 24 -0.40885724701565D+00 0.00000000000000D+00 3 10 3 24 0.48684240242133D-13 0.00000000000000D+00 1 11 3 24 0.27897093725930D-01 0.00000000000000D+00 2 11 3 24 0.40885724958644D+00 0.00000000000000D+00 3 11 3 24 0.20384551784624D-13 0.00000000000000D+00 1 12 3 24 -0.27897093724483D-01 0.00000000000000D+00 2 12 3 24 -0.40885724958676D+00 0.00000000000000D+00 3 12 3 24 -0.24188889706468D-13 0.00000000000000D+00 1 13 3 24 -0.32265876463600D+00 0.00000000000000D+00 2 13 3 24 0.24830978310878D+00 0.00000000000000D+00 3 13 3 24 0.77676655146262D+00 0.00000000000000D+00 1 14 3 24 0.32265876463678D+00 0.00000000000000D+00 2 14 3 24 -0.24830978310910D+00 0.00000000000000D+00 3 14 3 24 -0.77676655146309D+00 0.00000000000000D+00 1 15 3 24 0.32265876463658D+00 0.00000000000000D+00 2 15 3 24 -0.24830978310923D+00 0.00000000000000D+00 3 15 3 24 0.77676655146283D+00 0.00000000000000D+00 1 16 3 24 -0.32265876463602D+00 0.00000000000000D+00 2 16 3 24 0.24830978310861D+00 0.00000000000000D+00 3 16 3 24 -0.77676655146238D+00 0.00000000000000D+00 1 17 3 24 -0.32265875964081D+00 0.00000000000000D+00 2 17 3 24 -0.24830977860295D+00 0.00000000000000D+00 3 17 3 24 -0.77676654117826D+00 0.00000000000000D+00 1 18 3 24 0.32265875964149D+00 0.00000000000000D+00 2 18 3 24 0.24830977860311D+00 0.00000000000000D+00 3 18 3 24 0.77676654117846D+00 0.00000000000000D+00 1 19 3 24 0.32265875964118D+00 0.00000000000000D+00 2 19 3 24 0.24830977860320D+00 0.00000000000000D+00 3 19 3 24 -0.77676654117877D+00 0.00000000000000D+00 1 20 3 24 -0.32265875964084D+00 0.00000000000000D+00 2 20 3 24 -0.24830977860279D+00 0.00000000000000D+00 3 20 3 24 0.77676654117868D+00 0.00000000000000D+00 1 22 3 24 -0.66136177256641D-13 0.00000000000000D+00 2 22 3 24 0.16164140478746D-13 0.00000000000000D+00 3 22 3 24 -0.64921646461313D-14 0.00000000000000D+00 1 23 3 24 -0.13579444034168D-07 0.00000000000000D+00 2 23 3 24 -0.13576091241540D-07 0.00000000000000D+00 3 23 3 24 -0.13008869631055D-07 0.00000000000000D+00 1 24 3 24 0.49373187250021D-13 0.00000000000000D+00 2 24 3 24 0.15546802010506D-13 0.00000000000000D+00 3 24 3 24 0.69835502296926D+01 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 0.00000000E+00 0.00000000E+00 1.0 1 1 1 1 0.93997214749470D+01 0.00000000000000D+00 2 1 1 1 0.12669805341651D+01 0.56707772912160D-06 3 1 1 1 -0.42964443742191D-13 0.00000000000000D+00 1 2 1 1 0.10897109838317D+01 -0.32189825989427D-08 2 2 1 1 0.17233355688501D+00 -0.15531910925916D-07 3 2 1 1 0.20609427343650D-14 -0.17632748747406D-15 1 3 1 1 0.89815168331202D-01 -0.34956028362213D-14 2 3 1 1 0.46391553239624D-01 0.24934124793314D-08 3 3 1 1 0.37784571357245D-14 -0.78450518552960D-15 1 4 1 1 0.18553180634275D-13 -0.15185241937132D-07 2 4 1 1 -0.13087902084044D+00 0.50628358216367D-08 3 4 1 1 0.14893849135891D-13 0.14188465207102D-14 1 5 1 1 0.41459148040797D+01 -0.47906692044556D-02 2 5 1 1 -0.68984576298944D+00 0.25323577954598D-02 3 5 1 1 -0.22881076477143D+00 -0.72931471681151D-02 1 6 1 1 0.41459148040797D+01 -0.47906692044564D-02 2 6 1 1 -0.68984576298944D+00 0.25323577954597D-02 3 6 1 1 0.22881076477143D+00 0.72931471681164D-02 1 7 1 1 0.13361541043890D+00 -0.44153486286713D-08 2 7 1 1 0.40672906451281D+00 -0.58921908809886D-08 3 7 1 1 0.54342484007504D+01 -0.20688741706475D-07 1 8 1 1 0.13361541043889D+00 -0.44153511374596D-08 2 8 1 1 0.40672906451282D+00 -0.58921921178057D-08 3 8 1 1 -0.54342484007503D+01 0.20688741273883D-07 1 9 1 1 -0.15727436359372D+01 0.19293244659591D-07 2 9 1 1 -0.17021722332704D+00 0.17471615286083D-07 3 9 1 1 -0.17448930758118D-15 -0.33565692803943D-15 1 10 1 1 0.91094028615952D+00 0.21462945702464D-08 2 10 1 1 -0.10800215337626D+00 -0.25978548117144D-08 3 10 1 1 0.34171136610343D-14 0.35368066911360D-15 1 11 1 1 0.24302470502948D+00 -0.27640831250466D-08 2 11 1 1 -0.39371980731922D-01 0.17723282341141D-09 3 11 1 1 0.11030070627115D-13 -0.55792430658021D-15 1 12 1 1 -0.33669097512719D+01 0.83532829344920D-08 2 12 1 1 0.23688872566387D+00 0.47218103137153D-08 3 12 1 1 0.96067501641630D-15 -0.21375734440524D-15 1 13 1 1 0.13505761418087D+01 0.38777290124136D-08 2 13 1 1 0.81666934161534D+00 0.11466080368916D-08 3 13 1 1 -0.88204085885443D+00 -0.17236323833774D-07 1 14 1 1 -0.10413932964438D+01 0.21687425894923D-02 2 14 1 1 -0.83615108999649D+00 0.20828989450406D-02 3 14 1 1 -0.53793535376564D+00 0.17218116919611D-03 1 15 1 1 -0.10413932964438D+01 0.21687425894933D-02 2 15 1 1 -0.83615108999649D+00 0.20828989450404D-02 3 15 1 1 0.53793535376565D+00 -0.17218116919523D-03 1 16 1 1 0.13505761418087D+01 0.38777290580850D-08 2 16 1 1 0.81666934161532D+00 0.11466082059080D-08 3 16 1 1 0.88204085885442D+00 0.17236323744413D-07 1 17 1 1 0.18132533007096D+01 0.47530769157263D-02 2 17 1 1 -0.30117809923754D+00 0.56316188352035D-02 3 17 1 1 0.37152320846494D+00 0.14970024958012D-01 1 18 1 1 -0.12026903628936D+01 0.82154279193466D-02 2 18 1 1 0.10450540314164D+01 -0.21458121172627D-02 3 18 1 1 -0.87229731747195D+00 -0.11087385210481D-01 1 19 1 1 -0.12026903628936D+01 0.82154279193466D-02 2 19 1 1 0.10450540314164D+01 -0.21458121172631D-02 3 19 1 1 0.87229731747185D+00 0.11087385210481D-01 1 20 1 1 0.18132533007096D+01 0.47530769157264D-02 2 20 1 1 -0.30117809923755D+00 0.56316188352036D-02 3 20 1 1 -0.37152320846493D+00 -0.14970024958012D-01 1 1 2 1 0.12669774131178D+01 0.62963247344663D-06 2 1 2 1 0.80004662339525D+01 0.00000000000000D+00 3 1 2 1 -0.28862031926092D-13 0.00000000000000D+00 1 2 2 1 0.17233433603424D+00 0.88683079346214D-08 2 2 2 1 0.32158429759640D+00 0.12966335779994D-08 3 2 2 1 -0.12556911442689D-13 -0.22512919143627D-15 1 3 2 1 -0.46391553239281D-01 0.24934124793314D-08 2 3 2 1 0.37795024425616D+00 -0.26307839431057D-14 3 3 2 1 -0.30447512368394D-14 0.12654712836802D-15 1 4 2 1 -0.13087902084044D+00 -0.50628360228349D-08 2 4 2 1 -0.64332147788477D-14 0.17230484454493D-08 3 4 2 1 -0.81897340770988D-15 0.11333638906950D-15 1 5 2 1 0.23792062273921D+00 0.52956604204228D-03 2 5 2 1 -0.34762720614300D+01 0.48943671269857D-02 3 5 2 1 0.18697896599543D+01 -0.51240298166188D-02 1 6 2 1 0.23792062273921D+00 0.52956604204215D-03 2 6 2 1 -0.34762720614299D+01 0.48943671269851D-02 3 6 2 1 -0.18697896599543D+01 0.51240298166186D-02 1 7 2 1 0.39354977651034D+00 0.12796629213374D-08 2 7 2 1 -0.63364291431506D+00 -0.15952751289710D-09 3 7 2 1 -0.16919166734278D+00 -0.22089811977591D-08 1 8 2 1 0.39354977651034D+00 0.12796616844922D-08 2 8 2 1 -0.63364291431505D+00 -0.15952843235449D-09 3 8 2 1 0.16919166734278D+00 0.22089811590875D-08 1 9 2 1 -0.38698390888552D+00 -0.64342471723992D-08 2 9 2 1 0.11076702982744D+00 0.11066499627392D-08 3 9 2 1 0.38154378056854D-16 -0.32053600443344D-15 1 10 2 1 0.84278587224156D-01 0.27250361054355D-08 2 10 2 1 -0.27960957653770D+00 0.20657964361413D-08 3 10 2 1 -0.38740753544897D-14 -0.25398668516835D-16 1 11 2 1 0.82932068486495D-01 -0.55746736988359D-08 2 11 2 1 0.14122606994466D+00 0.45013045485935D-08 3 11 2 1 0.92121196699510D-15 -0.11181664048897D-17 1 12 2 1 0.21828633112945D+00 0.20847359786571D-08 2 12 2 1 -0.24626508420675D+00 0.12408394430883D-09 3 12 2 1 0.20730390282521D-14 0.17848561884160D-15 1 13 2 1 0.38250106498101D+00 -0.56178692536607D-08 2 13 2 1 0.39742552040037D+00 0.17814612958480D-09 3 13 2 1 0.45425891865290D+00 0.10717213167542D-07 1 14 2 1 -0.20608507553581D+00 -0.31656792789800D-03 2 14 2 1 0.27225118200816D+00 -0.35497944298521D-03 3 14 2 1 0.23505711426166D+00 0.21136134881316D-03 1 15 2 1 -0.20608507553581D+00 -0.31656792789816D-03 2 15 2 1 0.27225118200816D+00 -0.35497944298418D-03 3 15 2 1 -0.23505711426167D+00 -0.21136134881312D-03 1 16 2 1 0.38250106498101D+00 -0.56178690846443D-08 2 16 2 1 0.39742552040037D+00 0.17814623965919D-09 3 16 2 1 -0.45425891865290D+00 -0.10717213134763D-07 1 17 2 1 0.53612210623466D+00 0.45155218654886D-02 2 17 2 1 0.79186286634333D+00 0.81935811546418D-02 3 17 2 1 0.87893240916726D+00 0.16417684723853D-01 1 18 2 1 0.31248864877211D+00 0.53155363258309D-03 2 18 2 1 -0.11531177325472D+00 0.12687788388845D-02 3 18 2 1 -0.57330019971578D+00 -0.60569890989333D-02 1 19 2 1 0.31248864877211D+00 0.53155363258263D-03 2 19 2 1 -0.11531177325472D+00 0.12687788388846D-02 3 19 2 1 0.57330019971579D+00 0.60569890989331D-02 1 20 2 1 0.53612210623467D+00 0.45155218654886D-02 2 20 2 1 0.79186286634332D+00 0.81935811546418D-02 3 20 2 1 -0.87893240916726D+00 -0.16417684723853D-01 1 1 3 1 -0.42964443745500D-13 0.00000000000000D+00 2 1 3 1 -0.28862031926092D-13 0.00000000000000D+00 3 1 3 1 0.14650341002773D+02 0.00000000000000D+00 1 2 3 1 0.20609427342357D-14 -0.17618622441708D-15 2 2 3 1 -0.12556911441668D-13 -0.22518339737274D-15 3 2 3 1 -0.32792647624970D+01 0.10874688324065D-07 1 3 3 1 0.37784571356223D-14 -0.78472968916511D-15 2 3 3 1 -0.30447512364223D-14 0.12658703692585D-15 3 3 3 1 -0.71763572278871D+00 0.12435090464062D-14 1 4 3 1 0.14893849136176D-13 0.14187318116338D-14 2 4 3 1 -0.81897340844508D-15 0.11334297222944D-15 3 4 3 1 -0.49008006236103D-13 -0.19828143993685D-07 1 5 3 1 0.78857699776042D+00 0.49385839617423D-02 2 5 3 1 0.14319857911360D+01 -0.75143822495542D-02 3 5 3 1 -0.19010851186979D+01 -0.55721782336895D-02 1 6 3 1 -0.78857699776042D+00 -0.49385839617411D-02 2 6 3 1 -0.14319857911360D+01 0.75143822495540D-02 3 6 3 1 -0.19010851186979D+01 -0.55721782336719D-02 1 7 3 1 0.58257296579092D+01 0.76630372512528D-02 2 7 3 1 -0.15666301749174D+00 -0.27419237277449D-02 3 7 3 1 0.16211550928830D+01 -0.18700113001135D-02 1 8 3 1 -0.58257296579091D+01 -0.76630372512532D-02 2 8 3 1 0.15666301749174D+00 0.27419237277448D-02 3 8 3 1 0.16211550928830D+01 -0.18700113001126D-02 1 9 3 1 -0.17448930675400D-15 -0.33565692803943D-15 2 9 3 1 0.38154374748134D-16 -0.31880128095747D-15 3 9 3 1 -0.31432188357888D+01 0.32327910221159D-07 1 10 3 1 0.34171136610199D-14 0.35483494971299D-15 2 10 3 1 -0.38740753550300D-14 -0.24895243411880D-16 3 10 3 1 -0.18036365225666D+01 0.33471000645721D-08 1 11 3 1 0.11030070627428D-13 -0.55794811244892D-15 2 11 3 1 0.92121196788533D-15 -0.15807630663905D-17 3 11 3 1 -0.55303514789221D+00 0.10408827623452D-07 1 12 3 1 0.96067501721506D-15 -0.21322887446028D-15 2 12 3 1 0.20730390301548D-14 0.17900235900514D-15 3 12 3 1 -0.66456196054453D+00 0.63555385670519D-07 1 13 3 1 -0.82118588407746D+00 0.13780377708115D-07 2 13 3 1 0.91963428263787D-01 -0.14963375779377D-07 3 13 3 1 0.27311697623750D-01 0.16587181521566D-07 1 14 3 1 -0.10799786650728D+01 0.11528597573801D-02 2 14 3 1 -0.42674156748695D-01 0.11388164245968D-02 3 14 3 1 0.45218019499646D+00 0.13429359757366D-03 1 15 3 1 0.10799786650728D+01 -0.11528597573792D-02 2 15 3 1 0.42674156748706D-01 -0.11388164245968D-02 3 15 3 1 0.45218019499643D+00 0.13429359757402D-03 1 16 3 1 0.82118588407748D+00 -0.13780377797693D-07 2 16 3 1 -0.91963428263823D-01 0.14963375812156D-07 3 16 3 1 0.27311697623785D-01 0.16587178607422D-07 1 17 3 1 0.40884331380708D+00 -0.36635333128341D-02 2 17 3 1 0.96222188575302D+00 -0.16681063109167D-02 3 17 3 1 0.21356746809929D+01 0.64518719928322D-02 1 18 3 1 -0.14444766199701D+01 0.14756595536311D-08 2 18 3 1 -0.23803547453742D+00 -0.15358580473029D-06 3 18 3 1 0.69375072072499D+00 0.12776078107689D-06 1 19 3 1 0.14444766199700D+01 -0.14756589229224D-08 2 19 3 1 0.23803547453743D+00 0.15358580449686D-06 3 19 3 1 0.69375072072507D+00 0.12776078206891D-06 1 20 3 1 -0.40884331380708D+00 0.36635333128342D-02 2 20 3 1 -0.96222188575302D+00 0.16681063109167D-02 3 20 3 1 0.21356746809929D+01 0.64518719928304D-02 1 1 1 2 0.10897109838317D+01 -0.32189832532760D-08 2 1 1 2 0.17233355688501D+00 -0.15531911183527D-07 3 1 1 2 0.20609427343650D-14 0.17632748747406D-15 1 2 1 2 0.93997214749470D+01 0.00000000000000D+00 2 2 1 2 0.12669805341649D+01 0.56707772912160D-06 3 2 1 2 -0.33187959658539D-15 0.00000000000000D+00 1 3 1 2 -0.22527302229714D-14 0.15185239214420D-07 2 3 1 2 0.13087902084045D+00 -0.50628358033914D-08 3 3 1 2 -0.65295926065143D-14 0.32909531988510D-15 1 4 1 2 -0.89815168331167D-01 -0.14125851488990D-14 2 4 1 2 -0.46391553239478D-01 -0.24934119910298D-08 3 4 1 2 -0.16136283717038D-13 0.21037702779713D-14 1 5 1 2 0.41459148040797D+01 -0.47906692044563D-02 2 5 1 2 -0.68984576298944D+00 0.25323577954597D-02 3 5 1 2 -0.22881076477142D+00 -0.72931471681177D-02 1 6 1 2 0.41459148040797D+01 -0.47906692044594D-02 2 6 1 2 -0.68984576298945D+00 0.25323577954596D-02 3 6 1 2 0.22881076477142D+00 0.72931471681173D-02 1 7 1 2 -0.13361541043890D+00 0.44153408145904D-08 2 7 1 2 -0.40672906451286D+00 0.58921911613246D-08 3 7 1 2 -0.54342484007504D+01 0.20688740932225D-07 1 8 1 2 -0.13361541043889D+00 0.44153360952347D-08 2 8 1 2 -0.40672906451284D+00 0.58921915463155D-08 3 8 1 2 0.54342484007504D+01 -0.20688740159322D-07 1 9 1 2 -0.91094028615952D+00 -0.21462936265756D-08 2 9 1 2 0.10800215337626D+00 0.25978546969953D-08 3 9 1 2 0.11604424160123D-14 0.24662022911182D-15 1 10 1 2 0.15727436359371D+01 -0.19293239470211D-07 2 10 1 2 0.17021722332707D+00 -0.17471618347232D-07 3 10 1 2 -0.48590977079080D-14 0.32547964102087D-15 1 11 1 2 0.33669097512718D+01 -0.83533077072420D-08 2 11 1 2 -0.23688872566418D+00 -0.47218073202964D-08 3 11 1 2 -0.75522630749867D-14 0.29963219235760D-16 1 12 1 2 -0.24302470502948D+00 0.27640817602389D-08 2 12 1 2 0.39371980731900D-01 -0.17723304669109D-09 3 12 1 2 -0.31979708594030D-14 0.15258096103173D-14 1 13 1 2 0.10413932964438D+01 -0.21687425894975D-02 2 13 1 2 0.83615108999650D+00 -0.20828989450391D-02 3 13 1 2 0.53793535376568D+00 -0.17218116919339D-03 1 14 1 2 -0.13505761418088D+01 -0.38777333264845D-08 2 14 1 2 -0.81666934161532D+00 -0.11466037162238D-08 3 14 1 2 0.88204085885429D+00 0.17236315640321D-07 1 15 1 2 -0.13505761418088D+01 -0.38777323841190D-08 2 15 1 2 -0.81666934161537D+00 -0.11466036395090D-08 3 15 1 2 -0.88204085885436D+00 -0.17236315532314D-07 1 16 1 2 0.10413932964438D+01 -0.21687425894946D-02 2 16 1 2 0.83615108999652D+00 -0.20828989450392D-02 3 16 1 2 -0.53793535376568D+00 0.17218116919380D-03 1 17 1 2 0.12026903628937D+01 -0.82154279193479D-02 2 17 1 2 -0.10450540314163D+01 0.21458121172610D-02 3 17 1 2 0.87229731747169D+00 0.11087385210488D-01 1 18 1 2 -0.18132533007096D+01 -0.47530769157231D-02 2 18 1 2 0.30117809923759D+00 -0.56316188352095D-02 3 18 1 2 -0.37152320846480D+00 -0.14970024958021D-01 1 19 1 2 -0.18132533007096D+01 -0.47530769157247D-02 2 19 1 2 0.30117809923765D+00 -0.56316188352094D-02 3 19 1 2 0.37152320846471D+00 0.14970024958021D-01 1 20 1 2 0.12026903628937D+01 -0.82154279193457D-02 2 20 1 2 -0.10450540314164D+01 0.21458121172613D-02 3 20 1 2 -0.87229731747186D+00 -0.11087385210488D-01 1 1 2 2 0.17233433603424D+00 0.88683076770109D-08 2 1 2 2 0.32158429759640D+00 0.12966313136836D-08 3 1 2 2 -0.12556911442689D-13 0.22512919143627D-15 1 2 2 2 0.12669774131175D+01 0.62963247344663D-06 2 2 2 2 0.80004662339525D+01 0.00000000000000D+00 3 2 2 2 -0.35967459263013D-13 0.00000000000000D+00 1 3 2 2 0.13087902084045D+00 0.50628360410802D-08 2 3 2 2 -0.94059914847766D-15 -0.17230488065860D-08 3 3 2 2 0.67026460413034D-15 0.19230069821173D-15 1 4 2 2 0.46391553239427D-01 -0.24934119910298D-08 2 4 2 2 -0.37795024425623D+00 -0.24109366972446D-14 3 4 2 2 0.95083008224040D-14 0.10260941179389D-15 1 5 2 2 0.23792062273921D+00 0.52956604204217D-03 2 5 2 2 -0.34762720614300D+01 0.48943671269849D-02 3 5 2 2 0.18697896599545D+01 -0.51240298166188D-02 1 6 2 2 0.23792062273920D+00 0.52956604204207D-03 2 6 2 2 -0.34762720614300D+01 0.48943671269850D-02 3 6 2 2 -0.18697896599545D+01 0.51240298166189D-02 1 7 2 2 -0.39354977651038D+00 -0.12796626410014D-08 2 7 2 2 0.63364291431510D+00 0.15953179562721D-09 3 7 2 2 0.16919166734277D+00 0.22089798797311D-08 1 8 2 2 -0.39354977651036D+00 -0.12796622559825D-08 2 8 2 2 0.63364291431509D+00 0.15953122691950D-09 3 8 2 2 -0.16919166734278D+00 -0.22089798640182D-08 1 9 2 2 -0.84278587224155D-01 -0.27250362201549D-08 2 9 2 2 0.27960957653770D+00 -0.20657971065100D-08 3 9 2 2 0.87670705475125D-15 0.72944582750033D-16 1 10 2 2 0.38698390888555D+00 0.64342441112497D-08 2 10 2 2 -0.11076702982718D+00 -0.11066710380957D-08 3 10 2 2 0.31974507203090D-14 -0.29669298812224D-15 1 11 2 2 -0.21828633112977D+00 -0.20847329852382D-08 2 11 2 2 0.24626508420686D+00 -0.12407799244895D-09 3 11 2 2 -0.24681585645879D-14 0.12281677474933D-15 1 12 2 2 -0.82932068486516D-01 0.55746734755562D-08 2 12 2 2 -0.14122606994465D+00 -0.45013043206156D-08 3 12 2 2 0.46916257933248D-16 -0.33497586509180D-16 1 13 2 2 0.20608507553582D+00 0.31656792789944D-03 2 13 2 2 -0.27225118200812D+00 0.35497944298389D-03 3 13 2 2 -0.23505711426169D+00 -0.21136134881560D-03 1 14 2 2 -0.38250106498099D+00 0.56178735743286D-08 2 14 2 2 -0.39742552040029D+00 -0.17814838787544D-09 3 14 2 2 -0.45425891865288D+00 -0.10717205898902D-07 1 15 2 2 -0.38250106498106D+00 0.56178736510434D-08 2 15 2 2 -0.39742552040025D+00 -0.17814885479117D-09 3 15 2 2 0.45425891865290D+00 0.10717205652342D-07 1 16 2 2 0.20608507553583D+00 0.31656792789933D-03 2 16 2 2 -0.27225118200813D+00 0.35497944298382D-03 3 16 2 2 0.23505711426170D+00 0.21136134881553D-03 1 17 2 2 -0.31248864877209D+00 -0.53155363258469D-03 2 17 2 2 0.11531177325463D+00 -0.12687788388830D-02 3 17 2 2 0.57330019971577D+00 0.60569890989386D-02 1 18 2 2 -0.53612210623461D+00 -0.45155218654945D-02 2 18 2 2 -0.79186286634346D+00 -0.81935811546455D-02 3 18 2 2 -0.87893240916720D+00 -0.16417684723865D-01 1 19 2 2 -0.53612210623457D+00 -0.45155218654944D-02 2 19 2 2 -0.79186286634342D+00 -0.81935811546455D-02 3 19 2 2 0.87893240916711D+00 0.16417684723865D-01 1 20 2 2 -0.31248864877213D+00 -0.53155363258447D-03 2 20 2 2 0.11531177325466D+00 -0.12687788388837D-02 3 20 2 2 -0.57330019971585D+00 -0.60569890989388D-02 1 1 3 2 0.20609427341710D-14 0.17653938205954D-15 2 1 3 2 -0.12556911441571D-13 0.22504788253157D-15 3 1 3 2 -0.32792647624970D+01 0.10874688204600D-07 1 2 3 2 -0.33187959989411D-15 0.00000000000000D+00 2 2 3 2 -0.35967459263013D-13 0.00000000000000D+00 3 2 3 2 0.14650341002773D+02 0.00000000000000D+00 1 3 3 2 -0.65295926067998D-14 0.32921002896152D-15 2 3 3 2 0.67026460486553D-15 0.19229411505179D-15 3 3 3 2 -0.26781830163272D-13 0.19828141223402D-07 1 4 3 2 -0.16136283716936D-13 0.21039947816068D-14 2 4 3 2 0.95083008219869D-14 0.10256950323606D-15 3 4 3 2 0.71763572278882D+00 0.59023915877586D-15 1 5 3 2 0.78857699776043D+00 0.49385839617397D-02 2 5 3 2 0.14319857911361D+01 -0.75143822495543D-02 3 5 3 2 -0.19010851186978D+01 -0.55721782336828D-02 1 6 3 2 -0.78857699776043D+00 -0.49385839617401D-02 2 6 3 2 -0.14319857911362D+01 0.75143822495543D-02 3 6 3 2 -0.19010851186978D+01 -0.55721782336824D-02 1 7 3 2 -0.58257296579093D+01 -0.76630372512536D-02 2 7 3 2 0.15666301749174D+00 0.27419237277436D-02 3 7 3 2 -0.16211550928830D+01 0.18700113001053D-02 1 8 3 2 0.58257296579092D+01 0.76630372512543D-02 2 8 3 2 -0.15666301749174D+00 -0.27419237277435D-02 3 8 3 2 -0.16211550928830D+01 0.18700113001064D-02 1 9 3 2 0.11604424159874D-14 0.24585070871223D-15 2 9 3 2 0.87670705513729D-15 0.72898086592726D-16 3 9 3 2 0.18036365225666D+01 -0.33471019575980D-08 1 10 3 2 -0.48590977087352D-14 0.32547964102087D-15 2 10 3 2 0.31974507203090D-14 -0.29842771159822D-15 3 10 3 2 0.31432188357887D+01 -0.32327898890603D-07 1 11 3 2 -0.75522630757855D-14 0.29434749290794D-16 2 11 3 2 -0.24681585664907D-14 0.12230003458579D-15 3 11 3 2 0.66456196054462D+00 -0.63555373908981D-07 1 12 3 2 -0.31979708597158D-14 0.15258334161860D-14 2 12 3 2 0.46916257043017D-16 -0.33034989847679D-16 3 12 3 2 0.55303514789220D+00 -0.10408829957105D-07 1 13 3 2 0.10799786650728D+01 -0.11528597573773D-02 2 13 3 2 0.42674156748670D-01 -0.11388164245993D-02 3 13 3 2 -0.45218019499650D+00 -0.13429359758121D-03 1 14 3 2 0.82118588407732D+00 -0.13780385901568D-07 2 14 3 2 -0.91963428263773D-01 0.14963383047584D-07 3 14 3 2 -0.27311697623842D-01 -0.16587185996447D-07 1 15 3 2 -0.82118588407742D+00 0.13780386009792D-07 2 15 3 2 0.91963428263823D-01 -0.14963383294577D-07 3 15 3 2 -0.27311697623863D-01 -0.16587184242586D-07 1 16 3 2 -0.10799786650728D+01 0.11528597573777D-02 2 16 3 2 -0.42674156748667D-01 0.11388164245992D-02 3 16 3 2 -0.45218019499651D+00 -0.13429359758058D-03 1 17 3 2 0.14444766199698D+01 -0.14756525954353D-08 2 17 3 2 0.23803547453741D+00 0.15358581004368D-06 3 17 3 2 -0.69375072072487D+00 -0.12776079630561D-06 1 18 3 2 -0.40884331380694D+00 0.36635333128252D-02 2 18 3 2 -0.96222188575296D+00 0.16681063109043D-02 3 18 3 2 -0.21356746809926D+01 -0.64518719928414D-02 1 19 3 2 0.40884331380687D+00 -0.36635333128249D-02 2 19 3 2 0.96222188575287D+00 -0.16681063109045D-02 3 19 3 2 -0.21356746809927D+01 -0.64518719928424D-02 1 20 3 2 -0.14444766199700D+01 0.14756526012532D-08 2 20 3 2 -0.23803547453749D+00 -0.15358581025008D-06 3 20 3 2 -0.69375072072507D+00 -0.12776079436280D-06 1 1 1 3 0.89815168331202D-01 0.34956028362213D-14 2 1 1 3 -0.46391553239281D-01 -0.24934124793314D-08 3 1 1 3 0.37784571356223D-14 0.78472968916511D-15 1 2 1 3 -0.22527302229714D-14 -0.15185239214420D-07 2 2 1 3 0.13087902084045D+00 -0.50628360410802D-08 3 2 1 3 -0.65295926067998D-14 -0.32921002896152D-15 1 3 1 3 0.93997214749488D+01 0.00000000000000D+00 2 3 1 3 -0.12669805341649D+01 -0.56707772912160D-06 3 3 1 3 -0.14542734311787D-13 0.00000000000000D+00 1 4 1 3 0.10897109838317D+01 -0.32189826590133D-08 2 4 1 3 -0.17233355688501D+00 0.15531911001493D-07 3 4 1 3 -0.91951323806461D-14 0.11552584063207D-15 1 5 1 3 0.13361541043889D+00 -0.44153339634547D-08 2 5 1 3 -0.40672906451292D+00 0.58921896399774D-08 3 5 1 3 -0.54342484007504D+01 0.20688726197549D-07 1 6 1 3 0.13361541043889D+00 -0.44153363817248D-08 2 6 1 3 -0.40672906451292D+00 0.58921890975712D-08 3 6 1 3 0.54342484007503D+01 -0.20688726821339D-07 1 7 1 3 0.41459148040797D+01 -0.47906692044600D-02 2 7 1 3 0.68984576298944D+00 -0.25323577954597D-02 3 7 1 3 0.22881076477144D+00 0.72931471681184D-02 1 8 1 3 0.41459148040797D+01 -0.47906692044559D-02 2 8 1 3 0.68984576298945D+00 -0.25323577954596D-02 3 8 1 3 -0.22881076477145D+00 -0.72931471681164D-02 1 9 1 3 -0.33669097512721D+01 0.83532952764691D-08 2 9 1 3 -0.23688872566411D+00 -0.47218120470145D-08 3 9 1 3 0.33637946315219D-14 -0.26660970287692D-14 1 10 1 3 -0.24302470502949D+00 0.27640828616381D-08 2 10 1 3 -0.39371980731897D-01 0.17723242281462D-09 3 10 1 3 0.22956933295934D-13 -0.35789273330913D-15 1 11 1 3 -0.91094028615951D+00 -0.21462941422964D-08 2 11 1 3 -0.10800215337626D+00 -0.25978547673684D-08 3 11 1 3 0.42778879830378D-14 0.18076652353812D-15 1 12 1 3 -0.15727436359371D+01 0.19293244224877D-07 2 12 1 3 0.17021722332714D+00 -0.17471615178113D-07 3 12 1 3 0.10812402512172D-14 0.48882796199310D-15 1 13 1 3 -0.18132533007096D+01 -0.47530769157255D-02 2 13 1 3 -0.30117809923761D+00 0.56316188352094D-02 3 13 1 3 0.37152320846471D+00 0.14970024958021D-01 1 14 1 3 -0.12026903628936D+01 0.82154279193474D-02 2 14 1 3 -0.10450540314164D+01 0.21458121172635D-02 3 14 1 3 0.87229731747186D+00 0.11087385210480D-01 1 15 1 3 -0.12026903628936D+01 0.82154279193498D-02 2 15 1 3 -0.10450540314164D+01 0.21458121172635D-02 3 15 1 3 -0.87229731747179D+00 -0.11087385210480D-01 1 16 1 3 -0.18132533007097D+01 -0.47530769157252D-02 2 16 1 3 -0.30117809923763D+00 0.56316188352093D-02 3 16 1 3 -0.37152320846468D+00 -0.14970024958021D-01 1 17 1 3 -0.13505761418087D+01 -0.38777348821269D-08 2 17 1 3 0.81666934161532D+00 0.11466033572228D-08 3 17 1 3 -0.88204085885432D+00 -0.17236315715669D-07 1 18 1 3 -0.10413932964438D+01 0.21687425894934D-02 2 18 1 3 0.83615108999652D+00 -0.20828989450412D-02 3 18 1 3 0.53793535376571D+00 -0.17218116919643D-03 1 19 1 3 -0.10413932964438D+01 0.21687425894930D-02 2 19 1 3 0.83615108999652D+00 -0.20828989450404D-02 3 19 1 3 -0.53793535376573D+00 0.17218116919583D-03 1 20 1 3 -0.13505761418087D+01 -0.38777357386618D-08 2 20 1 3 0.81666934161533D+00 0.11466034726327D-08 3 20 1 3 0.88204085885430D+00 0.17236316101294D-07 1 1 2 3 0.46391553239624D-01 -0.24934124793314D-08 2 1 2 3 0.37795024425616D+00 0.26307839431057D-14 3 1 2 3 -0.30447512364223D-14 -0.12658703692585D-15 1 2 2 3 0.13087902084045D+00 0.50628358033914D-08 2 2 2 3 -0.94059914847766D-15 0.17230488065860D-08 3 2 2 3 0.67026460486553D-15 -0.19229411505179D-15 1 3 2 3 -0.12669774131176D+01 -0.62963247344663D-06 2 3 2 3 0.80004662339543D+01 0.00000000000000D+00 3 3 2 3 -0.57283741335824D-13 0.00000000000000D+00 1 4 2 3 -0.17233433603424D+00 -0.88683078590452D-08 2 4 2 3 0.32158429759636D+00 0.12966319407835D-08 3 4 2 3 -0.87013083235068D-14 -0.28703036166894D-15 1 5 2 3 -0.39354977651044D+00 -0.12796641623311D-08 2 5 2 3 -0.63364291431506D+00 -0.15953190587602D-09 3 5 2 3 -0.16919166734277D+00 -0.22089796724684D-08 1 6 2 3 -0.39354977651044D+00 -0.12796647047654D-08 2 6 2 3 -0.63364291431506D+00 -0.15953202768004D-09 3 6 2 3 0.16919166734277D+00 0.22089797331946D-08 1 7 2 3 -0.23792062273920D+00 -0.52956604204216D-03 2 7 2 3 -0.34762720614299D+01 0.48943671269858D-02 3 7 2 3 0.18697896599546D+01 -0.51240298166196D-02 1 8 2 3 -0.23792062273920D+00 -0.52956604204213D-03 2 8 2 3 -0.34762720614299D+01 0.48943671269875D-02 3 8 2 3 -0.18697896599546D+01 0.51240298166196D-02 1 9 2 3 -0.21828633112969D+00 -0.20847377119563D-08 2 9 2 3 -0.24626508420672D+00 0.12408098007107D-09 3 9 2 3 -0.46089538597335D-15 0.56896741979544D-16 1 10 2 3 0.82932068486520D-01 -0.55746740994327D-08 2 10 2 3 -0.14122606994466D+00 -0.45013044463201D-08 3 10 2 3 0.42892473776905D-14 0.19943026718554D-16 1 11 2 3 0.84278587224158D-01 0.27250361497818D-08 2 11 2 3 0.27960957653769D+00 -0.20657969911742D-08 3 11 2 3 0.19777331372489D-14 -0.69572058895587D-16 1 12 2 3 0.38698390888561D+00 0.64342472803687D-08 2 12 2 3 0.11076702982727D+00 0.11066497979401D-08 3 12 2 3 0.25760679341729D-15 0.17584752070344D-15 1 13 2 3 0.53612210623460D+00 0.45155218654945D-02 2 13 2 3 -0.79186286634349D+00 -0.81935811546456D-02 3 13 2 3 -0.87893240916711D+00 -0.16417684723865D-01 1 14 2 3 -0.31248864877212D+00 -0.53155363258225D-03 2 14 2 3 -0.11531177325465D+00 0.12687788388845D-02 3 14 2 3 -0.57330019971582D+00 -0.60569890989335D-02 1 15 2 3 -0.31248864877212D+00 -0.53155363258227D-03 2 15 2 3 -0.11531177325465D+00 0.12687788388848D-02 3 15 2 3 0.57330019971582D+00 0.60569890989336D-02 1 16 2 3 0.53612210623457D+00 0.45155218654943D-02 2 16 2 3 -0.79186286634348D+00 -0.81935811546452D-02 3 16 2 3 0.87893240916714D+00 0.16417684723865D-01 1 17 2 3 0.38250106498101D+00 -0.56178739333295D-08 2 17 2 3 -0.39742552040028D+00 -0.17814891653544D-09 3 17 2 3 -0.45425891865288D+00 -0.10717205788317D-07 1 18 2 3 0.20608507553584D+00 0.31656792789731D-03 2 18 2 3 0.27225118200813D+00 -0.35497944298488D-03 3 18 2 3 0.23505711426173D+00 0.21136134881328D-03 1 19 2 3 0.20608507553585D+00 0.31656792789815D-03 2 19 2 3 0.27225118200814D+00 -0.35497944298533D-03 3 19 2 3 -0.23505711426173D+00 -0.21136134881317D-03 1 20 2 3 0.38250106498100D+00 -0.56178738179197D-08 2 20 2 3 -0.39742552040028D+00 -0.17814850614061D-09 3 20 2 3 0.45425891865290D+00 0.10717205890526D-07 1 1 3 3 0.37784571357245D-14 0.78450518552960D-15 2 1 3 3 -0.30447512368394D-14 -0.12654712836802D-15 3 1 3 3 -0.71763572278871D+00 -0.12435090464062D-14 1 2 3 3 -0.65295926065143D-14 -0.32909531988510D-15 2 2 3 3 0.67026460413034D-15 -0.19230069821173D-15 3 2 3 3 -0.26781830163272D-13 -0.19828141223402D-07 1 3 3 3 -0.14542734315096D-13 0.00000000000000D+00 2 3 3 3 -0.57283741335824D-13 0.00000000000000D+00 3 3 3 3 0.14650341002773D+02 0.00000000000000D+00 1 4 3 3 -0.91951323803746D-14 0.11559647216056D-15 2 4 3 3 -0.87013083242369D-14 -0.28722009913520D-15 3 4 3 3 -0.32792647624969D+01 0.10874688187683D-07 1 5 3 3 -0.58257296579092D+01 -0.76630372512683D-02 2 5 3 3 -0.15666301749174D+00 -0.27419237277434D-02 3 5 3 3 0.16211550928830D+01 -0.18700113001048D-02 1 6 3 3 0.58257296579092D+01 0.76630372512677D-02 2 6 3 3 0.15666301749173D+00 0.27419237277434D-02 3 6 3 3 0.16211550928831D+01 -0.18700113001049D-02 1 7 3 3 -0.78857699776041D+00 -0.49385839617390D-02 2 7 3 3 0.14319857911363D+01 -0.75143822495550D-02 3 7 3 3 -0.19010851186980D+01 -0.55721782336787D-02 1 8 3 3 0.78857699776041D+00 0.49385839617410D-02 2 8 3 3 -0.14319857911363D+01 0.75143822495551D-02 3 8 3 3 -0.19010851186980D+01 -0.55721782336781D-02 1 9 3 3 0.33637946317080D-14 -0.26685790176012D-14 2 9 3 3 -0.46089538482774D-15 0.56469827455503D-16 3 9 3 3 -0.66456196054433D+00 0.63555381122410D-07 1 10 3 3 0.22956933296332D-13 -0.35914225263101D-15 2 10 3 3 0.42892473768131D-14 0.20181387023562D-16 3 10 3 3 0.55303514789223D+00 -0.10408829665760D-07 1 11 3 3 0.42778879829737D-14 0.18211648681430D-15 2 11 3 3 0.19777331374566D-14 -0.69548810816933D-16 3 11 3 3 0.18036365225666D+01 -0.33471022102026D-08 1 12 3 3 0.10812402512172D-14 0.48882796199310D-15 2 12 3 3 0.25760679672601D-15 0.17411279722747D-15 3 12 3 3 -0.31432188357886D+01 0.32327909601045D-07 1 13 3 3 0.40884331380686D+00 -0.36635333128257D-02 2 13 3 3 -0.96222188575288D+00 0.16681063109044D-02 3 13 3 3 -0.21356746809926D+01 -0.64518719928423D-02 1 14 3 3 0.14444766199700D+01 -0.14756600821609D-08 2 14 3 3 -0.23803547453745D+00 -0.15358580491633D-06 3 14 3 3 0.69375072072493D+00 0.12776077927054D-06 1 15 3 3 -0.14444766199699D+01 0.14756599047121D-08 2 15 3 3 0.23803547453746D+00 0.15358580496652D-06 3 15 3 3 0.69375072072496D+00 0.12776078417228D-06 1 16 3 3 -0.40884331380683D+00 0.36635333128256D-02 2 16 3 3 0.96222188575290D+00 -0.16681063109044D-02 3 16 3 3 -0.21356746809927D+01 -0.64518719928417D-02 1 17 3 3 -0.82118588407738D+00 0.13780385826437D-07 2 17 3 3 -0.91963428263801D-01 0.14963383158602D-07 3 17 3 3 -0.27311697623849D-01 -0.16587187407511D-07 1 18 3 3 0.10799786650729D+01 -0.11528597573804D-02 2 18 3 3 -0.42674156748635D-01 0.11388164245970D-02 3 18 3 3 0.45218019499651D+00 0.13429359757691D-03 1 19 3 3 -0.10799786650729D+01 0.11528597573798D-02 2 19 3 3 0.42674156748628D-01 -0.11388164245969D-02 3 19 3 3 0.45218019499650D+00 0.13429359757766D-03 1 20 3 3 0.82118588407733D+00 -0.13780385440595D-07 2 20 3 3 0.91963428263787D-01 -0.14963383055960D-07 3 20 3 3 -0.27311697623856D-01 -0.16587185314778D-07 1 1 1 4 0.18553180634275D-13 0.15185241937132D-07 2 1 1 4 -0.13087902084044D+00 0.50628360228349D-08 3 1 1 4 0.14893849136176D-13 -0.14187318116338D-14 1 2 1 4 -0.89815168331167D-01 0.14125851488990D-14 2 2 1 4 0.46391553239427D-01 0.24934119910298D-08 3 2 1 4 -0.16136283716936D-13 -0.21039947816068D-14 1 3 1 4 0.10897109838317D+01 -0.32189831932054D-08 2 3 1 4 -0.17233355688501D+00 0.15531911107951D-07 3 3 1 4 -0.91951323805814D-14 -0.11559647216056D-15 1 4 1 4 0.93997214749470D+01 0.00000000000000D+00 2 4 1 4 -0.12669805341652D+01 -0.56707772912160D-06 3 4 1 4 -0.21648161669388D-13 0.00000000000000D+00 1 5 1 4 -0.13361541043890D+00 0.44153457381749D-08 2 5 1 4 0.40672906451289D+00 -0.58921893463146D-08 3 5 1 4 0.54342484007504D+01 -0.20688727441668D-07 1 6 1 4 -0.13361541043893D+00 0.44153458711989D-08 2 6 1 4 0.40672906451288D+00 -0.58921908704126D-08 3 6 1 4 -0.54342484007504D+01 0.20688727505763D-07 1 7 1 4 0.41459148040797D+01 -0.47906692044560D-02 2 7 1 4 0.68984576298945D+00 -0.25323577954598D-02 3 7 1 4 0.22881076477139D+00 0.72931471681180D-02 1 8 1 4 0.41459148040797D+01 -0.47906692044599D-02 2 8 1 4 0.68984576298945D+00 -0.25323577954598D-02 3 8 1 4 -0.22881076477139D+00 -0.72931471681178D-02 1 9 1 4 -0.24302470502943D+00 0.27640821944336D-08 2 9 1 4 -0.39371980731899D-01 0.17723280349508D-09 3 9 1 4 0.27281781261066D-13 0.51305653064445D-15 1 10 1 4 -0.33669097512718D+01 0.83532832962529D-08 2 10 1 4 -0.23688872566404D+00 -0.47218106000572D-08 3 10 1 4 -0.87546330986735D-14 -0.83235390383412D-15 1 11 1 4 -0.15727436359370D+01 0.19293244405018D-07 2 11 1 4 0.17021722332730D+00 -0.17471615394410D-07 3 11 1 4 -0.26629299780761D-15 -0.10776528514257D-15 1 12 1 4 -0.91094028615951D+00 -0.21462936888894D-08 2 12 1 4 -0.10800215337626D+00 -0.25978546111886D-08 3 12 1 4 0.56924547099352D-14 0.37736831691746D-16 1 13 1 4 -0.12026903628936D+01 0.82154279193468D-02 2 13 1 4 -0.10450540314163D+01 0.21458121172629D-02 3 13 1 4 0.87229731747165D+00 0.11087385210481D-01 1 14 1 4 -0.18132533007096D+01 -0.47530769157243D-02 2 14 1 4 -0.30117809923758D+00 0.56316188352094D-02 3 14 1 4 0.37152320846478D+00 0.14970024958021D-01 1 15 1 4 -0.18132533007096D+01 -0.47530769157262D-02 2 15 1 4 -0.30117809923768D+00 0.56316188352094D-02 3 15 1 4 -0.37152320846467D+00 -0.14970024958022D-01 1 16 1 4 -0.12026903628937D+01 0.82154279193485D-02 2 16 1 4 -0.10450540314164D+01 0.21458121172632D-02 3 16 1 4 -0.87229731747185D+00 -0.11087385210480D-01 1 17 1 4 -0.10413932964438D+01 0.21687425894935D-02 2 17 1 4 0.83615108999653D+00 -0.20828989450397D-02 3 17 1 4 0.53793535376571D+00 -0.17218116919601D-03 1 18 1 4 -0.13505761418087D+01 -0.38777309048109D-08 2 18 1 4 0.81666934161529D+00 0.11466029928077D-08 3 18 1 4 -0.88204085885429D+00 -0.17236314924958D-07 1 19 1 4 -0.13505761418087D+01 -0.38777300648971D-08 2 19 1 4 0.81666934161534D+00 0.11466029530038D-08 3 19 1 4 0.88204085885432D+00 0.17236314514978D-07 1 20 1 4 -0.10413932964438D+01 0.21687425894940D-02 2 20 1 4 0.83615108999653D+00 -0.20828989450404D-02 3 20 1 4 -0.53793535376571D+00 0.17218116919520D-03 1 1 2 4 -0.13087902084044D+00 -0.50628358216367D-08 2 1 2 4 -0.64332147788477D-14 -0.17230484454493D-08 3 1 2 4 -0.81897340844508D-15 -0.11334297222944D-15 1 2 2 4 -0.46391553239478D-01 0.24934119910298D-08 2 2 2 4 -0.37795024425623D+00 0.24109366972446D-14 3 2 2 4 0.95083008219869D-14 -0.10256950323606D-15 1 3 2 4 -0.17233433603424D+00 -0.88683077525871D-08 2 3 2 4 0.32158429759636D+00 0.12966329508995D-08 3 3 2 4 -0.87013083234097D-14 0.28743693956970D-15 1 4 2 4 -0.12669774131178D+01 -0.62963247344663D-06 2 4 2 4 0.80004662339525D+01 0.00000000000000D+00 3 4 2 4 0.81272092137403D-13 0.00000000000000D+00 1 5 2 4 0.39354977651042D+00 0.12796644559938D-08 2 5 2 4 0.63364291431509D+00 0.15952891233048D-09 3 5 2 4 0.16919166734276D+00 0.22089810377466D-08 1 6 2 4 0.39354977651040D+00 0.12796629319240D-08 2 6 2 4 0.63364291431511D+00 0.15952769196652D-09 3 6 2 4 -0.16919166734275D+00 -0.22089810313111D-08 1 7 2 4 -0.23792062273920D+00 -0.52956604204227D-03 2 7 2 4 -0.34762720614300D+01 0.48943671269845D-02 3 7 2 4 0.18697896599545D+01 -0.51240298166186D-02 1 8 2 4 -0.23792062273919D+00 -0.52956604204230D-03 2 8 2 4 -0.34762720614300D+01 0.48943671269855D-02 3 8 2 4 -0.18697896599546D+01 0.51240298166189D-02 1 9 2 4 0.82932068486518D-01 -0.55746737187522D-08 2 9 2 4 -0.14122606994465D+00 -0.45013040810459D-08 3 9 2 4 0.28456040850885D-14 -0.41278161020051D-16 1 10 2 4 -0.21828633112962D+00 -0.20847362649990D-08 2 10 2 4 -0.24626508420686D+00 0.12408419237229D-09 3 10 2 4 -0.24803517517081D-14 0.10135476104988D-15 1 11 2 4 0.38698390888577D+00 0.64342470640721D-08 2 11 2 4 0.11076702982693D+00 0.11066501096170D-08 3 11 2 4 0.20410495037683D-15 -0.14483970859615D-15 1 12 2 4 0.84278587224153D-01 0.27250363059616D-08 2 12 2 4 0.27960957653770D+00 -0.20657969755526D-08 3 12 2 4 0.46613540410428D-14 -0.14677858872184D-15 1 13 2 4 -0.31248864877209D+00 -0.53155363258285D-03 2 13 2 4 -0.11531177325463D+00 0.12687788388846D-02 3 13 2 4 -0.57330019971579D+00 -0.60569890989331D-02 1 14 2 4 0.53612210623463D+00 0.45155218654944D-02 2 14 2 4 -0.79186286634356D+00 -0.81935811546454D-02 3 14 2 4 -0.87893240916724D+00 -0.16417684723865D-01 1 15 2 4 0.53612210623452D+00 0.45155218654944D-02 2 15 2 4 -0.79186286634350D+00 -0.81935811546453D-02 3 15 2 4 0.87893240916706D+00 0.16417684723865D-01 1 16 2 4 -0.31248864877213D+00 -0.53155363258256D-03 2 16 2 4 -0.11531177325465D+00 0.12687788388843D-02 3 16 2 4 0.57330019971585D+00 0.60569890989332D-02 1 17 2 4 0.20608507553585D+00 0.31656792789884D-03 2 17 2 4 0.27225118200813D+00 -0.35497944298513D-03 3 17 2 4 0.23505711426174D+00 0.21136134881298D-03 1 18 2 4 0.38250106498099D+00 -0.56178742977447D-08 2 18 2 4 -0.39742552040029D+00 -0.17814894035737D-09 3 18 2 4 -0.45425891865283D+00 -0.10717205922671D-07 1 19 2 4 0.38250106498101D+00 -0.56178743375485D-08 2 19 2 4 -0.39742552040027D+00 -0.17814846361050D-09 3 19 2 4 0.45425891865285D+00 0.10717206188500D-07 1 20 2 4 0.20608507553585D+00 0.31656792789810D-03 2 20 2 4 0.27225118200813D+00 -0.35497944298492D-03 3 20 2 4 -0.23505711426173D+00 -0.21136134881318D-03 1 1 3 4 0.14893849135891D-13 -0.14188465207102D-14 2 1 3 4 -0.81897340770988D-15 -0.11333638906950D-15 3 1 3 4 -0.49008006236103D-13 0.19828143993685D-07 1 2 3 4 -0.16136283717038D-13 -0.21037702779713D-14 2 2 3 4 0.95083008224040D-14 -0.10260941179389D-15 3 2 3 4 0.71763572278882D+00 -0.59023915877586D-15 1 3 3 4 -0.91951323804393D-14 -0.11552584063207D-15 2 3 3 4 -0.87013083239204D-14 0.28724720210344D-15 3 3 3 4 -0.32792647624969D+01 0.10874688340982D-07 1 4 3 4 -0.21648161672697D-13 0.00000000000000D+00 2 4 3 4 0.81272092137403D-13 0.00000000000000D+00 3 4 3 4 0.14650341002769D+02 0.00000000000000D+00 1 5 3 4 0.58257296579092D+01 0.76630372512670D-02 2 5 3 4 0.15666301749172D+00 0.27419237277447D-02 3 5 3 4 -0.16211550928831D+01 0.18700113001126D-02 1 6 3 4 -0.58257296579092D+01 -0.76630372512670D-02 2 6 3 4 -0.15666301749172D+00 -0.27419237277447D-02 3 6 3 4 -0.16211550928831D+01 0.18700113001119D-02 1 7 3 4 -0.78857699776047D+00 -0.49385839617394D-02 2 7 3 4 0.14319857911362D+01 -0.75143822495541D-02 3 7 3 4 -0.19010851186977D+01 -0.55721782336813D-02 1 8 3 4 0.78857699776046D+00 0.49385839617396D-02 2 8 3 4 -0.14319857911362D+01 0.75143822495543D-02 3 8 3 4 -0.19010851186979D+01 -0.55721782336773D-02 1 9 3 4 0.27281781261464D-13 0.51180701132258D-15 2 9 3 4 0.28456040842111D-14 -0.41039800715043D-16 3 9 3 4 0.55303514789212D+00 -0.10408827946637D-07 1 10 3 4 -0.87546330984874D-14 -0.83483589266607D-15 2 10 3 4 -0.24803517505625D-14 0.10092784652584D-15 3 10 3 4 -0.66456196054467D+00 0.63555385403605D-07 1 11 3 4 -0.26629299946197D-15 -0.10776528514257D-15 2 11 3 4 0.20410495368554D-15 -0.14657443207213D-15 3 11 3 4 -0.31432188357885D+01 0.32327909565724D-07 1 12 3 4 0.56924547098102D-14 0.37741378811719D-16 2 12 3 4 0.46613540414256D-14 -0.14684918291123D-15 3 12 3 4 0.18036365225666D+01 -0.33471025711175D-08 1 13 3 4 0.14444766199698D+01 -0.14756593862336D-08 2 13 3 4 -0.23803547453742D+00 -0.15358580454152D-06 3 13 3 4 0.69375072072487D+00 0.12776078169780D-06 1 14 3 4 0.40884331380693D+00 -0.36635333128252D-02 2 14 3 4 -0.96222188575300D+00 0.16681063109047D-02 3 14 3 4 -0.21356746809927D+01 -0.64518719928399D-02 1 15 3 4 -0.40884331380681D+00 0.36635333128247D-02 2 15 3 4 0.96222188575282D+00 -0.16681063109045D-02 3 15 3 4 -0.21356746809927D+01 -0.64518719928400D-02 1 16 3 4 -0.14444766199700D+01 0.14756602975997D-08 2 16 3 4 0.23803547453749D+00 0.15358580463201D-06 3 16 3 4 0.69375072072505D+00 0.12776077929278D-06 1 17 3 4 0.10799786650729D+01 -0.11528597573800D-02 2 17 3 4 -0.42674156748628D-01 0.11388164245967D-02 3 17 3 4 0.45218019499657D+00 0.13429359757471D-03 1 18 3 4 -0.82118588407735D+00 0.13780386617148D-07 2 18 3 4 -0.91963428263751D-01 0.14963383024248D-07 3 18 3 4 -0.27311697623828D-01 -0.16587183460518D-07 1 19 3 4 0.82118588407735D+00 -0.13780387026911D-07 2 19 3 4 0.91963428263744D-01 -0.14963382757986D-07 3 19 3 4 -0.27311697623892D-01 -0.16587186005533D-07 1 20 3 4 -0.10799786650729D+01 0.11528597573791D-02 2 20 3 4 0.42674156748631D-01 -0.11388164245969D-02 3 20 3 4 0.45218019499654D+00 0.13429359757364D-03 1 1 1 5 0.41458843334221D+01 -0.95813167344357D-02 2 1 1 5 0.23792015891847D+00 0.10591086452178D-02 3 1 1 5 0.78857791965727D+00 -0.49390269094700D-02 1 2 1 5 0.41458843334221D+01 -0.95813167344349D-02 2 2 1 5 0.23792015891847D+00 0.10591086452179D-02 3 2 1 5 0.78857791965728D+00 -0.49390269094674D-02 1 3 1 5 0.13361541043889D+00 0.44153339634547D-08 2 3 1 5 -0.39354977651044D+00 0.12796641623311D-08 3 3 1 5 -0.58257296579092D+01 0.76630372512683D-02 1 4 1 5 -0.13361541043890D+00 -0.44153457381749D-08 2 4 1 5 0.39354977651042D+00 -0.12796644559938D-08 3 4 1 5 0.58257296579092D+01 -0.76630372512670D-02 1 5 1 5 0.26768383601689D+02 0.00000000000000D+00 2 5 1 5 -0.56942185647653D+00 -0.71883591409774D-07 3 5 1 5 -0.25621462395015D+01 -0.36817267012126D-07 1 6 1 5 0.52976878025470D+01 0.00000000000000D+00 2 6 1 5 -0.38061126980362D+00 0.46151868955637D-08 3 6 1 5 -0.39231039299319D+01 0.34115748211336D-08 1 7 1 5 0.68803253312377D-14 -0.72030580474440D-14 2 7 1 5 -0.16455860073860D-14 0.44986622738495D-15 3 7 1 5 -0.21806666789128D-19 0.35824027476648D-15 1 8 1 5 0.87268738945134D-14 -0.35159505080935D-14 2 8 1 5 0.30600555504138D-14 0.65865398744083D-15 3 8 1 5 0.62826031034956D-13 0.38847384724589D-15 1 9 1 5 -0.36212769713446D+01 0.14047465394696D+00 2 9 1 5 -0.78446652621208D-01 0.17514855993833D-01 3 9 1 5 0.59857203921953D+00 -0.27487427215193D+00 1 10 1 5 0.36212769713442D+01 -0.14047465394695D+00 2 10 1 5 0.78446652621190D-01 -0.17514855993832D-01 3 10 1 5 -0.59857203921963D+00 0.27487427215192D+00 1 11 1 5 0.76738579693580D+00 0.39066862394456D-08 2 11 1 5 -0.12976085826889D+00 0.22902560909383D-08 3 11 1 5 -0.49067269366484D+01 -0.28500698534778D-01 1 12 1 5 -0.76738579693578D+00 -0.39066915609547D-08 2 12 1 5 0.12976085826896D+00 -0.22902569258880D-08 3 12 1 5 0.49067269366484D+01 0.28500698534778D-01 1 13 1 5 0.55578809554998D+01 0.10036421920700D-01 2 13 1 5 0.17328686465240D+01 0.86035443403148D-02 3 13 1 5 -0.68447259755901D+00 0.24612205715123D-01 1 14 1 5 -0.55578809554996D+01 -0.10036421920719D-01 2 14 1 5 -0.17328686465236D+01 -0.86035443403375D-02 3 14 1 5 0.68447259755862D+00 -0.24612205715111D-01 1 15 1 5 -0.19362396073031D+01 0.11964887554201D-01 2 15 1 5 -0.83329143018954D+00 0.64728025028715D-02 3 15 1 5 -0.14256153319269D+00 -0.18984854898019D-01 1 16 1 5 0.19362396073031D+01 -0.11964887554200D-01 2 16 1 5 0.83329143018954D+00 -0.64728025028718D-02 3 16 1 5 0.14256153319272D+00 0.18984854898020D-01 1 17 1 5 0.50617432499133D+01 0.34881693369000D-02 2 17 1 5 -0.26913011930788D+01 -0.98995665567427D-02 3 17 1 5 -0.69596597002010D+00 0.16195095029629D-01 1 18 1 5 -0.50617432499133D+01 -0.34881693369051D-02 2 18 1 5 0.26913011930788D+01 0.98995665567647D-02 3 18 1 5 0.69596597002004D+00 -0.16195095029622D-01 1 19 1 5 -0.17794879776837D+01 0.19165567050890D-01 2 19 1 5 0.90366117840244D+00 -0.33076361382235D-01 3 19 1 5 -0.81120919759087D-01 -0.39032224875295D-01 1 20 1 5 0.17794879776837D+01 -0.19165567050889D-01 2 20 1 5 -0.90366117840244D+00 0.33076361382235D-01 3 20 1 5 0.81120919759103D-01 0.39032224875296D-01 1 1 2 5 -0.68984662268177D+00 0.50647128845796D-02 2 1 2 5 -0.34762329656509D+01 0.97887442961941D-02 3 1 2 5 0.14319831458146D+01 0.75153521126186D-02 1 2 2 5 -0.68984662268177D+00 0.50647128845797D-02 2 2 2 5 -0.34762329656510D+01 0.97887442961949D-02 3 2 2 5 0.14319831458148D+01 0.75153521126186D-02 1 3 2 5 -0.40672906451292D+00 -0.58921896399774D-08 2 3 2 5 -0.63364291431506D+00 0.15953190587602D-09 3 3 2 5 -0.15666301749174D+00 0.27419237277434D-02 1 4 2 5 0.40672906451289D+00 0.58921893463146D-08 2 4 2 5 0.63364291431509D+00 -0.15952891233048D-09 3 4 2 5 0.15666301749172D+00 -0.27419237277447D-02 1 5 2 5 -0.56940811001070D+00 0.76568204521129D-07 2 5 2 5 0.17768143654868D+02 0.00000000000000D+00 3 5 2 5 -0.24404980588634D+01 0.27781183928932D-06 1 6 2 5 -0.38061126980362D+00 -0.46151868955637D-08 2 6 2 5 0.77509538115117D+00 0.00000000000000D+00 3 6 2 5 0.91497323207694D+00 -0.60068050702558D-08 1 7 2 5 -0.16455862104588D-14 0.44986622738495D-15 2 7 2 5 -0.19283016003274D-13 -0.49120057071396D-14 3 7 2 5 -0.17597900579370D-19 -0.10625979283124D-15 1 8 2 5 0.30629280235992D-14 0.65865398744083D-15 2 8 2 5 -0.13675447976401D-13 -0.12275589453542D-14 3 8 2 5 0.80970316287865D-14 0.10245478511037D-15 1 9 2 5 0.12019035166440D+00 0.15121587861564D-01 2 9 2 5 -0.15360197481026D+01 0.18392548166201D+00 3 9 2 5 -0.10266869558605D+00 0.94599174760196D-01 1 10 2 5 -0.12019035166442D+00 -0.15121587861564D-01 2 10 2 5 0.15360197481023D+01 -0.18392548166200D+00 3 10 2 5 0.10266869558588D+00 -0.94599174760192D-01 1 11 2 5 -0.20243395290057D+00 -0.74255241623416D-09 2 11 2 5 -0.17442933858857D+00 0.39696679721609D-08 3 11 2 5 0.87816433546891D+00 0.87406908002361D-02 1 12 2 5 0.20243395290064D+00 0.74255158128440D-09 2 12 2 5 0.17442933858859D+00 -0.39696692447027D-08 3 12 2 5 -0.87816433546888D+00 -0.87406908002363D-02 1 13 2 5 -0.55079910428888D+00 0.47042237695696D-02 2 13 2 5 0.77559052844709D-01 -0.22939404689650D-02 3 13 2 5 -0.94452050145549D+00 0.49332111770546D-02 1 14 2 5 0.55079910428923D+00 -0.47042237695924D-02 2 14 2 5 -0.77559052844894D-01 0.22939404689608D-02 3 14 2 5 0.94452050145529D+00 -0.49332111770474D-02 1 15 2 5 0.59457960571179D-01 0.53575458752782D-02 2 15 2 5 0.39726271758556D-01 -0.30007940843049D-02 3 15 2 5 -0.31979338364590D+00 -0.74730631846224D-02 1 16 2 5 -0.59457960571177D-01 -0.53575458752785D-02 2 16 2 5 -0.39726271758561D-01 0.30007940843052D-02 3 16 2 5 0.31979338364591D+00 0.74730631846227D-02 1 17 2 5 0.63648666029938D+00 -0.36009329414409D-03 2 17 2 5 0.12512110340052D+01 0.12958961000945D-02 3 17 2 5 0.86659694614989D+00 -0.17054032197880D-01 1 18 2 5 -0.63648666029930D+00 0.36009329416609D-03 2 18 2 5 -0.12512110340054D+01 -0.12958961001168D-02 3 18 2 5 -0.86659694614982D+00 0.17054032197871D-01 1 19 2 5 0.29515759724765D+00 -0.27556222075908D-01 2 19 2 5 -0.18468761522584D+00 0.15233969912442D-01 3 19 2 5 0.15591637751355D+00 0.29754428369388D-01 1 20 2 5 -0.29515759724765D+00 0.27556222075908D-01 2 20 2 5 0.18468761522585D+00 -0.15233969912443D-01 3 20 2 5 -0.15591637751359D+00 -0.29754428369388D-01 1 1 3 5 -0.22868326833029D+00 -0.14586330252921D-01 2 1 3 5 0.18698683453975D+01 -0.10248094084865D-01 3 1 3 5 -0.19010841754099D+01 0.55720036936268D-02 1 2 3 5 -0.22868326833027D+00 -0.14586330252919D-01 2 2 3 5 0.18698683453976D+01 -0.10248094084865D-01 3 2 3 5 -0.19010841754097D+01 0.55720036936201D-02 1 3 3 5 -0.54342484007504D+01 -0.20688726197549D-07 2 3 3 5 -0.16919166734277D+00 0.22089796724684D-08 3 3 3 5 0.16211550928830D+01 0.18700113001048D-02 1 4 3 5 0.54342484007504D+01 0.20688727441668D-07 2 4 3 5 0.16919166734276D+00 -0.22089810377466D-08 3 4 3 5 -0.16211550928831D+01 -0.18700113001126D-02 1 5 3 5 -0.25621371785622D+01 0.68822802612515D-07 2 5 3 5 -0.24405125197431D+01 -0.31042772210814D-06 3 5 3 5 0.40427799625786D+02 0.00000000000000D+00 1 6 3 5 0.39231039299319D+01 0.34115748211336D-08 2 6 3 5 -0.91497323207694D+00 -0.60068050702558D-08 3 6 3 5 -0.30885903591145D+02 0.00000000000000D+00 1 7 3 5 -0.21667700446219D-19 0.35824027476648D-15 2 7 3 5 -0.17597900579321D-19 -0.10625979283124D-15 3 7 3 5 0.21906021954347D-14 0.29787572334487D-14 1 8 3 5 0.62826031034956D-13 0.38847384724589D-15 2 8 3 5 0.80967459369398D-14 0.10245478511037D-15 3 8 3 5 0.82971216006550D-14 -0.14175124084231D-14 1 9 3 5 -0.17324984411220D+01 -0.12079190423141D+00 2 9 3 5 0.53235148846542D+00 0.32034975474216D-01 3 9 3 5 -0.89292680740130D+00 -0.83005515325623D+00 1 10 3 5 0.17324984411219D+01 0.12079190423139D+00 2 10 3 5 -0.53235148846559D+00 -0.32034975474212D-01 3 10 3 5 0.89292680740215D+00 0.83005515325616D+00 1 11 3 5 -0.73226898376363D+00 -0.33980727753161D-08 2 11 3 5 0.18660580744282D-01 0.40067536513166D-08 3 11 3 5 0.15135227836615D+01 0.37224085019515D-01 1 12 3 5 0.73226898376369D+00 0.33980719652973D-08 2 12 3 5 -0.18660580744249D-01 -0.40067538976608D-08 3 12 3 5 -0.15135227836615D+01 -0.37224085019516D-01 1 13 3 5 -0.69763772027531D+00 0.75155024728743D-01 2 13 3 5 -0.78918702786854D+00 0.67553265526860D-01 3 13 3 5 0.31913514226335D+01 -0.83761560550949D-02 1 14 3 5 0.69763772027493D+00 -0.75155024728732D-01 2 14 3 5 0.78918702786834D+00 -0.67553265526853D-01 3 14 3 5 -0.31913514226336D+01 0.83761560551191D-02 1 15 3 5 -0.43103011435937D+00 -0.27533992276405D-02 2 15 3 5 0.20553089582641D+00 -0.25769569991209D-02 3 15 3 5 0.28719852129376D+01 -0.13816268237819D-01 1 16 3 5 0.43103011435940D+00 0.27533992276416D-02 2 16 3 5 -0.20553089582639D+00 0.25769569991213D-02 3 16 3 5 -0.28719852129375D+01 0.13816268237817D-01 1 17 3 5 -0.80124576135857D+00 0.67820350195880D-01 2 17 3 5 0.73183635481973D+00 -0.90035483846351D-01 3 17 3 5 0.34292263390703D+01 -0.36210999366896D-02 1 18 3 5 0.80124576135850D+00 -0.67820350195874D-01 2 18 3 5 -0.73183635481966D+00 0.90035483846342D-01 3 18 3 5 -0.34292263390702D+01 0.36210999367127D-02 1 19 3 5 -0.21959835619193D+00 -0.16128550211123D-01 2 19 3 5 -0.26552575294931D+00 0.41357278682110D-02 3 19 3 5 0.32265122528777D+01 -0.23561001641450D-01 1 20 3 5 0.21959835619194D+00 0.16128550211124D-01 2 20 3 5 0.26552575294928D+00 -0.41357278682119D-02 3 20 3 5 -0.32265122528777D+01 0.23561001641446D-01 1 1 1 6 0.41458843334221D+01 -0.95813167344349D-02 2 1 1 6 0.23792015891847D+00 0.10591086452180D-02 3 1 1 6 -0.78857791965727D+00 0.49390269094688D-02 1 2 1 6 0.41458843334221D+01 -0.95813167344318D-02 2 2 1 6 0.23792015891846D+00 0.10591086452180D-02 3 2 1 6 -0.78857791965728D+00 0.49390269094678D-02 1 3 1 6 0.13361541043889D+00 0.44153363817248D-08 2 3 1 6 -0.39354977651044D+00 0.12796647047654D-08 3 3 1 6 0.58257296579092D+01 -0.76630372512677D-02 1 4 1 6 -0.13361541043893D+00 -0.44153458711989D-08 2 4 1 6 0.39354977651040D+00 -0.12796629319240D-08 3 4 1 6 -0.58257296579092D+01 0.76630372512670D-02 1 5 1 6 0.52976878025470D+01 0.00000000000000D+00 2 5 1 6 -0.38061126980362D+00 0.46151868955637D-08 3 5 1 6 0.39231039299319D+01 -0.34115748211336D-08 1 6 1 6 0.26768383601689D+02 0.00000000000000D+00 2 6 1 6 -0.56942185647648D+00 -0.71883591409774D-07 3 6 1 6 0.25621462395017D+01 0.36817267012126D-07 1 7 1 6 0.41680358498454D-14 -0.35159505080935D-14 2 7 1 6 -0.49335483171664D-14 0.65865398744083D-15 3 7 1 6 -0.79565156468823D-13 0.38847384724589D-15 1 8 1 6 0.28835225291321D-14 -0.72030580474440D-14 2 8 1 6 -0.16455859776061D-14 0.44986622738495D-15 3 8 1 6 0.12726980518965D-13 0.35824027476647D-15 1 9 1 6 -0.36212769713446D+01 0.14047465394696D+00 2 9 1 6 -0.78446652621211D-01 0.17514855993833D-01 3 9 1 6 -0.59857203921955D+00 0.27487427215193D+00 1 10 1 6 0.36212769713442D+01 -0.14047465394695D+00 2 10 1 6 0.78446652621204D-01 -0.17514855993832D-01 3 10 1 6 0.59857203921983D+00 -0.27487427215192D+00 1 11 1 6 0.76738579693579D+00 0.39066876112910D-08 2 11 1 6 -0.12976085826889D+00 0.22902569106627D-08 3 11 1 6 0.49067269366484D+01 0.28500698534778D-01 1 12 1 6 -0.76738579693579D+00 -0.39066904714974D-08 2 12 1 6 0.12976085826896D+00 -0.22902570010668D-08 3 12 1 6 -0.49067269366485D+01 -0.28500698534778D-01 1 13 1 6 0.19362396073031D+01 -0.11964887554200D-01 2 13 1 6 0.83329143018955D+00 -0.64728025028718D-02 3 13 1 6 -0.14256153319272D+00 -0.18984854898020D-01 1 14 1 6 -0.19362396073031D+01 0.11964887554198D-01 2 14 1 6 -0.83329143018955D+00 0.64728025028716D-02 3 14 1 6 0.14256153319269D+00 0.18984854898019D-01 1 15 1 6 -0.55578809554996D+01 -0.10036421920718D-01 2 15 1 6 -0.17328686465238D+01 -0.86035443403376D-02 3 15 1 6 -0.68447259755858D+00 0.24612205715113D-01 1 16 1 6 0.55578809554998D+01 0.10036421920702D-01 2 16 1 6 0.17328686465238D+01 0.86035443403150D-02 3 16 1 6 0.68447259755900D+00 -0.24612205715122D-01 1 17 1 6 0.17794879776837D+01 -0.19165567050889D-01 2 17 1 6 -0.90366117840244D+00 0.33076361382235D-01 3 17 1 6 -0.81120919759108D-01 -0.39032224875295D-01 1 18 1 6 -0.17794879776837D+01 0.19165567050890D-01 2 18 1 6 0.90366117840245D+00 -0.33076361382235D-01 3 18 1 6 0.81120919759066D-01 0.39032224875296D-01 1 19 1 6 -0.50617432499133D+01 -0.34881693369036D-02 2 19 1 6 0.26913011930789D+01 0.98995665567645D-02 3 19 1 6 -0.69596597002003D+00 0.16195095029620D-01 1 20 1 6 0.50617432499134D+01 0.34881693369011D-02 2 20 1 6 -0.26913011930787D+01 -0.98995665567427D-02 3 20 1 6 0.69596597002010D+00 -0.16195095029626D-01 1 1 2 6 -0.68984662268177D+00 0.50647128845798D-02 2 1 2 6 -0.34762329656509D+01 0.97887442961948D-02 3 1 2 6 -0.14319831458146D+01 -0.75153521126184D-02 1 2 2 6 -0.68984662268178D+00 0.50647128845798D-02 2 2 2 6 -0.34762329656509D+01 0.97887442961948D-02 3 2 2 6 -0.14319831458148D+01 -0.75153521126187D-02 1 3 2 6 -0.40672906451292D+00 -0.58921890975712D-08 2 3 2 6 -0.63364291431506D+00 0.15953202768004D-09 3 3 2 6 0.15666301749173D+00 -0.27419237277434D-02 1 4 2 6 0.40672906451288D+00 0.58921908704126D-08 2 4 2 6 0.63364291431511D+00 -0.15952769196652D-09 3 4 2 6 -0.15666301749172D+00 0.27419237277447D-02 1 5 2 6 -0.38061126980362D+00 -0.46151868955637D-08 2 5 2 6 0.77509538115117D+00 0.00000000000000D+00 3 5 2 6 -0.91497323207694D+00 0.60068050702558D-08 1 6 2 6 -0.56940811001065D+00 0.76568204521129D-07 2 6 2 6 0.17768143654868D+02 0.00000000000000D+00 3 6 2 6 0.24404980588634D+01 -0.27781183928932D-06 1 7 2 6 -0.49306758439810D-14 0.65865398744083D-15 2 7 2 6 -0.10865192129715D-13 -0.12275589453542D-14 3 7 2 6 0.10313825631544D-15 0.10245478511037D-15 1 8 2 6 -0.16455861806790D-14 0.44986622738495D-15 2 8 2 6 -0.11289410218527D-13 -0.49120057071396D-14 3 8 2 6 -0.25074111159240D-14 -0.10625979283124D-15 1 9 2 6 0.12019035166440D+00 0.15121587861565D-01 2 9 2 6 -0.15360197481026D+01 0.18392548166201D+00 3 9 2 6 0.10266869558606D+00 -0.94599174760196D-01 1 10 2 6 -0.12019035166441D+00 -0.15121587861564D-01 2 10 2 6 0.15360197481024D+01 -0.18392548166200D+00 3 10 2 6 -0.10266869558590D+00 0.94599174760192D-01 1 11 2 6 -0.20243395290057D+00 -0.74255159637334D-09 2 11 2 6 -0.17442933858859D+00 0.39696673905503D-08 3 11 2 6 -0.87816433546890D+00 -0.87406908002361D-02 1 12 2 6 0.20243395290064D+00 0.74255150596926D-09 2 12 2 6 0.17442933858858D+00 -0.39696691615812D-08 3 12 2 6 0.87816433546887D+00 0.87406908002363D-02 1 13 2 6 -0.59457960571170D-01 -0.53575458752785D-02 2 13 2 6 -0.39726271758559D-01 0.30007940843054D-02 3 13 2 6 -0.31979338364591D+00 -0.74730631846226D-02 1 14 2 6 0.59457960571165D-01 0.53575458752783D-02 2 14 2 6 0.39726271758556D-01 -0.30007940843053D-02 3 14 2 6 0.31979338364590D+00 0.74730631846224D-02 1 15 2 6 0.55079910428914D+00 -0.47042237695924D-02 2 15 2 6 -0.77559052844887D-01 0.22939404689601D-02 3 15 2 6 -0.94452050145529D+00 0.49332111770475D-02 1 16 2 6 -0.55079910428906D+00 0.47042237695698D-02 2 16 2 6 0.77559052844720D-01 -0.22939404689653D-02 3 16 2 6 0.94452050145547D+00 -0.49332111770543D-02 1 17 2 6 -0.29515759724765D+00 0.27556222075908D-01 2 17 2 6 0.18468761522585D+00 -0.15233969912443D-01 3 17 2 6 0.15591637751359D+00 0.29754428369388D-01 1 18 2 6 0.29515759724765D+00 -0.27556222075908D-01 2 18 2 6 -0.18468761522585D+00 0.15233969912442D-01 3 18 2 6 -0.15591637751356D+00 -0.29754428369388D-01 1 19 2 6 -0.63648666029923D+00 0.36009329416588D-03 2 19 2 6 -0.12512110340054D+01 -0.12958961001170D-02 3 19 2 6 0.86659694614983D+00 -0.17054032197871D-01 1 20 2 6 0.63648666029944D+00 -0.36009329414410D-03 2 20 2 6 0.12512110340052D+01 0.12958961000948D-02 3 20 2 6 -0.86659694614986D+00 0.17054032197881D-01 1 1 3 6 0.22868326833029D+00 0.14586330252920D-01 2 1 3 6 -0.18698683453975D+01 0.10248094084865D-01 3 1 3 6 -0.19010841754099D+01 0.55720036936091D-02 1 2 3 6 0.22868326833028D+00 0.14586330252919D-01 2 2 3 6 -0.18698683453976D+01 0.10248094084865D-01 3 2 3 6 -0.19010841754098D+01 0.55720036936196D-02 1 3 3 6 0.54342484007503D+01 0.20688726821339D-07 2 3 3 6 0.16919166734277D+00 -0.22089797331946D-08 3 3 3 6 0.16211550928831D+01 0.18700113001049D-02 1 4 3 6 -0.54342484007504D+01 -0.20688727505763D-07 2 4 3 6 -0.16919166734275D+00 0.22089810313111D-08 3 4 3 6 -0.16211550928831D+01 -0.18700113001119D-02 1 5 3 6 -0.39231039299319D+01 -0.34115748211336D-08 2 5 3 6 0.91497323207694D+00 0.60068050702558D-08 3 5 3 6 -0.30885903591145D+02 0.00000000000000D+00 1 6 3 6 0.25621371785624D+01 -0.68822802612515D-07 2 6 3 6 0.24405125197431D+01 0.31042772210814D-06 3 6 3 6 0.40427799625787D+02 0.00000000000000D+00 1 7 3 6 -0.79565156468823D-13 0.38847384724589D-15 2 7 3 6 0.10342394816220D-15 0.10245478511037D-15 3 7 3 6 -0.79399053799177D-14 -0.14175124084231D-14 1 8 3 6 0.12726980379999D-13 0.35824027476647D-15 2 8 3 6 -0.25074111159240D-14 -0.10625979283124D-15 3 8 3 6 -0.78014048754358D-14 0.29787572334487D-14 1 9 3 6 0.17324984411220D+01 0.12079190423141D+00 2 9 3 6 -0.53235148846540D+00 -0.32034975474216D-01 3 9 3 6 -0.89292680740141D+00 -0.83005515325624D+00 1 10 3 6 -0.17324984411217D+01 -0.12079190423139D+00 2 10 3 6 0.53235148846557D+00 0.32034975474212D-01 3 10 3 6 0.89292680740186D+00 0.83005515325617D+00 1 11 3 6 0.73226898376367D+00 0.33980728443004D-08 2 11 3 6 -0.18660580744275D-01 -0.40067536272439D-08 3 11 3 6 0.15135227836615D+01 0.37224085019515D-01 1 12 3 6 -0.73226898376370D+00 -0.33980719747098D-08 2 12 3 6 0.18660580744247D-01 0.40067538745278D-08 3 12 3 6 -0.15135227836615D+01 -0.37224085019515D-01 1 13 3 6 -0.43103011435940D+00 -0.27533992276410D-02 2 13 3 6 0.20553089582640D+00 -0.25769569991211D-02 3 13 3 6 -0.28719852129375D+01 0.13816268237816D-01 1 14 3 6 0.43103011435936D+00 0.27533992276405D-02 2 14 3 6 -0.20553089582641D+00 0.25769569991209D-02 3 14 3 6 0.28719852129375D+01 -0.13816268237820D-01 1 15 3 6 -0.69763772027487D+00 0.75155024728733D-01 2 15 3 6 -0.78918702786833D+00 0.67553265526853D-01 3 15 3 6 -0.31913514226337D+01 0.83761560551195D-02 1 16 3 6 0.69763772027530D+00 -0.75155024728743D-01 2 16 3 6 0.78918702786852D+00 -0.67553265526859D-01 3 16 3 6 0.31913514226335D+01 -0.83761560550949D-02 1 17 3 6 -0.21959835619195D+00 -0.16128550211123D-01 2 17 3 6 -0.26552575294928D+00 0.41357278682119D-02 3 17 3 6 -0.32265122528777D+01 0.23561001641445D-01 1 18 3 6 0.21959835619191D+00 0.16128550211124D-01 2 18 3 6 0.26552575294931D+00 -0.41357278682111D-02 3 18 3 6 0.32265122528777D+01 -0.23561001641451D-01 1 19 3 6 -0.80124576135849D+00 0.67820350195872D-01 2 19 3 6 0.73183635481968D+00 -0.90035483846342D-01 3 19 3 6 -0.34292263390701D+01 0.36210999367134D-02 1 20 3 6 0.80124576135857D+00 -0.67820350195878D-01 2 20 3 6 -0.73183635481971D+00 0.90035483846352D-01 3 20 3 6 0.34292263390704D+01 -0.36210999366898D-02 1 1 1 7 0.13361541043890D+00 0.44153486286713D-08 2 1 1 7 0.39354977651034D+00 -0.12796629213374D-08 3 1 1 7 0.58257296579092D+01 -0.76630372512528D-02 1 2 1 7 -0.13361541043890D+00 -0.44153408145904D-08 2 2 1 7 -0.39354977651038D+00 0.12796626410014D-08 3 2 1 7 -0.58257296579093D+01 0.76630372512536D-02 1 3 1 7 0.41458843334221D+01 -0.95813167344312D-02 2 3 1 7 -0.23792015891846D+00 -0.10591086452180D-02 3 3 1 7 -0.78857791965726D+00 0.49390269094668D-02 1 4 1 7 0.41458843334222D+01 -0.95813167344352D-02 2 4 1 7 -0.23792015891846D+00 -0.10591086452178D-02 3 4 1 7 -0.78857791965732D+00 0.49390269094671D-02 1 5 1 7 0.68803253312377D-14 0.72030580474440D-14 2 5 1 7 -0.16455862104588D-14 -0.44986622738495D-15 3 5 1 7 -0.21667700446219D-19 -0.35824027476648D-15 1 6 1 7 0.41680358498454D-14 0.35159505080935D-14 2 6 1 7 -0.49306758439810D-14 -0.65865398744083D-15 3 6 1 7 -0.79565156468823D-13 -0.38847384724589D-15 1 7 1 7 0.26768383601689D+02 0.00000000000000D+00 2 7 1 7 0.56942185647658D+00 0.71883591409774D-07 3 7 1 7 0.25621462395019D+01 0.36817267012126D-07 1 8 1 7 0.52976878025470D+01 0.00000000000000D+00 2 8 1 7 0.38061126980362D+00 -0.46151868955637D-08 3 8 1 7 0.39231039299319D+01 -0.34115748211336D-08 1 9 1 7 -0.76738579693573D+00 -0.39066888102637D-08 2 9 1 7 -0.12976085826896D+00 0.22902568008272D-08 3 9 1 7 -0.49067269366485D+01 -0.28500698534776D-01 1 10 1 7 -0.76738579693580D+00 -0.39066903011159D-08 2 10 1 7 -0.12976085826894D+00 0.22902570405010D-08 3 10 1 7 -0.49067269366484D+01 -0.28500698534777D-01 1 11 1 7 -0.36212769713441D+01 0.14047465394696D+00 2 11 1 7 0.78446652621093D-01 -0.17514855993833D-01 3 11 1 7 -0.59857203921966D+00 0.27487427215193D+00 1 12 1 7 -0.36212769713443D+01 0.14047465394696D+00 2 12 1 7 0.78446652621248D-01 -0.17514855993833D-01 3 12 1 7 -0.59857203921980D+00 0.27487427215193D+00 1 13 1 7 -0.50617432499133D+01 -0.34881693369037D-02 2 13 1 7 -0.26913011930787D+01 -0.98995665567645D-02 3 13 1 7 -0.69596597002010D+00 0.16195095029620D-01 1 14 1 7 -0.50617432499134D+01 -0.34881693369058D-02 2 14 1 7 -0.26913011930791D+01 -0.98995665567652D-02 3 14 1 7 -0.69596597002012D+00 0.16195095029621D-01 1 15 1 7 -0.17794879776837D+01 0.19165567050889D-01 2 15 1 7 -0.90366117840244D+00 0.33076361382235D-01 3 15 1 7 0.81120919759094D-01 0.39032224875295D-01 1 16 1 7 -0.17794879776837D+01 0.19165567050890D-01 2 16 1 7 -0.90366117840244D+00 0.33076361382235D-01 3 16 1 7 0.81120919759107D-01 0.39032224875293D-01 1 17 1 7 -0.55578809554999D+01 -0.10036421920719D-01 2 17 1 7 0.17328686465240D+01 0.86035443403377D-02 3 17 1 7 -0.68447259755906D+00 0.24612205715110D-01 1 18 1 7 -0.55578809554997D+01 -0.10036421920717D-01 2 18 1 7 0.17328686465238D+01 0.86035443403386D-02 3 18 1 7 -0.68447259755870D+00 0.24612205715112D-01 1 19 1 7 -0.19362396073031D+01 0.11964887554201D-01 2 19 1 7 0.83329143018954D+00 -0.64728025028715D-02 3 19 1 7 0.14256153319270D+00 0.18984854898019D-01 1 20 1 7 -0.19362396073031D+01 0.11964887554198D-01 2 20 1 7 0.83329143018954D+00 -0.64728025028718D-02 3 20 1 7 0.14256153319272D+00 0.18984854898019D-01 1 1 2 7 0.40672906451281D+00 0.58921908809886D-08 2 1 2 7 -0.63364291431506D+00 0.15952751289710D-09 3 1 2 7 -0.15666301749174D+00 0.27419237277449D-02 1 2 2 7 -0.40672906451286D+00 -0.58921911613246D-08 2 2 2 7 0.63364291431510D+00 -0.15953179562721D-09 3 2 2 7 0.15666301749174D+00 -0.27419237277436D-02 1 3 2 7 0.68984662268178D+00 -0.50647128845798D-02 2 3 2 7 -0.34762329656508D+01 0.97887442961941D-02 3 3 2 7 0.14319831458149D+01 0.75153521126194D-02 1 4 2 7 0.68984662268178D+00 -0.50647128845796D-02 2 4 2 7 -0.34762329656509D+01 0.97887442961953D-02 3 4 2 7 0.14319831458148D+01 0.75153521126184D-02 1 5 2 7 -0.16455860073860D-14 -0.44986622738495D-15 2 5 2 7 -0.19283016003274D-13 0.49120057071396D-14 3 5 2 7 -0.17597900579321D-19 0.10625979283124D-15 1 6 2 7 -0.49335483171664D-14 -0.65865398744083D-15 2 6 2 7 -0.10865192129715D-13 0.12275589453542D-14 3 6 2 7 0.10342394816220D-15 -0.10245478511037D-15 1 7 2 7 0.56940811001076D+00 -0.76568204521129D-07 2 7 2 7 0.17768143654868D+02 0.00000000000000D+00 3 7 2 7 -0.24404980588643D+01 0.27781183928932D-06 1 8 2 7 0.38061126980362D+00 0.46151868955637D-08 2 8 2 7 0.77509538115117D+00 0.00000000000000D+00 3 8 2 7 0.91497323207694D+00 -0.60068050702558D-08 1 9 2 7 -0.20243395290064D+00 -0.74255170669076D-09 2 9 2 7 0.17442933858856D+00 -0.39696684043269D-08 3 9 2 7 -0.87816433546887D+00 -0.87406908002363D-02 1 10 2 7 -0.20243395290062D+00 -0.74255146701702D-09 2 10 2 7 0.17442933858856D+00 -0.39696693265519D-08 3 10 2 7 -0.87816433546888D+00 -0.87406908002364D-02 1 11 2 7 -0.12019035166452D+00 -0.15121587861564D-01 2 11 2 7 -0.15360197481024D+01 0.18392548166201D+00 3 11 2 7 -0.10266869558528D+00 0.94599174760196D-01 1 12 2 7 -0.12019035166436D+00 -0.15121587861564D-01 2 12 2 7 -0.15360197481025D+01 0.18392548166201D+00 3 12 2 7 -0.10266869558617D+00 0.94599174760196D-01 1 13 2 7 0.63648666029938D+00 -0.36009329416593D-03 2 13 2 7 -0.12512110340052D+01 -0.12958961001163D-02 3 13 2 7 -0.86659694614989D+00 0.17054032197871D-01 1 14 2 7 0.63648666029901D+00 -0.36009329416661D-03 2 14 2 7 -0.12512110340054D+01 -0.12958961001165D-02 3 14 2 7 -0.86659694614991D+00 0.17054032197871D-01 1 15 2 7 -0.29515759724765D+00 0.27556222075908D-01 2 15 2 7 -0.18468761522584D+00 0.15233969912443D-01 3 15 2 7 0.15591637751355D+00 0.29754428369387D-01 1 16 2 7 -0.29515759724765D+00 0.27556222075908D-01 2 16 2 7 -0.18468761522585D+00 0.15233969912443D-01 3 16 2 7 0.15591637751359D+00 0.29754428369387D-01 1 17 2 7 -0.55079910428887D+00 0.47042237695925D-02 2 17 2 7 -0.77559052844610D-01 0.22939404689600D-02 3 17 2 7 0.94452050145549D+00 -0.49332111770478D-02 1 18 2 7 -0.55079910428908D+00 0.47042237695934D-02 2 18 2 7 -0.77559052844826D-01 0.22939404689596D-02 3 18 2 7 0.94452050145532D+00 -0.49332111770475D-02 1 19 2 7 -0.59457960571177D-01 -0.53575458752781D-02 2 19 2 7 0.39726271758558D-01 -0.30007940843051D-02 3 19 2 7 -0.31979338364590D+00 -0.74730631846225D-02 1 20 2 7 -0.59457960571177D-01 -0.53575458752784D-02 2 20 2 7 0.39726271758569D-01 -0.30007940843051D-02 3 20 2 7 -0.31979338364592D+00 -0.74730631846219D-02 1 1 3 7 0.54342484007504D+01 0.20688741706475D-07 2 1 3 7 -0.16919166734278D+00 0.22089811977591D-08 3 1 3 7 0.16211550928830D+01 0.18700113001135D-02 1 2 3 7 -0.54342484007504D+01 -0.20688740932225D-07 2 2 3 7 0.16919166734277D+00 -0.22089798797311D-08 3 2 3 7 -0.16211550928830D+01 -0.18700113001053D-02 1 3 3 7 0.22868326833029D+00 0.14586330252918D-01 2 3 3 7 0.18698683453978D+01 -0.10248094084864D-01 3 3 3 7 -0.19010841754100D+01 0.55720036936159D-02 1 4 3 7 0.22868326833024D+00 0.14586330252919D-01 2 4 3 7 0.18698683453977D+01 -0.10248094084865D-01 3 4 3 7 -0.19010841754097D+01 0.55720036936185D-02 1 5 3 7 -0.21806666789128D-19 -0.35824027476648D-15 2 5 3 7 -0.17597900579370D-19 0.10625979283124D-15 3 5 3 7 0.21906021954347D-14 -0.29787572334487D-14 1 6 3 7 -0.79565156468823D-13 -0.38847384724589D-15 2 6 3 7 0.10313825631544D-15 -0.10245478511037D-15 3 6 3 7 -0.79399053799177D-14 0.14175124084231D-14 1 7 3 7 0.25621371785625D+01 -0.68822802612515D-07 2 7 3 7 -0.24405125197440D+01 -0.31042772210814D-06 3 7 3 7 0.40427799625787D+02 0.00000000000000D+00 1 8 3 7 -0.39231039299319D+01 -0.34115748211336D-08 2 8 3 7 -0.91497323207694D+00 -0.60068050702558D-08 3 8 3 7 -0.30885903591145D+02 0.00000000000000D+00 1 9 3 7 -0.73226898376369D+00 -0.33980705637437D-08 2 9 3 7 -0.18660580744243D-01 -0.40067538637479D-08 3 9 3 7 -0.15135227836615D+01 -0.37224085019515D-01 1 10 3 7 -0.73226898376363D+00 -0.33980716685107D-08 2 10 3 7 -0.18660580744251D-01 -0.40067539778207D-08 3 10 3 7 -0.15135227836615D+01 -0.37224085019515D-01 1 11 3 7 0.17324984411219D+01 0.12079190423141D+00 2 11 3 7 0.53235148846619D+00 0.32034975474216D-01 3 11 3 7 -0.89292680740232D+00 -0.83005515325623D+00 1 12 3 7 0.17324984411217D+01 0.12079190423141D+00 2 12 3 7 0.53235148846530D+00 0.32034975474216D-01 3 12 3 7 -0.89292680740147D+00 -0.83005515325623D+00 1 13 3 7 -0.80124576135857D+00 0.67820350195871D-01 2 13 3 7 -0.73183635481973D+00 0.90035483846342D-01 3 13 3 7 -0.34292263390703D+01 0.36210999367106D-02 1 14 3 7 -0.80124576135858D+00 0.67820350195872D-01 2 14 3 7 -0.73183635481974D+00 0.90035483846342D-01 3 14 3 7 -0.34292263390698D+01 0.36210999367142D-02 1 15 3 7 0.21959835619193D+00 0.16128550211123D-01 2 15 3 7 -0.26552575294931D+00 0.41357278682108D-02 3 15 3 7 0.32265122528776D+01 -0.23561001641450D-01 1 16 3 7 0.21959835619195D+00 0.16128550211121D-01 2 16 3 7 -0.26552575294927D+00 0.41357278682107D-02 3 16 3 7 0.32265122528777D+01 -0.23561001641450D-01 1 17 3 7 -0.69763772027537D+00 0.75155024728731D-01 2 17 3 7 0.78918702786855D+00 -0.67553265526853D-01 3 17 3 7 -0.31913514226333D+01 0.83761560551184D-02 1 18 3 7 -0.69763772027500D+00 0.75155024728733D-01 2 18 3 7 0.78918702786836D+00 -0.67553265526853D-01 3 18 3 7 -0.31913514226335D+01 0.83761560551179D-02 1 19 3 7 0.43103011435938D+00 0.27533992276408D-02 2 19 3 7 0.20553089582641D+00 -0.25769569991210D-02 3 19 3 7 0.28719852129375D+01 -0.13816268237820D-01 1 20 3 7 0.43103011435940D+00 0.27533992276399D-02 2 20 3 7 0.20553089582639D+00 -0.25769569991204D-02 3 20 3 7 0.28719852129375D+01 -0.13816268237824D-01 1 1 1 8 0.13361541043889D+00 0.44153511374596D-08 2 1 1 8 0.39354977651034D+00 -0.12796616844922D-08 3 1 1 8 -0.58257296579091D+01 0.76630372512532D-02 1 2 1 8 -0.13361541043889D+00 -0.44153360952347D-08 2 2 1 8 -0.39354977651036D+00 0.12796622559825D-08 3 2 1 8 0.58257296579092D+01 -0.76630372512543D-02 1 3 1 8 0.41458843334221D+01 -0.95813167344353D-02 2 3 1 8 -0.23792015891846D+00 -0.10591086452180D-02 3 3 1 8 0.78857791965726D+00 -0.49390269094687D-02 1 4 1 8 0.41458843334221D+01 -0.95813167344313D-02 2 4 1 8 -0.23792015891845D+00 -0.10591086452178D-02 3 4 1 8 0.78857791965731D+00 -0.49390269094673D-02 1 5 1 8 0.87268738945134D-14 0.35159505080935D-14 2 5 1 8 0.30629280235992D-14 -0.65865398744083D-15 3 5 1 8 0.62826031034956D-13 -0.38847384724589D-15 1 6 1 8 0.28835225291321D-14 0.72030580474440D-14 2 6 1 8 -0.16455861806790D-14 -0.44986622738495D-15 3 6 1 8 0.12726980379999D-13 -0.35824027476647D-15 1 7 1 8 0.52976878025470D+01 0.00000000000000D+00 2 7 1 8 0.38061126980362D+00 -0.46151868955637D-08 3 7 1 8 -0.39231039299319D+01 0.34115748211336D-08 1 8 1 8 0.26768383601689D+02 0.00000000000000D+00 2 8 1 8 0.56942185647667D+00 0.71883591409774D-07 3 8 1 8 -0.25621462395021D+01 -0.36817267012126D-07 1 9 1 8 -0.76738579693573D+00 -0.39066891803198D-08 2 9 1 8 -0.12976085826896D+00 0.22902573255755D-08 3 9 1 8 0.49067269366484D+01 0.28500698534776D-01 1 10 1 8 -0.76738579693580D+00 -0.39066899852764D-08 2 10 1 8 -0.12976085826895D+00 0.22902572183144D-08 3 10 1 8 0.49067269366484D+01 0.28500698534777D-01 1 11 1 8 -0.36212769713442D+01 0.14047465394696D+00 2 11 1 8 0.78446652621103D-01 -0.17514855993833D-01 3 11 1 8 0.59857203921983D+00 -0.27487427215193D+00 1 12 1 8 -0.36212769713444D+01 0.14047465394696D+00 2 12 1 8 0.78446652621244D-01 -0.17514855993833D-01 3 12 1 8 0.59857203921979D+00 -0.27487427215193D+00 1 13 1 8 -0.17794879776837D+01 0.19165567050890D-01 2 13 1 8 -0.90366117840244D+00 0.33076361382235D-01 3 13 1 8 -0.81120919759114D-01 -0.39032224875295D-01 1 14 1 8 -0.17794879776837D+01 0.19165567050890D-01 2 14 1 8 -0.90366117840245D+00 0.33076361382235D-01 3 14 1 8 -0.81120919759087D-01 -0.39032224875294D-01 1 15 1 8 -0.50617432499134D+01 -0.34881693369059D-02 2 15 1 8 -0.26913011930791D+01 -0.98995665567653D-02 3 15 1 8 0.69596597002012D+00 -0.16195095029621D-01 1 16 1 8 -0.50617432499133D+01 -0.34881693369047D-02 2 16 1 8 -0.26913011930786D+01 -0.98995665567647D-02 3 16 1 8 0.69596597002008D+00 -0.16195095029620D-01 1 17 1 8 -0.19362396073031D+01 0.11964887554201D-01 2 17 1 8 0.83329143018954D+00 -0.64728025028716D-02 3 17 1 8 -0.14256153319273D+00 -0.18984854898020D-01 1 18 1 8 -0.19362396073031D+01 0.11964887554202D-01 2 18 1 8 0.83329143018955D+00 -0.64728025028716D-02 3 18 1 8 -0.14256153319265D+00 -0.18984854898019D-01 1 19 1 8 -0.55578809554997D+01 -0.10036421920718D-01 2 19 1 8 0.17328686465239D+01 0.86035443403386D-02 3 19 1 8 0.68447259755866D+00 -0.24612205715113D-01 1 20 1 8 -0.55578809554999D+01 -0.10036421920720D-01 2 20 1 8 0.17328686465239D+01 0.86035443403376D-02 3 20 1 8 0.68447259755906D+00 -0.24612205715113D-01 1 1 2 8 0.40672906451282D+00 0.58921921178057D-08 2 1 2 8 -0.63364291431505D+00 0.15952843235449D-09 3 1 2 8 0.15666301749174D+00 -0.27419237277448D-02 1 2 2 8 -0.40672906451284D+00 -0.58921915463155D-08 2 2 2 8 0.63364291431509D+00 -0.15953122691950D-09 3 2 2 8 -0.15666301749174D+00 0.27419237277435D-02 1 3 2 8 0.68984662268178D+00 -0.50647128845798D-02 2 3 2 8 -0.34762329656508D+01 0.97887442961923D-02 3 3 2 8 -0.14319831458149D+01 -0.75153521126194D-02 1 4 2 8 0.68984662268179D+00 -0.50647128845796D-02 2 4 2 8 -0.34762329656509D+01 0.97887442961944D-02 3 4 2 8 -0.14319831458148D+01 -0.75153521126187D-02 1 5 2 8 0.30600555504138D-14 -0.65865398744083D-15 2 5 2 8 -0.13675447976401D-13 0.12275589453542D-14 3 5 2 8 0.80967459369398D-14 -0.10245478511037D-15 1 6 2 8 -0.16455859776061D-14 -0.44986622738495D-15 2 6 2 8 -0.11289410218527D-13 0.49120057071396D-14 3 6 2 8 -0.25074111159240D-14 0.10625979283124D-15 1 7 2 8 0.38061126980362D+00 0.46151868955637D-08 2 7 2 8 0.77509538115117D+00 0.00000000000000D+00 3 7 2 8 -0.91497323207694D+00 0.60068050702558D-08 1 8 2 8 0.56940811001085D+00 -0.76568204521129D-07 2 8 2 8 0.17768143654868D+02 0.00000000000000D+00 3 8 2 8 0.24404980588643D+01 -0.27781183928932D-06 1 9 2 8 -0.20243395290064D+00 -0.74255118207895D-09 2 9 2 8 0.17442933858856D+00 -0.39696685312934D-08 3 9 2 8 0.87816433546887D+00 0.87406908002363D-02 1 10 2 8 -0.20243395290062D+00 -0.74255128933996D-09 2 10 2 8 0.17442933858858D+00 -0.39696690765053D-08 3 10 2 8 0.87816433546888D+00 0.87406908002364D-02 1 11 2 8 -0.12019035166451D+00 -0.15121587861564D-01 2 11 2 8 -0.15360197481025D+01 0.18392548166201D+00 3 11 2 8 0.10266869558530D+00 -0.94599174760196D-01 1 12 2 8 -0.12019035166437D+00 -0.15121587861564D-01 2 12 2 8 -0.15360197481026D+01 0.18392548166201D+00 3 12 2 8 0.10266869558619D+00 -0.94599174760196D-01 1 13 2 8 -0.29515759724765D+00 0.27556222075908D-01 2 13 2 8 -0.18468761522585D+00 0.15233969912442D-01 3 13 2 8 -0.15591637751359D+00 -0.29754428369387D-01 1 14 2 8 -0.29515759724766D+00 0.27556222075908D-01 2 14 2 8 -0.18468761522584D+00 0.15233969912442D-01 3 14 2 8 -0.15591637751355D+00 -0.29754428369387D-01 1 15 2 8 0.63648666029901D+00 -0.36009329416669D-03 2 15 2 8 -0.12512110340053D+01 -0.12958961001168D-02 3 15 2 8 0.86659694614990D+00 -0.17054032197871D-01 1 16 2 8 0.63648666029955D+00 -0.36009329416610D-03 2 16 2 8 -0.12512110340052D+01 -0.12958961001165D-02 3 16 2 8 0.86659694614985D+00 -0.17054032197871D-01 1 17 2 8 -0.59457960571173D-01 -0.53575458752783D-02 2 17 2 8 0.39726271758569D-01 -0.30007940843056D-02 3 17 2 8 0.31979338364592D+00 0.74730631846220D-02 1 18 2 8 -0.59457960571168D-01 -0.53575458752783D-02 2 18 2 8 0.39726271758558D-01 -0.30007940843052D-02 3 18 2 8 0.31979338364590D+00 0.74730631846225D-02 1 19 2 8 -0.55079910428900D+00 0.47042237695934D-02 2 19 2 8 -0.77559052844823D-01 0.22939404689609D-02 3 19 2 8 -0.94452050145532D+00 0.49332111770478D-02 1 20 2 8 -0.55079910428900D+00 0.47042237695924D-02 2 20 2 8 -0.77559052844606D-01 0.22939404689601D-02 3 20 2 8 -0.94452050145549D+00 0.49332111770473D-02 1 1 3 8 -0.54342484007503D+01 -0.20688741273883D-07 2 1 3 8 0.16919166734278D+00 -0.22089811590875D-08 3 1 3 8 0.16211550928830D+01 0.18700113001126D-02 1 2 3 8 0.54342484007504D+01 0.20688740159322D-07 2 2 3 8 -0.16919166734278D+00 0.22089798640182D-08 3 2 3 8 -0.16211550928830D+01 -0.18700113001064D-02 1 3 3 8 -0.22868326833030D+00 -0.14586330252920D-01 2 3 3 8 -0.18698683453978D+01 0.10248094084864D-01 3 3 3 8 -0.19010841754100D+01 0.55720036936153D-02 1 4 3 8 -0.22868326833024D+00 -0.14586330252919D-01 2 4 3 8 -0.18698683453977D+01 0.10248094084865D-01 3 4 3 8 -0.19010841754099D+01 0.55720036936145D-02 1 5 3 8 0.62826031034956D-13 -0.38847384724589D-15 2 5 3 8 0.80970316287865D-14 -0.10245478511037D-15 3 5 3 8 0.82971216006550D-14 0.14175124084231D-14 1 6 3 8 0.12726980518965D-13 -0.35824027476647D-15 2 6 3 8 -0.25074111159240D-14 0.10625979283124D-15 3 6 3 8 -0.78014048754358D-14 -0.29787572334487D-14 1 7 3 8 0.39231039299319D+01 0.34115748211336D-08 2 7 3 8 0.91497323207694D+00 0.60068050702558D-08 3 7 3 8 -0.30885903591145D+02 0.00000000000000D+00 1 8 3 8 -0.25621371785627D+01 0.68822802612515D-07 2 8 3 8 0.24405125197440D+01 0.31042772210814D-06 3 8 3 8 0.40427799625786D+02 0.00000000000000D+00 1 9 3 8 0.73226898376368D+00 0.33980705871584D-08 2 9 3 8 0.18660580744241D-01 0.40067538653129D-08 3 9 3 8 -0.15135227836615D+01 -0.37224085019515D-01 1 10 3 8 0.73226898376367D+00 0.33980716014993D-08 2 10 3 8 0.18660580744250D-01 0.40067539507282D-08 3 10 3 8 -0.15135227836615D+01 -0.37224085019516D-01 1 11 3 8 -0.17324984411217D+01 -0.12079190423141D+00 2 11 3 8 -0.53235148846616D+00 -0.32034975474216D-01 3 11 3 8 -0.89292680740175D+00 -0.83005515325623D+00 1 12 3 8 -0.17324984411217D+01 -0.12079190423141D+00 2 12 3 8 -0.53235148846528D+00 -0.32034975474216D-01 3 12 3 8 -0.89292680740175D+00 -0.83005515325623D+00 1 13 3 8 -0.21959835619195D+00 -0.16128550211123D-01 2 13 3 8 0.26552575294927D+00 -0.41357278682107D-02 3 13 3 8 0.32265122528777D+01 -0.23561001641451D-01 1 14 3 8 -0.21959835619193D+00 -0.16128550211122D-01 2 14 3 8 0.26552575294932D+00 -0.41357278682108D-02 3 14 3 8 0.32265122528776D+01 -0.23561001641450D-01 1 15 3 8 0.80124576135859D+00 -0.67820350195872D-01 2 15 3 8 0.73183635481975D+00 -0.90035483846342D-01 3 15 3 8 -0.34292263390698D+01 0.36210999367121D-02 1 16 3 8 0.80124576135854D+00 -0.67820350195872D-01 2 16 3 8 0.73183635481971D+00 -0.90035483846342D-01 3 16 3 8 -0.34292263390704D+01 0.36210999367115D-02 1 17 3 8 -0.43103011435941D+00 -0.27533992276409D-02 2 17 3 8 -0.20553089582639D+00 0.25769569991205D-02 3 17 3 8 0.28719852129375D+01 -0.13816268237820D-01 1 18 3 8 -0.43103011435933D+00 -0.27533992276405D-02 2 18 3 8 -0.20553089582641D+00 0.25769569991210D-02 3 18 3 8 0.28719852129376D+01 -0.13816268237820D-01 1 19 3 8 0.69763772027495D+00 -0.75155024728733D-01 2 19 3 8 -0.78918702786837D+00 0.67553265526853D-01 3 19 3 8 -0.31913514226336D+01 0.83761560551178D-02 1 20 3 8 0.69763772027535D+00 -0.75155024728733D-01 2 20 3 8 -0.78918702786855D+00 0.67553265526852D-01 3 20 3 8 -0.31913514226334D+01 0.83761560551198D-02 1 1 1 9 -0.15727406755428D+01 -0.20372511837940D-07 2 1 1 9 -0.38698744487228D+00 -0.63355813971932D-08 3 1 1 9 -0.17448930758118D-15 0.33565692803943D-15 1 2 1 9 -0.91094028615952D+00 0.21462936265756D-08 2 2 1 9 -0.84278587224155D-01 0.27250362201549D-08 3 2 1 9 0.11604424159874D-14 -0.24585070871223D-15 1 3 1 9 -0.33669097512721D+01 -0.83532952764691D-08 2 3 1 9 -0.21828633112969D+00 0.20847377119563D-08 3 3 1 9 0.33637946317080D-14 0.26685790176012D-14 1 4 1 9 -0.24302470502943D+00 -0.27640821944336D-08 2 4 1 9 0.82932068486518D-01 0.55746737187522D-08 3 4 1 9 0.27281781261464D-13 -0.51180701132258D-15 1 5 1 9 -0.36210253121760D+01 -0.21071197992902D+00 2 5 1 9 0.12019588008029D+00 -0.22682378088324D-01 3 5 1 9 -0.17327205328378D+01 0.18118784761341D+00 1 6 1 9 -0.36210253121760D+01 -0.21071197992902D+00 2 6 1 9 0.12019588008029D+00 -0.22682378088324D-01 3 6 1 9 0.17327205328378D+01 -0.18118784761341D+00 1 7 1 9 -0.76738579693573D+00 0.39066883635724D-08 2 7 1 9 -0.20243395290064D+00 0.74255159653582D-09 3 7 1 9 -0.73226898376369D+00 0.33980691065760D-08 1 8 1 9 -0.76738579693573D+00 0.39066887337946D-08 2 8 1 9 -0.20243395290064D+00 0.74255107212102D-09 3 8 1 9 0.73226898376368D+00 -0.33980691289745D-08 1 9 1 9 0.97215569808077D+01 0.00000000000000D+00 2 9 1 9 0.88223974985047D+00 0.63313732685173D-07 3 9 1 9 -0.72249040123717D-14 0.00000000000000D+00 1 10 1 9 0.75847769274732D-01 -0.17207609244682D-09 2 10 1 9 -0.97923704581656D-01 -0.33253204327650D-08 3 10 1 9 0.93891325239288D-14 0.61612316703383D-15 1 11 1 9 0.19676204725524D-13 0.30374518202355D-08 2 11 1 9 0.35073613129928D-01 -0.33457759164025D-08 3 11 1 9 0.66619594728713D-14 -0.59670163187838D-16 1 12 1 9 0.22425088122241D+00 0.48083337307161D-15 2 12 1 9 -0.14906667381481D+00 -0.31235835907242D-08 3 12 1 9 -0.24645969165264D-15 -0.23625793234178D-15 1 13 1 9 0.64500728160354D+00 0.13664967114305D-08 2 13 1 9 0.96908271650748D+00 -0.19894659383495D-08 3 13 1 9 0.20859549147458D+01 0.20170642312621D-07 1 14 1 9 0.83973050441773D+00 -0.40454286633893D-02 2 14 1 9 -0.47399747041750D-01 -0.24013175352655D-02 3 14 1 9 0.12473814058502D+01 -0.58367097580721D-02 1 15 1 9 0.83973050441773D+00 -0.40454286633908D-02 2 15 1 9 -0.47399747041752D-01 -0.24013175352658D-02 3 15 1 9 -0.12473814058502D+01 0.58367097580725D-02 1 16 1 9 0.64500728160354D+00 0.13664962988382D-08 2 16 1 9 0.96908271650749D+00 -0.19894655302059D-08 3 16 1 9 -0.20859549147459D+01 -0.20170642377548D-07 1 17 1 9 -0.84858308199483D-01 0.95162401793025D-02 2 17 1 9 -0.75734874106881D+00 -0.13852106275147D-01 3 17 1 9 0.13448842329276D+01 0.83173225262596D-02 1 18 1 9 0.10580893994944D+01 -0.36597420284044D-02 2 18 1 9 -0.77547794034034D-01 0.77545064256824D-02 3 18 1 9 0.96527559763942D+00 -0.38063651834875D-02 1 19 1 9 0.10580893994944D+01 -0.36597420284048D-02 2 19 1 9 -0.77547794034041D-01 0.77545064256823D-02 3 19 1 9 -0.96527559763942D+00 0.38063651834879D-02 1 20 1 9 -0.84858308199483D-01 0.95162401793018D-02 2 20 1 9 -0.75734874106881D+00 -0.13852106275147D-01 3 20 1 9 -0.13448842329276D+01 -0.83173225262598D-02 1 1 2 9 -0.17022130410256D+00 -0.11602150045251D-07 2 1 2 9 0.11077294980914D+00 -0.21721008325792D-08 3 1 2 9 0.38154378056857D-16 0.32053600443344D-15 1 2 2 9 0.10800215337626D+00 -0.25978546969953D-08 2 2 2 9 0.27960957653770D+00 0.20657971065100D-08 3 2 2 9 0.87670705513729D-15 -0.72898086592726D-16 1 3 2 9 -0.23688872566411D+00 0.47218120470145D-08 2 3 2 9 -0.24626508420672D+00 -0.12408098007107D-09 3 3 2 9 -0.46089538482774D-15 -0.56469827455503D-16 1 4 2 9 -0.39371980731899D-01 -0.17723280349508D-09 2 4 2 9 -0.14122606994465D+00 0.45013040810459D-08 3 4 2 9 0.28456040842111D-14 0.41039800715043D-16 1 5 2 9 -0.78447063273195D-01 -0.26272281656969D-01 2 5 2 9 -0.15357291354311D+01 -0.27588821938913D+00 3 5 2 9 0.53247151643947D+00 -0.48052467411765D-01 1 6 2 9 -0.78447063273198D-01 -0.26272281656970D-01 2 6 2 9 -0.15357291354311D+01 -0.27588821938913D+00 3 6 2 9 -0.53247151643945D+00 0.48052467411765D-01 1 7 2 9 -0.12976085826896D+00 -0.22902568901655D-08 2 7 2 9 0.17442933858856D+00 0.39696687772924D-08 3 7 2 9 -0.18660580744243D-01 0.40067539101517D-08 1 8 2 9 -0.12976085826896D+00 -0.22902574154264D-08 2 8 2 9 0.17442933858856D+00 0.39696689041630D-08 3 8 2 9 0.18660580744241D-01 -0.40067539118103D-08 1 9 2 9 0.88223955649874D+00 -0.50852591773874D-07 2 9 2 9 0.67580468587837D+01 0.00000000000000D+00 3 9 2 9 -0.42791080236612D-13 0.00000000000000D+00 1 10 2 9 -0.97924213690214D-01 0.29320542712019D-08 2 10 2 9 0.36724906313497D+00 -0.38961767497579D-09 3 10 2 9 -0.62651727030843D-16 -0.46731337874262D-16 1 11 2 9 0.35073613129928D-01 0.33457750886462D-08 2 11 2 9 -0.10885095876255D-13 -0.98737440724067D-09 3 11 2 9 -0.39688164963119D-15 0.63105314718723D-16 1 12 2 9 0.14906667381483D+00 -0.31235835907242D-08 2 12 2 9 -0.46299408881780D+00 -0.96715565440654D-16 3 12 2 9 0.21545051380987D-15 0.40567448005034D-16 1 13 2 9 0.85398941792521D+00 0.38353727626140D-08 2 13 2 9 0.19337318769003D+00 0.17435075383369D-08 3 13 2 9 0.10619523875356D+01 0.15637796867138D-07 1 14 2 9 -0.57465210920280D+00 -0.25106305660083D-02 2 14 2 9 -0.42039068212618D+00 0.26586663307461D-03 3 14 2 9 0.12136238300823D+01 -0.32481178331010D-02 1 15 2 9 -0.57465210920280D+00 -0.25106305660086D-02 2 15 2 9 -0.42039068212617D+00 0.26586663307468D-03 3 15 2 9 -0.12136238300823D+01 0.32481178331010D-02 1 16 2 9 0.85398941792521D+00 0.38353731707577D-08 2 16 2 9 0.19337318769003D+00 0.17435076612758D-08 3 16 2 9 -0.10619523875356D+01 -0.15637796811934D-07 1 17 2 9 -0.91516509802232D+00 -0.15177272222111D-01 2 17 2 9 0.94564695760792D+00 0.13326912347394D-01 3 17 2 9 -0.95903492959707D+00 -0.38148153958582D-02 1 18 2 9 0.47957436773312D+00 0.96862129538429D-02 2 18 2 9 -0.49224197726739D+00 -0.84630629951610D-02 3 18 2 9 -0.16802883486709D+01 0.76536880282332D-02 1 19 2 9 0.47957436773311D+00 0.96862129538428D-02 2 19 2 9 -0.49224197726739D+00 -0.84630629951611D-02 3 19 2 9 0.16802883486709D+01 -0.76536880282333D-02 1 20 2 9 -0.91516509802233D+00 -0.15177272222112D-01 2 20 2 9 0.94564695760792D+00 0.13326912347394D-01 3 20 2 9 0.95903492959708D+00 0.38148153958583D-02 1 1 3 9 -0.17448930758118D-15 0.33912637499138D-15 2 1 3 9 0.38154378056858D-16 0.32053600443344D-15 3 1 3 9 -0.31432302419448D+01 -0.46167987137695D-07 1 2 3 9 0.11604424160123D-14 -0.24662022911182D-15 2 2 3 9 0.87670705475125D-15 -0.72944582750033D-16 3 2 3 9 0.18036365225666D+01 0.33471019575980D-08 1 3 3 9 0.33637946315219D-14 0.26660970287692D-14 2 3 3 9 -0.46089538597335D-15 -0.56896741979544D-16 3 3 3 9 -0.66456196054433D+00 -0.63555381122410D-07 1 4 3 9 0.27281781261066D-13 -0.51305653064445D-15 2 4 3 9 0.28456040850885D-14 0.41278161020051D-16 3 4 3 9 0.55303514789212D+00 0.10408827946637D-07 1 5 3 9 0.59857184343517D+00 0.27487557896266D+00 2 5 3 9 -0.10266865570006D+00 -0.94599385762890D-01 3 5 3 9 -0.89292157642546D+00 0.83005783090320D+00 1 6 3 9 -0.59857184343518D+00 -0.27487557896266D+00 2 6 3 9 0.10266865570008D+00 0.94599385762890D-01 3 6 3 9 -0.89292157642558D+00 0.83005783090320D+00 1 7 3 9 -0.49067269366484D+01 0.28500698534775D-01 2 7 3 9 -0.87816433546887D+00 0.87406908002363D-02 3 7 3 9 -0.15135227836615D+01 0.37224085019515D-01 1 8 3 9 0.49067269366484D+01 -0.28500698534775D-01 2 8 3 9 0.87816433546887D+00 -0.87406908002363D-02 3 8 3 9 -0.15135227836615D+01 0.37224085019516D-01 1 9 3 9 -0.72249040123717D-14 0.00000000000000D+00 2 9 3 9 -0.42791080239921D-13 0.34694469519537D-17 3 9 3 9 0.41491249633157D+02 0.00000000000000D+00 1 10 3 9 0.93891325227545D-14 0.63031565941373D-15 2 10 3 9 -0.62651726721588D-16 -0.42030009360274D-16 3 10 3 9 0.15104566186109D+02 -0.20866824194362D-09 1 11 3 9 0.66619594728867D-14 -0.60962653570763D-16 2 11 3 9 -0.39688164965144D-15 0.63069692468479D-16 3 11 3 9 -0.21444724758536D-13 0.69723248042204D-08 1 12 3 9 -0.24645969145429D-15 -0.23669259901990D-15 2 12 3 9 0.21545051375975D-15 0.40847570964118D-16 3 12 3 9 0.39153730773328D+00 -0.10308626092389D-15 1 13 3 9 0.34640302746413D+01 -0.20597515345622D-07 2 13 3 9 0.21345791990508D+01 -0.11296742416600D-07 3 13 3 9 0.16895072203213D+01 0.23405228762510D-07 1 14 3 9 0.25421435270823D+01 0.30759355796044D-01 2 14 3 9 0.24736807453372D+01 0.26768477335266D-01 3 14 3 9 -0.32589072432735D+01 0.29450819023954D-01 1 15 3 9 -0.25421435270823D+01 -0.30759355796044D-01 2 15 3 9 -0.24736807453372D+01 -0.26768477335266D-01 3 15 3 9 -0.32589072432735D+01 0.29450819023954D-01 1 16 3 9 -0.34640302746413D+01 0.20597515277225D-07 2 16 3 9 -0.21345791990508D+01 0.11296742464865D-07 3 16 3 9 0.16895072203213D+01 0.23405228697618D-07 1 17 3 9 0.26814814780431D+01 -0.29395659937317D-01 2 17 3 9 -0.24740388935626D+01 0.65954300175020D-01 3 17 3 9 0.15239622487681D+01 0.25908668518441D-01 1 18 3 9 0.22884251646869D+01 0.19464124322560D-06 2 18 3 9 -0.30330790543789D+01 0.75576197140786D-06 3 18 3 9 -0.37129030726314D+01 0.55580406329637D-06 1 19 3 9 -0.22884251646869D+01 -0.19464124282918D-06 2 19 3 9 0.30330790543789D+01 -0.75576197150860D-06 3 19 3 9 -0.37129030726313D+01 0.55580406428666D-06 1 20 3 9 -0.26814814780431D+01 0.29395659937317D-01 2 20 3 9 0.24740388935626D+01 -0.65954300175020D-01 3 20 3 9 0.15239622487681D+01 0.25908668518440D-01 1 1 1 10 0.91094028615952D+00 -0.21462945702464D-08 2 1 1 10 0.84278587224156D-01 -0.27250361054355D-08 3 1 1 10 0.34171136610199D-14 -0.35483494971299D-15 1 2 1 10 0.15727406755427D+01 0.20372506648560D-07 2 2 1 10 0.38698744487231D+00 0.63355844583427D-08 3 2 1 10 -0.48590977079080D-14 -0.32547964102087D-15 1 3 1 10 -0.24302470502949D+00 -0.27640828616381D-08 2 3 1 10 0.82932068486520D-01 0.55746740994327D-08 3 3 1 10 0.22956933296332D-13 0.35914225263101D-15 1 4 1 10 -0.33669097512718D+01 -0.83532832962529D-08 2 4 1 10 -0.21828633112962D+00 0.20847362649990D-08 3 4 1 10 -0.87546330984874D-14 0.83483589266607D-15 1 5 1 10 0.36210253121756D+01 0.21071197992901D+00 2 5 1 10 -0.12019588008031D+00 0.22682378088323D-01 3 5 1 10 0.17327205328376D+01 -0.18118784761340D+00 1 6 1 10 0.36210253121756D+01 0.21071197992901D+00 2 6 1 10 -0.12019588008030D+00 0.22682378088323D-01 3 6 1 10 -0.17327205328375D+01 0.18118784761340D+00 1 7 1 10 -0.76738579693580D+00 0.39066898544246D-08 2 7 1 10 -0.20243395290062D+00 0.74255135686208D-09 3 7 1 10 -0.73226898376364D+00 0.33980702113430D-08 1 8 1 10 -0.76738579693580D+00 0.39066895387512D-08 2 8 1 10 -0.20243395290062D+00 0.74255117938203D-09 3 8 1 10 0.73226898376367D+00 -0.33980701433154D-08 1 9 1 10 0.75847769274732D-01 -0.17207552561694D-09 2 9 1 10 -0.97923704581656D-01 -0.33253203326070D-08 3 9 1 10 0.93891325240888D-14 -0.61664767465398D-15 1 10 1 10 0.97215569808070D+01 0.00000000000000D+00 2 10 1 10 0.88223974985044D+00 0.63313732685173D-07 3 10 1 10 0.13488364313965D-12 0.00000000000000D+00 1 11 1 10 0.22425088122236D+00 0.75782160408163D-15 2 11 1 10 -0.14906667381491D+00 -0.31235836932896D-08 3 11 1 10 -0.38419547840789D-14 -0.33891261370410D-15 1 12 1 10 -0.30042341395960D-14 0.30374539330020D-08 2 12 1 10 0.35073613129919D-01 -0.33457755606215D-08 3 12 1 10 0.10532723950315D-13 -0.26681863342248D-15 1 13 1 10 0.83973050441770D+00 -0.40454286633891D-02 2 13 1 10 -0.47399747041773D-01 -0.24013175352657D-02 3 13 1 10 0.12473814058502D+01 -0.58367097580726D-02 1 14 1 10 0.64500728160352D+00 0.13665009338093D-08 2 14 1 10 0.96908271650752D+00 -0.19894617255859D-08 3 14 1 10 0.20859549147459D+01 0.20170651165622D-07 1 15 1 10 0.64500728160350D+00 0.13665009238948D-08 2 15 1 10 0.96908271650750D+00 -0.19894618373872D-08 3 15 1 10 -0.20859549147459D+01 -0.20170651290035D-07 1 16 1 10 0.83973050441770D+00 -0.40454286633878D-02 2 16 1 10 -0.47399747041759D-01 -0.24013175352658D-02 3 16 1 10 -0.12473814058502D+01 0.58367097580726D-02 1 17 1 10 0.10580893994944D+01 -0.36597420284042D-02 2 17 1 10 -0.77547794034025D-01 0.77545064256821D-02 3 17 1 10 0.96527559763944D+00 -0.38063651834880D-02 1 18 1 10 -0.84858308199530D-01 0.95162401793038D-02 2 18 1 10 -0.75734874106883D+00 -0.13852106275151D-01 3 18 1 10 0.13448842329276D+01 0.83173225262661D-02 1 19 1 10 -0.84858308199512D-01 0.95162401793026D-02 2 19 1 10 -0.75734874106881D+00 -0.13852106275151D-01 3 19 1 10 -0.13448842329276D+01 -0.83173225262662D-02 1 20 1 10 0.10580893994944D+01 -0.36597420284056D-02 2 20 1 10 -0.77547794034032D-01 0.77545064256822D-02 3 20 1 10 -0.96527559763943D+00 0.38063651834875D-02 1 1 2 10 -0.10800215337626D+00 0.25978548117144D-08 2 1 2 10 -0.27960957653770D+00 -0.20657964361413D-08 3 1 2 10 -0.38740753550300D-14 0.24895243411880D-16 1 2 2 10 0.17022130410259D+00 0.11602153106400D-07 2 2 2 10 -0.11077294980888D+00 0.21721219079357D-08 3 2 2 10 0.31974507203090D-14 0.29669298812224D-15 1 3 2 10 -0.39371980731897D-01 -0.17723242281462D-09 2 3 2 10 -0.14122606994466D+00 0.45013044463201D-08 3 3 2 10 0.42892473768131D-14 -0.20181387023562D-16 1 4 2 10 -0.23688872566404D+00 0.47218106000572D-08 2 4 2 10 -0.24626508420686D+00 -0.12408419237229D-09 3 4 2 10 -0.24803517505625D-14 -0.10092784652584D-15 1 5 2 10 0.78447063273177D-01 0.26272281656969D-01 2 5 2 10 0.15357291354308D+01 0.27588821938912D+00 3 5 2 10 -0.53247151643965D+00 0.48052467411761D-01 1 6 2 10 0.78447063273192D-01 0.26272281656969D-01 2 6 2 10 0.15357291354310D+01 0.27588821938912D+00 3 6 2 10 0.53247151643962D+00 -0.48052467411761D-01 1 7 2 10 -0.12976085826894D+00 -0.22902571298392D-08 2 7 2 10 0.17442933858856D+00 0.39696696995175D-08 3 7 2 10 -0.18660580744251D-01 0.40067540242245D-08 1 8 2 10 -0.12976085826895D+00 -0.22902573081654D-08 2 8 2 10 0.17442933858858D+00 0.39696694493750D-08 3 8 2 10 0.18660580744250D-01 -0.40067539972257D-08 1 9 2 10 -0.97924213690214D-01 0.29320543713599D-08 2 9 2 10 0.36724906313497D+00 -0.38961830033227D-09 3 9 2 10 -0.62651726927758D-16 0.44678201937538D-16 1 10 2 10 0.88223955649871D+00 -0.50852591773874D-07 2 10 2 10 0.67580468587837D+01 0.00000000000000D+00 3 10 2 10 -0.21474798163806D-13 0.00000000000000D+00 1 11 2 10 0.14906667381474D+00 -0.31235836932896D-08 2 11 2 10 -0.46299408881772D+00 0.43227967251858D-15 3 11 2 10 0.17221450694907D-14 0.53774086171156D-16 1 12 2 10 0.35073613129919D-01 0.33457754444272D-08 2 12 2 10 0.29957049211245D-14 -0.98737418593312D-09 3 12 2 10 -0.41089234205105D-14 -0.28119906904650D-16 1 13 2 10 -0.57465210920283D+00 -0.25106305660084D-02 2 13 2 10 -0.42039068212617D+00 0.26586663307494D-03 3 13 2 10 0.12136238300823D+01 -0.32481178331010D-02 1 14 2 10 0.85398941792525D+00 0.38353769753777D-08 2 14 2 10 0.19337318769003D+00 0.17435071318300D-08 3 14 2 10 0.10619523875356D+01 0.15637801343582D-07 1 15 2 10 0.85398941792523D+00 0.38353768635764D-08 2 15 2 10 0.19337318769003D+00 0.17435072676309D-08 3 15 2 10 -0.10619523875356D+01 -0.15637801237090D-07 1 16 2 10 -0.57465210920281D+00 -0.25106305660086D-02 2 16 2 10 -0.42039068212616D+00 0.26586663307450D-03 3 16 2 10 -0.12136238300823D+01 0.32481178331010D-02 1 17 2 10 0.47957436773313D+00 0.96862129538426D-02 2 17 2 10 -0.49224197726740D+00 -0.84630629951606D-02 3 17 2 10 -0.16802883486709D+01 0.76536880282333D-02 1 18 2 10 -0.91516509802234D+00 -0.15177272222116D-01 2 18 2 10 0.94564695760794D+00 0.13326912347397D-01 3 18 2 10 -0.95903492959713D+00 -0.38148153958645D-02 1 19 2 10 -0.91516509802233D+00 -0.15177272222116D-01 2 19 2 10 0.94564695760794D+00 0.13326912347398D-01 3 19 2 10 0.95903492959712D+00 0.38148153958645D-02 1 20 2 10 0.47957436773312D+00 0.96862129538427D-02 2 20 2 10 -0.49224197726741D+00 -0.84630629951609D-02 3 20 2 10 0.16802883486708D+01 -0.76536880282333D-02 1 1 3 10 0.34171136610343D-14 -0.35368066911360D-15 2 1 3 10 -0.38740753544897D-14 0.25398668516835D-16 3 1 3 10 -0.18036365225666D+01 -0.33471000645721D-08 1 2 3 10 -0.48590977079080D-14 -0.32894908797282D-15 2 2 3 10 0.31974507203090D-14 0.29669298812224D-15 3 2 3 10 0.31432302419447D+01 0.46167975807139D-07 1 3 3 10 0.22956933295934D-13 0.35789273330913D-15 2 3 3 10 0.42892473776905D-14 -0.19943026718554D-16 3 3 3 10 0.55303514789223D+00 0.10408829665760D-07 1 4 3 10 -0.87546330986735D-14 0.83235390383412D-15 2 4 3 10 -0.24803517517081D-14 -0.10135476104988D-15 3 4 3 10 -0.66456196054467D+00 -0.63555385403605D-07 1 5 3 10 -0.59857184343528D+00 -0.27487557896265D+00 2 5 3 10 0.10266865569989D+00 0.94599385762886D-01 3 5 3 10 0.89292157642632D+00 -0.83005783090313D+00 1 6 3 10 0.59857184343547D+00 0.27487557896265D+00 2 6 3 10 -0.10266865569992D+00 -0.94599385762886D-01 3 6 3 10 0.89292157642603D+00 -0.83005783090313D+00 1 7 3 10 -0.49067269366484D+01 0.28500698534776D-01 2 7 3 10 -0.87816433546888D+00 0.87406908002364D-02 3 7 3 10 -0.15135227836615D+01 0.37224085019515D-01 1 8 3 10 0.49067269366484D+01 -0.28500698534776D-01 2 8 3 10 0.87816433546888D+00 -0.87406908002364D-02 3 8 3 10 -0.15135227836615D+01 0.37224085019516D-01 1 9 3 10 0.93891325235817D-14 -0.60256008379810D-15 2 9 3 10 -0.62651726721588D-16 0.48968903264181D-16 3 9 3 10 0.15104566186109D+02 -0.20866106299017D-09 1 10 3 10 0.13488364313965D-12 0.00000000000000D+00 2 10 3 10 -0.21474798167115D-13 0.34694469519537D-17 3 10 3 10 0.41491249633158D+02 0.00000000000000D+00 1 11 3 10 -0.38419547838805D-14 -0.33934728038222D-15 2 11 3 10 0.17221450694406D-14 0.54054209130240D-16 3 11 3 10 0.39153730773322D+00 -0.64021636395100D-15 1 12 3 10 0.10532723950331D-13 -0.26811112380540D-15 2 12 3 10 -0.41089234205308D-14 -0.28155529154895D-16 3 12 3 10 0.14401446007220D-13 0.69723257080633D-08 1 13 3 10 0.25421435270823D+01 0.30759355796044D-01 2 13 3 10 0.24736807453372D+01 0.26768477335266D-01 3 13 3 10 -0.32589072432735D+01 0.29450819023952D-01 1 14 3 10 0.34640302746413D+01 -0.20597506489151D-07 2 14 3 10 0.21345791990508D+01 -0.11296737933216D-07 3 14 3 10 0.16895072203213D+01 0.23405232481019D-07 1 15 3 10 -0.34640302746413D+01 0.20597506368207D-07 2 15 3 10 -0.21345791990508D+01 0.11296738032769D-07 3 15 3 10 0.16895072203213D+01 0.23405233073728D-07 1 16 3 10 -0.25421435270824D+01 -0.30759355796044D-01 2 16 3 10 -0.24736807453372D+01 -0.26768477335266D-01 3 16 3 10 -0.32589072432735D+01 0.29450819023955D-01 1 17 3 10 0.22884251646869D+01 0.19464124263626D-06 2 17 3 10 -0.30330790543789D+01 0.75576197147776D-06 3 17 3 10 -0.37129030726312D+01 0.55580406183199D-06 1 18 3 10 0.26814814780431D+01 -0.29395659937310D-01 2 18 3 10 -0.24740388935627D+01 0.65954300175013D-01 3 18 3 10 0.15239622487681D+01 0.25908668518444D-01 1 19 3 10 -0.26814814780431D+01 0.29395659937310D-01 2 19 3 10 0.24740388935627D+01 -0.65954300175013D-01 3 19 3 10 0.15239622487682D+01 0.25908668518443D-01 1 20 3 10 -0.22884251646869D+01 -0.19464124321743D-06 2 20 3 10 0.30330790543788D+01 -0.75576197147400D-06 3 20 3 10 -0.37129030726312D+01 0.55580406618530D-06 1 1 1 11 0.24302470502948D+00 0.27640831250466D-08 2 1 1 11 0.82932068486495D-01 0.55746736988359D-08 3 1 1 11 0.11030070627428D-13 0.55794811244892D-15 1 2 1 11 0.33669097512718D+01 0.83533077072420D-08 2 2 1 11 -0.21828633112977D+00 0.20847329852382D-08 3 2 1 11 -0.75522630757855D-14 -0.29434749290794D-16 1 3 1 11 -0.91094028615951D+00 0.21462941422964D-08 2 3 1 11 0.84278587224158D-01 -0.27250361497818D-08 3 3 1 11 0.42778879829737D-14 -0.18211648681430D-15 1 4 1 11 -0.15727406755425D+01 -0.20372511583367D-07 2 4 1 11 0.38698744487254D+00 0.63355815055202D-08 3 4 1 11 -0.26629299780761D-15 0.10776528514257D-15 1 5 1 11 0.76738579693580D+00 -0.39066857929204D-08 2 5 1 11 -0.20243395290057D+00 0.74255230627624D-09 3 5 1 11 -0.73226898376363D+00 0.33980713171322D-08 1 6 1 11 0.76738579693579D+00 -0.39066871645997D-08 2 6 1 11 -0.20243395290057D+00 0.74255148621840D-09 3 6 1 11 0.73226898376367D+00 -0.33980713853979D-08 1 7 1 11 -0.36210253121756D+01 -0.21071197992902D+00 2 7 1 11 -0.12019588008041D+00 0.22682378088324D-01 3 7 1 11 0.17327205328376D+01 -0.18118784761341D+00 1 8 1 11 -0.36210253121757D+01 -0.21071197992902D+00 2 8 1 11 -0.12019588008040D+00 0.22682378088324D-01 3 8 1 11 -0.17327205328375D+01 0.18118784761341D+00 1 9 1 11 0.19676204725524D-13 -0.30374518202355D-08 2 9 1 11 0.35073613129928D-01 -0.33457750886462D-08 3 9 1 11 0.66619594728867D-14 0.60962653570764D-16 1 10 1 11 0.22425088122236D+00 -0.75782160408163D-15 2 10 1 11 0.14906667381474D+00 0.31235836932896D-08 3 10 1 11 -0.38419547838805D-14 0.33934728038222D-15 1 11 1 11 0.97215569808066D+01 0.00000000000000D+00 2 11 1 11 -0.88223974985036D+00 -0.63313732685173D-07 3 11 1 11 -0.12801716909159D-12 0.00000000000000D+00 1 12 1 11 -0.75847769274718D-01 0.17207581129278D-09 2 12 1 11 -0.97923704581659D-01 -0.33253204154283D-08 3 12 1 11 0.89280547327704D-14 0.24001397666855D-15 1 13 1 11 0.10580893994944D+01 -0.36597420284058D-02 2 13 1 11 0.77547794034011D-01 -0.77545064256822D-02 3 13 1 11 -0.96527559763949D+00 0.38063651834879D-02 1 14 1 11 0.84858308199533D-01 -0.95162401793028D-02 2 14 1 11 -0.75734874106881D+00 -0.13852106275149D-01 3 14 1 11 0.13448842329276D+01 0.83173225262630D-02 1 15 1 11 0.84858308199533D-01 -0.95162401793021D-02 2 15 1 11 -0.75734874106881D+00 -0.13852106275149D-01 3 15 1 11 -0.13448842329276D+01 -0.83173225262629D-02 1 16 1 11 0.10580893994944D+01 -0.36597420284049D-02 2 16 1 11 0.77547794034013D-01 -0.77545064256822D-02 3 16 1 11 0.96527559763949D+00 -0.38063651834879D-02 1 17 1 11 0.83973050441770D+00 -0.40454286633898D-02 2 17 1 11 0.47399747041774D-01 0.24013175352657D-02 3 17 1 11 -0.12473814058502D+01 0.58367097580728D-02 1 18 1 11 -0.64500728160354D+00 -0.13664967563081D-08 2 18 1 11 0.96908271650750D+00 -0.19894637320997D-08 3 18 1 11 0.20859549147459D+01 0.20170647414168D-07 1 19 1 11 -0.64500728160353D+00 -0.13664957130283D-08 2 19 1 11 0.96908271650748D+00 -0.19894635554214D-08 3 19 1 11 -0.20859549147459D+01 -0.20170647379672D-07 1 20 1 11 0.83973050441770D+00 -0.40454286633897D-02 2 20 1 11 0.47399747041750D-01 0.24013175352658D-02 3 20 1 11 0.12473814058501D+01 -0.58367097580724D-02 1 1 2 11 -0.39371980731922D-01 -0.17723282341141D-09 2 1 2 11 0.14122606994466D+00 -0.45013045485935D-08 3 1 2 11 0.92121196788533D-15 0.15807630663905D-17 1 2 2 11 -0.23688872566419D+00 0.47218073202964D-08 2 2 2 11 0.24626508420686D+00 0.12407799244895D-09 3 2 2 11 -0.24681585664907D-14 -0.12230003458579D-15 1 3 2 11 -0.10800215337626D+00 0.25978547673684D-08 2 3 2 11 0.27960957653769D+00 0.20657969911742D-08 3 3 2 11 0.19777331374566D-14 0.69548810816933D-16 1 4 2 11 0.17022130410282D+00 0.11602150153578D-07 2 4 2 11 0.11077294980863D+00 -0.21721009794570D-08 3 4 2 11 0.20410495037682D-15 0.14483970859615D-15 1 5 2 11 -0.12976085826889D+00 -0.22902561807892D-08 2 5 2 11 -0.17442933858857D+00 -0.39696683450306D-08 3 5 2 11 0.18660580744282D-01 -0.40067536978140D-08 1 6 2 11 -0.12976085826889D+00 -0.22902570008683D-08 2 6 2 11 -0.17442933858859D+00 -0.39696677635158D-08 3 6 2 11 -0.18660580744275D-01 0.40067536740814D-08 1 7 2 11 0.78447063273080D-01 0.26272281656969D-01 2 7 2 11 -0.15357291354309D+01 -0.27588821938913D+00 3 7 2 11 0.53247151644024D+00 -0.48052467411765D-01 1 8 2 11 0.78447063273090D-01 0.26272281656970D-01 2 8 2 11 -0.15357291354311D+01 -0.27588821938913D+00 3 8 2 11 -0.53247151644021D+00 0.48052467411765D-01 1 9 2 11 0.35073613129928D-01 0.33457759164025D-08 2 9 2 11 -0.10885095876255D-13 0.98737440724067D-09 3 9 2 11 -0.39688164965144D-15 -0.63069692468479D-16 1 10 2 11 -0.14906667381491D+00 0.31235836932896D-08 2 10 2 11 -0.46299408881772D+00 -0.43227967251858D-15 3 10 2 11 0.17221450694406D-14 -0.54054209130240D-16 1 11 2 11 -0.88223955649863D+00 0.50852591773874D-07 2 11 2 11 0.67580468587842D+01 0.00000000000000D+00 3 11 2 11 -0.42791080236612D-13 0.00000000000000D+00 1 12 2 11 -0.97924213690217D-01 0.29320542885385D-08 2 12 2 11 -0.36724906313498D+00 0.38961799830648D-09 3 12 2 11 0.27257220798322D-14 -0.93424836367827D-17 1 13 2 11 -0.47957436773314D+00 -0.96862129538427D-02 2 13 2 11 -0.49224197726735D+00 -0.84630629951607D-02 3 13 2 11 -0.16802883486709D+01 0.76536880282332D-02 1 14 2 11 -0.91516509802233D+00 -0.15177272222114D-01 2 14 2 11 -0.94564695760798D+00 -0.13326912347396D-01 3 14 2 11 0.95903492959713D+00 0.38148153958614D-02 1 15 2 11 -0.91516509802232D+00 -0.15177272222114D-01 2 15 2 11 -0.94564695760797D+00 -0.13326912347396D-01 3 15 2 11 -0.95903492959713D+00 -0.38148153958612D-02 1 16 2 11 -0.47957436773314D+00 -0.96862129538427D-02 2 16 2 11 -0.49224197726734D+00 -0.84630629951615D-02 3 16 2 11 0.16802883486709D+01 -0.76536880282334D-02 1 17 2 11 0.57465210920282D+00 0.25106305660085D-02 2 17 2 11 -0.42039068212620D+00 0.26586663307418D-03 3 17 2 11 0.12136238300823D+01 -0.32481178331009D-02 1 18 2 11 0.85398941792522D+00 0.38353749688639D-08 2 18 2 11 -0.19337318768998D+00 -0.17435073448493D-08 3 18 2 11 -0.10619523875356D+01 -0.15637798889427D-07 1 19 2 11 0.85398941792521D+00 0.38353751455422D-08 2 19 2 11 -0.19337318768998D+00 -0.17435075004200D-08 3 19 2 11 0.10619523875356D+01 0.15637798804542D-07 1 20 2 11 0.57465210920280D+00 0.25106305660086D-02 2 20 2 11 -0.42039068212620D+00 0.26586663307494D-03 3 20 2 11 -0.12136238300823D+01 0.32481178331010D-02 1 1 3 11 0.11030070627115D-13 0.55792430658021D-15 2 1 3 11 0.92121196699510D-15 0.11181664048897D-17 3 1 3 11 -0.55303514789221D+00 -0.10408827623452D-07 1 2 3 11 -0.75522630749867D-14 -0.29963219235760D-16 2 2 3 11 -0.24681585645879D-14 -0.12281677474933D-15 3 2 3 11 0.66456196054462D+00 0.63555373908981D-07 1 3 3 11 0.42778879830378D-14 -0.18076652353812D-15 2 3 3 11 0.19777331372489D-14 0.69572058895587D-16 3 3 3 11 0.18036365225666D+01 0.33471022102026D-08 1 4 3 11 -0.26629299780761D-15 0.11123473209452D-15 2 4 3 11 0.20410495037682D-15 0.14483970859615D-15 3 4 3 11 -0.31432302419445D+01 -0.46167986482260D-07 1 5 3 11 -0.49067269366484D+01 0.28500698534777D-01 2 5 3 11 0.87816433546891D+00 -0.87406908002361D-02 3 5 3 11 0.15135227836615D+01 -0.37224085019515D-01 1 6 3 11 0.49067269366484D+01 -0.28500698534777D-01 2 6 3 11 -0.87816433546890D+00 0.87406908002361D-02 3 6 3 11 0.15135227836615D+01 -0.37224085019515D-01 1 7 3 11 -0.59857184343529D+00 -0.27487557896266D+00 2 7 3 11 -0.10266865569929D+00 -0.94599385762890D-01 3 7 3 11 -0.89292157642649D+00 0.83005783090319D+00 1 8 3 11 0.59857184343548D+00 0.27487557896266D+00 2 8 3 11 0.10266865569931D+00 0.94599385762890D-01 3 8 3 11 -0.89292157642592D+00 0.83005783090319D+00 1 9 3 11 0.66619594728713D-14 0.59670163187838D-16 2 9 3 11 -0.39688164963119D-15 -0.63105314718723D-16 3 9 3 11 -0.21444724758536D-13 -0.69723248042204D-08 1 10 3 11 -0.38419547840789D-14 0.33891261370410D-15 2 10 3 11 0.17221450694907D-14 -0.53774086171156D-16 3 10 3 11 0.39153730773322D+00 0.64021636395100D-15 1 11 3 11 -0.12801716909159D-12 0.00000000000000D+00 2 11 3 11 -0.42791080233303D-13 -0.34694469519535D-17 3 11 3 11 0.41491249633158D+02 0.00000000000000D+00 1 12 3 11 0.89280547325169D-14 0.26072575685624D-15 2 12 3 11 0.27257220795223D-14 -0.14136026877368D-16 3 12 3 11 -0.15104566186109D+02 0.20866445034180D-09 1 13 3 11 -0.22884251646869D+01 -0.19464124279488D-06 2 13 3 11 -0.30330790543789D+01 0.75576197133692D-06 3 13 3 11 -0.37129030726314D+01 0.55580406330544D-06 1 14 3 11 0.26814814780430D+01 -0.29395659937313D-01 2 14 3 11 0.24740388935627D+01 -0.65954300175016D-01 3 14 3 11 -0.15239622487681D+01 -0.25908668518442D-01 1 15 3 11 -0.26814814780431D+01 0.29395659937313D-01 2 15 3 11 -0.24740388935627D+01 0.65954300175017D-01 3 15 3 11 -0.15239622487681D+01 -0.25908668518440D-01 1 16 3 11 0.22884251646869D+01 0.19464124274442D-06 2 16 3 11 0.30330790543789D+01 -0.75576197159088D-06 3 16 3 11 -0.37129030726314D+01 0.55580406295355D-06 1 17 3 11 -0.25421435270823D+01 -0.30759355796044D-01 2 17 3 11 0.24736807453372D+01 0.26768477335266D-01 3 17 3 11 -0.32589072432734D+01 0.29450819023953D-01 1 18 3 11 0.34640302746414D+01 -0.20597510244075D-07 2 18 3 11 -0.21345791990508D+01 0.11296740390841D-07 3 18 3 11 -0.16895072203213D+01 -0.23405230585438D-07 1 19 3 11 -0.34640302746414D+01 0.20597510276836D-07 2 19 3 11 0.21345791990508D+01 -0.11296740468787D-07 3 19 3 11 -0.16895072203213D+01 -0.23405230843012D-07 1 20 3 11 0.25421435270823D+01 0.30759355796044D-01 2 20 3 11 -0.24736807453371D+01 -0.26768477335266D-01 3 20 3 11 -0.32589072432733D+01 0.29450819023952D-01 1 1 1 12 -0.33669097512719D+01 -0.83532829344920D-08 2 1 1 12 0.21828633112945D+00 -0.20847359786571D-08 3 1 1 12 0.96067501721508D-15 0.21322887446028D-15 1 2 1 12 -0.24302470502948D+00 -0.27640817602389D-08 2 2 1 12 -0.82932068486516D-01 -0.55746734755562D-08 3 2 1 12 -0.31979708597158D-14 -0.15258334161860D-14 1 3 1 12 -0.15727406755426D+01 -0.20372511403226D-07 2 3 1 12 0.38698744487238D+00 0.63355812892237D-08 3 3 1 12 0.10812402512172D-14 -0.48882796199310D-15 1 4 1 12 -0.91094028615951D+00 0.21462936888894D-08 2 4 1 12 0.84278587224153D-01 -0.27250363059616D-08 3 4 1 12 0.56924547098102D-14 -0.37741378811719D-16 1 5 1 12 -0.76738579693578D+00 0.39066911144295D-08 2 5 1 12 0.20243395290064D+00 -0.74255147132648D-09 3 5 1 12 0.73226898376369D+00 -0.33980705071134D-08 1 6 1 12 -0.76738579693579D+00 0.39066900248061D-08 2 6 1 12 0.20243395290064D+00 -0.74255139581432D-09 3 6 1 12 -0.73226898376371D+00 0.33980705158074D-08 1 7 1 12 -0.36210253121758D+01 -0.21071197992902D+00 2 7 1 12 -0.12019588008025D+00 0.22682378088324D-01 3 7 1 12 0.17327205328375D+01 -0.18118784761341D+00 1 8 1 12 -0.36210253121759D+01 -0.21071197992902D+00 2 8 1 12 -0.12019588008026D+00 0.22682378088324D-01 3 8 1 12 -0.17327205328375D+01 0.18118784761341D+00 1 9 1 12 0.22425088122241D+00 -0.48083337307161D-15 2 9 1 12 0.14906667381483D+00 0.31235835907242D-08 3 9 1 12 -0.24645969145429D-15 0.23669259901990D-15 1 10 1 12 -0.30042341395960D-14 -0.30374539330020D-08 2 10 1 12 0.35073613129919D-01 -0.33457754444272D-08 3 10 1 12 0.10532723950331D-13 0.26811112380540D-15 1 11 1 12 -0.75847769274718D-01 0.17207580677099D-09 2 11 1 12 -0.97923704581659D-01 -0.33253203499436D-08 3 11 1 12 0.89280547329305D-14 -0.23990907514452D-15 1 12 1 12 0.97215569808075D+01 0.00000000000000D+00 2 12 1 12 -0.88223974985040D+00 -0.63313732685173D-07 3 12 1 12 -0.11947665477074D-15 0.00000000000000D+00 1 13 1 12 0.84858308199508D-01 -0.95162401793017D-02 2 13 1 12 -0.75734874106883D+00 -0.13852106275149D-01 3 13 1 12 0.13448842329276D+01 0.83173225262628D-02 1 14 1 12 0.10580893994944D+01 -0.36597420284047D-02 2 14 1 12 0.77547794034020D-01 -0.77545064256822D-02 3 14 1 12 -0.96527559763944D+00 0.38063651834878D-02 1 15 1 12 0.10580893994944D+01 -0.36597420284048D-02 2 15 1 12 0.77547794034024D-01 -0.77545064256822D-02 3 15 1 12 0.96527559763944D+00 -0.38063651834877D-02 1 16 1 12 0.84858308199508D-01 -0.95162401793035D-02 2 16 1 12 -0.75734874106883D+00 -0.13852106275150D-01 3 16 1 12 -0.13448842329276D+01 -0.83173225262625D-02 1 17 1 12 -0.64500728160351D+00 -0.13664980254664D-08 2 17 1 12 0.96908271650750D+00 -0.19894641808694D-08 3 17 1 12 0.20859549147459D+01 0.20170645769137D-07 1 18 1 12 0.83973050441769D+00 -0.40454286633899D-02 2 18 1 12 0.47399747041757D-01 0.24013175352659D-02 3 18 1 12 -0.12473814058502D+01 0.58367097580722D-02 1 19 1 12 0.83973050441770D+00 -0.40454286633897D-02 2 19 1 12 0.47399747041761D-01 0.24013175352658D-02 3 19 1 12 0.12473814058502D+01 -0.58367097580730D-02 1 20 1 12 -0.64500728160351D+00 -0.13664990748505D-08 2 20 1 12 0.96908271650749D+00 -0.19894644851159D-08 3 20 1 12 -0.20859549147459D+01 -0.20170645897966D-07 1 1 2 12 0.23688872566387D+00 -0.47218103137153D-08 2 1 2 12 -0.24626508420675D+00 -0.12408394430883D-09 3 1 2 12 0.20730390301548D-14 -0.17900235900514D-15 1 2 2 12 0.39371980731900D-01 0.17723304669109D-09 2 2 2 12 -0.14122606994465D+00 0.45013043206156D-08 3 2 2 12 0.46916257043017D-16 0.33034989847679D-16 1 3 2 12 0.17022130410266D+00 0.11602149937281D-07 2 3 2 12 0.11077294980897D+00 -0.21721006677801D-08 3 3 2 12 0.25760679341729D-15 -0.17584752070344D-15 1 4 2 12 -0.10800215337626D+00 0.25978546111886D-08 2 4 2 12 0.27960957653770D+00 0.20657969755526D-08 3 4 2 12 0.46613540414256D-14 0.14684918291123D-15 1 5 2 12 0.12976085826896D+00 0.22902570157390D-08 2 5 2 12 0.17442933858859D+00 0.39696696175723D-08 3 5 2 12 -0.18660580744249D-01 0.40067539441582D-08 1 6 2 12 0.12976085826896D+00 0.22902570912724D-08 2 6 2 12 0.17442933858858D+00 0.39696695345467D-08 3 6 2 12 0.18660580744247D-01 -0.40067539213653D-08 1 7 2 12 0.78447063273235D-01 0.26272281656970D-01 2 7 2 12 -0.15357291354311D+01 -0.27588821938913D+00 3 7 2 12 0.53247151643934D+00 -0.48052467411765D-01 1 8 2 12 0.78447063273231D-01 0.26272281656970D-01 2 8 2 12 -0.15357291354311D+01 -0.27588821938913D+00 3 8 2 12 -0.53247151643933D+00 0.48052467411765D-01 1 9 2 12 -0.14906667381481D+00 0.31235835907242D-08 2 9 2 12 -0.46299408881780D+00 0.96715565440654D-16 3 9 2 12 0.21545051375975D-15 -0.40847570964118D-16 1 10 2 12 0.35073613129919D-01 0.33457755606215D-08 2 10 2 12 0.29957049211245D-14 0.98737418593312D-09 3 10 2 12 -0.41089234205308D-14 0.28155529154895D-16 1 11 2 12 -0.97924213690217D-01 0.29320543540232D-08 2 11 2 12 -0.36724906313498D+00 0.38961797700158D-09 3 11 2 12 0.27257220797291D-14 0.10666579925415D-16 1 12 2 12 -0.88223955649867D+00 0.50852591773874D-07 2 12 2 12 0.67580468587839D+01 0.00000000000000D+00 3 12 2 12 -0.21474798163809D-13 0.00000000000000D+00 1 13 2 12 -0.91516509802235D+00 -0.15177272222114D-01 2 13 2 12 -0.94564695760794D+00 -0.13326912347396D-01 3 13 2 12 0.95903492959712D+00 0.38148153958612D-02 1 14 2 12 -0.47957436773313D+00 -0.96862129538428D-02 2 14 2 12 -0.49224197726739D+00 -0.84630629951610D-02 3 14 2 12 -0.16802883486709D+01 0.76536880282333D-02 1 15 2 12 -0.47957436773313D+00 -0.96862129538428D-02 2 15 2 12 -0.49224197726739D+00 -0.84630629951609D-02 3 15 2 12 0.16802883486709D+01 -0.76536880282334D-02 1 16 2 12 -0.91516509802234D+00 -0.15177272222114D-01 2 16 2 12 -0.94564695760793D+00 -0.13326912347396D-01 3 16 2 12 -0.95903492959713D+00 -0.38148153958613D-02 1 17 2 12 0.85398941792522D+00 0.38353745200942D-08 2 17 2 12 -0.19337318769002D+00 -0.17435073799548D-08 3 17 2 12 -0.10619523875356D+01 -0.15637799288816D-07 1 18 2 12 0.57465210920281D+00 0.25106305660087D-02 2 18 2 12 -0.42039068212616D+00 0.26586663307475D-03 3 18 2 12 0.12136238300823D+01 -0.32481178331011D-02 1 19 2 12 0.57465210920282D+00 0.25106305660086D-02 2 19 2 12 -0.42039068212616D+00 0.26586663307458D-03 3 19 2 12 -0.12136238300823D+01 0.32481178331012D-02 1 20 2 12 0.85398941792522D+00 0.38353742158477D-08 2 20 2 12 -0.19337318769003D+00 -0.17435074905594D-08 3 20 2 12 0.10619523875356D+01 0.15637799296238D-07 1 1 3 12 0.96067501641630D-15 0.21375734440524D-15 2 1 3 12 0.20730390282521D-14 -0.17848561884160D-15 3 1 3 12 -0.66456196054453D+00 -0.63555385670519D-07 1 2 3 12 -0.31979708594030D-14 -0.15258096103173D-14 2 2 3 12 0.46916257933248D-16 0.33497586509180D-16 3 2 3 12 0.55303514789220D+00 0.10408829957105D-07 1 3 3 12 0.10812402512172D-14 -0.48535851504115D-15 2 3 3 12 0.25760679341729D-15 -0.17584752070344D-15 3 3 3 12 -0.31432302419446D+01 -0.46167986517581D-07 1 4 3 12 0.56924547099352D-14 -0.37736831691746D-16 2 4 3 12 0.46613540410428D-14 0.14677858872184D-15 3 4 3 12 0.18036365225666D+01 0.33471025711175D-08 1 5 3 12 0.49067269366484D+01 -0.28500698534776D-01 2 5 3 12 -0.87816433546888D+00 0.87406908002363D-02 3 5 3 12 -0.15135227836615D+01 0.37224085019516D-01 1 6 3 12 -0.49067269366485D+01 0.28500698534776D-01 2 6 3 12 0.87816433546887D+00 -0.87406908002363D-02 3 6 3 12 -0.15135227836615D+01 0.37224085019516D-01 1 7 3 12 -0.59857184343544D+00 -0.27487557896266D+00 2 7 3 12 -0.10266865570019D+00 -0.94599385762890D-01 3 7 3 12 -0.89292157642569D+00 0.83005783090320D+00 1 8 3 12 0.59857184343542D+00 0.27487557896266D+00 2 8 3 12 0.10266865570020D+00 0.94599385762890D-01 3 8 3 12 -0.89292157642592D+00 0.83005783090319D+00 1 9 3 12 -0.24645969165264D-15 0.23625793234178D-15 2 9 3 12 0.21545051380987D-15 -0.40567448005034D-16 3 9 3 12 0.39153730773328D+00 0.10308626092389D-15 1 10 3 12 0.10532723950315D-13 0.26681863342248D-15 2 10 3 12 -0.41089234205105D-14 0.28119906904650D-16 3 10 3 12 0.14401446007220D-13 -0.69723257080633D-08 1 11 3 12 0.89280547323568D-14 -0.21919729495683D-15 2 11 3 12 0.27257220796254D-14 0.41383132088523D-17 3 11 3 12 -0.15104566186109D+02 0.20866485459199D-09 1 12 3 12 -0.11947665477074D-15 0.00000000000000D+00 2 12 3 12 -0.21474798160500D-13 -0.34694469519535D-17 3 12 3 12 0.41491249633158D+02 0.00000000000000D+00 1 13 3 12 0.26814814780431D+01 -0.29395659937314D-01 2 13 3 12 0.24740388935627D+01 -0.65954300175017D-01 3 13 3 12 -0.15239622487681D+01 -0.25908668518441D-01 1 14 3 12 -0.22884251646869D+01 -0.19464124287218D-06 2 14 3 12 -0.30330790543789D+01 0.75576197144752D-06 3 14 3 12 -0.37129030726313D+01 0.55580406247501D-06 1 15 3 12 0.22884251646869D+01 0.19464124296091D-06 2 15 3 12 0.30330790543789D+01 -0.75576197155404D-06 3 15 3 12 -0.37129030726313D+01 0.55580406339938D-06 1 16 3 12 -0.26814814780431D+01 0.29395659937314D-01 2 16 3 12 -0.24740388935627D+01 0.65954300175017D-01 3 16 3 12 -0.15239622487681D+01 -0.25908668518441D-01 1 17 3 12 0.34640302746413D+01 -0.20597511889105D-07 2 17 3 12 -0.21345791990508D+01 0.11296739991451D-07 3 17 3 12 -0.16895072203213D+01 -0.23405231322151D-07 1 18 3 12 -0.25421435270823D+01 -0.30759355796044D-01 2 18 3 12 0.24736807453372D+01 0.26768477335266D-01 3 18 3 12 -0.32589072432735D+01 0.29450819023955D-01 1 19 3 12 0.25421435270823D+01 0.30759355796044D-01 2 19 3 12 -0.24736807453372D+01 -0.26768477335266D-01 3 19 3 12 -0.32589072432735D+01 0.29450819023952D-01 1 20 3 12 -0.34640302746413D+01 0.20597511762011D-07 2 20 3 12 0.21345791990508D+01 -0.11296739984029D-07 3 20 3 12 -0.16895072203213D+01 -0.23405230847656D-07 1 1 1 13 0.13505994119705D+01 -0.72550054491436D-02 2 1 1 13 0.38251114594275D+00 0.68471011367710D-03 3 1 1 13 -0.82118323636510D+00 -0.68437938016462D-06 1 2 1 13 0.10413932964438D+01 0.21687425894997D-02 2 2 1 13 0.20608507553582D+00 -0.31656792789838D-03 3 2 1 13 0.10799786650728D+01 0.11528597573805D-02 1 3 1 13 -0.18132533007096D+01 0.47530769157255D-02 2 3 1 13 0.53612210623460D+00 -0.45155218654945D-02 3 3 1 13 0.40884331380686D+00 0.36635333128257D-02 1 4 1 13 -0.12026903628936D+01 -0.82154279193468D-02 2 4 1 13 -0.31248864877209D+00 0.53155363258285D-03 3 4 1 13 0.14444766199698D+01 0.14756593862336D-08 1 5 1 13 0.55578836778290D+01 -0.10032565449078D-01 2 5 1 13 -0.55080508470611D+00 -0.47058206966910D-02 3 5 1 13 -0.69764104738228D+00 -0.75154469464729D-01 1 6 1 13 0.19362396073031D+01 0.11964887554200D-01 2 6 1 13 -0.59457960571169D-01 0.53575458752785D-02 3 6 1 13 -0.43103011435940D+00 0.27533992276410D-02 1 7 1 13 -0.50617432499133D+01 0.34881693369037D-02 2 7 1 13 0.63648666029938D+00 0.36009329416593D-03 3 7 1 13 -0.80124576135857D+00 -0.67820350195871D-01 1 8 1 13 -0.17794875236901D+01 -0.19166045915723D-01 2 8 1 13 -0.29515693224249D+00 -0.27555489500578D-01 3 8 1 13 -0.21959540990302D+00 0.16129721571363D-01 1 9 1 13 0.64503548991630D+00 -0.29967134865111D-01 2 9 1 13 0.85390272525949D+00 -0.16940258999621D-01 3 9 1 13 0.34640414696726D+01 -0.13911557897713D-06 1 10 1 13 0.83973052237793D+00 0.12136267489986D-01 2 10 1 13 -0.57461793332310D+00 0.75318918695217D-02 3 10 1 13 0.25421490654402D+01 -0.92278078692358D-01 1 11 1 13 0.10580893994944D+01 0.36597420284058D-02 2 11 1 13 -0.47957436773314D+00 0.96862129538427D-02 3 11 1 13 -0.22884251646869D+01 0.19464124279488D-06 1 12 1 13 0.84858308199508D-01 0.95162401793007D-02 2 12 1 13 -0.91516509802235D+00 0.15177272222115D-01 3 12 1 13 0.26814814780431D+01 0.29395659937312D-01 1 13 1 13 0.15369761478102D+02 0.00000000000000D+00 2 13 1 13 0.71163047741876D+01 0.13903371760471D+00 3 13 1 13 -0.12852033538845D+01 -0.17818189147543D+00 1 14 1 13 0.66914053695301D+00 -0.31094867468296D-02 2 14 1 13 0.36012474597850D+00 -0.57432848977183D-03 3 14 1 13 -0.71641648901979D+00 -0.15828544427265D-01 1 15 1 13 -0.73506087478142D-01 -0.58291722548124D-15 2 15 1 13 0.13243688489238D+00 0.27414411095331D-03 3 15 1 13 0.19420996202345D-01 -0.23289753098669D-01 1 16 1 13 0.15388288188003D+01 -0.65392745337796D-16 2 16 1 13 0.72965505522404D+00 -0.36779492458601D-06 3 16 1 13 0.62759339862234D-01 0.22779958224558D-06 1 17 1 13 0.32917986690431D+01 0.40539807740207D-15 2 17 1 13 -0.21589756231115D+01 -0.41735635658018D-02 3 17 1 13 0.36956654762330D-01 -0.83818816840154D-02 1 18 1 13 -0.55150388700688D-14 -0.33271949170871D-06 2 18 1 13 -0.92770841255382D+00 0.16024586686892D-06 3 18 1 13 -0.16804002707632D+01 0.20905317829478D-06 1 19 1 13 -0.85896396553962D-14 -0.16078841618535D-02 2 19 1 13 -0.71895228811410D-02 0.64504261100501D-04 3 19 1 13 -0.69597199524331D-01 -0.11644500598342D-01 1 20 1 13 0.14802253550499D+01 0.21198298160659D-02 2 20 1 13 -0.67715961460253D+00 0.39974976356835D-02 3 20 1 13 -0.93827316446331D-02 0.14470375306415D-02 1 1 2 13 0.81666076196986D+00 -0.21026794867858D-02 2 1 2 13 0.39743085092929D+00 -0.10315485055375D-01 3 1 2 13 0.91963324317481D-01 0.21945276637704D-06 1 2 2 13 0.83615108999650D+00 0.20828989450402D-02 2 2 2 13 -0.27225118200812D+00 -0.35497944298480D-03 3 2 2 13 0.42674156748670D-01 0.11388164245978D-02 1 3 2 13 -0.30117809923761D+00 -0.56316188352094D-02 2 3 2 13 -0.79186286634349D+00 0.81935811546456D-02 3 3 2 13 -0.96222188575287D+00 -0.16681063109044D-02 1 4 2 13 -0.10450540314163D+01 -0.21458121172629D-02 2 4 2 13 -0.11531177325463D+00 -0.12687788388846D-02 3 4 2 13 -0.23803547453742D+00 0.15358580454152D-06 1 5 2 13 0.17328707863209D+01 -0.86063586808160D-02 2 5 2 13 0.77551224241866D-01 0.22947561680979D-02 3 5 2 13 -0.78918936688460D+00 -0.67554363629039D-01 1 6 2 13 0.83329143018955D+00 0.64728025028718D-02 2 6 2 13 -0.39726271758559D-01 -0.30007940843054D-02 3 6 2 13 0.20553089582640D+00 0.25769569991211D-02 1 7 2 13 -0.26913011930787D+01 0.98995665567645D-02 2 7 2 13 -0.12512110340052D+01 0.12958961001163D-02 3 7 2 13 -0.73183635481973D+00 -0.90035483846342D-01 1 8 2 13 -0.90366178062741D+00 -0.33076193264512D-01 2 8 2 13 -0.18468895195533D+00 -0.15233242387268D-01 3 8 2 13 0.26552653181972D+00 0.41374279779799D-02 1 9 2 13 0.96903006575378D+00 -0.23745150991560D-01 2 9 2 13 0.19337201599433D+00 -0.68831483010556D-02 3 9 2 13 0.21345880305997D+01 0.14467656614462D-05 1 10 2 13 -0.47373420869628D-01 0.72039518971676D-02 2 10 2 13 -0.42039545619561D+00 -0.79760655183776D-03 3 10 2 13 0.24736843662435D+01 -0.80305452092080D-01 1 11 2 13 0.77547794034011D-01 0.77545064256822D-02 2 11 2 13 -0.49224197726735D+00 0.84630629951607D-02 3 11 2 13 -0.30330790543789D+01 -0.75576197133692D-06 1 12 2 13 -0.75734874106883D+00 0.13852106275150D-01 2 12 2 13 -0.94564695760794D+00 0.13326912347397D-01 3 12 2 13 0.24740388935627D+01 0.65954300175015D-01 1 13 2 13 0.71163101684453D+01 -0.13903321095824D+00 2 13 2 13 0.14511487521269D+02 0.00000000000000D+00 3 13 2 13 0.19810951837565D+01 0.24729521639192D+00 1 14 2 13 0.36012575396470D+00 -0.57485669567982D-03 2 14 2 13 -0.89467395764157D+00 0.10552609969095D-02 3 14 2 13 -0.59647116774059D+00 -0.15822220767528D-01 1 15 2 13 0.13243688489238D+00 -0.27414411095337D-03 2 15 2 13 -0.17109939588368D+00 -0.31308769589919D-15 3 15 2 13 -0.18380719447032D+00 -0.10237317577535D-01 1 16 2 13 0.72965505522404D+00 0.36779492459503D-06 2 16 2 13 0.70915292279926D+00 -0.86783042232327D-16 3 16 2 13 -0.11453501208804D+00 0.36582976533913D-06 1 17 2 13 0.21589756231115D+01 -0.41735635658018D-02 2 17 2 13 -0.68932005377594D+01 -0.77820343043226D-16 3 17 2 13 0.13936910002660D+00 -0.33101839317914D-02 1 18 2 13 -0.92770841255382D+00 -0.16024587070021D-06 2 18 2 13 -0.61924955690595D-15 -0.23241084394102D-07 3 18 2 13 -0.19785367914050D+00 0.16870516740554D-06 1 19 2 13 -0.71901523276219D-02 -0.64680691296646D-04 2 19 2 13 -0.91373653373876D-15 -0.14073042758145D-02 3 19 2 13 -0.52015312565545D-01 -0.10425068151978D-01 1 20 2 13 0.67715919531537D+00 -0.39970087055471D-02 2 20 2 13 -0.59319074231792D+00 0.10191869453764D-01 3 20 2 13 -0.26281136448339D-01 0.84309517833734D-04 1 1 3 13 -0.88210296911936D+00 0.12263345485662D-02 2 1 3 13 0.45426285046140D+00 -0.31921345472136D-02 3 1 3 13 0.27311368293409D-01 -0.48749975656208D-06 1 2 3 13 0.53793535376568D+00 0.17218116919652D-03 2 2 3 13 -0.23505711426169D+00 0.21136134881407D-03 3 2 3 13 -0.45218019499650D+00 0.13429359757872D-03 1 3 3 13 0.37152320846471D+00 -0.14970024958021D-01 2 3 3 13 -0.87893240916711D+00 0.16417684723865D-01 3 3 3 13 -0.21356746809926D+01 0.64518719928423D-02 1 4 3 13 0.87229731747165D+00 -0.11087385210481D-01 2 4 3 13 -0.57330019971579D+00 0.60569890989331D-02 3 4 3 13 0.69375072072487D+00 -0.12776078169780D-06 1 5 3 13 -0.68445644208535D+00 -0.24609705990383D-01 2 5 3 13 -0.94450980494593D+00 -0.49306558978914D-02 3 5 3 13 0.31913455621638D+01 0.83731619352408D-02 1 6 3 13 -0.14256153319272D+00 0.18984854898020D-01 2 6 3 13 -0.31979338364591D+00 0.74730631846226D-02 3 6 3 13 -0.28719852129375D+01 -0.13816268237816D-01 1 7 3 13 -0.69596597002010D+00 -0.16195095029620D-01 2 7 3 13 -0.86659694614990D+00 -0.17054032197871D-01 3 7 3 13 -0.34292263390703D+01 -0.36210999367106D-02 1 8 3 13 -0.81124461966970D-01 0.39031612854896D-01 2 8 3 13 -0.15591755126556D+00 0.29754511771128D-01 3 8 3 13 0.32265073658012D+01 0.23559605926578D-01 1 9 3 13 0.20859864215896D+01 -0.14690242051900D-01 2 9 3 13 0.10619468710812D+01 -0.75971701552286D-02 3 9 3 13 0.16894989372113D+01 -0.24659193715274D-05 1 10 3 13 0.12472944190923D+01 0.17510119224745D-01 2 10 3 13 0.12135925753972D+01 0.97443674449892D-02 3 10 3 13 -0.32589073730359D+01 -0.88352482724324D-01 1 11 3 13 -0.96527559763949D+00 -0.38063651834879D-02 2 11 3 13 -0.16802883486709D+01 -0.76536880282332D-02 3 11 3 13 -0.37129030726314D+01 -0.55580406330544D-06 1 12 3 13 0.13448842329276D+01 -0.83173225262647D-02 2 12 3 13 0.95903492959712D+00 -0.38148153958625D-02 3 12 3 13 -0.15239622487681D+01 0.25908668518442D-01 1 13 3 13 -0.12851833412153D+01 0.17817987556316D+00 2 13 3 13 0.19811208736033D+01 -0.24729430122380D+00 3 13 3 13 0.15027371097683D+02 0.00000000000000D+00 1 14 3 13 -0.71641649205775D+00 -0.15828408045863D-01 2 14 3 13 -0.59646955176477D+00 -0.15822443951962D-01 3 14 3 13 0.32238387805641D+00 0.82757133622915D-03 1 15 3 13 -0.19420996202349D-01 -0.23289753098669D-01 2 15 3 13 0.18380719447032D+00 -0.10237317577535D-01 3 15 3 13 -0.46307096784144D+00 -0.15019843926597D-15 1 16 3 13 -0.62759339862234D-01 0.22779958224645D-06 2 16 3 13 0.11453501208804D+00 0.36582976533913D-06 3 16 3 13 -0.17520321069576D+01 -0.13810109940830D-14 1 17 3 13 -0.36956654762326D-01 -0.83818816840154D-02 2 17 3 13 0.13936910002660D+00 0.33101839317915D-02 3 17 3 13 0.15430748243887D+01 0.28844551848866D-16 1 18 3 13 -0.16804002707632D+01 -0.20905318868673D-06 2 18 3 13 0.19785367914050D+00 0.16870516738472D-06 3 18 3 13 -0.12319030388348D-13 -0.80739057440933D-07 1 19 3 13 0.69597573774599D-01 -0.11644810110962D-01 2 19 3 13 -0.52015356245708D-01 0.10425154650182D-01 3 19 3 13 -0.11904421764624D-13 0.15265542333782D-02 1 20 3 13 -0.93794468912922D-02 0.14465381142971D-02 2 20 3 13 0.26278876546407D-01 -0.84337482442200D-04 3 20 3 13 -0.73190121021802D+00 0.35296795122738D-02 1 1 1 14 -0.10413932964438D+01 -0.21687425894944D-02 2 1 1 14 -0.20608507553581D+00 0.31656792789693D-03 3 1 1 14 -0.10799786650728D+01 -0.11528597573832D-02 1 2 1 14 -0.13505994119705D+01 0.72550054491479D-02 2 2 1 14 -0.38251114594273D+00 -0.68471011368142D-03 3 2 1 14 0.82118323636496D+00 0.68437938835807D-06 1 3 1 14 -0.12026903628936D+01 -0.82154279193474D-02 2 3 1 14 -0.31248864877212D+00 0.53155363258225D-03 3 3 1 14 0.14444766199700D+01 0.14756600821609D-08 1 4 1 14 -0.18132533007096D+01 0.47530769157243D-02 2 4 1 14 0.53612210623463D+00 -0.45155218654944D-02 3 4 1 14 0.40884331380693D+00 0.36635333128252D-02 1 5 1 14 -0.55578836778288D+01 0.10032565449097D-01 2 5 1 14 0.55080508470645D+00 0.47058206967137D-02 3 5 1 14 0.69764104738190D+00 0.75154469464718D-01 1 6 1 14 -0.19362396073031D+01 -0.11964887554198D-01 2 6 1 14 0.59457960571165D-01 -0.53575458752783D-02 3 6 1 14 0.43103011435936D+00 -0.27533992276405D-02 1 7 1 14 -0.50617432499134D+01 0.34881693369058D-02 2 7 1 14 0.63648666029901D+00 0.36009329416661D-03 3 7 1 14 -0.80124576135858D+00 -0.67820350195872D-01 1 8 1 14 -0.17794875236901D+01 -0.19166045915723D-01 2 8 1 14 -0.29515693224249D+00 -0.27555489500578D-01 3 8 1 14 -0.21959540990299D+00 0.16129721571362D-01 1 9 1 14 0.83973052237797D+00 0.12136267489986D-01 2 9 1 14 -0.57461793332308D+00 0.75318918695216D-02 3 9 1 14 0.25421490654402D+01 -0.92278078692359D-01 1 10 1 14 0.64503548991627D+00 -0.29967134865115D-01 2 10 1 14 0.85390272525953D+00 -0.16940258999625D-01 3 10 1 14 0.34640414696727D+01 -0.13911558783013D-06 1 11 1 14 0.84858308199533D-01 0.95162401793018D-02 2 11 1 14 -0.91516509802233D+00 0.15177272222115D-01 3 11 1 14 0.26814814780430D+01 0.29395659937311D-01 1 12 1 14 0.10580893994944D+01 0.36597420284047D-02 2 12 1 14 -0.47957436773313D+00 0.96862129538428D-02 3 12 1 14 -0.22884251646869D+01 0.19464124287218D-06 1 13 1 14 0.66914053695301D+00 -0.31094867468326D-02 2 13 1 14 0.36012474597850D+00 -0.57432848977248D-03 3 13 1 14 -0.71641648901979D+00 -0.15828544427265D-01 1 14 1 14 0.15369761478101D+02 0.00000000000000D+00 2 14 1 14 0.71163047741881D+01 0.13903371760471D+00 3 14 1 14 -0.12852033538841D+01 -0.17818189147543D+00 1 15 1 14 0.15388288188003D+01 -0.25568681554587D-15 2 15 1 14 0.72965505522404D+00 -0.36779492458681D-06 3 15 1 14 0.62759339862232D-01 0.22779958238029D-06 1 16 1 14 -0.73506087478142D-01 0.86951517084865D-15 2 16 1 14 0.13243688489238D+00 0.27414411095331D-03 3 16 1 14 0.19420996202340D-01 -0.23289753098669D-01 1 17 1 14 -0.24756789293571D-14 -0.33271950166135D-06 2 17 1 14 -0.92770841255380D+00 0.16024586897867D-06 3 17 1 14 -0.16804002707632D+01 0.20905318392449D-06 1 18 1 14 0.32917986690431D+01 0.22169625675903D-15 2 18 1 14 -0.21589756231115D+01 -0.41735635658018D-02 3 18 1 14 0.36956654762321D-01 -0.83818816840154D-02 1 19 1 14 0.14802253550499D+01 0.21198298160670D-02 2 19 1 14 -0.67715961460253D+00 0.39974976356836D-02 3 19 1 14 -0.93827316446343D-02 0.14470375306414D-02 1 20 1 14 0.49676191703949D-14 -0.16078841618551D-02 2 20 1 14 -0.71895228811402D-02 0.64504261100761D-04 3 20 1 14 -0.69597199524328D-01 -0.11644500598344D-01 1 1 2 14 -0.83615108999649D+00 -0.20828989450416D-02 2 1 2 14 0.27225118200816D+00 0.35497944298612D-03 3 1 2 14 -0.42674156748695D-01 -0.11388164245953D-02 1 2 2 14 -0.81666076196984D+00 0.21026794867815D-02 2 2 2 14 -0.39743085092921D+00 0.10315485055377D-01 3 2 2 14 -0.91963324317467D-01 -0.21945277364612D-06 1 3 2 14 -0.10450540314164D+01 -0.21458121172635D-02 2 3 2 14 -0.11531177325465D+00 -0.12687788388845D-02 3 3 2 14 -0.23803547453745D+00 0.15358580491633D-06 1 4 2 14 -0.30117809923758D+00 -0.56316188352094D-02 2 4 2 14 -0.79186286634356D+00 0.81935811546454D-02 3 4 2 14 -0.96222188575300D+00 -0.16681063109047D-02 1 5 2 14 -0.17328707863205D+01 0.86063586808387D-02 2 5 2 14 -0.77551224242050D-01 -0.22947561680936D-02 3 5 2 14 0.78918936688440D+00 0.67554363629032D-01 1 6 2 14 -0.83329143018955D+00 -0.64728025028716D-02 2 6 2 14 0.39726271758556D-01 0.30007940843053D-02 3 6 2 14 -0.20553089582641D+00 -0.25769569991209D-02 1 7 2 14 -0.26913011930791D+01 0.98995665567652D-02 2 7 2 14 -0.12512110340054D+01 0.12958961001165D-02 3 7 2 14 -0.73183635481974D+00 -0.90035483846342D-01 1 8 2 14 -0.90366178062742D+00 -0.33076193264512D-01 2 8 2 14 -0.18468895195532D+00 -0.15233242387268D-01 3 8 2 14 0.26552653181976D+00 0.41374279779800D-02 1 9 2 14 -0.47373420869605D-01 0.72039518971675D-02 2 9 2 14 -0.42039545619563D+00 -0.79760655183742D-03 3 9 2 14 0.24736843662435D+01 -0.80305452092080D-01 1 10 2 14 0.96903006575382D+00 -0.23745150991564D-01 2 10 2 14 0.19337201599433D+00 -0.68831483010552D-02 3 10 2 14 0.21345880305998D+01 0.14467656569628D-05 1 11 2 14 -0.75734874106881D+00 0.13852106275151D-01 2 11 2 14 -0.94564695760798D+00 0.13326912347396D-01 3 11 2 14 0.24740388935627D+01 0.65954300175015D-01 1 12 2 14 0.77547794034020D-01 0.77545064256822D-02 2 12 2 14 -0.49224197726739D+00 0.84630629951610D-02 3 12 2 14 -0.30330790543789D+01 -0.75576197144752D-06 1 13 2 14 0.36012575396470D+00 -0.57485669568048D-03 2 13 2 14 -0.89467395764157D+00 0.10552609969090D-02 3 13 2 14 -0.59647116774059D+00 -0.15822220767527D-01 1 14 2 14 0.71163101684458D+01 -0.13903321095824D+00 2 14 2 14 0.14511487521270D+02 0.00000000000000D+00 3 14 2 14 0.19810951837569D+01 0.24729521639192D+00 1 15 2 14 0.72965505522404D+00 0.36779492459422D-06 2 15 2 14 0.70915292279925D+00 0.13508593651636D-16 3 15 2 14 -0.11453501208804D+00 0.36582976529199D-06 1 16 2 14 0.13243688489238D+00 -0.27414411095337D-03 2 16 2 14 -0.17109939588368D+00 0.27481934829092D-15 3 16 2 14 -0.18380719447032D+00 -0.10237317577535D-01 1 17 2 14 -0.92770841255380D+00 -0.16024586859047D-06 2 17 2 14 0.66136079515909D-14 -0.23241082212542D-07 3 17 2 14 -0.19785367914050D+00 0.16870516660188D-06 1 18 2 14 0.21589756231115D+01 -0.41735635658018D-02 2 18 2 14 -0.68932005377593D+01 -0.21354660230616D-16 3 18 2 14 0.13936910002660D+00 -0.33101839317915D-02 1 19 2 14 0.67715919531537D+00 -0.39970087055471D-02 2 19 2 14 -0.59319074231792D+00 0.10191869453764D-01 3 19 2 14 -0.26281136448341D-01 0.84309517833783D-04 1 20 2 14 -0.71901523276210D-02 -0.64680691296387D-04 2 20 2 14 0.10162947802969D-15 -0.14073042758146D-02 3 20 2 14 -0.52015312565543D-01 -0.10425068151978D-01 1 1 3 14 -0.53793535376564D+00 -0.17218116919923D-03 2 1 3 14 0.23505711426166D+00 -0.21136134881163D-03 3 1 3 14 0.45218019499646D+00 -0.13429359757117D-03 1 2 3 14 0.88210296911922D+00 -0.12263345485580D-02 2 2 3 14 -0.45426285046139D+00 0.31921345472063D-02 3 2 3 14 -0.27311368293502D-01 0.48749976103697D-06 1 3 3 14 0.87229731747186D+00 -0.11087385210480D-01 2 3 3 14 -0.57330019971582D+00 0.60569890989335D-02 3 3 3 14 0.69375072072493D+00 -0.12776077927054D-06 1 4 3 14 0.37152320846478D+00 -0.14970024958021D-01 2 4 3 14 -0.87893240916724D+00 0.16417684723865D-01 3 4 3 14 -0.21356746809927D+01 0.64518719928399D-02 1 5 3 14 0.68445644208497D+00 0.24609705990372D-01 2 5 3 14 0.94450980494572D+00 0.49306558978843D-02 3 5 3 14 -0.31913455621639D+01 -0.83731619352649D-02 1 6 3 14 0.14256153319269D+00 -0.18984854898019D-01 2 6 3 14 0.31979338364590D+00 -0.74730631846224D-02 3 6 3 14 0.28719852129375D+01 0.13816268237820D-01 1 7 3 14 -0.69596597002011D+00 -0.16195095029621D-01 2 7 3 14 -0.86659694614991D+00 -0.17054032197871D-01 3 7 3 14 -0.34292263390698D+01 -0.36210999367142D-02 1 8 3 14 -0.81124461966944D-01 0.39031612854895D-01 2 8 3 14 -0.15591755126552D+00 0.29754511771129D-01 3 8 3 14 0.32265073658011D+01 0.23559605926577D-01 1 9 3 14 0.12472944190922D+01 0.17510119224744D-01 2 9 3 14 0.12135925753972D+01 0.97443674449891D-02 3 9 3 14 -0.32589073730359D+01 -0.88352482724326D-01 1 10 3 14 0.20859864215896D+01 -0.14690242051909D-01 2 10 3 14 0.10619468710813D+01 -0.75971701552331D-02 3 10 3 14 0.16894989372113D+01 -0.24659193752476D-05 1 11 3 14 0.13448842329276D+01 -0.83173225262649D-02 2 11 3 14 0.95903492959713D+00 -0.38148153958627D-02 3 11 3 14 -0.15239622487681D+01 0.25908668518443D-01 1 12 3 14 -0.96527559763944D+00 -0.38063651834878D-02 2 12 3 14 -0.16802883486709D+01 -0.76536880282333D-02 3 12 3 14 -0.37129030726313D+01 -0.55580406247501D-06 1 13 3 14 -0.71641649205775D+00 -0.15828408045863D-01 2 13 3 14 -0.59646955176477D+00 -0.15822443951961D-01 3 13 3 14 0.32238387805641D+00 0.82757133622954D-03 1 14 3 14 -0.12851833412150D+01 0.17817987556316D+00 2 14 3 14 0.19811208736036D+01 -0.24729430122380D+00 3 14 3 14 0.15027371097683D+02 0.00000000000000D+00 1 15 3 14 -0.62759339862236D-01 0.22779958238116D-06 2 15 3 14 0.11453501208804D+00 0.36582976529199D-06 3 15 3 14 -0.17520321069576D+01 -0.10672891943562D-14 1 16 3 14 -0.19420996202354D-01 -0.23289753098669D-01 2 16 3 14 0.18380719447032D+00 -0.10237317577535D-01 3 16 3 14 -0.46307096784144D+00 -0.29165771691155D-16 1 17 3 14 -0.16804002707632D+01 -0.20905318305702D-06 2 17 3 14 0.19785367914049D+00 0.16870516657413D-06 3 17 3 14 0.20315112519999D-13 -0.80739054088816D-07 1 18 3 14 -0.36956654762335D-01 -0.83818816840154D-02 2 18 3 14 0.13936910002660D+00 0.33101839317914D-02 3 18 3 14 0.15430748243887D+01 0.95725637483525D-16 1 19 3 14 -0.93794468912936D-02 0.14465381142969D-02 2 19 3 14 0.26278876546406D-01 -0.84337482442151D-04 3 19 3 14 -0.73190121021802D+00 0.35296795122742D-02 1 20 3 14 0.69597573774601D-01 -0.11644810110965D-01 2 20 3 14 -0.52015356245706D-01 0.10425154650182D-01 3 20 3 14 -0.25066634953106D-13 0.15265542333765D-02 1 1 1 15 -0.10413932964438D+01 -0.21687425894955D-02 2 1 1 15 -0.20608507553581D+00 0.31656792789710D-03 3 1 1 15 0.10799786650728D+01 0.11528597573823D-02 1 2 1 15 -0.13505994119705D+01 0.72550054491470D-02 2 2 1 15 -0.38251114594280D+00 -0.68471011368149D-03 3 2 1 15 -0.82118323636503D+00 -0.68437938846629D-06 1 3 1 15 -0.12026903628936D+01 -0.82154279193498D-02 2 3 1 15 -0.31248864877212D+00 0.53155363258227D-03 3 3 1 15 -0.14444766199699D+01 -0.14756599047121D-08 1 4 1 15 -0.18132533007096D+01 0.47530769157262D-02 2 4 1 15 0.53612210623452D+00 -0.45155218654944D-02 3 4 1 15 -0.40884331380681D+00 -0.36635333128247D-02 1 5 1 15 -0.19362396073031D+01 -0.11964887554201D-01 2 5 1 15 0.59457960571178D-01 -0.53575458752782D-02 3 5 1 15 -0.43103011435937D+00 0.27533992276405D-02 1 6 1 15 -0.55578836778288D+01 0.10032565449095D-01 2 6 1 15 0.55080508470637D+00 0.47058206967138D-02 3 6 1 15 -0.69764104738184D+00 -0.75154469464719D-01 1 7 1 15 -0.17794875236901D+01 -0.19166045915723D-01 2 7 1 15 -0.29515693224249D+00 -0.27555489500578D-01 3 7 1 15 0.21959540990300D+00 -0.16129721571363D-01 1 8 1 15 -0.50617432499134D+01 0.34881693369059D-02 2 8 1 15 0.63648666029901D+00 0.36009329416669D-03 3 8 1 15 0.80124576135859D+00 0.67820350195872D-01 1 9 1 15 0.83973052237796D+00 0.12136267489988D-01 2 9 1 15 -0.57461793332308D+00 0.75318918695219D-02 3 9 1 15 -0.25421490654402D+01 0.92278078692358D-01 1 10 1 15 0.64503548991626D+00 -0.29967134865115D-01 2 10 1 15 0.85390272525951D+00 -0.16940258999625D-01 3 10 1 15 -0.34640414696727D+01 0.13911558795281D-06 1 11 1 15 0.84858308199533D-01 0.95162401793011D-02 2 11 1 15 -0.91516509802232D+00 0.15177272222115D-01 3 11 1 15 -0.26814814780431D+01 -0.29395659937312D-01 1 12 1 15 0.10580893994944D+01 0.36597420284048D-02 2 12 1 15 -0.47957436773313D+00 0.96862129538428D-02 3 12 1 15 0.22884251646869D+01 -0.19464124296091D-06 1 13 1 15 -0.73506087478142D-01 0.58291722548124D-15 2 13 1 15 0.13243688489238D+00 0.27414411095337D-03 3 13 1 15 -0.19420996202349D-01 0.23289753098669D-01 1 14 1 15 0.15388288188003D+01 0.25568681554587D-15 2 14 1 15 0.72965505522404D+00 -0.36779492459422D-06 3 14 1 15 -0.62759339862236D-01 -0.22779958238116D-06 1 15 1 15 0.15369761478101D+02 0.00000000000000D+00 2 15 1 15 0.71163047741881D+01 0.13903371760471D+00 3 15 1 15 0.12852033538841D+01 0.17818189147543D+00 1 16 1 15 0.66914053695301D+00 -0.31094867468312D-02 2 16 1 15 0.36012474597850D+00 -0.57432848977251D-03 3 16 1 15 0.71641648901979D+00 0.15828544427265D-01 1 17 1 15 0.57170809961631D-14 -0.16078841618552D-02 2 17 1 15 -0.71895228811423D-02 0.64504261100774D-04 3 17 1 15 0.69597199524324D-01 0.11644500598342D-01 1 18 1 15 0.14802253550499D+01 0.21198298160662D-02 2 18 1 15 -0.67715961460253D+00 0.39974976356836D-02 3 18 1 15 0.93827316446420D-02 -0.14470375306414D-02 1 19 1 15 0.32917986690431D+01 -0.29711754721984D-15 2 19 1 15 -0.21589756231115D+01 -0.41735635658017D-02 3 19 1 15 -0.36956654762328D-01 0.83818816840154D-02 1 20 1 15 -0.24755178931190D-14 -0.33271950001726D-06 2 20 1 15 -0.92770841255380D+00 0.16024586894668D-06 3 20 1 15 0.16804002707633D+01 -0.20905318348631D-06 1 1 2 15 -0.83615108999649D+00 -0.20828989450415D-02 2 1 2 15 0.27225118200816D+00 0.35497944298509D-03 3 1 2 15 0.42674156748706D-01 0.11388164245953D-02 1 2 2 15 -0.81666076196989D+00 0.21026794867814D-02 2 2 2 15 -0.39743085092918D+00 0.10315485055378D-01 3 2 2 15 0.91963324317502D-01 0.21945277389246D-06 1 3 2 15 -0.10450540314164D+01 -0.21458121172635D-02 2 3 2 15 -0.11531177325465D+00 -0.12687788388848D-02 3 3 2 15 0.23803547453746D+00 -0.15358580496652D-06 1 4 2 15 -0.30117809923768D+00 -0.56316188352094D-02 2 4 2 15 -0.79186286634350D+00 0.81935811546453D-02 3 4 2 15 0.96222188575282D+00 0.16681063109045D-02 1 5 2 15 -0.83329143018954D+00 -0.64728025028715D-02 2 5 2 15 0.39726271758556D-01 0.30007940843049D-02 3 5 2 15 0.20553089582641D+00 0.25769569991209D-02 1 6 2 15 -0.17328707863206D+01 0.86063586808388D-02 2 6 2 15 -0.77551224242040D-01 -0.22947561680930D-02 3 6 2 15 -0.78918936688439D+00 -0.67554363629032D-01 1 7 2 15 -0.90366178062741D+00 -0.33076193264512D-01 2 7 2 15 -0.18468895195532D+00 -0.15233242387269D-01 3 7 2 15 -0.26552653181976D+00 -0.41374279779800D-02 1 8 2 15 -0.26913011930791D+01 0.98995665567653D-02 2 8 2 15 -0.12512110340053D+01 0.12958961001168D-02 3 8 2 15 0.73183635481975D+00 0.90035483846342D-01 1 9 2 15 -0.47373420869609D-01 0.72039518971678D-02 2 9 2 15 -0.42039545619562D+00 -0.79760655183749D-03 3 9 2 15 -0.24736843662435D+01 0.80305452092080D-01 1 10 2 15 0.96903006575380D+00 -0.23745150991564D-01 2 10 2 15 0.19337201599433D+00 -0.68831483010554D-02 3 10 2 15 -0.21345880305997D+01 -0.14467656570693D-05 1 11 2 15 -0.75734874106881D+00 0.13852106275151D-01 2 11 2 15 -0.94564695760797D+00 0.13326912347397D-01 3 11 2 15 -0.24740388935627D+01 -0.65954300175015D-01 1 12 2 15 0.77547794034024D-01 0.77545064256822D-02 2 12 2 15 -0.49224197726739D+00 0.84630629951609D-02 3 12 2 15 0.30330790543789D+01 0.75576197155404D-06 1 13 2 15 0.13243688489238D+00 -0.27414411095331D-03 2 13 2 15 -0.17109939588368D+00 0.31308769589919D-15 3 13 2 15 0.18380719447032D+00 0.10237317577535D-01 1 14 2 15 0.72965505522404D+00 0.36779492458681D-06 2 14 2 15 0.70915292279925D+00 -0.13508593651636D-16 3 14 2 15 0.11453501208804D+00 -0.36582976529199D-06 1 15 2 15 0.71163101684458D+01 -0.13903321095824D+00 2 15 2 15 0.14511487521270D+02 0.00000000000000D+00 3 15 2 15 -0.19810951837567D+01 -0.24729521639192D+00 1 16 2 15 0.36012575396470D+00 -0.57485669568051D-03 2 16 2 15 -0.89467395764157D+00 0.10552609969087D-02 3 16 2 15 0.59647116774059D+00 0.15822220767528D-01 1 17 2 15 -0.71901523276233D-02 -0.64680691296374D-04 2 17 2 15 0.70404622966180D-16 -0.14073042758146D-02 3 17 2 15 0.52015312565544D-01 0.10425068151978D-01 1 18 2 15 0.67715919531537D+00 -0.39970087055471D-02 2 18 2 15 -0.59319074231792D+00 0.10191869453764D-01 3 18 2 15 0.26281136448339D-01 -0.84309517833734D-04 1 19 2 15 0.21589756231115D+01 -0.41735635658017D-02 2 19 2 15 -0.68932005377593D+01 0.16494303264833D-16 3 19 2 15 -0.13936910002660D+00 0.33101839317914D-02 1 20 2 15 -0.92770841255380D+00 -0.16024586862245D-06 2 20 2 15 0.46151371802715D-14 -0.23241082067709D-07 3 20 2 15 0.19785367914050D+00 -0.16870516663266D-06 1 1 3 15 0.53793535376565D+00 0.17218116919835D-03 2 1 3 15 -0.23505711426167D+00 0.21136134881160D-03 3 1 3 15 0.45218019499643D+00 -0.13429359757153D-03 1 2 3 15 -0.88210296911926D+00 0.12263345485579D-02 2 2 3 15 0.45426285046141D+00 -0.31921345472061D-02 3 2 3 15 -0.27311368293530D-01 0.48749975928311D-06 1 3 3 15 -0.87229731747179D+00 0.11087385210480D-01 2 3 3 15 0.57330019971582D+00 -0.60569890989336D-02 3 3 3 15 0.69375072072496D+00 -0.12776078417228D-06 1 4 3 15 -0.37152320846467D+00 0.14970024958022D-01 2 4 3 15 0.87893240916706D+00 -0.16417684723865D-01 3 4 3 15 -0.21356746809927D+01 0.64518719928400D-02 1 5 3 15 -0.14256153319269D+00 0.18984854898019D-01 2 5 3 15 -0.31979338364590D+00 0.74730631846224D-02 3 5 3 15 0.28719852129376D+01 0.13816268237819D-01 1 6 3 15 -0.68445644208492D+00 -0.24609705990373D-01 2 6 3 15 -0.94450980494572D+00 -0.49306558978844D-02 3 6 3 15 -0.31913455621640D+01 -0.83731619352653D-02 1 7 3 15 0.81124461966951D-01 -0.39031612854896D-01 2 7 3 15 0.15591755126552D+00 -0.29754511771128D-01 3 7 3 15 0.32265073658011D+01 0.23559605926578D-01 1 8 3 15 0.69596597002012D+00 0.16195095029621D-01 2 8 3 15 0.86659694614990D+00 0.17054032197871D-01 3 8 3 15 -0.34292263390698D+01 -0.36210999367121D-02 1 9 3 15 -0.12472944190922D+01 -0.17510119224745D-01 2 9 3 15 -0.12135925753972D+01 -0.97443674449891D-02 3 9 3 15 -0.32589073730359D+01 -0.88352482724325D-01 1 10 3 15 -0.20859864215896D+01 0.14690242051909D-01 2 10 3 15 -0.10619468710813D+01 0.75971701552330D-02 3 10 3 15 0.16894989372113D+01 -0.24659193758378D-05 1 11 3 15 -0.13448842329276D+01 0.83173225262648D-02 2 11 3 15 -0.95903492959713D+00 0.38148153958625D-02 3 11 3 15 -0.15239622487681D+01 0.25908668518441D-01 1 12 3 15 0.96527559763944D+00 0.38063651834877D-02 2 12 3 15 0.16802883486709D+01 0.76536880282334D-02 3 12 3 15 -0.37129030726313D+01 -0.55580406339938D-06 1 13 3 15 0.19420996202345D-01 0.23289753098669D-01 2 13 3 15 -0.18380719447032D+00 0.10237317577535D-01 3 13 3 15 -0.46307096784144D+00 0.15019843926597D-15 1 14 3 15 0.62759339862232D-01 -0.22779958238029D-06 2 14 3 15 -0.11453501208804D+00 -0.36582976529199D-06 3 14 3 15 -0.17520321069576D+01 0.10672891943562D-14 1 15 3 15 0.12851833412149D+01 -0.17817987556316D+00 2 15 3 15 -0.19811208736035D+01 0.24729430122380D+00 3 15 3 15 0.15027371097683D+02 0.00000000000000D+00 1 16 3 15 0.71641649205775D+00 0.15828408045863D-01 2 16 3 15 0.59646955176477D+00 0.15822443951961D-01 3 16 3 15 0.32238387805641D+00 0.82757133623014D-03 1 17 3 15 -0.69597573774606D-01 0.11644810110962D-01 2 17 3 15 0.52015356245707D-01 -0.10425154650182D-01 3 17 3 15 -0.21069831960231D-13 0.15265542333761D-02 1 18 3 15 0.93794468913024D-02 -0.14465381142969D-02 2 18 3 15 -0.26278876546407D-01 0.84337482442200D-04 3 18 3 15 -0.73190121021800D+00 0.35296795122739D-02 1 19 3 15 0.36956654762328D-01 0.83818816840154D-02 2 19 3 15 -0.13936910002660D+00 -0.33101839317914D-02 3 19 3 15 0.15430748243887D+01 -0.21744619057425D-15 1 20 3 15 0.16804002707633D+01 0.20905318349519D-06 2 20 3 15 -0.19785367914050D+00 -0.16870516661184D-06 3 20 3 15 0.24311393059019D-13 -0.80739054110334D-07 1 1 1 16 0.13505994119705D+01 -0.72550054491436D-02 2 1 1 16 0.38251114594275D+00 0.68471011367693D-03 3 1 1 16 0.82118323636508D+00 0.68437938025419D-06 1 2 1 16 0.10413932964438D+01 0.21687425894968D-02 2 2 1 16 0.20608507553583D+00 -0.31656792789827D-03 3 2 1 16 -0.10799786650728D+01 -0.11528597573809D-02 1 3 1 16 -0.18132533007097D+01 0.47530769157252D-02 2 3 1 16 0.53612210623457D+00 -0.45155218654943D-02 3 3 1 16 -0.40884331380683D+00 -0.36635333128256D-02 1 4 1 16 -0.12026903628937D+01 -0.82154279193485D-02 2 4 1 16 -0.31248864877213D+00 0.53155363258256D-03 3 4 1 16 -0.14444766199700D+01 -0.14756602975997D-08 1 5 1 16 0.19362396073031D+01 0.11964887554200D-01 2 5 1 16 -0.59457960571176D-01 0.53575458752785D-02 3 5 1 16 0.43103011435940D+00 -0.27533992276416D-02 1 6 1 16 0.55578836778290D+01 -0.10032565449080D-01 2 6 1 16 -0.55080508470628D+00 -0.47058206966912D-02 3 6 1 16 0.69764104738227D+00 0.75154469464729D-01 1 7 1 16 -0.17794875236901D+01 -0.19166045915723D-01 2 7 1 16 -0.29515693224249D+00 -0.27555489500579D-01 3 7 1 16 0.21959540990301D+00 -0.16129721571361D-01 1 8 1 16 -0.50617432499133D+01 0.34881693369047D-02 2 8 1 16 0.63648666029955D+00 0.36009329416610D-03 3 8 1 16 0.80124576135854D+00 0.67820350195872D-01 1 9 1 16 0.64503548991630D+00 -0.29967134865110D-01 2 9 1 16 0.85390272525949D+00 -0.16940258999621D-01 3 9 1 16 -0.34640414696727D+01 0.13911557903685D-06 1 10 1 16 0.83973052237793D+00 0.12136267489985D-01 2 10 1 16 -0.57461793332309D+00 0.75318918695219D-02 3 10 1 16 -0.25421490654402D+01 0.92278078692358D-01 1 11 1 16 0.10580893994944D+01 0.36597420284049D-02 2 11 1 16 -0.47957436773314D+00 0.96862129538427D-02 3 11 1 16 0.22884251646869D+01 -0.19464124274442D-06 1 12 1 16 0.84858308199508D-01 0.95162401793026D-02 2 12 1 16 -0.91516509802234D+00 0.15177272222115D-01 3 12 1 16 -0.26814814780431D+01 -0.29395659937312D-01 1 13 1 16 0.15388288188003D+01 0.65392745337796D-16 2 13 1 16 0.72965505522404D+00 -0.36779492459503D-06 3 13 1 16 -0.62759339862234D-01 -0.22779958224645D-06 1 14 1 16 -0.73506087478142D-01 -0.86951517084865D-15 2 14 1 16 0.13243688489238D+00 0.27414411095337D-03 3 14 1 16 -0.19420996202354D-01 0.23289753098669D-01 1 15 1 16 0.66914053695301D+00 -0.31094867468310D-02 2 15 1 16 0.36012474597850D+00 -0.57432848977180D-03 3 15 1 16 0.71641648901979D+00 0.15828544427265D-01 1 16 1 16 0.15369761478101D+02 0.00000000000000D+00 2 16 1 16 0.71163047741877D+01 0.13903371760471D+00 3 16 1 16 0.12852033538845D+01 0.17818189147543D+00 1 17 1 16 0.14802253550499D+01 0.21198298160666D-02 2 17 1 16 -0.67715961460253D+00 0.39974976356836D-02 3 17 1 16 0.93827316446327D-02 -0.14470375306412D-02 1 18 1 16 -0.14703345099874D-14 -0.16078841618533D-02 2 18 1 16 -0.71895228811406D-02 0.64504261100605D-04 3 18 1 16 0.69597199524340D-01 0.11644500598344D-01 1 19 1 16 0.24785900807101D-14 -0.33271949118899D-06 2 19 1 16 -0.92770841255382D+00 0.16024586696132D-06 3 19 1 16 0.16804002707632D+01 -0.20905317872883D-06 1 20 1 16 0.32917986690431D+01 -0.57636024691524D-15 2 20 1 16 -0.21589756231115D+01 -0.41735635658018D-02 3 20 1 16 -0.36956654762326D-01 0.83818816840150D-02 1 1 2 16 0.81666076196984D+00 -0.21026794867860D-02 2 1 2 16 0.39743085092929D+00 -0.10315485055375D-01 3 1 2 16 -0.91963324317503D-01 -0.21945276641004D-06 1 2 2 16 0.83615108999652D+00 0.20828989450403D-02 2 2 2 16 -0.27225118200813D+00 -0.35497944298473D-03 3 2 2 16 -0.42674156748667D-01 -0.11388164245977D-02 1 3 2 16 -0.30117809923763D+00 -0.56316188352093D-02 2 3 2 16 -0.79186286634348D+00 0.81935811546452D-02 3 3 2 16 0.96222188575290D+00 0.16681063109044D-02 1 4 2 16 -0.10450540314164D+01 -0.21458121172632D-02 2 4 2 16 -0.11531177325465D+00 -0.12687788388843D-02 3 4 2 16 0.23803547453749D+00 -0.15358580463201D-06 1 5 2 16 0.83329143018954D+00 0.64728025028718D-02 2 5 2 16 -0.39726271758561D-01 -0.30007940843052D-02 3 5 2 16 -0.20553089582639D+00 -0.25769569991213D-02 1 6 2 16 0.17328707863207D+01 -0.86063586808162D-02 2 6 2 16 0.77551224241869D-01 0.22947561680982D-02 3 6 2 16 0.78918936688457D+00 0.67554363629039D-01 1 7 2 16 -0.90366178062741D+00 -0.33076193264513D-01 2 7 2 16 -0.18468895195533D+00 -0.15233242387269D-01 3 7 2 16 -0.26552653181972D+00 -0.41374279779799D-02 1 8 2 16 -0.26913011930786D+01 0.98995665567647D-02 2 8 2 16 -0.12512110340052D+01 0.12958961001165D-02 3 8 2 16 0.73183635481971D+00 0.90035483846342D-01 1 9 2 16 0.96903006575378D+00 -0.23745150991560D-01 2 9 2 16 0.19337201599433D+00 -0.68831483010558D-02 3 9 2 16 -0.21345880305997D+01 -0.14467656614876D-05 1 10 2 16 -0.47373420869615D-01 0.72039518971678D-02 2 10 2 16 -0.42039545619561D+00 -0.79760655183731D-03 3 10 2 16 -0.24736843662435D+01 0.80305452092080D-01 1 11 2 16 0.77547794034013D-01 0.77545064256822D-02 2 11 2 16 -0.49224197726734D+00 0.84630629951615D-02 3 11 2 16 0.30330790543789D+01 0.75576197159088D-06 1 12 2 16 -0.75734874106883D+00 0.13852106275151D-01 2 12 2 16 -0.94564695760793D+00 0.13326912347397D-01 3 12 2 16 -0.24740388935627D+01 -0.65954300175015D-01 1 13 2 16 0.72965505522404D+00 0.36779492458601D-06 2 13 2 16 0.70915292279926D+00 0.86783042232327D-16 3 13 2 16 0.11453501208804D+00 -0.36582976533913D-06 1 14 2 16 0.13243688489238D+00 -0.27414411095331D-03 2 14 2 16 -0.17109939588368D+00 -0.27481934829092D-15 3 14 2 16 0.18380719447032D+00 0.10237317577535D-01 1 15 2 16 0.36012575396470D+00 -0.57485669567980D-03 2 15 2 16 -0.89467395764157D+00 0.10552609969098D-02 3 15 2 16 0.59647116774059D+00 0.15822220767528D-01 1 16 2 16 0.71163101684454D+01 -0.13903321095824D+00 2 16 2 16 0.14511487521270D+02 0.00000000000000D+00 3 16 2 16 -0.19810951837566D+01 -0.24729521639192D+00 1 17 2 16 0.67715919531537D+00 -0.39970087055471D-02 2 17 2 16 -0.59319074231792D+00 0.10191869453764D-01 3 17 2 16 0.26281136448340D-01 -0.84309517833695D-04 1 18 2 16 -0.71901523276215D-02 -0.64680691296543D-04 2 18 2 16 0.86608975261345D-15 -0.14073042758146D-02 3 18 2 16 0.52015312565545D-01 0.10425068151978D-01 1 19 2 16 -0.92770841255382D+00 -0.16024587060869D-06 2 19 2 16 -0.61923551122786D-15 -0.23241084252773D-07 3 19 2 16 0.19785367914050D+00 -0.16870516738155D-06 1 20 2 16 0.21589756231115D+01 -0.41735635658018D-02 2 20 2 16 -0.68932005377594D+01 0.42450193614584D-16 3 20 2 16 -0.13936910002660D+00 0.33101839317915D-02 1 1 3 16 0.88210296911932D+00 -0.12263345485661D-02 2 1 3 16 -0.45426285046141D+00 0.31921345472135D-02 3 1 3 16 0.27311368293451D-01 -0.48749975364794D-06 1 2 3 16 -0.53793535376568D+00 -0.17218116919692D-03 2 2 3 16 0.23505711426170D+00 -0.21136134881401D-03 3 2 3 16 -0.45218019499651D+00 0.13429359757809D-03 1 3 3 16 -0.37152320846468D+00 0.14970024958021D-01 2 3 3 16 0.87893240916714D+00 -0.16417684723865D-01 3 3 3 16 -0.21356746809927D+01 0.64518719928417D-02 1 4 3 16 -0.87229731747185D+00 0.11087385210480D-01 2 4 3 16 0.57330019971585D+00 -0.60569890989332D-02 3 4 3 16 0.69375072072505D+00 -0.12776077929278D-06 1 5 3 16 0.14256153319272D+00 -0.18984854898020D-01 2 5 3 16 0.31979338364591D+00 -0.74730631846227D-02 3 5 3 16 -0.28719852129375D+01 -0.13816268237817D-01 1 6 3 16 0.68445644208534D+00 0.24609705990383D-01 2 6 3 16 0.94450980494592D+00 0.49306558978911D-02 3 6 3 16 0.31913455621638D+01 0.83731619352407D-02 1 7 3 16 0.81124461966963D-01 -0.39031612854894D-01 2 7 3 16 0.15591755126556D+00 -0.29754511771128D-01 3 7 3 16 0.32265073658012D+01 0.23559605926578D-01 1 8 3 16 0.69596597002008D+00 0.16195095029620D-01 2 8 3 16 0.86659694614985D+00 0.17054032197871D-01 3 8 3 16 -0.34292263390704D+01 -0.36210999367115D-02 1 9 3 16 -0.20859864215896D+01 0.14690242051901D-01 2 9 3 16 -0.10619468710813D+01 0.75971701552285D-02 3 9 3 16 0.16894989372113D+01 -0.24659193714616D-05 1 10 3 16 -0.12472944190923D+01 -0.17510119224745D-01 2 10 3 16 -0.12135925753972D+01 -0.97443674449892D-02 3 10 3 16 -0.32589073730359D+01 -0.88352482724327D-01 1 11 3 16 0.96527559763949D+00 0.38063651834879D-02 2 11 3 16 0.16802883486709D+01 0.76536880282334D-02 3 11 3 16 -0.37129030726314D+01 -0.55580406295355D-06 1 12 3 16 -0.13448842329276D+01 0.83173225262645D-02 2 12 3 16 -0.95903492959713D+00 0.38148153958626D-02 3 12 3 16 -0.15239622487681D+01 0.25908668518442D-01 1 13 3 16 0.62759339862234D-01 -0.22779958224558D-06 2 13 3 16 -0.11453501208804D+00 -0.36582976533913D-06 3 13 3 16 -0.17520321069576D+01 0.13810109940830D-14 1 14 3 16 0.19420996202340D-01 0.23289753098669D-01 2 14 3 16 -0.18380719447032D+00 0.10237317577535D-01 3 14 3 16 -0.46307096784144D+00 0.29165771691155D-16 1 15 3 16 0.71641649205775D+00 0.15828408045863D-01 2 15 3 16 0.59646955176477D+00 0.15822443951962D-01 3 15 3 16 0.32238387805641D+00 0.82757133622855D-03 1 16 3 16 0.12851833412153D+01 -0.17817987556316D+00 2 16 3 16 -0.19811208736033D+01 0.24729430122380D+00 3 16 3 16 0.15027371097683D+02 0.00000000000000D+00 1 17 3 16 0.93794468912930D-02 -0.14465381142967D-02 2 17 3 16 -0.26278876546407D-01 0.84337482442239D-04 3 17 3 16 -0.73190121021802D+00 0.35296795122740D-02 1 18 3 16 -0.69597573774590D-01 0.11644810110965D-01 2 18 3 16 0.52015356245708D-01 -0.10425154650182D-01 3 18 3 16 0.19570400983500D-13 0.15265542333777D-02 1 19 3 16 0.16804002707632D+01 0.20905318825267D-06 2 19 3 16 -0.19785367914050D+00 -0.16870516735726D-06 3 19 3 16 0.19655508301066D-13 -0.80739057505060D-07 1 20 3 16 0.36956654762330D-01 0.83818816840150D-02 2 20 3 16 -0.13936910002660D+00 -0.33101839317914D-02 3 20 3 16 0.15430748243888D+01 0.82293555681949D-16 1 1 1 17 0.18132533007096D+01 -0.47530769157263D-02 2 1 1 17 0.53612210623466D+00 -0.45155218654886D-02 3 1 1 17 0.40884331380708D+00 0.36635333128341D-02 1 2 1 17 0.12026903628937D+01 0.82154279193479D-02 2 2 1 17 -0.31248864877209D+00 0.53155363258469D-03 3 2 1 17 0.14444766199698D+01 0.14756525954353D-08 1 3 1 17 -0.13505994119705D+01 0.72550054491495D-02 2 3 1 17 0.38251114594275D+00 0.68471011368178D-03 3 3 1 17 -0.82118323636498D+00 -0.68437938828294D-06 1 4 1 17 -0.10413932964438D+01 -0.21687425894956D-02 2 4 1 17 0.20608507553585D+00 -0.31656792789778D-03 3 4 1 17 0.10799786650729D+01 0.11528597573831D-02 1 5 1 17 0.50617432499133D+01 -0.34881693369000D-02 2 5 1 17 0.63648666029938D+00 0.36009329414409D-03 3 5 1 17 -0.80124576135857D+00 -0.67820350195880D-01 1 6 1 17 0.17794875236901D+01 0.19166045915723D-01 2 6 1 17 -0.29515693224248D+00 -0.27555489500579D-01 3 6 1 17 -0.21959540990301D+00 0.16129721571363D-01 1 7 1 17 -0.55578836778291D+01 0.10032565449097D-01 2 7 1 17 -0.55080508470610D+00 -0.47058206967139D-02 3 7 1 17 -0.69764104738233D+00 -0.75154469464717D-01 1 8 1 17 -0.19362396073031D+01 -0.11964887554201D-01 2 8 1 17 -0.59457960571172D-01 0.53575458752783D-02 3 8 1 17 -0.43103011435941D+00 0.27533992276409D-02 1 9 1 17 -0.84858308199483D-01 -0.95162401793015D-02 2 9 1 17 -0.91516509802232D+00 0.15177272222113D-01 3 9 1 17 0.26814814780431D+01 0.29395659937315D-01 1 10 1 17 0.10580893994944D+01 0.36597420284042D-02 2 10 1 17 0.47957436773313D+00 -0.96862129538426D-02 3 10 1 17 0.22884251646869D+01 -0.19464124263626D-06 1 11 1 17 0.83973052237794D+00 0.12136267489987D-01 2 11 1 17 0.57461793332310D+00 -0.75318918695218D-02 3 11 1 17 -0.25421490654402D+01 0.92278078692358D-01 1 12 1 17 -0.64503548991626D+00 0.29967134865112D-01 2 12 1 17 0.85390272525951D+00 -0.16940258999623D-01 3 12 1 17 0.34640414696727D+01 -0.13911558243018D-06 1 13 1 17 0.32917986690431D+01 -0.40539807740207D-15 2 13 1 17 0.21589756231115D+01 0.41735635658018D-02 3 13 1 17 -0.36956654762326D-01 0.83818816840154D-02 1 14 1 17 -0.24756789293571D-14 0.33271950166135D-06 2 14 1 17 -0.92770841255380D+00 0.16024586667273D-06 3 14 1 17 -0.16804002707632D+01 0.20905317869939D-06 1 15 1 17 0.57170809961631D-14 0.16078841618552D-02 2 15 1 17 -0.71895228811423D-02 0.64504261100419D-04 3 15 1 17 -0.69597199524331D-01 -0.11644500598342D-01 1 16 1 17 0.14802253550499D+01 0.21198298160659D-02 2 16 1 17 0.67715961460253D+00 -0.39974976356836D-02 3 16 1 17 0.93827316446325D-02 -0.14470375306417D-02 1 17 1 17 0.15369761478102D+02 0.00000000000000D+00 2 17 1 17 -0.71163047741875D+01 -0.13903371760471D+00 3 17 1 17 0.12852033538846D+01 0.17818189147543D+00 1 18 1 17 -0.66914053695301D+00 0.31094867468319D-02 2 18 1 17 0.36012474597852D+00 -0.57432848977092D-03 3 18 1 17 -0.71641648901980D+00 -0.15828544427265D-01 1 19 1 17 0.73506087478142D-01 0.23223141148406D-15 2 19 1 17 0.13243688489239D+00 0.27414411095340D-03 3 19 1 17 0.19420996202345D-01 -0.23289753098669D-01 1 20 1 17 0.15388288188003D+01 -0.85664757815543D-16 2 20 1 17 -0.72965505522404D+00 0.36779492458769D-06 3 20 1 17 -0.62759339862234D-01 -0.22779958185500D-06 1 1 2 17 -0.30117809923754D+00 -0.56316188352035D-02 2 1 2 17 0.79186286634333D+00 -0.81935811546418D-02 3 1 2 17 0.96222188575302D+00 0.16681063109167D-02 1 2 2 17 -0.10450540314163D+01 -0.21458121172610D-02 2 2 2 17 0.11531177325463D+00 0.12687788388830D-02 3 2 2 17 0.23803547453741D+00 -0.15358581004368D-06 1 3 2 17 0.81666076196984D+00 -0.21026794867811D-02 2 3 2 17 -0.39743085092921D+00 0.10315485055378D-01 3 3 2 17 -0.91963324317481D-01 -0.21945277375649D-06 1 4 2 17 0.83615108999653D+00 0.20828989450408D-02 2 4 2 17 0.27225118200813D+00 0.35497944298604D-03 3 4 2 17 -0.42674156748628D-01 -0.11388164245952D-02 1 5 2 17 -0.26913011930788D+01 0.98995665567427D-02 2 5 2 17 0.12512110340052D+01 -0.12958961000945D-02 3 5 2 17 0.73183635481973D+00 0.90035483846351D-01 1 6 2 17 -0.90366178062741D+00 -0.33076193264513D-01 2 6 2 17 0.18468895195534D+00 0.15233242387269D-01 3 6 2 17 -0.26552653181972D+00 -0.41374279779811D-02 1 7 2 17 0.17328707863209D+01 -0.86063586808389D-02 2 7 2 17 -0.77551224241763D-01 -0.22947561680928D-02 3 7 2 17 0.78918936688461D+00 0.67554363629032D-01 1 8 2 17 0.83329143018954D+00 0.64728025028716D-02 2 8 2 17 0.39726271758569D-01 0.30007940843056D-02 3 8 2 17 -0.20553089582639D+00 -0.25769569991205D-02 1 9 2 17 -0.75734874106881D+00 0.13852106275148D-01 2 9 2 17 0.94564695760792D+00 -0.13326912347395D-01 3 9 2 17 -0.24740388935626D+01 -0.65954300175018D-01 1 10 2 17 -0.77547794034025D-01 -0.77545064256821D-02 2 10 2 17 -0.49224197726740D+00 0.84630629951606D-02 3 10 2 17 -0.30330790543789D+01 -0.75576197147776D-06 1 11 2 17 0.47373420869628D-01 -0.72039518971677D-02 2 11 2 17 -0.42039545619565D+00 -0.79760655183700D-03 3 11 2 17 0.24736843662435D+01 -0.80305452092080D-01 1 12 2 17 0.96903006575380D+00 -0.23745150991562D-01 2 12 2 17 -0.19337201599432D+00 0.68831483010555D-02 3 12 2 17 -0.21345880305997D+01 -0.14467656590141D-05 1 13 2 17 -0.21589756231115D+01 0.41735635658018D-02 2 13 2 17 -0.68932005377594D+01 0.77820343043226D-16 3 13 2 17 0.13936910002660D+00 -0.33101839317915D-02 1 14 2 17 -0.92770841255380D+00 -0.16024587089727D-06 2 14 2 17 0.66136079515909D-14 0.23241082212542D-07 3 14 2 17 0.19785367914049D+00 -0.16870516660102D-06 1 15 2 17 -0.71901523276235D-02 -0.64680691296729D-04 2 15 2 17 0.70404622966180D-16 0.14073042758146D-02 3 15 2 17 0.52015312565544D-01 0.10425068151978D-01 1 16 2 17 -0.67715919531537D+00 0.39970087055471D-02 2 16 2 17 -0.59319074231792D+00 0.10191869453764D-01 3 16 2 17 -0.26281136448345D-01 0.84309517833695D-04 1 17 2 17 -0.71163101684452D+01 0.13903321095824D+00 2 17 2 17 0.14511487521269D+02 0.00000000000000D+00 3 17 2 17 0.19810951837565D+01 0.24729521639192D+00 1 18 2 17 0.36012575396471D+00 -0.57485669567892D-03 2 18 2 17 0.89467395764156D+00 -0.10552609969076D-02 3 18 2 17 0.59647116774059D+00 0.15822220767527D-01 1 19 2 17 0.13243688489239D+00 -0.27414411095328D-03 2 19 2 17 0.17109939588368D+00 0.25118340070874D-16 3 19 2 17 0.18380719447032D+00 0.10237317577535D-01 1 20 2 17 -0.72965505522404D+00 -0.36779492459334D-06 2 20 2 17 0.70915292279925D+00 -0.49145181152778D-17 3 20 2 17 -0.11453501208804D+00 0.36582976543344D-06 1 1 3 17 0.37152320846494D+00 -0.14970024958012D-01 2 1 3 17 0.87893240916726D+00 -0.16417684723853D-01 3 1 3 17 0.21356746809929D+01 -0.64518719928322D-02 1 2 3 17 0.87229731747169D+00 -0.11087385210488D-01 2 2 3 17 0.57330019971577D+00 -0.60569890989386D-02 3 2 3 17 -0.69375072072487D+00 0.12776079630561D-06 1 3 3 17 -0.88210296911922D+00 0.12263345485581D-02 2 3 3 17 -0.45426285046139D+00 0.31921345472062D-02 3 3 3 17 -0.27311368293516D-01 0.48749976244803D-06 1 4 3 17 0.53793535376571D+00 0.17218116919913D-03 2 4 3 17 0.23505711426174D+00 -0.21136134881146D-03 3 4 3 17 0.45218019499657D+00 -0.13429359757222D-03 1 5 3 17 -0.69596597002010D+00 -0.16195095029629D-01 2 5 3 17 0.86659694614989D+00 0.17054032197880D-01 3 5 3 17 0.34292263390703D+01 0.36210999366896D-02 1 6 3 17 -0.81124461966965D-01 0.39031612854896D-01 2 6 3 17 0.15591755126556D+00 -0.29754511771130D-01 3 6 3 17 -0.32265073658012D+01 -0.23559605926573D-01 1 7 3 17 -0.68445644208540D+00 -0.24609705990371D-01 2 7 3 17 0.94450980494594D+00 0.49306558978846D-02 3 7 3 17 -0.31913455621636D+01 -0.83731619352642D-02 1 8 3 17 -0.14256153319273D+00 0.18984854898020D-01 2 8 3 17 0.31979338364592D+00 -0.74730631846220D-02 3 8 3 17 0.28719852129375D+01 0.13816268237820D-01 1 9 3 17 0.13448842329276D+01 -0.83173225262616D-02 2 9 3 17 -0.95903492959707D+00 0.38148153958595D-02 3 9 3 17 0.15239622487681D+01 -0.25908668518441D-01 1 10 3 17 0.96527559763944D+00 0.38063651834880D-02 2 10 3 17 -0.16802883486709D+01 -0.76536880282333D-02 3 10 3 17 -0.37129030726312D+01 -0.55580406183199D-06 1 11 3 17 -0.12472944190922D+01 -0.17510119224745D-01 2 11 3 17 0.12135925753972D+01 0.97443674449890D-02 3 11 3 17 -0.32589073730358D+01 -0.88352482724324D-01 1 12 3 17 0.20859864215896D+01 -0.14690242051904D-01 2 12 3 17 -0.10619468710813D+01 0.75971701552310D-02 3 12 3 17 -0.16894989372113D+01 0.24659193740862D-05 1 13 3 17 0.36956654762330D-01 0.83818816840154D-02 2 13 3 17 0.13936910002660D+00 0.33101839317914D-02 3 13 3 17 0.15430748243887D+01 -0.28844551848866D-16 1 14 3 17 -0.16804002707632D+01 -0.20905318828211D-06 2 14 3 17 -0.19785367914050D+00 -0.16870516657499D-06 3 14 3 17 0.20315112519999D-13 0.80739054088816D-07 1 15 3 17 0.69597573774598D-01 -0.11644810110962D-01 2 15 3 17 0.52015356245707D-01 -0.10425154650182D-01 3 15 3 17 -0.21069831960231D-13 -0.15265542333761D-02 1 16 3 17 0.93794468912927D-02 -0.14465381142972D-02 2 16 3 17 0.26278876546401D-01 -0.84337482442239D-04 3 16 3 17 -0.73190121021802D+00 0.35296795122743D-02 1 17 3 17 0.12851833412154D+01 -0.17817987556316D+00 2 17 3 17 0.19811208736033D+01 -0.24729430122380D+00 3 17 3 17 0.15027371097683D+02 0.00000000000000D+00 1 18 3 17 -0.71641649205775D+00 -0.15828408045863D-01 2 18 3 17 0.59646955176477D+00 0.15822443951961D-01 3 18 3 17 -0.32238387805641D+00 -0.82757133622994D-03 1 19 3 17 -0.19420996202349D-01 -0.23289753098669D-01 2 19 3 17 -0.18380719447032D+00 0.10237317577535D-01 3 19 3 17 0.46307096784142D+00 0.12109169790195D-15 1 20 3 17 0.62759339862234D-01 -0.22779958185413D-06 2 20 3 17 0.11453501208804D+00 0.36582976543344D-06 3 20 3 17 -0.17520321069576D+01 -0.19592955708604D-14 1 1 1 18 -0.12026903628936D+01 -0.82154279193466D-02 2 1 1 18 0.31248864877211D+00 -0.53155363258309D-03 3 1 1 18 -0.14444766199701D+01 -0.14756595536311D-08 1 2 1 18 -0.18132533007096D+01 0.47530769157231D-02 2 2 1 18 -0.53612210623461D+00 0.45155218654945D-02 3 2 1 18 -0.40884331380694D+00 -0.36635333128252D-02 1 3 1 18 -0.10413932964438D+01 -0.21687425894956D-02 2 3 1 18 0.20608507553584D+00 -0.31656792789625D-03 3 3 1 18 0.10799786650729D+01 0.11528597573835D-02 1 4 1 18 -0.13505994119705D+01 0.72550054491455D-02 2 4 1 18 0.38251114594272D+00 0.68471011368214D-03 3 4 1 18 -0.82118323636496D+00 -0.68437938907365D-06 1 5 1 18 -0.50617432499133D+01 0.34881693369051D-02 2 5 1 18 -0.63648666029930D+00 -0.36009329416609D-03 3 5 1 18 0.80124576135850D+00 0.67820350195874D-01 1 6 1 18 -0.17794875236901D+01 -0.19166045915724D-01 2 6 1 18 0.29515693224249D+00 0.27555489500578D-01 3 6 1 18 0.21959540990297D+00 -0.16129721571364D-01 1 7 1 18 -0.55578836778290D+01 0.10032565449094D-01 2 7 1 18 -0.55080508470631D+00 -0.47058206967148D-02 3 7 1 18 -0.69764104738196D+00 -0.75154469464719D-01 1 8 1 18 -0.19362396073031D+01 -0.11964887554202D-01 2 8 1 18 -0.59457960571167D-01 0.53575458752783D-02 3 8 1 18 -0.43103011435933D+00 0.27533992276405D-02 1 9 1 18 0.10580893994944D+01 0.36597420284044D-02 2 9 1 18 0.47957436773312D+00 -0.96862129538429D-02 3 9 1 18 0.22884251646869D+01 -0.19464124322560D-06 1 10 1 18 -0.84858308199530D-01 -0.95162401793029D-02 2 10 1 18 -0.91516509802234D+00 0.15177272222117D-01 3 10 1 18 0.26814814780431D+01 0.29395659937308D-01 1 11 1 18 -0.64503548991630D+00 0.29967134865111D-01 2 11 1 18 0.85390272525951D+00 -0.16940258999623D-01 3 11 1 18 0.34640414696727D+01 -0.13911558407521D-06 1 12 1 18 0.83973052237793D+00 0.12136267489987D-01 2 12 1 18 0.57461793332309D+00 -0.75318918695219D-02 3 12 1 18 -0.25421490654402D+01 0.92278078692359D-01 1 13 1 18 -0.55150388700688D-14 0.33271949170871D-06 2 13 1 18 -0.92770841255382D+00 0.16024586878248D-06 3 13 1 18 -0.16804002707632D+01 0.20905318432910D-06 1 14 1 18 0.32917986690431D+01 -0.22169625675903D-15 2 14 1 18 0.21589756231115D+01 0.41735635658018D-02 3 14 1 18 -0.36956654762335D-01 0.83818816840154D-02 1 15 1 18 0.14802253550499D+01 0.21198298160663D-02 2 15 1 18 0.67715961460253D+00 -0.39974976356836D-02 3 15 1 18 0.93827316446420D-02 -0.14470375306415D-02 1 16 1 18 -0.14703345099874D-14 0.16078841618533D-02 2 16 1 18 -0.71895228811406D-02 0.64504261100588D-04 3 16 1 18 -0.69597199524316D-01 -0.11644500598344D-01 1 17 1 18 -0.66914053695301D+00 0.31094867468304D-02 2 17 1 18 0.36012474597852D+00 -0.57432848977339D-03 3 17 1 18 -0.71641648901980D+00 -0.15828544427265D-01 1 18 1 18 0.15369761478102D+02 0.00000000000000D+00 2 18 1 18 -0.71163047741879D+01 -0.13903371760471D+00 3 18 1 18 0.12852033538843D+01 0.17818189147543D+00 1 19 1 18 0.15388288188003D+01 0.33844618730430D-15 2 19 1 18 -0.72965505522404D+00 0.36779492460069D-06 3 19 1 18 -0.62759339862227D-01 -0.22779958230596D-06 1 20 1 18 0.73506087478148D-01 0.61980359578466D-15 2 20 1 18 0.13243688489239D+00 0.27414411095333D-03 3 20 1 18 0.19420996202360D-01 -0.23289753098669D-01 1 1 2 18 0.10450540314164D+01 0.21458121172627D-02 2 1 2 18 -0.11531177325472D+00 -0.12687788388845D-02 3 1 2 18 -0.23803547453742D+00 0.15358580473029D-06 1 2 2 18 0.30117809923759D+00 0.56316188352095D-02 2 2 2 18 -0.79186286634346D+00 0.81935811546455D-02 3 2 2 18 -0.96222188575296D+00 -0.16681063109043D-02 1 3 2 18 0.83615108999652D+00 0.20828989450423D-02 2 3 2 18 0.27225118200813D+00 0.35497944298579D-03 3 3 2 18 -0.42674156748635D-01 -0.11388164245955D-02 1 4 2 18 0.81666076196981D+00 -0.21026794867808D-02 2 4 2 18 -0.39743085092921D+00 0.10315485055378D-01 3 4 2 18 -0.91963324317431D-01 -0.21945277362213D-06 1 5 2 18 0.26913011930788D+01 -0.98995665567647D-02 2 5 2 18 -0.12512110340054D+01 0.12958961001168D-02 3 5 2 18 -0.73183635481966D+00 -0.90035483846342D-01 1 6 2 18 0.90366178062742D+00 0.33076193264512D-01 2 6 2 18 -0.18468895195533D+00 -0.15233242387268D-01 3 6 2 18 0.26552653181976D+00 0.41374279779802D-02 1 7 2 18 0.17328707863207D+01 -0.86063586808398D-02 2 7 2 18 -0.77551224241976D-01 -0.22947561680925D-02 3 7 2 18 0.78918936688442D+00 0.67554363629032D-01 1 8 2 18 0.83329143018955D+00 0.64728025028716D-02 2 8 2 18 0.39726271758558D-01 0.30007940843052D-02 3 8 2 18 -0.20553089582641D+00 -0.25769569991210D-02 1 9 2 18 -0.77547794034034D-01 -0.77545064256824D-02 2 9 2 18 -0.49224197726739D+00 0.84630629951610D-02 3 9 2 18 -0.30330790543789D+01 -0.75576197140786D-06 1 10 2 18 -0.75734874106883D+00 0.13852106275153D-01 2 10 2 18 0.94564695760794D+00 -0.13326912347398D-01 3 10 2 18 -0.24740388935627D+01 -0.65954300175012D-01 1 11 2 18 0.96903006575380D+00 -0.23745150991562D-01 2 11 2 18 -0.19337201599427D+00 0.68831483010554D-02 3 11 2 18 -0.21345880305997D+01 -0.14467656594135D-05 1 12 2 18 0.47373420869612D-01 -0.72039518971679D-02 2 12 2 18 -0.42039545619561D+00 -0.79760655183756D-03 3 12 2 18 0.24736843662435D+01 -0.80305452092080D-01 1 13 2 18 -0.92770841255382D+00 -0.16024586878753D-06 2 13 2 18 -0.61924955690595D-15 0.23241084394102D-07 3 13 2 18 0.19785367914050D+00 -0.16870516740641D-06 1 14 2 18 -0.21589756231115D+01 0.41735635658018D-02 2 14 2 18 -0.68932005377593D+01 0.21354660230616D-16 3 14 2 18 0.13936910002660D+00 -0.33101839317914D-02 1 15 2 18 -0.67715919531537D+00 0.39970087055471D-02 2 15 2 18 -0.59319074231792D+00 0.10191869453765D-01 3 15 2 18 -0.26281136448346D-01 0.84309517833734D-04 1 16 2 18 -0.71901523276217D-02 -0.64680691296559D-04 2 16 2 18 0.86608975261345D-15 0.14073042758146D-02 3 16 2 18 0.52015312565545D-01 0.10425068151978D-01 1 17 2 18 0.36012575396471D+00 -0.57485669568139D-03 2 17 2 18 0.89467395764156D+00 -0.10552609969109D-02 3 17 2 18 0.59647116774059D+00 0.15822220767528D-01 1 18 2 18 -0.71163101684456D+01 0.13903321095824D+00 2 18 2 18 0.14511487521270D+02 0.00000000000000D+00 3 18 2 18 0.19810951837566D+01 0.24729521639192D+00 1 19 2 18 -0.72965505522404D+00 -0.36779492458034D-06 2 19 2 18 0.70915292279925D+00 -0.17363331848808D-15 3 19 2 18 -0.11453501208804D+00 0.36582976526570D-06 1 20 2 18 0.13243688489239D+00 -0.27414411095335D-03 2 20 2 18 0.17109939588368D+00 0.64312665356527D-16 3 20 2 18 0.18380719447032D+00 0.10237317577535D-01 1 1 3 18 -0.87229731747195D+00 0.11087385210481D-01 2 1 3 18 -0.57330019971578D+00 0.60569890989333D-02 3 1 3 18 0.69375072072499D+00 -0.12776078107689D-06 1 2 3 18 -0.37152320846480D+00 0.14970024958021D-01 2 2 3 18 -0.87893240916720D+00 0.16417684723865D-01 3 2 3 18 -0.21356746809926D+01 0.64518719928414D-02 1 3 3 18 0.53793535376571D+00 0.17218116919955D-03 2 3 3 18 0.23505711426173D+00 -0.21136134881176D-03 3 3 3 18 0.45218019499651D+00 -0.13429359757442D-03 1 4 3 18 -0.88210296911919D+00 0.12263345485573D-02 2 4 3 18 -0.45426285046134D+00 0.31921345472063D-02 3 4 3 18 -0.27311368293494D-01 0.48749975850104D-06 1 5 3 18 0.69596597002003D+00 0.16195095029622D-01 2 5 3 18 -0.86659694614982D+00 -0.17054032197871D-01 3 5 3 18 -0.34292263390702D+01 -0.36210999367127D-02 1 6 3 18 0.81124461966922D-01 -0.39031612854897D-01 2 6 3 18 -0.15591755126553D+00 0.29754511771129D-01 3 6 3 18 0.32265073658012D+01 0.23559605926579D-01 1 7 3 18 -0.68445644208504D+00 -0.24609705990373D-01 2 7 3 18 0.94450980494575D+00 0.49306558978843D-02 3 7 3 18 -0.31913455621638D+01 -0.83731619352637D-02 1 8 3 18 -0.14256153319265D+00 0.18984854898019D-01 2 8 3 18 0.31979338364590D+00 -0.74730631846225D-02 3 8 3 18 0.28719852129376D+01 0.13816268237820D-01 1 9 3 18 0.96527559763942D+00 0.38063651834875D-02 2 9 3 18 -0.16802883486709D+01 -0.76536880282332D-02 3 9 3 18 -0.37129030726314D+01 -0.55580406329637D-06 1 10 3 18 0.13448842329276D+01 -0.83173225262680D-02 2 10 3 18 -0.95903492959713D+00 0.38148153958658D-02 3 10 3 18 0.15239622487681D+01 -0.25908668518444D-01 1 11 3 18 0.20859864215897D+01 -0.14690242051906D-01 2 11 3 18 -0.10619468710813D+01 0.75971701552306D-02 3 11 3 18 -0.16894989372113D+01 0.24659193733495D-05 1 12 3 18 -0.12472944190923D+01 -0.17510119224744D-01 2 12 3 18 0.12135925753972D+01 0.97443674449892D-02 3 12 3 18 -0.32589073730359D+01 -0.88352482724326D-01 1 13 3 18 -0.16804002707632D+01 -0.20905318265240D-06 2 13 3 18 -0.19785367914050D+00 -0.16870516738386D-06 3 13 3 18 -0.12319030388348D-13 0.80739057440933D-07 1 14 3 18 0.36956654762321D-01 0.83818816840154D-02 2 14 3 18 0.13936910002660D+00 0.33101839317915D-02 3 14 3 18 0.15430748243887D+01 -0.95725637483525D-16 1 15 3 18 0.93794468913020D-02 -0.14465381142970D-02 2 15 3 18 0.26278876546401D-01 -0.84337482442200D-04 3 15 3 18 -0.73190121021800D+00 0.35296795122744D-02 1 16 3 18 0.69597573774614D-01 -0.11644810110965D-01 2 16 3 18 0.52015356245708D-01 -0.10425154650182D-01 3 16 3 18 0.19570400983500D-13 -0.15265542333777D-02 1 17 3 18 -0.71641649205775D+00 -0.15828408045863D-01 2 17 3 18 0.59646955176477D+00 0.15822443951962D-01 3 17 3 18 -0.32238387805641D+00 -0.82757133622876D-03 1 18 3 18 0.12851833412152D+01 -0.17817987556316D+00 2 18 3 18 0.19811208736033D+01 -0.24729430122380D+00 3 18 3 18 0.15027371097683D+02 0.00000000000000D+00 1 19 3 18 0.62759339862241D-01 -0.22779958230509D-06 2 19 3 18 0.11453501208804D+00 0.36582976526570D-06 3 19 3 18 -0.17520321069576D+01 -0.56264328654196D-15 1 20 3 18 -0.19420996202335D-01 -0.23289753098669D-01 2 20 3 18 -0.18380719447032D+00 0.10237317577535D-01 3 20 3 18 0.46307096784143D+00 -0.11186149552219D-14 1 1 1 19 -0.12026903628936D+01 -0.82154279193466D-02 2 1 1 19 0.31248864877211D+00 -0.53155363258263D-03 3 1 1 19 0.14444766199700D+01 0.14756589229224D-08 1 2 1 19 -0.18132533007096D+01 0.47530769157247D-02 2 2 1 19 -0.53612210623457D+00 0.45155218654944D-02 3 2 1 19 0.40884331380687D+00 0.36635333128249D-02 1 3 1 19 -0.10413932964438D+01 -0.21687425894951D-02 2 3 1 19 0.20608507553585D+00 -0.31656792789709D-03 3 3 1 19 -0.10799786650729D+01 -0.11528597573829D-02 1 4 1 19 -0.13505994119705D+01 0.72550054491446D-02 2 4 1 19 0.38251114594275D+00 0.68471011368218D-03 3 4 1 19 0.82118323636499D+00 0.68437938948341D-06 1 5 1 19 -0.17794875236900D+01 -0.19166045915724D-01 2 5 1 19 0.29515693224249D+00 0.27555489500578D-01 3 5 1 19 -0.21959540990299D+00 0.16129721571363D-01 1 6 1 19 -0.50617432499133D+01 0.34881693369036D-02 2 6 1 19 -0.63648666029923D+00 -0.36009329416588D-03 3 6 1 19 -0.80124576135849D+00 -0.67820350195872D-01 1 7 1 19 -0.19362396073031D+01 -0.11964887554201D-01 2 7 1 19 -0.59457960571177D-01 0.53575458752781D-02 3 7 1 19 0.43103011435938D+00 -0.27533992276408D-02 1 8 1 19 -0.55578836778290D+01 0.10032565449095D-01 2 8 1 19 -0.55080508470623D+00 -0.47058206967148D-02 3 8 1 19 0.69764104738192D+00 0.75154469464719D-01 1 9 1 19 0.10580893994944D+01 0.36597420284048D-02 2 9 1 19 0.47957436773311D+00 -0.96862129538428D-02 3 9 1 19 -0.22884251646869D+01 0.19464124282918D-06 1 10 1 19 -0.84858308199512D-01 -0.95162401793017D-02 2 10 1 19 -0.91516509802233D+00 0.15177272222117D-01 3 10 1 19 -0.26814814780431D+01 -0.29395659937308D-01 1 11 1 19 -0.64503548991628D+00 0.29967134865110D-01 2 11 1 19 0.85390272525949D+00 -0.16940258999623D-01 3 11 1 19 -0.34640414696727D+01 0.13911558403724D-06 1 12 1 19 0.83973052237793D+00 0.12136267489987D-01 2 12 1 19 0.57461793332309D+00 -0.75318918695219D-02 3 12 1 19 0.25421490654402D+01 -0.92278078692358D-01 1 13 1 19 -0.85896396553962D-14 0.16078841618535D-02 2 13 1 19 -0.71895228811411D-02 0.64504261100692D-04 3 13 1 19 0.69597199524325D-01 0.11644500598342D-01 1 14 1 19 0.14802253550499D+01 0.21198298160655D-02 2 14 1 19 0.67715961460253D+00 -0.39974976356836D-02 3 14 1 19 -0.93827316446339D-02 0.14470375306415D-02 1 15 1 19 0.32917986690431D+01 0.29711754721984D-15 2 15 1 19 0.21589756231115D+01 0.41735635658017D-02 3 15 1 19 0.36956654762328D-01 -0.83818816840154D-02 1 16 1 19 0.24785900807101D-14 0.33271949118899D-06 2 16 1 19 -0.92770841255382D+00 0.16024586869095D-06 3 16 1 19 0.16804002707632D+01 -0.20905318390198D-06 1 17 1 19 0.73506087478142D-01 -0.23223141148406D-15 2 17 1 19 0.13243688489239D+00 0.27414411095328D-03 3 17 1 19 -0.19420996202349D-01 0.23289753098669D-01 1 18 1 19 0.15388288188003D+01 -0.33844618730430D-15 2 18 1 19 -0.72965505522404D+00 0.36779492458034D-06 3 18 1 19 0.62759339862241D-01 0.22779958230509D-06 1 19 1 19 0.15369761478102D+02 0.00000000000000D+00 2 19 1 19 -0.71163047741878D+01 -0.13903371760471D+00 3 19 1 19 -0.12852033538843D+01 -0.17818189147543D+00 1 20 1 19 -0.66914053695299D+00 0.31094867468288D-02 2 20 1 19 0.36012474597855D+00 -0.57432848977298D-03 3 20 1 19 0.71641648901980D+00 0.15828544427265D-01 1 1 2 19 0.10450540314164D+01 0.21458121172631D-02 2 1 2 19 -0.11531177325472D+00 -0.12687788388846D-02 3 1 2 19 0.23803547453743D+00 -0.15358580449686D-06 1 2 2 19 0.30117809923765D+00 0.56316188352094D-02 2 2 2 19 -0.79186286634342D+00 0.81935811546455D-02 3 2 2 19 0.96222188575287D+00 0.16681063109045D-02 1 3 2 19 0.83615108999652D+00 0.20828989450415D-02 2 3 2 19 0.27225118200814D+00 0.35497944298624D-03 3 3 2 19 0.42674156748628D-01 0.11388164245954D-02 1 4 2 19 0.81666076196986D+00 -0.21026794867807D-02 2 4 2 19 -0.39743085092919D+00 0.10315485055377D-01 3 4 2 19 0.91963324317438D-01 0.21945277335652D-06 1 5 2 19 0.90366178062741D+00 0.33076193264512D-01 2 5 2 19 -0.18468895195533D+00 -0.15233242387268D-01 3 5 2 19 -0.26552653181976D+00 -0.41374279779802D-02 1 6 2 19 0.26913011930789D+01 -0.98995665567645D-02 2 6 2 19 -0.12512110340054D+01 0.12958961001170D-02 3 6 2 19 0.73183635481968D+00 0.90035483846342D-01 1 7 2 19 0.83329143018954D+00 0.64728025028715D-02 2 7 2 19 0.39726271758558D-01 0.30007940843051D-02 3 7 2 19 0.20553089582641D+00 0.25769569991210D-02 1 8 2 19 0.17328707863208D+01 -0.86063586808398D-02 2 8 2 19 -0.77551224241979D-01 -0.22947561680937D-02 3 8 2 19 -0.78918936688443D+00 -0.67554363629032D-01 1 9 2 19 -0.77547794034041D-01 -0.77545064256823D-02 2 9 2 19 -0.49224197726739D+00 0.84630629951611D-02 3 9 2 19 0.30330790543789D+01 0.75576197150860D-06 1 10 2 19 -0.75734874106880D+00 0.13852106275153D-01 2 10 2 19 0.94564695760794D+00 -0.13326912347399D-01 3 10 2 19 0.24740388935627D+01 0.65954300175012D-01 1 11 2 19 0.96903006575378D+00 -0.23745150991562D-01 2 11 2 19 -0.19337201599428D+00 0.68831483010556D-02 3 11 2 19 0.21345880305997D+01 0.14467656595019D-05 1 12 2 19 0.47373420869617D-01 -0.72039518971678D-02 2 12 2 19 -0.42039545619561D+00 -0.79760655183740D-03 3 12 2 19 -0.24736843662435D+01 0.80305452092080D-01 1 13 2 19 -0.71901523276219D-02 -0.64680691296456D-04 2 13 2 19 -0.91373653373876D-15 0.14073042758145D-02 3 13 2 19 -0.52015312565545D-01 -0.10425068151977D-01 1 14 2 19 -0.67715919531537D+00 0.39970087055471D-02 2 14 2 19 -0.59319074231792D+00 0.10191869453765D-01 3 14 2 19 0.26281136448344D-01 -0.84309517833783D-04 1 15 2 19 -0.21589756231115D+01 0.41735635658017D-02 2 15 2 19 -0.68932005377593D+01 -0.16494303264833D-16 3 15 2 19 -0.13936910002660D+00 0.33101839317914D-02 1 16 2 19 -0.92770841255382D+00 -0.16024586887906D-06 2 16 2 19 -0.61923551122786D-15 0.23241084252773D-07 3 16 2 19 -0.19785367914050D+00 0.16870516738328D-06 1 17 2 19 0.13243688489239D+00 -0.27414411095340D-03 2 17 2 19 0.17109939588368D+00 -0.25118340070874D-16 3 17 2 19 -0.18380719447032D+00 -0.10237317577535D-01 1 18 2 19 -0.72965505522404D+00 -0.36779492460069D-06 2 18 2 19 0.70915292279925D+00 0.17363331848808D-15 3 18 2 19 0.11453501208804D+00 -0.36582976526570D-06 1 19 2 19 -0.71163101684455D+01 0.13903321095824D+00 2 19 2 19 0.14511487521269D+02 0.00000000000000D+00 3 19 2 19 -0.19810951837566D+01 -0.24729521639192D+00 1 20 2 19 0.36012575396474D+00 -0.57485669568098D-03 2 20 2 19 0.89467395764158D+00 -0.10552609969112D-02 3 20 2 19 -0.59647116774058D+00 -0.15822220767528D-01 1 1 3 19 0.87229731747185D+00 -0.11087385210481D-01 2 1 3 19 0.57330019971579D+00 -0.60569890989331D-02 3 1 3 19 0.69375072072507D+00 -0.12776078206891D-06 1 2 3 19 0.37152320846471D+00 -0.14970024958021D-01 2 2 3 19 0.87893240916711D+00 -0.16417684723865D-01 3 2 3 19 -0.21356746809927D+01 0.64518719928424D-02 1 3 3 19 -0.53793535376573D+00 -0.17218116919896D-03 2 3 3 19 -0.23505711426173D+00 0.21136134881164D-03 3 3 3 19 0.45218019499650D+00 -0.13429359757516D-03 1 4 3 19 0.88210296911925D+00 -0.12263345485569D-02 2 4 3 19 0.45426285046136D+00 -0.31921345472066D-02 3 4 3 19 -0.27311368293551D-01 0.48749976104605D-06 1 5 3 19 -0.81124461966944D-01 0.39031612854896D-01 2 5 3 19 0.15591755126552D+00 -0.29754511771129D-01 3 5 3 19 0.32265073658012D+01 0.23559605926578D-01 1 6 3 19 -0.69596597002003D+00 -0.16195095029620D-01 2 6 3 19 0.86659694614983D+00 0.17054032197871D-01 3 6 3 19 -0.34292263390701D+01 -0.36210999367134D-02 1 7 3 19 0.14256153319270D+00 -0.18984854898019D-01 2 7 3 19 -0.31979338364590D+00 0.74730631846225D-02 3 7 3 19 0.28719852129375D+01 0.13816268237820D-01 1 8 3 19 0.68445644208499D+00 0.24609705990373D-01 2 8 3 19 -0.94450980494576D+00 -0.49306558978847D-02 3 8 3 19 -0.31913455621638D+01 -0.83731619352636D-02 1 9 3 19 -0.96527559763942D+00 -0.38063651834879D-02 2 9 3 19 0.16802883486709D+01 0.76536880282333D-02 3 9 3 19 -0.37129030726313D+01 -0.55580406428666D-06 1 10 3 19 -0.13448842329276D+01 0.83173225262681D-02 2 10 3 19 0.95903492959712D+00 -0.38148153958658D-02 3 10 3 19 0.15239622487682D+01 -0.25908668518443D-01 1 11 3 19 -0.20859864215897D+01 0.14690242051906D-01 2 11 3 19 0.10619468710813D+01 -0.75971701552305D-02 3 11 3 19 -0.16894989372113D+01 0.24659193736079D-05 1 12 3 19 0.12472944190922D+01 0.17510119224745D-01 2 12 3 19 -0.12135925753971D+01 -0.97443674449893D-02 3 12 3 19 -0.32589073730359D+01 -0.88352482724324D-01 1 13 3 19 -0.69597573774605D-01 0.11644810110962D-01 2 13 3 19 -0.52015356245708D-01 0.10425154650182D-01 3 13 3 19 -0.11904421764624D-13 -0.15265542333782D-02 1 14 3 19 -0.93794468912944D-02 0.14465381142970D-02 2 14 3 19 -0.26278876546402D-01 0.84337482442151D-04 3 14 3 19 -0.73190121021802D+00 0.35296795122741D-02 1 15 3 19 -0.36956654762328D-01 -0.83818816840154D-02 2 15 3 19 -0.13936910002660D+00 -0.33101839317914D-02 3 15 3 19 0.15430748243887D+01 0.21744619057425D-15 1 16 3 19 0.16804002707632D+01 0.20905318307952D-06 2 16 3 19 0.19785367914050D+00 0.16870516735553D-06 3 16 3 19 0.19655508301066D-13 0.80739057505060D-07 1 17 3 19 0.19420996202345D-01 0.23289753098669D-01 2 17 3 19 0.18380719447032D+00 -0.10237317577535D-01 3 17 3 19 0.46307096784142D+00 -0.12109169790195D-15 1 18 3 19 -0.62759339862227D-01 0.22779958230596D-06 2 18 3 19 -0.11453501208804D+00 -0.36582976526570D-06 3 18 3 19 -0.17520321069576D+01 0.56264328654196D-15 1 19 3 19 -0.12851833412152D+01 0.17817987556316D+00 2 19 3 19 -0.19811208736033D+01 0.24729430122380D+00 3 19 3 19 0.15027371097683D+02 0.00000000000000D+00 1 20 3 19 0.71641649205776D+00 0.15828408045863D-01 2 20 3 19 -0.59646955176476D+00 -0.15822443951962D-01 3 20 3 19 -0.32238387805638D+00 -0.82757133622767D-03 1 1 1 20 0.18132533007096D+01 -0.47530769157264D-02 2 1 1 20 0.53612210623467D+00 -0.45155218654886D-02 3 1 1 20 -0.40884331380708D+00 -0.36635333128342D-02 1 2 1 20 0.12026903628937D+01 0.82154279193457D-02 2 2 1 20 -0.31248864877213D+00 0.53155363258447D-03 3 2 1 20 -0.14444766199700D+01 -0.14756526012532D-08 1 3 1 20 -0.13505994119705D+01 0.72550054491503D-02 2 3 1 20 0.38251114594274D+00 0.68471011368166D-03 3 3 1 20 0.82118323636497D+00 0.68437938789710D-06 1 4 1 20 -0.10413932964438D+01 -0.21687425894961D-02 2 4 1 20 0.20608507553585D+00 -0.31656792789704D-03 3 4 1 20 -0.10799786650729D+01 -0.11528597573823D-02 1 5 1 20 0.17794875236901D+01 0.19166045915722D-01 2 5 1 20 -0.29515693224249D+00 -0.27555489500579D-01 3 5 1 20 0.21959540990301D+00 -0.16129721571364D-01 1 6 1 20 0.50617432499134D+01 -0.34881693369011D-02 2 6 1 20 0.63648666029944D+00 0.36009329414410D-03 3 6 1 20 0.80124576135857D+00 0.67820350195878D-01 1 7 1 20 -0.19362396073031D+01 -0.11964887554198D-01 2 7 1 20 -0.59457960571177D-01 0.53575458752784D-02 3 7 1 20 0.43103011435940D+00 -0.27533992276399D-02 1 8 1 20 -0.55578836778291D+01 0.10032565449097D-01 2 8 1 20 -0.55080508470623D+00 -0.47058206967138D-02 3 8 1 20 0.69764104738233D+00 0.75154469464719D-01 1 9 1 20 -0.84858308199483D-01 -0.95162401793008D-02 2 9 1 20 -0.91516509802233D+00 0.15177272222113D-01 3 9 1 20 -0.26814814780431D+01 -0.29395659937315D-01 1 10 1 20 0.10580893994944D+01 0.36597420284056D-02 2 10 1 20 0.47957436773312D+00 -0.96862129538427D-02 3 10 1 20 -0.22884251646869D+01 0.19464124321743D-06 1 11 1 20 0.83973052237793D+00 0.12136267489987D-01 2 11 1 20 0.57461793332308D+00 -0.75318918695219D-02 3 11 1 20 0.25421490654401D+01 -0.92278078692358D-01 1 12 1 20 -0.64503548991626D+00 0.29967134865113D-01 2 12 1 20 0.85390272525950D+00 -0.16940258999622D-01 3 12 1 20 -0.34640414696727D+01 0.13911558256247D-06 1 13 1 20 0.14802253550499D+01 0.21198298160666D-02 2 13 1 20 0.67715961460253D+00 -0.39974976356835D-02 3 13 1 20 -0.93827316446327D-02 0.14470375306413D-02 1 14 1 20 0.49676191703949D-14 0.16078841618551D-02 2 14 1 20 -0.71895228811401D-02 0.64504261100432D-04 3 14 1 20 0.69597199524327D-01 0.11644500598344D-01 1 15 1 20 -0.24755178931190D-14 0.33271950001726D-06 2 15 1 20 -0.92770841255380D+00 0.16024586670472D-06 3 15 1 20 0.16804002707633D+01 -0.20905317914451D-06 1 16 1 20 0.32917986690431D+01 0.57636024691524D-15 2 16 1 20 0.21589756231115D+01 0.41735635658018D-02 3 16 1 20 0.36956654762330D-01 -0.83818816840150D-02 1 17 1 20 0.15388288188003D+01 0.85664757815543D-16 2 17 1 20 -0.72965505522404D+00 0.36779492459334D-06 3 17 1 20 0.62759339862234D-01 0.22779958185413D-06 1 18 1 20 0.73506087478148D-01 -0.61980359578466D-15 2 18 1 20 0.13243688489239D+00 0.27414411095335D-03 3 18 1 20 -0.19420996202335D-01 0.23289753098669D-01 1 19 1 20 -0.66914053695299D+00 0.31094867468335D-02 2 19 1 20 0.36012474597854D+00 -0.57432848977132D-03 3 19 1 20 0.71641648901980D+00 0.15828544427265D-01 1 20 1 20 0.15369761478102D+02 0.00000000000000D+00 2 20 1 20 -0.71163047741875D+01 -0.13903371760471D+00 3 20 1 20 -0.12852033538846D+01 -0.17818189147543D+00 1 1 2 20 -0.30117809923755D+00 -0.56316188352036D-02 2 1 2 20 0.79186286634332D+00 -0.81935811546418D-02 3 1 2 20 -0.96222188575302D+00 -0.16681063109167D-02 1 2 2 20 -0.10450540314164D+01 -0.21458121172613D-02 2 2 2 20 0.11531177325466D+00 0.12687788388837D-02 3 2 2 20 -0.23803547453749D+00 0.15358581025008D-06 1 3 2 20 0.81666076196985D+00 -0.21026794867812D-02 2 3 2 20 -0.39743085092920D+00 0.10315485055377D-01 3 3 2 20 0.91963324317481D-01 0.21945277365449D-06 1 4 2 20 0.83615108999653D+00 0.20828989450415D-02 2 4 2 20 0.27225118200813D+00 0.35497944298583D-03 3 4 2 20 0.42674156748631D-01 0.11388164245954D-02 1 5 2 20 -0.90366178062741D+00 -0.33076193264513D-01 2 5 2 20 0.18468895195534D+00 0.15233242387269D-01 3 5 2 20 0.26552653181972D+00 0.41374279779811D-02 1 6 2 20 -0.26913011930787D+01 0.98995665567427D-02 2 6 2 20 0.12512110340052D+01 -0.12958961000948D-02 3 6 2 20 -0.73183635481971D+00 -0.90035483846352D-01 1 7 2 20 0.83329143018954D+00 0.64728025028718D-02 2 7 2 20 0.39726271758569D-01 0.30007940843051D-02 3 7 2 20 0.20553089582639D+00 0.25769569991204D-02 1 8 2 20 0.17328707863208D+01 -0.86063586808388D-02 2 8 2 20 -0.77551224241763D-01 -0.22947561680930D-02 3 8 2 20 -0.78918936688460D+00 -0.67554363629032D-01 1 9 2 20 -0.75734874106880D+00 0.13852106275148D-01 2 9 2 20 0.94564695760792D+00 -0.13326912347395D-01 3 9 2 20 0.24740388935626D+01 0.65954300175018D-01 1 10 2 20 -0.77547794034032D-01 -0.77545064256822D-02 2 10 2 20 -0.49224197726741D+00 0.84630629951609D-02 3 10 2 20 0.30330790543788D+01 0.75576197147400D-06 1 11 2 20 0.47373420869604D-01 -0.72039518971678D-02 2 11 2 20 -0.42039545619565D+00 -0.79760655183775D-03 3 11 2 20 -0.24736843662435D+01 0.80305452092080D-01 1 12 2 20 0.96903006575378D+00 -0.23745150991562D-01 2 12 2 20 -0.19337201599432D+00 0.68831483010556D-02 3 12 2 20 0.21345880305997D+01 0.14467656590102D-05 1 13 2 20 -0.67715919531537D+00 0.39970087055471D-02 2 13 2 20 -0.59319074231792D+00 0.10191869453764D-01 3 13 2 20 0.26281136448346D-01 -0.84309517833734D-04 1 14 2 20 -0.71901523276210D-02 -0.64680691296715D-04 2 14 2 20 0.10162947802969D-15 0.14073042758146D-02 3 14 2 20 -0.52015312565543D-01 -0.10425068151977D-01 1 15 2 20 -0.92770841255380D+00 -0.16024587086442D-06 2 15 2 20 0.46151371802715D-14 0.23241082067709D-07 3 15 2 20 -0.19785367914050D+00 0.16870516663439D-06 1 16 2 20 -0.21589756231115D+01 0.41735635658018D-02 2 16 2 20 -0.68932005377594D+01 -0.42450193614584D-16 3 16 2 20 -0.13936910002660D+00 0.33101839317914D-02 1 17 2 20 -0.72965505522404D+00 -0.36779492458769D-06 2 17 2 20 0.70915292279925D+00 0.49145181152778D-17 3 17 2 20 0.11453501208804D+00 -0.36582976543344D-06 1 18 2 20 0.13243688489239D+00 -0.27414411095333D-03 2 18 2 20 0.17109939588368D+00 -0.64312665356527D-16 3 18 2 20 -0.18380719447032D+00 -0.10237317577535D-01 1 19 2 20 0.36012575396474D+00 -0.57485669567932D-03 2 19 2 20 0.89467395764158D+00 -0.10552609969073D-02 3 19 2 20 -0.59647116774058D+00 -0.15822220767527D-01 1 20 2 20 -0.71163101684452D+01 0.13903321095824D+00 2 20 2 20 0.14511487521269D+02 0.00000000000000D+00 3 20 2 20 -0.19810951837567D+01 -0.24729521639192D+00 1 1 3 20 -0.37152320846493D+00 0.14970024958012D-01 2 1 3 20 -0.87893240916726D+00 0.16417684723853D-01 3 1 3 20 0.21356746809929D+01 -0.64518719928304D-02 1 2 3 20 -0.87229731747186D+00 0.11087385210488D-01 2 2 3 20 -0.57330019971585D+00 0.60569890989388D-02 3 2 3 20 -0.69375072072507D+00 0.12776079436280D-06 1 3 3 20 0.88210296911924D+00 -0.12263345485585D-02 2 3 3 20 0.45426285046140D+00 -0.31921345472063D-02 3 3 3 20 -0.27311368293515D-01 0.48749976035530D-06 1 4 3 20 -0.53793535376571D+00 -0.17218116919833D-03 2 4 3 20 -0.23505711426173D+00 0.21136134881166D-03 3 4 3 20 0.45218019499654D+00 -0.13429359757115D-03 1 5 3 20 0.81124461966960D-01 -0.39031612854897D-01 2 5 3 20 -0.15591755126556D+00 0.29754511771130D-01 3 5 3 20 -0.32265073658012D+01 -0.23559605926573D-01 1 6 3 20 0.69596597002010D+00 0.16195095029626D-01 2 6 3 20 -0.86659694614985D+00 -0.17054032197881D-01 3 6 3 20 0.34292263390704D+01 0.36210999366898D-02 1 7 3 20 0.14256153319272D+00 -0.18984854898019D-01 2 7 3 20 -0.31979338364592D+00 0.74730631846219D-02 3 7 3 20 0.28719852129375D+01 0.13816268237824D-01 1 8 3 20 0.68445644208540D+00 0.24609705990373D-01 2 8 3 20 -0.94450980494593D+00 -0.49306558978841D-02 3 8 3 20 -0.31913455621637D+01 -0.83731619352656D-02 1 9 3 20 -0.13448842329276D+01 0.83173225262617D-02 2 9 3 20 0.95903492959708D+00 -0.38148153958596D-02 3 9 3 20 0.15239622487681D+01 -0.25908668518440D-01 1 10 3 20 -0.96527559763943D+00 -0.38063651834875D-02 2 10 3 20 0.16802883486708D+01 0.76536880282333D-02 3 10 3 20 -0.37129030726312D+01 -0.55580406618530D-06 1 11 3 20 0.12472944190922D+01 0.17510119224745D-01 2 11 3 20 -0.12135925753971D+01 -0.97443674449892D-02 3 11 3 20 -0.32589073730358D+01 -0.88352482724323D-01 1 12 3 20 -0.20859864215896D+01 0.14690242051904D-01 2 12 3 20 0.10619468710813D+01 -0.75971701552310D-02 3 12 3 20 -0.16894989372113D+01 0.24659193736108D-05 1 13 3 20 -0.93794468912931D-02 0.14465381142969D-02 2 13 3 20 -0.26278876546401D-01 0.84337482442200D-04 3 13 3 20 -0.73190121021802D+00 0.35296795122745D-02 1 14 3 20 -0.69597573774603D-01 0.11644810110965D-01 2 14 3 20 -0.52015356245706D-01 0.10425154650182D-01 3 14 3 20 -0.25066634953106D-13 -0.15265542333765D-02 1 15 3 20 0.16804002707633D+01 0.20905318783700D-06 2 15 3 20 0.19785367914050D+00 0.16870516661010D-06 3 15 3 20 0.24311393059019D-13 0.80739054110334D-07 1 16 3 20 -0.36956654762326D-01 -0.83818816840150D-02 2 16 3 20 -0.13936910002660D+00 -0.33101839317915D-02 3 16 3 20 0.15430748243888D+01 -0.82293555681949D-16 1 17 3 20 -0.62759339862234D-01 0.22779958185500D-06 2 17 3 20 -0.11453501208804D+00 -0.36582976543344D-06 3 17 3 20 -0.17520321069576D+01 0.19592955708604D-14 1 18 3 20 0.19420996202360D-01 0.23289753098669D-01 2 18 3 20 0.18380719447032D+00 -0.10237317577535D-01 3 18 3 20 0.46307096784143D+00 0.11186149552219D-14 1 19 3 20 0.71641649205776D+00 0.15828408045863D-01 2 19 3 20 -0.59646955176476D+00 -0.15822443951961D-01 3 19 3 20 -0.32238387805638D+00 -0.82757133623102D-03 1 20 3 20 -0.12851833412155D+01 0.17817987556316D+00 2 20 3 20 -0.19811208736034D+01 0.24729430122380D+00 3 20 3 20 0.15027371097683D+02 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 3600 qpt 0.00000000E+00 5.00000000E-01 0.00000000E+00 1.0 1 1 1 1 0.81101763433835D+01 0.00000000000000D+00 2 1 1 1 0.13411441435579D+01 0.57068282343976D-06 3 1 1 1 -0.42341419265024D-13 0.00000000000000D+00 1 2 1 1 -0.36276863171947D+00 -0.11989790858426D-08 2 2 1 1 -0.19209349629714D+00 0.14670636523227D-07 3 2 1 1 -0.14228885975987D-14 0.30461922256397D-16 1 3 1 1 0.15051069402328D-12 0.29453607031279D-08 2 3 1 1 0.84471420843343D-01 0.27483402967792D-08 3 3 1 1 -0.97474355513378D-15 0.82927798749943D-16 1 4 1 1 -0.15562863989261D+00 0.87926706859983D-16 2 4 1 1 -0.32946762254022D-01 0.84978504365561D-08 3 4 1 1 0.85949219539237D-14 -0.19177013383189D-15 1 5 1 1 0.53435286521323D+00 0.44385687380677D-03 2 5 1 1 0.12820431883205D+00 0.18235400061326D-02 3 5 1 1 0.20894608884872D+00 0.90634560144194D-04 1 6 1 1 0.53435286521322D+00 0.44385687380678D-03 2 6 1 1 0.12820431883205D+00 0.18235400061325D-02 3 6 1 1 -0.20894608884872D+00 -0.90634560144182D-04 1 7 1 1 -0.34739790734432D+01 -0.88547588111040D-09 2 7 1 1 0.45407510740998D-02 -0.22541774075895D-08 3 7 1 1 0.22378761700954D+00 0.40029090361391D-08 1 8 1 1 -0.34739790734432D+01 -0.88547169199573D-09 2 8 1 1 0.45407510740984D-02 -0.22541775603061D-08 3 8 1 1 -0.22378761700955D+00 -0.40029090399354D-08 1 9 1 1 -0.34067595583720D+00 0.13815604787250D-07 2 9 1 1 0.60756791989550D-01 0.18911858432923D-07 3 9 1 1 -0.91074152268092D-15 0.16914474231633D-16 1 10 1 1 -0.90847243655284D-01 -0.10096856678440D-07 2 10 1 1 -0.69495458873908D-02 0.38816360706264D-08 3 10 1 1 -0.39774835668548D-15 -0.49933998567366D-16 1 11 1 1 0.27086826803723D+00 -0.28246234247617D-08 2 11 1 1 -0.10288537780560D-01 0.56733237514132D-08 3 11 1 1 0.16129894448164D-14 -0.20745265814122D-15 1 12 1 1 0.11748780754743D+01 -0.20743046980769D-07 2 12 1 1 -0.44442567613515D+00 -0.15885677436475D-07 3 12 1 1 -0.83137797485674D-16 -0.23847034529998D-15 1 13 1 1 -0.18590741189155D+00 -0.72134374123399D-08 2 13 1 1 -0.31686007888679D+00 0.14912578971223D-08 3 13 1 1 0.52525060974991D+00 0.15267510657437D-07 1 14 1 1 -0.18627785637425D-01 -0.21012580137554D-03 2 14 1 1 0.32726503947587D+00 -0.81391347136053D-03 3 14 1 1 0.29524272141786D+00 0.22397157633299D-03 1 15 1 1 -0.18627785637427D-01 -0.21012580137574D-03 2 15 1 1 0.32726503947588D+00 -0.81391347136077D-03 3 15 1 1 -0.29524272141784D+00 -0.22397157633306D-03 1 16 1 1 -0.18590741189156D+00 -0.72134376521586D-08 2 16 1 1 -0.31686007888680D+00 0.14912581682323D-08 3 16 1 1 -0.52525060974991D+00 -0.15267510627171D-07 1 17 1 1 0.39631777278968D+00 0.16656258511057D-02 2 17 1 1 0.42349060819953D+00 0.90267832783264D-02 3 17 1 1 0.58852109688804D+00 0.15680990687216D-01 1 18 1 1 0.25144422357387D-01 0.30885780243654D-02 2 18 1 1 0.27520775231614D+00 0.18559808744829D-02 3 18 1 1 -0.73325324000050D+00 -0.13507992412825D-01 1 19 1 1 0.25144422357387D-01 0.30885780243653D-02 2 19 1 1 0.27520775231614D+00 0.18559808744829D-02 3 19 1 1 0.73325324000050D+00 0.13507992412825D-01 1 20 1 1 0.39631777278968D+00 0.16656258511050D-02 2 20 1 1 0.42349060819953D+00 0.90267832783270D-02 3 20 1 1 -0.58852109688807D+00 -0.15680990687216D-01 1 1 2 1 0.13411378199716D+01 0.62445455851852D-06 2 1 2 1 0.92689969471940D+01 0.00000000000000D+00 3 1 2 1 -0.28402913369793D-13 0.00000000000000D+00 1 2 2 1 -0.19209482885814D+00 -0.42071828994023D-08 2 2 2 1 -0.10637963373164D+01 -0.19393787956531D-08 3 2 2 1 -0.18608803165565D-14 -0.86258122735748D-15 1 3 2 1 0.84471420843343D-01 -0.27483412534550D-08 2 3 2 1 -0.92988356307624D-13 -0.13414832008200D-07 3 3 2 1 -0.11864405819073D-13 -0.10529925030500D-14 1 4 2 1 0.32946762254018D-01 0.84978504365561D-08 2 4 2 1 0.15490076597232D+00 0.66292108737698D-15 3 4 2 1 0.10732522526422D-13 -0.78075157699636D-15 1 5 2 1 0.28245309356687D-01 0.22437261175111D-02 2 5 2 1 -0.44552797138270D+00 0.15198122804666D-02 3 5 2 1 0.53357376639834D+01 -0.11102714251348D-01 1 6 2 1 0.28245309356688D-01 0.22437261175109D-02 2 6 2 1 -0.44552797138269D+00 0.15198122804659D-02 3 6 2 1 -0.53357376639834D+01 0.11102714251348D-01 1 7 2 1 -0.68537920293003D+00 -0.78117112718764D-09 2 7 2 1 0.41365193551445D+01 -0.12492129097404D-08 3 7 2 1 -0.89081693609245D+00 0.21996920786455D-08 1 8 2 1 -0.68537920293003D+00 -0.78117127966995D-09 2 8 2 1 0.41365193551445D+01 -0.12492120087100D-08 3 8 2 1 0.89081693609241D+00 -0.21996926811692D-08 1 9 2 1 -0.42462188945386D+00 0.39108544985383D-08 2 9 2 1 -0.22294748005275D+01 0.93386595573720D-08 3 9 2 1 -0.92948916655977D-15 0.26488463839633D-15 1 10 2 1 -0.73000920128042D-01 0.69602992668835D-08 2 10 2 1 0.27633383791820D-03 0.10177183586110D-07 3 10 2 1 0.15783669026557D-13 0.65545142904037D-15 1 11 2 1 0.16366317516938D+00 -0.98162996602175D-08 2 11 2 1 -0.95093453917009D+00 0.10155836155401D-08 3 11 2 1 -0.13466280437887D-14 -0.55752352955156D-16 1 12 2 1 -0.63249916978185D+00 -0.75795662949125D-08 2 12 2 1 0.14506871895840D+01 -0.84332650906702D-08 3 12 2 1 0.67413579715682D-16 0.17939118726800D-15 1 13 2 1 -0.90025678873822D+00 0.98563492906430D-08 2 13 2 1 -0.16404728917975D+01 -0.31219665400644D-08 3 13 2 1 -0.64604799336343D+00 -0.25110321685270D-07 1 14 2 1 0.66650992669084D+00 -0.15958688660321D-02 2 14 2 1 0.75893449639926D+00 -0.18091601147792D-02 3 14 2 1 -0.66671587413015D+00 0.10683385518576D-02 1 15 2 1 0.66650992669084D+00 -0.15958688660323D-02 2 15 2 1 0.75893449639926D+00 -0.18091601147786D-02 3 15 2 1 0.66671587413015D+00 -0.10683385518588D-02 1 16 2 1 -0.90025678873822D+00 0.98563495617531D-08 2 16 2 1 -0.16404728917975D+01 -0.31219695246899D-08 3 16 2 1 0.64604799336342D+00 0.25110322455548D-07 1 17 2 1 -0.18325830586093D+00 0.29427663472241D-02 2 17 2 1 0.20887133686633D+01 0.10053792221442D-01 3 17 2 1 0.56434041082929D+00 0.14139490556701D-01 1 18 2 1 0.10029332792676D+01 -0.42170134288039D-02 2 18 2 1 -0.15089106015210D+01 0.75631303211634D-02 3 18 2 1 -0.76652726720671D+00 -0.69414717873122D-02 1 19 2 1 0.10029332792676D+01 -0.42170134288039D-02 2 19 2 1 -0.15089106015210D+01 0.75631303211634D-02 3 19 2 1 0.76652726720668D+00 0.69414717873127D-02 1 20 2 1 -0.18325830586093D+00 0.29427663472247D-02 2 20 2 1 0.20887133686633D+01 0.10053792221444D-01 3 20 2 1 -0.56434041082926D+00 -0.14139490556700D-01 1 1 3 1 -0.42341419265024D-13 0.00000000000000D+00 2 1 3 1 -0.28402913369793D-13 -0.11102230246252D-15 3 1 3 1 0.14574890059892D+02 0.00000000000000D+00 1 2 3 1 -0.14228885976037D-14 0.30893087528487D-16 2 2 3 1 -0.18608803166722D-14 -0.86292938827117D-15 3 2 3 1 0.32405254610749D+01 -0.82746173497623D-08 1 3 3 1 -0.97474355509861D-15 0.82943840135699D-16 2 3 3 1 -0.11864405819119D-13 -0.10532804135797D-14 3 3 3 1 -0.22481512784405D-12 -0.63756719060770D-08 1 4 3 1 0.85949219538802D-14 -0.19171716550677D-15 2 4 3 1 0.10732522526407D-13 -0.78080701327177D-15 3 4 3 1 -0.51058392511606D+00 -0.31946917109930D-15 1 5 3 1 -0.34544467547428D-01 0.29537549460747D-02 2 5 3 1 0.61716601375008D+01 -0.42040274325361D-02 3 5 3 1 -0.64438804769714D+00 -0.55120817600532D-03 1 6 3 1 0.34544467547427D-01 -0.29537549460746D-02 2 6 3 1 -0.61716601375008D+01 0.42040274325367D-02 3 6 3 1 -0.64438804769714D+00 -0.55120817600661D-03 1 7 3 1 -0.43975167368966D+00 0.14395926504082D-01 2 7 3 1 -0.68394290283075D+00 -0.11779748011195D-02 3 7 3 1 -0.16810370817580D+01 0.98905860945142D-02 1 8 3 1 0.43975167368966D+00 -0.14395926504082D-01 2 8 3 1 0.68394290283071D+00 0.11779748011189D-02 3 8 3 1 -0.16810370817580D+01 0.98905860945137D-02 1 9 3 1 -0.91074152268092D-15 0.16914474231633D-16 2 9 3 1 -0.92948916738695D-15 0.26661936187231D-15 3 9 3 1 -0.11521353089179D+01 0.25800159656049D-07 1 10 3 1 -0.39774835648916D-15 -0.49926056351195D-16 2 10 3 1 0.15783669026687D-13 0.65442059148506D-15 3 10 3 1 0.14087185061612D+00 0.36345535623397D-09 1 11 3 1 0.16129894453027D-14 -0.20805885958878D-15 2 11 3 1 -0.13466280437957D-14 -0.55583954725063D-16 3 11 3 1 0.17860256660851D+01 -0.15336967048172D-07 1 12 3 1 -0.83137797883945D-16 -0.24070126161861D-15 2 12 3 1 0.67413577976069D-16 0.17929074406845D-15 3 12 3 1 0.29843300792446D+01 -0.13044294353993D-06 1 13 3 1 -0.37629434814472D-01 -0.15933136403036D-07 2 13 3 1 -0.10171320710695D+01 0.13645316944265D-07 3 13 3 1 -0.12410077114876D+00 -0.90218564989274D-08 1 14 3 1 -0.24459026156728D-01 0.14667797057901D-02 2 14 3 1 -0.10416370308126D+01 0.74936709422972D-03 3 14 3 1 -0.61524493664583D+00 -0.19236340652559D-03 1 15 3 1 0.24459026156749D-01 -0.14667797057902D-02 2 15 3 1 0.10416370308126D+01 -0.74936709423091D-03 3 15 3 1 -0.61524493664583D+00 -0.19236340652547D-03 1 16 3 1 0.37629434814472D-01 0.15933136433192D-07 2 16 3 1 0.10171320710695D+01 -0.13645316174421D-07 3 16 3 1 -0.12410077114878D+00 -0.90218544762165D-08 1 17 3 1 0.98985970064588D+00 -0.70221971410176D-02 2 17 3 1 0.12605127499428D+00 -0.17367804720354D-03 3 17 3 1 0.22355539557404D+01 0.40605244129951D-02 1 18 3 1 -0.44240345177316D+00 -0.11654722498244D-06 2 18 3 1 -0.10376008111885D+01 0.22639750259907D-06 3 18 3 1 0.86413724239495D+00 0.43621189609078D-07 1 19 3 1 0.44240345177314D+00 0.11654722489119D-06 2 19 3 1 0.10376008111885D+01 -0.22639750208068D-06 3 19 3 1 0.86413724239495D+00 0.43621190046815D-07 1 20 3 1 -0.98985970064590D+00 0.70221971410177D-02 2 20 3 1 -0.12605127499422D+00 0.17367804720381D-03 3 20 3 1 0.22355539557405D+01 0.40605244129946D-02 1 1 1 2 -0.36276863171947D+00 -0.11989806595003D-08 2 1 1 2 -0.19209349629714D+00 0.14670636404205D-07 3 1 1 2 -0.14228885975987D-14 -0.30461922256397D-16 1 2 1 2 0.81101763433835D+01 0.00000000000000D+00 2 2 1 2 0.13411441435576D+01 0.57068282343976D-06 3 2 1 2 0.29114488058211D-15 0.00000000000000D+00 1 3 1 2 -0.15562863989262D+00 -0.20753865426104D-15 2 3 1 2 -0.32946762254022D-01 0.84978506379211D-08 3 3 1 2 -0.57284260902174D-15 -0.79146415425546D-17 1 4 1 2 0.21785058977234D-13 0.29453664051161D-08 2 4 1 2 0.84471420843396D-01 0.27483412345780D-08 3 4 1 2 0.67416309856635D-14 -0.82369562123896D-16 1 5 1 2 0.53435286521328D+00 0.44385687380500D-03 2 5 1 2 0.12820431883205D+00 0.18235400061320D-02 3 5 1 2 0.20894608884872D+00 0.90634560144021D-04 1 6 1 2 0.53435286521328D+00 0.44385687380416D-03 2 6 1 2 0.12820431883206D+00 0.18235400061321D-02 3 6 1 2 -0.20894608884872D+00 -0.90634560144067D-04 1 7 1 2 0.34739790734433D+01 0.88548133988891D-09 2 7 1 2 -0.45407510740964D-02 0.22541774618211D-08 3 7 1 2 -0.22378761700955D+00 -0.40029080004123D-08 1 8 1 2 0.34739790734432D+01 0.88548237133639D-09 2 8 1 2 -0.45407510740940D-02 0.22541775350261D-08 3 8 1 2 0.22378761700953D+00 0.40029079096413D-08 1 9 1 2 -0.90847243655278D-01 -0.10096858123899D-07 2 9 1 2 -0.69495458873882D-02 0.38816360615929D-08 3 9 1 2 -0.30168507176265D-14 0.53036062177578D-17 1 10 1 2 -0.34067595583708D+00 0.13815601890003D-07 2 10 1 2 0.60756791989614D-01 0.18911856279930D-07 3 10 1 2 0.49023141616434D-15 0.24057813688887D-16 1 11 1 2 0.11748780754741D+01 -0.20743000875829D-07 2 11 1 2 -0.44442567613532D+00 -0.15885683017945D-07 3 11 1 2 -0.65673060466247D-15 0.26768469542421D-15 1 12 1 2 0.27086826803725D+00 -0.28246234366367D-08 2 12 1 2 -0.10288537780566D-01 0.56733240326505D-08 3 12 1 2 0.48712738987882D-14 0.37702862562143D-16 1 13 1 2 -0.18627785637442D-01 -0.21012580137408D-03 2 13 1 2 0.32726503947588D+00 -0.81391347136329D-03 3 13 1 2 0.29524272141789D+00 0.22397157632931D-03 1 14 1 2 -0.18590741189163D+00 -0.72134378637328D-08 2 14 1 2 -0.31686007888678D+00 0.14912574719490D-08 3 14 1 2 0.52525060974981D+00 0.15267510765989D-07 1 15 1 2 -0.18590741189160D+00 -0.72134378548902D-08 2 15 1 2 -0.31686007888685D+00 0.14912583354384D-08 3 15 1 2 -0.52525060974985D+00 -0.15267510783668D-07 1 16 1 2 -0.18627785637451D-01 -0.21012580137409D-03 2 16 1 2 0.32726503947589D+00 -0.81391347136339D-03 3 16 1 2 -0.29524272141790D+00 -0.22397157632900D-03 1 17 1 2 0.25144422357362D-01 0.30885780243653D-02 2 17 1 2 0.27520775231612D+00 0.18559808744827D-02 3 17 1 2 -0.73325324000035D+00 -0.13507992412825D-01 1 18 1 2 0.39631777278964D+00 0.16656258511048D-02 2 18 1 2 0.42349060819950D+00 0.90267832783382D-02 3 18 1 2 0.58852109688794D+00 0.15680990687234D-01 1 19 1 2 0.39631777278962D+00 0.16656258511049D-02 2 19 1 2 0.42349060819943D+00 0.90267832783377D-02 3 19 1 2 -0.58852109688782D+00 -0.15680990687235D-01 1 20 1 2 0.25144422357362D-01 0.30885780243649D-02 2 20 1 2 0.27520775231616D+00 0.18559808744827D-02 3 20 1 2 0.73325324000045D+00 0.13507992412825D-01 1 1 2 2 -0.19209482885814D+00 -0.42071830184244D-08 2 1 2 2 -0.10637963373164D+01 -0.19393848138921D-08 3 1 2 2 -0.18608803161429D-14 0.86301490822648D-15 1 2 2 2 0.13411378199713D+01 0.62445455851852D-06 2 2 2 2 0.92689969471940D+01 0.00000000000000D+00 3 2 2 2 -0.35508340706714D-13 0.00000000000000D+00 1 3 2 2 0.32946762254017D-01 0.84978506379211D-08 2 3 2 2 0.15490076597238D+00 0.11418181213921D-14 3 3 2 2 -0.27265407606013D-13 -0.14009297241720D-14 1 4 2 2 0.84471420843396D-01 -0.27483403156561D-08 2 4 2 2 -0.29639100024077D-13 -0.13414830556070D-07 3 4 2 2 0.19971542364281D-13 0.10643030431117D-14 1 5 2 2 0.28245309356685D-01 0.22437261175104D-02 2 5 2 2 -0.44552797138271D+00 0.15198122804780D-02 3 5 2 2 0.53357376639835D+01 -0.11102714251339D-01 1 6 2 2 0.28245309356689D-01 0.22437261175106D-02 2 6 2 2 -0.44552797138273D+00 0.15198122804737D-02 3 6 2 2 -0.53357376639835D+01 0.11102714251339D-01 1 7 2 2 0.68537920293003D+00 0.78117118141928D-09 2 7 2 2 -0.41365193551445D+01 0.12492029053882D-08 3 7 2 2 0.89081693609250D+00 -0.21996921473994D-08 1 8 2 2 0.68537920293003D+00 0.78117125438994D-09 2 8 2 2 -0.41365193551446D+01 0.12492099207445D-08 3 8 2 2 -0.89081693609252D+00 0.21996924397541D-08 1 9 2 2 -0.73000920128040D-01 0.69602992578500D-08 2 9 2 2 0.27633383794748D-03 0.10177183910418D-07 3 9 2 2 0.24448724996915D-14 0.23666198086793D-14 1 10 2 2 -0.42462188945380D+00 0.39108523455449D-08 2 10 2 2 -0.22294748005279D+01 0.93386738554444D-08 3 10 2 2 0.12540582998351D-13 -0.15262921199118D-14 1 11 2 2 -0.63249916978202D+00 -0.75795718763825D-08 2 11 2 2 0.14506871895842D+01 -0.84332778792843D-08 3 11 2 2 -0.12168372074944D-14 -0.76199787024524D-16 1 12 2 2 0.16366317516937D+00 -0.98162993789802D-08 2 12 2 2 -0.95093453917009D+00 0.10155834165445D-08 3 12 2 2 0.10511814630886D-14 0.13344609693577D-16 1 13 2 2 0.66650992669084D+00 -0.15958688660348D-02 2 13 2 2 0.75893449639934D+00 -0.18091601147797D-02 3 13 2 2 -0.66671587413012D+00 0.10683385518641D-02 1 14 2 2 -0.90025678873822D+00 0.98563488654697D-08 2 14 2 2 -0.16404728917973D+01 -0.31219641611256D-08 3 14 2 2 -0.64604799336346D+00 -0.25110321358136D-07 1 15 2 2 -0.90025678873827D+00 0.98563497289592D-08 2 15 2 2 -0.16404728917973D+01 -0.31219654982815D-08 3 15 2 2 0.64604799336350D+00 0.25110321219020D-07 1 16 2 2 0.66650992669085D+00 -0.15958688660349D-02 2 16 2 2 0.75893449639932D+00 -0.18091601147775D-02 3 16 2 2 0.66671587413014D+00 -0.10683385518639D-02 1 17 2 2 0.10029332792676D+01 -0.42170134288040D-02 2 17 2 2 -0.15089106015210D+01 0.75631303211622D-02 3 17 2 2 -0.76652726720668D+00 -0.69414717873127D-02 1 18 2 2 -0.18325830586096D+00 0.29427663472359D-02 2 18 2 2 0.20887133686634D+01 0.10053792221448D-01 3 18 2 2 0.56434041082929D+00 0.14139490556726D-01 1 19 2 2 -0.18325830586103D+00 0.29427663472354D-02 2 19 2 2 0.20887133686634D+01 0.10053792221448D-01 3 19 2 2 -0.56434041082920D+00 -0.14139490556726D-01 1 20 2 2 0.10029332792677D+01 -0.42170134288040D-02 2 20 2 2 -0.15089106015209D+01 0.75631303211613D-02 3 20 2 2 0.76652726720680D+00 0.69414717873124D-02 1 1 3 2 -0.14228885976063D-14 -0.29815174348261D-16 2 1 3 2 -0.18608803167301D-14 0.86314318815944D-15 3 1 3 2 0.32405254610749D+01 -0.82745917808264D-08 1 2 3 2 0.29114488058211D-15 0.00000000000000D+00 2 2 3 2 -0.35508340706714D-13 -0.11102230246252D-15 3 2 3 2 0.14574890059892D+02 0.00000000000000D+00 1 3 3 2 -0.57284260906527D-15 -0.78616732174358D-17 2 3 3 2 -0.27265407606027D-13 -0.14009851604474D-14 3 3 3 2 -0.51058392511619D+00 -0.59284354121634D-15 1 4 3 2 0.67416309856987D-14 -0.82353520738139D-16 2 4 3 2 0.19971542364234D-13 0.10640151325819D-14 3 4 3 2 -0.27981033919398D-13 -0.63756730338910D-08 1 5 3 2 -0.34544467547424D-01 0.29537549460745D-02 2 5 3 2 0.61716601375009D+01 -0.42040274325271D-02 3 5 3 2 -0.64438804769716D+00 -0.55120817600099D-03 1 6 3 2 0.34544467547424D-01 -0.29537549460745D-02 2 6 3 2 -0.61716601375009D+01 0.42040274325269D-02 3 6 3 2 -0.64438804769720D+00 -0.55120817600137D-03 1 7 3 2 0.43975167368966D+00 -0.14395926504081D-01 2 7 3 2 0.68394290283080D+00 0.11779748011194D-02 3 7 3 2 0.16810370817578D+01 -0.98905860945003D-02 1 8 3 2 -0.43975167368967D+00 0.14395926504081D-01 2 8 3 2 -0.68394290283081D+00 -0.11779748011191D-02 3 8 3 2 0.16810370817578D+01 -0.98905860945009D-02 1 9 3 2 -0.30168507174267D-14 0.53089010285382D-17 2 9 3 2 0.24448724999850D-14 0.23659325836425D-14 3 9 3 2 0.14087185061603D+00 0.36345818109285D-09 1 10 3 2 0.49023141616435D-15 0.24057813688887D-16 2 10 3 2 0.12540582997524D-13 -0.15245573964358D-14 3 10 3 2 -0.11521353089176D+01 0.25800154610377D-07 1 11 3 2 -0.65673060506074D-15 0.26545377910558D-15 2 11 3 2 -0.12168372092340D-14 -0.76300230224073D-16 3 11 3 2 0.29843300792447D+01 -0.13044296979411D-06 1 12 3 2 0.48712738992746D-14 0.37096661114581D-16 2 12 3 2 0.10511814630816D-14 0.13513007923670D-16 3 12 3 2 0.17860256660851D+01 -0.15336967287265D-07 1 13 3 2 -0.24459026156699D-01 0.14667797057864D-02 2 13 3 2 -0.10416370308126D+01 0.74936709423614D-03 3 13 3 2 -0.61524493664588D+00 -0.19236340651834D-03 1 14 3 2 -0.37629434814572D-01 -0.15933136294483D-07 2 14 3 2 -0.10171320710695D+01 0.13645317271400D-07 3 14 3 2 -0.12410077114880D+00 -0.90218561041032D-08 1 15 3 2 0.37629434814529D-01 0.15933136276695D-07 2 15 3 2 0.10171320710695D+01 -0.13645317410949D-07 3 15 3 2 -0.12410077114884D+00 -0.90218559692762D-08 1 16 3 2 0.24459026156692D-01 -0.14667797057861D-02 2 16 3 2 0.10416370308126D+01 -0.74936709423597D-03 3 16 3 2 -0.61524493664591D+00 -0.19236340652034D-03 1 17 3 2 -0.44240345177301D+00 -0.11654722499866D-06 2 17 3 2 -0.10376008111885D+01 0.22639750213420D-06 3 17 3 2 0.86413724239475D+00 0.43621182869894D-07 1 18 3 2 0.98985970064578D+00 -0.70221971409993D-02 2 18 3 2 0.12605127499428D+00 -0.17367804717866D-03 3 18 3 2 0.22355539557402D+01 0.40605244130139D-02 1 19 3 2 -0.98985970064566D+00 0.70221971409991D-02 2 19 3 2 -0.12605127499416D+00 0.17367804717772D-03 3 19 3 2 0.22355539557403D+01 0.40605244130143D-02 1 20 3 2 0.44240345177309D+00 0.11654722499208D-06 2 20 3 2 0.10376008111886D+01 -0.22639750246368D-06 3 20 3 2 0.86413724239489D+00 0.43621189308003D-07 1 1 1 3 0.15051069402328D-12 -0.29453607031279D-08 2 1 1 3 0.84471420843343D-01 0.27483412534550D-08 3 1 1 3 -0.97474355509861D-15 -0.82943840135699D-16 1 2 1 3 -0.15562863989262D+00 0.20753865426104D-15 2 2 1 3 0.32946762254017D-01 -0.84978506379211D-08 3 2 1 3 -0.57284260906527D-15 0.78616732174359D-17 1 3 1 3 0.81101763433835D+01 0.00000000000000D+00 2 3 1 3 -0.13411441435577D+01 -0.57068282343976D-06 3 3 1 3 -0.13919709834620D-13 0.00000000000000D+00 1 4 1 3 0.36276863171944D+00 0.11989795136252D-08 2 4 1 3 -0.19209349629714D+00 0.14670636492349D-07 3 4 1 3 -0.64059835462056D-15 0.48497778561309D-16 1 5 1 3 -0.34739790734432D+01 -0.88547368917528D-09 2 5 1 3 -0.45407510740924D-02 0.22541775318337D-08 3 5 1 3 -0.22378761700955D+00 -0.40029092246582D-08 1 6 1 3 -0.34739790734432D+01 -0.88547296214208D-09 2 6 1 3 -0.45407510740898D-02 0.22541776369290D-08 3 6 1 3 0.22378761700954D+00 0.40029091038997D-08 1 7 1 3 -0.53435286521332D+00 -0.44385687380647D-03 2 7 1 3 0.12820431883206D+00 0.18235400061321D-02 3 7 1 3 0.20894608884872D+00 0.90634560144300D-04 1 8 1 3 -0.53435286521332D+00 -0.44385687380502D-03 2 8 1 3 0.12820431883205D+00 0.18235400061317D-02 3 8 1 3 -0.20894608884873D+00 -0.90634560144288D-04 1 9 1 3 -0.11748780754741D+01 0.20743023930629D-07 2 9 1 3 -0.44442567613534D+00 -0.15885680287403D-07 3 9 1 3 0.30160744112848D-15 0.12430192443174D-15 1 10 1 3 0.27086826803724D+00 -0.28246234201797D-08 2 10 1 3 0.10288537780567D-01 -0.56733238680431D-08 3 10 1 3 0.13545865205782D-13 0.26252953052473D-15 1 11 1 3 0.90847243655284D-01 0.10096856703250D-07 2 11 1 3 -0.69495458873944D-02 0.38816361208912D-08 3 11 1 3 -0.43722370104569D-15 -0.13650806825351D-16 1 12 1 3 -0.34067595583705D+00 0.13815604860470D-07 2 12 1 3 -0.60756791989571D-01 -0.18911858447407D-07 3 12 1 3 0.23710462383634D-16 -0.81901317454608D-16 1 13 1 3 -0.39631777278964D+00 -0.16656258511048D-02 2 13 1 3 0.42349060819948D+00 0.90267832783326D-02 3 13 1 3 0.58852109688780D+00 0.15680990687225D-01 1 14 1 3 0.25144422357394D-01 0.30885780243655D-02 2 14 1 3 -0.27520775231615D+00 -0.18559808744826D-02 3 14 1 3 0.73325324000044D+00 0.13507992412825D-01 1 15 1 3 0.25144422357393D-01 0.30885780243650D-02 2 15 1 3 -0.27520775231615D+00 -0.18559808744825D-02 3 15 1 3 -0.73325324000046D+00 -0.13507992412825D-01 1 16 1 3 -0.39631777278964D+00 -0.16656258511050D-02 2 16 1 3 0.42349060819948D+00 0.90267832783326D-02 3 16 1 3 -0.58852109688784D+00 -0.15680990687225D-01 1 17 1 3 -0.18590741189160D+00 -0.72134376292242D-08 2 17 1 3 0.31686007888682D+00 -0.14912577652808D-08 3 17 1 3 -0.52525060974981D+00 -0.15267510721415D-07 1 18 1 3 0.18627785637451D-01 0.21012580137492D-03 2 18 1 3 0.32726503947590D+00 -0.81391347136205D-03 3 18 1 3 0.29524272141792D+00 0.22397157633117D-03 1 19 1 3 0.18627785637453D-01 0.21012580137497D-03 2 19 1 3 0.32726503947591D+00 -0.81391347136193D-03 3 19 1 3 -0.29524272141791D+00 -0.22397157633105D-03 1 20 1 3 -0.18590741189160D+00 -0.72134376457942D-08 2 20 1 3 0.31686007888681D+00 -0.14912581253357D-08 3 20 1 3 0.52525060974981D+00 0.15267510443232D-07 1 1 2 3 0.84471420843343D-01 -0.27483402967792D-08 2 1 2 3 -0.92988356307624D-13 0.13414832008200D-07 3 1 2 3 -0.11864405819119D-13 0.10532804135797D-14 1 2 2 3 -0.32946762254022D-01 -0.84978506379211D-08 2 2 2 3 0.15490076597238D+00 -0.11418181213921D-14 3 2 2 3 -0.27265407606027D-13 0.14009851604474D-14 1 3 2 3 -0.13411378199714D+01 -0.62445455851852D-06 2 3 2 3 0.92689969471940D+01 0.00000000000000D+00 3 3 2 3 -0.56824622779526D-13 0.00000000000000D+00 1 4 2 3 -0.19209482885814D+00 -0.42071829302796D-08 2 4 2 3 0.10637963373163D+01 0.19393815160900D-08 3 4 2 3 -0.27217310663234D-14 0.37196216846149D-15 1 5 2 3 0.68537920293004D+00 0.78117125132523D-09 2 5 2 3 0.41365193551444D+01 -0.12492123481578D-08 3 5 2 3 -0.89081693609259D+00 0.21996940087597D-08 1 6 2 3 0.68537920293004D+00 0.78117135622118D-09 2 6 2 3 0.41365193551445D+01 -0.12492149535782D-08 3 6 2 3 0.89081693609256D+00 -0.21996918820171D-08 1 7 2 3 0.28245309356689D-01 0.22437261175106D-02 2 7 2 3 0.44552797138264D+00 -0.15198122804606D-02 3 7 2 3 -0.53357376639834D+01 0.11102714251335D-01 1 8 2 3 0.28245309356688D-01 0.22437261175101D-02 2 8 2 3 0.44552797138264D+00 -0.15198122804618D-02 3 8 2 3 0.53357376639834D+01 -0.11102714251334D-01 1 9 2 3 -0.63249916978203D+00 -0.75795691458406D-08 2 9 2 3 -0.14506871895841D+01 0.84332717282187D-08 3 9 2 3 -0.46753226868575D-14 -0.42007649967871D-15 1 10 2 3 -0.16366317516937D+00 0.98162995435876D-08 2 10 2 3 -0.95093453917009D+00 0.10155837970395D-08 3 10 2 3 0.11489454957776D-14 -0.14638333935634D-15 1 11 2 3 -0.73000920128046D-01 0.69602993171484D-08 2 11 2 3 -0.27633383793016D-03 -0.10177181625541D-07 3 11 2 3 0.22592842473336D-15 -0.61224203623444D-15 1 12 2 3 0.42462188945384D+00 -0.39108545130222D-08 2 12 2 3 -0.22294748005280D+01 0.93386619345692D-08 3 12 2 3 -0.85115420170685D-15 0.62398481586961D-15 1 13 2 3 -0.18325830586098D+00 0.29427663472302D-02 2 13 2 3 -0.20887133686635D+01 -0.10053792221447D-01 3 13 2 3 -0.56434041082926D+00 -0.14139490556713D-01 1 14 2 3 -0.10029332792676D+01 0.42170134288041D-02 2 14 2 3 -0.15089106015209D+01 0.75631303211636D-02 3 14 2 3 -0.76652726720675D+00 -0.69414717873122D-02 1 15 2 3 -0.10029332792676D+01 0.42170134288043D-02 2 15 2 3 -0.15089106015209D+01 0.75631303211644D-02 3 15 2 3 0.76652726720675D+00 0.69414717873130D-02 1 16 2 3 -0.18325830586098D+00 0.29427663472303D-02 2 16 2 3 -0.20887133686635D+01 -0.10053792221446D-01 3 16 2 3 0.56434041082915D+00 0.14139490556714D-01 1 17 2 3 0.90025678873825D+00 -0.98563491588016D-08 2 17 2 3 -0.16404728917974D+01 -0.31219671710687D-08 3 17 2 3 -0.64604799336346D+00 -0.25110322329583D-07 1 18 2 3 0.66650992669086D+00 -0.15958688660336D-02 2 18 2 3 -0.75893449639934D+00 0.18091601147810D-02 3 18 2 3 0.66671587413017D+00 -0.10683385518618D-02 1 19 2 3 0.66650992669087D+00 -0.15958688660335D-02 2 19 2 3 -0.75893449639933D+00 0.18091601147780D-02 3 19 2 3 -0.66671587413018D+00 0.10683385518620D-02 1 20 2 3 0.90025678873825D+00 -0.98563495188565D-08 2 20 2 3 -0.16404728917974D+01 -0.31219679954378D-08 3 20 2 3 0.64604799336348D+00 0.25110322081805D-07 1 1 3 3 -0.97474355513378D-15 -0.82927798749943D-16 2 1 3 3 -0.11864405819073D-13 0.10529925030500D-14 3 1 3 3 -0.22481512784405D-12 0.63756719060770D-08 1 2 3 3 -0.57284260902174D-15 0.79146415425546D-17 2 2 3 3 -0.27265407606013D-13 0.14009297241720D-14 3 2 3 3 -0.51058392511619D+00 0.59284354121634D-15 1 3 3 3 -0.13919709834620D-13 0.00000000000000D+00 2 3 3 3 -0.56824622779526D-13 0.11102230246252D-15 3 3 3 3 0.14574890059888D+02 0.00000000000000D+00 1 4 3 3 -0.64059835462310D-15 0.49149557663253D-16 2 4 3 3 -0.27217310662655D-14 0.37157124757015D-15 3 4 3 3 -0.32405254610749D+01 0.82746051533069D-08 1 5 3 3 0.43975167368965D+00 -0.14395926504082D-01 2 5 3 3 -0.68394290283089D+00 -0.11779748011175D-02 3 5 3 3 -0.16810370817580D+01 0.98905860945129D-02 1 6 3 3 -0.43975167368966D+00 0.14395926504082D-01 2 6 3 3 0.68394290283086D+00 0.11779748011197D-02 3 6 3 3 -0.16810370817579D+01 0.98905860945116D-02 1 7 3 3 -0.34544467547421D-01 0.29537549460748D-02 2 7 3 3 -0.61716601375008D+01 0.42040274325227D-02 3 7 3 3 0.64438804769740D+00 0.55120817600943D-03 1 8 3 3 0.34544467547418D-01 -0.29537549460748D-02 2 8 3 3 0.61716601375008D+01 -0.42040274325219D-02 3 8 3 3 0.64438804769736D+00 0.55120817600821D-03 1 9 3 3 0.30160744123360D-15 0.12206408949674D-15 2 9 3 3 -0.46753226852398D-14 -0.42141026647708D-15 3 9 3 3 -0.29843300792445D+01 0.13044295665286D-06 1 10 3 3 0.13545865205744D-13 0.26293651096916D-15 2 10 3 3 0.11489454956125D-14 -0.14618637850569D-15 3 10 3 3 0.17860256660852D+01 -0.15336967239002D-07 1 11 3 3 -0.43722370093880D-15 -0.13639901703585D-16 2 11 3 3 0.22592842488008D-15 -0.61171828701489D-15 3 11 3 3 -0.14087185061614D+00 -0.36345499949345D-09 1 12 3 3 0.23710462383636D-16 -0.81901317454608D-16 2 12 3 3 -0.85115420087967D-15 0.62225009239363D-15 3 12 3 3 -0.11521353089175D+01 0.25800160789107D-07 1 13 3 3 0.98985970064562D+00 -0.70221971410086D-02 2 13 3 3 -0.12605127499425D+00 0.17367804719088D-03 3 13 3 3 -0.22355539557402D+01 -0.40605244129984D-02 1 14 3 3 0.44240345177309D+00 0.11654722501160D-06 2 14 3 3 -0.10376008111886D+01 0.22639750264708D-06 3 14 3 3 0.86413724239483D+00 0.43621186697018D-07 1 15 3 3 -0.44240345177310D+00 -0.11654722503451D-06 2 15 3 3 0.10376008111886D+01 -0.22639750183624D-06 3 15 3 3 0.86413724239483D+00 0.43621190564523D-07 1 16 3 3 -0.98985970064568D+00 0.70221971410087D-02 2 16 3 3 0.12605127499414D+00 -0.17367804719044D-03 3 16 3 3 -0.22355539557402D+01 -0.40605244130026D-02 1 17 3 3 0.37629434814572D-01 0.15933136338949D-07 2 17 3 3 -0.10171320710695D+01 0.13645316300386D-07 3 17 3 3 -0.12410077114883D+00 -0.90218539292149D-08 1 18 3 3 -0.24459026156668D-01 0.14667797057883D-02 2 18 3 3 0.10416370308126D+01 -0.74936709423388D-03 3 18 3 3 0.61524493664593D+00 0.19236340652355D-03 1 19 3 3 0.24459026156678D-01 -0.14667797057882D-02 2 19 3 3 -0.10416370308127D+01 0.74936709423410D-03 3 19 3 3 0.61524493664593D+00 0.19236340652296D-03 1 20 3 3 -0.37629434814573D-01 -0.15933136617240D-07 2 20 3 3 0.10171320710695D+01 -0.13645316547730D-07 3 20 3 3 -0.12410077114881D+00 -0.90218578486230D-08 1 1 1 4 -0.15562863989261D+00 -0.87926706859983D-16 2 1 1 4 0.32946762254018D-01 -0.84978504365561D-08 3 1 1 4 0.85949219538802D-14 0.19171716550677D-15 1 2 1 4 0.21785058977234D-13 -0.29453664051161D-08 2 2 1 4 0.84471420843396D-01 0.27483403156561D-08 3 2 1 4 0.67416309856987D-14 0.82353520738140D-16 1 3 1 4 0.36276863171944D+00 0.11989802317177D-08 2 3 1 4 -0.19209349629714D+00 0.14670636435082D-07 3 3 1 4 -0.64059835462310D-15 -0.49149557663253D-16 1 4 1 4 0.81101763433835D+01 0.00000000000000D+00 2 4 1 4 -0.13411441435579D+01 -0.57068282343976D-06 3 4 1 4 -0.21025137192221D-13 0.00000000000000D+00 1 5 1 4 -0.34739790734434D+01 -0.88547233056797D-09 2 5 1 4 -0.45407510740805D-02 0.22541775601184D-08 3 5 1 4 -0.22378761700946D+00 -0.40029091834603D-08 1 6 1 4 -0.34739790734432D+01 -0.88547389635740D-09 2 6 1 4 -0.45407510740782D-02 0.22541774619853D-08 3 6 1 4 0.22378761700938D+00 0.40029089549996D-08 1 7 1 4 0.53435286521329D+00 0.44385687380304D-03 2 7 1 4 -0.12820431883204D+00 -0.18235400061320D-02 3 7 1 4 -0.20894608884873D+00 -0.90634560143947D-04 1 8 1 4 0.53435286521330D+00 0.44385687380329D-03 2 8 1 4 -0.12820431883204D+00 -0.18235400061322D-02 3 8 1 4 0.20894608884873D+00 0.90634560144020D-04 1 9 1 4 0.27086826803725D+00 -0.28246235853566D-08 2 9 1 4 0.10288537780566D-01 -0.56733237329886D-08 3 9 1 4 0.23443021790094D-14 -0.17231116655192D-15 1 10 1 4 -0.11748780754741D+01 0.20743023956414D-07 2 10 1 4 -0.44442567613522D+00 -0.15885680100852D-07 3 10 1 4 -0.72475985152282D-15 -0.13814408458626D-15 1 11 1 4 -0.34067595583692D+00 0.13815601688870D-07 2 11 1 4 -0.60756791989450D-01 -0.18911856335717D-07 3 11 1 4 0.83241429804828D-15 0.72433729038211D-16 1 12 1 4 0.90847243655280D-01 0.10096858087019D-07 2 12 1 4 -0.69495458873913D-02 0.38816361418133D-08 3 12 1 4 -0.22321114902226D-15 -0.10859195477819D-15 1 13 1 4 0.25144422357356D-01 0.30885780243656D-02 2 13 1 4 -0.27520775231612D+00 -0.18559808744822D-02 3 13 1 4 0.73325324000034D+00 0.13507992412826D-01 1 14 1 4 -0.39631777278961D+00 -0.16656258511052D-02 2 14 1 4 0.42349060819950D+00 0.90267832783322D-02 3 14 1 4 0.58852109688790D+00 0.15680990687225D-01 1 15 1 4 -0.39631777278960D+00 -0.16656258511047D-02 2 15 1 4 0.42349060819940D+00 0.90267832783319D-02 3 15 1 4 -0.58852109688773D+00 -0.15680990687225D-01 1 16 1 4 0.25144422357362D-01 0.30885780243651D-02 2 16 1 4 -0.27520775231616D+00 -0.18559808744826D-02 3 16 1 4 -0.73325324000046D+00 -0.13507992412826D-01 1 17 1 4 0.18627785637451D-01 0.21012580137512D-03 2 17 1 4 0.32726503947590D+00 -0.81391347136216D-03 3 17 1 4 0.29524272141792D+00 0.22397157633064D-03 1 18 1 4 -0.18590741189161D+00 -0.72134376366983D-08 2 18 1 4 0.31686007888678D+00 -0.14912590610316D-08 3 18 1 4 -0.52525060974979D+00 -0.15267510881372D-07 1 19 1 4 -0.18590741189158D+00 -0.72134378720150D-08 2 19 1 4 0.31686007888680D+00 -0.14912583802603D-08 3 19 1 4 0.52525060974982D+00 0.15267510767510D-07 1 20 1 4 0.18627785637450D-01 0.21012580137490D-03 2 20 1 4 0.32726503947589D+00 -0.81391347136172D-03 3 20 1 4 -0.29524272141792D+00 -0.22397157633108D-03 1 1 2 4 -0.32946762254022D-01 -0.84978504365561D-08 2 1 2 4 0.15490076597232D+00 -0.66292108737698D-15 3 1 2 4 0.10732522526407D-13 0.78080701327177D-15 1 2 2 4 0.84471420843396D-01 -0.27483412345780D-08 2 2 2 4 -0.29639100024077D-13 0.13414830556070D-07 3 2 2 4 0.19971542364234D-13 -0.10640151325819D-14 1 3 2 4 -0.19209482885814D+00 -0.42071829875470D-08 2 3 2 4 0.10637963373163D+01 0.19393820934552D-08 3 3 2 4 -0.27217310670927D-14 -0.37113756670116D-15 1 4 2 4 -0.13411378199716D+01 -0.62445455851852D-06 2 4 2 4 0.92689969471940D+01 0.00000000000000D+00 3 4 2 4 0.81731210693702D-13 0.00000000000000D+00 1 5 2 4 0.68537920293005D+00 0.78117127960992D-09 2 5 2 4 0.41365193551445D+01 -0.12492132474321D-08 3 5 2 4 -0.89081693609256D+00 0.21996937503204D-08 1 6 2 4 0.68537920293005D+00 0.78117118127744D-09 2 6 2 4 0.41365193551445D+01 -0.12492115272200D-08 3 6 2 4 0.89081693609256D+00 -0.21996947260131D-08 1 7 2 4 -0.28245309356670D-01 -0.22437261175104D-02 2 7 2 4 -0.44552797138275D+00 0.15198122804835D-02 3 7 2 4 0.53357376639835D+01 -0.11102714251339D-01 1 8 2 4 -0.28245309356671D-01 -0.22437261175106D-02 2 8 2 4 -0.44552797138277D+00 0.15198122804763D-02 3 8 2 4 -0.53357376639835D+01 0.11102714251339D-01 1 9 2 4 -0.16366317516937D+00 0.98162996786421D-08 2 9 2 4 -0.95093453917009D+00 0.10155840565792D-08 3 9 2 4 -0.96348179634062D-15 0.12897300588180D-15 1 10 2 4 -0.63249916978192D+00 -0.75795689592897D-08 2 10 2 4 -0.14506871895841D+01 0.84332715235047D-08 3 10 2 4 -0.14452484955147D-14 -0.63096658243496D-15 1 11 2 4 0.42462188945396D+00 -0.39108524013321D-08 2 11 2 4 -0.22294748005283D+01 0.93386711957882D-08 3 11 2 4 -0.60685013976947D-14 -0.26361124240747D-14 1 12 2 4 -0.73000920128043D-01 0.69602993380705D-08 2 12 2 4 -0.27633383797593D-03 -0.10177184732306D-07 3 12 2 4 0.14644739203054D-14 0.84764085712639D-16 1 13 2 4 -0.10029332792676D+01 0.42170134288046D-02 2 13 2 4 -0.15089106015210D+01 0.75631303211643D-02 3 13 2 4 -0.76652726720671D+00 -0.69414717873133D-02 1 14 2 4 -0.18325830586095D+00 0.29427663472298D-02 2 14 2 4 -0.20887133686635D+01 -0.10053792221446D-01 3 14 2 4 -0.56434041082935D+00 -0.14139490556713D-01 1 15 2 4 -0.18325830586105D+00 0.29427663472295D-02 2 15 2 4 -0.20887133686635D+01 -0.10053792221447D-01 3 15 2 4 0.56434041082920D+00 0.14139490556712D-01 1 16 2 4 -0.10029332792677D+01 0.42170134288042D-02 2 16 2 4 -0.15089106015210D+01 0.75631303211615D-02 3 16 2 4 0.76652726720682D+00 0.69414717873126D-02 1 17 2 4 0.66650992669086D+00 -0.15958688660337D-02 2 17 2 4 -0.75893449639935D+00 0.18091601147803D-02 3 17 2 4 0.66671587413015D+00 -0.10683385518610D-02 1 18 2 4 0.90025678873820D+00 -0.98563504545524D-08 2 18 2 4 -0.16404728917973D+01 -0.31219657253164D-08 3 18 2 4 -0.64604799336336D+00 -0.25110321584804D-07 1 19 2 4 0.90025678873823D+00 -0.98563497737811D-08 2 19 2 4 -0.16404728917974D+01 -0.31219672818333D-08 3 19 2 4 0.64604799336345D+00 0.25110321812530D-07 1 20 2 4 0.66650992669085D+00 -0.15958688660333D-02 2 20 2 4 -0.75893449639935D+00 0.18091601147809D-02 3 20 2 4 -0.66671587413018D+00 0.10683385518606D-02 1 1 3 4 0.85949219539237D-14 0.19177013383189D-15 2 1 3 4 0.10732522526422D-13 0.78075157699636D-15 3 1 3 4 -0.51058392511606D+00 0.31946917109930D-15 1 2 3 4 0.67416309856635D-14 0.82369562123896D-16 2 2 3 4 0.19971542364281D-13 -0.10643030431117D-14 3 2 3 4 -0.27981033919398D-13 0.63756730338910D-08 1 3 3 4 -0.64059835462057D-15 -0.48497778561309D-16 2 3 3 4 -0.27217310663234D-14 -0.37174532802700D-15 3 3 3 4 -0.32405254610749D+01 0.82746039772818D-08 1 4 3 4 -0.21025137192221D-13 0.00000000000000D+00 2 4 3 4 0.81731210693702D-13 0.11102230246252D-15 3 4 3 4 0.14574890059892D+02 0.00000000000000D+00 1 5 3 4 0.43975167368975D+00 -0.14395926504082D-01 2 5 3 4 -0.68394290283086D+00 -0.11779748011178D-02 3 5 3 4 -0.16810370817577D+01 0.98905860945112D-02 1 6 3 4 -0.43975167368982D+00 0.14395926504082D-01 2 6 3 4 0.68394290283086D+00 0.11779748011168D-02 3 6 3 4 -0.16810370817578D+01 0.98905860945174D-02 1 7 3 4 0.34544467547415D-01 -0.29537549460744D-02 2 7 3 4 0.61716601375008D+01 -0.42040274325272D-02 3 7 3 4 -0.64438804769720D+00 -0.55120817600193D-03 1 8 3 4 -0.34544467547416D-01 0.29537549460745D-02 2 8 3 4 -0.61716601375009D+01 0.42040274325268D-02 3 8 3 4 -0.64438804769726D+00 -0.55120817600249D-03 1 9 3 4 0.23443021789715D-14 -0.17190418610749D-15 2 9 3 4 -0.96348179650572D-15 0.12916996673244D-15 3 9 3 4 0.17860256660851D+01 -0.15336967254658D-07 1 10 3 4 -0.72475985141770D-15 -0.14038191952125D-15 2 10 3 4 -0.14452484938970D-14 -0.63230034923333D-15 3 10 3 4 -0.29843300792447D+01 0.13044295672560D-06 1 11 3 4 0.83241429804829D-15 0.72433729038212D-16 2 11 3 4 -0.60685013968675D-14 -0.26378471475506D-14 3 11 3 4 -0.11521353089171D+01 0.25800153300770D-07 1 12 3 4 -0.22321114892532D-15 -0.10857870657523D-15 2 12 3 4 0.14644739200338D-14 0.85771384787307D-16 3 12 3 4 -0.14087185061598D+00 -0.36345785109082D-09 1 13 3 4 0.44240345177299D+00 0.11654722509409D-06 2 13 3 4 -0.10376008111885D+01 0.22639750149163D-06 3 13 3 4 0.86413724239475D+00 0.43621188061545D-07 1 14 3 4 0.98985970064572D+00 -0.70221971410084D-02 2 14 3 4 -0.12605127499434D+00 0.17367804719102D-03 3 14 3 4 -0.22355539557403D+01 -0.40605244130072D-02 1 15 3 4 -0.98985970064556D+00 0.70221971410085D-02 2 15 3 4 0.12605127499419D+00 -0.17367804719217D-03 3 15 3 4 -0.22355539557402D+01 -0.40605244130013D-02 1 16 3 4 -0.44240345177311D+00 -0.11654722509521D-06 2 16 3 4 0.10376008111886D+01 -0.22639750222649D-06 3 16 3 4 0.86413724239492D+00 0.43621186060680D-07 1 17 3 4 -0.24459026156664D-01 0.14667797057878D-02 2 17 3 4 0.10416370308126D+01 -0.74936709423311D-03 3 17 3 4 0.61524493664595D+00 0.19236340652185D-03 1 18 3 4 0.37629434814586D-01 0.15933136178991D-07 2 18 3 4 -0.10171320710694D+01 0.13645317045165D-07 3 18 3 4 -0.12410077114879D+00 -0.90218552009581D-08 1 19 3 4 -0.37629434814558D-01 -0.15933136292962D-07 2 19 3 4 0.10171320710695D+01 -0.13645316817006D-07 3 19 3 4 -0.12410077114888D+00 -0.90218535675119D-08 1 20 3 4 0.24459026156668D-01 -0.14667797057882D-02 2 20 3 4 -0.10416370308127D+01 0.74936709423263D-03 3 20 3 4 0.61524493664593D+00 0.19236340652300D-03 1 1 1 5 0.53432111858778D+00 0.88771390239262D-03 2 1 1 5 0.28205507708318D-01 0.44874730179367D-02 3 1 1 5 -0.34542834473133D-01 -0.29535935175403D-02 1 2 1 5 0.53432111858784D+00 0.88771390239439D-03 2 2 1 5 0.28205507708316D-01 0.44874730179373D-02 3 2 1 5 -0.34542834473129D-01 -0.29535935175402D-02 1 3 1 5 -0.34739790734432D+01 0.88547368917528D-09 2 3 1 5 0.68537920293004D+00 -0.78117125132523D-09 3 3 1 5 0.43975167368965D+00 0.14395926504082D-01 1 4 1 5 -0.34739790734434D+01 0.88547233056797D-09 2 4 1 5 0.68537920293005D+00 -0.78117127960992D-09 3 4 1 5 0.43975167368975D+00 0.14395926504082D-01 1 5 1 5 0.17032235679795D+02 0.00000000000000D+00 2 5 1 5 0.13008018820259D+01 -0.84449587720246D-07 3 5 1 5 -0.11775168613240D+00 -0.42171026902080D-07 1 6 1 5 0.14183565285401D+01 0.00000000000000D+00 2 6 1 5 0.43331506645509D-02 0.37269986739726D-09 3 6 1 5 -0.43133549922910D+01 -0.48126889764435D-09 1 7 1 5 -0.59201998543929D-14 0.36453585289745D-14 2 7 1 5 0.21861162354999D-14 0.27876495812912D-15 3 7 1 5 -0.10548673656662D-17 0.15160753293697D-17 1 8 1 5 -0.98584043929047D-15 0.41003390653009D-15 2 8 1 5 -0.26264620429562D-14 -0.27781378479316D-15 3 8 1 5 -0.45013287456730D-17 0.14733469102317D-17 1 9 1 5 -0.16195405218010D+01 0.13847969061544D+00 2 9 1 5 -0.90065158085639D-01 0.16654270979538D-01 3 9 1 5 0.45096495312507D+00 -0.28904022487875D+00 1 10 1 5 -0.16195405218006D+01 0.13847969061544D+00 2 10 1 5 -0.90065158085617D-01 0.16654270979538D-01 3 10 1 5 0.45096495312512D+00 -0.28904022487875D+00 1 11 1 5 0.64637539596326D-01 -0.95134618349728D-10 2 11 1 5 0.25313561100868D-01 -0.28691428191925D-08 3 11 1 5 0.86856186557536D+00 0.88069222136633D-02 1 12 1 5 0.64637539596383D-01 -0.95137092753472D-10 2 12 1 5 0.25313561100879D-01 -0.28691422789965D-08 3 12 1 5 0.86856186557539D+00 0.88069222136628D-02 1 13 1 5 -0.14132858478809D+01 -0.16780058856161D-01 2 13 1 5 0.43386576755758D+00 -0.89129393016624D-02 3 13 1 5 0.77009826948023D+00 -0.16551616775286D-01 1 14 1 5 -0.14132858478807D+01 -0.16780058856161D-01 2 14 1 5 0.43386576755786D+00 -0.89129393016618D-02 3 14 1 5 0.77009826947987D+00 -0.16551616775286D-01 1 15 1 5 -0.31076334350387D+00 0.97508677259309D-02 2 15 1 5 -0.27322497593675D+00 0.66212463350024D-02 3 15 1 5 0.11574704131345D+00 -0.15169791020613D-01 1 16 1 5 -0.31076334350387D+00 0.97508677259311D-02 2 16 1 5 -0.27322497593675D+00 0.66212463350021D-02 3 16 1 5 0.11574704131345D+00 -0.15169791020613D-01 1 17 1 5 0.11975170767614D+00 -0.98203798255541D-02 2 17 1 5 -0.71405983092762D+00 0.99047118005322D-02 3 17 1 5 0.98932719077390D+00 -0.77813748561253D-02 1 18 1 5 0.11975170767610D+00 -0.98203798255542D-02 2 18 1 5 -0.71405983092725D+00 0.99047118005330D-02 3 18 1 5 0.98932719077383D+00 -0.77813748561255D-02 1 19 1 5 -0.41860808482343D-01 0.13715067473218D-01 2 19 1 5 0.60402079476125D-02 -0.32115839925080D-01 3 19 1 5 0.20564018406032D+00 -0.28648551012425D-01 1 20 1 5 -0.41860808482348D-01 0.13715067473218D-01 2 20 1 5 0.60402079476081D-02 -0.32115839925080D-01 3 20 1 5 0.20564018406030D+00 -0.28648551012425D-01 1 1 2 5 0.12824360441077D+00 0.36471075147193D-02 2 1 2 5 -0.44548204137474D+00 0.30396572270224D-02 3 1 2 5 0.61716593510246D+01 0.42033921524917D-02 1 2 2 5 0.12824360441076D+00 0.36471075147199D-02 2 2 2 5 -0.44548204137475D+00 0.30396572270110D-02 3 2 2 5 0.61716593510247D+01 0.42033921524827D-02 1 3 2 5 -0.45407510740924D-02 -0.22541775318337D-08 2 3 2 5 0.41365193551444D+01 0.12492123481578D-08 3 3 2 5 -0.68394290283089D+00 0.11779748011175D-02 1 4 2 5 -0.45407510740805D-02 -0.22541775601184D-08 2 4 2 5 0.41365193551445D+01 0.12492132474321D-08 3 4 2 5 -0.68394290283086D+00 0.11779748011178D-02 1 5 2 5 0.13007947808518D+01 0.92979494467397D-07 2 5 2 5 0.28255601903496D+02 0.00000000000000D+00 3 5 2 5 -0.28470657431608D+01 0.29541115483351D-06 1 6 2 5 0.43331506645509D-02 -0.37269986739726D-09 2 6 2 5 0.49497625398612D+01 0.00000000000000D+00 3 6 2 5 0.13585497355038D+01 -0.13554577267503D-07 1 7 2 5 0.21874312745974D-14 0.27876495812912D-15 2 7 2 5 -0.39829436223762D-13 0.30156400470859D-14 3 7 2 5 -0.60066278264103D-17 -0.15960105041923D-14 1 8 2 5 -0.26264621946275D-14 -0.27781378479316D-15 2 8 2 5 -0.32733902617851D-13 -0.18859651819363D-14 3 8 2 5 -0.80513651475737D-13 -0.91466918707509D-15 1 9 2 5 -0.19136626185786D+00 0.15197064924277D-01 2 9 2 5 -0.34305302337379D+01 0.18581713521824D+00 3 9 2 5 -0.22296174836245D+00 0.77409466642936D-01 1 10 2 5 -0.19136626185784D+00 0.15197064924277D-01 2 10 2 5 -0.34305302337377D+01 0.18581713521824D+00 3 10 2 5 -0.22296174836224D+00 0.77409466642936D-01 1 11 2 5 -0.76864195703410D-01 -0.17698092776245D-08 2 11 2 5 -0.37783647993467D+00 -0.54721539775295D-10 3 11 2 5 0.50596657091991D+01 0.22843272391442D-01 1 12 2 5 -0.76864195703400D-01 -0.17698087374285D-08 2 12 2 5 -0.37783647993477D+00 -0.54724178379749D-10 3 12 2 5 0.50596657091991D+01 0.22843272391444D-01 1 13 2 5 -0.29325622775832D+01 0.40133603037763D-02 2 13 2 5 -0.56047356324624D+01 0.69297330690930D-02 3 13 2 5 0.41102064508718D+00 -0.14635914271648D-01 1 14 2 5 -0.29325622775829D+01 0.40133603037770D-02 2 14 2 5 -0.56047356324625D+01 0.69297330690931D-02 3 14 2 5 0.41102064508697D+00 -0.14635914271647D-01 1 15 2 5 -0.84458994063050D+00 0.80772866284178D-02 2 15 2 5 -0.19712272332279D+01 -0.48238814018633D-03 3 15 2 5 -0.46565926400898D+00 -0.96578056394336D-02 1 16 2 5 -0.84458994063050D+00 0.80772866284176D-02 2 16 2 5 -0.19712272332279D+01 -0.48238814018270D-03 3 16 2 5 -0.46565926400901D+00 -0.96578056394316D-02 1 17 2 5 0.16406849123270D+01 -0.32328470040599D-02 2 17 2 5 -0.57399295574616D+01 0.25035389652168D-03 3 17 2 5 -0.49419589443972D+00 0.23665373738744D-01 1 18 2 5 0.16406849123273D+01 -0.32328470040591D-02 2 18 2 5 -0.57399295574619D+01 0.25035389652277D-03 3 18 2 5 -0.49419589443961D+00 0.23665373738744D-01 1 19 2 5 0.86364268745081D+00 -0.31244453421060D-01 2 19 2 5 -0.19627813396923D+01 0.22171759650072D-01 3 19 2 5 0.49064510769629D+00 0.48289991207568D-01 1 20 2 5 0.86364268745080D+00 -0.31244453421059D-01 2 20 2 5 -0.19627813396923D+01 0.22171759650075D-01 3 20 2 5 0.49064510769632D+00 0.48289991207568D-01 1 1 3 5 0.20900339623782D+00 0.18126319184378D-03 2 1 3 5 0.53359140394452D+01 -0.22205331350655D-01 3 1 3 5 -0.64438559312219D+00 0.55134499776671D-03 1 2 3 5 0.20900339623782D+00 0.18126319184395D-03 2 2 3 5 0.53359140394453D+01 -0.22205331350664D-01 3 2 3 5 -0.64438559312222D+00 0.55134499776238D-03 1 3 3 5 -0.22378761700955D+00 0.40029092246582D-08 2 3 3 5 -0.89081693609259D+00 -0.21996940087597D-08 3 3 3 5 -0.16810370817580D+01 -0.98905860945129D-02 1 4 3 5 -0.22378761700946D+00 0.40029091834603D-08 2 4 3 5 -0.89081693609256D+00 -0.21996937503204D-08 3 4 3 5 -0.16810370817577D+01 -0.98905860945112D-02 1 5 3 5 -0.11774096893409D+00 0.72995172042819D-07 2 5 3 5 -0.28470716517157D+01 -0.32936070742274D-06 3 5 3 5 0.39864613984769D+02 0.00000000000000D+00 1 6 3 5 0.43133549922910D+01 -0.48126889764435D-09 2 6 3 5 -0.13585497355038D+01 -0.13554577267503D-07 3 6 3 5 -0.31041399857622D+02 0.00000000000000D+00 1 7 3 5 0.10681588848755D-17 0.15160753293697D-17 2 7 3 5 -0.60066278264103D-17 -0.15960105041924D-14 3 7 3 5 -0.31449209244319D-13 0.12888310085190D-14 1 8 3 5 -0.45013287424418D-17 0.14733469102315D-17 2 8 3 5 -0.80513651459303D-13 -0.91466918707509D-15 3 8 3 5 -0.91529225785495D-14 0.56854378544587D-14 1 9 3 5 -0.23325028865521D+01 -0.12055524764948D+00 2 9 3 5 0.42446620651855D+00 0.31095994092535D-01 3 9 3 5 -0.84039943674560D+00 -0.82345547420193D+00 1 10 3 5 -0.23325028865521D+01 -0.12055524764948D+00 2 10 3 5 0.42446620651876D+00 0.31095994092535D-01 3 10 3 5 -0.84039943674617D+00 -0.82345547420193D+00 1 11 3 5 -0.83892502093507D-01 0.25500722000109D-08 2 11 3 5 0.55708549824360D+00 0.30160418565335D-08 3 11 3 5 0.77235024357356D-02 -0.92952290049535D-02 1 12 3 5 -0.83892502093477D-01 0.25500716877046D-08 2 12 3 5 0.55708549824363D+00 0.30160438374922D-08 3 12 3 5 0.77235024357654D-02 -0.92952290049538D-02 1 13 3 5 -0.37229864838553D+00 -0.71952141488996D-01 2 13 3 5 -0.35637835461180D+00 -0.67733380454438D-01 3 13 3 5 -0.38187926021983D+01 0.83435389186050D-02 1 14 3 5 -0.37229864838589D+00 -0.71952141488996D-01 2 14 3 5 -0.35637835461201D+00 -0.67733380454437D-01 3 14 3 5 -0.38187926021984D+01 0.83435389186069D-02 1 15 3 5 -0.42333913530498D+00 0.57653228107844D-03 2 15 3 5 -0.13123301985444D+00 -0.52540686046652D-02 3 15 3 5 0.33113979864878D+01 -0.10995496813762D-01 1 16 3 5 -0.42333913530498D+00 0.57653228107839D-03 2 16 3 5 -0.13123301985447D+00 -0.52540686046633D-02 3 16 3 5 0.33113979864876D+01 -0.10995496813763D-01 1 17 3 5 -0.20245841920847D+00 -0.64972512946613D-01 2 17 3 5 0.53594074220148D+00 0.89956128772503D-01 3 17 3 5 -0.33040214403575D+01 -0.17968918688659D-02 1 18 3 5 -0.20245841920854D+00 -0.64972512946613D-01 2 18 3 5 0.53594074220160D+00 0.89956128772503D-01 3 18 3 5 -0.33040214403572D+01 -0.17968918688690D-02 1 19 3 5 -0.27108133047545D+00 -0.12033131126891D-01 2 19 3 5 0.31948038827917D+00 0.20095564767296D-01 3 19 3 5 0.29726339901638D+01 -0.22414061714860D-01 1 20 3 5 -0.27108133047548D+00 -0.12033131126891D-01 2 20 3 5 0.31948038827920D+00 0.20095564767297D-01 3 20 3 5 0.29726339901638D+01 -0.22414061714861D-01 1 1 1 6 0.53432111858778D+00 0.88771390239261D-03 2 1 1 6 0.28205507708318D-01 0.44874730179369D-02 3 1 1 6 0.34542834473132D-01 0.29535935175403D-02 1 2 1 6 0.53432111858783D+00 0.88771390239523D-03 2 2 1 6 0.28205507708320D-01 0.44874730179372D-02 3 2 1 6 0.34542834473129D-01 0.29535935175402D-02 1 3 1 6 -0.34739790734432D+01 0.88547296214208D-09 2 3 1 6 0.68537920293004D+00 -0.78117135622118D-09 3 3 1 6 -0.43975167368966D+00 -0.14395926504082D-01 1 4 1 6 -0.34739790734432D+01 0.88547389635740D-09 2 4 1 6 0.68537920293005D+00 -0.78117118127744D-09 3 4 1 6 -0.43975167368982D+00 -0.14395926504082D-01 1 5 1 6 0.14183565285401D+01 0.00000000000000D+00 2 5 1 6 0.43331506645509D-02 0.37269986739726D-09 3 5 1 6 0.43133549922910D+01 0.48126889764435D-09 1 6 1 6 0.17032235679794D+02 0.00000000000000D+00 2 6 1 6 0.13008018820260D+01 -0.84449587720246D-07 3 6 1 6 0.11775168613261D+00 0.42171026902080D-07 1 7 1 6 -0.24846272324594D-14 0.41003390653009D-15 2 7 1 6 0.16201448339865D-14 -0.27781378479316D-15 3 7 1 6 -0.15033098067775D-14 0.14733469102315D-17 1 8 1 6 -0.59202150147924D-14 0.36453585289745D-14 2 8 1 6 0.10179722043509D-13 0.27876495812912D-15 3 8 1 6 0.13285982646520D-15 0.15160753293701D-17 1 9 1 6 -0.16195405218009D+01 0.13847969061544D+00 2 9 1 6 -0.90065158085638D-01 0.16654270979538D-01 3 9 1 6 -0.45096495312509D+00 0.28904022487875D+00 1 10 1 6 -0.16195405218007D+01 0.13847969061544D+00 2 10 1 6 -0.90065158085628D-01 0.16654270979538D-01 3 10 1 6 -0.45096495312526D+00 0.28904022487875D+00 1 11 1 6 0.64637539596325D-01 -0.95135500632640D-10 2 11 1 6 0.25313561100885D-01 -0.28691427197591D-08 3 11 1 6 -0.86856186557537D+00 -0.88069222136633D-02 1 12 1 6 0.64637539596386D-01 -0.95136032773330D-10 2 12 1 6 0.25313561100883D-01 -0.28691421151919D-08 3 12 1 6 -0.86856186557539D+00 -0.88069222136625D-02 1 13 1 6 -0.31076334350387D+00 0.97508677259310D-02 2 13 1 6 -0.27322497593674D+00 0.66212463350026D-02 3 13 1 6 -0.11574704131344D+00 0.15169791020614D-01 1 14 1 6 -0.31076334350386D+00 0.97508677259307D-02 2 14 1 6 -0.27322497593675D+00 0.66212463350022D-02 3 14 1 6 -0.11574704131345D+00 0.15169791020614D-01 1 15 1 6 -0.14132858478807D+01 -0.16780058856161D-01 2 15 1 6 0.43386576755789D+00 -0.89129393016622D-02 3 15 1 6 -0.77009826947990D+00 0.16551616775286D-01 1 16 1 6 -0.14132858478808D+01 -0.16780058856161D-01 2 16 1 6 0.43386576755765D+00 -0.89129393016629D-02 3 16 1 6 -0.77009826948019D+00 0.16551616775286D-01 1 17 1 6 -0.41860808482349D-01 0.13715067473218D-01 2 17 1 6 0.60402079476072D-02 -0.32115839925080D-01 3 17 1 6 -0.20564018406031D+00 0.28648551012425D-01 1 18 1 6 -0.41860808482344D-01 0.13715067473218D-01 2 18 1 6 0.60402079476081D-02 -0.32115839925080D-01 3 18 1 6 -0.20564018406032D+00 0.28648551012425D-01 1 19 1 6 0.11975170767610D+00 -0.98203798255542D-02 2 19 1 6 -0.71405983092730D+00 0.99047118005331D-02 3 19 1 6 -0.98932719077384D+00 0.77813748561256D-02 1 20 1 6 0.11975170767615D+00 -0.98203798255539D-02 2 20 1 6 -0.71405983092751D+00 0.99047118005320D-02 3 20 1 6 -0.98932719077387D+00 0.77813748561257D-02 1 1 2 6 0.12824360441077D+00 0.36471075147194D-02 2 1 2 6 -0.44548204137473D+00 0.30396572270230D-02 3 1 2 6 -0.61716593510246D+01 -0.42033921524923D-02 1 2 2 6 0.12824360441077D+00 0.36471075147198D-02 2 2 2 6 -0.44548204137477D+00 0.30396572270153D-02 3 2 2 6 -0.61716593510246D+01 -0.42033921524825D-02 1 3 2 6 -0.45407510740898D-02 -0.22541776369290D-08 2 3 2 6 0.41365193551445D+01 0.12492149535782D-08 3 3 2 6 0.68394290283086D+00 -0.11779748011197D-02 1 4 2 6 -0.45407510740782D-02 -0.22541774619853D-08 2 4 2 6 0.41365193551445D+01 0.12492115272200D-08 3 4 2 6 0.68394290283086D+00 -0.11779748011168D-02 1 5 2 6 0.43331506645509D-02 -0.37269986739726D-09 2 5 2 6 0.49497625398612D+01 0.00000000000000D+00 3 5 2 6 -0.13585497355038D+01 0.13554577267503D-07 1 6 2 6 0.13007947808519D+01 0.92979494467397D-07 2 6 2 6 0.28255601903496D+02 0.00000000000000D+00 3 6 2 6 0.28470657431607D+01 -0.29541115483351D-06 1 7 2 6 0.16201446823152D-14 -0.27781378479316D-15 2 7 2 6 -0.20618593865584D-13 -0.18859651819363D-14 3 7 2 6 0.57376059631766D-13 -0.91466918707509D-15 1 8 2 6 0.10181037082606D-13 0.27876495812912D-15 2 8 2 6 -0.31835830442740D-13 0.30156400470859D-14 3 8 2 6 0.13996579188311D-13 -0.15960105041924D-14 1 9 2 6 -0.19136626185786D+00 0.15197064924277D-01 2 9 2 6 -0.34305302337379D+01 0.18581713521824D+00 3 9 2 6 0.22296174836244D+00 -0.77409466642936D-01 1 10 2 6 -0.19136626185785D+00 0.15197064924277D-01 2 10 2 6 -0.34305302337377D+01 0.18581713521824D+00 3 10 2 6 0.22296174836229D+00 -0.77409466642935D-01 1 11 2 6 -0.76864195703394D-01 -0.17698091781108D-08 2 11 2 6 -0.37783647993466D+00 -0.54721150244392D-10 3 11 2 6 -0.50596657091992D+01 -0.22843272391442D-01 1 12 2 6 -0.76864195703395D-01 -0.17698085735436D-08 2 12 2 6 -0.37783647993477D+00 -0.54721466751918D-10 3 12 2 6 -0.50596657091991D+01 -0.22843272391444D-01 1 13 2 6 -0.84458994063049D+00 0.80772866284181D-02 2 13 2 6 -0.19712272332279D+01 -0.48238814018279D-03 3 13 2 6 0.46565926400900D+00 0.96578056394315D-02 1 14 2 6 -0.84458994063050D+00 0.80772866284177D-02 2 14 2 6 -0.19712272332279D+01 -0.48238814018761D-03 3 14 2 6 0.46565926400899D+00 0.96578056394324D-02 1 15 2 6 -0.29325622775829D+01 0.40133603037766D-02 2 15 2 6 -0.56047356324625D+01 0.69297330690951D-02 3 15 2 6 -0.41102064508695D+00 0.14635914271648D-01 1 16 2 6 -0.29325622775831D+01 0.40133603037759D-02 2 16 2 6 -0.56047356324624D+01 0.69297330690910D-02 3 16 2 6 -0.41102064508716D+00 0.14635914271646D-01 1 17 2 6 0.86364268745080D+00 -0.31244453421059D-01 2 17 2 6 -0.19627813396923D+01 0.22171759650072D-01 3 17 2 6 -0.49064510769632D+00 -0.48289991207568D-01 1 18 2 6 0.86364268745080D+00 -0.31244453421059D-01 2 18 2 6 -0.19627813396923D+01 0.22171759650074D-01 3 18 2 6 -0.49064510769627D+00 -0.48289991207571D-01 1 19 2 6 0.16406849123273D+01 -0.32328470040590D-02 2 19 2 6 -0.57399295574618D+01 0.25035389652313D-03 3 19 2 6 0.49419589443961D+00 -0.23665373738743D-01 1 20 2 6 0.16406849123271D+01 -0.32328470040601D-02 2 20 2 6 -0.57399295574617D+01 0.25035389652162D-03 3 20 2 6 0.49419589443965D+00 -0.23665373738742D-01 1 1 3 6 -0.20900339623782D+00 -0.18126319184379D-03 2 1 3 6 -0.53359140394452D+01 0.22205331350655D-01 3 1 3 6 -0.64438559312219D+00 0.55134499776800D-03 1 2 3 6 -0.20900339623782D+00 -0.18126319184390D-03 2 2 3 6 -0.53359140394452D+01 0.22205331350665D-01 3 2 3 6 -0.64438559312225D+00 0.55134499776276D-03 1 3 3 6 0.22378761700954D+00 -0.40029091038997D-08 2 3 3 6 0.89081693609256D+00 0.21996918820171D-08 3 3 3 6 -0.16810370817579D+01 -0.98905860945116D-02 1 4 3 6 0.22378761700938D+00 -0.40029089549996D-08 2 4 3 6 0.89081693609256D+00 0.21996947260131D-08 3 4 3 6 -0.16810370817578D+01 -0.98905860945174D-02 1 5 3 6 -0.43133549922910D+01 0.48126889764435D-09 2 5 3 6 0.13585497355038D+01 0.13554577267503D-07 3 5 3 6 -0.31041399857622D+02 0.00000000000000D+00 1 6 3 6 0.11774096893431D+00 -0.72995172042819D-07 2 6 3 6 0.28470716517157D+01 0.32936070742274D-06 3 6 3 6 0.39864613984769D+02 0.00000000000000D+00 1 7 3 6 -0.15033098067807D-14 0.14733469102317D-17 2 7 3 6 0.57376059615332D-13 -0.91466918707509D-15 3 7 3 6 0.28816708674349D-13 0.56854378544587D-14 1 8 3 6 0.13073680021466D-15 0.15160753293701D-17 2 8 3 6 0.13996579188311D-13 -0.15960105041923D-14 3 8 3 6 -0.11465194648453D-13 0.12888310085190D-14 1 9 3 6 0.23325028865521D+01 0.12055524764948D+00 2 9 3 6 -0.42446620651857D+00 -0.31095994092535D-01 3 9 3 6 -0.84039943674549D+00 -0.82345547420193D+00 1 10 3 6 0.23325028865519D+01 0.12055524764948D+00 2 10 3 6 -0.42446620651871D+00 -0.31095994092534D-01 3 10 3 6 -0.84039943674611D+00 -0.82345547420193D+00 1 11 3 6 0.83892502093497D-01 -0.25500722212940D-08 2 11 3 6 -0.55708549824364D+00 -0.30160418074997D-08 3 11 3 6 0.77235024357454D-02 -0.92952290049533D-02 1 12 3 6 0.83892502093475D-01 -0.25500713483026D-08 2 12 3 6 -0.55708549824362D+00 -0.30160438555978D-08 3 12 3 6 0.77235024357667D-02 -0.92952290049542D-02 1 13 3 6 0.42333913530499D+00 -0.57653228107802D-03 2 13 3 6 0.13123301985446D+00 0.52540686046631D-02 3 13 3 6 0.33113979864878D+01 -0.10995496813759D-01 1 14 3 6 0.42333913530498D+00 -0.57653228107817D-03 2 14 3 6 0.13123301985445D+00 0.52540686046641D-02 3 14 3 6 0.33113979864878D+01 -0.10995496813760D-01 1 15 3 6 0.37229864838586D+00 0.71952141488996D-01 2 15 3 6 0.35637835461202D+00 0.67733380454438D-01 3 15 3 6 -0.38187926021984D+01 0.83435389186058D-02 1 16 3 6 0.37229864838558D+00 0.71952141488996D-01 2 16 3 6 0.35637835461180D+00 0.67733380454437D-01 3 16 3 6 -0.38187926021982D+01 0.83435389186067D-02 1 17 3 6 0.27108133047547D+00 0.12033131126891D-01 2 17 3 6 -0.31948038827920D+00 -0.20095564767297D-01 3 17 3 6 0.29726339901639D+01 -0.22414061714861D-01 1 18 3 6 0.27108133047546D+00 0.12033131126891D-01 2 18 3 6 -0.31948038827915D+00 -0.20095564767300D-01 3 18 3 6 0.29726339901638D+01 -0.22414061714862D-01 1 19 3 6 0.20245841920853D+00 0.64972512946613D-01 2 19 3 6 -0.53594074220157D+00 -0.89956128772503D-01 3 19 3 6 -0.33040214403572D+01 -0.17968918688676D-02 1 20 3 6 0.20245841920850D+00 0.64972512946613D-01 2 20 3 6 -0.53594074220155D+00 -0.89956128772501D-01 3 20 3 6 -0.33040214403575D+01 -0.17968918688670D-02 1 1 1 7 -0.34739790734432D+01 0.88547588111040D-09 2 1 1 7 -0.68537920293003D+00 0.78117112718764D-09 3 1 1 7 -0.43975167368966D+00 -0.14395926504082D-01 1 2 1 7 0.34739790734433D+01 -0.88548133988891D-09 2 2 1 7 0.68537920293003D+00 -0.78117118141928D-09 3 2 1 7 0.43975167368966D+00 0.14395926504081D-01 1 3 1 7 -0.53432111858787D+00 -0.88771390239292D-03 2 3 1 7 0.28205507708319D-01 0.44874730179372D-02 3 3 1 7 -0.34542834473126D-01 -0.29535935175404D-02 1 4 1 7 0.53432111858785D+00 0.88771390239635D-03 2 4 1 7 -0.28205507708301D-01 -0.44874730179373D-02 3 4 1 7 0.34542834473121D-01 0.29535935175401D-02 1 5 1 7 -0.59201998543929D-14 -0.36453585289745D-14 2 5 1 7 0.21874312745974D-14 -0.27876495812912D-15 3 5 1 7 0.10681588848755D-17 -0.15160753293697D-17 1 6 1 7 -0.24846272324594D-14 -0.41003390653009D-15 2 6 1 7 0.16201446823152D-14 0.27781378479316D-15 3 6 1 7 -0.15033098067807D-14 -0.14733469102317D-17 1 7 1 7 0.17032235679795D+02 0.00000000000000D+00 2 7 1 7 -0.13008018820259D+01 0.84449587720246D-07 3 7 1 7 0.11775168613278D+00 0.42171026902080D-07 1 8 1 7 0.14183565285401D+01 0.00000000000000D+00 2 8 1 7 -0.43331506645519D-02 -0.37269986739726D-09 3 8 1 7 0.43133549922910D+01 0.48126889764435D-09 1 9 1 7 0.64637539596383D-01 -0.95135644334034D-10 2 9 1 7 -0.25313561100863D-01 0.28691422307362D-08 3 9 1 7 -0.86856186557539D+00 -0.88069222136628D-02 1 10 1 7 -0.64637539596365D-01 0.95136001065480D-10 2 10 1 7 0.25313561100866D-01 -0.28691417077216D-08 3 10 1 7 0.86856186557539D+00 0.88069222136634D-02 1 11 1 7 -0.16195405218007D+01 0.13847969061544D+00 2 11 1 7 0.90065158085519D-01 -0.16654270979538D-01 3 11 1 7 -0.45096495312515D+00 0.28904022487875D+00 1 12 1 7 0.16195405218008D+01 -0.13847969061543D+00 2 12 1 7 -0.90065158085672D-01 0.16654270979537D-01 3 12 1 7 0.45096495312526D+00 -0.28904022487874D+00 1 13 1 7 0.11975170767615D+00 -0.98203798255541D-02 2 13 1 7 0.71405983092761D+00 -0.99047118005321D-02 3 13 1 7 -0.98932719077391D+00 0.77813748561254D-02 1 14 1 7 -0.11975170767603D+00 0.98203798255504D-02 2 14 1 7 -0.71405983092700D+00 0.99047118005103D-02 3 14 1 7 0.98932719077391D+00 -0.77813748561317D-02 1 15 1 7 0.41860808482337D-01 -0.13715067473217D-01 2 15 1 7 0.60402079476107D-02 -0.32115839925080D-01 3 15 1 7 0.20564018406033D+00 -0.28648551012426D-01 1 16 1 7 -0.41860808482347D-01 0.13715067473217D-01 2 16 1 7 -0.60402079476054D-02 0.32115839925080D-01 3 16 1 7 -0.20564018406030D+00 0.28648551012425D-01 1 17 1 7 0.14132858478811D+01 0.16780058856140D-01 2 17 1 7 0.43386576755758D+00 -0.89129393016400D-02 3 17 1 7 0.77009826948032D+00 -0.16551616775295D-01 1 18 1 7 -0.14132858478808D+01 -0.16780058856160D-01 2 18 1 7 -0.43386576755773D+00 0.89129393016628D-02 3 18 1 7 -0.77009826947993D+00 0.16551616775286D-01 1 19 1 7 -0.31076334350387D+00 0.97508677259309D-02 2 19 1 7 0.27322497593675D+00 -0.66212463350018D-02 3 19 1 7 -0.11574704131345D+00 0.15169791020613D-01 1 20 1 7 0.31076334350387D+00 -0.97508677259313D-02 2 20 1 7 -0.27322497593675D+00 0.66212463350027D-02 3 20 1 7 0.11574704131344D+00 -0.15169791020614D-01 1 1 2 7 0.45407510740998D-02 0.22541774075895D-08 2 1 2 7 0.41365193551445D+01 0.12492129097404D-08 3 1 2 7 -0.68394290283075D+00 0.11779748011195D-02 1 2 2 7 -0.45407510740964D-02 -0.22541774618211D-08 2 2 2 7 -0.41365193551445D+01 -0.12492029053882D-08 3 2 2 7 0.68394290283080D+00 -0.11779748011194D-02 1 3 2 7 0.12824360441077D+00 0.36471075147198D-02 2 3 2 7 0.44548204137468D+00 -0.30396572270284D-02 3 3 2 7 -0.61716593510246D+01 -0.42033921524783D-02 1 4 2 7 -0.12824360441075D+00 -0.36471075147199D-02 2 4 2 7 -0.44548204137479D+00 0.30396572270055D-02 3 4 2 7 0.61716593510246D+01 0.42033921524828D-02 1 5 2 7 0.21861162354999D-14 -0.27876495812912D-15 2 5 2 7 -0.39829436223762D-13 -0.30156400470859D-14 3 5 2 7 -0.60066278264103D-17 0.15960105041924D-14 1 6 2 7 0.16201448339865D-14 0.27781378479316D-15 2 6 2 7 -0.20618593865584D-13 0.18859651819363D-14 3 6 2 7 0.57376059615332D-13 0.91466918707509D-15 1 7 2 7 -0.13007947808517D+01 -0.92979494467397D-07 2 7 2 7 0.28255601903494D+02 0.00000000000000D+00 3 7 2 7 -0.28470657431617D+01 0.29541115483351D-06 1 8 2 7 -0.43331506645519D-02 0.37269986739726D-09 2 8 2 7 0.49497625398612D+01 0.00000000000000D+00 3 8 2 7 0.13585497355038D+01 -0.13554577267503D-07 1 9 2 7 0.76864195703414D-01 0.17698086892247D-08 2 9 2 7 -0.37783647993475D+00 -0.54724888938289D-10 3 9 2 7 0.50596657091991D+01 0.22843272391444D-01 1 10 2 7 -0.76864195703412D-01 -0.17698081662101D-08 2 10 2 7 0.37783647993471D+00 0.54719916549085D-10 3 10 2 7 -0.50596657091991D+01 -0.22843272391444D-01 1 11 2 7 0.19136626185774D+00 -0.15197064924277D-01 2 11 2 7 -0.34305302337378D+01 0.18581713521824D+00 3 11 2 7 -0.22296174836162D+00 0.77409466642935D-01 1 12 2 7 -0.19136626185789D+00 0.15197064924276D-01 2 12 2 7 0.34305302337379D+01 -0.18581713521823D+00 3 12 2 7 0.22296174836258D+00 -0.77409466642932D-01 1 13 2 7 -0.16406849123270D+01 0.32328470040600D-02 2 13 2 7 -0.57399295574616D+01 0.25035389651710D-03 3 13 2 7 -0.49419589443971D+00 0.23665373738743D-01 1 14 2 7 0.16406849123276D+01 -0.32328470040818D-02 2 14 2 7 0.57399295574618D+01 -0.25035389654274D-03 3 14 2 7 0.49419589443968D+00 -0.23665373738754D-01 1 15 2 7 0.86364268745080D+00 -0.31244453421060D-01 2 15 2 7 0.19627813396923D+01 -0.22171759650069D-01 3 15 2 7 -0.49064510769629D+00 -0.48289991207569D-01 1 16 2 7 -0.86364268745080D+00 0.31244453421059D-01 2 16 2 7 -0.19627813396923D+01 0.22171759650073D-01 3 16 2 7 0.49064510769632D+00 0.48289991207568D-01 1 17 2 7 -0.29325622775832D+01 0.40133603037988D-02 2 17 2 7 0.56047356324623D+01 -0.69297330690977D-02 3 17 2 7 -0.41102064508721D+00 0.14635914271655D-01 1 18 2 7 0.29325622775830D+01 -0.40133603037760D-02 2 18 2 7 -0.56047356324624D+01 0.69297330690936D-02 3 18 2 7 0.41102064508699D+00 -0.14635914271647D-01 1 19 2 7 0.84458994063050D+00 -0.80772866284173D-02 2 19 2 7 -0.19712272332279D+01 -0.48238814018513D-03 3 19 2 7 -0.46565926400898D+00 -0.96578056394333D-02 1 20 2 7 -0.84458994063050D+00 0.80772866284182D-02 2 20 2 7 0.19712272332279D+01 0.48238814018454D-03 3 20 2 7 0.46565926400901D+00 0.96578056394326D-02 1 1 3 7 0.22378761700954D+00 -0.40029090361391D-08 2 1 3 7 -0.89081693609245D+00 -0.21996920786455D-08 3 1 3 7 -0.16810370817580D+01 -0.98905860945142D-02 1 2 3 7 -0.22378761700955D+00 0.40029080004123D-08 2 2 3 7 0.89081693609250D+00 0.21996921473994D-08 3 2 3 7 0.16810370817578D+01 0.98905860945003D-02 1 3 3 7 0.20900339623783D+00 0.18126319184367D-03 2 3 3 7 -0.53359140394452D+01 0.22205331350669D-01 3 3 3 7 0.64438559312245D+00 -0.55134499777082D-03 1 4 3 7 -0.20900339623783D+00 -0.18126319184402D-03 2 4 3 7 0.53359140394452D+01 -0.22205331350664D-01 3 4 3 7 -0.64438559312226D+00 0.55134499776332D-03 1 5 3 7 -0.10548673656662D-17 -0.15160753293697D-17 2 5 3 7 -0.60066278264103D-17 0.15960105041923D-14 3 5 3 7 -0.31449209244319D-13 -0.12888310085190D-14 1 6 3 7 -0.15033098067775D-14 -0.14733469102315D-17 2 6 3 7 0.57376059631766D-13 0.91466918707509D-15 3 6 3 7 0.28816708674349D-13 -0.56854378544587D-14 1 7 3 7 0.11774096893447D+00 -0.72995172042819D-07 2 7 3 7 -0.28470716517167D+01 -0.32936070742274D-06 3 7 3 7 0.39864613984768D+02 0.00000000000000D+00 1 8 3 7 -0.43133549922910D+01 0.48126889764435D-09 2 8 3 7 -0.13585497355038D+01 -0.13554577267503D-07 3 8 3 7 -0.31041399857622D+02 0.00000000000000D+00 1 9 3 7 0.83892502093471D-01 -0.25500716470827D-08 2 9 3 7 0.55708549824362D+00 0.30160438479455D-08 3 9 3 7 0.77235024357667D-02 -0.92952290049538D-02 1 10 3 7 -0.83892502093477D-01 0.25500722634719D-08 2 10 3 7 -0.55708549824363D+00 -0.30160439467443D-08 3 10 3 7 -0.77235024357596D-02 0.92952290049537D-02 1 11 3 7 0.23325028865520D+01 0.12055524764948D+00 2 11 3 7 0.42446620651938D+00 0.31095994092534D-01 3 11 3 7 -0.84039943674622D+00 -0.82345547420193D+00 1 12 3 7 -0.23325028865519D+01 -0.12055524764946D+00 2 12 3 7 -0.42446620651842D+00 -0.31095994092532D-01 3 12 3 7 0.84039943674605D+00 0.82345547420186D+00 1 13 3 7 0.20245841920845D+00 0.64972512946613D-01 2 13 3 7 0.53594074220148D+00 0.89956128772502D-01 3 13 3 7 -0.33040214403575D+01 -0.17968918688677D-02 1 14 3 7 -0.20245841920845D+00 -0.64972512946619D-01 2 14 3 7 -0.53594074220151D+00 -0.89956128772513D-01 3 14 3 7 0.33040214403569D+01 0.17968918688902D-02 1 15 3 7 -0.27108133047545D+00 -0.12033131126892D-01 2 15 3 7 -0.31948038827916D+00 -0.20095564767297D-01 3 15 3 7 -0.29726339901638D+01 0.22414061714856D-01 1 16 3 7 0.27108133047548D+00 0.12033131126891D-01 2 16 3 7 0.31948038827920D+00 0.20095564767296D-01 3 16 3 7 0.29726339901639D+01 -0.22414061714862D-01 1 17 3 7 -0.37229864838545D+00 -0.71952141489005D-01 2 17 3 7 0.35637835461176D+00 0.67733380454445D-01 3 17 3 7 0.38187926021982D+01 -0.83435389185819D-02 1 18 3 7 0.37229864838584D+00 0.71952141488996D-01 2 18 3 7 -0.35637835461198D+00 -0.67733380454437D-01 3 18 3 7 -0.38187926021983D+01 0.83435389186069D-02 1 19 3 7 0.42333913530498D+00 -0.57653228107830D-03 2 19 3 7 -0.13123301985444D+00 -0.52540686046649D-02 3 19 3 7 0.33113979864878D+01 -0.10995496813760D-01 1 20 3 7 -0.42333913530499D+00 0.57653228107768D-03 2 20 3 7 0.13123301985447D+00 0.52540686046643D-02 3 20 3 7 -0.33113979864877D+01 0.10995496813757D-01 1 1 1 8 -0.34739790734432D+01 0.88547169199573D-09 2 1 1 8 -0.68537920293003D+00 0.78117127966995D-09 3 1 1 8 0.43975167368966D+00 0.14395926504082D-01 1 2 1 8 0.34739790734432D+01 -0.88548237133639D-09 2 2 1 8 0.68537920293003D+00 -0.78117125438994D-09 3 2 1 8 -0.43975167368967D+00 -0.14395926504081D-01 1 3 1 8 -0.53432111858787D+00 -0.88771390239437D-03 2 3 1 8 0.28205507708318D-01 0.44874730179376D-02 3 3 1 8 0.34542834473123D-01 0.29535935175404D-02 1 4 1 8 0.53432111858786D+00 0.88771390239610D-03 2 4 1 8 -0.28205507708301D-01 -0.44874730179371D-02 3 4 1 8 -0.34542834473121D-01 -0.29535935175402D-02 1 5 1 8 -0.98584043929047D-15 -0.41003390653009D-15 2 5 1 8 -0.26264621946275D-14 0.27781378479316D-15 3 5 1 8 -0.45013287424418D-17 -0.14733469102315D-17 1 6 1 8 -0.59202150147924D-14 -0.36453585289745D-14 2 6 1 8 0.10181037082606D-13 -0.27876495812912D-15 3 6 1 8 0.13073680021466D-15 -0.15160753293701D-17 1 7 1 8 0.14183565285401D+01 0.00000000000000D+00 2 7 1 8 -0.43331506645519D-02 -0.37269986739726D-09 3 7 1 8 -0.43133549922910D+01 -0.48126889764435D-09 1 8 1 8 0.17032235679795D+02 0.00000000000000D+00 2 8 1 8 -0.13008018820258D+01 0.84449587720246D-07 3 8 1 8 -0.11775168613298D+00 -0.42171026902080D-07 1 9 1 8 0.64637539596384D-01 -0.95136437953752D-10 2 9 1 8 -0.25313561100861D-01 0.28691419605040D-08 3 9 1 8 0.86856186557539D+00 0.88069222136626D-02 1 10 1 8 -0.64637539596369D-01 0.95135804827623D-10 2 10 1 8 0.25313561100885D-01 -0.28691425343709D-08 3 10 1 8 -0.86856186557539D+00 -0.88069222136634D-02 1 11 1 8 -0.16195405218008D+01 0.13847969061544D+00 2 11 1 8 0.90065158085533D-01 -0.16654270979538D-01 3 11 1 8 0.45096495312529D+00 -0.28904022487875D+00 1 12 1 8 0.16195405218008D+01 -0.13847969061543D+00 2 12 1 8 -0.90065158085669D-01 0.16654270979538D-01 3 12 1 8 -0.45096495312531D+00 0.28904022487874D+00 1 13 1 8 -0.41860808482341D-01 0.13715067473218D-01 2 13 1 8 -0.60402079476032D-02 0.32115839925080D-01 3 13 1 8 0.20564018406031D+00 -0.28648551012425D-01 1 14 1 8 0.41860808482345D-01 -0.13715067473217D-01 2 14 1 8 0.60402079476076D-02 -0.32115839925080D-01 3 14 1 8 -0.20564018406032D+00 0.28648551012426D-01 1 15 1 8 -0.11975170767603D+00 0.98203798255507D-02 2 15 1 8 -0.71405983092713D+00 0.99047118005101D-02 3 15 1 8 -0.98932719077393D+00 0.77813748561320D-02 1 16 1 8 0.11975170767615D+00 -0.98203798255544D-02 2 16 1 8 0.71405983092755D+00 -0.99047118005319D-02 3 16 1 8 0.98932719077387D+00 -0.77813748561257D-02 1 17 1 8 0.31076334350387D+00 -0.97508677259313D-02 2 17 1 8 -0.27322497593675D+00 0.66212463350025D-02 3 17 1 8 -0.11574704131344D+00 0.15169791020614D-01 1 18 1 8 -0.31076334350387D+00 0.97508677259312D-02 2 18 1 8 0.27322497593675D+00 -0.66212463350025D-02 3 18 1 8 0.11574704131345D+00 -0.15169791020613D-01 1 19 1 8 -0.14132858478809D+01 -0.16780058856161D-01 2 19 1 8 -0.43386576755773D+00 0.89129393016618D-02 3 19 1 8 0.77009826947994D+00 -0.16551616775286D-01 1 20 1 8 0.14132858478810D+01 0.16780058856140D-01 2 20 1 8 0.43386576755755D+00 -0.89129393016400D-02 3 20 1 8 -0.77009826948025D+00 0.16551616775295D-01 1 1 2 8 0.45407510740984D-02 0.22541775603061D-08 2 1 2 8 0.41365193551445D+01 0.12492120087100D-08 3 1 2 8 0.68394290283071D+00 -0.11779748011189D-02 1 2 2 8 -0.45407510740940D-02 -0.22541775350261D-08 2 2 2 8 -0.41365193551446D+01 -0.12492099207445D-08 3 2 2 8 -0.68394290283081D+00 0.11779748011191D-02 1 3 2 8 0.12824360441077D+00 0.36471075147202D-02 2 3 2 8 0.44548204137468D+00 -0.30396572270272D-02 3 3 2 8 0.61716593510246D+01 0.42033921524775D-02 1 4 2 8 -0.12824360441075D+00 -0.36471075147197D-02 2 4 2 8 -0.44548204137481D+00 0.30396572270126D-02 3 4 2 8 -0.61716593510246D+01 -0.42033921524824D-02 1 5 2 8 -0.26264620429562D-14 0.27781378479316D-15 2 5 2 8 -0.32733902617851D-13 0.18859651819363D-14 3 5 2 8 -0.80513651459303D-13 0.91466918707509D-15 1 6 2 8 0.10179722043509D-13 -0.27876495812912D-15 2 6 2 8 -0.31835830442740D-13 -0.30156400470859D-14 3 6 2 8 0.13996579188311D-13 0.15960105041923D-14 1 7 2 8 -0.43331506645519D-02 0.37269986739726D-09 2 7 2 8 0.49497625398612D+01 0.00000000000000D+00 3 7 2 8 -0.13585497355038D+01 0.13554577267503D-07 1 8 2 8 -0.13007947808517D+01 -0.92979494467397D-07 2 8 2 8 0.28255601903494D+02 0.00000000000000D+00 3 8 2 8 0.28470657431617D+01 -0.29541115483351D-06 1 9 2 8 0.76864195703418D-01 0.17698084182055D-08 2 9 2 8 -0.37783647993476D+00 -0.54724407839926D-10 3 9 2 8 -0.50596657091991D+01 -0.22843272391443D-01 1 10 2 8 -0.76864195703393D-01 -0.17698089920724D-08 2 10 2 8 0.37783647993470D+00 0.54719209561108D-10 3 10 2 8 0.50596657091991D+01 0.22843272391444D-01 1 11 2 8 0.19136626185775D+00 -0.15197064924277D-01 2 11 2 8 -0.34305302337378D+01 0.18581713521824D+00 3 11 2 8 0.22296174836167D+00 -0.77409466642933D-01 1 12 2 8 -0.19136626185789D+00 0.15197064924276D-01 2 12 2 8 0.34305302337379D+01 -0.18581713521823D+00 3 12 2 8 -0.22296174836258D+00 0.77409466642932D-01 1 13 2 8 -0.86364268745080D+00 0.31244453421060D-01 2 13 2 8 -0.19627813396923D+01 0.22171759650070D-01 3 13 2 8 -0.49064510769632D+00 -0.48289991207567D-01 1 14 2 8 0.86364268745080D+00 -0.31244453421060D-01 2 14 2 8 0.19627813396923D+01 -0.22171759650072D-01 3 14 2 8 0.49064510769630D+00 0.48289991207569D-01 1 15 2 8 0.16406849123275D+01 -0.32328470040820D-02 2 15 2 8 0.57399295574618D+01 -0.25035389653984D-03 3 15 2 8 -0.49419589443971D+00 0.23665373738754D-01 1 16 2 8 -0.16406849123270D+01 0.32328470040602D-02 2 16 2 8 -0.57399295574616D+01 0.25035389651674D-03 3 16 2 8 0.49419589443966D+00 -0.23665373738743D-01 1 17 2 8 -0.84458994063049D+00 0.80772866284179D-02 2 17 2 8 0.19712272332279D+01 0.48238814018308D-03 3 17 2 8 -0.46565926400900D+00 -0.96578056394326D-02 1 18 2 8 0.84458994063050D+00 -0.80772866284180D-02 2 18 2 8 -0.19712272332279D+01 -0.48238814018265D-03 3 18 2 8 0.46565926400897D+00 0.96578056394329D-02 1 19 2 8 0.29325622775830D+01 -0.40133603037770D-02 2 19 2 8 -0.56047356324624D+01 0.69297330690927D-02 3 19 2 8 -0.41102064508696D+00 0.14635914271647D-01 1 20 2 8 -0.29325622775832D+01 0.40133603037987D-02 2 20 2 8 0.56047356324623D+01 -0.69297330690955D-02 3 20 2 8 0.41102064508721D+00 -0.14635914271654D-01 1 1 3 8 -0.22378761700954D+00 0.40029090399354D-08 2 1 3 8 0.89081693609241D+00 0.21996926811692D-08 3 1 3 8 -0.16810370817580D+01 -0.98905860945137D-02 1 2 3 8 0.22378761700953D+00 -0.40029079096413D-08 2 2 3 8 -0.89081693609252D+00 -0.21996924397541D-08 3 2 3 8 0.16810370817578D+01 0.98905860945009D-02 1 3 3 8 -0.20900339623783D+00 -0.18126319184368D-03 2 3 3 8 0.53359140394452D+01 -0.22205331350670D-01 3 3 3 8 0.64438559312242D+00 -0.55134499776960D-03 1 4 3 8 0.20900339623783D+00 0.18126319184395D-03 2 4 3 8 -0.53359140394452D+01 0.22205331350665D-01 3 4 3 8 -0.64438559312232D+00 0.55134499776388D-03 1 5 3 8 -0.45013287456730D-17 -0.14733469102317D-17 2 5 3 8 -0.80513651475737D-13 0.91466918707509D-15 3 5 3 8 -0.91529225785495D-14 -0.56854378544587D-14 1 6 3 8 0.13285982646520D-15 -0.15160753293701D-17 2 6 3 8 0.13996579188311D-13 0.15960105041924D-14 3 6 3 8 -0.11465194648453D-13 -0.12888310085190D-14 1 7 3 8 0.43133549922910D+01 -0.48126889764435D-09 2 7 3 8 0.13585497355038D+01 0.13554577267503D-07 3 7 3 8 -0.31041399857622D+02 0.00000000000000D+00 1 8 3 8 -0.11774096893468D+00 0.72995172042819D-07 2 8 3 8 0.28470716517166D+01 0.32936070742274D-06 3 8 3 8 0.39864613984767D+02 0.00000000000000D+00 1 9 3 8 -0.83892502093469D-01 0.25500714607874D-08 2 9 3 8 -0.55708549824361D+00 -0.30160437135466D-08 3 9 3 8 0.77235024357685D-02 -0.92952290049547D-02 1 10 3 8 0.83892502093479D-01 -0.25500722637918D-08 2 10 3 8 0.55708549824363D+00 0.30160442725943D-08 3 10 3 8 -0.77235024357571D-02 0.92952290049534D-02 1 11 3 8 -0.23325028865519D+01 -0.12055524764948D+00 2 11 3 8 -0.42446620651933D+00 -0.31095994092533D-01 3 11 3 8 -0.84039943674566D+00 -0.82345547420193D+00 1 12 3 8 0.23325028865519D+01 0.12055524764946D+00 2 12 3 8 0.42446620651843D+00 0.31095994092531D-01 3 12 3 8 0.84039943674583D+00 0.82345547420186D+00 1 13 3 8 -0.27108133047547D+00 -0.12033131126891D-01 2 13 3 8 -0.31948038827920D+00 -0.20095564767295D-01 3 13 3 8 0.29726339901639D+01 -0.22414061714861D-01 1 14 3 8 0.27108133047546D+00 0.12033131126892D-01 2 14 3 8 0.31948038827917D+00 0.20095564767297D-01 3 14 3 8 -0.29726339901637D+01 0.22414061714855D-01 1 15 3 8 0.20245841920844D+00 0.64972512946619D-01 2 15 3 8 0.53594074220148D+00 0.89956128772514D-01 3 15 3 8 0.33040214403568D+01 0.17968918688886D-02 1 16 3 8 -0.20245841920850D+00 -0.64972512946613D-01 2 16 3 8 -0.53594074220154D+00 -0.89956128772503D-01 3 16 3 8 -0.33040214403575D+01 -0.17968918688658D-02 1 17 3 8 0.42333913530499D+00 -0.57653228107734D-03 2 17 3 8 -0.13123301985446D+00 -0.52540686046643D-02 3 17 3 8 -0.33113979864878D+01 0.10995496813756D-01 1 18 3 8 -0.42333913530498D+00 0.57653228107836D-03 2 18 3 8 0.13123301985443D+00 0.52540686046646D-02 3 18 3 8 0.33113979864877D+01 -0.10995496813761D-01 1 19 3 8 -0.37229864838583D+00 -0.71952141488996D-01 2 19 3 8 0.35637835461201D+00 0.67733380454437D-01 3 19 3 8 -0.38187926021983D+01 0.83435389186056D-02 1 20 3 8 0.37229864838551D+00 0.71952141489005D-01 2 20 3 8 -0.35637835461177D+00 -0.67733380454444D-01 3 20 3 8 0.38187926021982D+01 -0.83435389185832D-02 1 1 1 9 -0.34067507200395D+00 -0.14638563778116D-07 2 1 1 9 -0.42462063461765D+00 -0.17518729013103D-07 3 1 1 9 -0.91074152268092D-15 -0.16914474231633D-16 1 2 1 9 -0.90847243655278D-01 0.10096858123899D-07 2 2 1 9 -0.73000920128040D-01 -0.69602992578500D-08 3 2 1 9 -0.30168507174267D-14 -0.53089010285382D-17 1 3 1 9 -0.11748780754741D+01 -0.20743023930629D-07 2 3 1 9 -0.63249916978203D+00 0.75795691458406D-08 3 3 1 9 0.30160744123360D-15 -0.12206408949675D-15 1 4 1 9 0.27086826803725D+00 0.28246235853566D-08 2 4 1 9 -0.16366317516937D+00 -0.98162996786421D-08 3 4 1 9 0.23443021789715D-14 0.17190418610749D-15 1 5 1 9 -0.16192500572110D+01 -0.20771954063255D+00 2 5 1 9 -0.19137110159127D+00 -0.22795595111421D-01 3 5 1 9 -0.23327673293651D+01 0.18083286316607D+00 1 6 1 9 -0.16192500572110D+01 -0.20771954063255D+00 2 6 1 9 -0.19137110159126D+00 -0.22795595111421D-01 3 6 1 9 0.23327673293651D+01 -0.18083286316607D+00 1 7 1 9 0.64637539596383D-01 0.95135727817601D-10 2 7 1 9 0.76864195703413D-01 -0.17698090483125D-08 3 7 1 9 0.83892502093471D-01 0.25500716054494D-08 1 8 1 9 0.64637539596384D-01 0.95136521446099D-10 2 8 1 9 0.76864195703418D-01 -0.17698087772360D-08 3 8 1 9 -0.83892502093469D-01 -0.25500714191924D-08 1 9 1 9 0.89476770944812D+01 0.00000000000000D+00 2 9 1 9 0.93232038040180D+00 0.69777959362267D-07 3 9 1 9 -0.70006152005915D-14 0.00000000000000D+00 1 10 1 9 -0.52394473368438D+00 0.39063163538297D-09 2 10 1 9 0.11377012462632D+00 0.20545503336390D-08 3 10 1 9 -0.82827380307036D-14 0.28896789275904D-15 1 11 1 9 0.38569229888580D-01 0.16716310652498D-15 2 11 1 9 -0.13720769706464D+00 -0.11649704608812D-08 3 11 1 9 -0.25302931235554D-14 -0.63307181647194D-16 1 12 1 9 0.57021290435032D-15 0.38046141169366D-09 2 12 1 9 -0.53662203100369D+00 -0.73080995945652D-09 3 12 1 9 -0.87809088422253D-15 0.26497254948193D-16 1 13 1 9 -0.14934665198589D+01 0.12031749826188D-08 2 13 1 9 -0.80425400214361D+00 0.24420574973700D-08 3 13 1 9 -0.13064333069258D+01 -0.11424269791884D-07 1 14 1 9 0.64982840858896D-02 -0.31004102515301D-02 2 14 1 9 -0.43679226663016D+00 -0.30988760905921D-02 3 14 1 9 0.12554524805744D+01 -0.59655618165022D-02 1 15 1 9 0.64982840858881D-02 -0.31004102515300D-02 2 15 1 9 -0.43679226663016D+00 -0.30988760905923D-02 3 15 1 9 -0.12554524805744D+01 0.59655618165023D-02 1 16 1 9 -0.14934665198589D+01 0.12031748463520D-08 2 16 1 9 -0.80425400214361D+00 0.24420576605566D-08 3 16 1 9 0.13064333069258D+01 0.11424269674591D-07 1 17 1 9 -0.73442613606824D+00 -0.73271357183325D-02 2 17 1 9 0.95475056913762D+00 0.13338005088368D-01 3 17 1 9 -0.66564031357815D+00 -0.53613601460756D-02 1 18 1 9 0.17171534193013D-01 -0.18215668653421D-02 2 18 1 9 0.46172911400710D+00 0.92326164388086D-02 3 18 1 9 0.95501543360746D+00 -0.40511861185109D-02 1 19 1 9 0.17171534193013D-01 -0.18215668653424D-02 2 19 1 9 0.46172911400710D+00 0.92326164388082D-02 3 19 1 9 -0.95501543360746D+00 0.40511861185110D-02 1 20 1 9 -0.73442613606824D+00 -0.73271357183324D-02 2 20 1 9 0.95475056913762D+00 0.13338005088368D-01 3 20 1 9 0.66564031357816D+00 0.53613601460755D-02 1 1 2 9 0.60757540101622D-01 -0.27052685705195D-07 2 1 2 9 -0.22294686253607D+01 -0.68545561409291D-08 3 1 2 9 -0.92948916655978D-15 -0.26488463839633D-15 1 2 2 9 -0.69495458873882D-02 -0.38816360615929D-08 2 2 2 9 0.27633383794748D-03 -0.10177183910418D-07 3 2 2 9 0.24448724999850D-14 -0.23659325836425D-14 1 3 2 9 -0.44442567613534D+00 0.15885680287403D-07 2 3 2 9 -0.14506871895841D+01 -0.84332717282187D-08 3 3 2 9 -0.46753226852398D-14 0.42141026647708D-15 1 4 2 9 0.10288537780566D-01 0.56733237329886D-08 2 4 2 9 -0.95093453917009D+00 -0.10155840565792D-08 3 4 2 9 -0.96348179650572D-15 -0.12916996673244D-15 1 5 2 9 -0.90066967558262D-01 -0.24981407868869D-01 2 5 2 9 -0.34302706964864D+01 -0.27872569876803D+00 3 5 2 9 0.42457655352300D+00 -0.46643992746653D-01 1 6 2 9 -0.90066967558261D-01 -0.24981407868869D-01 2 6 2 9 -0.34302706964865D+01 -0.27872569876803D+00 3 6 2 9 -0.42457655352301D+00 0.46643992746653D-01 1 7 2 9 -0.25313561100864D-01 -0.28691425603337D-08 2 7 2 9 -0.37783647993475D+00 0.54724740619432D-10 3 7 2 9 0.55708549824362D+00 -0.30160422519999D-08 1 8 2 9 -0.25313561100861D-01 -0.28691422893251D-08 2 8 2 9 -0.37783647993476D+00 0.54724259616298D-10 3 8 2 9 -0.55708549824361D+00 0.30160421185664D-08 1 9 2 9 0.93231833163941D+00 -0.57246956840947D-07 2 9 2 9 0.74017914710930D+01 0.00000000000000D+00 3 9 2 9 -0.42625797556344D-13 0.00000000000000D+00 1 10 2 9 0.11377091585428D+00 -0.15442713217906D-08 2 10 2 9 0.12182169613776D+00 0.69648457819328D-09 3 10 2 9 0.13628947926812D-15 -0.19467876440385D-15 1 11 2 9 0.13720769706465D+00 -0.11649704608812D-08 2 11 2 9 0.22743408462265D+00 -0.61321718674966D-15 3 11 2 9 -0.17397915136559D-14 0.35983966847824D-15 1 12 2 9 -0.53662203100369D+00 0.73081260835702D-09 2 12 2 9 -0.72689843229068D-14 -0.63051053254213D-08 3 12 2 9 -0.54002353137025D-14 0.65702458462301D-15 1 13 2 9 -0.41575685832010D+00 -0.14435272915806D-07 2 13 2 9 0.77887176800124D+00 -0.88619877416840D-08 3 13 2 9 -0.10413264263538D+01 -0.10860401318780D-07 1 14 2 9 -0.19480650971428D+00 -0.31376545498053D-02 2 14 2 9 0.31596115616934D+00 0.50862222149238D-03 3 14 2 9 0.13160594003879D+01 -0.28535538357909D-02 1 15 2 9 -0.19480650971428D+00 -0.31376545498056D-02 2 15 2 9 0.31596115616933D+00 0.50862222149168D-03 3 15 2 9 -0.13160594003879D+01 0.28535538357909D-02 1 16 2 9 -0.41575685832010D+00 -0.14435272752620D-07 2 16 2 9 0.77887176800125D+00 -0.88619878179040D-08 3 16 2 9 0.10413264263538D+01 0.10860401687294D-07 1 17 2 9 0.87044227676283D+00 0.15194833848588D-01 2 17 2 9 -0.19735520769818D-01 -0.14451739772077D-01 3 17 2 9 0.17154731050668D+01 0.48289889671000D-02 1 18 2 9 -0.63146529951685D-02 0.89196694456554D-02 2 18 2 9 0.29291042281994D+00 -0.81021931314561D-02 3 18 2 9 -0.17197215205557D+01 0.76217125311953D-02 1 19 2 9 -0.63146529951665D-02 0.89196694456549D-02 2 19 2 9 0.29291042281995D+00 -0.81021931314543D-02 3 19 2 9 0.17197215205557D+01 -0.76217125311949D-02 1 20 2 9 0.87044227676282D+00 0.15194833848588D-01 2 20 2 9 -0.19735520769806D-01 -0.14451739772077D-01 3 20 2 9 -0.17154731050668D+01 -0.48289889670997D-02 1 1 3 9 -0.91074152268092D-15 -0.16914474231633D-16 2 1 3 9 -0.92948916614618D-15 -0.26488463839633D-15 3 1 3 9 -0.11521352310824D+01 -0.48540217403477D-07 1 2 3 9 -0.30168507176265D-14 -0.53036062177577D-17 2 2 3 9 0.24448724996915D-14 -0.23666198086793D-14 3 2 3 9 0.14087185061603D+00 -0.36345818109285D-09 1 3 3 9 0.30160744112848D-15 -0.12430192443174D-15 2 3 3 9 -0.46753226868575D-14 0.42007649967871D-15 3 3 3 9 -0.29843300792445D+01 -0.13044295665286D-06 1 4 3 9 0.23443021790094D-14 0.17231116655192D-15 2 4 3 9 -0.96348179634062D-15 -0.12897300588180D-15 3 4 3 9 0.17860256660851D+01 0.15336967254658D-07 1 5 3 9 0.45096516641649D+00 0.28904115117430D+00 2 5 3 9 -0.22296202286228D+00 -0.77409455086048D-01 3 5 3 9 -0.84039452125535D+00 0.82345773040978D+00 1 6 3 9 -0.45096516641652D+00 -0.28904115117430D+00 2 6 3 9 0.22296202286227D+00 0.77409455086048D-01 3 6 3 9 -0.84039452125523D+00 0.82345773040978D+00 1 7 3 9 -0.86856186557539D+00 0.88069222136627D-02 2 7 3 9 0.50596657091991D+01 -0.22843272391442D-01 3 7 3 9 0.77235024357667D-02 0.92952290049538D-02 1 8 3 9 0.86856186557539D+00 -0.88069222136625D-02 2 8 3 9 -0.50596657091991D+01 0.22843272391442D-01 3 8 3 9 0.77235024357685D-02 0.92952290049547D-02 1 9 3 9 -0.70006152005915D-14 0.13877787807814D-16 2 9 3 9 -0.42625797556344D-13 0.00000000000000D+00 3 9 3 9 0.41534743982116D+02 0.00000000000000D+00 1 10 3 9 -0.82827380301623D-14 0.27145253403428D-15 2 10 3 9 0.13628947915782D-15 -0.19368248531807D-15 3 10 3 9 -0.15205234919070D+02 0.25716317027629D-09 1 11 3 9 -0.25302931235778D-14 -0.63801874382545D-16 2 11 3 9 -0.17397915137434D-14 0.36576420450446D-15 3 11 3 9 -0.20035517264249D+00 0.58485311422133D-15 1 12 3 9 -0.87809088419499D-15 0.27340468090294D-16 2 12 3 9 -0.54002353139890D-14 0.65763845701821D-15 3 12 3 9 -0.15417375275082D-13 0.41412220282377D-07 1 13 3 9 -0.29406371989934D+01 0.18619026968786D-07 2 13 3 9 -0.23657867743271D+01 0.12929810262905D-07 3 13 3 9 -0.15996529498805D+01 -0.18746695174516D-07 1 14 3 9 0.22145513347881D+01 0.27619719981107D-01 2 14 3 9 0.28565669353928D+01 0.21959744064957D-01 3 14 3 9 -0.33825879169125D+01 0.21969610404842D-01 1 15 3 9 -0.22145513347881D+01 -0.27619719981107D-01 2 15 3 9 -0.28565669353928D+01 -0.21959744064957D-01 3 15 3 9 -0.33825879169125D+01 0.21969610404843D-01 1 16 3 9 0.29406371989934D+01 -0.18619027089548D-07 2 16 3 9 0.23657867743271D+01 -0.12929809897861D-07 3 16 3 9 -0.15996529498805D+01 -0.18746694232686D-07 1 17 3 9 -0.23717968961453D+01 0.36889848857991D-01 2 17 3 9 0.29062589369672D+01 -0.47548968402089D-01 3 17 3 9 -0.14454180791777D+01 -0.21075224935321D-01 1 18 3 9 0.19208973171480D+01 -0.10914982302531D-07 2 18 3 9 -0.35022316799165D+01 0.89237683719750D-06 3 18 3 9 -0.38199648074239D+01 0.59547118846551D-06 1 19 3 9 -0.19208973171480D+01 0.10914982358578D-07 2 19 3 9 0.35022316799165D+01 -0.89237683675400D-06 3 19 3 9 -0.38199648074239D+01 0.59547118874576D-06 1 20 3 9 0.23717968961453D+01 -0.36889848857992D-01 2 20 3 9 -0.29062589369672D+01 0.47548968402089D-01 3 20 3 9 -0.14454180791777D+01 -0.21075224935322D-01 1 1 1 10 -0.90847243655284D-01 0.10096856678440D-07 2 1 1 10 -0.73000920128042D-01 -0.69602992668835D-08 3 1 1 10 -0.39774835648916D-15 0.49926056351195D-16 1 2 1 10 -0.34067507200383D+00 -0.14638560880868D-07 2 2 1 10 -0.42462063461758D+00 -0.17518726860110D-07 3 2 1 10 0.49023141616434D-15 -0.24057813688887D-16 1 3 1 10 0.27086826803724D+00 0.28246234201797D-08 2 3 1 10 -0.16366317516937D+00 -0.98162995435876D-08 3 3 1 10 0.13545865205744D-13 -0.26293651096916D-15 1 4 1 10 -0.11748780754741D+01 -0.20743023956414D-07 2 4 1 10 -0.63249916978192D+00 0.75795689592897D-08 3 4 1 10 -0.72475985141770D-15 0.14038191952125D-15 1 5 1 10 -0.16192500572107D+01 -0.20771954063255D+00 2 5 1 10 -0.19137110159124D+00 -0.22795595111420D-01 3 5 1 10 -0.23327673293651D+01 0.18083286316607D+00 1 6 1 10 -0.16192500572108D+01 -0.20771954063255D+00 2 6 1 10 -0.19137110159126D+00 -0.22795595111421D-01 3 6 1 10 0.23327673293649D+01 -0.18083286316607D+00 1 7 1 10 -0.64637539596365D-01 -0.95136084549047D-10 2 7 1 10 -0.76864195703412D-01 0.17698085252979D-08 3 7 1 10 -0.83892502093478D-01 -0.25500722218386D-08 1 8 1 10 -0.64637539596369D-01 -0.95135888319970D-10 2 8 1 10 -0.76864195703393D-01 0.17698093511029D-08 3 8 1 10 0.83892502093479D-01 0.25500722221968D-08 1 9 1 10 -0.52394473368438D+00 0.39063133437574D-09 2 9 1 10 0.11377012462632D+00 0.20545500201139D-08 3 9 1 10 -0.82827380307989D-14 -0.28290527456413D-15 1 10 1 10 0.89476770944805D+01 0.00000000000000D+00 2 10 1 10 0.93232038040176D+00 0.69777959362267D-07 3 10 1 10 0.13510793195143D-12 0.00000000000000D+00 1 11 1 10 -0.40704908416976D-13 0.38046253161825D-09 2 11 1 10 -0.53662203100364D+00 -0.73081255182460D-09 3 11 1 10 0.87904369770970D-15 -0.48525708552720D-17 1 12 1 10 0.38569229888588D-01 0.34294300470936D-15 2 12 1 10 -0.13720769706465D+00 -0.11649703721440D-08 3 12 1 10 0.31546306736502D-14 -0.23346086820042D-16 1 13 1 10 0.64982840858628D-02 -0.31004102515302D-02 2 13 1 10 -0.43679226663017D+00 -0.30988760905923D-02 3 13 1 10 0.12554524805744D+01 -0.59655618165022D-02 1 14 1 10 -0.14934665198589D+01 0.12031750261005D-08 2 14 1 10 -0.80425400214366D+00 0.24420575297223D-08 3 14 1 10 -0.13064333069258D+01 -0.11424269629610D-07 1 15 1 10 -0.14934665198589D+01 0.12031751555149D-08 2 15 1 10 -0.80425400214363D+00 0.24420575286144D-08 3 15 1 10 0.13064333069258D+01 0.11424269610358D-07 1 16 1 10 0.64982840858677D-02 -0.31004102515300D-02 2 16 1 10 -0.43679226663016D+00 -0.30988760905924D-02 3 16 1 10 -0.12554524805744D+01 0.59655618165021D-02 1 17 1 10 0.17171534192990D-01 -0.18215668653423D-02 2 17 1 10 0.46172911400711D+00 0.92326164388082D-02 3 17 1 10 0.95501543360748D+00 -0.40511861185109D-02 1 18 1 10 -0.73442613606822D+00 -0.73271357183325D-02 2 18 1 10 0.95475056913764D+00 0.13338005088368D-01 3 18 1 10 -0.66564031357820D+00 -0.53613601460753D-02 1 19 1 10 -0.73442613606821D+00 -0.73271357183324D-02 2 19 1 10 0.95475056913763D+00 0.13338005088368D-01 3 19 1 10 0.66564031357818D+00 0.53613601460754D-02 1 20 1 10 0.17171534192977D-01 -0.18215668653424D-02 2 20 1 10 0.46172911400710D+00 0.92326164388085D-02 3 20 1 10 -0.95501543360746D+00 0.40511861185110D-02 1 1 2 10 -0.69495458873908D-02 -0.38816360706264D-08 2 1 2 10 0.27633383791820D-03 -0.10177183586110D-07 3 1 2 10 0.15783669026687D-13 -0.65442059148506D-15 1 2 2 10 0.60757540101686D-01 -0.27052683552202D-07 2 2 2 10 -0.22294686253611D+01 -0.68545704390015D-08 3 2 2 10 0.12540582998351D-13 0.15262921199118D-14 1 3 2 10 0.10288537780567D-01 0.56733238680431D-08 2 3 2 10 -0.95093453917009D+00 -0.10155837970395D-08 3 3 2 10 0.11489454956125D-14 0.14618637850569D-15 1 4 2 10 -0.44442567613522D+00 0.15885680100852D-07 2 4 2 10 -0.14506871895841D+01 -0.84332715235047D-08 3 4 2 10 -0.14452484938970D-14 0.63230034923333D-15 1 5 2 10 -0.90066967558240D-01 -0.24981407868869D-01 2 5 2 10 -0.34302706964863D+01 -0.27872569876803D+00 3 5 2 10 0.42457655352320D+00 -0.46643992746653D-01 1 6 2 10 -0.90066967558251D-01 -0.24981407868869D-01 2 6 2 10 -0.34302706964863D+01 -0.27872569876803D+00 3 6 2 10 -0.42457655352315D+00 0.46643992746652D-01 1 7 2 10 0.25313561100867D-01 0.28691420373191D-08 2 7 2 10 0.37783647993471D+00 -0.54719768230228D-10 3 7 2 10 -0.55708549824363D+00 0.30160423507987D-08 1 8 2 10 0.25313561100886D-01 0.28691428631919D-08 2 8 2 10 0.37783647993470D+00 -0.54719061337480D-10 3 8 2 10 0.55708549824363D+00 -0.30160426776141D-08 1 9 2 10 0.11377091585428D+00 -0.15442716353158D-08 2 9 2 10 0.12182169613776D+00 0.69648409492853D-09 3 9 2 10 0.13628947936921D-15 0.19880071084748D-15 1 10 2 10 0.93231833163937D+00 -0.57246956840947D-07 2 10 2 10 0.74017914710930D+01 0.00000000000000D+00 3 10 2 10 -0.21309515483538D-13 0.00000000000000D+00 1 11 2 10 -0.53662203100364D+00 0.73081001598894D-09 2 11 2 10 -0.26186368807564D-14 -0.63051012975220D-08 3 11 2 10 -0.39298695253711D-14 0.40404844709461D-15 1 12 2 10 0.13720769706465D+00 -0.11649703721440D-08 2 12 2 10 0.22743408462261D+00 -0.89226759347090D-15 3 12 2 10 0.22734794049619D-14 -0.36907949730659D-15 1 13 2 10 -0.19480650971429D+00 -0.31376545498056D-02 2 13 2 10 0.31596115616935D+00 0.50862222149310D-03 3 13 2 10 0.13160594003879D+01 -0.28535538357905D-02 1 14 2 10 -0.41575685832014D+00 -0.14435272883454D-07 2 14 2 10 0.77887176800125D+00 -0.88619880892418D-08 3 14 2 10 -0.10413264263539D+01 -0.10860401337753D-07 1 15 2 10 -0.41575685832012D+00 -0.14435272884562D-07 2 15 2 10 0.77887176800122D+00 -0.88619882170450D-08 3 15 2 10 0.10413264263539D+01 0.10860401690504D-07 1 16 2 10 -0.19480650971428D+00 -0.31376545498057D-02 2 16 2 10 0.31596115616934D+00 0.50862222149155D-03 3 16 2 10 -0.13160594003879D+01 0.28535538357908D-02 1 17 2 10 -0.63146529951543D-02 0.89196694456549D-02 2 17 2 10 0.29291042281993D+00 -0.81021931314551D-02 3 17 2 10 -0.17197215205557D+01 0.76217125311956D-02 1 18 2 10 0.87044227676285D+00 0.15194833848588D-01 2 18 2 10 -0.19735520769818D-01 -0.14451739772075D-01 3 18 2 10 0.17154731050669D+01 0.48289889671005D-02 1 19 2 10 0.87044227676284D+00 0.15194833848588D-01 2 19 2 10 -0.19735520769815D-01 -0.14451739772076D-01 3 19 2 10 -0.17154731050669D+01 -0.48289889671004D-02 1 20 2 10 -0.63146529951594D-02 0.89196694456553D-02 2 20 2 10 0.29291042281993D+00 -0.81021931314559D-02 3 20 2 10 0.17197215205557D+01 -0.76217125311950D-02 1 1 3 10 -0.39774835668548D-15 0.49933998567366D-16 2 1 3 10 0.15783669026557D-13 -0.65545142904037D-15 3 1 3 10 0.14087185061612D+00 -0.36345535623397D-09 1 2 3 10 0.49023141616435D-15 -0.24057813688887D-16 2 2 3 10 0.12540582998765D-13 0.15262921199118D-14 3 2 3 10 -0.11521352310822D+01 -0.48540212357805D-07 1 3 3 10 0.13545865205782D-13 -0.26252953052473D-15 2 3 3 10 0.11489454957776D-14 0.14638333935634D-15 3 3 3 10 0.17860256660852D+01 0.15336967239002D-07 1 4 3 10 -0.72475985152282D-15 0.13814408458626D-15 2 4 3 10 -0.14452484955147D-14 0.63096658243496D-15 3 4 3 10 -0.29843300792447D+01 -0.13044295672560D-06 1 5 3 10 0.45096516641655D+00 0.28904115117430D+00 2 5 3 10 -0.22296202286207D+00 -0.77409455086048D-01 3 5 3 10 -0.84039452125592D+00 0.82345773040978D+00 1 6 3 10 -0.45096516641669D+00 -0.28904115117430D+00 2 6 3 10 0.22296202286212D+00 0.77409455086047D-01 3 6 3 10 -0.84039452125586D+00 0.82345773040978D+00 1 7 3 10 0.86856186557539D+00 -0.88069222136633D-02 2 7 3 10 -0.50596657091991D+01 0.22843272391442D-01 3 7 3 10 -0.77235024357596D-02 -0.92952290049537D-02 1 8 3 10 -0.86856186557539D+00 0.88069222136633D-02 2 8 3 10 0.50596657091991D+01 -0.22843272391442D-01 3 8 3 10 -0.77235024357571D-02 -0.92952290049534D-02 1 9 3 10 -0.82827380309895D-14 -0.29920810964991D-15 2 9 3 10 0.13628947957141D-15 0.20062137922198D-15 3 9 3 10 -0.15205234919070D+02 0.25716340554322D-09 1 10 3 10 0.13510793195143D-12 0.13877787807814D-16 2 10 3 10 -0.21309515483538D-13 0.00000000000000D+00 3 10 3 10 0.41534743982117D+02 0.00000000000000D+00 1 11 3 10 0.87904369773724D-15 -0.40093577131708D-17 2 11 3 10 -0.39298695256576D-14 0.40466231948981D-15 3 11 3 10 0.99805969406061D-13 0.41412218753502D-07 1 12 3 10 0.31546306736278D-14 -0.23840779555393D-16 2 12 3 10 0.22734794048744D-14 -0.36315496128037D-15 3 12 3 10 -0.20035517264243D+00 0.24592596925143D-15 1 13 3 10 0.22145513347882D+01 0.27619719981107D-01 2 13 3 10 0.28565669353928D+01 0.21959744064957D-01 3 13 3 10 -0.33825879169125D+01 0.21969610404843D-01 1 14 3 10 -0.29406371989934D+01 0.18619027131060D-07 2 14 3 10 -0.23657867743271D+01 0.12929810243932D-07 3 14 3 10 -0.15996529498806D+01 -0.18746691755740D-07 1 15 3 10 0.29406371989934D+01 -0.18619027153782D-07 2 15 3 10 0.23657867743271D+01 -0.12929809894651D-07 3 15 3 10 -0.15996529498806D+01 -0.18746692663989D-07 1 16 3 10 -0.22145513347881D+01 -0.27619719981107D-01 2 16 3 10 -0.28565669353928D+01 -0.21959744064957D-01 3 16 3 10 -0.33825879169125D+01 0.21969610404842D-01 1 17 3 10 0.19208973171480D+01 -0.10914982246333D-07 2 17 3 10 -0.35022316799164D+01 0.89237683749152D-06 3 17 3 10 -0.38199648074238D+01 0.59547118822711D-06 1 18 3 10 -0.23717968961453D+01 0.36889848857992D-01 2 18 3 10 0.29062589369672D+01 -0.47548968402088D-01 3 18 3 10 -0.14454180791777D+01 -0.21075224935320D-01 1 19 3 10 0.23717968961453D+01 -0.36889848857992D-01 2 19 3 10 -0.29062589369673D+01 0.47548968402089D-01 3 19 3 10 -0.14454180791777D+01 -0.21075224935321D-01 1 20 3 10 -0.19208973171480D+01 0.10914982367720D-07 2 20 3 10 0.35022316799164D+01 -0.89237683681644D-06 3 20 3 10 -0.38199648074238D+01 0.59547118801820D-06 1 1 1 11 0.27086826803723D+00 0.28246234247617D-08 2 1 1 11 0.16366317516938D+00 0.98162996602175D-08 3 1 1 11 0.16129894453027D-14 0.20805885958878D-15 1 2 1 11 0.11748780754741D+01 0.20743000875829D-07 2 2 1 11 -0.63249916978202D+00 0.75795718763825D-08 3 2 1 11 -0.65673060506074D-15 -0.26545377910558D-15 1 3 1 11 0.90847243655284D-01 -0.10096856703250D-07 2 3 1 11 -0.73000920128046D-01 -0.69602993171484D-08 3 3 1 11 -0.43722370093880D-15 0.13639901703585D-16 1 4 1 11 -0.34067507200367D+00 -0.14638560679735D-07 2 4 1 11 0.42462063461775D+00 0.17518726915897D-07 3 4 1 11 0.83241429804828D-15 -0.72433729038211D-16 1 5 1 11 0.64637539596326D-01 0.95134701842075D-10 2 5 1 11 -0.76864195703410D-01 0.17698096366550D-08 3 5 1 11 -0.83892502093507D-01 -0.25500721584160D-08 1 6 1 11 0.64637539596325D-01 0.95135584116208D-10 2 6 1 11 -0.76864195703394D-01 0.17698095371985D-08 3 6 1 11 0.83892502093497D-01 0.25500721796606D-08 1 7 1 11 -0.16192500572107D+01 -0.20771954063255D+00 2 7 1 11 0.19137110159115D+00 0.22795595111421D-01 3 7 1 11 0.23327673293650D+01 -0.18083286316607D+00 1 8 1 11 -0.16192500572108D+01 -0.20771954063255D+00 2 8 1 11 0.19137110159116D+00 0.22795595111420D-01 3 8 1 11 -0.23327673293649D+01 0.18083286316607D+00 1 9 1 11 0.38569229888580D-01 -0.16716310652498D-15 2 9 1 11 0.13720769706465D+00 0.11649704608812D-08 3 9 1 11 -0.25302931235778D-14 0.63801874382545D-16 1 10 1 11 -0.40704908416976D-13 -0.38046253161825D-09 2 10 1 11 -0.53662203100364D+00 -0.73081001598894D-09 3 10 1 11 0.87904369773724D-15 0.40093577131708D-17 1 11 1 11 0.89476770944805D+01 0.00000000000000D+00 2 11 1 11 -0.93232038040168D+00 -0.69777959362267D-07 3 11 1 11 -0.12779288027981D-12 0.00000000000000D+00 1 12 1 11 0.52394473368437D+00 -0.39063117408788D-09 2 12 1 11 0.11377012462632D+00 0.20545502123456D-08 3 12 1 11 -0.53628903318436D-14 -0.18739722124772D-15 1 13 1 11 0.17171534193013D-01 -0.18215668653429D-02 2 13 1 11 -0.46172911400712D+00 -0.92326164388082D-02 3 13 1 11 -0.95501543360752D+00 0.40511861185110D-02 1 14 1 11 0.73442613606819D+00 0.73271357183314D-02 2 14 1 11 0.95475056913764D+00 0.13338005088366D-01 3 14 1 11 -0.66564031357816D+00 -0.53613601460727D-02 1 15 1 11 0.73442613606819D+00 0.73271357183313D-02 2 15 1 11 0.95475056913764D+00 0.13338005088366D-01 3 15 1 11 0.66564031357817D+00 0.53613601460727D-02 1 16 1 11 0.17171534193005D-01 -0.18215668653424D-02 2 16 1 11 -0.46172911400712D+00 -0.92326164388083D-02 3 16 1 11 0.95501543360752D+00 -0.40511861185109D-02 1 17 1 11 -0.64982840858623D-02 0.31004102515302D-02 2 17 1 11 -0.43679226663018D+00 -0.30988760905913D-02 3 17 1 11 0.12554524805744D+01 -0.59655618165052D-02 1 18 1 11 -0.14934665198590D+01 0.12031750558032D-08 2 18 1 11 0.80425400214363D+00 -0.24420575641536D-08 3 18 1 11 0.13064333069259D+01 0.11424269790870D-07 1 19 1 11 -0.14934665198589D+01 0.12031749891779D-08 2 19 1 11 0.80425400214362D+00 -0.24420576450847D-08 3 19 1 11 -0.13064333069259D+01 -0.11424269856389D-07 1 20 1 11 -0.64982840858634D-02 0.31004102515302D-02 2 20 1 11 -0.43679226663015D+00 -0.30988760905910D-02 3 20 1 11 -0.12554524805743D+01 0.59655618165051D-02 1 1 2 11 -0.10288537780560D-01 -0.56733237514132D-08 2 1 2 11 -0.95093453917009D+00 -0.10155836155401D-08 3 1 2 11 -0.13466280437957D-14 0.55583954725064D-16 1 2 2 11 -0.44442567613532D+00 0.15885683017945D-07 2 2 2 11 0.14506871895842D+01 0.84332778792843D-08 3 2 2 11 -0.12168372092340D-14 0.76300230224073D-16 1 3 2 11 -0.69495458873944D-02 -0.38816361208912D-08 2 3 2 11 -0.27633383793016D-03 0.10177181625541D-07 3 3 2 11 0.22592842488008D-15 0.61171828701489D-15 1 4 2 11 -0.60757540101522D-01 0.27052683607989D-07 2 4 2 11 -0.22294686253615D+01 -0.68545677793453D-08 3 4 2 11 -0.60685013976947D-14 0.26361124240747D-14 1 5 2 11 0.25313561100868D-01 0.28691431480135D-08 2 5 2 11 -0.37783647993467D+00 0.54721391551667D-10 3 5 2 11 0.55708549824360D+00 -0.30160402615533D-08 1 6 2 11 0.25313561100885D-01 0.28691430484892D-08 2 6 2 11 -0.37783647993466D+00 0.54721001925535D-10 3 6 2 11 -0.55708549824364D+00 0.30160402132888D-08 1 7 2 11 0.90066967558142D-01 0.24981407868869D-01 2 7 2 11 -0.34302706964863D+01 -0.27872569876803D+00 3 7 2 11 0.42457655352382D+00 -0.46643992746652D-01 1 8 2 11 0.90066967558156D-01 0.24981407868869D-01 2 8 2 11 -0.34302706964864D+01 -0.27872569876803D+00 3 8 2 11 -0.42457655352378D+00 0.46643992746651D-01 1 9 2 11 -0.13720769706464D+00 0.11649704608812D-08 2 9 2 11 0.22743408462265D+00 0.61321718674966D-15 3 9 2 11 -0.17397915137434D-14 -0.36576420450446D-15 1 10 2 11 -0.53662203100364D+00 0.73081255182460D-09 2 10 2 11 -0.26186368807564D-14 0.63051012975220D-08 3 10 2 11 -0.39298695256576D-14 -0.40466231948981D-15 1 11 2 11 -0.93231833163929D+00 0.57246956840947D-07 2 11 2 11 0.74017914710932D+01 0.00000000000000D+00 3 11 2 11 -0.42625797556344D-13 0.00000000000000D+00 1 12 2 11 0.11377091585428D+00 -0.15442714430840D-08 2 12 2 11 -0.12182169613775D+00 -0.69648362712673D-09 3 12 2 11 -0.11212630629653D-14 -0.13662940664294D-15 1 13 2 11 0.63146529951419D-02 -0.89196694456550D-02 2 13 2 11 0.29291042281998D+00 -0.81021931314563D-02 3 13 2 11 -0.17197215205557D+01 0.76217125311954D-02 1 14 2 11 0.87044227676285D+00 0.15194833848586D-01 2 14 2 11 0.19735520769853D-01 0.14451739772075D-01 3 14 2 11 -0.17154731050669D+01 -0.48289889670967D-02 1 15 2 11 0.87044227676285D+00 0.15194833848586D-01 2 15 2 11 0.19735520769864D-01 0.14451739772075D-01 3 15 2 11 0.17154731050669D+01 0.48289889670968D-02 1 16 2 11 0.63146529951472D-02 -0.89196694456551D-02 2 16 2 11 0.29291042282000D+00 -0.81021931314551D-02 3 16 2 11 0.17197215205557D+01 -0.76217125311951D-02 1 17 2 11 -0.19480650971429D+00 -0.31376545498046D-02 2 17 2 11 -0.31596115616930D+00 -0.50862222149208D-03 3 17 2 11 -0.13160594003879D+01 0.28535538357947D-02 1 18 2 11 0.41575685832012D+00 0.14435272849023D-07 2 18 2 11 0.77887176800132D+00 -0.88619882959359D-08 3 18 2 11 -0.10413264263538D+01 -0.10860401448434D-07 1 19 2 11 0.41575685832010D+00 0.14435272768091D-07 2 19 2 11 0.77887176800130D+00 -0.88619882311547D-08 3 19 2 11 0.10413264263538D+01 0.10860401813822D-07 1 20 2 11 -0.19480650971427D+00 -0.31376545498043D-02 2 20 2 11 -0.31596115616931D+00 -0.50862222149188D-03 3 20 2 11 0.13160594003879D+01 -0.28535538357942D-02 1 1 3 11 0.16129894448164D-14 0.20745265814122D-15 2 1 3 11 -0.13466280437887D-14 0.55752352955156D-16 3 1 3 11 0.17860256660851D+01 0.15336967048172D-07 1 2 3 11 -0.65673060466247D-15 -0.26768469542421D-15 2 2 3 11 -0.12168372074944D-14 0.76199787024524D-16 3 2 3 11 0.29843300792447D+01 0.13044296979411D-06 1 3 3 11 -0.43722370104569D-15 0.13650806825351D-16 2 3 3 11 0.22592842473336D-15 0.61224203623444D-15 3 3 3 11 -0.14087185061614D+00 0.36345499949345D-09 1 4 3 11 0.83241429804829D-15 -0.72433729038211D-16 2 4 3 11 -0.60685013981083D-14 0.26361124240747D-14 3 4 3 11 -0.11521352310816D+01 -0.48540211048198D-07 1 5 3 11 0.86856186557536D+00 -0.88069222136632D-02 2 5 3 11 0.50596657091991D+01 -0.22843272391440D-01 3 5 3 11 0.77235024357356D-02 0.92952290049536D-02 1 6 3 11 -0.86856186557537D+00 0.88069222136632D-02 2 6 3 11 -0.50596657091992D+01 0.22843272391440D-01 3 6 3 11 0.77235024357454D-02 0.92952290049533D-02 1 7 3 11 -0.45096516641658D+00 -0.28904115117430D+00 2 7 3 11 -0.22296202286145D+00 -0.77409455086047D-01 3 7 3 11 -0.84039452125597D+00 0.82345773040977D+00 1 8 3 11 0.45096516641674D+00 0.28904115117430D+00 2 8 3 11 0.22296202286150D+00 0.77409455086045D-01 3 8 3 11 -0.84039452125540D+00 0.82345773040978D+00 1 9 3 11 -0.25302931235554D-14 0.63307181647194D-16 2 9 3 11 -0.17397915136559D-14 -0.35983966847824D-15 3 9 3 11 -0.20035517264249D+00 -0.58485311422133D-15 1 10 3 11 0.87904369770970D-15 0.48525708552720D-17 2 10 3 11 -0.39298695253711D-14 -0.40404844709461D-15 3 10 3 11 0.99805969406061D-13 -0.41412218753502D-07 1 11 3 11 -0.12779288027981D-12 0.13877787807814D-16 2 11 3 11 -0.42625797556344D-13 0.00000000000000D+00 3 11 3 11 0.41534743982117D+02 0.00000000000000D+00 1 12 3 11 -0.53628903319389D-14 -0.19312359151265D-15 2 12 3 11 -0.11212630632732D-14 -0.13224962550374D-15 3 12 3 11 0.15205234919070D+02 -0.25716731009086D-09 1 13 3 11 -0.19208973171480D+01 0.10914982315115D-07 2 13 3 11 -0.35022316799165D+01 0.89237683720232D-06 3 13 3 11 -0.38199648074240D+01 0.59547118571521D-06 1 14 3 11 -0.23717968961453D+01 0.36889848857994D-01 2 14 3 11 -0.29062589369673D+01 0.47548968402092D-01 3 14 3 11 0.14454180791777D+01 0.21075224935318D-01 1 15 3 11 0.23717968961453D+01 -0.36889848857994D-01 2 15 3 11 0.29062589369673D+01 -0.47548968402092D-01 3 15 3 11 0.14454180791777D+01 0.21075224935319D-01 1 16 3 11 0.19208973171480D+01 -0.10914982262853D-07 2 16 3 11 0.35022316799165D+01 -0.89237683692162D-06 3 16 3 11 -0.38199648074240D+01 0.59547118603724D-06 1 17 3 11 0.22145513347881D+01 0.27619719981104D-01 2 17 3 11 -0.28565669353929D+01 -0.21959744064953D-01 3 17 3 11 0.33825879169124D+01 -0.21969610404849D-01 1 18 3 11 0.29406371989935D+01 -0.18619026973270D-07 2 18 3 11 -0.23657867743271D+01 0.12929810136721D-07 3 18 3 11 -0.15996529498806D+01 -0.18746691921203D-07 1 19 3 11 -0.29406371989935D+01 0.18619026904281D-07 2 19 3 11 0.23657867743271D+01 -0.12929809767864D-07 3 19 3 11 -0.15996529498806D+01 -0.18746693223386D-07 1 20 3 11 -0.22145513347881D+01 -0.27619719981104D-01 2 20 3 11 0.28565669353928D+01 0.21959744064953D-01 3 20 3 11 0.33825879169124D+01 -0.21969610404847D-01 1 1 1 12 0.11748780754743D+01 0.20743046980769D-07 2 1 1 12 -0.63249916978185D+00 0.75795662949125D-08 3 1 1 12 -0.83137797883945D-16 0.24070126161861D-15 1 2 1 12 0.27086826803725D+00 0.28246234366367D-08 2 2 1 12 0.16366317516937D+00 0.98162993789802D-08 3 2 1 12 0.48712738992746D-14 -0.37096661114581D-16 1 3 1 12 -0.34067507200380D+00 -0.14638563851335D-07 2 3 1 12 0.42462063461763D+00 0.17518729027587D-07 3 3 1 12 0.23710462383632D-16 0.81901317454608D-16 1 4 1 12 0.90847243655280D-01 -0.10096858087019D-07 2 4 1 12 -0.73000920128043D-01 -0.69602993380705D-08 3 4 1 12 -0.22321114892532D-15 0.10857870657523D-15 1 5 1 12 0.64637539596383D-01 0.95137176245819D-10 2 5 1 12 -0.76864195703400D-01 0.17698090964590D-08 3 5 1 12 -0.83892502093477D-01 -0.25500716461096D-08 1 6 1 12 0.64637539596386D-01 0.95136116256897D-10 2 6 1 12 -0.76864195703395D-01 0.17698089326313D-08 3 6 1 12 0.83892502093475D-01 0.25500713066692D-08 1 7 1 12 0.16192500572109D+01 0.20771954063254D+00 2 7 1 12 -0.19137110159130D+00 -0.22795595111420D-01 3 7 1 12 -0.23327673293649D+01 0.18083286316605D+00 1 8 1 12 0.16192500572108D+01 0.20771954063254D+00 2 8 1 12 -0.19137110159129D+00 -0.22795595111420D-01 3 8 1 12 0.23327673293649D+01 -0.18083286316605D+00 1 9 1 12 0.57021290435032D-15 -0.38046141169366D-09 2 9 1 12 -0.53662203100369D+00 -0.73081260835702D-09 3 9 1 12 -0.87809088419499D-15 -0.27340468090294D-16 1 10 1 12 0.38569229888588D-01 -0.34294300470936D-15 2 10 1 12 0.13720769706465D+00 0.11649703721440D-08 3 10 1 12 0.31546306736278D-14 0.23840779555393D-16 1 11 1 12 0.52394473368437D+00 -0.39063179567083D-09 2 11 1 12 0.11377012462632D+00 0.20545501414072D-08 3 11 1 12 -0.53628903315253D-14 0.19312359151265D-15 1 12 1 12 0.89476770944809D+01 0.00000000000000D+00 2 12 1 12 -0.93232038040173D+00 -0.69777959362267D-07 3 12 1 12 0.10481215700956D-15 0.00000000000000D+00 1 13 1 12 0.73442613606822D+00 0.73271357183334D-02 2 13 1 12 0.95475056913764D+00 0.13338005088370D-01 3 13 1 12 -0.66564031357818D+00 -0.53613601460783D-02 1 14 1 12 0.17171534193002D-01 -0.18215668653423D-02 2 14 1 12 -0.46172911400710D+00 -0.92326164388084D-02 3 14 1 12 -0.95501543360747D+00 0.40511861185110D-02 1 15 1 12 0.17171534193002D-01 -0.18215668653424D-02 2 15 1 12 -0.46172911400711D+00 -0.92326164388084D-02 3 15 1 12 0.95501543360748D+00 -0.40511861185110D-02 1 16 1 12 0.73442613606822D+00 0.73271357183334D-02 2 16 1 12 0.95475056913765D+00 0.13338005088370D-01 3 16 1 12 0.66564031357820D+00 0.53613601460781D-02 1 17 1 12 -0.14934665198589D+01 0.12031754621473D-08 2 17 1 12 0.80425400214363D+00 -0.24420574396409D-08 3 17 1 12 0.13064333069258D+01 0.11424269771943D-07 1 18 1 12 -0.64982840858703D-02 0.31004102515301D-02 2 18 1 12 -0.43679226663016D+00 -0.30988760905932D-02 3 18 1 12 0.12554524805744D+01 -0.59655618164992D-02 1 19 1 12 -0.64982840858680D-02 0.31004102515299D-02 2 19 1 12 -0.43679226663016D+00 -0.30988760905936D-02 3 19 1 12 -0.12554524805744D+01 0.59655618164992D-02 1 20 1 12 -0.14934665198589D+01 0.12031747211285D-08 2 20 1 12 0.80425400214363D+00 -0.24420573241093D-08 3 20 1 12 -0.13064333069258D+01 -0.11424269855105D-07 1 1 2 12 -0.44442567613515D+00 0.15885677436475D-07 2 1 2 12 0.14506871895840D+01 0.84332650906702D-08 3 1 2 12 0.67413577976069D-16 -0.17929074406845D-15 1 2 2 12 -0.10288537780566D-01 -0.56733240326505D-08 2 2 2 12 -0.95093453917009D+00 -0.10155834165445D-08 3 2 2 12 0.10511814630816D-14 -0.13513007923669D-16 1 3 2 12 -0.60757540101643D-01 0.27052685719679D-07 2 3 2 12 -0.22294686253612D+01 -0.68545585181263D-08 3 3 2 12 -0.85115420170684D-15 -0.62398481586961D-15 1 4 2 12 -0.69495458873913D-02 -0.38816361418133D-08 2 4 2 12 -0.27633383797593D-03 0.10177184732306D-07 3 4 2 12 0.14644739200338D-14 -0.85771384787307D-16 1 5 2 12 0.25313561100879D-01 0.28691426078175D-08 2 5 2 12 -0.37783647993477D+00 0.54724030156121D-10 3 5 2 12 0.55708549824363D+00 -0.30160422425120D-08 1 6 2 12 0.25313561100883D-01 0.28691424439220D-08 2 6 2 12 -0.37783647993477D+00 0.54721318433060D-10 3 6 2 12 -0.55708549824362D+00 0.30160422613870D-08 1 7 2 12 -0.90066967558295D-01 -0.24981407868868D-01 2 7 2 12 0.34302706964864D+01 0.27872569876802D+00 3 7 2 12 -0.42457655352287D+00 0.46643992746650D-01 1 8 2 12 -0.90066967558292D-01 -0.24981407868869D-01 2 8 2 12 0.34302706964865D+01 0.27872569876802D+00 3 8 2 12 0.42457655352287D+00 -0.46643992746649D-01 1 9 2 12 -0.53662203100369D+00 0.73080995945652D-09 2 9 2 12 -0.72689843229068D-14 0.63051053254213D-08 3 9 2 12 -0.54002353139890D-14 -0.65763845701821D-15 1 10 2 12 -0.13720769706465D+00 0.11649703721440D-08 2 10 2 12 0.22743408462261D+00 0.89226759347090D-15 3 10 2 12 0.22734794048744D-14 0.36315496128037D-15 1 11 2 12 0.11377091585428D+00 -0.15442715140223D-08 2 11 2 12 -0.12182169613775D+00 -0.69648504599508D-09 3 11 2 12 -0.11212630630664D-14 0.13398434897971D-15 1 12 2 12 -0.93231833163934D+00 0.57246956840947D-07 2 12 2 12 0.74017914710928D+01 0.00000000000000D+00 3 12 2 12 -0.21309515483541D-13 0.00000000000000D+00 1 13 2 12 0.87044227676285D+00 0.15194833848590D-01 2 13 2 12 0.19735520769805D-01 0.14451739772077D-01 3 13 2 12 -0.17154731050669D+01 -0.48289889671034D-02 1 14 2 12 0.63146529951579D-02 -0.89196694456552D-02 2 14 2 12 0.29291042281994D+00 -0.81021931314561D-02 3 14 2 12 -0.17197215205557D+01 0.76217125311948D-02 1 15 2 12 0.63146529951597D-02 -0.89196694456551D-02 2 15 2 12 0.29291042281993D+00 -0.81021931314549D-02 3 15 2 12 0.17197215205557D+01 -0.76217125311949D-02 1 16 2 12 0.87044227676286D+00 0.15194833848590D-01 2 16 2 12 0.19735520769796D-01 0.14451739772077D-01 3 16 2 12 0.17154731050669D+01 0.48289889671037D-02 1 17 2 12 0.41575685832012D+00 0.14435272973535D-07 2 17 2 12 0.77887176800124D+00 -0.88619877522463D-08 3 17 2 12 -0.10413264263539D+01 -0.10860401369427D-07 1 18 2 12 -0.19480650971428D+00 -0.31376545498065D-02 2 18 2 12 -0.31596115616935D+00 -0.50862222149102D-03 3 18 2 12 -0.13160594003879D+01 0.28535538357872D-02 1 19 2 12 -0.19480650971428D+00 -0.31376545498069D-02 2 19 2 12 -0.31596115616935D+00 -0.50862222149146D-03 3 19 2 12 0.13160594003879D+01 -0.28535538357873D-02 1 20 2 12 0.41575685832012D+00 0.14435273089067D-07 2 20 2 12 0.77887176800125D+00 -0.88619881842232D-08 3 20 2 12 0.10413264263538D+01 0.10860401615763D-07 1 1 3 12 -0.83137797485674D-16 0.23847034529998D-15 2 1 3 12 0.67413579715682D-16 -0.17939118726800D-15 3 1 3 12 0.29843300792446D+01 0.13044294353993D-06 1 2 3 12 0.48712738987882D-14 -0.37702862562143D-16 2 2 3 12 0.10511814630886D-14 -0.13344609693577D-16 3 2 3 12 0.17860256660851D+01 0.15336967287265D-07 1 3 3 12 0.23710462383636D-16 0.81901317454608D-16 2 3 3 12 -0.85115420212044D-15 -0.62398481586961D-15 3 3 3 12 -0.11521352310820D+01 -0.48540218536536D-07 1 4 3 12 -0.22321114902226D-15 0.10859195477819D-15 2 4 3 12 0.14644739203054D-14 -0.84764085712639D-16 3 4 3 12 -0.14087185061598D+00 0.36345785109082D-09 1 5 3 12 0.86856186557539D+00 -0.88069222136627D-02 2 5 3 12 0.50596657091991D+01 -0.22843272391442D-01 3 5 3 12 0.77235024357654D-02 0.92952290049538D-02 1 6 3 12 -0.86856186557539D+00 0.88069222136624D-02 2 6 3 12 -0.50596657091991D+01 0.22843272391442D-01 3 6 3 12 0.77235024357667D-02 0.92952290049542D-02 1 7 3 12 0.45096516641669D+00 0.28904115117429D+00 2 7 3 12 0.22296202286241D+00 0.77409455086044D-01 3 7 3 12 0.84039452125586D+00 -0.82345773040971D+00 1 8 3 12 -0.45096516641674D+00 -0.28904115117429D+00 2 8 3 12 -0.22296202286240D+00 -0.77409455086044D-01 3 8 3 12 0.84039452125558D+00 -0.82345773040971D+00 1 9 3 12 -0.87809088422253D-15 -0.26497254948193D-16 2 9 3 12 -0.54002353137025D-14 -0.65702458462301D-15 3 9 3 12 -0.15417375275082D-13 -0.41412220282377D-07 1 10 3 12 0.31546306736502D-14 0.23346086820042D-16 2 10 3 12 0.22734794049619D-14 0.36907949730659D-15 3 10 3 12 -0.20035517264243D+00 -0.24592596925143D-15 1 11 3 12 -0.53628903301892D-14 0.18045832734382D-15 2 11 3 12 -0.11212630623449D-14 0.13836413011892D-15 3 11 3 12 0.15205234919070D+02 -0.25715926572865D-09 1 12 3 12 0.10481215700956D-15 0.13877787807814D-16 2 12 3 12 -0.21309515483541D-13 0.00000000000000D+00 3 12 3 12 0.41534743982118D+02 0.00000000000000D+00 1 13 3 12 -0.23717968961453D+01 0.36889848857989D-01 2 13 3 12 -0.29062589369673D+01 0.47548968402086D-01 3 13 3 12 0.14454180791777D+01 0.21075224935323D-01 1 14 3 12 -0.19208973171480D+01 0.10914982382527D-07 2 14 3 12 -0.35022316799165D+01 0.89237683668537D-06 3 14 3 12 -0.38199648074239D+01 0.59547118617894D-06 1 15 3 12 0.19208973171480D+01 -0.10914982342947D-07 2 15 3 12 0.35022316799165D+01 -0.89237683677325D-06 3 15 3 12 -0.38199648074239D+01 0.59547118761243D-06 1 16 3 12 0.23717968961453D+01 -0.36889848857989D-01 2 16 3 12 0.29062589369672D+01 -0.47548968402085D-01 3 16 3 12 0.14454180791777D+01 0.21075224935323D-01 1 17 3 12 0.29406371989934D+01 -0.18619026992197D-07 2 17 3 12 -0.23657867743271D+01 0.12929810215728D-07 3 17 3 12 -0.15996529498805D+01 -0.18746693686936D-07 1 18 3 12 0.22145513347881D+01 0.27619719981110D-01 2 18 3 12 -0.28565669353928D+01 -0.21959744064960D-01 3 18 3 12 0.33825879169125D+01 -0.21969610404834D-01 1 19 3 12 -0.22145513347881D+01 -0.27619719981110D-01 2 19 3 12 0.28565669353928D+01 0.21959744064960D-01 3 19 3 12 0.33825879169125D+01 -0.21969610404837D-01 1 20 3 12 -0.29406371989934D+01 0.18619026905565D-07 2 20 3 12 0.23657867743271D+01 -0.12929809965922D-07 3 20 3 12 -0.15996529498805D+01 -0.18746693449670D-07 1 1 1 13 -0.18591191906728D+00 0.17939914049752D-02 2 1 1 13 -0.90026468815003D+00 0.11789234466966D-02 3 1 1 13 -0.37629219597444D-01 0.38205164724475D-07 1 2 1 13 -0.18627785637442D-01 0.21012580137455D-03 2 2 1 13 0.66650992669084D+00 0.15958688660337D-02 3 2 1 13 -0.24459026156699D-01 -0.14667797057877D-02 1 3 1 13 -0.39631777278964D+00 0.16656258511048D-02 2 3 1 13 -0.18325830586098D+00 -0.29427663472302D-02 3 3 1 13 0.98985970064562D+00 0.70221971410086D-02 1 4 1 13 0.25144422357356D-01 -0.30885780243656D-02 2 4 1 13 -0.10029332792676D+01 -0.42170134288046D-02 3 4 1 13 0.44240345177299D+00 -0.11654722509409D-06 1 5 1 13 -0.14132827669591D+01 0.16778780763755D-01 2 5 1 13 -0.29325625873652D+01 -0.40121880979463D-02 3 5 1 13 -0.37229547086809D+00 0.71956096608917D-01 1 6 1 13 -0.31076334350387D+00 -0.97508677259310D-02 2 6 1 13 -0.84458994063049D+00 -0.80772866284181D-02 3 6 1 13 0.42333913530499D+00 0.57653228107802D-03 1 7 1 13 0.11975170767615D+00 0.98203798255548D-02 2 7 1 13 -0.16406849123270D+01 -0.32328470040546D-02 3 7 1 13 0.20245841920845D+00 -0.64972512946611D-01 1 8 1 13 -0.41859550399764D-01 -0.13715393663127D-01 2 8 1 13 -0.86364077739423D+00 -0.31243896307693D-01 3 8 1 13 -0.27107925689621D+00 0.12034302390373D-01 1 9 1 13 -0.14934460445475D+01 0.24838384143342D-01 2 9 1 13 -0.41569964933525D+00 0.21437584582276D-01 3 9 1 13 -0.29406501250588D+01 0.82743793855561D-07 1 10 1 13 0.65091568533056D-02 0.93012107904106D-02 2 10 1 13 -0.19477953011356D+00 0.94129551087462D-02 3 10 1 13 0.22145572656932D+01 -0.82859171484277D-01 1 11 1 13 0.17171534193013D-01 0.18215668653429D-02 2 11 1 13 0.63146529951419D-02 0.89196694456550D-02 3 11 1 13 -0.19208973171480D+01 -0.10914982315115D-07 1 12 1 13 0.73442613606822D+00 -0.73271357183338D-02 2 12 1 13 0.87044227676285D+00 -0.15194833848591D-01 3 12 1 13 -0.23717968961453D+01 -0.36889848857988D-01 1 13 1 13 0.13281113930983D+02 0.00000000000000D+00 2 13 1 13 0.71826014189155D+01 0.13979109054849D+00 3 13 1 13 -0.12076101657739D+01 -0.17933368183392D+00 1 14 1 13 -0.97733751767875D+00 0.31622574160496D-02 2 14 1 13 0.23613571627540D+00 0.19231436639707D-03 3 14 1 13 0.73237303227026D+00 0.14548070139897D-01 1 15 1 13 -0.15749731011419D+00 -0.10120844011320D-15 2 15 1 13 0.15117986666873D+00 0.57695902243442D-04 3 15 1 13 -0.43632794082818D-01 0.17406243555828D-01 1 16 1 13 0.68328166505078D+00 0.58947624595497D-16 2 16 1 13 0.76015030895172D+00 -0.11839658803165D-06 3 16 1 13 0.16481974863657D-01 0.26205469350212D-06 1 17 1 13 0.30537934851343D-15 -0.17480545157797D-02 2 17 1 13 -0.93267625267633D+00 0.48459772409223D-02 3 17 1 13 -0.28701547608895D+00 -0.25278758042201D-01 1 18 1 13 -0.61907660529897D+01 -0.18578395270111D-15 2 18 1 13 0.21064030177164D+01 -0.88195580812820D-07 3 18 1 13 0.24605958406478D-03 -0.29252181174882D-06 1 19 1 13 -0.47787634030002D+00 -0.90112502728089D-07 2 19 1 13 0.75145899227435D+00 0.30416819069580D-02 3 19 1 13 -0.11433259996273D+00 -0.13854177625741D-02 1 20 1 13 -0.66256674147922D-15 0.18424820898467D-06 2 20 1 13 -0.62995622893073D-01 -0.93487793350767D-03 3 20 1 13 0.14363884105381D+00 -0.47095587187194D-02 1 1 2 13 -0.31686715648499D+00 -0.75760419285128D-02 2 1 2 13 -0.16404765908637D+01 0.12652863075468D-01 3 1 2 13 -0.10171296516120D+01 -0.45526650333509D-07 1 2 2 13 0.32726503947588D+00 0.81391347136216D-03 2 2 2 13 0.75893449639934D+00 0.18091601147780D-02 3 2 2 13 -0.10416370308126D+01 -0.74936709423248D-03 1 3 2 13 0.42349060819948D+00 -0.90267832783326D-02 2 3 2 13 -0.20887133686635D+01 0.10053792221447D-01 3 3 2 13 -0.12605127499425D+00 -0.17367804719088D-03 1 4 2 13 -0.27520775231612D+00 0.18559808744822D-02 2 4 2 13 -0.15089106015210D+01 -0.75631303211643D-02 3 4 2 13 -0.10376008111885D+01 -0.22639750149163D-06 1 5 2 13 0.43386917041248D+00 0.89139711311273D-02 2 5 2 13 -0.56047361781017D+01 -0.69295610230415D-02 3 5 2 13 -0.35637188164228D+00 0.67736081061716D-01 1 6 2 13 -0.27322497593674D+00 -0.66212463350026D-02 2 6 2 13 -0.19712272332279D+01 0.48238814018279D-03 3 6 2 13 0.13123301985446D+00 -0.52540686046631D-02 1 7 2 13 0.71405983092760D+00 0.99047118005376D-02 2 7 2 13 -0.57399295574616D+01 -0.25035389651492D-03 3 7 2 13 0.53594074220148D+00 -0.89956128772500D-01 1 8 2 13 -0.60390887309065D-02 -0.32115589159745D-01 2 8 2 13 -0.19627782024968D+01 -0.22171585459856D-01 3 8 2 13 -0.31948107143717D+00 0.20096264537441D-01 1 9 2 13 -0.80418738571386D+00 0.25530227544933D-01 2 9 2 13 0.77883076299127D+00 0.92341284513325D-02 3 9 2 13 -0.23657963913107D+01 -0.10268497672982D-05 1 10 2 13 -0.43675767475460D+00 0.92966318914350D-02 2 10 2 13 0.31593779458368D+00 -0.15258830031242D-02 3 10 2 13 0.28565703852058D+01 -0.65879253351045D-01 1 11 2 13 -0.46172911400712D+00 0.92326164388082D-02 2 11 2 13 0.29291042281998D+00 0.81021931314563D-02 3 11 2 13 -0.35022316799165D+01 -0.89237683720232D-06 1 12 2 13 0.95475056913764D+00 -0.13338005088371D-01 2 12 2 13 0.19735520769805D-01 -0.14451739772076D-01 3 12 2 13 -0.29062589369673D+01 -0.47548968402083D-01 1 13 2 13 0.71826056682818D+01 -0.13979063280100D+00 2 13 2 13 0.16980139277633D+02 0.00000000000000D+00 3 13 2 13 0.20712557483682D+01 0.24785524218975D+00 1 14 2 13 0.23613536008034D+00 0.19237132705910D-03 2 14 2 13 0.66673109866710D+00 -0.21510066108847D-02 3 14 2 13 0.99634253689593D+00 0.15758001046142D-01 1 15 2 13 0.15117986666873D+00 -0.57695902243325D-04 2 15 2 13 0.64591501749743D-01 0.10171200723129D-14 3 15 2 13 -0.71059163567540D-02 0.24563030454912D-01 1 16 2 13 0.76015030895172D+00 0.11839658800769D-06 2 16 2 13 0.17314326962186D+01 0.52874320522331D-15 3 16 2 13 -0.17779933115966D+00 0.22313226315733D-06 1 17 2 13 -0.93267625267633D+00 -0.48459772409181D-02 2 17 2 13 0.20343554054110D-13 0.28114949348548D-02 3 17 2 13 -0.19657751149757D-01 -0.34560078058959D-01 1 18 2 13 -0.21064030177164D+01 -0.88195580812820D-07 2 18 2 13 0.35233322690473D+01 -0.18730646424296D-15 3 18 2 13 -0.30766317313185D+00 0.10308124045993D-06 1 19 2 13 -0.75146054059527D+00 0.30415856890043D-02 2 19 2 13 0.15579327054328D+01 0.40018818748949D-07 3 19 2 13 -0.11171791278783D-01 -0.40426306225290D-02 1 20 2 13 -0.62997787618651D-01 -0.93428785486425D-03 2 20 2 13 -0.16261213672244D-13 -0.19079360432929D-06 3 20 2 13 -0.34654244736437D+00 -0.34462583141573D-02 1 1 3 13 0.52523419709060D+00 0.21665446929420D-02 2 1 3 13 -0.64607194557477D+00 0.43467172148254D-02 3 1 3 13 -0.12410017819341D+00 0.21217364884568D-06 1 2 3 13 0.29524272141789D+00 -0.22397157633062D-03 2 2 3 13 -0.66671587413012D+00 -0.10683385518604D-02 3 2 3 13 -0.61524493664588D+00 0.19236340652068D-03 1 3 3 13 0.58852109688780D+00 -0.15680990687225D-01 2 3 3 13 -0.56434041082926D+00 0.14139490556713D-01 3 3 3 13 -0.22355539557402D+01 0.40605244129984D-02 1 4 3 13 0.73325324000034D+00 -0.13507992412826D-01 2 4 3 13 -0.76652726720671D+00 0.69414717873133D-02 3 4 3 13 0.86413724239475D+00 -0.43621188061545D-07 1 5 3 13 0.77008098638764D+00 0.16550095159033D-01 2 5 3 13 0.41101651657511D+00 0.14633391495208D-01 3 5 3 13 -0.38187858707145D+01 -0.83398926245814D-02 1 6 3 13 -0.11574704131344D+00 -0.15169791020614D-01 2 6 3 13 0.46565926400900D+00 -0.96578056394315D-02 3 6 3 13 0.33113979864878D+01 0.10995496813759D-01 1 7 3 13 -0.98932719077391D+00 -0.77813748561240D-02 2 7 3 13 -0.49419589443971D+00 -0.23665373738740D-01 3 7 3 13 -0.33040214403575D+01 0.17968918688611D-02 1 8 3 13 0.20564180761398D+00 0.28648166579906D-01 2 8 3 13 -0.49064448143153D+00 0.48289929063165D-01 3 8 3 13 0.29726299654675D+01 0.22412377616584D-01 1 9 3 13 -0.13065437590370D+01 0.13274932927196D-01 2 9 3 13 -0.10413070221578D+01 0.89206689404533D-02 3 9 3 13 -0.15996441794863D+01 0.22175483998304D-05 1 10 3 13 0.12553718318911D+01 0.17896677689910D-01 2 10 3 13 0.13160138097076D+01 0.85606723896021D-02 3 10 3 13 -0.33825892305504D+01 -0.65908846273702D-01 1 11 3 13 -0.95501543360752D+00 -0.40511861185110D-02 2 11 3 13 -0.17197215205557D+01 -0.76217125311954D-02 3 11 3 13 -0.38199648074240D+01 -0.59547118571521D-06 1 12 3 13 -0.66564031357818D+00 0.53613601460795D-02 2 12 3 13 -0.17154731050669D+01 0.48289889671056D-02 3 12 3 13 0.14454180791777D+01 -0.21075224935323D-01 1 13 3 13 -0.12075921112688D+01 0.17933139462464D+00 2 13 3 13 0.20712817804932D+01 -0.24785480103441D+00 3 13 3 13 0.15199907007337D+02 0.00000000000000D+00 1 14 3 13 0.73237358986143D+00 0.14548041350846D-01 2 14 3 13 0.99634061540388D+00 0.15757697354718D-01 3 14 3 13 0.28614716333105D+00 -0.66939125962415D-03 1 15 3 13 0.43632794082819D-01 0.17406243555828D-01 2 15 3 13 0.71059163567384D-02 0.24563030454912D-01 3 15 3 13 -0.47302865594405D+00 -0.37722053214600D-15 1 16 3 13 -0.16481974863656D-01 0.26205469350212D-06 2 16 3 13 0.17779933115965D+00 0.22313226315733D-06 3 16 3 13 -0.18130548827795D+01 0.30272254329930D-15 1 17 3 13 -0.28701547608895D+00 0.25278758042201D-01 2 17 3 13 0.19657751149751D-01 -0.34560078058959D-01 3 17 3 13 -0.13375936957890D-13 0.46236086934915D-02 1 18 3 13 -0.24605958406120D-03 -0.29252181174882D-06 2 18 3 13 -0.30766317313185D+00 -0.10308124031085D-06 3 18 3 13 0.93373692662097D+00 0.89190814317247D-15 1 19 3 13 -0.11433356198722D+00 0.13854815198983D-02 2 19 3 13 0.11172645839056D-01 -0.40424793648482D-02 3 19 3 13 -0.55289935268936D+00 0.52213956983423D-08 1 20 3 13 -0.14363873573459D+00 0.47098595949132D-02 2 20 3 13 -0.34654275540796D+00 -0.34465516954449D-02 3 20 3 13 -0.63967050429561D-14 0.38706733149292D-07 1 1 1 14 -0.18627785637425D-01 0.21012580137601D-03 2 1 1 14 0.66650992669084D+00 0.15958688660309D-02 3 1 1 14 -0.24459026156728D-01 -0.14667797057914D-02 1 2 1 14 -0.18591191906736D+00 0.17939914049756D-02 2 2 1 14 -0.90026468815002D+00 0.11789234466970D-02 3 2 1 14 -0.37629219597544D-01 0.38205164615922D-07 1 3 1 14 0.25144422357394D-01 -0.30885780243655D-02 2 3 1 14 -0.10029332792676D+01 -0.42170134288041D-02 3 3 1 14 0.44240345177309D+00 -0.11654722501160D-06 1 4 1 14 -0.39631777278961D+00 0.16656258511052D-02 2 4 1 14 -0.18325830586095D+00 -0.29427663472298D-02 3 4 1 14 0.98985970064572D+00 0.70221971410084D-02 1 5 1 14 -0.14132827669589D+01 0.16778780763755D-01 2 5 1 14 -0.29325625873649D+01 -0.40121880979469D-02 3 5 1 14 -0.37229547086845D+00 0.71956096608916D-01 1 6 1 14 -0.31076334350386D+00 -0.97508677259307D-02 2 6 1 14 -0.84458994063050D+00 -0.80772866284177D-02 3 6 1 14 0.42333913530498D+00 0.57653228107817D-03 1 7 1 14 -0.11975170767603D+00 -0.98203798255511D-02 2 7 1 14 0.16406849123276D+01 0.32328470040763D-02 3 7 1 14 -0.20245841920845D+00 0.64972512946618D-01 1 8 1 14 0.41859550399768D-01 0.13715393663127D-01 2 8 1 14 0.86364077739423D+00 0.31243896307693D-01 3 8 1 14 0.27107925689619D+00 -0.12034302390373D-01 1 9 1 14 0.65091568533324D-02 0.93012107904105D-02 2 9 1 14 -0.19477953011355D+00 0.94129551087459D-02 3 9 1 14 0.22145572656932D+01 -0.82859171484277D-01 1 10 1 14 -0.14934460445475D+01 0.24838384143342D-01 2 10 1 14 -0.41569964933530D+00 0.21437584582276D-01 3 10 1 14 -0.29406501250589D+01 0.82743793693287D-07 1 11 1 14 0.73442613606819D+00 -0.73271357183318D-02 2 11 1 14 0.87044227676285D+00 -0.15194833848587D-01 3 11 1 14 -0.23717968961453D+01 -0.36889848857993D-01 1 12 1 14 0.17171534193002D-01 0.18215668653423D-02 2 12 1 14 0.63146529951579D-02 0.89196694456552D-02 3 12 1 14 -0.19208973171480D+01 -0.10914982382527D-07 1 13 1 14 -0.97733751767875D+00 0.31622574160510D-02 2 13 1 14 0.23613571627540D+00 0.19231436639775D-03 3 13 1 14 0.73237303227026D+00 0.14548070139898D-01 1 14 1 14 0.13281113930983D+02 0.00000000000000D+00 2 14 1 14 0.71826014189159D+01 0.13979109054849D+00 3 14 1 14 -0.12076101657735D+01 -0.17933368183392D+00 1 15 1 14 0.68328166505077D+00 -0.12989607834477D-15 2 15 1 14 0.76015030895172D+00 -0.11839658801925D-06 3 15 1 14 0.16481974863655D-01 0.26205469346586D-06 1 16 1 14 -0.15749731011419D+00 0.10202482904542D-15 2 16 1 14 0.15117986666873D+00 0.57695902243325D-04 3 16 1 14 -0.43632794082821D-01 0.17406243555827D-01 1 17 1 14 -0.61907660529897D+01 0.54485774380114D-15 2 17 1 14 0.21064030177164D+01 -0.88195580870488D-07 3 17 1 14 0.24605958404918D-03 -0.29252181175309D-06 1 18 1 14 -0.21514935718595D-15 -0.17480545157822D-02 2 18 1 14 -0.93267625267633D+00 0.48459772409200D-02 3 18 1 14 -0.28701547608896D+00 -0.25278758042201D-01 1 19 1 14 -0.81356704404412D-15 0.18424820885026D-06 2 19 1 14 -0.62995622893072D-01 -0.93487793350770D-03 3 19 1 14 0.14363884105381D+00 -0.47095587187192D-02 1 20 1 14 -0.47787634030003D+00 -0.90112502502396D-07 2 20 1 14 0.75145899227435D+00 0.30416819069580D-02 3 20 1 14 -0.11433259996273D+00 -0.13854177625741D-02 1 1 2 14 0.32726503947587D+00 0.81391347135940D-03 2 1 2 14 0.75893449639926D+00 0.18091601147775D-02 3 1 2 14 -0.10416370308126D+01 -0.74936709422606D-03 1 2 2 14 -0.31686715648498D+00 -0.75760419285123D-02 2 2 2 14 -0.16404765908636D+01 0.12652863075466D-01 3 2 2 14 -0.10171296516120D+01 -0.45526650660644D-07 1 3 2 14 -0.27520775231615D+00 0.18559808744826D-02 2 3 2 14 -0.15089106015209D+01 -0.75631303211636D-02 3 3 2 14 -0.10376008111886D+01 -0.22639750264708D-06 1 4 2 14 0.42349060819950D+00 -0.90267832783322D-02 2 4 2 14 -0.20887133686635D+01 0.10053792221446D-01 3 4 2 14 -0.12605127499434D+00 -0.17367804719102D-03 1 5 2 14 0.43386917041276D+00 0.89139711311267D-02 2 5 2 14 -0.56047361781018D+01 -0.69295610230417D-02 3 5 2 14 -0.35637188164249D+00 0.67736081061715D-01 1 6 2 14 -0.27322497593675D+00 -0.66212463350022D-02 2 6 2 14 -0.19712272332279D+01 0.48238814018761D-03 3 6 2 14 0.13123301985445D+00 -0.52540686046641D-02 1 7 2 14 -0.71405983092700D+00 -0.99047118005158D-02 2 7 2 14 0.57399295574618D+01 0.25035389654056D-03 3 7 2 14 -0.53594074220151D+00 0.89956128772511D-01 1 8 2 14 0.60390887309110D-02 0.32115589159745D-01 2 8 2 14 0.19627782024968D+01 0.22171585459858D-01 3 8 2 14 0.31948107143714D+00 -0.20096264537443D-01 1 9 2 14 -0.43675767475458D+00 0.92966318914347D-02 2 9 2 14 0.31593779458367D+00 -0.15258830031235D-02 3 9 2 14 0.28565703852058D+01 -0.65879253351044D-01 1 10 2 14 -0.80418738571390D+00 0.25530227544933D-01 2 10 2 14 0.77883076299128D+00 0.92341284513329D-02 3 10 2 14 -0.23657963913107D+01 -0.10268497672792D-05 1 11 2 14 0.95475056913764D+00 -0.13338005088367D-01 2 11 2 14 0.19735520769853D-01 -0.14451739772074D-01 3 11 2 14 -0.29062589369673D+01 -0.47548968402090D-01 1 12 2 14 -0.46172911400710D+00 0.92326164388084D-02 2 12 2 14 0.29291042281994D+00 0.81021931314561D-02 3 12 2 14 -0.35022316799165D+01 -0.89237683668537D-06 1 13 2 14 0.23613536008034D+00 0.19237132705979D-03 2 13 2 14 0.66673109866710D+00 -0.21510066108812D-02 3 13 2 14 0.99634253689593D+00 0.15758001046143D-01 1 14 2 14 0.71826056682822D+01 -0.13979063280100D+00 2 14 2 14 0.16980139277633D+02 0.00000000000000D+00 3 14 2 14 0.20712557483685D+01 0.24785524218975D+00 1 15 2 14 0.76015030895172D+00 0.11839658802009D-06 2 15 2 14 0.17314326962186D+01 0.12192603991448D-15 3 15 2 14 -0.17779933115967D+00 0.22313226366759D-06 1 16 2 14 0.15117986666873D+00 -0.57695902243442D-04 2 16 2 14 0.64591501749751D-01 0.74731863971804D-15 3 16 2 14 -0.71059163567356D-02 0.24563030454913D-01 1 17 2 14 -0.21064030177164D+01 -0.88195580870488D-07 2 17 2 14 0.35233322690473D+01 -0.65418159714518D-16 3 17 2 14 -0.30766317313183D+00 0.10308124045063D-06 1 18 2 14 -0.93267625267633D+00 -0.48459772409203D-02 2 18 2 14 -0.67550016568029D-13 0.28114949348625D-02 3 18 2 14 -0.19657751149769D-01 -0.34560078058958D-01 1 19 2 14 -0.62997787618651D-01 -0.93428785486428D-03 2 19 2 14 -0.70268986204276D-14 -0.19079360121623D-06 3 19 2 14 -0.34654244736436D+00 -0.34462583141583D-02 1 20 2 14 -0.75146054059527D+00 0.30415856890043D-02 2 20 2 14 0.15579327054328D+01 0.40018819564443D-07 3 20 2 14 -0.11171791278786D-01 -0.40426306225293D-02 1 1 3 14 0.29524272141786D+00 -0.22397157633430D-03 2 1 3 14 -0.66671587413015D+00 -0.10683385518540D-02 3 1 3 14 -0.61524493664583D+00 0.19236340652794D-03 1 2 3 14 0.52523419709050D+00 0.21665446929419D-02 2 2 3 14 -0.64607194557480D+00 0.43467172148250D-02 3 2 3 14 -0.12410017819345D+00 0.21217364845086D-06 1 3 3 14 0.73325324000044D+00 -0.13507992412825D-01 2 3 3 14 -0.76652726720675D+00 0.69414717873122D-02 3 3 3 14 0.86413724239483D+00 -0.43621186697018D-07 1 4 3 14 0.58852109688790D+00 -0.15680990687225D-01 2 4 3 14 -0.56434041082935D+00 0.14139490556713D-01 3 4 3 14 -0.22355539557403D+01 0.40605244130072D-02 1 5 3 14 0.77008098638728D+00 0.16550095159032D-01 2 5 3 14 0.41101651657490D+00 0.14633391495207D-01 3 5 3 14 -0.38187858707146D+01 -0.83398926245834D-02 1 6 3 14 -0.11574704131345D+00 -0.15169791020614D-01 2 6 3 14 0.46565926400899D+00 -0.96578056394324D-02 3 6 3 14 0.33113979864878D+01 0.10995496813760D-01 1 7 3 14 0.98932719077391D+00 0.77813748561304D-02 2 7 3 14 0.49419589443968D+00 0.23665373738751D-01 3 7 3 14 0.33040214403569D+01 -0.17968918688836D-02 1 8 3 14 -0.20564180761400D+00 -0.28648166579907D-01 2 8 3 14 0.49064448143151D+00 -0.48289929063167D-01 3 8 3 14 -0.29726299654673D+01 -0.22412377616578D-01 1 9 3 14 0.12553718318911D+01 0.17896677689910D-01 2 9 3 14 0.13160138097076D+01 0.85606723896025D-02 3 9 3 14 -0.33825892305505D+01 -0.65908846273701D-01 1 10 3 14 -0.13065437590370D+01 0.13274932927196D-01 2 10 3 14 -0.10413070221578D+01 0.89206689404533D-02 3 10 3 14 -0.15996441794864D+01 0.22175483964117D-05 1 11 3 14 -0.66564031357816D+00 0.53613601460739D-02 2 11 3 14 -0.17154731050669D+01 0.48289889670989D-02 3 11 3 14 0.14454180791777D+01 -0.21075224935318D-01 1 12 3 14 -0.95501543360747D+00 -0.40511861185110D-02 2 12 3 14 -0.17197215205557D+01 -0.76217125311948D-02 3 12 3 14 -0.38199648074239D+01 -0.59547118617894D-06 1 13 3 14 0.73237358986143D+00 0.14548041350846D-01 2 13 3 14 0.99634061540388D+00 0.15757697354719D-01 3 13 3 14 0.28614716333105D+00 -0.66939125962499D-03 1 14 3 14 -0.12075921112685D+01 0.17933139462464D+00 2 14 3 14 0.20712817804936D+01 -0.24785480103441D+00 3 14 3 14 0.15199907007336D+02 0.00000000000000D+00 1 15 3 14 -0.16481974863659D-01 0.26205469346586D-06 2 15 3 14 0.17779933115965D+00 0.22313226366759D-06 3 15 3 14 -0.18130548827797D+01 -0.40369144638045D-17 1 16 3 14 0.43632794082817D-01 0.17406243555827D-01 2 16 3 14 0.71059163567568D-02 0.24563030454913D-01 3 16 3 14 -0.47302865594401D+00 0.87392933189479D-16 1 17 3 14 -0.24605958407678D-03 -0.29252181175309D-06 2 17 3 14 -0.30766317313183D+00 -0.10308124032014D-06 3 17 3 14 0.93373692662099D+00 0.37132935104097D-15 1 18 3 14 -0.28701547608896D+00 0.25278758042201D-01 2 18 3 14 0.19657751149740D-01 -0.34560078058958D-01 3 18 3 14 -0.44647336839777D-13 0.46236086934862D-02 1 19 3 14 -0.14363873573459D+00 0.47098595949134D-02 2 19 3 14 -0.34654275540795D+00 -0.34465516954459D-02 3 19 3 14 0.40123403350460D-13 0.38706735144755D-07 1 20 3 14 -0.11433356198721D+00 0.13854815198983D-02 2 20 3 14 0.11172645839052D-01 -0.40424793648484D-02 3 20 3 14 -0.55289935268936D+00 0.52213957832613D-08 1 1 1 15 -0.18627785637427D-01 0.21012580137621D-03 2 1 1 15 0.66650992669084D+00 0.15958688660312D-02 3 1 1 15 0.24459026156749D-01 0.14667797057915D-02 1 2 1 15 -0.18591191906733D+00 0.17939914049756D-02 2 2 1 15 -0.90026468815008D+00 0.11789234466961D-02 3 2 1 15 0.37629219597501D-01 -0.38205164598135D-07 1 3 1 15 0.25144422357393D-01 -0.30885780243650D-02 2 3 1 15 -0.10029332792676D+01 -0.42170134288043D-02 3 3 1 15 -0.44240345177310D+00 0.11654722503451D-06 1 4 1 15 -0.39631777278960D+00 0.16656258511047D-02 2 4 1 15 -0.18325830586105D+00 -0.29427663472295D-02 3 4 1 15 -0.98985970064556D+00 -0.70221971410085D-02 1 5 1 15 -0.31076334350387D+00 -0.97508677259309D-02 2 5 1 15 -0.84458994063050D+00 -0.80772866284178D-02 3 5 1 15 -0.42333913530498D+00 -0.57653228107844D-03 1 6 1 15 -0.14132827669589D+01 0.16778780763755D-01 2 6 1 15 -0.29325625873649D+01 -0.40121880979466D-02 3 6 1 15 0.37229547086843D+00 -0.71956096608917D-01 1 7 1 15 0.41859550399760D-01 0.13715393663127D-01 2 7 1 15 0.86364077739424D+00 0.31243896307693D-01 3 7 1 15 -0.27107925689619D+00 0.12034302390374D-01 1 8 1 15 -0.11975170767603D+00 -0.98203798255515D-02 2 8 1 15 0.16406849123275D+01 0.32328470040766D-02 3 8 1 15 0.20245841920844D+00 -0.64972512946618D-01 1 9 1 15 0.65091568533314D-02 0.93012107904103D-02 2 9 1 15 -0.19477953011355D+00 0.94129551087462D-02 3 9 1 15 -0.22145572656932D+01 0.82859171484277D-01 1 10 1 15 -0.14934460445475D+01 0.24838384143342D-01 2 10 1 15 -0.41569964933528D+00 0.21437584582276D-01 3 10 1 15 0.29406501250589D+01 -0.82743793674034D-07 1 11 1 15 0.73442613606819D+00 -0.73271357183318D-02 2 11 1 15 0.87044227676285D+00 -0.15194833848587D-01 3 11 1 15 0.23717968961453D+01 0.36889848857993D-01 1 12 1 15 0.17171534193002D-01 0.18215668653424D-02 2 12 1 15 0.63146529951597D-02 0.89196694456551D-02 3 12 1 15 0.19208973171480D+01 0.10914982342947D-07 1 13 1 15 -0.15749731011419D+00 0.10120844011320D-15 2 13 1 15 0.15117986666873D+00 0.57695902243325D-04 3 13 1 15 0.43632794082819D-01 -0.17406243555828D-01 1 14 1 15 0.68328166505077D+00 0.12989607834477D-15 2 14 1 15 0.76015030895172D+00 -0.11839658802009D-06 3 14 1 15 -0.16481974863659D-01 -0.26205469346586D-06 1 15 1 15 0.13281113930984D+02 0.00000000000000D+00 2 15 1 15 0.71826014189160D+01 0.13979109054849D+00 3 15 1 15 0.12076101657735D+01 0.17933368183392D+00 1 16 1 15 -0.97733751767875D+00 0.31622574160506D-02 2 16 1 15 0.23613571627540D+00 0.19231436639784D-03 3 16 1 15 -0.73237303227026D+00 -0.14548070139898D-01 1 17 1 15 -0.47787634030003D+00 -0.90112502503832D-07 2 17 1 15 0.75145899227435D+00 0.30416819069579D-02 3 17 1 15 0.11433259996273D+00 0.13854177625741D-02 1 18 1 15 -0.69192429273716D-15 0.18424820869345D-06 2 18 1 15 -0.62995622893074D-01 -0.93487793350763D-03 3 18 1 15 -0.14363884105381D+00 0.47095587187192D-02 1 19 1 15 -0.21515189828479D-15 -0.17480545157825D-02 2 19 1 15 -0.93267625267633D+00 0.48459772409201D-02 3 19 1 15 0.28701547608896D+00 0.25278758042201D-01 1 20 1 15 -0.61907660529897D+01 -0.17830773489592D-15 2 20 1 15 0.21064030177164D+01 -0.88195580844250D-07 3 20 1 15 -0.24605958405119D-03 0.29252181174974D-06 1 1 2 15 0.32726503947588D+00 0.81391347135964D-03 2 1 2 15 0.75893449639926D+00 0.18091601147769D-02 3 1 2 15 0.10416370308126D+01 0.74936709422725D-03 1 2 2 15 -0.31686715648504D+00 -0.75760419285132D-02 2 2 2 15 -0.16404765908636D+01 0.12652863075467D-01 3 2 2 15 0.10171296516121D+01 0.45526650800193D-07 1 3 2 15 -0.27520775231615D+00 0.18559808744825D-02 2 3 2 15 -0.15089106015209D+01 -0.75631303211644D-02 3 3 2 15 0.10376008111886D+01 0.22639750183624D-06 1 4 2 15 0.42349060819940D+00 -0.90267832783319D-02 2 4 2 15 -0.20887133686635D+01 0.10053792221447D-01 3 4 2 15 0.12605127499419D+00 0.17367804719217D-03 1 5 2 15 -0.27322497593675D+00 -0.66212463350024D-02 2 5 2 15 -0.19712272332279D+01 0.48238814018633D-03 3 5 2 15 -0.13123301985444D+00 0.52540686046652D-02 1 6 2 15 0.43386917041278D+00 0.89139711311270D-02 2 6 2 15 -0.56047361781019D+01 -0.69295610230437D-02 3 6 2 15 0.35637188164250D+00 -0.67736081061716D-01 1 7 2 15 0.60390887309136D-02 0.32115589159745D-01 2 7 2 15 0.19627782024968D+01 0.22171585459855D-01 3 7 2 15 -0.31948107143713D+00 0.20096264537443D-01 1 8 2 15 -0.71405983092713D+00 -0.99047118005155D-02 2 8 2 15 0.57399295574618D+01 0.25035389653767D-03 3 8 2 15 0.53594074220149D+00 -0.89956128772511D-01 1 9 2 15 -0.43675767475458D+00 0.92966318914350D-02 2 9 2 15 0.31593779458366D+00 -0.15258830031227D-02 3 9 2 15 -0.28565703852058D+01 0.65879253351044D-01 1 10 2 15 -0.80418738571387D+00 0.25530227544933D-01 2 10 2 15 0.77883076299126D+00 0.92341284513330D-02 3 10 2 15 0.23657963913107D+01 0.10268497669299D-05 1 11 2 15 0.95475056913764D+00 -0.13338005088367D-01 2 11 2 15 0.19735520769864D-01 -0.14451739772074D-01 3 11 2 15 0.29062589369673D+01 0.47548968402090D-01 1 12 2 15 -0.46172911400711D+00 0.92326164388084D-02 2 12 2 15 0.29291042281993D+00 0.81021931314549D-02 3 12 2 15 0.35022316799165D+01 0.89237683677325D-06 1 13 2 15 0.15117986666873D+00 -0.57695902243442D-04 2 13 2 15 0.64591501749743D-01 -0.10171200723129D-14 3 13 2 15 0.71059163567384D-02 -0.24563030454912D-01 1 14 2 15 0.76015030895172D+00 0.11839658801925D-06 2 14 2 15 0.17314326962186D+01 -0.12192603991448D-15 3 14 2 15 0.17779933115965D+00 -0.22313226366759D-06 1 15 2 15 0.71826056682823D+01 -0.13979063280100D+00 2 15 2 15 0.16980139277633D+02 0.00000000000000D+00 3 15 2 15 -0.20712557483684D+01 -0.24785524218975D+00 1 16 2 15 0.23613536008034D+00 0.19237132705987D-03 2 16 2 15 0.66673109866711D+00 -0.21510066108831D-02 3 16 2 15 -0.99634253689594D+00 -0.15758001046143D-01 1 17 2 15 -0.75146054059527D+00 0.30415856890043D-02 2 17 2 15 0.15579327054328D+01 0.40018819279939D-07 3 17 2 15 0.11171791278783D-01 0.40426306225295D-02 1 18 2 15 -0.62997787618652D-01 -0.93428785486421D-03 2 18 2 15 -0.10633357766190D-13 -0.19079360058192D-06 3 18 2 15 0.34654244736435D+00 0.34462583141583D-02 1 19 2 15 -0.93267625267633D+00 -0.48459772409203D-02 2 19 2 15 -0.51562803742877D-13 0.28114949348630D-02 3 19 2 15 0.19657751149759D-01 0.34560078058959D-01 1 20 2 15 -0.21064030177164D+01 -0.88195580844250D-07 2 20 2 15 0.35233322690473D+01 -0.16934985122054D-15 3 20 2 15 0.30766317313184D+00 -0.10308124043128D-06 1 1 3 15 -0.29524272141784D+00 0.22397157633438D-03 2 1 3 15 0.66671587413015D+00 0.10683385518552D-02 3 1 3 15 -0.61524493664583D+00 0.19236340652782D-03 1 2 3 15 -0.52523419709054D+00 -0.21665446929419D-02 2 2 3 15 0.64607194557484D+00 -0.43467172148249D-02 3 2 3 15 -0.12410017819349D+00 0.21217364831603D-06 1 3 3 15 -0.73325324000046D+00 0.13507992412825D-01 2 3 3 15 0.76652726720675D+00 -0.69414717873130D-02 3 3 3 15 0.86413724239483D+00 -0.43621190564523D-07 1 4 3 15 -0.58852109688773D+00 0.15680990687225D-01 2 4 3 15 0.56434041082920D+00 -0.14139490556712D-01 3 4 3 15 -0.22355539557402D+01 0.40605244130013D-02 1 5 3 15 0.11574704131345D+00 0.15169791020613D-01 2 5 3 15 -0.46565926400898D+00 0.96578056394336D-02 3 5 3 15 0.33113979864878D+01 0.10995496813762D-01 1 6 3 15 -0.77008098638731D+00 -0.16550095159033D-01 2 6 3 15 -0.41101651657488D+00 -0.14633391495208D-01 3 6 3 15 -0.38187858707145D+01 -0.83398926245822D-02 1 7 3 15 0.20564180761400D+00 0.28648166579907D-01 2 7 3 15 -0.49064448143150D+00 0.48289929063167D-01 3 7 3 15 -0.29726299654673D+01 -0.22412377616580D-01 1 8 3 15 -0.98932719077393D+00 -0.77813748561306D-02 2 8 3 15 -0.49419589443972D+00 -0.23665373738752D-01 3 8 3 15 0.33040214403568D+01 -0.17968918688819D-02 1 9 3 15 -0.12553718318911D+01 -0.17896677689910D-01 2 9 3 15 -0.13160138097076D+01 -0.85606723896025D-02 3 9 3 15 -0.33825892305504D+01 -0.65908846273701D-01 1 10 3 15 0.13065437590370D+01 -0.13274932927196D-01 2 10 3 15 0.10413070221578D+01 -0.89206689404537D-02 3 10 3 15 -0.15996441794864D+01 0.22175483973199D-05 1 11 3 15 0.66564031357817D+00 -0.53613601460739D-02 2 11 3 15 0.17154731050669D+01 -0.48289889670990D-02 3 11 3 15 0.14454180791777D+01 -0.21075224935319D-01 1 12 3 15 0.95501543360748D+00 0.40511861185110D-02 2 12 3 15 0.17197215205557D+01 0.76217125311949D-02 3 12 3 15 -0.38199648074239D+01 -0.59547118761243D-06 1 13 3 15 -0.43632794082818D-01 -0.17406243555828D-01 2 13 3 15 -0.71059163567540D-02 -0.24563030454912D-01 3 13 3 15 -0.47302865594405D+00 0.37722053214600D-15 1 14 3 15 0.16481974863655D-01 -0.26205469346586D-06 2 14 3 15 -0.17779933115967D+00 -0.22313226366759D-06 3 14 3 15 -0.18130548827797D+01 0.40369144638045D-17 1 15 3 15 0.12075921112684D+01 -0.17933139462464D+00 2 15 3 15 -0.20712817804934D+01 0.24785480103441D+00 3 15 3 15 0.15199907007336D+02 0.00000000000000D+00 1 16 3 15 -0.73237358986143D+00 -0.14548041350846D-01 2 16 3 15 -0.99634061540389D+00 -0.15757697354718D-01 3 16 3 15 0.28614716333107D+00 -0.66939125962420D-03 1 17 3 15 0.11433356198722D+00 -0.13854815198983D-02 2 17 3 15 -0.11172645839055D-01 0.40424793648487D-02 3 17 3 15 -0.55289935268936D+00 0.52213960861409D-08 1 18 3 15 0.14363873573459D+00 -0.47098595949134D-02 2 18 3 15 0.34654275540794D+00 0.34465516954459D-02 3 18 3 15 0.21089294254310D-13 0.38706734483839D-07 1 19 3 15 0.28701547608896D+00 -0.25278758042201D-01 2 19 3 15 -0.19657751149749D-01 0.34560078058959D-01 3 19 3 15 -0.46793079532716D-14 0.46236086934858D-02 1 20 3 15 0.24605958407478D-03 0.29252181174974D-06 2 20 3 15 0.30766317313184D+00 0.10308124033949D-06 3 20 3 15 0.93373692662100D+00 0.25753339365829D-15 1 1 1 16 -0.18591191906729D+00 0.17939914049754D-02 2 1 1 16 -0.90026468815003D+00 0.11789234466963D-02 3 1 1 16 0.37629219597444D-01 -0.38205164754632D-07 1 2 1 16 -0.18627785637451D-01 0.21012580137456D-03 2 2 1 16 0.66650992669085D+00 0.15958688660338D-02 3 2 1 16 0.24459026156692D-01 0.14667797057874D-02 1 3 1 16 -0.39631777278964D+00 0.16656258511050D-02 2 3 1 16 -0.18325830586098D+00 -0.29427663472303D-02 3 3 1 16 -0.98985970064568D+00 -0.70221971410087D-02 1 4 1 16 0.25144422357362D-01 -0.30885780243651D-02 2 4 1 16 -0.10029332792677D+01 -0.42170134288042D-02 3 4 1 16 -0.44240345177311D+00 0.11654722509521D-06 1 5 1 16 -0.31076334350387D+00 -0.97508677259311D-02 2 5 1 16 -0.84458994063050D+00 -0.80772866284176D-02 3 5 1 16 -0.42333913530498D+00 -0.57653228107839D-03 1 6 1 16 -0.14132827669591D+01 0.16778780763755D-01 2 6 1 16 -0.29325625873651D+01 -0.40121880979459D-02 3 6 1 16 0.37229547086815D+00 -0.71956096608917D-01 1 7 1 16 -0.41859550399770D-01 -0.13715393663127D-01 2 7 1 16 -0.86364077739423D+00 -0.31243896307692D-01 3 7 1 16 0.27107925689621D+00 -0.12034302390373D-01 1 8 1 16 0.11975170767615D+00 0.98203798255551D-02 2 8 1 16 -0.16406849123270D+01 -0.32328470040547D-02 3 8 1 16 -0.20245841920850D+00 0.64972512946612D-01 1 9 1 16 -0.14934460445475D+01 0.24838384143342D-01 2 9 1 16 -0.41569964933526D+00 0.21437584582276D-01 3 9 1 16 0.29406501250588D+01 -0.82743793738268D-07 1 10 1 16 0.65091568533109D-02 0.93012107904103D-02 2 10 1 16 -0.19477953011355D+00 0.94129551087463D-02 3 10 1 16 -0.22145572656932D+01 0.82859171484277D-01 1 11 1 16 0.17171534193005D-01 0.18215668653424D-02 2 11 1 16 0.63146529951472D-02 0.89196694456551D-02 3 11 1 16 0.19208973171480D+01 0.10914982262853D-07 1 12 1 16 0.73442613606822D+00 -0.73271357183339D-02 2 12 1 16 0.87044227676286D+00 -0.15194833848591D-01 3 12 1 16 0.23717968961453D+01 0.36889848857988D-01 1 13 1 16 0.68328166505078D+00 -0.58947624595497D-16 2 13 1 16 0.76015030895172D+00 -0.11839658800769D-06 3 13 1 16 -0.16481974863656D-01 -0.26205469350212D-06 1 14 1 16 -0.15749731011419D+00 -0.10202482904542D-15 2 14 1 16 0.15117986666873D+00 0.57695902243442D-04 3 14 1 16 0.43632794082817D-01 -0.17406243555827D-01 1 15 1 16 -0.97733751767875D+00 0.31622574160501D-02 2 15 1 16 0.23613571627540D+00 0.19231436639698D-03 3 15 1 16 -0.73237303227026D+00 -0.14548070139897D-01 1 16 1 16 0.13281113930984D+02 0.00000000000000D+00 2 16 1 16 0.71826014189156D+01 0.13979109054849D+00 3 16 1 16 0.12076101657739D+01 0.17933368183392D+00 1 17 1 16 0.96007125054510D-15 0.18424820871544D-06 2 17 1 16 -0.62995622893073D-01 -0.93487793350766D-03 3 17 1 16 -0.14363884105381D+00 0.47095587187193D-02 1 18 1 16 -0.47787634030002D+00 -0.90112502689691D-07 2 18 1 16 0.75145899227435D+00 0.30416819069580D-02 3 18 1 16 0.11433259996273D+00 0.13854177625741D-02 1 19 1 16 -0.61907660529897D+01 0.50684791775923D-16 2 19 1 16 0.21064030177164D+01 -0.88195580857998D-07 3 19 1 16 -0.24605958406279D-03 0.29252181180732D-06 1 20 1 16 -0.16930229428448D-14 -0.17480545157803D-02 2 20 1 16 -0.93267625267633D+00 0.48459772409223D-02 3 20 1 16 0.28701547608895D+00 0.25278758042201D-01 1 1 2 16 -0.31686715648499D+00 -0.75760419285130D-02 2 1 2 16 -0.16404765908637D+01 0.12652863075471D-01 3 1 2 16 0.10171296516120D+01 0.45526649563665D-07 1 2 2 16 0.32726503947589D+00 0.81391347136225D-03 2 2 2 16 0.75893449639932D+00 0.18091601147758D-02 3 2 2 16 0.10416370308126D+01 0.74936709423231D-03 1 3 2 16 0.42349060819948D+00 -0.90267832783326D-02 2 3 2 16 -0.20887133686635D+01 0.10053792221446D-01 3 3 2 16 0.12605127499414D+00 0.17367804719044D-03 1 4 2 16 -0.27520775231616D+00 0.18559808744826D-02 2 4 2 16 -0.15089106015210D+01 -0.75631303211615D-02 3 4 2 16 0.10376008111886D+01 0.22639750222649D-06 1 5 2 16 -0.27322497593675D+00 -0.66212463350021D-02 2 5 2 16 -0.19712272332279D+01 0.48238814018270D-03 3 5 2 16 -0.13123301985447D+00 0.52540686046633D-02 1 6 2 16 0.43386917041254D+00 0.89139711311277D-02 2 6 2 16 -0.56047361781017D+01 -0.69295610230396D-02 3 6 2 16 0.35637188164228D+00 -0.67736081061714D-01 1 7 2 16 -0.60390887309087D-02 -0.32115589159744D-01 2 7 2 16 -0.19627782024968D+01 -0.22171585459859D-01 3 7 2 16 0.31948107143717D+00 -0.20096264537441D-01 1 8 2 16 0.71405983092755D+00 0.99047118005374D-02 2 8 2 16 -0.57399295574616D+01 -0.25035389651456D-03 3 8 2 16 -0.53594074220154D+00 0.89956128772500D-01 1 9 2 16 -0.80418738571386D+00 0.25530227544932D-01 2 9 2 16 0.77883076299129D+00 0.92341284513326D-02 3 9 2 16 0.23657963913107D+01 0.10268497669331D-05 1 10 2 16 -0.43675767475459D+00 0.92966318914351D-02 2 10 2 16 0.31593779458367D+00 -0.15258830031226D-02 3 10 2 16 -0.28565703852057D+01 0.65879253351044D-01 1 11 2 16 -0.46172911400712D+00 0.92326164388083D-02 2 11 2 16 0.29291042282000D+00 0.81021931314551D-02 3 11 2 16 0.35022316799165D+01 0.89237683692162D-06 1 12 2 16 0.95475056913765D+00 -0.13338005088371D-01 2 12 2 16 0.19735520769796D-01 -0.14451739772076D-01 3 12 2 16 0.29062589369672D+01 0.47548968402083D-01 1 13 2 16 0.76015030895172D+00 0.11839658803165D-06 2 13 2 16 0.17314326962186D+01 -0.52874320522331D-15 3 13 2 16 0.17779933115965D+00 -0.22313226315733D-06 1 14 2 16 0.15117986666873D+00 -0.57695902243325D-04 2 14 2 16 0.64591501749751D-01 -0.74731863971804D-15 3 14 2 16 0.71059163567568D-02 -0.24563030454913D-01 1 15 2 16 0.23613536008034D+00 0.19237132705902D-03 2 15 2 16 0.66673109866711D+00 -0.21510066108828D-02 3 15 2 16 -0.99634253689594D+00 -0.15758001046143D-01 1 16 2 16 0.71826056682819D+01 -0.13979063280100D+00 2 16 2 16 0.16980139277633D+02 0.00000000000000D+00 3 16 2 16 -0.20712557483683D+01 -0.24785524218975D+00 1 17 2 16 -0.62997787618651D-01 -0.93428785486424D-03 2 17 2 16 -0.11531437350170D-13 -0.19079360092951D-06 3 17 2 16 0.34654244736437D+00 0.34462583141580D-02 1 18 2 16 -0.75146054059527D+00 0.30415856890043D-02 2 18 2 16 0.15579327054328D+01 0.40018818745672D-07 3 18 2 16 0.11171791278786D-01 0.40426306225292D-02 1 19 2 16 -0.21064030177164D+01 -0.88195580857998D-07 2 19 2 16 0.35233322690473D+01 -0.38687003379252D-16 3 19 2 16 0.30766317313185D+00 -0.10308124023169D-06 1 20 2 16 -0.93267625267633D+00 -0.48459772409181D-02 2 20 2 16 0.20343554477626D-13 0.28114949348547D-02 3 20 2 16 0.19657751149758D-01 0.34560078058958D-01 1 1 3 16 -0.52523419709060D+00 -0.21665446929421D-02 2 1 3 16 0.64607194557476D+00 -0.43467172148261D-02 3 1 3 16 -0.12410017819342D+00 0.21217364682297D-06 1 2 3 16 -0.29524272141790D+00 0.22397157633031D-03 2 2 3 16 0.66671587413014D+00 0.10683385518603D-02 3 2 3 16 -0.61524493664591D+00 0.19236340652269D-03 1 3 3 16 -0.58852109688784D+00 0.15680990687225D-01 2 3 3 16 0.56434041082915D+00 -0.14139490556714D-01 3 3 3 16 -0.22355539557402D+01 0.40605244130026D-02 1 4 3 16 -0.73325324000046D+00 0.13507992412826D-01 2 4 3 16 0.76652726720682D+00 -0.69414717873126D-02 3 4 3 16 0.86413724239492D+00 -0.43621186060680D-07 1 5 3 16 0.11574704131344D+00 0.15169791020613D-01 2 5 3 16 -0.46565926400901D+00 0.96578056394316D-02 3 5 3 16 0.33113979864876D+01 0.10995496813763D-01 1 6 3 16 -0.77008098638760D+00 -0.16550095159033D-01 2 6 3 16 -0.41101651657510D+00 -0.14633391495206D-01 3 6 3 16 -0.38187858707144D+01 -0.83398926245831D-02 1 7 3 16 -0.20564180761398D+00 -0.28648166579906D-01 2 7 3 16 0.49064448143153D+00 -0.48289929063166D-01 3 7 3 16 0.29726299654674D+01 0.22412377616585D-01 1 8 3 16 0.98932719077387D+00 0.77813748561243D-02 2 8 3 16 0.49419589443966D+00 0.23665373738741D-01 3 8 3 16 -0.33040214403575D+01 0.17968918688591D-02 1 9 3 16 0.13065437590370D+01 -0.13274932927196D-01 2 9 3 16 0.10413070221577D+01 -0.89206689404537D-02 3 9 3 16 -0.15996441794863D+01 0.22175483988886D-05 1 10 3 16 -0.12553718318911D+01 -0.17896677689910D-01 2 10 3 16 -0.13160138097076D+01 -0.85606723896025D-02 3 10 3 16 -0.33825892305505D+01 -0.65908846273701D-01 1 11 3 16 0.95501543360752D+00 0.40511861185109D-02 2 11 3 16 0.17197215205557D+01 0.76217125311951D-02 3 11 3 16 -0.38199648074240D+01 -0.59547118603724D-06 1 12 3 16 0.66564031357820D+00 -0.53613601460792D-02 2 12 3 16 0.17154731050669D+01 -0.48289889671060D-02 3 12 3 16 0.14454180791777D+01 -0.21075224935324D-01 1 13 3 16 0.16481974863657D-01 -0.26205469350212D-06 2 13 3 16 -0.17779933115966D+00 -0.22313226315733D-06 3 13 3 16 -0.18130548827795D+01 -0.30272254329930D-15 1 14 3 16 -0.43632794082821D-01 -0.17406243555827D-01 2 14 3 16 -0.71059163567356D-02 -0.24563030454913D-01 3 14 3 16 -0.47302865594401D+00 -0.87392933189479D-16 1 15 3 16 -0.73237358986143D+00 -0.14548041350846D-01 2 15 3 16 -0.99634061540389D+00 -0.15757697354719D-01 3 15 3 16 0.28614716333107D+00 -0.66939125962493D-03 1 16 3 16 0.12075921112688D+01 -0.17933139462464D+00 2 16 3 16 -0.20712817804933D+01 0.24785480103441D+00 3 16 3 16 0.15199907007336D+02 0.00000000000000D+00 1 17 3 16 0.14363873573459D+00 -0.47098595949133D-02 2 17 3 16 0.34654275540796D+00 0.34465516954456D-02 3 17 3 16 0.12880333653088D-13 0.38706734132394D-07 1 18 3 16 0.11433356198722D+00 -0.13854815198983D-02 2 18 3 16 -0.11172645839053D-01 0.40424793648483D-02 3 18 3 16 -0.55289935268935D+00 0.52213958874206D-08 1 19 3 16 0.24605958406319D-03 0.29252181180732D-06 2 19 3 16 0.30766317313185D+00 0.10308124053909D-06 3 19 3 16 0.93373692662097D+00 0.30205926824632D-15 1 20 3 16 0.28701547608895D+00 -0.25278758042201D-01 2 20 3 16 -0.19657751149750D-01 0.34560078058958D-01 3 20 3 16 -0.13855282919380D-14 0.46236086934912D-02 1 1 1 17 0.39631777278968D+00 -0.16656258511057D-02 2 1 1 17 -0.18325830586093D+00 -0.29427663472241D-02 3 1 1 17 0.98985970064588D+00 0.70221971410176D-02 1 2 1 17 0.25144422357362D-01 -0.30885780243653D-02 2 2 1 17 0.10029332792676D+01 0.42170134288040D-02 3 2 1 17 -0.44240345177301D+00 0.11654722499866D-06 1 3 1 17 -0.18591191906733D+00 0.17939914049754D-02 2 3 1 17 0.90026468815005D+00 -0.11789234466967D-02 3 3 1 17 0.37629219597544D-01 -0.38205164660388D-07 1 4 1 17 0.18627785637451D-01 -0.21012580137559D-03 2 4 1 17 0.66650992669086D+00 0.15958688660326D-02 3 4 1 17 -0.24459026156664D-01 -0.14667797057891D-02 1 5 1 17 0.11975170767614D+00 0.98203798255548D-02 2 5 1 17 0.16406849123270D+01 0.32328470040545D-02 3 5 1 17 -0.20245841920847D+00 0.64972512946611D-01 1 6 1 17 -0.41859550399772D-01 -0.13715393663127D-01 2 6 1 17 0.86364077739423D+00 0.31243896307693D-01 3 6 1 17 0.27107925689621D+00 -0.12034302390373D-01 1 7 1 17 0.14132827669593D+01 -0.16778780763734D-01 2 7 1 17 -0.29325625873652D+01 -0.40121880979688D-02 3 7 1 17 -0.37229547086801D+00 0.71956096608926D-01 1 8 1 17 0.31076334350387D+00 0.97508677259313D-02 2 8 1 17 -0.84458994063049D+00 -0.80772866284179D-02 3 8 1 17 0.42333913530499D+00 0.57653228107734D-03 1 9 1 17 -0.73442613606824D+00 0.73271357183329D-02 2 9 1 17 0.87044227676282D+00 -0.15194833848589D-01 3 9 1 17 -0.23717968961453D+01 -0.36889848857990D-01 1 10 1 17 0.17171534192990D-01 0.18215668653423D-02 2 10 1 17 -0.63146529951543D-02 -0.89196694456549D-02 3 10 1 17 0.19208973171480D+01 0.10914982246333D-07 1 11 1 17 -0.65091568533054D-02 -0.93012107904106D-02 2 11 1 17 -0.19477953011356D+00 0.94129551087452D-02 3 11 1 17 0.22145572656932D+01 -0.82859171484274D-01 1 12 1 17 -0.14934460445475D+01 0.24838384143342D-01 2 12 1 17 0.41569964933528D+00 -0.21437584582276D-01 3 12 1 17 0.29406501250589D+01 -0.82743793835619D-07 1 13 1 17 0.30516250807893D-15 0.17480545157797D-02 2 13 1 17 -0.93267625267633D+00 0.48459772409201D-02 3 13 1 17 -0.28701547608895D+00 -0.25278758042201D-01 1 14 1 17 -0.61907660529897D+01 -0.54485774380114D-15 2 14 1 17 -0.21064030177164D+01 0.88195580870488D-07 3 14 1 17 -0.24605958407678D-03 0.29252181175309D-06 1 15 1 17 -0.47787634030003D+00 -0.90112502605129D-07 2 15 1 17 -0.75145899227435D+00 -0.30416819069579D-02 3 15 1 17 0.11433259996273D+00 0.13854177625741D-02 1 16 1 17 0.96007125054510D-15 -0.18424820871544D-06 2 16 1 17 -0.62995622893073D-01 -0.93487793350769D-03 3 16 1 17 0.14363884105381D+00 -0.47095587187193D-02 1 17 1 17 0.13281113930984D+02 0.00000000000000D+00 2 17 1 17 -0.71826014189154D+01 -0.13979109054849D+00 3 17 1 17 0.12076101657740D+01 0.17933368183392D+00 1 18 1 17 0.97733751767876D+00 -0.31622574160490D-02 2 18 1 17 0.23613571627540D+00 0.19231436639854D-03 3 18 1 17 0.73237303227025D+00 0.14548070139897D-01 1 19 1 17 0.15749731011419D+00 -0.23635652872216D-15 2 19 1 17 0.15117986666873D+00 0.57695902243410D-04 3 19 1 17 -0.43632794082818D-01 0.17406243555827D-01 1 20 1 17 0.68328166505078D+00 0.12840123866887D-15 2 20 1 17 -0.76015030895172D+00 0.11839658803503D-06 3 20 1 17 -0.16481974863657D-01 -0.26205469350160D-06 1 1 2 17 0.42349060819953D+00 -0.90267832783264D-02 2 1 2 17 0.20887133686633D+01 -0.10053792221442D-01 3 1 2 17 0.12605127499428D+00 0.17367804720354D-03 1 2 2 17 0.27520775231612D+00 -0.18559808744827D-02 2 2 2 17 -0.15089106015210D+01 -0.75631303211622D-02 3 2 2 17 -0.10376008111885D+01 -0.22639750213420D-06 1 3 2 17 0.31686715648501D+00 0.75760419285126D-02 2 3 2 17 -0.16404765908636D+01 0.12652863075469D-01 3 3 2 17 -0.10171296516120D+01 -0.45526649689630D-07 1 4 2 17 0.32726503947590D+00 0.81391347136102D-03 2 4 2 17 -0.75893449639935D+00 -0.18091601147785D-02 3 4 2 17 0.10416370308126D+01 0.74936709422945D-03 1 5 2 17 -0.71405983092762D+00 -0.99047118005377D-02 2 5 2 17 -0.57399295574616D+01 -0.25035389651950D-03 3 5 2 17 0.53594074220148D+00 -0.89956128772501D-01 1 6 2 17 0.60390887309101D-02 0.32115589159744D-01 2 6 2 17 -0.19627782024968D+01 -0.22171585459858D-01 3 6 2 17 -0.31948107143717D+00 0.20096264537442D-01 1 7 2 17 0.43386917041245D+00 0.89139711311048D-02 2 7 2 17 0.56047361781016D+01 0.69295610230462D-02 3 7 2 17 0.35637188164225D+00 -0.67736081061723D-01 1 8 2 17 -0.27322497593675D+00 -0.66212463350025D-02 2 8 2 17 0.19712272332279D+01 -0.48238814018308D-03 3 8 2 17 -0.13123301985446D+00 0.52540686046643D-02 1 9 2 17 0.95475056913762D+00 -0.13338005088369D-01 2 9 2 17 -0.19735520769818D-01 0.14451739772076D-01 3 9 2 17 0.29062589369672D+01 0.47548968402087D-01 1 10 2 17 0.46172911400711D+00 -0.92326164388082D-02 2 10 2 17 0.29291042281993D+00 0.81021931314551D-02 3 10 2 17 -0.35022316799164D+01 -0.89237683749152D-06 1 11 2 17 -0.43675767475460D+00 0.92966318914340D-02 2 11 2 17 -0.31593779458364D+00 0.15258830031232D-02 3 11 2 17 -0.28565703852058D+01 0.65879253351040D-01 1 12 2 17 0.80418738571388D+00 -0.25530227544933D-01 2 12 2 17 0.77883076299128D+00 0.92341284513325D-02 3 12 2 17 -0.23657963913107D+01 -0.10268497672510D-05 1 13 2 17 -0.93267625267633D+00 -0.48459772409203D-02 2 13 2 17 0.20343899643552D-13 -0.28114949348548D-02 3 13 2 17 0.19657751149751D-01 0.34560078058959D-01 1 14 2 17 0.21064030177164D+01 0.88195580870488D-07 2 14 2 17 0.35233322690473D+01 0.65418159714518D-16 3 14 2 17 -0.30766317313183D+00 0.10308124032014D-06 1 15 2 17 0.75146054059526D+00 -0.30415856890043D-02 2 15 2 17 0.15579327054328D+01 0.40018819119795D-07 3 15 2 17 -0.11171791278783D-01 -0.40426306225295D-02 1 16 2 17 -0.62997787618651D-01 -0.93428785486427D-03 2 16 2 17 -0.11531437350170D-13 0.19079360092951D-06 3 16 2 17 0.34654244736437D+00 0.34462583141578D-02 1 17 2 17 -0.71826056682817D+01 0.13979063280100D+00 2 17 2 17 0.16980139277632D+02 0.00000000000000D+00 3 17 2 17 0.20712557483682D+01 0.24785524218975D+00 1 18 2 17 0.23613536008034D+00 0.19237132706057D-03 2 18 2 17 -0.66673109866714D+00 0.21510066108847D-02 3 18 2 17 -0.99634253689593D+00 -0.15758001046144D-01 1 19 2 17 0.15117986666873D+00 -0.57695902243357D-04 2 19 2 17 -0.64591501749768D-01 0.37462662702880D-15 3 19 2 17 0.71059163567482D-02 -0.24563030454913D-01 1 20 2 17 -0.76015030895172D+00 -0.11839658800432D-06 2 20 2 17 0.17314326962186D+01 0.99118092456260D-16 3 20 2 17 -0.17779933115966D+00 0.22313226353753D-06 1 1 3 17 0.58852109688804D+00 -0.15680990687216D-01 2 1 3 17 0.56434041082929D+00 -0.14139490556701D-01 3 1 3 17 0.22355539557404D+01 -0.40605244129951D-02 1 2 3 17 -0.73325324000035D+00 0.13507992412825D-01 2 2 3 17 -0.76652726720668D+00 0.69414717873127D-02 3 2 3 17 0.86413724239475D+00 -0.43621182869894D-07 1 3 3 17 -0.52523419709050D+00 -0.21665446929420D-02 2 3 3 17 -0.64607194557480D+00 0.43467172148260D-02 3 3 3 17 -0.12410017819347D+00 0.21217364627597D-06 1 4 3 17 0.29524272141792D+00 -0.22397157633196D-03 2 4 3 17 0.66671587413015D+00 0.10683385518574D-02 3 4 3 17 0.61524493664595D+00 -0.19236340652419D-03 1 5 3 17 0.98932719077390D+00 0.77813748561239D-02 2 5 3 17 -0.49419589443971D+00 -0.23665373738741D-01 3 5 3 17 -0.33040214403575D+01 0.17968918688592D-02 1 6 3 17 -0.20564180761398D+00 -0.28648166579906D-01 2 6 3 17 -0.49064448143153D+00 0.48289929063167D-01 3 6 3 17 0.29726299654675D+01 0.22412377616585D-01 1 7 3 17 0.77008098638773D+00 0.16550095159042D-01 2 7 3 17 -0.41101651657514D+00 -0.14633391495215D-01 3 7 3 17 0.38187858707143D+01 0.83398926245583D-02 1 8 3 17 -0.11574704131344D+00 -0.15169791020614D-01 2 8 3 17 -0.46565926400900D+00 0.96578056394326D-02 3 8 3 17 -0.33113979864878D+01 -0.10995496813756D-01 1 9 3 17 -0.66564031357815D+00 0.53613601460768D-02 2 9 3 17 0.17154731050668D+01 -0.48289889671023D-02 3 9 3 17 -0.14454180791777D+01 0.21075224935322D-01 1 10 3 17 0.95501543360748D+00 0.40511861185109D-02 2 10 3 17 -0.17197215205557D+01 -0.76217125311956D-02 3 10 3 17 -0.38199648074238D+01 -0.59547118822711D-06 1 11 3 17 0.12553718318911D+01 0.17896677689913D-01 2 11 3 17 -0.13160138097076D+01 -0.85606723896063D-02 3 11 3 17 0.33825892305504D+01 0.65908846273708D-01 1 12 3 17 0.13065437590370D+01 -0.13274932927196D-01 2 12 3 17 -0.10413070221578D+01 0.89206689404534D-02 3 12 3 17 -0.15996441794863D+01 0.22175483983429D-05 1 13 3 17 -0.28701547608895D+00 0.25278758042201D-01 2 13 3 17 -0.19657751149757D-01 0.34560078058959D-01 3 13 3 17 -0.13375371139881D-13 -0.46236086934915D-02 1 14 3 17 0.24605958404918D-03 0.29252181175309D-06 2 14 3 17 -0.30766317313183D+00 -0.10308124045063D-06 3 14 3 17 0.93373692662099D+00 -0.37132935104097D-15 1 15 3 17 0.11433356198722D+00 -0.13854815198983D-02 2 15 3 17 0.11172645839056D-01 -0.40424793648487D-02 3 15 3 17 -0.55289935268936D+00 0.52213959824359D-08 1 16 3 17 -0.14363873573459D+00 0.47098595949133D-02 2 16 3 17 0.34654275540796D+00 0.34465516954454D-02 3 16 3 17 0.12880333653088D-13 -0.38706734132394D-07 1 17 3 17 0.12075921112689D+01 -0.17933139462464D+00 2 17 3 17 0.20712817804932D+01 -0.24785480103441D+00 3 17 3 17 0.15199907007337D+02 0.00000000000000D+00 1 18 3 17 0.73237358986143D+00 0.14548041350845D-01 2 18 3 17 -0.99634061540388D+00 -0.15757697354720D-01 3 18 3 17 -0.28614716333109D+00 0.66939125962398D-03 1 19 3 17 0.43632794082819D-01 0.17406243555827D-01 2 19 3 17 -0.71059163567441D-02 -0.24563030454913D-01 3 19 3 17 0.47302865594406D+00 -0.66051618888657D-16 1 20 3 17 0.16481974863657D-01 -0.26205469350160D-06 2 20 3 17 0.17779933115966D+00 0.22313226353753D-06 3 20 3 17 -0.18130548827795D+01 -0.12857920593548D-15 1 1 1 18 0.25144422357387D-01 -0.30885780243654D-02 2 1 1 18 0.10029332792676D+01 0.42170134288039D-02 3 1 1 18 -0.44240345177316D+00 0.11654722498244D-06 1 2 1 18 0.39631777278964D+00 -0.16656258511048D-02 2 2 1 18 -0.18325830586096D+00 -0.29427663472359D-02 3 2 1 18 0.98985970064578D+00 0.70221971409993D-02 1 3 1 18 0.18627785637451D-01 -0.21012580137539D-03 2 3 1 18 0.66650992669086D+00 0.15958688660324D-02 3 3 1 18 -0.24459026156668D-01 -0.14667797057896D-02 1 4 1 18 -0.18591191906734D+00 0.17939914049754D-02 2 4 1 18 0.90026468815001D+00 -0.11789234466954D-02 3 4 1 18 0.37629219597558D-01 -0.38205164500431D-07 1 5 1 18 0.11975170767610D+00 0.98203798255550D-02 2 5 1 18 0.16406849123273D+01 0.32328470040536D-02 3 5 1 18 -0.20245841920854D+00 0.64972512946611D-01 1 6 1 18 -0.41859550399767D-01 -0.13715393663127D-01 2 6 1 18 0.86364077739423D+00 0.31243896307693D-01 3 6 1 18 0.27107925689619D+00 -0.12034302390373D-01 1 7 1 18 -0.14132827669590D+01 0.16778780763754D-01 2 7 1 18 0.29325625873651D+01 0.40121880979459D-02 3 7 1 18 0.37229547086840D+00 -0.71956096608917D-01 1 8 1 18 -0.31076334350387D+00 -0.97508677259312D-02 2 8 1 18 0.84458994063050D+00 0.80772866284180D-02 3 8 1 18 -0.42333913530498D+00 -0.57653228107836D-03 1 9 1 18 0.17171534193013D-01 0.18215668653421D-02 2 9 1 18 -0.63146529951685D-02 -0.89196694456554D-02 3 9 1 18 0.19208973171480D+01 0.10914982302531D-07 1 10 1 18 -0.73442613606822D+00 0.73271357183329D-02 2 10 1 18 0.87044227676285D+00 -0.15194833848589D-01 3 10 1 18 -0.23717968961453D+01 -0.36889848857991D-01 1 11 1 18 -0.14934460445476D+01 0.24838384143342D-01 2 11 1 18 0.41569964933528D+00 -0.21437584582276D-01 3 11 1 18 0.29406501250589D+01 -0.82743793854547D-07 1 12 1 18 -0.65091568533134D-02 -0.93012107904104D-02 2 12 1 18 -0.19477953011355D+00 0.94129551087471D-02 3 12 1 18 0.22145572656932D+01 -0.82859171484280D-01 1 13 1 18 -0.61907660529897D+01 0.18578395270111D-15 2 13 1 18 -0.21064030177164D+01 0.88195580812820D-07 3 13 1 18 -0.24605958406120D-03 0.29252181174882D-06 1 14 1 18 -0.21536619762044D-15 0.17480545157822D-02 2 14 1 18 -0.93267625267633D+00 0.48459772409223D-02 3 14 1 18 -0.28701547608896D+00 -0.25278758042201D-01 1 15 1 18 -0.69192429273716D-15 -0.18424820869345D-06 2 15 1 18 -0.62995622893074D-01 -0.93487793350772D-03 3 15 1 18 0.14363884105381D+00 -0.47095587187192D-02 1 16 1 18 -0.47787634030002D+00 -0.90112502419270D-07 2 16 1 18 -0.75145899227435D+00 -0.30416819069580D-02 3 16 1 18 0.11433259996273D+00 0.13854177625741D-02 1 17 1 18 0.97733751767876D+00 -0.31622574160517D-02 2 17 1 18 0.23613571627540D+00 0.19231436639628D-03 3 17 1 18 0.73237303227025D+00 0.14548070139898D-01 1 18 1 18 0.13281113930984D+02 0.00000000000000D+00 2 18 1 18 -0.71826014189157D+01 -0.13979109054849D+00 3 18 1 18 0.12076101657737D+01 0.17933368183392D+00 1 19 1 18 0.68328166505077D+00 -0.13288460689018D-15 2 19 1 18 -0.76015030895172D+00 0.11839658803484D-06 3 19 1 18 -0.16481974863657D-01 -0.26205469345028D-06 1 20 1 18 0.15749731011419D+00 -0.11613215835564D-16 2 20 1 18 0.15117986666873D+00 0.57695902243387D-04 3 20 1 18 -0.43632794082818D-01 0.17406243555828D-01 1 1 2 18 0.27520775231614D+00 -0.18559808744829D-02 2 1 2 18 -0.15089106015210D+01 -0.75631303211634D-02 3 1 2 18 -0.10376008111885D+01 -0.22639750259907D-06 1 2 2 18 0.42349060819950D+00 -0.90267832783382D-02 2 2 2 18 0.20887133686634D+01 -0.10053792221448D-01 3 2 2 18 0.12605127499428D+00 0.17367804717866D-03 1 3 2 18 0.32726503947590D+00 0.81391347136092D-03 2 3 2 18 -0.75893449639934D+00 -0.18091601147793D-02 3 3 2 18 0.10416370308126D+01 0.74936709423022D-03 1 4 2 18 0.31686715648497D+00 0.75760419285139D-02 2 4 2 18 -0.16404765908636D+01 0.12652863075467D-01 3 4 2 18 -0.10171296516119D+01 -0.45526650434409D-07 1 5 2 18 -0.71405983092725D+00 -0.99047118005385D-02 2 5 2 18 -0.57399295574619D+01 -0.25035389652059D-03 3 5 2 18 0.53594074220159D+00 -0.89956128772501D-01 1 6 2 18 0.60390887309105D-02 0.32115589159745D-01 2 6 2 18 -0.19627782024968D+01 -0.22171585459859D-01 3 6 2 18 -0.31948107143712D+00 0.20096264537445D-01 1 7 2 18 -0.43386917041262D+00 -0.89139711311277D-02 2 7 2 18 -0.56047361781017D+01 -0.69295610230421D-02 3 7 2 18 -0.35637188164245D+00 0.67736081061715D-01 1 8 2 18 0.27322497593675D+00 0.66212463350025D-02 2 8 2 18 -0.19712272332279D+01 0.48238814018265D-03 3 8 2 18 0.13123301985443D+00 -0.52540686046646D-02 1 9 2 18 0.46172911400710D+00 -0.92326164388086D-02 2 9 2 18 0.29291042281994D+00 0.81021931314561D-02 3 9 2 18 -0.35022316799165D+01 -0.89237683719750D-06 1 10 2 18 0.95475056913764D+00 -0.13338005088369D-01 2 10 2 18 -0.19735520769818D-01 0.14451739772075D-01 3 10 2 18 0.29062589369672D+01 0.47548968402086D-01 1 11 2 18 0.80418738571387D+00 -0.25530227544933D-01 2 11 2 18 0.77883076299136D+00 0.92341284513331D-02 3 11 2 18 -0.23657963913107D+01 -0.10268497671720D-05 1 12 2 18 -0.43675767475459D+00 0.92966318914359D-02 2 12 2 18 -0.31593779458368D+00 0.15258830031221D-02 3 12 2 18 -0.28565703852057D+01 0.65879253351048D-01 1 13 2 18 0.21064030177164D+01 0.88195580812820D-07 2 13 2 18 0.35233322690473D+01 0.18730646424296D-15 3 13 2 18 -0.30766317313185D+00 0.10308124031085D-06 1 14 2 18 -0.93267625267633D+00 -0.48459772409180D-02 2 14 2 18 -0.67549670978586D-13 -0.28114949348625D-02 3 14 2 18 0.19657751149740D-01 0.34560078058958D-01 1 15 2 18 -0.62997787618652D-01 -0.93428785486430D-03 2 15 2 18 -0.10633357766190D-13 0.19079360058192D-06 3 15 2 18 0.34654244736434D+00 0.34462583141575D-02 1 16 2 18 0.75146054059527D+00 -0.30415856890043D-02 2 16 2 18 0.15579327054328D+01 0.40018819654062D-07 3 16 2 18 -0.11171791278781D-01 -0.40426306225292D-02 1 17 2 18 0.23613536008034D+00 0.19237132705832D-03 2 17 2 18 -0.66673109866714D+00 0.21510066108812D-02 3 17 2 18 -0.99634253689593D+00 -0.15758001046142D-01 1 18 2 18 -0.71826056682821D+01 0.13979063280100D+00 2 18 2 18 0.16980139277633D+02 0.00000000000000D+00 3 18 2 18 0.20712557483683D+01 0.24785524218975D+00 1 19 2 18 -0.76015030895172D+00 -0.11839658800451D-06 2 19 2 18 0.17314326962186D+01 0.28556855928569D-15 3 19 2 18 -0.17779933115966D+00 0.22313226357868D-06 1 20 2 18 0.15117986666873D+00 -0.57695902243381D-04 2 20 2 18 -0.64591501749765D-01 -0.43409998260296D-15 3 20 2 18 0.71059163567491D-02 -0.24563030454912D-01 1 1 3 18 -0.73325324000050D+00 0.13507992412825D-01 2 1 3 18 -0.76652726720671D+00 0.69414717873122D-02 3 1 3 18 0.86413724239495D+00 -0.43621189609078D-07 1 2 3 18 0.58852109688794D+00 -0.15680990687234D-01 2 2 3 18 0.56434041082929D+00 -0.14139490556726D-01 3 2 3 18 0.22355539557402D+01 -0.40605244130139D-02 1 3 3 18 0.29524272141792D+00 -0.22397157633248D-03 2 3 3 18 0.66671587413017D+00 0.10683385518582D-02 3 3 3 18 0.61524493664593D+00 -0.19236340652590D-03 1 4 3 18 -0.52523419709049D+00 -0.21665446929418D-02 2 4 3 18 -0.64607194557470D+00 0.43467172148253D-02 3 4 3 18 -0.12410017819344D+00 0.21217364754771D-06 1 5 3 18 0.98932719077383D+00 0.77813748561241D-02 2 5 3 18 -0.49419589443961D+00 -0.23665373738741D-01 3 5 3 18 -0.33040214403572D+01 0.17968918688623D-02 1 6 3 18 -0.20564180761400D+00 -0.28648166579906D-01 2 6 3 18 -0.49064448143148D+00 0.48289929063170D-01 3 6 3 18 0.29726299654674D+01 0.22412377616586D-01 1 7 3 18 -0.77008098638734D+00 -0.16550095159032D-01 2 7 3 18 0.41101651657493D+00 0.14633391495207D-01 3 7 3 18 -0.38187858707144D+01 -0.83398926245833D-02 1 8 3 18 0.11574704131345D+00 0.15169791020613D-01 2 8 3 18 0.46565926400897D+00 -0.96578056394329D-02 3 8 3 18 0.33113979864877D+01 0.10995496813761D-01 1 9 3 18 0.95501543360746D+00 0.40511861185109D-02 2 9 3 18 -0.17197215205557D+01 -0.76217125311953D-02 3 9 3 18 -0.38199648074239D+01 -0.59547118846551D-06 1 10 3 18 -0.66564031357820D+00 0.53613601460765D-02 2 10 3 18 0.17154731050669D+01 -0.48289889671027D-02 3 10 3 18 -0.14454180791777D+01 0.21075224935321D-01 1 11 3 18 0.13065437590371D+01 -0.13274932927196D-01 2 11 3 18 -0.10413070221577D+01 0.89206689404534D-02 3 11 3 18 -0.15996441794863D+01 0.22175483965771D-05 1 12 3 18 0.12553718318911D+01 0.17896677689907D-01 2 12 3 18 -0.13160138097076D+01 -0.85606723895989D-02 3 12 3 18 0.33825892305505D+01 0.65908846273693D-01 1 13 3 18 0.24605958406478D-03 0.29252181174882D-06 2 13 3 18 -0.30766317313185D+00 -0.10308124045993D-06 3 13 3 18 0.93373692662097D+00 -0.89190814317247D-15 1 14 3 18 -0.28701547608896D+00 0.25278758042201D-01 2 14 3 18 -0.19657751149769D-01 0.34560078058958D-01 3 14 3 18 -0.44646771021768D-13 -0.46236086934862D-02 1 15 3 18 -0.14363873573459D+00 0.47098595949134D-02 2 15 3 18 0.34654275540794D+00 0.34465516954451D-02 3 15 3 18 0.21089294254310D-13 -0.38706734483839D-07 1 16 3 18 0.11433356198722D+00 -0.13854815198983D-02 2 16 3 18 0.11172645839058D-01 -0.40424793648483D-02 3 16 3 18 -0.55289935268935D+00 0.52213961811562D-08 1 17 3 18 0.73237358986143D+00 0.14548041350846D-01 2 17 3 18 -0.99634061540388D+00 -0.15757697354717D-01 3 17 3 18 -0.28614716333109D+00 0.66939125962515D-03 1 18 3 18 0.12075921112687D+01 -0.17933139462464D+00 2 18 3 18 0.20712817804933D+01 -0.24785480103441D+00 3 18 3 18 0.15199907007336D+02 0.00000000000000D+00 1 19 3 18 0.16481974863657D-01 -0.26205469345028D-06 2 19 3 18 0.17779933115966D+00 0.22313226357868D-06 3 19 3 18 -0.18130548827796D+01 0.47966774672209D-15 1 20 3 18 0.43632794082819D-01 0.17406243555828D-01 2 20 3 18 -0.71059163567433D-02 -0.24563030454912D-01 3 20 3 18 0.47302865594406D+00 -0.64327960201251D-15 1 1 1 19 0.25144422357387D-01 -0.30885780243653D-02 2 1 1 19 0.10029332792676D+01 0.42170134288039D-02 3 1 1 19 0.44240345177314D+00 -0.11654722489119D-06 1 2 1 19 0.39631777278962D+00 -0.16656258511049D-02 2 2 1 19 -0.18325830586103D+00 -0.29427663472354D-02 3 2 1 19 -0.98985970064566D+00 -0.70221971409991D-02 1 3 1 19 0.18627785637453D-01 -0.21012580137544D-03 2 3 1 19 0.66650992669087D+00 0.15958688660323D-02 3 3 1 19 0.24459026156678D-01 0.14667797057895D-02 1 4 1 19 -0.18591191906731D+00 0.17939914049756D-02 2 4 1 19 0.90026468815004D+00 -0.11789234466961D-02 3 4 1 19 -0.37629219597529D-01 0.38205164614402D-07 1 5 1 19 -0.41859550399766D-01 -0.13715393663127D-01 2 5 1 19 0.86364077739424D+00 0.31243896307693D-01 3 5 1 19 -0.27107925689619D+00 0.12034302390373D-01 1 6 1 19 0.11975170767610D+00 0.98203798255550D-02 2 6 1 19 0.16406849123273D+01 0.32328470040536D-02 3 6 1 19 0.20245841920853D+00 -0.64972512946612D-01 1 7 1 19 -0.31076334350387D+00 -0.97508677259309D-02 2 7 1 19 0.84458994063050D+00 0.80772866284173D-02 3 7 1 19 0.42333913530498D+00 0.57653228107830D-03 1 8 1 19 -0.14132827669591D+01 0.16778780763755D-01 2 8 1 19 0.29325625873651D+01 0.40121880979470D-02 3 8 1 19 -0.37229547086838D+00 0.71956096608917D-01 1 9 1 19 0.17171534193013D-01 0.18215668653424D-02 2 9 1 19 -0.63146529951668D-02 -0.89196694456549D-02 3 9 1 19 -0.19208973171480D+01 -0.10914982358578D-07 1 10 1 19 -0.73442613606821D+00 0.73271357183329D-02 2 10 1 19 0.87044227676284D+00 -0.15194833848589D-01 3 10 1 19 0.23717968961453D+01 0.36889848857991D-01 1 11 1 19 -0.14934460445475D+01 0.24838384143342D-01 2 11 1 19 0.41569964933526D+00 -0.21437584582276D-01 3 11 1 19 -0.29406501250589D+01 0.82743793920065D-07 1 12 1 19 -0.65091568533108D-02 -0.93012107904102D-02 2 12 1 19 -0.19477953011355D+00 0.94129551087475D-02 3 12 1 19 -0.22145572656932D+01 0.82859171484280D-01 1 13 1 19 -0.47787634030002D+00 -0.90112502380872D-07 2 13 1 19 -0.75145899227435D+00 -0.30416819069580D-02 3 13 1 19 -0.11433259996273D+00 -0.13854177625741D-02 1 14 1 19 -0.81356704404412D-15 -0.18424820885026D-06 2 14 1 19 -0.62995622893072D-01 -0.93487793350765D-03 3 14 1 19 -0.14363884105381D+00 0.47095587187192D-02 1 15 1 19 -0.21536535058750D-15 0.17480545157825D-02 2 15 1 19 -0.93267625267633D+00 0.48459772409223D-02 3 15 1 19 0.28701547608896D+00 0.25278758042201D-01 1 16 1 19 -0.61907660529897D+01 -0.50684791775923D-16 2 16 1 19 -0.21064030177164D+01 0.88195580857998D-07 3 16 1 19 0.24605958406319D-03 -0.29252181180732D-06 1 17 1 19 0.15749731011419D+00 0.23635652872216D-15 2 17 1 19 0.15117986666873D+00 0.57695902243357D-04 3 17 1 19 0.43632794082819D-01 -0.17406243555827D-01 1 18 1 19 0.68328166505077D+00 0.13288460689018D-15 2 18 1 19 -0.76015030895172D+00 0.11839658800451D-06 3 18 1 19 0.16481974863657D-01 0.26205469345028D-06 1 19 1 19 0.13281113930984D+02 0.00000000000000D+00 2 19 1 19 -0.71826014189157D+01 -0.13979109054849D+00 3 19 1 19 -0.12076101657738D+01 -0.17933368183392D+00 1 20 1 19 0.97733751767877D+00 -0.31622574160524D-02 2 20 1 19 0.23613571627541D+00 0.19231436639644D-03 3 20 1 19 -0.73237303227025D+00 -0.14548070139898D-01 1 1 2 19 0.27520775231614D+00 -0.18559808744829D-02 2 1 2 19 -0.15089106015210D+01 -0.75631303211634D-02 3 1 2 19 0.10376008111885D+01 0.22639750208068D-06 1 2 2 19 0.42349060819943D+00 -0.90267832783377D-02 2 2 2 19 0.20887133686634D+01 -0.10053792221448D-01 3 2 2 19 -0.12605127499416D+00 -0.17367804717772D-03 1 3 2 19 0.32726503947591D+00 0.81391347136079D-03 2 3 2 19 -0.75893449639933D+00 -0.18091601147763D-02 3 3 2 19 -0.10416370308127D+01 -0.74936709423044D-03 1 4 2 19 0.31686715648500D+00 0.75760419285132D-02 2 4 2 19 -0.16404765908636D+01 0.12652863075469D-01 3 4 2 19 0.10171296516120D+01 0.45526650206250D-07 1 5 2 19 0.60390887309154D-02 0.32115589159745D-01 2 5 2 19 -0.19627782024968D+01 -0.22171585459858D-01 3 5 2 19 0.31948107143713D+00 -0.20096264537442D-01 1 6 2 19 -0.71405983092728D+00 -0.99047118005386D-02 2 6 2 19 -0.57399295574618D+01 -0.25035389652095D-03 3 6 2 19 -0.53594074220157D+00 0.89956128772501D-01 1 7 2 19 0.27322497593675D+00 0.66212463350018D-02 2 7 2 19 -0.19712272332279D+01 0.48238814018513D-03 3 7 2 19 -0.13123301985444D+00 0.52540686046649D-02 1 8 2 19 -0.43386917041261D+00 -0.89139711311266D-02 2 8 2 19 -0.56047361781017D+01 -0.69295610230412D-02 3 8 2 19 0.35637188164250D+00 -0.67736081061715D-01 1 9 2 19 0.46172911400710D+00 -0.92326164388082D-02 2 9 2 19 0.29291042281995D+00 0.81021931314543D-02 3 9 2 19 0.35022316799165D+01 0.89237683675400D-06 1 10 2 19 0.95475056913763D+00 -0.13338005088369D-01 2 10 2 19 -0.19735520769815D-01 0.14451739772075D-01 3 10 2 19 -0.29062589369673D+01 -0.47548968402086D-01 1 11 2 19 0.80418738571386D+00 -0.25530227544932D-01 2 11 2 19 0.77883076299133D+00 0.92341284513330D-02 3 11 2 19 0.23657963913107D+01 0.10268497668031D-05 1 12 2 19 -0.43675767475459D+00 0.92966318914362D-02 2 12 2 19 -0.31593779458369D+00 0.15258830031225D-02 3 12 2 19 0.28565703852058D+01 -0.65879253351048D-01 1 13 2 19 0.75146054059527D+00 -0.30415856890043D-02 2 13 2 19 0.15579327054328D+01 0.40018819650785D-07 3 13 2 19 0.11171791278783D-01 0.40426306225290D-02 1 14 2 19 -0.62997787618650D-01 -0.93428785486423D-03 2 14 2 19 -0.70268986204276D-14 0.19079360121623D-06 3 14 2 19 -0.34654244736436D+00 -0.34462583141576D-02 1 15 2 19 -0.93267625267633D+00 -0.48459772409181D-02 2 15 2 19 -0.51562459847501D-13 -0.28114949348630D-02 3 15 2 19 -0.19657751149749D-01 -0.34560078058959D-01 1 16 2 19 0.21064030177164D+01 0.88195580857998D-07 2 16 2 19 0.35233322690473D+01 0.38687003379252D-16 3 16 2 19 0.30766317313185D+00 -0.10308124053909D-06 1 17 2 19 0.15117986666873D+00 -0.57695902243410D-04 2 17 2 19 -0.64591501749768D-01 -0.37462662702880D-15 3 17 2 19 -0.71059163567441D-02 0.24563030454913D-01 1 18 2 19 -0.76015030895172D+00 -0.11839658803484D-06 2 18 2 19 0.17314326962186D+01 -0.28556855928569D-15 3 18 2 19 0.17779933115966D+00 -0.22313226357868D-06 1 19 2 19 -0.71826056682821D+01 0.13979063280100D+00 2 19 2 19 0.16980139277633D+02 0.00000000000000D+00 3 19 2 19 -0.20712557483682D+01 -0.24785524218975D+00 1 20 2 19 0.23613536008035D+00 0.19237132705848D-03 2 20 2 19 -0.66673109866712D+00 0.21510066108811D-02 3 20 2 19 0.99634253689594D+00 0.15758001046143D-01 1 1 3 19 0.73325324000050D+00 -0.13507992412825D-01 2 1 3 19 0.76652726720668D+00 -0.69414717873127D-02 3 1 3 19 0.86413724239495D+00 -0.43621190046815D-07 1 2 3 19 -0.58852109688782D+00 0.15680990687235D-01 2 2 3 19 -0.56434041082920D+00 0.14139490556726D-01 3 2 3 19 0.22355539557403D+01 -0.40605244130143D-02 1 3 3 19 -0.29524272141791D+00 0.22397157633237D-03 2 3 3 19 -0.66671587413019D+00 -0.10683385518584D-02 3 3 3 19 0.61524493664593D+00 -0.19236340652530D-03 1 4 3 19 0.52523419709052D+00 0.21665446929419D-02 2 4 3 19 0.64607194557478D+00 -0.43467172148255D-02 3 4 3 19 -0.12410017819354D+00 0.21217364591427D-06 1 5 3 19 0.20564180761400D+00 0.28648166579906D-01 2 5 3 19 0.49064448143150D+00 -0.48289929063167D-01 3 5 3 19 0.29726299654673D+01 0.22412377616584D-01 1 6 3 19 -0.98932719077384D+00 -0.77813748561243D-02 2 6 3 19 0.49419589443961D+00 0.23665373738741D-01 3 6 3 19 -0.33040214403572D+01 0.17968918688609D-02 1 7 3 19 -0.11574704131345D+00 -0.15169791020613D-01 2 7 3 19 -0.46565926400898D+00 0.96578056394333D-02 3 7 3 19 0.33113979864878D+01 0.10995496813760D-01 1 8 3 19 0.77008098638736D+00 0.16550095159033D-01 2 8 3 19 -0.41101651657488D+00 -0.14633391495207D-01 3 8 3 19 -0.38187858707145D+01 -0.83398926245820D-02 1 9 3 19 -0.95501543360746D+00 -0.40511861185110D-02 2 9 3 19 0.17197215205557D+01 0.76217125311949D-02 3 9 3 19 -0.38199648074239D+01 -0.59547118874576D-06 1 10 3 19 0.66564031357818D+00 -0.53613601460765D-02 2 10 3 19 -0.17154731050669D+01 0.48289889671026D-02 3 10 3 19 -0.14454180791777D+01 0.21075224935321D-01 1 11 3 19 -0.13065437590371D+01 0.13274932927196D-01 2 11 3 19 0.10413070221577D+01 -0.89206689404538D-02 3 11 3 19 -0.15996441794864D+01 0.22175483978793D-05 1 12 3 19 -0.12553718318911D+01 -0.17896677689907D-01 2 12 3 19 0.13160138097076D+01 0.85606723895989D-02 3 12 3 19 0.33825892305504D+01 0.65908846273695D-01 1 13 3 19 -0.11433356198722D+00 0.13854815198983D-02 2 13 3 19 -0.11172645839056D-01 0.40424793648482D-02 3 13 3 19 -0.55289935268936D+00 0.52213963702345D-08 1 14 3 19 0.14363873573459D+00 -0.47098595949134D-02 2 14 3 19 -0.34654275540795D+00 -0.34465516954452D-02 3 14 3 19 0.40123403350460D-13 -0.38706735144755D-07 1 15 3 19 0.28701547608896D+00 -0.25278758042201D-01 2 15 3 19 0.19657751149759D-01 -0.34560078058959D-01 3 15 3 19 -0.46787421352628D-14 -0.46236086934858D-02 1 16 3 19 -0.24605958406279D-03 -0.29252181180732D-06 2 16 3 19 0.30766317313185D+00 0.10308124023169D-06 3 16 3 19 0.93373692662097D+00 -0.30205926824632D-15 1 17 3 19 -0.43632794082818D-01 -0.17406243555827D-01 2 17 3 19 0.71059163567483D-02 0.24563030454913D-01 3 17 3 19 0.47302865594406D+00 0.66051618888657D-16 1 18 3 19 -0.16481974863657D-01 0.26205469345028D-06 2 18 3 19 -0.17779933115966D+00 -0.22313226357868D-06 3 18 3 19 -0.18130548827796D+01 -0.47966774672209D-15 1 19 3 19 -0.12075921112687D+01 0.17933139462464D+00 2 19 3 19 -0.20712817804933D+01 0.24785480103441D+00 3 19 3 19 0.15199907007336D+02 0.00000000000000D+00 1 20 3 19 -0.73237358986143D+00 -0.14548041350847D-01 2 20 3 19 0.99634061540390D+00 0.15757697354718D-01 3 20 3 19 -0.28614716333108D+00 0.66939125962429D-03 1 1 1 20 0.39631777278968D+00 -0.16656258511050D-02 2 1 1 20 -0.18325830586093D+00 -0.29427663472247D-02 3 1 1 20 -0.98985970064590D+00 -0.70221971410177D-02 1 2 1 20 0.25144422357362D-01 -0.30885780243649D-02 2 2 1 20 0.10029332792677D+01 0.42170134288040D-02 3 2 1 20 0.44240345177309D+00 -0.11654722499208D-06 1 3 1 20 -0.18591191906733D+00 0.17939914049754D-02 2 3 1 20 0.90026468815005D+00 -0.11789234466964D-02 3 3 1 20 -0.37629219597544D-01 0.38205164938679D-07 1 4 1 20 0.18627785637450D-01 -0.21012580137537D-03 2 4 1 20 0.66650992669085D+00 0.15958688660321D-02 3 4 1 20 0.24459026156668D-01 0.14667797057895D-02 1 5 1 20 -0.41859550399771D-01 -0.13715393663127D-01 2 5 1 20 0.86364077739423D+00 0.31243896307693D-01 3 5 1 20 -0.27107925689621D+00 0.12034302390373D-01 1 6 1 20 0.11975170767615D+00 0.98203798255547D-02 2 6 1 20 0.16406849123271D+01 0.32328470040547D-02 3 6 1 20 0.20245841920850D+00 -0.64972512946612D-01 1 7 1 20 0.31076334350387D+00 0.97508677259313D-02 2 7 1 20 -0.84458994063050D+00 -0.80772866284182D-02 3 7 1 20 -0.42333913530499D+00 -0.57653228107768D-03 1 8 1 20 0.14132827669592D+01 -0.16778780763734D-01 2 8 1 20 -0.29325625873653D+01 -0.40121880979687D-02 3 8 1 20 0.37229547086807D+00 -0.71956096608926D-01 1 9 1 20 -0.73442613606824D+00 0.73271357183329D-02 2 9 1 20 0.87044227676282D+00 -0.15194833848589D-01 3 9 1 20 0.23717968961453D+01 0.36889848857990D-01 1 10 1 20 0.17171534192977D-01 0.18215668653424D-02 2 10 1 20 -0.63146529951594D-02 -0.89196694456553D-02 3 10 1 20 -0.19208973171480D+01 -0.10914982367720D-07 1 11 1 20 -0.65091568533067D-02 -0.93012107904106D-02 2 11 1 20 -0.19477953011354D+00 0.94129551087449D-02 3 11 1 20 -0.22145572656931D+01 0.82859171484274D-01 1 12 1 20 -0.14934460445475D+01 0.24838384143342D-01 2 12 1 20 0.41569964933528D+00 -0.21437584582276D-01 3 12 1 20 -0.29406501250589D+01 0.82743793918782D-07 1 13 1 20 -0.66256674147922D-15 -0.18424820898467D-06 2 13 1 20 -0.62995622893073D-01 -0.93487793350768D-03 3 13 1 20 -0.14363884105381D+00 0.47095587187194D-02 1 14 1 20 -0.47787634030003D+00 -0.90112502606565D-07 2 14 1 20 -0.75145899227435D+00 -0.30416819069580D-02 3 14 1 20 -0.11433259996273D+00 -0.13854177625741D-02 1 15 1 20 -0.61907660529897D+01 0.17830773489592D-15 2 15 1 20 -0.21064030177164D+01 0.88195580844250D-07 3 15 1 20 0.24605958407478D-03 -0.29252181174974D-06 1 16 1 20 -0.16932363951475D-14 0.17480545157803D-02 2 16 1 20 -0.93267625267633D+00 0.48459772409201D-02 3 16 1 20 0.28701547608895D+00 0.25278758042201D-01 1 17 1 20 0.68328166505078D+00 -0.12840123866887D-15 2 17 1 20 -0.76015030895172D+00 0.11839658800432D-06 3 17 1 20 0.16481974863657D-01 0.26205469350160D-06 1 18 1 20 0.15749731011419D+00 0.11613215835564D-16 2 18 1 20 0.15117986666873D+00 0.57695902243381D-04 3 18 1 20 0.43632794082819D-01 -0.17406243555828D-01 1 19 1 20 0.97733751767877D+00 -0.31622574160482D-02 2 19 1 20 0.23613571627541D+00 0.19231436639838D-03 3 19 1 20 -0.73237303227025D+00 -0.14548070139897D-01 1 20 1 20 0.13281113930984D+02 0.00000000000000D+00 2 20 1 20 -0.71826014189154D+01 -0.13979109054849D+00 3 20 1 20 -0.12076101657740D+01 -0.17933368183392D+00 1 1 2 20 0.42349060819953D+00 -0.90267832783270D-02 2 1 2 20 0.20887133686633D+01 -0.10053792221444D-01 3 1 2 20 -0.12605127499422D+00 -0.17367804720381D-03 1 2 2 20 0.27520775231616D+00 -0.18559808744827D-02 2 2 2 20 -0.15089106015209D+01 -0.75631303211613D-02 3 2 2 20 0.10376008111886D+01 0.22639750246368D-06 1 3 2 20 0.31686715648501D+00 0.75760419285130D-02 2 3 2 20 -0.16404765908636D+01 0.12652863075469D-01 3 3 2 20 0.10171296516120D+01 0.45526649936975D-07 1 4 2 20 0.32726503947589D+00 0.81391347136059D-03 2 4 2 20 -0.75893449639935D+00 -0.18091601147792D-02 3 4 2 20 -0.10416370308127D+01 -0.74936709422897D-03 1 5 2 20 0.60390887309110D-02 0.32115589159745D-01 2 5 2 20 -0.19627782024968D+01 -0.22171585459861D-01 3 5 2 20 0.31948107143717D+00 -0.20096264537442D-01 1 6 2 20 -0.71405983092751D+00 -0.99047118005375D-02 2 6 2 20 -0.57399295574617D+01 -0.25035389651944D-03 3 6 2 20 -0.53594074220155D+00 0.89956128772499D-01 1 7 2 20 -0.27322497593675D+00 -0.66212463350027D-02 2 7 2 20 0.19712272332279D+01 -0.48238814018454D-03 3 7 2 20 0.13123301985447D+00 -0.52540686046643D-02 1 8 2 20 0.43386917041245D+00 0.89139711311049D-02 2 8 2 20 0.56047361781016D+01 0.69295610230441D-02 3 8 2 20 -0.35637188164225D+00 0.67736081061722D-01 1 9 2 20 0.95475056913762D+00 -0.13338005088369D-01 2 9 2 20 -0.19735520769806D-01 0.14451739772076D-01 3 9 2 20 -0.29062589369672D+01 -0.47548968402087D-01 1 10 2 20 0.46172911400710D+00 -0.92326164388085D-02 2 10 2 20 0.29291042281993D+00 0.81021931314559D-02 3 10 2 20 0.35022316799164D+01 0.89237683681644D-06 1 11 2 20 -0.43675767475458D+00 0.92966318914337D-02 2 11 2 20 -0.31593779458364D+00 0.15258830031230D-02 3 11 2 20 0.28565703852057D+01 -0.65879253351041D-01 1 12 2 20 0.80418738571388D+00 -0.25530227544933D-01 2 12 2 20 0.77883076299128D+00 0.92341284513330D-02 3 12 2 20 0.23657963913107D+01 0.10268497670012D-05 1 13 2 20 -0.62997787618651D-01 -0.93428785486426D-03 2 13 2 20 -0.16261213672244D-13 0.19079360432929D-06 3 13 2 20 -0.34654244736437D+00 -0.34462583141585D-02 1 14 2 20 0.75146054059527D+00 -0.30415856890043D-02 2 14 2 20 0.15579327054328D+01 0.40018818835291D-07 3 14 2 20 0.11171791278780D-01 0.40426306225293D-02 1 15 2 20 0.21064030177164D+01 0.88195580844250D-07 2 15 2 20 0.35233322690473D+01 0.16934985122054D-15 3 15 2 20 0.30766317313184D+00 -0.10308124033949D-06 1 16 2 20 -0.93267625267633D+00 -0.48459772409203D-02 2 16 2 20 0.20343898373003D-13 -0.28114949348547D-02 3 16 2 20 -0.19657751149750D-01 -0.34560078058958D-01 1 17 2 20 -0.76015030895172D+00 -0.11839658803503D-06 2 17 2 20 0.17314326962186D+01 -0.99118092456260D-16 3 17 2 20 0.17779933115966D+00 -0.22313226353753D-06 1 18 2 20 0.15117986666873D+00 -0.57695902243387D-04 2 18 2 20 -0.64591501749765D-01 0.43409998260296D-15 3 18 2 20 -0.71059163567433D-02 0.24563030454912D-01 1 19 2 20 0.23613536008035D+00 0.19237132706041D-03 2 19 2 20 -0.66673109866712D+00 0.21510066108848D-02 3 19 2 20 0.99634253689594D+00 0.15758001046143D-01 1 20 2 20 -0.71826056682817D+01 0.13979063280100D+00 2 20 2 20 0.16980139277632D+02 0.00000000000000D+00 3 20 2 20 -0.20712557483684D+01 -0.24785524218975D+00 1 1 3 20 -0.58852109688807D+00 0.15680990687216D-01 2 1 3 20 -0.56434041082926D+00 0.14139490556700D-01 3 1 3 20 0.22355539557405D+01 -0.40605244129946D-02 1 2 3 20 0.73325324000045D+00 -0.13507992412825D-01 2 2 3 20 0.76652726720680D+00 -0.69414717873124D-02 3 2 3 20 0.86413724239489D+00 -0.43621189308003D-07 1 3 3 20 0.52523419709050D+00 0.21665446929423D-02 2 3 3 20 0.64607194557481D+00 -0.43467172148258D-02 3 3 3 20 -0.12410017819346D+00 0.21217365019538D-06 1 4 3 20 -0.29524272141792D+00 0.22397157633240D-03 2 4 3 20 -0.66671587413018D+00 -0.10683385518569D-02 3 4 3 20 0.61524493664593D+00 -0.19236340652535D-03 1 5 3 20 0.20564180761398D+00 0.28648166579906D-01 2 5 3 20 0.49064448143153D+00 -0.48289929063167D-01 3 5 3 20 0.29726299654674D+01 0.22412377616585D-01 1 6 3 20 -0.98932719077387D+00 -0.77813748561243D-02 2 6 3 20 0.49419589443965D+00 0.23665373738739D-01 3 6 3 20 -0.33040214403575D+01 0.17968918688603D-02 1 7 3 20 0.11574704131344D+00 0.15169791020614D-01 2 7 3 20 0.46565926400901D+00 -0.96578056394326D-02 3 7 3 20 -0.33113979864877D+01 -0.10995496813757D-01 1 8 3 20 -0.77008098638766D+00 -0.16550095159042D-01 2 8 3 20 0.41101651657513D+00 0.14633391495214D-01 3 8 3 20 0.38187858707144D+01 0.83398926245596D-02 1 9 3 20 0.66564031357816D+00 -0.53613601460766D-02 2 9 3 20 -0.17154731050668D+01 0.48289889671019D-02 3 9 3 20 -0.14454180791777D+01 0.21075224935323D-01 1 10 3 20 -0.95501543360746D+00 -0.40511861185110D-02 2 10 3 20 0.17197215205557D+01 0.76217125311950D-02 3 10 3 20 -0.38199648074238D+01 -0.59547118801820D-06 1 11 3 20 -0.12553718318910D+01 -0.17896677689913D-01 2 11 3 20 0.13160138097076D+01 0.85606723896059D-02 3 11 3 20 0.33825892305503D+01 0.65908846273706D-01 1 12 3 20 -0.13065437590370D+01 0.13274932927196D-01 2 12 3 20 0.10413070221578D+01 -0.89206689404536D-02 3 12 3 20 -0.15996441794863D+01 0.22175483981056D-05 1 13 3 20 0.14363873573459D+00 -0.47098595949132D-02 2 13 3 20 -0.34654275540796D+00 -0.34465516954461D-02 3 13 3 20 -0.63967050429561D-14 -0.38706733149292D-07 1 14 3 20 -0.11433356198721D+00 0.13854815198983D-02 2 14 3 20 -0.11172645839059D-01 0.40424793648484D-02 3 14 3 20 -0.55289935268936D+00 0.52213962853155D-08 1 15 3 20 -0.24605958405119D-03 -0.29252181174974D-06 2 15 3 20 0.30766317313184D+00 0.10308124043128D-06 3 15 3 20 0.93373692662100D+00 -0.25753339365829D-15 1 16 3 20 0.28701547608895D+00 -0.25278758042201D-01 2 16 3 20 0.19657751149758D-01 -0.34560078058958D-01 3 16 3 20 -0.13849624739292D-14 -0.46236086934912D-02 1 17 3 20 -0.16481974863657D-01 0.26205469350160D-06 2 17 3 20 -0.17779933115966D+00 -0.22313226353753D-06 3 17 3 20 -0.18130548827795D+01 0.12857920593548D-15 1 18 3 20 -0.43632794082818D-01 -0.17406243555828D-01 2 18 3 20 0.71059163567491D-02 0.24563030454912D-01 3 18 3 20 0.47302865594406D+00 0.64327960201251D-15 1 19 3 20 -0.73237358986143D+00 -0.14548041350845D-01 2 19 3 20 0.99634061540390D+00 0.15757697354719D-01 3 19 3 20 -0.28614716333108D+00 0.66939125962484D-03 1 20 3 20 -0.12075921112690D+01 0.17933139462464D+00 2 20 3 20 -0.20712817804934D+01 0.24785480103441D+00 3 20 3 20 0.15199907007335D+02 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 5.00000000E-01 0.00000000E+00 1.0 1 1 1 1 0.91791587439220D+01 0.00000000000000D+00 2 1 1 1 0.13772139281218D+01 0.57171827219290D-06 3 1 1 1 -0.41788963180379D-13 0.00000000000000D+00 1 2 1 1 -0.91115557569266D+00 0.96633415111665D-09 2 2 1 1 -0.25163483277610D+00 0.17351135590425D-07 3 2 1 1 -0.71603274258008D-14 0.64132077979969D-16 1 3 1 1 0.50696491373287D-15 -0.97070091608302D-08 2 3 1 1 -0.24697006100925D+01 -0.49360520638669D-08 3 3 1 1 0.12969883372326D-14 0.22249176881878D-17 1 4 1 1 0.44152499754399D-14 -0.15829149424820D-07 2 4 1 1 -0.80139165027213D+00 0.12209004459453D-07 3 4 1 1 0.11826458153671D-13 0.12060173680465D-14 1 5 1 1 0.61785285138948D+00 0.47584016671684D-03 2 5 1 1 0.27404867942924D+00 0.17864480588415D-02 3 5 1 1 0.22575183399690D+00 0.10153804990146D-02 1 6 1 1 0.61785285138947D+00 0.47584016671004D-03 2 6 1 1 0.27404867942924D+00 0.17864480588395D-02 3 6 1 1 -0.22575183399690D+00 -0.10153804990146D-02 1 7 1 1 0.14196865593326D-01 0.30870219464353D-09 2 7 1 1 0.43091913283068D+00 -0.11657335051805D-08 3 7 1 1 0.53077092998001D+01 -0.19568105539748D-07 1 8 1 1 0.14196865593327D-01 0.30870213139259D-09 2 8 1 1 0.43091913283066D+00 -0.11657385109498D-08 3 8 1 1 -0.53077092998001D+01 0.19568104993416D-07 1 9 1 1 -0.36172695740989D+00 0.14254659753576D-07 2 9 1 1 0.13496843910713D+00 0.20167333667233D-07 3 9 1 1 -0.54463979023064D-14 0.37281458057223D-15 1 10 1 1 0.13065003929993D+00 0.52795468091175D-08 2 10 1 1 0.11362851269806D+00 -0.10673654441333D-08 3 10 1 1 -0.12157801708622D-13 -0.57717646587578D-15 1 11 1 1 0.23137836817498D+00 -0.42466433177951D-08 2 11 1 1 0.43811931371854D-01 0.22301121214041D-08 3 11 1 1 0.14507809620080D-13 0.45087654566842D-16 1 12 1 1 0.33282156738927D+01 -0.68875799274928D-08 2 12 1 1 -0.80808543337908D-01 -0.30625074891142D-08 3 12 1 1 -0.10393528621015D-13 0.88393053613887D-15 1 13 1 1 0.10068875849351D+01 0.12154396525275D-08 2 13 1 1 0.11550920008749D+01 -0.47717343425211D-08 3 13 1 1 -0.69566126400816D+00 -0.18064485275918D-07 1 14 1 1 0.55109143599850D+00 -0.16859470164449D-02 2 14 1 1 0.10457860794229D+01 -0.21886711657059D-02 3 14 1 1 0.59817842655171D+00 -0.88572067146316D-03 1 15 1 1 0.55109143599849D+00 -0.16859470164446D-02 2 15 1 1 0.10457860794229D+01 -0.21886711657073D-02 3 15 1 1 -0.59817842655171D+00 0.88572067146340D-03 1 16 1 1 0.10068875849351D+01 0.12154400086260D-08 2 16 1 1 0.11550920008749D+01 -0.47717350967895D-08 3 16 1 1 0.69566126400815D+00 0.18064487137609D-07 1 17 1 1 -0.13160036258649D+01 -0.39440115589894D-02 2 17 1 1 0.24946234683046D+00 -0.65656601002124D-02 3 17 1 1 -0.38956142221468D+00 -0.13481471670719D-01 1 18 1 1 -0.71675581434649D+00 0.64643204087177D-02 2 18 1 1 0.78575631330611D+00 -0.12548032918742D-02 3 18 1 1 -0.95826380163168D+00 -0.12094229383055D-01 1 19 1 1 -0.71675581434649D+00 0.64643204087180D-02 2 19 1 1 0.78575631330610D+00 -0.12548032918746D-02 3 19 1 1 0.95826380163169D+00 0.12094229383054D-01 1 20 1 1 -0.13160036258649D+01 -0.39440115589883D-02 2 20 1 1 0.24946234683043D+00 -0.65656601002118D-02 3 20 1 1 0.38956142221469D+00 0.13481471670719D-01 1 1 2 1 0.13772125059793D+01 0.62610147890101D-06 2 1 2 1 0.90169130276790D+01 0.00000000000000D+00 3 1 2 1 -0.30040538760915D-13 0.00000000000000D+00 1 2 2 1 -0.25163368371930D+00 -0.57816451842871D-08 2 2 2 1 -0.85097819111141D+00 -0.37533424387328D-08 3 2 2 1 0.13508348505171D-13 -0.13448388147701D-15 1 3 2 1 -0.24697006100925D+01 0.49360681863246D-08 2 3 2 1 0.78220649560602D-14 -0.73083860394288D-08 3 3 2 1 0.19626417369691D-15 0.17948719302939D-15 1 4 2 1 -0.80139165027214D+00 -0.12209002566962D-07 2 4 2 1 0.29688049252269D-16 -0.17945371304497D-07 3 4 2 1 0.76819625720432D-14 -0.91633611493912D-16 1 5 2 1 -0.22850983113631D-01 0.27624678139527D-02 2 5 2 1 -0.70369167550632D+00 0.23073912552774D-02 3 5 2 1 0.52526907385762D+01 -0.94558926742200D-02 1 6 2 1 -0.22850983113627D-01 0.27624678139506D-02 2 6 2 1 -0.70369167550632D+00 0.23073912552781D-02 3 6 2 1 -0.52526907385762D+01 0.94558926742204D-02 1 7 2 1 0.57844668973428D+00 -0.42020364872323D-08 2 7 2 1 -0.58296009246916D+00 0.45000906476477D-08 3 7 2 1 -0.15477292984609D+00 -0.33495939027174D-08 1 8 2 1 0.57844668973426D+00 -0.42020414930337D-08 2 8 2 1 -0.58296009246915D+00 0.45000872647521D-08 3 8 2 1 0.15477292984609D+00 0.33495937527467D-08 1 9 2 1 -0.16123218273363D+00 0.64755260914630D-08 2 9 2 1 -0.21153417980671D+01 0.78856789423678D-08 3 9 2 1 -0.24026214277380D-14 -0.63474123049100D-15 1 10 2 1 0.19701072520445D+00 0.92413184308883D-09 2 10 2 1 -0.52632133627159D-01 -0.13117718594308D-07 3 10 2 1 -0.22412744227169D-13 -0.33168750969515D-15 1 11 2 1 0.41044526200018D-01 -0.81463562651120D-08 2 11 2 1 0.16311114054322D+00 0.39850752826578D-08 3 11 2 1 0.16538195323706D-13 0.56967372322346D-16 1 12 2 1 -0.15354487276502D+00 -0.52421170902712D-08 2 12 2 1 0.35840601747481D+00 0.29847658443105D-08 3 12 2 1 -0.27994344791368D-14 -0.24131094939038D-15 1 13 2 1 0.98294883532375D+00 -0.56159688231892D-08 2 13 2 1 0.10331801108356D+01 0.71683566617666D-08 3 13 2 1 0.57471389885982D+00 0.17475578338433D-07 1 14 2 1 0.99309514956424D+00 -0.22828829356225D-02 2 14 2 1 0.44556139274740D+00 -0.17908386303753D-02 3 14 2 1 -0.62614459687664D+00 0.14714487593205D-02 1 15 2 1 0.99309514956421D+00 -0.22828829356239D-02 2 15 2 1 0.44556139274739D+00 -0.17908386303749D-02 3 15 2 1 0.62614459687666D+00 -0.14714487593201D-02 1 16 2 1 0.98294883532377D+00 -0.56159695774577D-08 2 16 2 1 0.10331801108356D+01 0.71683558893185D-08 3 16 2 1 -0.57471389885982D+00 -0.17475577764819D-07 1 17 2 1 0.15794604274557D+00 -0.19553670742051D-02 2 17 2 1 -0.17254708423937D+01 -0.11015428189470D-01 3 17 2 1 -0.70195143547449D+00 -0.15254249492223D-01 1 18 2 1 0.81535905389243D+00 -0.28061440144172D-02 2 18 2 1 -0.85394703937680D+00 0.48041569582791D-02 3 18 2 1 -0.84183351782022D+00 -0.70212322370557D-02 1 19 2 1 0.81535905389243D+00 -0.28061440144175D-02 2 19 2 1 -0.85394703937679D+00 0.48041569582787D-02 3 19 2 1 0.84183351782022D+00 0.70212322370555D-02 1 20 2 1 0.15794604274555D+00 -0.19553670742045D-02 2 20 2 1 -0.17254708423937D+01 -0.11015428189467D-01 3 20 2 1 0.70195143547449D+00 0.15254249492223D-01 1 1 3 1 -0.41788963180379D-13 0.11102230246252D-15 2 1 3 1 -0.30040538760915D-13 0.11102230246252D-15 3 1 3 1 0.14332138621132D+02 0.00000000000000D+00 1 2 3 1 -0.71603274257902D-14 0.65297025090958D-16 2 2 3 1 0.13508348504483D-13 -0.13498522718085D-15 3 2 3 1 0.30029765055764D+01 -0.13895256170028D-07 1 3 3 1 0.12969883372212D-14 0.22767982805170D-17 2 3 3 1 0.19626417300784D-15 0.17942379373817D-15 3 3 3 1 0.19695965827206D-13 -0.61858568078470D-08 1 4 3 1 0.11826458153786D-13 0.12059733609379D-14 2 4 3 1 0.76819625723271D-14 -0.91613839814402D-16 3 4 3 1 0.26871889523028D-14 -0.17070105178194D-07 1 5 3 1 -0.20481552077899D+00 0.27268975716815D-02 2 5 3 1 0.53915354466516D+01 -0.24772797766737D-02 3 5 3 1 -0.65892265794331D+00 0.36390399576755D-03 1 6 3 1 0.20481552077899D+00 -0.27268975716815D-02 2 6 3 1 -0.53915354466516D+01 0.24772797766741D-02 3 6 3 1 -0.65892265794332D+00 0.36390399576713D-03 1 7 3 1 0.50120406576588D+01 0.78590532211649D-02 2 7 3 1 -0.28770540691925D+00 -0.31864594806069D-02 3 7 3 1 0.13477910186055D+01 -0.13062225379033D-02 1 8 3 1 -0.50120406576589D+01 -0.78590532211655D-02 2 8 3 1 0.28770540691924D+00 0.31864594806068D-02 3 8 3 1 0.13477910186055D+01 -0.13062225379030D-02 1 9 3 1 -0.54463979014792D-14 0.37281458057223D-15 2 9 3 1 -0.24026214293923D-14 -0.63474123049100D-15 3 9 3 1 -0.10363902286753D+01 0.25549010285252D-07 1 10 3 1 -0.12157801708632D-13 -0.57730516256881D-15 2 10 3 1 -0.22412744226985D-13 -0.33188463285635D-15 3 10 3 1 -0.10694750080719D+00 -0.71288044406183D-08 1 11 3 1 0.14507809620041D-13 0.44783372341556D-16 2 11 3 1 0.16538195323705D-13 0.56230138728200D-16 3 11 3 1 -0.45198706458874D+00 0.41599824946954D-08 1 12 3 1 -0.10393528622009D-13 0.88560100106848D-15 2 12 3 1 -0.27994344791003D-14 -0.23909328895244D-15 3 12 3 1 0.67483083842958D+00 -0.66874266838036D-07 1 13 3 1 -0.44153493756761D+00 0.14934091465842D-07 2 13 3 1 0.71923361310960D+00 -0.16315786659145D-07 3 13 3 1 -0.44958778618903D-01 0.18600451860708D-07 1 14 3 1 0.57842585428567D+00 0.65392177610117D-03 2 14 3 1 -0.52686513852279D+00 -0.25246145760649D-03 3 14 3 1 -0.44381121288763D+00 0.16889012571114D-02 1 15 3 1 -0.57842585428567D+00 -0.65392177610093D-03 2 15 3 1 0.52686513852280D+00 0.25246145760682D-03 3 15 3 1 -0.44381121288767D+00 0.16889012571127D-02 1 16 3 1 0.44153493756763D+00 -0.14934089604151D-07 2 16 3 1 -0.71923361310960D+00 0.16315787232542D-07 3 16 3 1 -0.44958778618917D-01 0.18600451254024D-07 1 17 3 1 -0.69577824832151D+00 0.49956770034411D-02 2 17 3 1 -0.37915633795141D+00 -0.91334163740530D-04 3 17 3 1 -0.20184457421977D+01 0.33650333214228D-03 1 18 3 1 -0.10601158843440D+01 0.13474040882782D-06 2 18 3 1 -0.69431667125023D+00 0.21940594227210D-07 3 18 3 1 0.65032357226175D+00 -0.35819904084301D-07 1 19 3 1 0.10601158843441D+01 -0.13474040929707D-06 2 19 3 1 0.69431667125025D+00 -0.21940594395287D-07 3 19 3 1 0.65032357226186D+00 -0.35819907301323D-07 1 20 3 1 0.69577824832154D+00 -0.49956770034411D-02 2 20 3 1 0.37915633795141D+00 0.91334163740795D-04 3 20 3 1 -0.20184457421977D+01 0.33650333214056D-03 1 1 1 2 -0.91115557569266D+00 0.96633139456072D-09 2 1 1 2 -0.25163483277610D+00 0.17351135402880D-07 3 1 1 2 -0.71603274257749D-14 -0.65866801455946D-16 1 2 1 2 0.91791587439220D+01 0.00000000000000D+00 2 2 1 2 0.13772139281215D+01 0.57171827219290D-06 3 2 1 2 0.84360096522751D-15 0.00000000000000D+00 1 3 1 2 0.15588408637211D-14 0.15829149636782D-07 2 3 1 2 0.80139165027212D+00 -0.12209004454300D-07 3 3 1 2 -0.12340665184651D-13 0.34628502441884D-16 1 4 1 2 0.10401501445046D-13 0.97070095190894D-08 2 4 1 2 0.24697006100925D+01 0.49360606075068D-08 3 4 1 2 0.40374882834834D-15 -0.11284762439668D-16 1 5 1 2 0.61785285138953D+00 0.47584016670953D-03 2 5 1 2 0.27404867942924D+00 0.17864480588402D-02 3 5 1 2 0.22575183399690D+00 0.10153804990144D-02 1 6 1 2 0.61785285138953D+00 0.47584016670807D-03 2 6 1 2 0.27404867942924D+00 0.17864480588422D-02 3 6 1 2 -0.22575183399690D+00 -0.10153804990145D-02 1 7 1 2 0.14196865593327D-01 0.30871370905601D-09 2 7 1 2 0.43091913283071D+00 -0.11657340471676D-08 3 7 1 2 0.53077092998002D+01 -0.19568089598291D-07 1 8 1 2 0.14196865593314D-01 0.30871457182346D-09 2 8 1 2 0.43091913283071D+00 -0.11657325954794D-08 3 8 1 2 -0.53077092998002D+01 0.19568090317548D-07 1 9 1 2 -0.13065003929992D+00 -0.52795488725362D-08 2 9 1 2 -0.11362851269804D+00 0.10673649358226D-08 3 9 1 2 -0.12699314879520D-13 -0.12543648758788D-15 1 10 1 2 0.36172695740977D+00 -0.14254656420229D-07 2 10 1 2 -0.13496843910722D+00 -0.20167335525551D-07 3 10 1 2 -0.21702109665999D-13 -0.42600878165687D-15 1 11 1 2 -0.33282156738926D+01 0.68875806001246D-08 2 11 1 2 0.80808543338262D-01 0.30625153291344D-08 3 11 1 2 0.84976795424821D-15 0.59981775554913D-15 1 12 1 2 -0.23137836817497D+00 0.42466430353785D-08 2 12 1 2 -0.43811931371897D-01 -0.22301125714888D-08 3 12 1 2 -0.12420187412125D-13 -0.11712892249517D-14 1 13 1 2 -0.55109143599850D+00 0.16859470164451D-02 2 13 1 2 -0.10457860794229D+01 0.21886711657089D-02 3 13 1 2 -0.59817842655174D+00 0.88572067146593D-03 1 14 1 2 -0.10068875849351D+01 -0.12154427602466D-08 2 14 1 2 -0.11550920008749D+01 0.47717422475985D-08 3 14 1 2 0.69566126400801D+00 0.18064477443729D-07 1 15 1 2 -0.10068875849351D+01 -0.12154435457377D-08 2 15 1 2 -0.11550920008750D+01 0.47717403007472D-08 3 15 1 2 -0.69566126400808D+00 -0.18064478629250D-07 1 16 1 2 -0.55109143599850D+00 0.16859470164446D-02 2 16 1 2 -0.10457860794229D+01 0.21886711657086D-02 3 16 1 2 0.59817842655178D+00 -0.88572067146617D-03 1 17 1 2 0.71675581434649D+00 -0.64643204087180D-02 2 17 1 2 -0.78575631330609D+00 0.12548032918728D-02 3 17 1 2 0.95826380163157D+00 0.12094229383061D-01 1 18 1 2 0.13160036258649D+01 0.39440115589865D-02 2 18 1 2 -0.24946234683043D+00 0.65656601002296D-02 3 18 1 2 0.38956142221453D+00 0.13481471670747D-01 1 19 1 2 0.13160036258649D+01 0.39440115589874D-02 2 19 1 2 -0.24946234683047D+00 0.65656601002292D-02 3 19 1 2 -0.38956142221445D+00 -0.13481471670747D-01 1 20 1 2 0.71675581434651D+00 -0.64643204087172D-02 2 20 1 2 -0.78575631330613D+00 0.12548032918718D-02 3 20 1 2 -0.95826380163168D+00 -0.12094229383062D-01 1 1 2 2 -0.25163368371930D+00 -0.57816453718318D-08 2 1 2 2 -0.85097819111141D+00 -0.37533437254703D-08 3 1 2 2 0.13508348504343D-13 0.13491756234600D-15 1 2 2 2 0.13772125059790D+01 0.62610147890101D-06 2 2 2 2 0.90169130276809D+01 0.00000000000000D+00 3 2 2 2 -0.37145966139195D-13 0.00000000000000D+00 1 3 2 2 0.80139165027214D+00 0.12209002572115D-07 2 3 2 2 0.45401506977901D-14 0.17945371325626D-07 3 3 2 2 -0.23658375804678D-15 -0.13197679847443D-15 1 4 2 2 0.24697006100925D+01 -0.49360596426848D-08 2 4 2 2 0.40819905134629D-15 0.73083868196082D-08 3 4 2 2 -0.15225814757819D-15 0.49212910670282D-16 1 5 2 2 -0.22850983113629D-01 0.27624678139514D-02 2 5 2 2 -0.70369167550638D+00 0.23073912552930D-02 3 5 2 2 0.52526907385763D+01 -0.94558926742111D-02 1 6 2 2 -0.22850983113630D-01 0.27624678139534D-02 2 6 2 2 -0.70369167550640D+00 0.23073912552865D-02 3 6 2 2 -0.52526907385762D+01 0.94558926742112D-02 1 7 2 2 0.57844668973431D+00 -0.42020370291652D-08 2 7 2 2 -0.58296009246920D+00 0.45000871991600D-08 3 7 2 2 -0.15477292984610D+00 -0.33495923062002D-08 1 8 2 2 0.57844668973431D+00 -0.42020355775091D-08 2 8 2 2 -0.58296009246920D+00 0.45000849064867D-08 3 8 2 2 0.15477292984609D+00 0.33495922874527D-08 1 9 2 2 -0.19701072520443D+00 -0.92413235139958D-09 2 9 2 2 0.52632133627170D-01 0.13117720151042D-07 3 9 2 2 0.79142712487603D-14 -0.10798252270273D-14 1 10 2 2 0.16123218273354D+00 -0.64755279497814D-08 2 10 2 2 0.21153417980675D+01 -0.78856997112400D-08 3 10 2 2 -0.88719050746798D-14 -0.15179942888243D-14 1 11 2 2 0.15354487276537D+00 0.52421249302914D-08 2 11 2 2 -0.35840601747494D+00 -0.29847641390425D-08 3 11 2 2 0.16413406772946D-13 0.10329628757114D-15 1 12 2 2 -0.41044526200061D-01 0.81463558150274D-08 2 12 2 2 -0.16311114054321D+00 -0.39850756068874D-08 3 12 2 2 -0.48334051107077D-15 0.21554731404739D-15 1 13 2 2 -0.99309514956420D+00 0.22828829356255D-02 2 13 2 2 -0.44556139274742D+00 0.17908386303731D-02 3 13 2 2 0.62614459687664D+00 -0.14714487593225D-02 1 14 2 2 -0.98294883532374D+00 0.56159767282666D-08 2 14 2 2 -0.10331801108355D+01 -0.71683565180519D-08 3 14 2 2 -0.57471389885983D+00 -0.17475570122769D-07 1 15 2 2 -0.98294883532382D+00 0.56159747814154D-08 2 15 2 2 -0.10331801108355D+01 -0.71683560699283D-08 3 15 2 2 0.57471389885990D+00 0.17475569930734D-07 1 16 2 2 -0.99309514956425D+00 0.22828829356253D-02 2 16 2 2 -0.44556139274741D+00 0.17908386303727D-02 3 16 2 2 -0.62614459687667D+00 0.14714487593227D-02 1 17 2 2 -0.81535905389242D+00 0.28061440144157D-02 2 17 2 2 0.85394703937671D+00 -0.48041569582777D-02 3 17 2 2 0.84183351782020D+00 0.70212322370611D-02 1 18 2 2 -0.15794604274555D+00 0.19553670742223D-02 2 18 2 2 0.17254708423938D+01 0.11015428189478D-01 3 18 2 2 0.70195143547452D+00 0.15254249492261D-01 1 19 2 2 -0.15794604274559D+00 0.19553670742218D-02 2 19 2 2 0.17254708423938D+01 0.11015428189477D-01 3 19 2 2 -0.70195143547449D+00 -0.15254249492261D-01 1 20 2 2 -0.81535905389246D+00 0.28061440144148D-02 2 20 2 2 0.85394703937677D+00 -0.48041569582769D-02 3 20 2 2 -0.84183351782026D+00 -0.70212322370613D-02 1 1 3 2 -0.71603274257913D-14 -0.64553061658456D-16 2 1 3 2 0.13508348504553D-13 0.13481606509373D-15 3 1 3 2 0.30029765055764D+01 -0.13895232268231D-07 1 2 3 2 0.84360096522751D-15 0.11102230246252D-15 2 2 3 2 -0.37145966139195D-13 0.11102230246252D-15 3 2 3 2 0.14332138621128D+02 0.00000000000000D+00 1 3 3 2 -0.12340665184766D-13 0.34672509550534D-16 2 3 3 2 -0.23658375833071D-15 -0.13199657015394D-15 3 3 3 2 -0.35758306347377D-14 0.17070104185407D-07 1 4 3 2 0.40374882835978D-15 -0.11336643031997D-16 2 4 3 2 -0.15225814709591D-15 0.49276309961508D-16 3 4 3 2 0.77521541460236D-15 0.61858561974078D-08 1 5 3 2 -0.20481552077899D+00 0.27268975716813D-02 2 5 3 2 0.53915354466517D+01 -0.24772797766648D-02 3 5 3 2 -0.65892265794334D+00 0.36390399577081D-03 1 6 3 2 0.20481552077899D+00 -0.27268975716814D-02 2 6 3 2 -0.53915354466515D+01 0.24772797766648D-02 3 6 3 2 -0.65892265794338D+00 0.36390399577086D-03 1 7 3 2 0.50120406576590D+01 0.78590532211809D-02 2 7 3 2 -0.28770540691925D+00 -0.31864594806053D-02 3 7 3 2 0.13477910186055D+01 -0.13062225378949D-02 1 8 3 2 -0.50120406576589D+01 -0.78590532211802D-02 2 8 3 2 0.28770540691924D+00 0.31864594806053D-02 3 8 3 2 0.13477910186055D+01 -0.13062225378949D-02 1 9 3 2 -0.12699314879535D-13 -0.12532358473822D-15 2 9 3 2 0.79142712482927D-14 -0.10796938115865D-14 3 9 3 2 0.10694750080711D+00 0.71288046925418D-08 1 10 3 2 -0.21702109666826D-13 -0.42600878165687D-15 2 10 3 2 -0.88719050746798D-14 -0.15179942888243D-14 3 10 3 2 0.10363902286751D+01 -0.25548997912420D-07 1 11 3 2 0.84976795524219D-15 0.59814729061952D-15 2 11 3 2 0.16413406772909D-13 0.10107862713321D-15 3 11 3 2 -0.67483083842971D+00 0.66874269502060D-07 1 12 3 2 -0.12420187412085D-13 -0.11709849427264D-14 2 12 3 2 -0.48334051106957D-15 0.21628454764153D-15 3 12 3 2 0.45198706458874D+00 -0.41599854978095D-08 1 13 3 2 -0.57842585428570D+00 -0.65392177609840D-03 2 13 3 2 0.52686513852279D+00 0.25246145760448D-03 3 13 3 2 0.44381121288772D+00 -0.16889012571152D-02 1 14 3 2 0.44153493756746D+00 -0.14934099298085D-07 2 14 3 2 -0.71923361310961D+00 0.16315794874591D-07 3 14 3 2 0.44958778618903D-01 -0.18600456203081D-07 1 15 3 2 -0.44153493756756D+00 0.14934098112564D-07 2 15 3 2 0.71923361310968D+00 -0.16315795066844D-07 3 15 3 2 0.44958778618831D-01 -0.18600456986964D-07 1 16 3 2 0.57842585428574D+00 0.65392177609816D-03 2 16 3 2 -0.52686513852281D+00 -0.25246145760428D-03 3 16 3 2 0.44381121288773D+00 -0.16889012571152D-02 1 17 3 2 0.10601158843439D+01 -0.13474040200727D-06 2 17 3 2 0.69431667125021D+00 -0.21940588786129D-07 3 17 3 2 -0.65032357226161D+00 0.35819892962452D-07 1 18 3 2 0.69577824832137D+00 -0.49956770034128D-02 2 18 3 2 0.37915633795144D+00 0.91334163778467D-04 3 18 3 2 0.20184457421975D+01 -0.33650333211274D-03 1 19 3 2 -0.69577824832130D+00 0.49956770034128D-02 2 19 3 2 -0.37915633795141D+00 -0.91334163778488D-04 3 19 3 2 0.20184457421975D+01 -0.33650333210863D-03 1 20 3 2 -0.10601158843441D+01 0.13474040178195D-06 2 20 3 2 -0.69431667125029D+00 0.21940588601265D-07 3 20 3 2 -0.65032357226175D+00 0.35819893517031D-07 1 1 1 3 0.50696491373287D-15 0.97070091608302D-08 2 1 1 3 -0.24697006100925D+01 -0.49360681863246D-08 3 1 1 3 0.12969883372212D-14 -0.22767982805168D-17 1 2 1 3 0.15588408637211D-14 -0.15829149636782D-07 2 2 1 3 0.80139165027214D+00 -0.12209002572115D-07 3 2 1 3 -0.12340665184766D-13 -0.34672509550534D-16 1 3 1 3 0.91791587439238D+01 0.00000000000000D+00 2 3 1 3 -0.13772139281216D+01 -0.57171827219290D-06 3 3 1 3 -0.13367253749975D-13 0.00000000000000D+00 1 4 1 3 0.91115557569262D+00 -0.96633302412606D-09 2 4 1 3 -0.25163483277611D+00 0.17351135099394D-07 3 4 1 3 -0.55149112743953D-14 0.38464090137186D-15 1 5 1 3 0.14196865593336D-01 0.30871515121207D-09 2 5 1 3 -0.43091913283082D+00 0.11657338036154D-08 3 5 1 3 -0.53077092998001D+01 0.19568089929848D-07 1 6 1 3 0.14196865593336D-01 0.30871397895346D-09 2 6 1 3 -0.43091913283080D+00 0.11657297031230D-08 3 6 1 3 0.53077092998001D+01 -0.19568090308344D-07 1 7 1 3 -0.61785285138962D+00 -0.47584016671754D-03 2 7 1 3 0.27404867942925D+00 0.17864480588421D-02 3 7 1 3 0.22575183399690D+00 0.10153804990147D-02 1 8 1 3 -0.61785285138960D+00 -0.47584016671241D-03 2 8 1 3 0.27404867942925D+00 0.17864480588417D-02 3 8 1 3 -0.22575183399690D+00 -0.10153804990150D-02 1 9 1 3 -0.33282156738928D+01 0.68875809317257D-08 2 9 1 3 -0.80808543338177D-01 -0.30625185654931D-08 3 9 1 3 0.36739192810892D-14 0.13297717873350D-14 1 10 1 3 -0.23137836817497D+00 0.42466423848163D-08 2 10 1 3 0.43811931371908D-01 0.22301094130538D-08 3 10 1 3 0.28276538431668D-13 0.12431319428237D-15 1 11 1 3 0.13065003929994D+00 0.52795461635066D-08 2 11 1 3 -0.11362851269805D+00 0.10673659707103D-08 3 11 1 3 -0.13995273214664D-13 -0.11720819852688D-16 1 12 1 3 -0.36172695740971D+00 0.14254658030659D-07 2 12 1 3 -0.13496843910719D+00 -0.20167333313751D-07 3 12 1 3 0.20081817915971D-15 0.23697390331568D-15 1 13 1 3 -0.13160036258649D+01 -0.39440115589896D-02 2 13 1 3 -0.24946234683046D+00 0.65656601002246D-02 3 13 1 3 0.38956142221442D+00 0.13481471670737D-01 1 14 1 3 -0.71675581434647D+00 0.64643204087186D-02 2 14 1 3 -0.78575631330612D+00 0.12548032918744D-02 3 14 1 3 0.95826380163159D+00 0.12094229383054D-01 1 15 1 3 -0.71675581434646D+00 0.64643204087164D-02 2 15 1 3 -0.78575631330613D+00 0.12548032918745D-02 3 15 1 3 -0.95826380163162D+00 -0.12094229383054D-01 1 16 1 3 -0.13160036258649D+01 -0.39440115589873D-02 2 16 1 3 -0.24946234683046D+00 0.65656601002254D-02 3 16 1 3 -0.38956142221445D+00 -0.13481471670738D-01 1 17 1 3 -0.10068875849351D+01 -0.12154425870558D-08 2 17 1 3 0.11550920008749D+01 -0.47717393174775D-08 3 17 1 3 -0.69566126400806D+00 -0.18064477902601D-07 1 18 1 3 -0.55109143599850D+00 0.16859470164466D-02 2 18 1 3 0.10457860794230D+01 -0.21886711657099D-02 3 18 1 3 0.59817842655181D+00 -0.88572067146535D-03 1 19 1 3 -0.55109143599851D+00 0.16859470164454D-02 2 19 1 3 0.10457860794229D+01 -0.21886711657092D-02 3 19 1 3 -0.59817842655179D+00 0.88572067146643D-03 1 20 1 3 -0.10068875849351D+01 -0.12154439464089D-08 2 20 1 3 0.11550920008749D+01 -0.47717397112750D-08 3 20 1 3 0.69566126400804D+00 0.18064477963482D-07 1 1 2 3 -0.24697006100925D+01 0.49360520638669D-08 2 1 2 3 0.78220649560602D-14 0.73083860394288D-08 3 1 2 3 0.19626417300784D-15 -0.17942379373817D-15 1 2 2 3 0.80139165027212D+00 0.12209004454300D-07 2 2 2 3 0.45401506977901D-14 -0.17945371325626D-07 3 2 2 3 -0.23658375833071D-15 0.13199657015394D-15 1 3 2 3 -0.13772125059791D+01 -0.62610147890101D-06 2 3 2 3 0.90169130276809D+01 0.00000000000000D+00 3 3 2 3 -0.58462248212006D-13 0.00000000000000D+00 1 4 2 3 -0.25163368371931D+00 -0.57816456753177D-08 2 4 2 3 0.85097819111133D+00 0.37533437955283D-08 3 4 2 3 -0.11986308842765D-13 -0.10846905038034D-15 1 5 2 3 -0.57844668973442D+00 0.42020367857308D-08 2 5 2 3 -0.58296009246914D+00 0.45000859335590D-08 3 5 2 3 -0.15477292984609D+00 -0.33495925360486D-08 1 6 2 3 -0.57844668973440D+00 0.42020326852062D-08 2 6 2 3 -0.58296009246914D+00 0.45000871802561D-08 3 6 2 3 0.15477292984609D+00 0.33495924473225D-08 1 7 2 3 -0.22850983113618D-01 0.27624678139533D-02 2 7 2 3 0.70369167550636D+00 -0.23073912552763D-02 3 7 2 3 -0.52526907385762D+01 0.94558926742063D-02 1 8 2 3 -0.22850983113616D-01 0.27624678139529D-02 2 8 2 3 0.70369167550637D+00 -0.23073912552795D-02 3 8 2 3 0.52526907385763D+01 -0.94558926742064D-02 1 9 2 3 -0.15354487276529D+00 -0.52421281666501D-08 2 9 2 3 -0.35840601747473D+00 -0.29847639639218D-08 3 9 2 3 0.34552363871342D-14 0.24536766143420D-15 1 10 2 3 0.41044526200072D-01 -0.81463589734624D-08 2 10 2 3 -0.16311114054321D+00 -0.39850746037394D-08 3 10 2 3 0.11392153102535D-13 -0.63293519782771D-16 1 11 2 3 -0.19701072520445D+00 -0.92413131651183D-09 2 11 2 3 -0.52632133627149D-01 -0.13117719969066D-07 3 11 2 3 -0.22598672814301D-13 0.72165563228788D-15 1 12 2 3 0.16123218273356D+00 -0.64755257379813D-08 2 12 2 3 -0.21153417980675D+01 0.78856794280909D-08 3 12 2 3 0.39910917955911D-14 -0.72691639364058D-15 1 13 2 3 -0.15794604274555D+00 0.19553670742172D-02 2 13 2 3 -0.17254708423938D+01 -0.11015428189472D-01 3 13 2 3 -0.70195143547442D+00 -0.15254249492247D-01 1 14 2 3 -0.81535905389245D+00 0.28061440144173D-02 2 14 2 3 -0.85394703937676D+00 0.48041569582790D-02 3 14 2 3 -0.84183351782026D+00 -0.70212322370556D-02 1 15 2 3 -0.81535905389245D+00 0.28061440144175D-02 2 15 2 3 -0.85394703937674D+00 0.48041569582770D-02 3 15 2 3 0.84183351782028D+00 0.70212322370550D-02 1 16 2 3 -0.15794604274556D+00 0.19553670742181D-02 2 16 2 3 -0.17254708423938D+01 -0.11015428189473D-01 3 16 2 3 0.70195143547442D+00 0.15254249492249D-01 1 17 2 3 0.98294883532377D+00 -0.56159737981457D-08 2 17 2 3 -0.10331801108355D+01 -0.71683564771512D-08 3 17 2 3 -0.57471389885983D+00 -0.17475570059432D-07 1 18 2 3 0.99309514956425D+00 -0.22828829356266D-02 2 18 2 3 -0.44556139274741D+00 0.17908386303746D-02 3 18 2 3 0.62614459687669D+00 -0.14714487593231D-02 1 19 2 3 0.99309514956424D+00 -0.22828829356258D-02 2 19 2 3 -0.44556139274742D+00 0.17908386303754D-02 3 19 2 3 -0.62614459687669D+00 0.14714487593231D-02 1 20 2 3 0.98294883532375D+00 -0.56159741919432D-08 2 20 2 3 -0.10331801108355D+01 -0.71683558791601D-08 3 20 2 3 0.57471389885983D+00 0.17475569860898D-07 1 1 3 3 0.12969883372326D-14 -0.22249176881878D-17 2 1 3 3 0.19626417369691D-15 -0.17948719302939D-15 3 1 3 3 0.19695965827206D-13 0.61858568078470D-08 1 2 3 3 -0.12340665184651D-13 -0.34628502441884D-16 2 2 3 3 -0.23658375804678D-15 0.13197679847443D-15 3 2 3 3 -0.35758306347377D-14 -0.17070104185407D-07 1 3 3 3 -0.13367253749975D-13 0.11102230246252D-15 2 3 3 3 -0.58462248212006D-13 -0.11102230246252D-15 3 3 3 3 0.14332138621128D+02 0.00000000000000D+00 1 4 3 3 -0.55149112744030D-14 0.38449210868536D-15 2 4 3 3 -0.11986308841594D-13 -0.10871972323226D-15 3 4 3 3 -0.30029765055763D+01 0.13895243706818D-07 1 5 3 3 -0.50120406576589D+01 -0.78590532211806D-02 2 5 3 3 -0.28770540691924D+00 -0.31864594806055D-02 3 5 3 3 0.13477910186055D+01 -0.13062225378956D-02 1 6 3 3 0.50120406576589D+01 0.78590532211802D-02 2 6 3 3 0.28770540691924D+00 0.31864594806055D-02 3 6 3 3 0.13477910186055D+01 -0.13062225378951D-02 1 7 3 3 -0.20481552077899D+00 0.27268975716816D-02 2 7 3 3 -0.53915354466516D+01 0.24772797766599D-02 3 7 3 3 0.65892265794353D+00 -0.36390399576364D-03 1 8 3 3 0.20481552077899D+00 -0.27268975716819D-02 2 8 3 3 0.53915354466517D+01 -0.24772797766600D-02 3 8 3 3 0.65892265794355D+00 -0.36390399576261D-03 1 9 3 3 0.36739192796928D-14 0.13313214337983D-14 2 9 3 3 0.34552363871161D-14 0.24391888169057D-15 3 9 3 3 -0.67483083842939D+00 0.66874268827837D-07 1 10 3 3 0.28276538431553D-13 0.12506731032881D-15 2 10 3 3 0.11392153102314D-13 -0.62700671087942D-16 3 10 3 3 0.45198706458876D+00 -0.41599855787609D-08 1 11 3 3 -0.13995273214650D-13 -0.11560430843025D-16 2 11 3 3 -0.22598672813914D-13 0.72172134000828D-15 3 11 3 3 -0.10694750080719D+00 -0.71288031009829D-08 1 12 3 3 0.20081817998689D-15 0.23697390331568D-15 2 12 3 3 0.39910917972455D-14 -0.72691639364058D-15 3 12 3 3 -0.10363902286750D+01 0.25549007820033D-07 1 13 3 3 0.69577824832127D+00 -0.49956770034228D-02 2 13 3 3 -0.37915633795134D+00 -0.91334163764999D-04 3 13 3 3 -0.20184457421974D+01 0.33650333211633D-03 1 14 3 3 0.10601158843440D+01 -0.13474040931372D-06 2 14 3 3 -0.69431667125029D+00 0.21940594282474D-07 3 14 3 3 0.65032357226161D+00 -0.35819906274507D-07 1 15 3 3 -0.10601158843440D+01 0.13474040959229D-06 2 15 3 3 0.69431667125028D+00 -0.21940594887424D-07 3 15 3 3 0.65032357226169D+00 -0.35819907728856D-07 1 16 3 3 -0.69577824832129D+00 0.49956770034225D-02 2 16 3 3 0.37915633795134D+00 0.91334163766715D-04 3 16 3 3 -0.20184457421974D+01 0.33650333211986D-03 1 17 3 3 -0.44153493756754D+00 0.14934098839214D-07 2 17 3 3 -0.71923361310961D+00 0.16315794938145D-07 3 17 3 3 0.44958778618824D-01 -0.18600456302173D-07 1 18 3 3 0.57842585428576D+00 0.65392177609898D-03 2 18 3 3 0.52686513852284D+00 0.25246145760384D-03 3 18 3 3 0.44381121288777D+00 -0.16889012571165D-02 1 19 3 3 -0.57842585428575D+00 -0.65392177609790D-03 2 19 3 3 -0.52686513852285D+00 -0.25246145760382D-03 3 19 3 3 0.44381121288777D+00 -0.16889012571149D-02 1 20 3 3 0.44153493756748D+00 -0.14934098778332D-07 2 20 3 3 0.71923361310961D+00 -0.16315795136463D-07 3 20 3 3 0.44958778618825D-01 -0.18600458820428D-07 1 1 1 4 0.44152499754399D-14 0.15829149424820D-07 2 1 1 4 -0.80139165027214D+00 0.12209002566962D-07 3 1 1 4 0.11826458153786D-13 -0.12059733609379D-14 1 2 1 4 0.10401501445046D-13 -0.97070095190894D-08 2 2 1 4 0.24697006100925D+01 0.49360596426848D-08 3 2 1 4 0.40374882835978D-15 0.11336643031997D-16 1 3 1 4 0.91115557569262D+00 -0.96633252155131D-09 2 3 1 4 -0.25163483277611D+00 0.17351135893910D-07 3 3 1 4 -0.55149112743965D-14 -0.38362474694737D-15 1 4 1 4 0.91791587439220D+01 0.00000000000000D+00 2 4 1 4 -0.13772139281218D+01 -0.57171827219290D-06 3 4 1 4 -0.20472681107575D-13 0.00000000000000D+00 1 5 1 4 -0.14196865593351D-01 -0.30870336709064D-09 2 5 1 4 0.43091913283076D+00 -0.11657319756352D-08 3 5 1 4 0.53077092998002D+01 -0.19568091783379D-07 1 6 1 4 -0.14196865593391D-01 -0.30870422452000D-09 2 6 1 4 0.43091913283077D+00 -0.11657294485764D-08 3 6 1 4 -0.53077092998001D+01 0.19568091232906D-07 1 7 1 4 0.61785285138957D+00 0.47584016671401D-03 2 7 1 4 -0.27404867942922D+00 -0.17864480588417D-02 3 7 1 4 -0.22575183399690D+00 -0.10153804990143D-02 1 8 1 4 0.61785285138957D+00 0.47584016671427D-03 2 8 1 4 -0.27404867942922D+00 -0.17864480588421D-02 3 8 1 4 0.22575183399690D+00 0.10153804990145D-02 1 9 1 4 -0.23137836817495D+00 0.42466428233556D-08 2 9 1 4 0.43811931371904D-01 0.22301090572386D-08 3 9 1 4 0.27356271097286D-13 -0.10289344270934D-14 1 10 1 4 -0.33282156738925D+01 0.68875686250855D-08 2 10 1 4 -0.80808543338092D-01 -0.30625146605143D-08 3 10 1 4 -0.48573076697253D-14 -0.19596067417094D-15 1 11 1 4 -0.36172695740951D+00 0.14254659026087D-07 2 11 1 4 -0.13496843910707D+00 -0.20167330897179D-07 3 11 1 4 0.87253536607513D-14 -0.96424374158166D-16 1 12 1 4 0.13065003929990D+00 0.52795451885864D-08 2 12 1 4 -0.11362851269806D+00 0.10673651496971D-08 3 12 1 4 -0.41810521063719D-14 -0.28419530191813D-15 1 13 1 4 -0.71675581434648D+00 0.64643204087173D-02 2 13 1 4 -0.78575631330609D+00 0.12548032918743D-02 3 13 1 4 0.95826380163155D+00 0.12094229383055D-01 1 14 1 4 -0.13160036258648D+01 -0.39440115589854D-02 2 14 1 4 -0.24946234683041D+00 0.65656601002238D-02 3 14 1 4 0.38956142221451D+00 0.13481471670738D-01 1 15 1 4 -0.13160036258649D+01 -0.39440115589863D-02 2 15 1 4 -0.24946234683054D+00 0.65656601002237D-02 3 15 1 4 -0.38956142221438D+00 -0.13481471670738D-01 1 16 1 4 -0.71675581434650D+00 0.64643204087174D-02 2 16 1 4 -0.78575631330615D+00 0.12548032918755D-02 3 16 1 4 -0.95826380163167D+00 -0.12094229383054D-01 1 17 1 4 -0.55109143599849D+00 0.16859470164460D-02 2 17 1 4 0.10457860794229D+01 -0.21886711657089D-02 3 17 1 4 0.59817842655179D+00 -0.88572067146620D-03 1 18 1 4 -0.10068875849351D+01 -0.12154408441580D-08 2 18 1 4 0.11550920008749D+01 -0.47717415047608D-08 3 18 1 4 -0.69566126400798D+00 -0.18064477306923D-07 1 19 1 4 -0.10068875849351D+01 -0.12154416461885D-08 2 19 1 4 0.11550920008750D+01 -0.47717404252532D-08 3 19 1 4 0.69566126400804D+00 0.18064477480546D-07 1 20 1 4 -0.55109143599850D+00 0.16859470164449D-02 2 20 1 4 0.10457860794230D+01 -0.21886711657072D-02 3 20 1 4 -0.59817842655181D+00 0.88572067146555D-03 1 1 2 4 -0.80139165027213D+00 -0.12209004459453D-07 2 1 2 4 0.29688049252269D-16 0.17945371304497D-07 3 1 2 4 0.76819625723271D-14 0.91613839814402D-16 1 2 2 4 0.24697006100925D+01 -0.49360606075068D-08 2 2 2 4 0.40819905134629D-15 -0.73083868196082D-08 3 2 2 4 -0.15225814709591D-15 -0.49276309961508D-16 1 3 2 4 -0.25163368371931D+00 -0.57816448808014D-08 2 3 2 4 0.85097819111133D+00 0.37533423686748D-08 3 3 2 4 -0.11986308841180D-13 0.10893656366676D-15 1 4 2 4 -0.13772125059793D+01 -0.62610147890101D-06 2 4 2 4 0.90169130276809D+01 0.00000000000000D+00 3 4 2 4 0.80093585261221D-13 0.00000000000000D+00 1 5 2 4 0.57844668973436D+00 -0.42020349577506D-08 2 5 2 4 0.58296009246921D+00 -0.45000907301570D-08 3 5 2 4 0.15477292984608D+00 0.33495937534032D-08 1 6 2 4 0.57844668973437D+00 -0.42020324306596D-08 2 6 2 4 0.58296009246924D+00 -0.45000902611731D-08 3 6 2 4 -0.15477292984607D+00 -0.33495935158560D-08 1 7 2 4 0.22850983113644D-01 -0.27624678139529D-02 2 7 2 4 -0.70369167550641D+00 0.23073912552826D-02 3 7 2 4 0.52526907385763D+01 -0.94558926742109D-02 1 8 2 4 0.22850983113647D-01 -0.27624678139533D-02 2 8 2 4 -0.70369167550642D+00 0.23073912552885D-02 3 8 2 4 -0.52526907385762D+01 0.94558926742108D-02 1 9 2 4 0.41044526200068D-01 -0.81463593292775D-08 2 9 2 4 -0.16311114054318D+00 -0.39850757874032D-08 3 9 2 4 -0.47489538823086D-14 -0.60560864109665D-15 1 10 2 4 -0.15354487276520D+00 -0.52421242616713D-08 2 10 2 4 -0.35840601747494D+00 -0.29847621657435D-08 3 10 2 4 -0.10543255596805D-13 0.15464074892681D-15 1 11 2 4 0.16123218273369D+00 -0.64755233214093D-08 2 11 2 4 -0.21153417980679D+01 0.78856874138644D-08 3 11 2 4 -0.64146239899135D-14 -0.15131767865514D-14 1 12 2 4 -0.19701072520445D+00 -0.92413213752502D-09 2 12 2 4 -0.52632133627178D-01 -0.13117717980316D-07 3 12 2 4 -0.25779489965879D-13 -0.13176586005548D-14 1 13 2 4 -0.81535905389242D+00 0.28061440144173D-02 2 13 2 4 -0.85394703937670D+00 0.48041569582788D-02 3 13 2 4 -0.84183351782021D+00 -0.70212322370559D-02 1 14 2 4 -0.15794604274550D+00 0.19553670742165D-02 2 14 2 4 -0.17254708423938D+01 -0.11015428189474D-01 3 14 2 4 -0.70195143547452D+00 -0.15254249492248D-01 1 15 2 4 -0.15794604274565D+00 0.19553670742164D-02 2 15 2 4 -0.17254708423938D+01 -0.11015428189474D-01 3 15 2 4 0.70195143547441D+00 0.15254249492248D-01 1 16 2 4 -0.81535905389247D+00 0.28061440144184D-02 2 16 2 4 -0.85394703937675D+00 0.48041569582779D-02 3 16 2 4 0.84183351782030D+00 0.70212322370555D-02 1 17 2 4 0.99309514956422D+00 -0.22828829356255D-02 2 17 2 4 -0.44556139274741D+00 0.17908386303745D-02 3 17 2 4 0.62614459687668D+00 -0.14714487593229D-02 1 18 2 4 0.98294883532374D+00 -0.56159759854289D-08 2 18 2 4 -0.10331801108355D+01 -0.71683558668952D-08 3 18 2 4 -0.57471389885979D+00 -0.17475570087409D-07 1 19 2 4 0.98294883532380D+00 -0.56159749059213D-08 2 19 2 4 -0.10331801108355D+01 -0.71683573792479D-08 3 19 2 4 0.57471389885986D+00 0.17475570367662D-07 1 20 2 4 0.99309514956425D+00 -0.22828829356239D-02 2 20 2 4 -0.44556139274742D+00 0.17908386303741D-02 3 20 2 4 -0.62614459687668D+00 0.14714487593227D-02 1 1 3 4 0.11826458153671D-13 -0.12060173680465D-14 2 1 3 4 0.76819625720432D-14 0.91633611493912D-16 3 1 3 4 0.26871889523028D-14 0.17070105178194D-07 1 2 3 4 0.40374882834834D-15 0.11284762439668D-16 2 2 3 4 -0.15225814757819D-15 -0.49212910670282D-16 3 2 3 4 0.77521541460236D-15 -0.61858561974078D-08 1 3 3 4 -0.55149112744083D-14 -0.38377353963387D-15 2 3 3 4 -0.11986308841938D-13 0.10868589081484D-15 3 3 3 4 -0.30029765055763D+01 0.13895244731441D-07 1 4 3 4 -0.20472681107575D-13 0.11102230246252D-15 2 4 3 4 0.80093585261221D-13 -0.11102230246252D-15 3 4 3 4 0.14332138621132D+02 0.00000000000000D+00 1 5 3 4 0.50120406576590D+01 0.78590532211787D-02 2 5 3 4 0.28770540691923D+00 0.31864594806068D-02 3 5 3 4 -0.13477910186055D+01 0.13062225379020D-02 1 6 3 4 -0.50120406576588D+01 -0.78590532211793D-02 2 6 3 4 -0.28770540691922D+00 -0.31864594806065D-02 3 6 3 4 -0.13477910186056D+01 0.13062225379023D-02 1 7 3 4 0.20481552077898D+00 -0.27268975716812D-02 2 7 3 4 0.53915354466517D+01 -0.24772797766646D-02 3 7 3 4 -0.65892265794338D+00 0.36390399577058D-03 1 8 3 4 -0.20481552077898D+00 0.27268975716814D-02 2 8 3 4 -0.53915354466516D+01 0.24772797766645D-02 3 8 3 4 -0.65892265794342D+00 0.36390399577041D-03 1 9 3 4 0.27356271097171D-13 -0.10281803110469D-14 2 9 3 4 -0.47489538825303D-14 -0.60501579240182D-15 3 9 3 4 0.45198706458866D+00 -0.41599848488585D-08 1 10 3 4 -0.48573076711216D-14 -0.19441102770759D-15 2 10 3 4 -0.10543255596823D-13 0.15319196918317D-15 3 10 3 4 -0.67483083842969D+00 0.66874273976316D-07 1 11 3 4 0.87253536615785D-14 -0.96424374158166D-16 2 11 3 4 -0.64146239882592D-14 -0.15131767865514D-14 3 11 3 4 -0.10363902286746D+01 0.25549005290055D-07 1 12 3 4 -0.41810521063619D-14 -0.28421412875418D-15 2 12 3 4 -0.25779489965403D-13 -0.13175785915064D-14 3 12 3 4 -0.10694750080709D+00 -0.71288068625385D-08 1 13 3 4 0.10601158843439D+01 -0.13474040885307D-06 2 13 3 4 -0.69431667125023D+00 0.21940593988053D-07 3 13 3 4 0.65032357226164D+00 -0.35819907862076D-07 1 14 3 4 0.69577824832136D+00 -0.49956770034226D-02 2 14 3 4 -0.37915633795144D+00 -0.91334163765621D-04 3 14 3 4 -0.20184457421974D+01 0.33650333212146D-03 1 15 3 4 -0.69577824832121D+00 0.49956770034217D-02 2 15 3 4 0.37915633795133D+00 0.91334163765766D-04 3 15 3 4 -0.20184457421975D+01 0.33650333212189D-03 1 16 3 4 -0.10601158843440D+01 0.13474040907494D-06 2 16 3 4 0.69431667125030D+00 -0.21940594421151D-07 3 16 3 4 0.65032357226169D+00 -0.35819906570914D-07 1 17 3 4 0.57842585428575D+00 0.65392177609813D-03 2 17 3 4 0.52686513852283D+00 0.25246145760410D-03 3 17 3 4 0.44381121288779D+00 -0.16889012571133D-02 1 18 3 4 -0.44153493756746D+00 0.14934099434891D-07 2 18 3 4 -0.71923361310957D+00 0.16315794910169D-07 3 18 3 4 0.44958778618860D-01 -0.18600454899332D-07 1 19 3 4 0.44153493756748D+00 -0.14934099261268D-07 2 19 3 4 0.71923361310964D+00 -0.16315794629699D-07 3 19 3 4 0.44958778618761D-01 -0.18600456303261D-07 1 20 3 4 -0.57842585428576D+00 -0.65392177609878D-03 2 20 3 4 -0.52686513852283D+00 -0.25246145760424D-03 3 20 3 4 0.44381121288776D+00 -0.16889012571153D-02 1 1 1 5 0.61782658536660D+00 0.95168082387859D-03 2 1 1 5 -0.22879020495671D-01 0.55249529946962D-02 3 1 1 5 -0.20481178733484D+00 -0.27271301515583D-02 1 2 1 5 0.61782658536665D+00 0.95168082388590D-03 2 2 1 5 -0.22879020495669D-01 0.55249529946974D-02 3 2 1 5 -0.20481178733484D+00 -0.27271301515580D-02 1 3 1 5 0.14196865593336D-01 -0.30871515121207D-09 2 3 1 5 -0.57844668973442D+00 -0.42020367857308D-08 3 3 1 5 -0.50120406576589D+01 0.78590532211806D-02 1 4 1 5 -0.14196865593351D-01 0.30870336709064D-09 2 4 1 5 0.57844668973436D+00 0.42020349577506D-08 3 4 1 5 0.50120406576590D+01 -0.78590532211787D-02 1 5 1 5 0.18910117189205D+02 0.00000000000000D+00 2 5 1 5 0.34210003123047D+00 -0.75449475546075D-07 3 5 1 5 -0.27892469889627D+00 -0.35366111672092D-07 1 6 1 5 0.16845704064195D+01 0.00000000000000D+00 2 6 1 5 -0.18944397192879D+00 -0.82136231039716D-10 3 6 1 5 -0.48105850063564D+01 -0.36105220941019D-08 1 7 1 5 -0.88511358749813D-15 0.18385237170166D-07 2 7 1 5 0.16248635278159D+02 -0.86990592572845D-08 3 7 1 5 0.68674811068094D+00 -0.45624650982181D-08 1 8 1 5 0.25722598854539D-14 -0.18127730597390D-09 2 8 1 5 0.94298622900392D+00 -0.30997457684428D-08 3 8 1 5 0.32035791511017D+00 0.43831931650114D-08 1 9 1 5 -0.21881152116258D+01 0.13825947814848D+00 2 9 1 5 0.77559806050584D-02 0.15898773107516D-01 3 9 1 5 0.49555145897725D+00 -0.27340856142325D+00 1 10 1 5 0.21881152116255D+01 -0.13825947814847D+00 2 10 1 5 -0.77559806050909D-02 -0.15898773107516D-01 3 10 1 5 -0.49555145897733D+00 0.27340856142323D+00 1 11 1 5 0.21341603871672D-02 -0.19838940221509D-08 2 11 1 5 -0.19145017835138D+01 0.17698233234609D-08 3 11 1 5 -0.27731420957055D+00 0.39615690911785D-02 1 12 1 5 -0.21341603871757D-02 0.19838939508972D-08 2 12 1 5 0.19145017835138D+01 -0.17698224126078D-08 3 12 1 5 0.27731420957065D+00 -0.39615690911810D-02 1 13 1 5 0.23453152791021D+01 0.16678481292263D-01 2 13 1 5 -0.21977973795745D+01 0.11959758316339D-01 3 13 1 5 -0.90732738122318D+00 0.15660185344886D-01 1 14 1 5 -0.23453152791019D+01 -0.16678481292284D-01 2 14 1 5 0.21977973795746D+01 -0.11959758316360D-01 3 14 1 5 0.90732738122282D+00 -0.15660185344878D-01 1 15 1 5 -0.39544003264495D+00 0.10151579064273D-01 2 15 1 5 0.38309205658961D+00 0.35535921356545D-02 3 15 1 5 0.49487343110552D-01 -0.14477814241088D-01 1 16 1 5 0.39544003264495D+00 -0.10151579064275D-01 2 16 1 5 -0.38309205658962D+00 -0.35535921356556D-02 3 16 1 5 -0.49487343110544D-01 0.14477814241089D-01 1 17 1 5 0.10827856698304D+01 0.98483646079537D-02 2 17 1 5 0.12608295382431D+01 -0.12204994699724D-01 3 17 1 5 -0.96407854234453D+00 0.86948716823837D-02 1 18 1 5 -0.10827856698305D+01 -0.98483646079585D-02 2 18 1 5 -0.12608295382428D+01 0.12204994699749D-01 3 18 1 5 0.96407854234447D+00 -0.86948716823767D-02 1 19 1 5 -0.11020997013611D+00 0.11188134076724D-01 2 19 1 5 -0.89173255839761D-01 -0.26609503360623D-01 3 19 1 5 0.65420891526019D-01 -0.32434875877203D-01 1 20 1 5 0.11020997013614D+00 -0.11188134076723D-01 2 20 1 5 0.89173255839741D-01 0.26609503360625D-01 3 20 1 5 -0.65420891526005D-01 0.32434875877202D-01 1 1 2 5 0.27412098593956D+00 0.35729222940309D-02 2 1 2 5 -0.70363270083289D+00 0.46148053164145D-02 3 1 2 5 0.53915352609181D+01 0.24777809343411D-02 1 2 2 5 0.27412098593956D+00 0.35729222940322D-02 2 2 2 5 -0.70363270083295D+00 0.46148053163989D-02 3 2 2 5 0.53915352609182D+01 0.24777809343322D-02 1 3 2 5 -0.43091913283082D+00 -0.11657338036154D-08 2 3 2 5 -0.58296009246914D+00 -0.45000859335590D-08 3 3 2 5 -0.28770540691924D+00 0.31864594806055D-02 1 4 2 5 0.43091913283076D+00 0.11657319756352D-08 2 4 2 5 0.58296009246921D+00 0.45000907301570D-08 3 4 2 5 0.28770540691923D+00 -0.31864594806068D-02 1 5 2 5 0.34208830822792D+00 0.82495495801611D-07 2 5 2 5 0.19661052058775D+02 0.00000000000000D+00 3 5 2 5 -0.28812580498043D+01 0.28363896075741D-06 1 6 2 5 -0.18944397192879D+00 0.82136231039716D-10 2 6 2 5 0.10315332826134D+01 0.00000000000000D+00 3 6 2 5 0.12411420792622D+01 -0.19554323336561D-07 1 7 2 5 0.16248635278159D+02 0.86990592572845D-08 2 7 2 5 0.32957817931870D-14 0.66652598890291D-08 3 7 2 5 0.44862169353480D+01 0.63662961712403D-08 1 8 2 5 0.94298645666080D+00 0.32828542899729D-08 2 8 2 5 0.35557553587071D-14 -0.10608730643894D-08 3 8 2 5 0.50687966608252D-01 -0.10490662013178D-08 1 9 2 5 -0.96702763266685D-02 0.15615448338125D-01 2 9 2 5 -0.18849522389694D+01 0.18373904947083D+00 3 9 2 5 -0.10823834313310D+00 0.85902488057707D-01 1 10 2 5 0.96702763266356D-02 -0.15615448338125D-01 2 10 2 5 0.18849522389690D+01 -0.18373904947081D+00 3 10 2 5 0.10823834313289D+00 -0.85902488057702D-01 1 11 2 5 -0.19102253674039D+01 0.48441103890342D-08 2 11 2 5 0.87508242795246D-01 -0.41774358005991D-08 3 11 2 5 -0.41366878460155D+00 0.81464236242487D-02 1 12 2 5 0.19102253674039D+01 -0.48441094781812D-08 2 12 2 5 -0.87508242795253D-01 0.41774349511540D-08 3 12 2 5 0.41366878460157D+00 -0.81464236242502D-02 1 13 2 5 -0.98466830470983D+00 0.58600208529767D-02 2 13 2 5 0.12873711358941D+01 0.13777757604804D-02 3 13 2 5 -0.13162330433725D+01 0.79774179397017D-02 1 14 2 5 0.98466830470991D+00 -0.58600208529985D-02 2 14 2 5 -0.12873711358942D+01 -0.13777757604857D-02 3 14 2 5 0.13162330433723D+01 -0.79774179396939D-02 1 15 2 5 0.14944663858130D+00 0.46910145595009D-02 2 15 2 5 -0.49139147588205D-01 -0.25472336714017D-02 3 15 2 5 -0.51299136639815D+00 -0.68963283496949D-02 1 16 2 5 -0.14944663858132D+00 -0.46910145595019D-02 2 16 2 5 0.49139147588194D-01 0.25472336714024D-02 3 16 2 5 0.51299136639816D+00 0.68963283496954D-02 1 17 2 5 0.24617870014946D+01 -0.81223136744578D-02 2 17 2 5 0.23175373615651D+01 0.57779753515352D-02 3 17 2 5 0.12447197071311D+01 -0.19064598607915D-01 1 18 2 5 -0.24617870014943D+01 0.81223136744821D-02 2 18 2 5 -0.23175373615653D+01 -0.57779753515513D-02 3 18 2 5 -0.12447197071310D+01 0.19064598607904D-01 1 19 2 5 -0.35913944563347D+00 -0.20901073508292D-01 2 19 2 5 -0.27797133824927D+00 0.10194209073261D-01 3 19 2 5 0.29788044684198D+00 0.29759930187467D-01 1 20 2 5 0.35913944563345D+00 0.20901073508293D-01 2 20 2 5 0.27797133824928D+00 -0.10194209073261D-01 3 20 2 5 -0.29788044684201D+00 -0.29759930187468D-01 1 1 3 5 0.22581630858633D+00 0.20307765000361D-02 2 1 3 5 0.52528265821401D+01 -0.18911704112528D-01 3 1 3 5 -0.65892105666508D+00 -0.36356041041527D-03 1 2 3 5 0.22581630858633D+00 0.20307765000363D-02 2 2 3 5 0.52528265821402D+01 -0.18911704112537D-01 3 2 3 5 -0.65892105666511D+00 -0.36356041041854D-03 1 3 3 5 -0.53077092998001D+01 -0.19568089929848D-07 2 3 3 5 -0.15477292984609D+00 0.33495925360486D-08 3 3 3 5 0.13477910186055D+01 0.13062225378956D-02 1 4 3 5 0.53077092998002D+01 0.19568091783379D-07 2 4 3 5 0.15477292984608D+00 -0.33495937534032D-08 3 4 3 5 -0.13477910186055D+01 -0.13062225379020D-02 1 5 3 5 -0.27891634472950D+00 0.69645035864310D-07 2 5 3 5 -0.28812774441778D+01 -0.31642090624636D-06 3 5 3 5 0.39343679974651D+02 0.00000000000000D+00 1 6 3 5 0.48105850063564D+01 -0.36105220941019D-08 2 6 3 5 -0.12411420792622D+01 -0.19554323336561D-07 3 6 3 5 -0.30271317074665D+02 0.00000000000000D+00 1 7 3 5 0.68674811068094D+00 0.45624650982181D-08 2 7 3 5 -0.44862169353480D+01 0.63662961712403D-08 3 7 3 5 -0.19207886676493D-15 0.52820338054762D-07 1 8 3 5 -0.32035677858130D+00 0.48400273590566D-08 2 8 3 5 0.50691514744931D-01 0.41347375083704D-09 3 8 3 5 0.69592719321920D-15 -0.50187004690180D-09 1 9 3 5 -0.20898068340127D+01 -0.11814891006816D+00 2 9 3 5 0.48849797486998D+00 0.30452641988901D-01 3 9 3 5 -0.83666971121852D+00 -0.83595200946110D+00 1 10 3 5 0.20898068340126D+01 0.11814891006814D+00 2 10 3 5 -0.48849797487019D+00 -0.30452641988896D-01 3 10 3 5 0.83666971121909D+00 0.83595200946103D+00 1 11 3 5 0.19409225590814D-01 0.20459768933689D-09 2 11 3 5 -0.93495707286655D-01 0.56187789554180D-08 3 11 3 5 0.15132431734958D+00 0.16123029826871D-02 1 12 3 5 -0.19409225590715D-01 -0.20460024159510D-09 2 12 3 5 0.93495707286669D-01 -0.56187804271151D-08 3 12 3 5 -0.15132431734954D+00 -0.16123029826886D-02 1 13 3 5 0.11000545595058D+00 0.70034984234107D-01 2 13 3 5 0.37608143009031D+00 0.65008013740986D-01 3 13 3 5 0.32211264804366D+01 -0.75245839031040D-02 1 14 3 5 -0.11000545595093D+00 -0.70034984234100D-01 2 14 3 5 -0.37608143009050D+00 -0.65008013740978D-01 3 14 3 5 -0.32211264804368D+01 0.75245839031272D-02 1 15 3 5 -0.73236565614060D+00 -0.22460210510022D-02 2 15 3 5 -0.62837224393659D-02 -0.45528123343564D-02 3 15 3 5 0.28377039333194D+01 -0.13288858565879D-01 1 16 3 5 0.73236565614061D+00 0.22460210510033D-02 2 16 3 5 0.62837224393766D-02 0.45528123343568D-02 3 16 3 5 -0.28377039333194D+01 0.13288858565875D-01 1 17 3 5 0.16328383843283D+00 0.62236888688054D-01 2 17 3 5 -0.65422004179177D+00 -0.85498412820511D-01 3 17 3 5 0.29576833739170D+01 -0.87886963382329D-03 1 18 3 5 -0.16328383843289D+00 -0.62236888688047D-01 2 18 3 5 0.65422004179181D+00 0.85498412820500D-01 3 18 3 5 -0.29576833739167D+01 0.87886963384430D-03 1 19 3 5 -0.37343963415799D+00 -0.15954043812434D-01 2 19 3 5 0.20766913822667D+00 0.94043432756836D-02 3 19 3 5 0.27182122046449D+01 -0.31902639594482D-01 1 20 3 5 0.37343963415800D+00 0.15954043812433D-01 2 20 3 5 -0.20766913822670D+00 -0.94043432756845D-02 3 20 3 5 -0.27182122046449D+01 0.31902639594479D-01 1 1 1 6 0.61782658536659D+00 0.95168082388540D-03 2 1 1 6 -0.22879020495667D-01 0.55249529946982D-02 3 1 1 6 0.20481178733484D+00 0.27271301515582D-02 1 2 1 6 0.61782658536665D+00 0.95168082388736D-03 2 2 1 6 -0.22879020495670D-01 0.55249529946954D-02 3 2 1 6 0.20481178733484D+00 0.27271301515581D-02 1 3 1 6 0.14196865593336D-01 -0.30871397895346D-09 2 3 1 6 -0.57844668973440D+00 -0.42020326852062D-08 3 3 1 6 0.50120406576589D+01 -0.78590532211802D-02 1 4 1 6 -0.14196865593391D-01 0.30870422452000D-09 2 4 1 6 0.57844668973437D+00 0.42020324306596D-08 3 4 1 6 -0.50120406576588D+01 0.78590532211793D-02 1 5 1 6 0.16845704064195D+01 0.00000000000000D+00 2 5 1 6 -0.18944397192879D+00 -0.82136231039716D-10 3 5 1 6 0.48105850063564D+01 0.36105220941019D-08 1 6 1 6 0.18910117189205D+02 0.00000000000000D+00 2 6 1 6 0.34210003123052D+00 -0.75449475546075D-07 3 6 1 6 0.27892469889648D+00 0.35366111672092D-07 1 7 1 6 0.25722446424669D-14 -0.18127730597390D-09 2 7 1 6 0.94298622900392D+00 -0.30997457684428D-08 3 7 1 6 -0.32035791511017D+00 -0.43831931650114D-08 1 8 1 6 -0.88511367404066D-15 0.18385237170166D-07 2 8 1 6 0.16248635278159D+02 -0.86990592572845D-08 3 8 1 6 -0.68674811068094D+00 0.45624650982181D-08 1 9 1 6 -0.21881152116259D+01 0.13825947814848D+00 2 9 1 6 0.77559806050638D-02 0.15898773107516D-01 3 9 1 6 -0.49555145897726D+00 0.27340856142325D+00 1 10 1 6 0.21881152116255D+01 -0.13825947814847D+00 2 10 1 6 -0.77559806050651D-02 -0.15898773107516D-01 3 10 1 6 0.49555145897749D+00 -0.27340856142323D+00 1 11 1 6 0.21341603871497D-02 -0.19838948460767D-08 2 11 1 6 -0.19145017835138D+01 0.17698230215342D-08 3 11 1 6 0.27731420957053D+00 -0.39615690911787D-02 1 12 1 6 -0.21341603871787D-02 0.19838942892434D-08 2 12 1 6 0.19145017835138D+01 -0.17698225883176D-08 3 12 1 6 -0.27731420957065D+00 0.39615690911808D-02 1 13 1 6 0.39544003264494D+00 -0.10151579064274D-01 2 13 1 6 -0.38309205658963D+00 -0.35535921356563D-02 3 13 1 6 0.49487343110543D-01 -0.14477814241088D-01 1 14 1 6 -0.39544003264495D+00 0.10151579064273D-01 2 14 1 6 0.38309205658961D+00 0.35535921356545D-02 3 14 1 6 -0.49487343110576D-01 0.14477814241088D-01 1 15 1 6 -0.23453152791019D+01 -0.16678481292282D-01 2 15 1 6 0.21977973795746D+01 -0.11959758316359D-01 3 15 1 6 -0.90732738122281D+00 0.15660185344876D-01 1 16 1 6 0.23453152791021D+01 0.16678481292263D-01 2 16 1 6 -0.21977973795744D+01 0.11959758316338D-01 3 16 1 6 0.90732738122317D+00 -0.15660185344887D-01 1 17 1 6 0.11020997013613D+00 -0.11188134076724D-01 2 17 1 6 0.89173255839755D-01 0.26609503360624D-01 3 17 1 6 0.65420891526005D-01 -0.32434875877203D-01 1 18 1 6 -0.11020997013611D+00 0.11188134076725D-01 2 18 1 6 -0.89173255839754D-01 -0.26609503360624D-01 3 18 1 6 -0.65420891526026D-01 0.32434875877202D-01 1 19 1 6 -0.10827856698304D+01 -0.98483646079588D-02 2 19 1 6 -0.12608295382428D+01 0.12204994699750D-01 3 19 1 6 -0.96407854234447D+00 0.86948716823787D-02 1 20 1 6 0.10827856698304D+01 0.98483646079542D-02 2 20 1 6 0.12608295382429D+01 -0.12204994699725D-01 3 20 1 6 0.96407854234451D+00 -0.86948716823848D-02 1 1 2 6 0.27412098593956D+00 0.35729222940330D-02 2 1 2 6 -0.70363270083289D+00 0.46148053164138D-02 3 1 2 6 -0.53915352609181D+01 -0.24777809343414D-02 1 2 2 6 0.27412098593956D+00 0.35729222940302D-02 2 2 2 6 -0.70363270083297D+00 0.46148053164054D-02 3 2 2 6 -0.53915352609180D+01 -0.24777809343322D-02 1 3 2 6 -0.43091913283080D+00 -0.11657297031230D-08 2 3 2 6 -0.58296009246914D+00 -0.45000871802561D-08 3 3 2 6 0.28770540691924D+00 -0.31864594806055D-02 1 4 2 6 0.43091913283077D+00 0.11657294485764D-08 2 4 2 6 0.58296009246924D+00 0.45000902611731D-08 3 4 2 6 -0.28770540691922D+00 0.31864594806065D-02 1 5 2 6 -0.18944397192879D+00 0.82136231039716D-10 2 5 2 6 0.10315332826134D+01 0.00000000000000D+00 3 5 2 6 -0.12411420792622D+01 0.19554323336561D-07 1 6 2 6 0.34208830822797D+00 0.82495495801611D-07 2 6 2 6 0.19661052058775D+02 0.00000000000000D+00 3 6 2 6 0.28812580498042D+01 -0.28363896075741D-06 1 7 2 6 0.94298645666080D+00 0.32828542899729D-08 2 7 2 6 0.35557515510138D-14 -0.10608730643894D-08 3 7 2 6 -0.50687966608251D-01 0.10490662013178D-08 1 8 2 6 0.16248635278159D+02 0.86990592572845D-08 2 8 2 6 0.32957817857437D-14 0.66652598890291D-08 3 8 2 6 -0.44862169353480D+01 -0.63662961712403D-08 1 9 2 6 -0.96702763266632D-02 0.15615448338125D-01 2 9 2 6 -0.18849522389693D+01 0.18373904947083D+00 3 9 2 6 0.10823834313309D+00 -0.85902488057709D-01 1 10 2 6 0.96702763266623D-02 -0.15615448338125D-01 2 10 2 6 0.18849522389692D+01 -0.18373904947081D+00 3 10 2 6 -0.10823834313292D+00 0.85902488057704D-01 1 11 2 6 -0.19102253674039D+01 0.48441100871528D-08 2 11 2 6 0.87508242795229D-01 -0.41774365331175D-08 3 11 2 6 0.41366878460158D+00 -0.81464236242485D-02 1 12 2 6 0.19102253674039D+01 -0.48441096539362D-08 2 12 2 6 -0.87508242795253D-01 0.41774346047377D-08 3 12 2 6 -0.41366878460157D+00 0.81464236242496D-02 1 13 2 6 -0.14944663858132D+00 -0.46910145595026D-02 2 13 2 6 0.49139147588201D-01 0.25472336714022D-02 3 13 2 6 -0.51299136639816D+00 -0.68963283496951D-02 1 14 2 6 0.14944663858130D+00 0.46910145595009D-02 2 14 2 6 -0.49139147588210D-01 -0.25472336713988D-02 3 14 2 6 0.51299136639813D+00 0.68963283496942D-02 1 15 2 6 0.98466830470997D+00 -0.58600208529971D-02 2 15 2 6 -0.12873711358942D+01 -0.13777757604835D-02 3 15 2 6 -0.13162330433723D+01 0.79774179396952D-02 1 16 2 6 -0.98466830470980D+00 0.58600208529757D-02 2 16 2 6 0.12873711358941D+01 0.13777757604811D-02 3 16 2 6 0.13162330433725D+01 -0.79774179397016D-02 1 17 2 6 0.35913944563346D+00 0.20901073508293D-01 2 17 2 6 0.27797133824928D+00 -0.10194209073259D-01 3 17 2 6 0.29788044684201D+00 0.29759930187468D-01 1 18 2 6 -0.35913944563346D+00 -0.20901073508293D-01 2 18 2 6 -0.27797133824927D+00 0.10194209073260D-01 3 18 2 6 -0.29788044684198D+00 -0.29759930187468D-01 1 19 2 6 -0.24617870014944D+01 0.81223136744832D-02 2 19 2 6 -0.23175373615653D+01 -0.57779753515504D-02 3 19 2 6 0.12447197071310D+01 -0.19064598607904D-01 1 20 2 6 0.24617870014945D+01 -0.81223136744581D-02 2 20 2 6 0.23175373615651D+01 0.57779753515342D-02 3 20 2 6 -0.12447197071311D+01 0.19064598607915D-01 1 1 3 6 -0.22581630858633D+00 -0.20307765000361D-02 2 1 3 6 -0.52528265821401D+01 0.18911704112528D-01 3 1 3 6 -0.65892105666508D+00 -0.36356041041486D-03 1 2 3 6 -0.22581630858634D+00 -0.20307765000362D-02 2 2 3 6 -0.52528265821401D+01 0.18911704112537D-01 3 2 3 6 -0.65892105666514D+00 -0.36356041041859D-03 1 3 3 6 0.53077092998001D+01 0.19568090308344D-07 2 3 3 6 0.15477292984609D+00 -0.33495924473225D-08 3 3 3 6 0.13477910186055D+01 0.13062225378951D-02 1 4 3 6 -0.53077092998001D+01 -0.19568091232906D-07 2 4 3 6 -0.15477292984607D+00 0.33495935158560D-08 3 4 3 6 -0.13477910186056D+01 -0.13062225379023D-02 1 5 3 6 -0.48105850063564D+01 0.36105220941019D-08 2 5 3 6 0.12411420792622D+01 0.19554323336561D-07 3 5 3 6 -0.30271317074665D+02 0.00000000000000D+00 1 6 3 6 0.27891634472972D+00 -0.69645035864310D-07 2 6 3 6 0.28812774441778D+01 0.31642090624636D-06 3 6 3 6 0.39343679974651D+02 0.00000000000000D+00 1 7 3 6 0.32035677858131D+00 -0.48400273590566D-08 2 7 3 6 -0.50691514744930D-01 -0.41347375083704D-09 3 7 3 6 0.69594244097547D-15 -0.50187004690180D-09 1 8 3 6 -0.68674811068094D+00 -0.45624650982181D-08 2 8 3 6 0.44862169353480D+01 -0.63662961712403D-08 3 8 3 6 -0.19207901751644D-15 0.52820338054762D-07 1 9 3 6 0.20898068340127D+01 0.11814891006816D+00 2 9 3 6 -0.48849797486999D+00 -0.30452641988902D-01 3 9 3 6 -0.83666971121841D+00 -0.83595200946110D+00 1 10 3 6 -0.20898068340124D+01 -0.11814891006814D+00 2 10 3 6 0.48849797487015D+00 0.30452641988898D-01 3 10 3 6 0.83666971121897D+00 0.83595200946103D+00 1 11 3 6 -0.19409225590830D-01 -0.20459797605248D-09 2 11 3 6 0.93495707286680D-01 -0.56187787593039D-08 3 11 3 6 0.15132431734953D+00 0.16123029826876D-02 1 12 3 6 0.19409225590718D-01 0.20460004553646D-09 2 12 3 6 -0.93495707286667D-01 0.56187798646344D-08 3 12 3 6 -0.15132431734954D+00 -0.16123029826879D-02 1 13 3 6 -0.73236565614061D+00 -0.22460210510026D-02 2 13 3 6 -0.62837224393801D-02 -0.45528123343565D-02 3 13 3 6 -0.28377039333194D+01 0.13288858565875D-01 1 14 3 6 0.73236565614058D+00 0.22460210510024D-02 2 14 3 6 0.62837224393464D-02 0.45528123343556D-02 3 14 3 6 0.28377039333194D+01 -0.13288858565880D-01 1 15 3 6 0.11000545595095D+00 0.70034984234097D-01 2 15 3 6 0.37608143009054D+00 0.65008013740979D-01 3 15 3 6 -0.32211264804368D+01 0.75245839031244D-02 1 16 3 6 -0.11000545595060D+00 -0.70034984234108D-01 2 16 3 6 -0.37608143009032D+00 -0.65008013740986D-01 3 16 3 6 0.32211264804367D+01 -0.75245839031044D-02 1 17 3 6 -0.37343963415800D+00 -0.15954043812434D-01 2 17 3 6 0.20766913822671D+00 0.94043432756847D-02 3 17 3 6 -0.27182122046450D+01 0.31902639594479D-01 1 18 3 6 0.37343963415798D+00 0.15954043812433D-01 2 18 3 6 -0.20766913822667D+00 -0.94043432756844D-02 3 18 3 6 0.27182122046449D+01 -0.31902639594484D-01 1 19 3 6 0.16328383843290D+00 0.62236888688049D-01 2 19 3 6 -0.65422004179184D+00 -0.85498412820500D-01 3 19 3 6 -0.29576833739166D+01 0.87886963384441D-03 1 20 3 6 -0.16328383843285D+00 -0.62236888688055D-01 2 20 3 6 0.65422004179176D+00 0.85498412820510D-01 3 20 3 6 0.29576833739171D+01 -0.87886963382323D-03 1 1 1 7 0.14196865593326D-01 -0.30870219464353D-09 2 1 1 7 0.57844668973428D+00 0.42020364872323D-08 3 1 1 7 0.50120406576588D+01 -0.78590532211649D-02 1 2 1 7 0.14196865593327D-01 -0.30871370905601D-09 2 2 1 7 0.57844668973431D+00 0.42020370291652D-08 3 2 1 7 0.50120406576590D+01 -0.78590532211809D-02 1 3 1 7 -0.61782658536675D+00 -0.95168082387789D-03 2 3 1 7 -0.22879020495658D-01 0.55249529946955D-02 3 3 1 7 -0.20481178733484D+00 -0.27271301515583D-02 1 4 1 7 0.61782658536670D+00 0.95168082388142D-03 2 4 1 7 0.22879020495684D-01 -0.55249529946959D-02 3 4 1 7 0.20481178733484D+00 0.27271301515580D-02 1 5 1 7 -0.88511358749813D-15 -0.18385237170166D-07 2 5 1 7 0.16248635278159D+02 -0.86990592572845D-08 3 5 1 7 0.68674811068094D+00 -0.45624650982181D-08 1 6 1 7 0.25722446424669D-14 0.18127730597390D-09 2 6 1 7 0.94298622900392D+00 -0.30997457684428D-08 3 6 1 7 0.32035791511017D+00 0.43831931650114D-08 1 7 1 7 0.18910117189206D+02 0.00000000000000D+00 2 7 1 7 -0.34210003123041D+00 0.75449475546075D-07 3 7 1 7 0.27892469889665D+00 0.35366111672092D-07 1 8 1 7 0.16845704064195D+01 0.00000000000000D+00 2 8 1 7 0.18944397192879D+00 0.82136231039716D-10 3 8 1 7 0.48105850063564D+01 0.36105220941019D-08 1 9 1 7 -0.21341603871638D-02 0.19838944530665D-08 2 9 1 7 -0.19145017835138D+01 0.17698226190928D-08 3 9 1 7 -0.27731420957066D+00 0.39615690911809D-02 1 10 1 7 0.21341603871660D-02 -0.19838936735703D-08 2 10 1 7 0.19145017835138D+01 -0.17698220551992D-08 3 10 1 7 0.27731420957062D+00 -0.39615690911777D-02 1 11 1 7 -0.21881152116255D+01 0.13825947814848D+00 2 11 1 7 -0.77559806051948D-02 -0.15898773107517D-01 3 11 1 7 -0.49555145897730D+00 0.27340856142325D+00 1 12 1 7 0.21881152116257D+01 -0.13825947814847D+00 2 12 1 7 0.77559806050296D-02 0.15898773107516D-01 3 12 1 7 0.49555145897750D+00 -0.27340856142323D+00 1 13 1 7 -0.10827856698304D+01 -0.98483646079579D-02 2 13 1 7 0.12608295382431D+01 -0.12204994699747D-01 3 13 1 7 -0.96407854234451D+00 0.86948716823776D-02 1 14 1 7 0.10827856698305D+01 0.98483646079548D-02 2 14 1 7 -0.12608295382425D+01 0.12204994699725D-01 3 14 1 7 0.96407854234460D+00 -0.86948716823854D-02 1 15 1 7 0.11020997013612D+00 -0.11188134076723D-01 2 15 1 7 -0.89173255839768D-01 -0.26609503360624D-01 3 15 1 7 0.65420891526024D-01 -0.32434875877203D-01 1 16 1 7 -0.11020997013613D+00 0.11188134076725D-01 2 16 1 7 0.89173255839745D-01 0.26609503360623D-01 3 16 1 7 -0.65420891526010D-01 0.32434875877203D-01 1 17 1 7 0.23453152791022D+01 0.16678481292268D-01 2 17 1 7 0.21977973795744D+01 -0.11959758316337D-01 3 17 1 7 0.90732738122325D+00 -0.15660185344887D-01 1 18 1 7 -0.23453152791020D+01 -0.16678481292281D-01 2 18 1 7 -0.21977973795744D+01 0.11959758316361D-01 3 18 1 7 -0.90732738122287D+00 0.15660185344876D-01 1 19 1 7 -0.39544003264493D+00 0.10151579064274D-01 2 19 1 7 -0.38309205658961D+00 -0.35535921356553D-02 3 19 1 7 -0.49487343110555D-01 0.14477814241087D-01 1 20 1 7 0.39544003264493D+00 -0.10151579064272D-01 2 20 1 7 0.38309205658961D+00 0.35535921356569D-02 3 20 1 7 0.49487343110530D-01 -0.14477814241088D-01 1 1 2 7 0.43091913283068D+00 0.11657335051805D-08 2 1 2 7 -0.58296009246916D+00 -0.45000906476477D-08 3 1 2 7 -0.28770540691925D+00 0.31864594806069D-02 1 2 2 7 0.43091913283071D+00 0.11657340471676D-08 2 2 2 7 -0.58296009246920D+00 -0.45000871991600D-08 3 2 2 7 -0.28770540691925D+00 0.31864594806053D-02 1 3 2 7 0.27412098593957D+00 0.35729222940303D-02 2 3 2 7 0.70363270083293D+00 -0.46148053164156D-02 3 3 2 7 -0.53915352609180D+01 -0.24777809343273D-02 1 4 2 7 -0.27412098593954D+00 -0.35729222940307D-02 2 4 2 7 -0.70363270083298D+00 0.46148053164093D-02 3 4 2 7 0.53915352609181D+01 0.24777809343320D-02 1 5 2 7 0.16248635278159D+02 0.86990592572845D-08 2 5 2 7 0.32957817931870D-14 -0.66652598890291D-08 3 5 2 7 -0.44862169353480D+01 -0.63662961712403D-08 1 6 2 7 0.94298645666080D+00 0.32828542899729D-08 2 6 2 7 0.35557515510138D-14 0.10608730643894D-08 3 6 2 7 -0.50687966608251D-01 0.10490662013178D-08 1 7 2 7 -0.34208830822786D+00 -0.82495495801611D-07 2 7 2 7 0.19661052058775D+02 0.00000000000000D+00 3 7 2 7 -0.28812580498052D+01 0.28363896075741D-06 1 8 2 7 0.18944397192879D+00 -0.82136231039716D-10 2 8 2 7 0.10315332826134D+01 0.00000000000000D+00 3 8 2 7 0.12411420792622D+01 -0.19554323336561D-07 1 9 2 7 -0.19102253674039D+01 0.48441096846821D-08 2 9 2 7 -0.87508242795244D-01 0.41774350182596D-08 3 9 2 7 0.41366878460152D+00 -0.81464236242488D-02 1 10 2 7 0.19102253674038D+01 -0.48441091207885D-08 2 10 2 7 0.87508242795242D-01 -0.41774353671456D-08 3 10 2 7 -0.41366878460155D+00 0.81464236242498D-02 1 11 2 7 0.96702763265317D-02 -0.15615448338126D-01 2 11 2 7 -0.18849522389691D+01 0.18373904947083D+00 3 11 2 7 -0.10823834313226D+00 0.85902488057708D-01 1 12 2 7 -0.96702763266974D-02 0.15615448338125D-01 2 12 2 7 0.18849522389694D+01 -0.18373904947081D+00 3 12 2 7 0.10823834313322D+00 -0.85902488057703D-01 1 13 2 7 0.24617870014946D+01 -0.81223136744807D-02 2 13 2 7 -0.23175373615651D+01 -0.57779753515532D-02 3 13 2 7 -0.12447197071311D+01 0.19064598607905D-01 1 14 2 7 -0.24617870014940D+01 0.81223136744588D-02 2 14 2 7 0.23175373615654D+01 0.57779753515306D-02 3 14 2 7 0.12447197071312D+01 -0.19064598607914D-01 1 15 2 7 -0.35913944563347D+00 -0.20901073508293D-01 2 15 2 7 0.27797133824926D+00 -0.10194209073261D-01 3 15 2 7 -0.29788044684199D+00 -0.29759930187469D-01 1 16 2 7 0.35913944563345D+00 0.20901073508291D-01 2 16 2 7 -0.27797133824927D+00 0.10194209073260D-01 3 16 2 7 0.29788044684201D+00 0.29759930187468D-01 1 17 2 7 0.98466830470974D+00 -0.58600208529748D-02 2 17 2 7 0.12873711358940D+01 0.13777757604806D-02 3 17 2 7 -0.13162330433725D+01 0.79774179397016D-02 1 18 2 7 -0.98466830470977D+00 0.58600208529990D-02 2 18 2 7 -0.12873711358942D+01 -0.13777757604852D-02 3 18 2 7 0.13162330433723D+01 -0.79774179396953D-02 1 19 2 7 -0.14944663858130D+00 -0.46910145595017D-02 2 19 2 7 -0.49139147588201D-01 -0.25472336714032D-02 3 19 2 7 -0.51299136639815D+00 -0.68963283496959D-02 1 20 2 7 0.14944663858130D+00 0.46910145595033D-02 2 20 2 7 0.49139147588191D-01 0.25472336714021D-02 3 20 2 7 0.51299136639817D+00 0.68963283496957D-02 1 1 3 7 0.53077092998001D+01 0.19568105539748D-07 2 1 3 7 -0.15477292984609D+00 0.33495939027174D-08 3 1 3 7 0.13477910186055D+01 0.13062225379033D-02 1 2 3 7 0.53077092998002D+01 0.19568089598291D-07 2 2 3 7 -0.15477292984610D+00 0.33495923062002D-08 3 2 3 7 0.13477910186055D+01 0.13062225378949D-02 1 3 3 7 0.22581630858634D+00 0.20307765000360D-02 2 3 3 7 -0.52528265821401D+01 0.18911704112542D-01 3 3 3 7 0.65892105666530D+00 0.36356041041137D-03 1 4 3 7 -0.22581630858634D+00 -0.20307765000364D-02 2 4 3 7 0.52528265821402D+01 -0.18911704112537D-01 3 4 3 7 -0.65892105666515D+00 -0.36356041041831D-03 1 5 3 7 0.68674811068094D+00 0.45624650982181D-08 2 5 3 7 0.44862169353480D+01 -0.63662961712403D-08 3 5 3 7 -0.19207886676493D-15 -0.52820338054762D-07 1 6 3 7 -0.32035677858130D+00 0.48400273590566D-08 2 6 3 7 -0.50691514744930D-01 -0.41347375083704D-09 3 6 3 7 0.69594244097547D-15 0.50187004690180D-09 1 7 3 7 0.27891634472988D+00 -0.69645035864310D-07 2 7 3 7 -0.28812774441787D+01 -0.31642090624636D-06 3 7 3 7 0.39343679974651D+02 0.00000000000000D+00 1 8 3 7 -0.48105850063564D+01 0.36105220941019D-08 2 8 3 7 -0.12411420792622D+01 -0.19554323336561D-07 3 8 3 7 -0.30271317074665D+02 0.00000000000000D+00 1 9 3 7 0.19409225590699D-01 0.20460016631893D-09 2 9 3 7 0.93495707286623D-01 -0.56187790708039D-08 3 9 3 7 -0.15132431734954D+00 -0.16123029826879D-02 1 10 3 7 -0.19409225590748D-01 -0.20459693165941D-09 2 10 3 7 -0.93495707286655D-01 0.56187800672592D-08 3 10 3 7 0.15132431734952D+00 0.16123029826878D-02 1 11 3 7 0.20898068340126D+01 0.11814891006816D+00 2 11 3 7 0.48849797487081D+00 0.30452641988901D-01 3 11 3 7 -0.83666971121920D+00 -0.83595200946109D+00 1 12 3 7 -0.20898068340124D+01 -0.11814891006814D+00 2 12 3 7 -0.48849797486986D+00 -0.30452641988897D-01 3 12 3 7 0.83666971121880D+00 0.83595200946103D+00 1 13 3 7 0.16328383843285D+00 0.62236888688048D-01 2 13 3 7 0.65422004179177D+00 0.85498412820500D-01 3 13 3 7 -0.29576833739170D+01 0.87886963384547D-03 1 14 3 7 -0.16328383843277D+00 -0.62236888688056D-01 2 14 3 7 -0.65422004179167D+00 -0.85498412820509D-01 3 14 3 7 0.29576833739164D+01 -0.87886963382234D-03 1 15 3 7 -0.37343963415799D+00 -0.15954043812434D-01 2 15 3 7 -0.20766913822668D+00 -0.94043432756857D-02 3 15 3 7 -0.27182122046448D+01 0.31902639594479D-01 1 16 3 7 0.37343963415800D+00 0.15954043812434D-01 2 16 3 7 0.20766913822670D+00 0.94043432756845D-02 3 16 3 7 0.27182122046449D+01 -0.31902639594482D-01 1 17 3 7 -0.11000545595052D+00 -0.70034984234108D-01 2 17 3 7 0.37608143009030D+00 0.65008013740986D-01 3 17 3 7 0.32211264804365D+01 -0.75245839031051D-02 1 18 3 7 0.11000545595090D+00 0.70034984234098D-01 2 18 3 7 -0.37608143009049D+00 -0.65008013740979D-01 3 18 3 7 -0.32211264804366D+01 0.75245839031268D-02 1 19 3 7 0.73236565614060D+00 0.22460210510010D-02 2 19 3 7 -0.62837224393748D-02 -0.45528123343574D-02 3 19 3 7 0.28377039333194D+01 -0.13288858565878D-01 1 20 3 7 -0.73236565614063D+00 -0.22460210510024D-02 2 20 3 7 0.62837224393899D-02 0.45528123343571D-02 3 20 3 7 -0.28377039333194D+01 0.13288858565876D-01 1 1 1 8 0.14196865593327D-01 -0.30870213139259D-09 2 1 1 8 0.57844668973426D+00 0.42020414930337D-08 3 1 1 8 -0.50120406576589D+01 0.78590532211655D-02 1 2 1 8 0.14196865593314D-01 -0.30871457182346D-09 2 2 1 8 0.57844668973431D+00 0.42020355775091D-08 3 2 1 8 -0.50120406576589D+01 0.78590532211802D-02 1 3 1 8 -0.61782658536672D+00 -0.95168082388302D-03 2 3 1 8 -0.22879020495655D-01 0.55249529946959D-02 3 3 1 8 0.20481178733484D+00 0.27271301515586D-02 1 4 1 8 0.61782658536670D+00 0.95168082388116D-03 2 4 1 8 0.22879020495687D-01 -0.55249529946956D-02 3 4 1 8 -0.20481178733483D+00 -0.27271301515582D-02 1 5 1 8 0.25722598854539D-14 0.18127730597390D-09 2 5 1 8 0.94298622900392D+00 -0.30997457684428D-08 3 5 1 8 -0.32035791511017D+00 -0.43831931650114D-08 1 6 1 8 -0.88511367404066D-15 -0.18385237170166D-07 2 6 1 8 0.16248635278159D+02 -0.86990592572845D-08 3 6 1 8 -0.68674811068094D+00 0.45624650982181D-08 1 7 1 8 0.16845704064195D+01 0.00000000000000D+00 2 7 1 8 0.18944397192879D+00 0.82136231039716D-10 3 7 1 8 -0.48105850063564D+01 -0.36105220941019D-08 1 8 1 8 0.18910117189205D+02 0.00000000000000D+00 2 8 1 8 -0.34210003123032D+00 0.75449475546075D-07 3 8 1 8 -0.27892469889685D+00 -0.35366111672092D-07 1 9 1 8 -0.21341603871603D-02 0.19838944189757D-08 2 9 1 8 -0.19145017835138D+01 0.17698225932028D-08 3 9 1 8 0.27731420957066D+00 -0.39615690911802D-02 1 10 1 8 0.21341603871786D-02 -0.19838935037887D-08 2 10 1 8 0.19145017835138D+01 -0.17698218791838D-08 3 10 1 8 -0.27731420957062D+00 0.39615690911788D-02 1 11 1 8 -0.21881152116255D+01 0.13825947814848D+00 2 11 1 8 -0.77559806051921D-02 -0.15898773107517D-01 3 11 1 8 0.49555145897753D+00 -0.27340856142325D+00 1 12 1 8 0.21881152116258D+01 -0.13825947814847D+00 2 12 1 8 0.77559806050256D-02 0.15898773107516D-01 3 12 1 8 -0.49555145897746D+00 0.27340856142323D+00 1 13 1 8 -0.11020997013614D+00 0.11188134076723D-01 2 13 1 8 0.89173255839745D-01 0.26609503360624D-01 3 13 1 8 0.65420891526005D-01 -0.32434875877202D-01 1 14 1 8 0.11020997013611D+00 -0.11188134076724D-01 2 14 1 8 -0.89173255839761D-01 -0.26609503360624D-01 3 14 1 8 -0.65420891526047D-01 0.32434875877202D-01 1 15 1 8 0.10827856698305D+01 0.98483646079543D-02 2 15 1 8 -0.12608295382426D+01 0.12204994699725D-01 3 15 1 8 -0.96407854234457D+00 0.86948716823838D-02 1 16 1 8 -0.10827856698304D+01 -0.98483646079584D-02 2 16 1 8 0.12608295382430D+01 -0.12204994699748D-01 3 16 1 8 0.96407854234452D+00 -0.86948716823759D-02 1 17 1 8 0.39544003264494D+00 -0.10151579064274D-01 2 17 1 8 0.38309205658961D+00 0.35535921356560D-02 3 17 1 8 -0.49487343110528D-01 0.14477814241087D-01 1 18 1 8 -0.39544003264494D+00 0.10151579064274D-01 2 18 1 8 -0.38309205658961D+00 -0.35535921356547D-02 3 18 1 8 0.49487343110558D-01 -0.14477814241087D-01 1 19 1 8 -0.23453152791020D+01 -0.16678481292282D-01 2 19 1 8 -0.21977973795745D+01 0.11959758316362D-01 3 19 1 8 0.90732738122288D+00 -0.15660185344877D-01 1 20 1 8 0.23453152791022D+01 0.16678481292267D-01 2 20 1 8 0.21977973795743D+01 -0.11959758316337D-01 3 20 1 8 -0.90732738122322D+00 0.15660185344888D-01 1 1 2 8 0.43091913283066D+00 0.11657385109498D-08 2 1 2 8 -0.58296009246915D+00 -0.45000872647521D-08 3 1 2 8 0.28770540691924D+00 -0.31864594806068D-02 1 2 2 8 0.43091913283071D+00 0.11657325954794D-08 2 2 2 8 -0.58296009246920D+00 -0.45000849064867D-08 3 2 2 8 0.28770540691924D+00 -0.31864594806053D-02 1 3 2 8 0.27412098593957D+00 0.35729222940307D-02 2 3 2 8 0.70363270083294D+00 -0.46148053164124D-02 3 3 2 8 0.53915352609181D+01 0.24777809343274D-02 1 4 2 8 -0.27412098593954D+00 -0.35729222940303D-02 2 4 2 8 -0.70363270083299D+00 0.46148053164033D-02 3 4 2 8 -0.53915352609181D+01 -0.24777809343318D-02 1 5 2 8 0.94298645666080D+00 0.32828542899729D-08 2 5 2 8 0.35557553587071D-14 0.10608730643894D-08 3 5 2 8 0.50687966608252D-01 -0.10490662013178D-08 1 6 2 8 0.16248635278159D+02 0.86990592572845D-08 2 6 2 8 0.32957817857437D-14 -0.66652598890291D-08 3 6 2 8 0.44862169353480D+01 0.63662961712403D-08 1 7 2 8 0.18944397192879D+00 -0.82136231039716D-10 2 7 2 8 0.10315332826134D+01 0.00000000000000D+00 3 7 2 8 -0.12411420792622D+01 0.19554323336561D-07 1 8 2 8 -0.34208830822776D+00 -0.82495495801611D-07 2 8 2 8 0.19661052058775D+02 0.00000000000000D+00 3 8 2 8 0.28812580498052D+01 -0.28363896075741D-06 1 9 2 8 -0.19102253674039D+01 0.48441096587469D-08 2 9 2 8 -0.87508242795242D-01 0.41774350123487D-08 3 9 2 8 -0.41366878460152D+00 0.81464236242486D-02 1 10 2 8 0.19102253674039D+01 -0.48441089447279D-08 2 10 2 8 0.87508242795253D-01 -0.41774361646374D-08 3 10 2 8 0.41366878460157D+00 -0.81464236242507D-02 1 11 2 8 0.96702763265348D-02 -0.15615448338126D-01 2 11 2 8 -0.18849522389693D+01 0.18373904947083D+00 3 11 2 8 0.10823834313232D+00 -0.85902488057707D-01 1 12 2 8 -0.96702763267014D-02 0.15615448338125D-01 2 12 2 8 0.18849522389693D+01 -0.18373904947081D+00 3 12 2 8 -0.10823834313322D+00 0.85902488057702D-01 1 13 2 8 0.35913944563345D+00 0.20901073508292D-01 2 13 2 8 -0.27797133824927D+00 0.10194209073261D-01 3 13 2 8 -0.29788044684201D+00 -0.29759930187468D-01 1 14 2 8 -0.35913944563347D+00 -0.20901073508292D-01 2 14 2 8 0.27797133824924D+00 -0.10194209073261D-01 3 14 2 8 0.29788044684196D+00 0.29759930187467D-01 1 15 2 8 -0.24617870014941D+01 0.81223136744587D-02 2 15 2 8 0.23175373615654D+01 0.57779753515311D-02 3 15 2 8 -0.12447197071311D+01 0.19064598607913D-01 1 16 2 8 0.24617870014945D+01 -0.81223136744812D-02 2 16 2 8 -0.23175373615651D+01 -0.57779753515542D-02 3 16 2 8 0.12447197071311D+01 -0.19064598607906D-01 1 17 2 8 0.14944663858130D+00 0.46910145595024D-02 2 17 2 8 0.49139147588193D-01 0.25472336714014D-02 3 17 2 8 -0.51299136639817D+00 -0.68963283496956D-02 1 18 2 8 -0.14944663858130D+00 -0.46910145595011D-02 2 18 2 8 -0.49139147588201D-01 -0.25472336714019D-02 3 18 2 8 0.51299136639815D+00 0.68963283496947D-02 1 19 2 8 -0.98466830470986D+00 0.58600208529998D-02 2 19 2 8 -0.12873711358942D+01 -0.13777757604858D-02 3 19 2 8 -0.13162330433723D+01 0.79774179396950D-02 1 20 2 8 0.98466830470969D+00 -0.58600208529748D-02 2 20 2 8 0.12873711358940D+01 0.13777757604812D-02 3 20 2 8 0.13162330433725D+01 -0.79774179397020D-02 1 1 3 8 -0.53077092998001D+01 -0.19568104993416D-07 2 1 3 8 0.15477292984609D+00 -0.33495937527467D-08 3 1 3 8 0.13477910186055D+01 0.13062225379030D-02 1 2 3 8 -0.53077092998001D+01 -0.19568090317548D-07 2 2 3 8 0.15477292984609D+00 -0.33495922874527D-08 3 2 3 8 0.13477910186055D+01 0.13062225378949D-02 1 3 3 8 -0.22581630858633D+00 -0.20307765000357D-02 2 3 3 8 0.52528265821402D+01 -0.18911704112542D-01 3 3 3 8 0.65892105666532D+00 0.36356041041034D-03 1 4 3 8 0.22581630858634D+00 0.20307765000362D-02 2 4 3 8 -0.52528265821401D+01 0.18911704112537D-01 3 4 3 8 -0.65892105666518D+00 -0.36356041041814D-03 1 5 3 8 0.32035677858130D+00 -0.48400273590566D-08 2 5 3 8 0.50691514744931D-01 0.41347375083704D-09 3 5 3 8 0.69592719321920D-15 0.50187004690180D-09 1 6 3 8 -0.68674811068094D+00 -0.45624650982181D-08 2 6 3 8 -0.44862169353480D+01 0.63662961712403D-08 3 6 3 8 -0.19207901751644D-15 -0.52820338054762D-07 1 7 3 8 0.48105850063564D+01 -0.36105220941019D-08 2 7 3 8 0.12411420792622D+01 0.19554323336561D-07 3 7 3 8 -0.30271317074665D+02 0.00000000000000D+00 1 8 3 8 -0.27891634473009D+00 0.69645035864310D-07 2 8 3 8 0.28812774441787D+01 0.31642090624636D-06 3 8 3 8 0.39343679974651D+02 0.00000000000000D+00 1 9 3 8 -0.19409225590703D-01 -0.20459945137703D-09 2 9 3 8 -0.93495707286619D-01 0.56187788813870D-08 3 9 3 8 -0.15132431734952D+00 -0.16123029826879D-02 1 10 3 8 0.19409225590743D-01 0.20459801176396D-09 2 10 3 8 0.93495707286669D-01 -0.56187809091463D-08 3 10 3 8 0.15132431734957D+00 0.16123029826878D-02 1 11 3 8 -0.20898068340124D+01 -0.11814891006816D+00 2 11 3 8 -0.48849797487075D+00 -0.30452641988901D-01 3 11 3 8 -0.83666971121875D+00 -0.83595200946109D+00 1 12 3 8 0.20898068340124D+01 0.11814891006814D+00 2 12 3 8 0.48849797486986D+00 0.30452641988896D-01 3 12 3 8 0.83666971121852D+00 0.83595200946103D+00 1 13 3 8 -0.37343963415801D+00 -0.15954043812433D-01 2 13 3 8 -0.20766913822670D+00 -0.94043432756840D-02 3 13 3 8 0.27182122046450D+01 -0.31902639594481D-01 1 14 3 8 0.37343963415796D+00 0.15954043812433D-01 2 14 3 8 0.20766913822666D+00 0.94043432756835D-02 3 14 3 8 -0.27182122046449D+01 0.31902639594478D-01 1 15 3 8 0.16328383843279D+00 0.62236888688054D-01 2 15 3 8 0.65422004179174D+00 0.85498412820509D-01 3 15 3 8 0.29576833739164D+01 -0.87886963382193D-03 1 16 3 8 -0.16328383843285D+00 -0.62236888688046D-01 2 16 3 8 -0.65422004179175D+00 -0.85498412820502D-01 3 16 3 8 -0.29576833739170D+01 0.87886963384463D-03 1 17 3 8 0.73236565614063D+00 0.22460210510019D-02 2 17 3 8 -0.62837224393961D-02 -0.45528123343570D-02 3 17 3 8 -0.28377039333194D+01 0.13288858565876D-01 1 18 3 8 -0.73236565614060D+00 -0.22460210510018D-02 2 18 3 8 0.62837224393668D-02 0.45528123343562D-02 3 18 3 8 0.28377039333194D+01 -0.13288858565879D-01 1 19 3 8 -0.11000545595088D+00 -0.70034984234099D-01 2 19 3 8 0.37608143009051D+00 0.65008013740979D-01 3 19 3 8 -0.32211264804367D+01 0.75245839031272D-02 1 20 3 8 0.11000545595054D+00 0.70034984234110D-01 2 20 3 8 -0.37608143009031D+00 -0.65008013740986D-01 3 20 3 8 0.32211264804366D+01 -0.75245839031049D-02 1 1 1 9 -0.36172381347646D+00 -0.12143592510336D-07 2 1 1 9 -0.16123279486189D+00 -0.20140307716290D-07 3 1 1 9 -0.54463979023064D-14 -0.37281458057223D-15 1 2 1 9 -0.13065003929992D+00 0.52795488725362D-08 2 2 1 9 -0.19701072520443D+00 0.92413235139958D-09 3 2 1 9 -0.12699314879535D-13 0.12532358473822D-15 1 3 1 9 -0.33282156738928D+01 -0.68875809317257D-08 2 3 1 9 -0.15354487276529D+00 0.52421281666501D-08 3 3 1 9 0.36739192796928D-14 -0.13313214337983D-14 1 4 1 9 -0.23137836817495D+00 -0.42466428233556D-08 2 4 1 9 0.41044526200068D-01 0.81463593292775D-08 3 4 1 9 0.27356271097171D-13 0.10281803110469D-14 1 5 1 9 -0.21878423655580D+01 -0.20738921948090D+00 2 5 1 9 -0.96682828952699D-02 -0.23423170337500D-01 3 5 1 9 -0.20900314481476D+01 0.17722335537008D+00 1 6 1 9 -0.21878423655580D+01 -0.20738921948090D+00 2 6 1 9 -0.96682828952646D-02 -0.23423170337500D-01 3 6 1 9 0.20900314481476D+01 -0.17722335537008D+00 1 7 1 9 -0.21341603871638D-02 -0.19838944702511D-08 2 7 1 9 -0.19102253674039D+01 -0.48441135012906D-08 3 7 1 9 0.19409225590699D-01 -0.20460045956851D-09 1 8 1 9 -0.21341603871603D-02 -0.19838944361608D-08 2 8 1 9 -0.19102253674039D+01 -0.48441134753274D-08 3 8 1 9 -0.19409225590702D-01 0.20459974461704D-09 1 9 1 9 0.93264867146540D+01 0.00000000000000D+00 2 9 1 9 0.87863662414357D+00 0.69201663948975D-07 3 9 1 9 -0.68017310101191D-14 0.00000000000000D+00 1 10 1 9 0.44324041969416D+00 -0.25690580942537D-09 2 10 1 9 -0.85446127777930D-01 0.66695847636335D-09 3 10 1 9 0.87374939216316D-14 -0.10850526294032D-15 1 11 1 9 0.37026076986375D-15 0.13221568425800D-07 2 11 1 9 0.51756298170430D+00 -0.18050936698885D-08 3 11 1 9 0.15383083557275D-14 -0.48633772363359D-16 1 12 1 9 -0.21406075682086D-14 0.37346912229987D-08 2 12 1 9 -0.10349349737145D+01 -0.45504936514603D-09 3 12 1 9 0.29850763537122D-15 -0.45538454837974D-16 1 13 1 9 0.11792840981585D+01 0.14657541942197D-08 2 13 1 9 0.15290618345528D+01 -0.21912298335384D-09 3 13 1 9 0.20198192734156D+01 0.20136477580881D-07 1 14 1 9 0.12559601067698D+00 -0.41103341452900D-02 2 14 1 9 -0.67873933551284D+00 -0.31114792136694D-02 3 14 1 9 0.11814514531565D+01 -0.38817394447906D-02 1 15 1 9 0.12559601067698D+00 -0.41103341452899D-02 2 15 1 9 -0.67873933551281D+00 -0.31114792136695D-02 3 15 1 9 -0.11814514531565D+01 0.38817394447905D-02 1 16 1 9 0.11792840981585D+01 0.14657533937822D-08 2 16 1 9 0.15290618345528D+01 -0.21912148302783D-09 3 16 1 9 -0.20198192734156D+01 -0.20136477723236D-07 1 17 1 9 0.51208103388208D+00 0.73998515644727D-02 2 17 1 9 -0.13787632836625D+01 -0.12509683799566D-01 3 17 1 9 0.12577055527437D+01 0.79309320047516D-02 1 18 1 9 0.28672537569089D+00 -0.36001205228426D-02 2 18 1 9 0.40928988517286D+00 0.90318035260557D-02 3 18 1 9 0.87343912340415D+00 -0.72677952405787D-04 1 19 1 9 0.28672537569089D+00 -0.36001205228415D-02 2 19 1 9 0.40928988517286D+00 0.90318035260555D-02 3 19 1 9 -0.87343912340415D+00 0.72677952405556D-04 1 20 1 9 0.51208103388208D+00 0.73998515644725D-02 2 20 1 9 -0.13787632836625D+01 -0.12509683799566D-01 3 20 1 9 -0.12577055527437D+01 -0.79309320047519D-02 1 1 2 9 0.13496539410442D+00 -0.27761404652582D-07 2 1 2 9 -0.21153409858905D+01 -0.49798893709648D-08 3 1 2 9 -0.24026214277380D-14 0.63474123049100D-15 1 2 2 9 -0.11362851269804D+00 -0.10673649358226D-08 2 2 2 9 0.52632133627170D-01 -0.13117720151042D-07 3 2 2 9 0.79142712482927D-14 0.10796938115865D-14 1 3 2 9 -0.80808543338177D-01 0.30625185654931D-08 2 3 2 9 -0.35840601747473D+00 0.29847639639218D-08 3 3 2 9 0.34552363871161D-14 -0.24391888169057D-15 1 4 2 9 0.43811931371904D-01 -0.22301090572386D-08 2 4 2 9 -0.16311114054318D+00 0.39850757874032D-08 3 4 2 9 -0.47489538825303D-14 0.60501579240182D-15 1 5 2 9 0.77546100932659D-02 -0.23848159771395D-01 2 5 2 9 -0.18846576428242D+01 -0.27560857113652D+00 3 5 2 9 0.48860436788215D+00 -0.45678966139999D-01 1 6 2 9 0.77546100932713D-02 -0.23848159771395D-01 2 6 2 9 -0.18846576428241D+01 -0.27560857113652D+00 3 6 2 9 -0.48860436788217D+00 0.45678966140001D-01 1 7 2 9 -0.19145017835138D+01 -0.17698264231245D-08 2 7 2 9 -0.87508242795244D-01 -0.41774350443347D-08 3 7 2 9 0.93495707286625D-01 0.56187801957720D-08 1 8 2 9 -0.19145017835138D+01 -0.17698263973263D-08 2 8 2 9 -0.87508242795242D-01 -0.41774350383809D-08 3 8 2 9 -0.93495707286619D-01 -0.56187800061614D-08 1 9 2 9 0.87863431263830D+00 -0.56754310355654D-07 2 9 2 9 0.70083826622392D+01 0.00000000000000D+00 3 9 2 9 -0.43215342712037D-13 0.00000000000000D+00 1 10 2 9 -0.85445693898901D-01 -0.13544669261343D-08 2 10 2 9 0.28496653650629D+00 -0.48149309063917D-09 3 10 2 9 -0.77245448309429D-15 -0.46693154904164D-16 1 11 2 9 0.51756298170430D+00 0.18050934403552D-08 2 11 2 9 0.20613829415870D-15 0.76663885055684D-08 3 11 2 9 0.16771076384940D-14 -0.27802749575238D-16 1 12 2 9 -0.10349349737145D+01 0.45505374942841D-09 2 12 2 9 0.71749420967103D-14 -0.92199641870399D-08 3 12 2 9 0.14591787124494D-14 -0.73510720392552D-15 1 13 2 9 0.96788075964936D+00 0.33760300340028D-08 2 13 2 9 0.15028776992843D+00 0.12123581545551D-08 3 13 2 9 0.11306285642217D+01 0.18957272395751D-07 1 14 2 9 -0.71345382285085D+00 -0.28956415681481D-02 2 14 2 9 -0.33477642938886D+00 0.65465492851246D-03 3 14 2 9 0.12228105029199D+01 -0.24804778549793D-02 1 15 2 9 -0.71345382285082D+00 -0.28956415681482D-02 2 15 2 9 -0.33477642938885D+00 0.65465492851200D-03 3 15 2 9 -0.12228105029199D+01 0.24804778549789D-02 1 16 2 9 0.96788075964937D+00 0.33760315343288D-08 2 16 2 9 0.15028776992843D+00 0.12123581555867D-08 3 16 2 9 -0.11306285642217D+01 -0.18957272229146D-07 1 17 2 9 -0.15309479480782D+01 -0.12027406262379D-01 2 17 2 9 0.65000998327061D+00 0.12586852879374D-01 3 17 2 9 -0.16372026278765D+01 -0.25871656357054D-02 1 18 2 9 0.63256779803005D+00 0.81669387408802D-02 2 18 2 9 -0.34620334871824D+00 -0.69950907808253D-02 3 18 2 9 -0.16621987530293D+01 0.36014268524247D-02 1 19 2 9 0.63256779803006D+00 0.81669387408800D-02 2 19 2 9 -0.34620334871824D+00 -0.69950907808249D-02 3 19 2 9 0.16621987530294D+01 -0.36014268524245D-02 1 20 2 9 -0.15309479480782D+01 -0.12027406262379D-01 2 20 2 9 0.65000998327061D+00 0.12586852879374D-01 3 20 2 9 0.16372026278765D+01 0.25871656357057D-02 1 1 3 9 -0.54463979023064D-14 -0.37238089970324D-15 2 1 3 9 -0.24026214285652D-14 0.62780233658710D-15 3 1 3 9 -0.10363869185446D+01 -0.52224047712544D-07 1 2 3 9 -0.12699314879520D-13 0.12543648758788D-15 2 2 3 9 0.79142712487603D-14 0.10798252270273D-14 3 2 3 9 0.10694750080711D+00 -0.71288046925418D-08 1 3 3 9 0.36739192810892D-14 -0.13297717873350D-14 2 3 3 9 0.34552363871342D-14 -0.24536766143420D-15 3 3 3 9 -0.67483083842939D+00 -0.66874268827837D-07 1 4 3 9 0.27356271097286D-13 0.10289344270934D-14 2 4 3 9 -0.47489538823086D-14 0.60560864109665D-15 3 4 3 9 0.45198706458866D+00 0.41599848488585D-08 1 5 3 9 0.49555160195311D+00 0.27340884384046D+00 2 5 3 9 -0.10823867431967D+00 -0.85902608025652D-01 3 5 3 9 -0.83666465134479D+00 0.83595431870830D+00 1 6 3 9 -0.49555160195312D+00 -0.27340884384046D+00 2 6 3 9 0.10823867431966D+00 0.85902608025653D-01 3 6 3 9 -0.83666465134468D+00 0.83595431870830D+00 1 7 3 9 -0.27731420957066D+00 -0.39615690911813D-02 2 7 3 9 0.41366878460152D+00 0.81464236242500D-02 3 7 3 9 -0.15132431734954D+00 0.16123029826879D-02 1 8 3 9 0.27731420957066D+00 0.39615690911805D-02 2 8 3 9 -0.41366878460152D+00 -0.81464236242498D-02 3 8 3 9 -0.15132431734952D+00 0.16123029826879D-02 1 9 3 9 -0.68017310101191D-14 -0.13877787807815D-16 2 9 3 9 -0.43215342708729D-13 0.00000000000000D+00 3 9 3 9 0.41321132866859D+02 0.00000000000000D+00 1 10 3 9 0.87374939225770D-14 -0.91618336691578D-16 2 10 3 9 -0.77245448337971D-15 -0.49233760151061D-16 3 10 3 9 0.15044194495700D+02 -0.20703249753841D-09 1 11 3 9 0.15383083558900D-14 -0.49367988714095D-16 2 11 3 9 0.16771076380922D-14 -0.28817985184431D-16 3 11 3 9 -0.58459449376137D-14 0.69644005028677D-08 1 12 3 9 0.29850763540835D-15 -0.45164458847199D-16 2 12 3 9 0.14591787124151D-14 -0.73357465699017D-15 3 12 3 9 -0.31977105055763D-14 0.53866301404187D-08 1 13 3 9 0.31923995749106D+01 -0.16948072899245D-07 2 13 3 9 0.21396415006660D+01 -0.21295309069188D-07 3 13 3 9 0.17035299470639D+01 0.19985561748114D-07 1 14 3 9 0.23135024108146D+01 0.31545977923777D-01 2 14 3 9 0.26016443436610D+01 0.27437419579306D-01 3 14 3 9 -0.34057645311672D+01 0.25437250854663D-01 1 15 3 9 -0.23135024108146D+01 -0.31545977923777D-01 2 15 3 9 -0.26016443436611D+01 -0.27437419579307D-01 3 15 3 9 -0.34057645311671D+01 0.25437250854660D-01 1 16 3 9 -0.31923995749106D+01 0.16948072755155D-07 2 16 3 9 -0.21396415006660D+01 0.21295309242732D-07 3 16 3 9 0.17035299470639D+01 0.19985562889245D-07 1 17 3 9 0.23940770338269D+01 -0.29573251647822D-01 2 17 3 9 -0.26120744864271D+01 0.55407714197695D-01 3 17 3 9 0.15656387372481D+01 0.11391631286557D-01 1 18 3 9 0.20382482901667D+01 -0.92247872934603D-06 2 18 3 9 -0.31960816568676D+01 0.14956826096216D-05 3 18 3 9 -0.38509075865804D+01 0.51020608879537D-06 1 19 3 9 -0.20382482901667D+01 0.92247872911135D-06 2 19 3 9 0.31960816568676D+01 -0.14956826093713D-05 3 19 3 9 -0.38509075865804D+01 0.51020608859169D-06 1 20 3 9 -0.23940770338269D+01 0.29573251647821D-01 2 20 3 9 0.26120744864271D+01 -0.55407714197695D-01 3 20 3 9 0.15656387372480D+01 0.11391631286559D-01 1 1 1 10 0.13065003929993D+00 -0.52795468091175D-08 2 1 1 10 0.19701072520445D+00 -0.92413184308883D-09 3 1 1 10 -0.12157801708632D-13 0.57730516256881D-15 1 2 1 10 0.36172381347634D+00 0.12143589176989D-07 2 2 1 10 0.16123279486180D+00 0.20140309574608D-07 3 2 1 10 -0.21702109665999D-13 0.42600878165687D-15 1 3 1 10 -0.23137836817497D+00 -0.42466423848163D-08 2 3 1 10 0.41044526200072D-01 0.81463589734624D-08 3 3 1 10 0.28276538431553D-13 -0.12506731032881D-15 1 4 1 10 -0.33282156738925D+01 -0.68875686250855D-08 2 4 1 10 -0.15354487276520D+00 0.52421242616713D-08 3 4 1 10 -0.48573076711216D-14 0.19441102770759D-15 1 5 1 10 0.21878423655576D+01 0.20738921948089D+00 2 5 1 10 0.96682828952370D-02 0.23423170337501D-01 3 5 1 10 0.20900314481476D+01 -0.17722335537006D+00 1 6 1 10 0.21878423655577D+01 0.20738921948089D+00 2 6 1 10 0.96682828952637D-02 0.23423170337500D-01 3 6 1 10 -0.20900314481474D+01 0.17722335537006D+00 1 7 1 10 0.21341603871660D-02 0.19838936907549D-08 2 7 1 10 0.19102253674038D+01 0.48441129373970D-08 3 7 1 10 -0.19409225590748D-01 0.20459722490899D-09 1 8 1 10 0.21341603871786D-02 0.19838935209737D-08 2 8 1 10 0.19102253674039D+01 0.48441127613084D-08 3 8 1 10 0.19409225590743D-01 -0.20459830500397D-09 1 9 1 10 0.44324041969416D+00 -0.25690570404528D-09 2 9 1 10 -0.85446127777930D-01 0.66695764811116D-09 3 9 1 10 0.87374939216710D-14 0.10349003220544D-15 1 10 1 10 0.93264867146534D+01 0.00000000000000D+00 2 10 1 10 0.87863662414354D+00 0.69201663948975D-07 3 10 1 10 0.13530681614190D-12 0.00000000000000D+00 1 11 1 10 -0.25486208656843D-14 0.37346915793958D-08 2 11 1 10 -0.10349349737145D+01 -0.45505385063467D-09 3 11 1 10 -0.13259883576444D-16 -0.59111093055216D-16 1 12 1 10 0.19605444544821D-14 0.13221568436196D-07 2 12 1 10 0.51756298170431D+00 -0.18050933311066D-08 3 12 1 10 0.41526735201698D-14 0.53080236456384D-16 1 13 1 10 0.12559601067696D+00 -0.41103341452894D-02 2 13 1 10 -0.67873933551282D+00 -0.31114792136697D-02 3 13 1 10 0.11814514531565D+01 -0.38817394447903D-02 1 14 1 10 0.11792840981585D+01 0.14657584091277D-08 2 14 1 10 0.15290618345528D+01 -0.21911883218554D-09 3 14 1 10 0.20198192734156D+01 0.20136486446079D-07 1 15 1 10 0.11792840981585D+01 0.14657583832400D-08 2 15 1 10 0.15290618345528D+01 -0.21911771999111D-09 3 15 1 10 -0.20198192734156D+01 -0.20136485816527D-07 1 16 1 10 0.12559601067696D+00 -0.41103341452901D-02 2 16 1 10 -0.67873933551283D+00 -0.31114792136689D-02 3 16 1 10 -0.11814514531565D+01 0.38817394447903D-02 1 17 1 10 0.28672537569087D+00 -0.36001205228421D-02 2 17 1 10 0.40928988517290D+00 0.90318035260556D-02 3 17 1 10 0.87343912340417D+00 -0.72677952405233D-04 1 18 1 10 0.51208103388205D+00 0.73998515644744D-02 2 18 1 10 -0.13787632836625D+01 -0.12509683799571D-01 3 18 1 10 0.12577055527437D+01 0.79309320047573D-02 1 19 1 10 0.51208103388207D+00 0.73998515644733D-02 2 19 1 10 -0.13787632836625D+01 -0.12509683799571D-01 3 19 1 10 -0.12577055527437D+01 -0.79309320047574D-02 1 20 1 10 0.28672537569085D+00 -0.36001205228410D-02 2 20 1 10 0.40928988517288D+00 0.90318035260554D-02 3 20 1 10 -0.87343912340415D+00 0.72677952405171D-04 1 1 2 10 0.11362851269806D+00 0.10673654441333D-08 2 1 2 10 -0.52632133627159D-01 0.13117718594308D-07 3 1 2 10 -0.22412744226985D-13 0.33188463285635D-15 1 2 2 10 -0.13496539410451D+00 0.27761406510901D-07 2 2 2 10 0.21153409858909D+01 0.49799101398370D-08 3 2 2 10 -0.88719050746798D-14 0.15179942888243D-14 1 3 2 10 0.43811931371908D-01 -0.22301094130538D-08 2 3 2 10 -0.16311114054321D+00 0.39850746037394D-08 3 3 2 10 0.11392153102314D-13 0.62700671087942D-16 1 4 2 10 -0.80808543338092D-01 0.30625146605143D-08 2 4 2 10 -0.35840601747494D+00 0.29847621657435D-08 3 4 2 10 -0.10543255596823D-13 -0.15319196918317D-15 1 5 2 10 -0.77546100932993D-02 0.23848159771395D-01 2 5 2 10 0.18846576428237D+01 0.27560857113650D+00 3 5 2 10 -0.48860436788237D+00 0.45678966139995D-01 1 6 2 10 -0.77546100932726D-02 0.23848159771395D-01 2 6 2 10 0.18846576428240D+01 0.27560857113650D+00 3 6 2 10 0.48860436788233D+00 -0.45678966139997D-01 1 7 2 10 0.19145017835138D+01 0.17698258592309D-08 2 7 2 10 0.87508242795242D-01 0.41774353932206D-08 3 7 2 10 -0.93495707286657D-01 -0.56187811922273D-08 1 8 2 10 0.19145017835138D+01 0.17698256833073D-08 2 8 2 10 0.87508242795253D-01 0.41774361906697D-08 3 8 2 10 0.93495707286669D-01 0.56187820339207D-08 1 9 2 10 -0.85445693898901D-01 -0.13544677543865D-08 2 9 2 10 0.28496653650629D+00 -0.48149404541751D-09 3 9 2 10 -0.77245448318943D-15 0.50927496982328D-16 1 10 2 10 0.87863431263827D+00 -0.56754310355654D-07 2 10 2 10 0.70083826622390D+01 0.00000000000000D+00 3 10 2 10 -0.21899060639231D-13 0.00000000000000D+00 1 11 2 10 -0.10349349737145D+01 0.45504926393977D-09 2 11 2 10 -0.30017759613404D-13 -0.92199609031527D-08 3 11 2 10 -0.24918261816817D-14 0.67590702739363D-16 1 12 2 10 0.51756298170431D+00 0.18050937791372D-08 2 12 2 10 0.19184416374247D-14 0.76663885260865D-08 3 12 2 10 0.82463003576642D-15 0.25029551594017D-16 1 13 2 10 -0.71345382285083D+00 -0.28956415681484D-02 2 13 2 10 -0.33477642938885D+00 0.65465492851217D-03 3 13 2 10 0.12228105029200D+01 -0.24804778549786D-02 1 14 2 10 0.96788075964939D+00 0.33760341851711D-08 2 14 2 10 0.15028776992841D+00 0.12123575193271D-08 3 14 2 10 0.11306285642218D+01 0.18957276817664D-07 1 15 2 10 0.96788075964937D+00 0.33760352973655D-08 2 15 2 10 0.15028776992842D+00 0.12123577711683D-08 3 15 2 10 -0.11306285642218D+01 -0.18957277050011D-07 1 16 2 10 -0.71345382285084D+00 -0.28956415681477D-02 2 16 2 10 -0.33477642938884D+00 0.65465492851201D-03 3 16 2 10 -0.12228105029199D+01 0.24804778549787D-02 1 17 2 10 0.63256779803009D+00 0.81669387408801D-02 2 17 2 10 -0.34620334871824D+00 -0.69950907808238D-02 3 17 2 10 -0.16621987530293D+01 0.36014268524253D-02 1 18 2 10 -0.15309479480783D+01 -0.12027406262384D-01 2 18 2 10 0.65000998327061D+00 0.12586852879375D-01 3 18 2 10 -0.16372026278766D+01 -0.25871656357134D-02 1 19 2 10 -0.15309479480783D+01 -0.12027406262384D-01 2 19 2 10 0.65000998327061D+00 0.12586852879375D-01 3 19 2 10 0.16372026278766D+01 0.25871656357134D-02 1 20 2 10 0.63256779803007D+00 0.81669387408799D-02 2 20 2 10 -0.34620334871824D+00 -0.69950907808254D-02 3 20 2 10 0.16621987530293D+01 -0.36014268524255D-02 1 1 3 10 -0.12157801708622D-13 0.57717646587578D-15 2 1 3 10 -0.22412744227169D-13 0.33168750969515D-15 3 1 3 10 -0.10694750080719D+00 0.71288044406183D-08 1 2 3 10 -0.21702109665379D-13 0.42557510078788D-15 2 2 3 10 -0.88719050738526D-14 0.15249331827282D-14 3 2 3 10 0.10363869185444D+01 0.52224035339712D-07 1 3 3 10 0.28276538431668D-13 -0.12431319428237D-15 2 3 3 10 0.11392153102535D-13 0.63293519782771D-16 3 3 3 10 0.45198706458876D+00 0.41599855787609D-08 1 4 3 10 -0.48573076697253D-14 0.19596067417094D-15 2 4 3 10 -0.10543255596805D-13 -0.15464074892681D-15 3 4 3 10 -0.67483083842969D+00 -0.66874273976316D-07 1 5 3 10 -0.49555160195320D+00 -0.27340884384044D+00 2 5 3 10 0.10823867431946D+00 0.85902608025647D-01 3 5 3 10 0.83666465134536D+00 -0.83595431870823D+00 1 6 3 10 0.49555160195335D+00 0.27340884384044D+00 2 6 3 10 -0.10823867431949D+00 -0.85902608025649D-01 3 6 3 10 0.83666465134525D+00 -0.83595431870823D+00 1 7 3 10 0.27731420957062D+00 0.39615690911780D-02 2 7 3 10 -0.41366878460155D+00 -0.81464236242510D-02 3 7 3 10 0.15132431734952D+00 -0.16123029826878D-02 1 8 3 10 -0.27731420957062D+00 -0.39615690911791D-02 2 8 3 10 0.41366878460157D+00 0.81464236242518D-02 3 8 3 10 0.15132431734957D+00 -0.16123029826878D-02 1 9 3 10 0.87374939225770D-14 0.10549612449939D-15 2 9 3 10 -0.77245448296612D-15 0.49233760151061D-16 3 9 3 10 0.15044194495700D+02 -0.20702483770173D-09 1 10 3 10 0.13530681614190D-12 -0.13877787807815D-16 2 10 3 10 -0.21899060635923D-13 0.00000000000000D+00 3 10 3 10 0.41321132866859D+02 0.00000000000000D+00 1 11 3 10 -0.13259883539319D-16 -0.58737097064441D-16 2 11 3 10 -0.24918261817161D-14 0.69123249674715D-16 3 11 3 10 0.66029444177706D-13 0.53866289033277D-08 1 12 3 10 0.41526735203323D-14 0.52346020105648D-16 2 12 3 10 0.82463003536462D-15 0.24014315984825D-16 3 12 3 10 -0.12110647171777D-14 0.69644006807297D-08 1 13 3 10 0.23135024108147D+01 0.31545977923778D-01 2 13 3 10 0.26016443436611D+01 0.27437419579307D-01 3 13 3 10 -0.34057645311671D+01 0.25437250854662D-01 1 14 3 10 0.31923995749106D+01 -0.16948064034046D-07 2 14 3 10 0.21396415006660D+01 -0.21295304654214D-07 3 14 3 10 0.17035299470639D+01 0.19985566126263D-07 1 15 3 10 -0.31923995749106D+01 0.16948064661864D-07 2 15 3 10 -0.21396415006660D+01 0.21295304428806D-07 3 15 3 10 0.17035299470640D+01 0.19985565358431D-07 1 16 3 10 -0.23135024108146D+01 -0.31545977923778D-01 2 16 3 10 -0.26016443436610D+01 -0.27437419579307D-01 3 16 3 10 -0.34057645311672D+01 0.25437250854662D-01 1 17 3 10 0.20382482901667D+01 -0.92247872879158D-06 2 17 3 10 -0.31960816568676D+01 0.14956826101997D-05 3 17 3 10 -0.38509075865803D+01 0.51020608901390D-06 1 18 3 10 0.23940770338270D+01 -0.29573251647816D-01 2 18 3 10 -0.26120744864272D+01 0.55407714197687D-01 3 18 3 10 0.15656387372481D+01 0.11391631286562D-01 1 19 3 10 -0.23940770338269D+01 0.29573251647816D-01 2 19 3 10 0.26120744864272D+01 -0.55407714197687D-01 3 19 3 10 0.15656387372481D+01 0.11391631286561D-01 1 20 3 10 -0.20382482901667D+01 0.92247872872600D-06 2 20 3 10 0.31960816568676D+01 -0.14956826104499D-05 3 20 3 10 -0.38509075865803D+01 0.51020608976021D-06 1 1 1 11 0.23137836817498D+00 0.42466433177951D-08 2 1 1 11 0.41044526200018D-01 0.81463562651120D-08 3 1 1 11 0.14507809620041D-13 -0.44783372341556D-16 1 2 1 11 -0.33282156738926D+01 -0.68875806001246D-08 2 2 1 11 0.15354487276537D+00 -0.52421249302914D-08 3 2 1 11 0.84976795524219D-15 -0.59814729061952D-15 1 3 1 11 0.13065003929994D+00 -0.52795461635066D-08 2 3 1 11 -0.19701072520445D+00 0.92413131651183D-09 3 3 1 11 -0.13995273214650D-13 0.11560430843025D-16 1 4 1 11 -0.36172381347609D+00 -0.12143591782847D-07 2 4 1 11 0.16123279486195D+00 0.20140304946236D-07 3 4 1 11 0.87253536607513D-14 0.96424374158166D-16 1 5 1 11 0.21341603871672D-02 0.19838940393360D-08 2 5 1 11 -0.19102253674039D+01 -0.48441142056148D-08 3 5 1 11 0.19409225590813D-01 -0.20459798257690D-09 1 6 1 11 0.21341603871497D-02 0.19838948632613D-08 2 6 1 11 -0.19102253674039D+01 -0.48441139037613D-08 3 6 1 11 -0.19409225590830D-01 0.20459826930206D-09 1 7 1 11 -0.21878423655577D+01 -0.20738921948090D+00 2 7 1 11 0.96682828951331D-02 0.23423170337501D-01 3 7 1 11 0.20900314481476D+01 -0.17722335537008D+00 1 8 1 11 -0.21878423655577D+01 -0.20738921948091D+00 2 8 1 11 0.96682828951358D-02 0.23423170337501D-01 3 8 1 11 -0.20900314481474D+01 0.17722335537008D+00 1 9 1 11 0.37026076986375D-15 -0.13221568425800D-07 2 9 1 11 0.51756298170430D+00 -0.18050934403552D-08 3 9 1 11 0.15383083558900D-14 0.49367988714095D-16 1 10 1 11 -0.25486208656843D-14 -0.37346915793958D-08 2 10 1 11 -0.10349349737145D+01 -0.45504926393977D-09 3 10 1 11 -0.13259883539319D-16 0.58737097064441D-16 1 11 1 11 0.93264867146529D+01 0.00000000000000D+00 2 11 1 11 -0.87863662414346D+00 -0.69201663948975D-07 3 11 1 11 -0.12759399608934D-12 0.00000000000000D+00 1 12 1 11 0.44324041969416D+00 -0.25690572763886D-09 2 12 1 11 0.85446127777938D-01 -0.66695868361367D-09 3 12 1 11 -0.91042851261485D-14 0.14654408640004D-15 1 13 1 11 0.28672537569090D+00 -0.36001205228405D-02 2 13 1 11 -0.40928988517289D+00 -0.90318035260557D-02 3 13 1 11 -0.87343912340423D+00 0.72677952405507D-04 1 14 1 11 0.51208103388207D+00 0.73998515644730D-02 2 14 1 11 0.13787632836625D+01 0.12509683799567D-01 3 14 1 11 -0.12577055527436D+01 -0.79309320047515D-02 1 15 1 11 0.51208103388207D+00 0.73998515644725D-02 2 15 1 11 0.13787632836625D+01 0.12509683799566D-01 3 15 1 11 0.12577055527436D+01 0.79309320047513D-02 1 16 1 11 0.28672537569089D+00 -0.36001205228421D-02 2 16 1 11 -0.40928988517289D+00 -0.90318035260556D-02 3 16 1 11 0.87343912340423D+00 -0.72677952405305D-04 1 17 1 11 -0.12559601067695D+00 0.41103341452903D-02 2 17 1 11 -0.67873933551283D+00 -0.31114792136682D-02 3 17 1 11 0.11814514531565D+01 -0.38817394447937D-02 1 18 1 11 -0.11792840981585D+01 -0.14657556693048D-08 2 18 1 11 0.15290618345528D+01 -0.21912009089350D-09 3 18 1 11 0.20198192734156D+01 0.20136482262939D-07 1 19 1 11 -0.11792840981585D+01 -0.14657555128453D-08 2 19 1 11 0.15290618345527D+01 -0.21912035027438D-09 3 19 1 11 -0.20198192734156D+01 -0.20136482687841D-07 1 20 1 11 -0.12559601067694D+00 0.41103341452900D-02 2 20 1 11 -0.67873933551282D+00 -0.31114792136678D-02 3 20 1 11 -0.11814514531565D+01 0.38817394447936D-02 1 1 2 11 0.43811931371854D-01 -0.22301121214041D-08 2 1 2 11 0.16311114054322D+00 -0.39850752826578D-08 3 1 2 11 0.16538195323705D-13 -0.56230138728199D-16 1 2 2 11 0.80808543338262D-01 -0.30625153291344D-08 2 2 2 11 -0.35840601747494D+00 0.29847641390425D-08 3 2 2 11 0.16413406772909D-13 -0.10107862713321D-15 1 3 2 11 -0.11362851269805D+00 -0.10673659707103D-08 2 3 2 11 -0.52632133627149D-01 0.13117719969066D-07 3 3 2 11 -0.22598672813914D-13 -0.72172134000828D-15 1 4 2 11 -0.13496539410436D+00 0.27761401882528D-07 2 4 2 11 -0.21153409858913D+01 -0.49798978424614D-08 3 4 2 11 -0.64146239899135D-14 0.15131767865514D-14 1 5 2 11 -0.19145017835138D+01 -0.17698271275843D-08 2 5 2 11 0.87508242795246D-01 0.41774358266314D-08 3 5 2 11 -0.93495707286655D-01 -0.56187800801924D-08 1 6 2 11 -0.19145017835138D+01 -0.17698268255660D-08 2 6 2 11 0.87508242795229D-01 0.41774365591383D-08 3 6 2 11 0.93495707286680D-01 0.56187798838384D-08 1 7 2 11 -0.77546100934018D-02 0.23848159771396D-01 2 7 2 11 -0.18846576428238D+01 -0.27560857113652D+00 3 7 2 11 0.48860436788299D+00 -0.45678966140000D-01 1 8 2 11 -0.77546100933996D-02 0.23848159771396D-01 2 8 2 11 -0.18846576428241D+01 -0.27560857113652D+00 3 8 2 11 -0.48860436788294D+00 0.45678966139999D-01 1 9 2 11 0.51756298170430D+00 0.18050936698885D-08 2 9 2 11 0.20613829415870D-15 -0.76663885055684D-08 3 9 2 11 0.16771076380922D-14 0.28817985184431D-16 1 10 2 11 -0.10349349737145D+01 0.45505385063467D-09 2 10 2 11 -0.30017759613404D-13 0.92199609031527D-08 3 10 2 11 -0.24918261817161D-14 -0.69123249674715D-16 1 11 2 11 -0.87863431263819D+00 0.56754310355654D-07 2 11 2 11 0.70083826622397D+01 0.00000000000000D+00 3 11 2 11 -0.43215342712037D-13 0.00000000000000D+00 1 12 2 11 0.85445693898909D-01 0.13544667188838D-08 2 12 2 11 0.28496653650629D+00 -0.48149309081583D-09 3 12 2 11 -0.55441395907651D-14 0.11743909896211D-15 1 13 2 11 -0.63256779803009D+00 -0.81669387408802D-02 2 13 2 11 -0.34620334871821D+00 -0.69950907808244D-02 3 13 2 11 -0.16621987530293D+01 0.36014268524251D-02 1 14 2 11 0.15309479480783D+01 0.12027406262380D-01 2 14 2 11 0.65000998327064D+00 0.12586852879373D-01 3 14 2 11 -0.16372026278766D+01 -0.25871656357060D-02 1 15 2 11 0.15309479480783D+01 0.12027406262379D-01 2 15 2 11 0.65000998327064D+00 0.12586852879373D-01 3 15 2 11 0.16372026278766D+01 0.25871656357058D-02 1 16 2 11 -0.63256779803008D+00 -0.81669387408801D-02 2 16 2 11 -0.34620334871820D+00 -0.69950907808249D-02 3 16 2 11 0.16621987530293D+01 -0.36014268524251D-02 1 17 2 11 -0.71345382285084D+00 -0.28956415681469D-02 2 17 2 11 0.33477642938887D+00 -0.65465492851225D-03 3 17 2 11 -0.12228105029200D+01 0.24804778549823D-02 1 18 2 11 0.96788075964935D+00 0.33760329264631D-08 2 18 2 11 -0.15028776992837D+00 -0.12123576778434D-08 3 18 2 11 -0.11306285642218D+01 -0.18957274229241D-07 1 19 2 11 0.96788075964931D+00 0.33760326670822D-08 2 19 2 11 -0.15028776992838D+00 -0.12123581544866D-08 3 19 2 11 0.11306285642217D+01 0.18957274629635D-07 1 20 2 11 -0.71345382285084D+00 -0.28956415681465D-02 2 20 2 11 0.33477642938888D+00 -0.65465492851263D-03 3 20 2 11 0.12228105029199D+01 -0.24804778549823D-02 1 1 3 11 0.14507809620080D-13 -0.45087654566841D-16 2 1 3 11 0.16538195323706D-13 -0.56967372322346D-16 3 1 3 11 -0.45198706458874D+00 -0.41599824946954D-08 1 2 3 11 0.84976795424821D-15 -0.59981775554913D-15 2 2 3 11 0.16413406772946D-13 -0.10329628757114D-15 3 2 3 11 -0.67483083842971D+00 -0.66874269502060D-07 1 3 3 11 -0.13995273214664D-13 0.11720819852689D-16 2 3 3 11 -0.22598672814301D-13 -0.72165563228788D-15 3 3 3 11 -0.10694750080719D+00 0.71288031009829D-08 1 4 3 11 0.87253536607513D-14 0.96858055027160D-16 2 4 3 11 -0.64146239890863D-14 0.15201156804553D-14 3 4 3 11 -0.10363869185439D+01 -0.52224042717348D-07 1 5 3 11 -0.27731420957055D+00 -0.39615690911788D-02 2 5 3 11 -0.41366878460155D+00 -0.81464236242499D-02 3 5 3 11 0.15132431734958D+00 -0.16123029826871D-02 1 6 3 11 0.27731420957053D+00 0.39615690911791D-02 2 6 3 11 0.41366878460158D+00 0.81464236242497D-02 3 6 3 11 0.15132431734953D+00 -0.16123029826877D-02 1 7 3 11 -0.49555160195317D+00 -0.27340884384046D+00 2 7 3 11 -0.10823867431883D+00 -0.85902608025652D-01 3 7 3 11 -0.83666465134547D+00 0.83595431870830D+00 1 8 3 11 0.49555160195339D+00 0.27340884384046D+00 2 8 3 11 0.10823867431889D+00 0.85902608025652D-01 3 8 3 11 -0.83666465134502D+00 0.83595431870830D+00 1 9 3 11 0.15383083557275D-14 0.48633772363359D-16 2 9 3 11 0.16771076384940D-14 0.27802749575238D-16 3 9 3 11 -0.58459449376137D-14 -0.69644005028677D-08 1 10 3 11 -0.13259883576444D-16 0.59111093055216D-16 2 10 3 11 -0.24918261816817D-14 -0.67590702739363D-16 3 10 3 11 0.66029444177706D-13 -0.53866289033277D-08 1 11 3 11 -0.12759399608934D-12 -0.13877787807814D-16 2 11 3 11 -0.43215342715346D-13 0.00000000000000D+00 3 11 3 11 0.41321132866860D+02 0.00000000000000D+00 1 12 3 11 -0.91042851270151D-14 0.14754713254702D-15 2 12 3 11 -0.55441395908603D-14 0.11655124390176D-15 3 12 3 11 0.15044194495700D+02 -0.20703279262363D-09 1 13 3 11 -0.20382482901667D+01 0.92247872906222D-06 2 13 3 11 -0.31960816568676D+01 0.14956826099818D-05 3 13 3 11 -0.38509075865805D+01 0.51020608893075D-06 1 14 3 11 -0.23940770338269D+01 0.29573251647822D-01 2 14 3 11 -0.26120744864272D+01 0.55407714197694D-01 3 14 3 11 0.15656387372481D+01 0.11391631286557D-01 1 15 3 11 0.23940770338269D+01 -0.29573251647822D-01 2 15 3 11 0.26120744864272D+01 -0.55407714197695D-01 3 15 3 11 0.15656387372481D+01 0.11391631286559D-01 1 16 3 11 0.20382482901667D+01 -0.92247872886413D-06 2 16 3 11 0.31960816568676D+01 -0.14956826099440D-05 3 16 3 11 -0.38509075865805D+01 0.51020608759785D-06 1 17 3 11 0.23135024108146D+01 0.31545977923774D-01 2 17 3 11 -0.26016443436611D+01 -0.27437419579303D-01 3 17 3 11 0.34057645311671D+01 -0.25437250854667D-01 1 18 3 11 0.31923995749107D+01 -0.16948068215452D-07 2 18 3 11 -0.21396415006660D+01 0.21295307242637D-07 3 18 3 11 -0.17035299470640D+01 -0.19985564036336D-07 1 19 3 11 -0.31923995749107D+01 0.16948067792285D-07 2 19 3 11 0.21396415006660D+01 -0.21295306849182D-07 3 19 3 11 -0.17035299470640D+01 -0.19985565470849D-07 1 20 3 11 -0.23135024108146D+01 -0.31545977923774D-01 2 20 3 11 0.26016443436610D+01 0.27437419579303D-01 3 20 3 11 0.34057645311670D+01 -0.25437250854667D-01 1 1 1 12 0.33282156738927D+01 0.68875799274928D-08 2 1 1 12 -0.15354487276502D+00 0.52421170902712D-08 3 1 1 12 -0.10393528622009D-13 -0.88560100106848D-15 1 2 1 12 -0.23137836817497D+00 -0.42466430353785D-08 2 2 1 12 -0.41044526200061D-01 -0.81463558150274D-08 3 2 1 12 -0.12420187412085D-13 0.11709849427264D-14 1 3 1 12 -0.36172381347628D+00 -0.12143590787418D-07 2 3 1 12 0.16123279486183D+00 0.20140307362808D-07 3 3 1 12 0.20081817915971D-15 -0.23697390331568D-15 1 4 1 12 0.13065003929990D+00 -0.52795451885864D-08 2 4 1 12 -0.19701072520445D+00 0.92413213752502D-09 3 4 1 12 -0.41810521063619D-14 0.28421412875418D-15 1 5 1 12 -0.21341603871757D-02 -0.19838939680823D-08 2 5 1 12 0.19102253674039D+01 0.48441132947618D-08 3 5 1 12 -0.19409225590714D-01 0.20460053483511D-09 1 6 1 12 -0.21341603871787D-02 -0.19838943064280D-08 2 6 1 12 0.19102253674039D+01 0.48441134705447D-08 3 6 1 12 0.19409225590718D-01 -0.20460033878605D-09 1 7 1 12 0.21878423655578D+01 0.20738921948089D+00 2 7 1 12 -0.96682828952988D-02 -0.23423170337500D-01 3 7 1 12 -0.20900314481474D+01 0.17722335537006D+00 1 8 1 12 0.21878423655579D+01 0.20738921948089D+00 2 8 1 12 -0.96682828953027D-02 -0.23423170337500D-01 3 8 1 12 0.20900314481474D+01 -0.17722335537006D+00 1 9 1 12 -0.21406075682086D-14 -0.37346912229987D-08 2 9 1 12 -0.10349349737145D+01 -0.45505374942841D-09 3 9 1 12 0.29850763540835D-15 0.45164458847199D-16 1 10 1 12 0.19605444544821D-14 -0.13221568436196D-07 2 10 1 12 0.51756298170431D+00 -0.18050937791372D-08 3 10 1 12 0.41526735203323D-14 -0.52346020105648D-16 1 11 1 12 0.44324041969416D+00 -0.25690578583180D-09 2 11 1 12 0.85446127777938D-01 -0.66695744086074D-09 3 11 1 12 -0.91042851261879D-14 -0.14754713254702D-15 1 12 1 12 0.93264867146538D+01 0.00000000000000D+00 2 12 1 12 -0.87863662414351D+00 -0.69201663948975D-07 3 12 1 12 0.30369634748191D-15 0.00000000000000D+00 1 13 1 12 0.51208103388207D+00 0.73998515644743D-02 2 13 1 12 0.13787632836625D+01 0.12509683799571D-01 3 13 1 12 -0.12577055527437D+01 -0.79309320047573D-02 1 14 1 12 0.28672537569088D+00 -0.36001205228428D-02 2 14 1 12 -0.40928988517289D+00 -0.90318035260554D-02 3 14 1 12 -0.87343912340418D+00 0.72677952405411D-04 1 15 1 12 0.28672537569088D+00 -0.36001205228423D-02 2 15 1 12 -0.40928988517289D+00 -0.90318035260559D-02 3 15 1 12 0.87343912340419D+00 -0.72677952405091D-04 1 16 1 12 0.51208103388207D+00 0.73998515644741D-02 2 16 1 12 0.13787632836625D+01 0.12509683799571D-01 3 16 1 12 0.12577055527437D+01 0.79309320047572D-02 1 17 1 12 -0.11792840981585D+01 -0.14657569181534D-08 2 17 1 12 0.15290618345528D+01 -0.21912183753698D-09 3 17 1 12 0.20198192734156D+01 0.20136481210591D-07 1 18 1 12 -0.12559601067695D+00 0.41103341452887D-02 2 18 1 12 -0.67873933551284D+00 -0.31114792136712D-02 3 18 1 12 0.11814514531565D+01 -0.38817394447873D-02 1 19 1 12 -0.12559601067695D+00 0.41103341452887D-02 2 19 1 12 -0.67873933551282D+00 -0.31114792136706D-02 3 19 1 12 -0.11814514531565D+01 0.38817394447874D-02 1 20 1 12 -0.11792840981585D+01 -0.14657572047461D-08 2 20 1 12 0.15290618345528D+01 -0.21912266691688D-09 3 20 1 12 -0.20198192734156D+01 -0.20136480994888D-07 1 1 2 12 -0.80808543337907D-01 0.30625074891142D-08 2 1 2 12 0.35840601747481D+00 -0.29847658443105D-08 3 1 2 12 -0.27994344791003D-14 0.23909328895244D-15 1 2 2 12 -0.43811931371897D-01 0.22301125714888D-08 2 2 2 12 -0.16311114054321D+00 0.39850756068874D-08 3 2 2 12 -0.48334051106957D-15 -0.21628454764153D-15 1 3 2 12 -0.13496539410449D+00 0.27761404299100D-07 2 3 2 12 -0.21153409858909D+01 -0.49798898566879D-08 3 3 2 12 0.39910917955911D-14 0.72691639364058D-15 1 4 2 12 -0.11362851269806D+00 -0.10673651496971D-08 2 4 2 12 -0.52632133627178D-01 0.13117717980316D-07 3 4 2 12 -0.25779489965403D-13 0.13175785915064D-14 1 5 2 12 0.19145017835138D+01 0.17698262167313D-08 2 5 2 12 -0.87508242795253D-01 -0.41774349771863D-08 3 5 2 12 0.93495707286669D-01 0.56187815518895D-08 1 6 2 12 0.19145017835138D+01 0.17698263923493D-08 2 6 2 12 -0.87508242795253D-01 -0.41774346307585D-08 3 6 2 12 -0.93495707286669D-01 -0.56187809891689D-08 1 7 2 12 0.77546100932371D-02 -0.23848159771395D-01 2 7 2 12 0.18846576428241D+01 0.27560857113650D+00 3 7 2 12 -0.48860436788204D+00 0.45678966139995D-01 1 8 2 12 0.77546100932331D-02 -0.23848159771395D-01 2 8 2 12 0.18846576428241D+01 0.27560857113651D+00 3 8 2 12 0.48860436788204D+00 -0.45678966139995D-01 1 9 2 12 -0.10349349737145D+01 0.45504936514603D-09 2 9 2 12 0.71749420967103D-14 0.92199641870399D-08 3 9 2 12 0.14591787124151D-14 0.73357465699017D-15 1 10 2 12 0.51756298170431D+00 0.18050933311066D-08 2 10 2 12 0.19184416374247D-14 -0.76663885260865D-08 3 10 2 12 0.82463003536462D-15 -0.24014315984825D-16 1 11 2 12 0.85445693898909D-01 0.13544679616368D-08 2 11 2 12 0.28496653650629D+00 -0.48149404524085D-09 3 11 2 12 -0.55441395908603D-14 -0.11481652042579D-15 1 12 2 12 -0.87863431263823D+00 0.56754310355654D-07 2 12 2 12 0.70083826622392D+01 0.00000000000000D+00 3 12 2 12 -0.21899060639234D-13 0.00000000000000D+00 1 13 2 12 0.15309479480782D+01 0.12027406262383D-01 2 13 2 12 0.65000998327061D+00 0.12586852879376D-01 3 13 2 12 -0.16372026278766D+01 -0.25871656357126D-02 1 14 2 12 -0.63256779803008D+00 -0.81669387408799D-02 2 14 2 12 -0.34620334871824D+00 -0.69950907808249D-02 3 14 2 12 -0.16621987530293D+01 0.36014268524249D-02 1 15 2 12 -0.63256779803008D+00 -0.81669387408804D-02 2 15 2 12 -0.34620334871824D+00 -0.69950907808249D-02 3 15 2 12 0.16621987530293D+01 -0.36014268524248D-02 1 16 2 12 0.15309479480782D+01 0.12027406262384D-01 2 16 2 12 0.65000998327061D+00 0.12586852879376D-01 3 16 2 12 0.16372026278766D+01 0.25871656357126D-02 1 17 2 12 0.96788075964937D+00 0.33760311798196D-08 2 17 2 12 -0.15028776992840D+00 -0.12123573050105D-08 3 17 2 12 -0.11306285642218D+01 -0.18957275030468D-07 1 18 2 12 -0.71345382285085D+00 -0.28956415681499D-02 2 18 2 12 0.33477642938885D+00 -0.65465492851223D-03 3 18 2 12 -0.12228105029199D+01 0.24804778549755D-02 1 19 2 12 -0.71345382285083D+00 -0.28956415681493D-02 2 19 2 12 0.33477642938885D+00 -0.65465492851267D-03 3 19 2 12 0.12228105029199D+01 -0.24804778549758D-02 1 20 2 12 0.96788075964937D+00 0.33760303504397D-08 2 20 2 12 -0.15028776992840D+00 -0.12123572892465D-08 3 20 2 12 0.11306285642218D+01 0.18957275321937D-07 1 1 3 12 -0.10393528621015D-13 -0.88393053613887D-15 2 1 3 12 -0.27994344791368D-14 0.24131094939038D-15 3 1 3 12 0.67483083842958D+00 0.66874266838036D-07 1 2 3 12 -0.12420187412125D-13 0.11712892249517D-14 2 2 3 12 -0.48334051107077D-15 -0.21554731404739D-15 3 2 3 12 0.45198706458874D+00 0.41599854978095D-08 1 3 3 12 0.20081817915971D-15 -0.23654022244669D-15 2 3 3 12 0.39910917964183D-14 0.73385528754448D-15 3 3 3 12 -0.10363869185443D+01 -0.52224045247325D-07 1 4 3 12 -0.41810521063719D-14 0.28419530191813D-15 2 4 3 12 -0.25779489965879D-13 0.13176586005548D-14 3 4 3 12 -0.10694750080709D+00 0.71288068625385D-08 1 5 3 12 0.27731420957065D+00 0.39615690911813D-02 2 5 3 12 0.41366878460157D+00 0.81464236242514D-02 3 5 3 12 -0.15132431734954D+00 0.16123029826887D-02 1 6 3 12 -0.27731420957064D+00 -0.39615690911811D-02 2 6 3 12 -0.41366878460157D+00 -0.81464236242508D-02 3 6 3 12 -0.15132431734954D+00 0.16123029826879D-02 1 7 3 12 0.49555160195337D+00 0.27340884384044D+00 2 7 3 12 0.10823867431979D+00 0.85902608025647D-01 3 7 3 12 0.83666465134502D+00 -0.83595431870823D+00 1 8 3 12 -0.49555160195334D+00 -0.27340884384044D+00 2 8 3 12 -0.10823867431979D+00 -0.85902608025647D-01 3 8 3 12 0.83666465134479D+00 -0.83595431870823D+00 1 9 3 12 0.29850763537122D-15 0.45538454837974D-16 2 9 3 12 0.14591787124494D-14 0.73510720392552D-15 3 9 3 12 -0.31977105055763D-14 -0.53866301404187D-08 1 10 3 12 0.41526735201698D-14 -0.53080236456384D-16 2 10 3 12 0.82463003576642D-15 -0.25029551594017D-16 3 10 3 12 -0.12110647171777D-14 -0.69644006807297D-08 1 11 3 12 -0.91042851269757D-14 -0.14654408640004D-15 2 11 3 12 -0.55441395907651D-14 -0.11570437548613D-15 3 11 3 12 0.15044194495700D+02 -0.20702454261651D-09 1 12 3 12 0.30369634748191D-15 -0.13877787807814D-16 2 12 3 12 -0.21899060642543D-13 0.00000000000000D+00 3 12 3 12 0.41321132866860D+02 0.00000000000000D+00 1 13 3 12 -0.23940770338270D+01 0.29573251647816D-01 2 13 3 12 -0.26120744864271D+01 0.55407714197688D-01 3 13 3 12 0.15656387372481D+01 0.11391631286561D-01 1 14 3 12 -0.20382482901667D+01 0.92247872896678D-06 2 14 3 12 -0.31960816568676D+01 0.14956826097548D-05 3 14 3 12 -0.38509075865804D+01 0.51020608952109D-06 1 15 3 12 0.20382482901667D+01 -0.92247872864995D-06 2 15 3 12 0.31960816568676D+01 -0.14956826097164D-05 3 15 3 12 -0.38509075865804D+01 0.51020608768106D-06 1 16 3 12 0.23940770338270D+01 -0.29573251647816D-01 2 16 3 12 0.26120744864271D+01 -0.55407714197688D-01 3 16 3 12 0.15656387372481D+01 0.11391631286562D-01 1 17 3 12 0.31923995749106D+01 -0.16948069267800D-07 2 17 3 12 -0.21396415006660D+01 0.21295306441410D-07 3 17 3 12 -0.17035299470640D+01 -0.19985564345777D-07 1 18 3 12 0.23135024108146D+01 0.31545977923781D-01 2 18 3 12 -0.26016443436610D+01 -0.27437419579310D-01 3 18 3 12 0.34057645311672D+01 -0.25437250854655D-01 1 19 3 12 -0.23135024108147D+01 -0.31545977923781D-01 2 19 3 12 0.26016443436611D+01 0.27437419579310D-01 3 19 3 12 0.34057645311672D+01 -0.25437250854655D-01 1 20 3 12 -0.31923995749106D+01 0.16948069485237D-07 2 20 3 12 0.21396415006660D+01 -0.21295306143002D-07 3 20 3 12 -0.17035299470640D+01 -0.19985565727951D-07 1 1 1 13 0.10069046520912D+01 -0.75801891297609D-02 2 1 1 13 0.98296591948538D+00 -0.11414437978986D-03 3 1 1 13 -0.44153365123546D+00 -0.32937483978255D-06 1 2 1 13 -0.55109143599850D+00 -0.16859470164451D-02 2 2 1 13 -0.99309514956420D+00 -0.22828829356255D-02 3 2 1 13 -0.57842585428570D+00 0.65392177609840D-03 1 3 1 13 -0.13160036258649D+01 0.39440115589896D-02 2 3 1 13 -0.15794604274555D+00 -0.19553670742172D-02 3 3 1 13 0.69577824832127D+00 0.49956770034228D-02 1 4 1 13 -0.71675581434648D+00 -0.64643204087173D-02 2 4 1 13 -0.81535905389242D+00 -0.28061440144173D-02 3 4 1 13 0.10601158843439D+01 0.13474040885307D-06 1 5 1 13 0.23453182885643D+01 -0.16674234083550D-01 2 5 1 13 -0.98466804978321D+00 -0.58611420646953D-02 3 5 1 13 0.11000385517933D+00 -0.70037218515900D-01 1 6 1 13 0.39544003264494D+00 0.10151579064274D-01 2 6 1 13 -0.14944663858132D+00 0.46910145595026D-02 3 6 1 13 -0.73236565614061D+00 0.22460210510026D-02 1 7 1 13 -0.10827856698304D+01 0.98483646079575D-02 2 7 1 13 0.24617870014946D+01 0.81223136744872D-02 3 7 1 13 0.16328383843285D+00 -0.62236888688046D-01 1 8 1 13 -0.11021003754773D+00 -0.11188285938630D-01 2 8 1 13 0.35913873778794D+00 -0.20900740470024D-01 3 8 1 13 -0.37344062582968D+00 0.15954711032810D-01 1 9 1 13 0.11792543453489D+01 -0.25928368317276D-01 2 9 1 13 0.96776936133487D+00 -0.15465194806862D-01 3 9 1 13 0.31924106243957D+01 0.25898797161304D-06 1 10 1 13 0.12560827012672D+00 0.12330983344348D-01 2 10 1 13 -0.71340983732439D+00 0.86869267897178D-02 3 10 1 13 0.23135068875126D+01 -0.94637920869666D-01 1 11 1 13 0.28672537569090D+00 0.36001205228405D-02 2 11 1 13 -0.63256779803009D+00 0.81669387408802D-02 3 11 1 13 -0.20382482901667D+01 -0.92247872906222D-06 1 12 1 13 0.51208103388207D+00 -0.73998515644737D-02 2 12 1 13 0.15309479480782D+01 -0.12027406262387D-01 3 12 1 13 -0.23940770338270D+01 -0.29573251647813D-01 1 13 1 13 0.14018771555323D+02 0.00000000000000D+00 2 13 1 13 0.65412930989867D+01 0.13867832533663D+00 3 13 1 13 -0.12534211744677D+01 -0.17848228615364D+00 1 14 1 13 0.40053634807070D+01 -0.13755915305201D-01 2 14 1 13 0.45407403845477D+01 -0.11005341543043D-01 3 14 1 13 -0.15890369664996D+00 0.69597593046970D-03 1 15 1 13 0.55662578533547D+00 -0.97468182131708D-16 2 15 1 13 0.95303860896536D+00 -0.60150321622908D-02 3 15 1 13 -0.27845449107735D-01 -0.31834257981196D-02 1 16 1 13 0.79957387128997D+00 -0.21950053658972D-15 2 16 1 13 0.42416844527457D+00 0.55006316855568D-06 3 16 1 13 0.13494353405146D-01 0.14591325901365D-06 1 17 1 13 -0.90824189549487D-14 0.27701138385525D-02 2 17 1 13 -0.11328492275163D+01 0.17771686275287D-02 3 17 1 13 -0.31475421745964D+00 -0.23119860455358D-01 1 18 1 13 -0.55152217924512D-14 -0.14541765375485D-06 2 18 1 13 -0.11972185995970D+01 0.18151935751482D-07 3 18 1 13 -0.17805383791154D+01 0.27936845729824D-06 1 19 1 13 -0.47098368995403D-15 -0.17988293595823D-02 2 19 1 13 -0.16402152340575D+00 -0.13007202038280D-02 3 19 1 13 0.49779003552929D-01 -0.76211479211266D-02 1 20 1 13 -0.18781594496572D-14 -0.63244999801768D-07 2 20 1 13 -0.17425885055314D+00 0.67634282606850D-03 3 20 1 13 0.23410909939360D+00 -0.23039730995278D-02 1 1 2 13 0.11550840835894D+01 -0.16430291573635D-02 2 1 2 13 0.10331870704529D+01 -0.10190726007475D-01 3 1 2 13 0.71922953309456D+00 -0.71558839958530D-06 1 2 2 13 -0.10457860794229D+01 -0.21886711657089D-02 2 2 2 13 -0.44556139274742D+00 -0.17908386303731D-02 3 2 2 13 0.52686513852279D+00 -0.25246145760448D-03 1 3 2 13 -0.24946234683046D+00 -0.65656601002246D-02 2 3 2 13 -0.17254708423938D+01 0.11015428189472D-01 3 3 2 13 -0.37915633795134D+00 0.91334163764999D-04 1 4 2 13 -0.78575631330609D+00 -0.12548032918743D-02 2 4 2 13 -0.85394703937670D+00 -0.48041569582788D-02 3 4 2 13 -0.69431667125023D+00 -0.21940593988053D-07 1 5 2 13 -0.21977909173431D+01 -0.11960701918880D-01 2 5 2 13 0.12873738576442D+01 -0.13769741829539D-02 3 5 2 13 0.37607978775016D+00 -0.65012570417141D-01 1 6 2 13 -0.38309205658963D+00 0.35535921356563D-02 2 6 2 13 0.49139147588201D-01 -0.25472336714022D-02 3 6 2 13 -0.62837224393801D-02 0.45528123343565D-02 1 7 2 13 0.12608295382431D+01 0.12204994699754D-01 2 7 2 13 -0.23175373615651D+01 0.57779753515564D-02 3 7 2 13 0.65422004179177D+00 -0.85498412820498D-01 1 8 2 13 0.89171766890264D-01 -0.26609451199874D-01 2 8 2 13 -0.27797187308837D+00 -0.10193949992741D-01 3 8 2 13 -0.20767249716440D+00 0.94054658540127D-02 1 9 2 13 0.15289641943779D+01 -0.22584548497021D-01 2 9 2 13 0.15027919413291D+00 -0.23594633032802D-02 3 9 2 13 0.21396494930190D+01 0.94417468446850D-06 1 10 2 13 -0.67869591569542D+00 0.93344425159557D-02 2 10 2 13 -0.33478353757330D+00 -0.19639679643250D-02 3 10 2 13 0.26016470698638D+01 -0.82312268288987D-01 1 11 2 13 -0.40928988517289D+00 0.90318035260557D-02 2 11 2 13 -0.34620334871821D+00 0.69950907808244D-02 3 11 2 13 -0.31960816568676D+01 -0.14956826099818D-05 1 12 2 13 0.13787632836625D+01 -0.12509683799575D-01 2 12 2 13 0.65000998327061D+00 -0.12586852879376D-01 3 12 2 13 -0.26120744864271D+01 -0.55407714197684D-01 1 13 2 13 0.65413004175264D+01 -0.13867893823385D+00 2 13 2 13 0.15438927152218D+02 0.00000000000000D+00 3 13 2 13 0.19966755567862D+01 0.24576842909646D+00 1 14 2 13 0.45407401985304D+01 -0.11004733036747D-01 2 14 2 13 0.42698097218778D+01 -0.74181966107356D-02 3 14 2 13 0.20446992695352D+00 0.36024759921536D-02 1 15 2 13 0.95303860896536D+00 0.60150321622909D-02 2 15 2 13 0.67736820099816D+00 0.21751428916985D-15 3 15 2 13 -0.18117068988275D+00 0.92204988686867D-02 1 16 2 13 0.42416844527457D+00 -0.55006316865666D-06 2 16 2 13 0.84707703179603D+00 -0.45047149551894D-16 3 16 2 13 -0.14916776242601D+00 0.30621673933086D-07 1 17 2 13 -0.11328492275163D+01 -0.17771686275233D-02 2 17 2 13 0.32820005379261D-13 0.14887989700285D-02 3 17 2 13 0.11586323857779D-01 -0.28862187909305D-01 1 18 2 13 -0.11972185995970D+01 -0.18151939183384D-07 2 18 2 13 -0.86233742755156D-14 0.81956009689501D-07 3 18 2 13 -0.46319515530405D+00 0.28298393583996D-06 1 19 2 13 -0.16402406394416D+00 0.13007313982918D-02 2 19 2 13 -0.72557715125494D-15 -0.41697473675394D-02 3 19 2 13 0.84250477741826D-01 -0.61727387437711D-02 1 20 2 13 -0.17425918532635D+00 0.67679638551982D-03 2 20 2 13 0.23131123037650D-14 0.55626929812878D-07 3 20 2 13 -0.21238404067058D+00 0.11160471241759D-02 1 1 3 13 -0.69570235660940D+00 0.27898016116085D-02 2 1 3 13 0.57473179760962D+00 -0.59719574030926D-02 3 1 3 13 -0.44958523427849D-01 -0.12310374104438D-06 1 2 3 13 -0.59817842655174D+00 -0.88572067146593D-03 2 2 3 13 0.62614459687664D+00 0.14714487593225D-02 3 2 3 13 0.44381121288772D+00 0.16889012571152D-02 1 3 3 13 0.38956142221442D+00 -0.13481471670737D-01 2 3 3 13 -0.70195143547442D+00 0.15254249492247D-01 3 3 3 13 -0.20184457421974D+01 -0.33650333211633D-03 1 4 3 13 0.95826380163155D+00 -0.12094229383055D-01 2 4 3 13 -0.84183351782021D+00 0.70212322370559D-02 3 4 3 13 0.65032357226164D+00 0.35819907862076D-07 1 5 3 13 -0.90731475143181D+00 -0.15657512190464D-01 2 5 3 13 -0.13162303149503D+01 -0.79750112227116D-02 3 5 3 13 0.32211215966645D+01 0.75223812782802D-02 1 6 3 13 0.49487343110543D-01 0.14477814241088D-01 2 6 3 13 -0.51299136639816D+00 0.68963283496951D-02 3 6 3 13 -0.28377039333194D+01 -0.13288858565875D-01 1 7 3 13 -0.96407854234451D+00 -0.86948716823761D-02 2 7 3 13 -0.12447197071311D+01 -0.19064598607902D-01 3 7 3 13 -0.29576833739170D+01 -0.87886963385164D-03 1 8 3 13 0.65422170228906D-01 0.32433958052623D-01 2 8 3 13 -0.29787887214579D+00 0.29759813823276D-01 3 8 3 13 0.27182085584869D+01 0.31900596381034D-01 1 9 3 13 0.20198802719664D+01 -0.15121631187525D-01 2 9 3 13 0.11306710335159D+01 -0.24693145586140D-02 3 9 3 13 0.17035198209407D+01 -0.26680844381145D-05 1 10 3 13 0.11813973042934D+01 0.11645223633927D-01 2 10 3 13 0.12227658592657D+01 0.74414564454605D-02 3 10 3 13 -0.34057657659554D+01 -0.76311774053895D-01 1 11 3 13 -0.87343912340423D+00 -0.72677952405507D-04 2 11 3 13 -0.16621987530293D+01 -0.36014268524251D-02 3 11 3 13 -0.38509075865805D+01 -0.51020608893075D-06 1 12 3 13 -0.12577055527437D+01 0.79309320047604D-02 2 12 3 13 -0.16372026278766D+01 0.25871656357161D-02 3 12 3 13 0.15656387372481D+01 -0.11391631286562D-01 1 13 3 13 -0.12533989959841D+01 0.17847971290829D+00 2 13 3 13 0.19967038258309D+01 -0.24576823034110D+00 3 13 3 13 0.14944819687402D+02 0.00000000000000D+00 1 14 3 13 -0.15890551258367D+00 0.69581532588610D-03 2 14 3 13 0.20446752567252D+00 0.36016952142046D-02 3 14 3 13 0.12056623485434D+01 -0.99040090716819D-02 1 15 3 13 0.27845449107742D-01 -0.31834257981196D-02 2 15 3 13 0.18117068988274D+00 0.92204988686867D-02 3 15 3 13 0.34417987723533D+00 0.10954072179878D-15 1 16 3 13 -0.13494353405142D-01 0.14591325901191D-06 2 16 3 13 0.14916776242601D+00 0.30621673933086D-07 3 16 3 13 -0.17429667864103D+01 0.19788023486907D-15 1 17 3 13 -0.31475421745964D+00 0.23119860455358D-01 2 17 3 13 -0.11586323857773D-01 -0.28862187909305D-01 3 17 3 13 -0.17543527708521D-13 0.50784577220555D-02 1 18 3 13 -0.17805383791154D+01 -0.27936846582211D-06 2 18 3 13 0.46319515530405D+00 0.28298393578185D-06 3 18 3 13 -0.12325867550466D-13 -0.27808464282407D-07 1 19 3 13 -0.49779657171117D-01 -0.76213733339868D-02 2 19 3 13 0.84249717343221D-01 0.61730325793652D-02 3 19 3 13 0.12076159388629D-13 -0.39435543142286D-03 1 20 3 13 -0.23410832737731D+00 0.23050707619879D-02 2 20 3 13 -0.21238464665666D+00 0.11150492717772D-02 3 20 3 13 0.71555242791750D-14 0.89405304253812D-07 1 1 1 14 0.55109143599850D+00 0.16859470164449D-02 2 1 1 14 0.99309514956424D+00 0.22828829356225D-02 3 1 1 14 0.57842585428567D+00 -0.65392177610117D-03 1 2 1 14 -0.10069046520912D+01 0.75801891297640D-02 2 2 1 14 -0.98296591948537D+00 0.11414437978195D-03 3 2 1 14 0.44153365123531D+00 0.32937484761479D-06 1 3 1 14 -0.71675581434647D+00 -0.64643204087186D-02 2 3 1 14 -0.81535905389245D+00 -0.28061440144173D-02 3 3 1 14 0.10601158843440D+01 0.13474040931372D-06 1 4 1 14 -0.13160036258648D+01 0.39440115589854D-02 2 4 1 14 -0.15794604274550D+00 -0.19553670742165D-02 3 4 1 14 0.69577824832136D+00 0.49956770034226D-02 1 5 1 14 -0.23453182885641D+01 0.16674234083571D-01 2 5 1 14 0.98466804978332D+00 0.58611420647171D-02 3 5 1 14 -0.11000385517968D+00 0.70037218515893D-01 1 6 1 14 -0.39544003264495D+00 -0.10151579064273D-01 2 6 1 14 0.14944663858130D+00 -0.46910145595009D-02 3 6 1 14 0.73236565614058D+00 -0.22460210510024D-02 1 7 1 14 0.10827856698305D+01 -0.98483646079545D-02 2 7 1 14 -0.24617870014940D+01 -0.81223136744652D-02 3 7 1 14 -0.16328383843277D+00 0.62236888688054D-01 1 8 1 14 0.11021003754771D+00 0.11188285938630D-01 2 8 1 14 -0.35913873778796D+00 0.20900740470024D-01 3 8 1 14 0.37344062582964D+00 -0.15954711032811D-01 1 9 1 14 0.12560827012674D+00 0.12330983344349D-01 2 9 1 14 -0.71340983732440D+00 0.86869267897176D-02 3 9 1 14 0.23135068875126D+01 -0.94637920869665D-01 1 10 1 14 0.11792543453489D+01 -0.25928368317281D-01 2 10 1 14 0.96776936133490D+00 -0.15465194806866D-01 3 10 1 14 0.31924106243957D+01 0.25898796274784D-06 1 11 1 14 0.51208103388207D+00 -0.73998515644725D-02 2 11 1 14 0.15309479480783D+01 -0.12027406262383D-01 3 11 1 14 -0.23940770338269D+01 -0.29573251647819D-01 1 12 1 14 0.28672537569088D+00 0.36001205228428D-02 2 12 1 14 -0.63256779803008D+00 0.81669387408799D-02 3 12 1 14 -0.20382482901667D+01 -0.92247872896678D-06 1 13 1 14 0.40053634807070D+01 -0.13755915305202D-01 2 13 1 14 0.45407403845477D+01 -0.11005341543044D-01 3 13 1 14 -0.15890369664996D+00 0.69597593046959D-03 1 14 1 14 0.14018771555323D+02 0.00000000000000D+00 2 14 1 14 0.65412930989871D+01 0.13867832533663D+00 3 14 1 14 -0.12534211744674D+01 -0.17848228615364D+00 1 15 1 14 0.79957387128999D+00 0.22720875933690D-17 2 15 1 14 0.42416844527457D+00 0.55006316863695D-06 3 15 1 14 0.13494353405145D-01 0.14591325917473D-06 1 16 1 14 0.55662578533547D+00 -0.13689665905240D-15 2 16 1 14 0.95303860896536D+00 -0.60150321622907D-02 3 16 1 14 -0.27845449107739D-01 -0.31834257981196D-02 1 17 1 14 -0.10475868386107D-13 -0.14541766335727D-06 2 17 1 14 -0.11972185995970D+01 0.18151936912774D-07 3 17 1 14 -0.17805383791154D+01 0.27936846099929D-06 1 18 1 14 0.11768783755295D-14 0.27701138385504D-02 2 18 1 14 -0.11328492275163D+01 0.17771686275265D-02 3 18 1 14 -0.31475421745964D+00 -0.23119860455358D-01 1 19 1 14 -0.36558554319528D-14 -0.63245000677012D-07 2 19 1 14 -0.17425885055315D+00 0.67634282606905D-03 3 19 1 14 0.23410909939359D+00 -0.23039730995281D-02 1 20 1 14 0.90890382790055D-14 -0.17988293595832D-02 2 20 1 14 -0.16402152340575D+00 -0.13007202038268D-02 3 20 1 14 0.49779003552928D-01 -0.76211479211258D-02 1 1 2 14 0.10457860794229D+01 0.21886711657059D-02 2 1 2 14 0.44556139274740D+00 0.17908386303753D-02 3 1 2 14 -0.52686513852279D+00 0.25246145760649D-03 1 2 2 14 -0.11550840835894D+01 0.16430291573555D-02 2 2 2 14 -0.10331870704528D+01 0.10190726007475D-01 3 2 2 14 -0.71922953309458D+00 0.71558839136986D-06 1 3 2 14 -0.78575631330612D+00 -0.12548032918744D-02 2 3 2 14 -0.85394703937676D+00 -0.48041569582790D-02 3 3 2 14 -0.69431667125029D+00 -0.21940594282474D-07 1 4 2 14 -0.24946234683041D+00 -0.65656601002238D-02 2 4 2 14 -0.17254708423938D+01 0.11015428189474D-01 3 4 2 14 -0.37915633795144D+00 0.91334163765621D-04 1 5 2 14 0.21977909173432D+01 0.11960701918901D-01 2 5 2 14 -0.12873738576443D+01 0.13769741829592D-02 3 5 2 14 -0.37607978775035D+00 0.65012570417133D-01 1 6 2 14 0.38309205658961D+00 -0.35535921356545D-02 2 6 2 14 -0.49139147588210D-01 0.25472336713988D-02 3 6 2 14 0.62837224393464D-02 -0.45528123343556D-02 1 7 2 14 -0.12608295382425D+01 -0.12204994699732D-01 2 7 2 14 0.23175373615654D+01 -0.57779753515338D-02 3 7 2 14 -0.65422004179168D+00 0.85498412820507D-01 1 8 2 14 -0.89171766890280D-01 0.26609451199874D-01 2 8 2 14 0.27797187308835D+00 0.10193949992741D-01 3 8 2 14 0.20767249716435D+00 -0.94054658540122D-02 1 9 2 14 -0.67869591569544D+00 0.93344425159554D-02 2 9 2 14 -0.33478353757331D+00 -0.19639679643253D-02 3 9 2 14 0.26016470698638D+01 -0.82312268288986D-01 1 10 2 14 0.15289641943779D+01 -0.22584548497025D-01 2 10 2 14 0.15027919413290D+00 -0.23594633032796D-02 3 10 2 14 0.21396494930190D+01 0.94417468004659D-06 1 11 2 14 0.13787632836625D+01 -0.12509683799571D-01 2 11 2 14 0.65000998327064D+00 -0.12586852879373D-01 3 11 2 14 -0.26120744864272D+01 -0.55407714197691D-01 1 12 2 14 -0.40928988517289D+00 0.90318035260554D-02 2 12 2 14 -0.34620334871824D+00 0.69950907808249D-02 3 12 2 14 -0.31960816568676D+01 -0.14956826097548D-05 1 13 2 14 0.45407401985304D+01 -0.11004733036748D-01 2 13 2 14 0.42698097218778D+01 -0.74181966107343D-02 3 13 2 14 0.20446992695352D+00 0.36024759921548D-02 1 14 2 14 0.65413004175269D+01 -0.13867893823385D+00 2 14 2 14 0.15438927152218D+02 0.00000000000000D+00 3 14 2 14 0.19966755567866D+01 0.24576842909646D+00 1 15 2 14 0.42416844527457D+00 -0.55006316857538D-06 2 15 2 14 0.84707703179603D+00 0.61110973554079D-16 3 15 2 14 -0.14916776242600D+00 0.30621673669863D-07 1 16 2 14 0.95303860896536D+00 0.60150321622911D-02 2 16 2 14 0.67736820099816D+00 0.22450182719220D-15 3 16 2 14 -0.18117068988275D+00 0.92204988686866D-02 1 17 2 14 -0.11972185995970D+01 -0.18151938022093D-07 2 17 2 14 0.14603795158533D-13 0.81956012768501D-07 3 17 2 14 -0.46319515530406D+00 0.28298393519172D-06 1 18 2 14 -0.11328492275163D+01 -0.17771686275254D-02 2 18 2 14 -0.30236090323004D-13 0.14887989700400D-02 3 18 2 14 0.11586323857787D-01 -0.28862187909308D-01 1 19 2 14 -0.17425918532636D+00 0.67679638552038D-03 2 19 2 14 -0.15310374462656D-14 0.55626931135157D-07 3 19 2 14 -0.21238404067057D+00 0.11160471241741D-02 1 20 2 14 -0.16402406394416D+00 0.13007313982930D-02 2 20 2 14 0.95627589521253D-14 -0.41697473675394D-02 3 20 2 14 0.84250477741830D-01 -0.61727387437713D-02 1 1 3 14 0.59817842655171D+00 0.88572067146316D-03 2 1 3 14 -0.62614459687664D+00 -0.14714487593205D-02 3 1 3 14 -0.44381121288763D+00 -0.16889012571114D-02 1 2 3 14 0.69570235660924D+00 -0.27898016116007D-02 2 2 3 14 -0.57473179760963D+00 0.59719574030843D-02 3 2 3 14 0.44958523427849D-01 0.12310374538675D-06 1 3 3 14 0.95826380163159D+00 -0.12094229383054D-01 2 3 3 14 -0.84183351782026D+00 0.70212322370556D-02 3 3 3 14 0.65032357226161D+00 0.35819906274507D-07 1 4 3 14 0.38956142221451D+00 -0.13481471670738D-01 2 4 3 14 -0.70195143547452D+00 0.15254249492248D-01 3 4 3 14 -0.20184457421974D+01 -0.33650333212146D-03 1 5 3 14 0.90731475143145D+00 0.15657512190456D-01 2 5 3 14 0.13162303149501D+01 0.79750112227039D-02 3 5 3 14 -0.32211215966647D+01 -0.75223812783034D-02 1 6 3 14 -0.49487343110575D-01 -0.14477814241088D-01 2 6 3 14 0.51299136639813D+00 -0.68963283496942D-02 3 6 3 14 0.28377039333194D+01 0.13288858565880D-01 1 7 3 14 0.96407854234460D+00 0.86948716823839D-02 2 7 3 14 0.12447197071312D+01 0.19064598607912D-01 3 7 3 14 0.29576833739164D+01 0.87886963382850D-03 1 8 3 14 -0.65422170228949D-01 -0.32433958052623D-01 2 8 3 14 0.29787887214575D+00 -0.29759813823276D-01 3 8 3 14 -0.27182085584869D+01 -0.31900596381031D-01 1 9 3 14 0.11813973042934D+01 0.11645223633927D-01 2 9 3 14 0.12227658592656D+01 0.74414564454611D-02 3 9 3 14 -0.34057657659554D+01 -0.76311774053895D-01 1 10 3 14 0.20198802719665D+01 -0.15121631187534D-01 2 10 3 14 0.11306710335160D+01 -0.24693145586184D-02 3 10 3 14 0.17035198209407D+01 -0.26680844424926D-05 1 11 3 14 -0.12577055527436D+01 0.79309320047546D-02 2 11 3 14 -0.16372026278766D+01 0.25871656357096D-02 3 11 3 14 0.15656387372481D+01 -0.11391631286558D-01 1 12 3 14 -0.87343912340418D+00 -0.72677952405411D-04 2 12 3 14 -0.16621987530293D+01 -0.36014268524249D-02 3 12 3 14 -0.38509075865804D+01 -0.51020608952109D-06 1 13 3 14 -0.15890551258367D+00 0.69581532588598D-03 2 13 3 14 0.20446752567252D+00 0.36016952142057D-02 3 13 3 14 0.12056623485434D+01 -0.99040090716815D-02 1 14 3 14 -0.12533989959837D+01 0.17847971290829D+00 2 14 3 14 0.19967038258313D+01 -0.24576823034110D+00 3 14 3 14 0.14944819687401D+02 0.00000000000000D+00 1 15 3 14 -0.13494353405143D-01 0.14591325917300D-06 2 15 3 14 0.14916776242601D+00 0.30621673669863D-07 3 15 3 14 -0.17429667864102D+01 0.72149631162847D-15 1 16 3 14 0.27845449107739D-01 -0.31834257981196D-02 2 16 3 14 0.18117068988275D+00 0.92204988686866D-02 3 16 3 14 0.34417987723533D+00 -0.60642834822139D-15 1 17 3 14 -0.17805383791154D+01 -0.27936846212106D-06 2 17 3 14 0.46319515530405D+00 0.28298393513187D-06 3 17 3 14 0.10323471197079D-13 -0.27808461156050D-07 1 18 3 14 -0.31475421745964D+00 0.23119860455358D-01 2 18 3 14 -0.11586323857766D-01 -0.28862187909308D-01 3 18 3 14 0.16648424535036D-13 0.50784577220494D-02 1 19 3 14 -0.23410832737731D+00 0.23050707619876D-02 2 19 3 14 -0.21238464665665D+00 0.11150492717754D-02 3 19 3 14 -0.30771083728822D-14 0.89405305320594D-07 1 20 3 14 -0.49779657171118D-01 -0.76213733339861D-02 2 20 3 14 0.84249717343225D-01 0.61730325793650D-02 3 20 3 14 0.29110177685894D-14 -0.39435543142434D-03 1 1 1 15 0.55109143599849D+00 0.16859470164446D-02 2 1 1 15 0.99309514956421D+00 0.22828829356239D-02 3 1 1 15 -0.57842585428567D+00 0.65392177610093D-03 1 2 1 15 -0.10069046520912D+01 0.75801891297648D-02 2 2 1 15 -0.98296591948545D+00 0.11414437978390D-03 3 2 1 15 -0.44153365123539D+00 -0.32937484642927D-06 1 3 1 15 -0.71675581434646D+00 -0.64643204087164D-02 2 3 1 15 -0.81535905389245D+00 -0.28061440144175D-02 3 3 1 15 -0.10601158843440D+01 -0.13474040959229D-06 1 4 1 15 -0.13160036258649D+01 0.39440115589863D-02 2 4 1 15 -0.15794604274565D+00 -0.19553670742164D-02 3 4 1 15 -0.69577824832121D+00 -0.49956770034217D-02 1 5 1 15 -0.39544003264495D+00 -0.10151579064273D-01 2 5 1 15 0.14944663858130D+00 -0.46910145595009D-02 3 5 1 15 -0.73236565614060D+00 0.22460210510022D-02 1 6 1 15 -0.23453182885641D+01 0.16674234083568D-01 2 6 1 15 0.98466804978338D+00 0.58611420647157D-02 3 6 1 15 0.11000385517971D+00 -0.70037218515890D-01 1 7 1 15 0.11021003754771D+00 0.11188285938630D-01 2 7 1 15 -0.35913873778796D+00 0.20900740470025D-01 3 7 1 15 -0.37344062582966D+00 0.15954711032811D-01 1 8 1 15 0.10827856698305D+01 -0.98483646079540D-02 2 8 1 15 -0.24617870014941D+01 -0.81223136744652D-02 3 8 1 15 0.16328383843279D+00 -0.62236888688053D-01 1 9 1 15 0.12560827012674D+00 0.12330983344349D-01 2 9 1 15 -0.71340983732437D+00 0.86869267897177D-02 3 9 1 15 -0.23135068875126D+01 0.94637920869665D-01 1 10 1 15 0.11792543453488D+01 -0.25928368317281D-01 2 10 1 15 0.96776936133486D+00 -0.15465194806867D-01 3 10 1 15 -0.31924106243957D+01 -0.25898796337740D-06 1 11 1 15 0.51208103388207D+00 -0.73998515644720D-02 2 11 1 15 0.15309479480783D+01 -0.12027406262382D-01 3 11 1 15 0.23940770338269D+01 0.29573251647819D-01 1 12 1 15 0.28672537569088D+00 0.36001205228423D-02 2 12 1 15 -0.63256779803008D+00 0.81669387408804D-02 3 12 1 15 0.20382482901667D+01 0.92247872864995D-06 1 13 1 15 0.55662578533547D+00 0.97468182131708D-16 2 13 1 15 0.95303860896536D+00 -0.60150321622909D-02 3 13 1 15 0.27845449107742D-01 0.31834257981196D-02 1 14 1 15 0.79957387128999D+00 -0.22720875933690D-17 2 14 1 15 0.42416844527457D+00 0.55006316857538D-06 3 14 1 15 -0.13494353405143D-01 -0.14591325917300D-06 1 15 1 15 0.14018771555323D+02 0.00000000000000D+00 2 15 1 15 0.65412930989872D+01 0.13867832533663D+00 3 15 1 15 0.12534211744673D+01 0.17848228615364D+00 1 16 1 15 0.40053634807070D+01 -0.13755915305201D-01 2 16 1 15 0.45407403845477D+01 -0.11005341543043D-01 3 16 1 15 0.15890369664995D+00 -0.69597593046996D-03 1 17 1 15 0.69656754602417D-14 -0.17988293595836D-02 2 17 1 15 -0.16402152340575D+00 -0.13007202038268D-02 3 17 1 15 -0.49779003552916D-01 0.76211479211266D-02 1 18 1 15 -0.10300199825801D-14 -0.63245002334032D-07 2 18 1 15 -0.17425885055315D+00 0.67634282606851D-03 3 18 1 15 -0.23410909939359D+00 0.23039730995280D-02 1 19 1 15 -0.68167274017716D-14 0.27701138385510D-02 2 19 1 15 -0.11328492275163D+01 0.17771686275260D-02 3 19 1 15 0.31475421745964D+00 0.23119860455358D-01 1 20 1 15 -0.10475649533341D-13 -0.14541766393400D-06 2 20 1 15 -0.11972185995970D+01 0.18151936424437D-07 3 20 1 15 0.17805383791154D+01 -0.27936846136631D-06 1 1 2 15 0.10457860794229D+01 0.21886711657073D-02 2 1 2 15 0.44556139274739D+00 0.17908386303749D-02 3 1 2 15 0.52686513852280D+00 -0.25246145760682D-03 1 2 2 15 -0.11550840835895D+01 0.16430291573575D-02 2 2 2 15 -0.10331870704528D+01 0.10190726007474D-01 3 2 2 15 0.71922953309465D+00 -0.71558839117739D-06 1 3 2 15 -0.78575631330613D+00 -0.12548032918745D-02 2 3 2 15 -0.85394703937674D+00 -0.48041569582770D-02 3 3 2 15 0.69431667125028D+00 0.21940594887424D-07 1 4 2 15 -0.24946234683054D+00 -0.65656601002237D-02 2 4 2 15 -0.17254708423938D+01 0.11015428189474D-01 3 4 2 15 0.37915633795133D+00 -0.91334163765766D-04 1 5 2 15 0.38309205658961D+00 -0.35535921356545D-02 2 5 2 15 -0.49139147588205D-01 0.25472336714017D-02 3 5 2 15 -0.62837224393659D-02 0.45528123343564D-02 1 6 2 15 0.21977909173432D+01 0.11960701918900D-01 2 6 2 15 -0.12873738576443D+01 0.13769741829570D-02 3 6 2 15 0.37607978775038D+00 -0.65012570417135D-01 1 7 2 15 -0.89171766890285D-01 0.26609451199874D-01 2 7 2 15 0.27797187308836D+00 0.10193949992741D-01 3 7 2 15 -0.20767249716438D+00 0.94054658540145D-02 1 8 2 15 -0.12608295382426D+01 -0.12204994699732D-01 2 8 2 15 0.23175373615654D+01 -0.57779753515343D-02 3 8 2 15 0.65422004179174D+00 -0.85498412820506D-01 1 9 2 15 -0.67869591569541D+00 0.93344425159555D-02 2 9 2 15 -0.33478353757330D+00 -0.19639679643248D-02 3 9 2 15 -0.26016470698638D+01 0.82312268288987D-01 1 10 2 15 0.15289641943779D+01 -0.22584548497026D-01 2 10 2 15 0.15027919413291D+00 -0.23594633032799D-02 3 10 2 15 -0.21396494930190D+01 -0.94417467981077D-06 1 11 2 15 0.13787632836625D+01 -0.12509683799570D-01 2 11 2 15 0.65000998327064D+00 -0.12586852879373D-01 3 11 2 15 0.26120744864272D+01 0.55407714197691D-01 1 12 2 15 -0.40928988517289D+00 0.90318035260559D-02 2 12 2 15 -0.34620334871824D+00 0.69950907808249D-02 3 12 2 15 0.31960816568676D+01 0.14956826097164D-05 1 13 2 15 0.95303860896536D+00 0.60150321622908D-02 2 13 2 15 0.67736820099816D+00 -0.21751428916985D-15 3 13 2 15 0.18117068988274D+00 -0.92204988686867D-02 1 14 2 15 0.42416844527457D+00 -0.55006316863695D-06 2 14 2 15 0.84707703179603D+00 -0.61110973554079D-16 3 14 2 15 0.14916776242601D+00 -0.30621673669863D-07 1 15 2 15 0.65413004175269D+01 -0.13867893823385D+00 2 15 2 15 0.15438927152218D+02 0.00000000000000D+00 3 15 2 15 -0.19966755567864D+01 -0.24576842909646D+00 1 16 2 15 0.45407401985304D+01 -0.11004733036748D-01 2 16 2 15 0.42698097218778D+01 -0.74181966107346D-02 3 16 2 15 -0.20446992695352D+00 -0.36024759921544D-02 1 17 2 15 -0.16402406394416D+00 0.13007313982929D-02 2 17 2 15 0.93754086492157D-14 -0.41697473675397D-02 3 17 2 15 -0.84250477741827D-01 0.61727387437712D-02 1 18 2 15 -0.17425918532636D+00 0.67679638551983D-03 2 18 2 15 0.55391001805019D-15 0.55626930453773D-07 3 18 2 15 0.21238404067056D+00 -0.11160471241739D-02 1 19 2 15 -0.11328492275163D+01 -0.17771686275259D-02 2 19 2 15 -0.38229696100305D-13 0.14887989700403D-02 3 19 2 15 -0.11586323857776D-01 0.28862187909307D-01 1 20 2 15 -0.11972185995970D+01 -0.18151938511296D-07 2 20 2 15 0.16602252790088D-13 0.81956012037514D-07 3 20 2 15 0.46319515530406D+00 -0.28298393521428D-06 1 1 3 15 -0.59817842655171D+00 -0.88572067146340D-03 2 1 3 15 0.62614459687666D+00 0.14714487593201D-02 3 1 3 15 -0.44381121288767D+00 -0.16889012571127D-02 1 2 3 15 -0.69570235660931D+00 0.27898016116018D-02 2 2 3 15 0.57473179760972D+00 -0.59719574030842D-02 3 2 3 15 0.44958523427777D-01 0.12310374617063D-06 1 3 3 15 -0.95826380163162D+00 0.12094229383054D-01 2 3 3 15 0.84183351782028D+00 -0.70212322370550D-02 3 3 3 15 0.65032357226169D+00 0.35819907728856D-07 1 4 3 15 -0.38956142221438D+00 0.13481471670738D-01 2 4 3 15 0.70195143547441D+00 -0.15254249492248D-01 3 4 3 15 -0.20184457421975D+01 -0.33650333212189D-03 1 5 3 15 0.49487343110552D-01 0.14477814241088D-01 2 5 3 15 -0.51299136639815D+00 0.68963283496949D-02 3 5 3 15 0.28377039333194D+01 0.13288858565879D-01 1 6 3 15 -0.90731475143144D+00 -0.15657512190454D-01 2 6 3 15 -0.13162303149501D+01 -0.79750112227052D-02 3 6 3 15 -0.32211215966647D+01 -0.75223812783006D-02 1 7 3 15 0.65422170228926D-01 0.32433958052624D-01 2 7 3 15 -0.29787887214577D+00 0.29759813823278D-01 3 7 3 15 -0.27182085584868D+01 -0.31900596381032D-01 1 8 3 15 -0.96407854234457D+00 -0.86948716823824D-02 2 8 3 15 -0.12447197071311D+01 -0.19064598607911D-01 3 8 3 15 0.29576833739164D+01 0.87886963382810D-03 1 9 3 15 -0.11813973042934D+01 -0.11645223633927D-01 2 9 3 15 -0.12227658592656D+01 -0.74414564454608D-02 3 9 3 15 -0.34057657659554D+01 -0.76311774053893D-01 1 10 3 15 -0.20198802719665D+01 0.15121631187533D-01 2 10 3 15 -0.11306710335160D+01 0.24693145586187D-02 3 10 3 15 0.17035198209407D+01 -0.26680844417248D-05 1 11 3 15 0.12577055527436D+01 -0.79309320047544D-02 2 11 3 15 0.16372026278766D+01 -0.25871656357094D-02 3 11 3 15 0.15656387372481D+01 -0.11391631286559D-01 1 12 3 15 0.87343912340419D+00 0.72677952405091D-04 2 12 3 15 0.16621987530293D+01 0.36014268524248D-02 3 12 3 15 -0.38509075865804D+01 -0.51020608768106D-06 1 13 3 15 -0.27845449107735D-01 0.31834257981196D-02 2 13 3 15 -0.18117068988275D+00 -0.92204988686867D-02 3 13 3 15 0.34417987723533D+00 -0.10954072179878D-15 1 14 3 15 0.13494353405145D-01 -0.14591325917473D-06 2 14 3 15 -0.14916776242600D+00 -0.30621673669863D-07 3 14 3 15 -0.17429667864102D+01 -0.72149631162847D-15 1 15 3 15 0.12533989959837D+01 -0.17847971290829D+00 2 15 3 15 -0.19967038258312D+01 0.24576823034110D+00 3 15 3 15 0.14944819687402D+02 0.00000000000000D+00 1 16 3 15 0.15890551258366D+00 -0.69581532588636D-03 2 16 3 15 -0.20446752567252D+00 -0.36016952142053D-02 3 16 3 15 0.12056623485435D+01 -0.99040090716815D-02 1 17 3 15 0.49779657171130D-01 0.76213733339868D-02 2 17 3 15 -0.84249717343222D-01 -0.61730325793651D-02 3 17 3 15 -0.60817888350996D-14 -0.39435543142427D-03 1 18 3 15 0.23410832737731D+00 -0.23050707619877D-02 2 18 3 15 0.21238464665665D+00 -0.11150492717752D-02 3 18 3 15 0.57904019005508D-14 0.89405306693695D-07 1 19 3 15 0.31475421745964D+00 -0.23119860455358D-01 2 19 3 15 0.11586323857777D-01 0.28862187909307D-01 3 19 3 15 -0.11329195473760D-13 0.50784577220504D-02 1 20 3 15 0.17805383791154D+01 0.27936846175144D-06 2 20 3 15 -0.46319515530405D+00 -0.28298393515443D-06 3 20 3 15 0.20315565853314D-13 -0.27808461071126D-07 1 1 1 16 0.10069046520912D+01 -0.75801891297613D-02 2 1 1 16 0.98296591948539D+00 -0.11414437978910D-03 3 1 1 16 0.44153365123546D+00 0.32937483792086D-06 1 2 1 16 -0.55109143599850D+00 -0.16859470164446D-02 2 2 1 16 -0.99309514956425D+00 -0.22828829356253D-02 3 2 1 16 0.57842585428574D+00 -0.65392177609816D-03 1 3 1 16 -0.13160036258649D+01 0.39440115589873D-02 2 3 1 16 -0.15794604274556D+00 -0.19553670742181D-02 3 3 1 16 -0.69577824832129D+00 -0.49956770034225D-02 1 4 1 16 -0.71675581434650D+00 -0.64643204087174D-02 2 4 1 16 -0.81535905389247D+00 -0.28061440144184D-02 3 4 1 16 -0.10601158843440D+01 -0.13474040907494D-06 1 5 1 16 0.39544003264495D+00 0.10151579064275D-01 2 5 1 16 -0.14944663858132D+00 0.46910145595019D-02 3 5 1 16 0.73236565614061D+00 -0.22460210510033D-02 1 6 1 16 0.23453182885644D+01 -0.16674234083550D-01 2 6 1 16 -0.98466804978318D+00 -0.58611420646943D-02 3 6 1 16 -0.11000385517935D+00 0.70037218515901D-01 1 7 1 16 -0.11021003754773D+00 -0.11188285938631D-01 2 7 1 16 0.35913873778794D+00 -0.20900740470023D-01 3 7 1 16 0.37344062582968D+00 -0.15954711032811D-01 1 8 1 16 -0.10827856698304D+01 0.98483646079581D-02 2 8 1 16 0.24617870014945D+01 0.81223136744876D-02 3 8 1 16 -0.16328383843285D+00 0.62236888688045D-01 1 9 1 16 0.11792543453489D+01 -0.25928368317276D-01 2 9 1 16 0.96776936133487D+00 -0.15465194806863D-01 3 9 1 16 -0.31924106243957D+01 -0.25898797147069D-06 1 10 1 16 0.12560827012672D+00 0.12330983344349D-01 2 10 1 16 -0.71340983732439D+00 0.86869267897171D-02 3 10 1 16 -0.23135068875126D+01 0.94637920869666D-01 1 11 1 16 0.28672537569089D+00 0.36001205228421D-02 2 11 1 16 -0.63256779803008D+00 0.81669387408801D-02 3 11 1 16 0.20382482901667D+01 0.92247872886413D-06 1 12 1 16 0.51208103388207D+00 -0.73998515644735D-02 2 12 1 16 0.15309479480782D+01 -0.12027406262388D-01 3 12 1 16 0.23940770338270D+01 0.29573251647813D-01 1 13 1 16 0.79957387128997D+00 0.21950053658972D-15 2 13 1 16 0.42416844527457D+00 0.55006316865666D-06 3 13 1 16 -0.13494353405142D-01 -0.14591325901191D-06 1 14 1 16 0.55662578533547D+00 0.13689665905240D-15 2 14 1 16 0.95303860896536D+00 -0.60150321622911D-02 3 14 1 16 0.27845449107739D-01 0.31834257981196D-02 1 15 1 16 0.40053634807070D+01 -0.13755915305201D-01 2 15 1 16 0.45407403845477D+01 -0.11005341543043D-01 3 15 1 16 0.15890369664995D+00 -0.69597593046933D-03 1 16 1 16 0.14018771555323D+02 0.00000000000000D+00 2 16 1 16 0.65412930989868D+01 0.13867832533663D+00 3 16 1 16 0.12534211744677D+01 0.17848228615364D+00 1 17 1 16 -0.37134095965800D-15 -0.63245001381313D-07 2 17 1 16 -0.17425885055314D+00 0.67634282606872D-03 3 17 1 16 -0.23410909939360D+00 0.23039730995280D-02 1 18 1 16 -0.23444850440090D-14 -0.17988293595826D-02 2 18 1 16 -0.16402152340575D+00 -0.13007202038268D-02 3 18 1 16 -0.49779003552923D-01 0.76211479211268D-02 1 19 1 16 -0.55152234286274D-14 -0.14541765345512D-06 2 19 1 16 -0.11972185995970D+01 0.18151934701795D-07 3 19 1 16 0.17805383791154D+01 -0.27936845545428D-06 1 20 1 16 -0.70840175106234D-14 0.27701138385526D-02 2 20 1 16 -0.11328492275163D+01 0.17771686275282D-02 3 20 1 16 0.31475421745964D+00 0.23119860455358D-01 1 1 2 16 0.11550840835894D+01 -0.16430291573627D-02 2 1 2 16 0.10331870704529D+01 -0.10190726007474D-01 3 1 2 16 -0.71922953309456D+00 0.71558839901169D-06 1 2 2 16 -0.10457860794229D+01 -0.21886711657086D-02 2 2 2 16 -0.44556139274741D+00 -0.17908386303727D-02 3 2 2 16 -0.52686513852281D+00 0.25246145760428D-03 1 3 2 16 -0.24946234683046D+00 -0.65656601002254D-02 2 3 2 16 -0.17254708423938D+01 0.11015428189473D-01 3 3 2 16 0.37915633795134D+00 -0.91334163766715D-04 1 4 2 16 -0.78575631330615D+00 -0.12548032918755D-02 2 4 2 16 -0.85394703937675D+00 -0.48041569582779D-02 3 4 2 16 0.69431667125030D+00 0.21940594421151D-07 1 5 2 16 -0.38309205658962D+00 0.35535921356556D-02 2 5 2 16 0.49139147588194D-01 -0.25472336714024D-02 3 5 2 16 0.62837224393766D-02 -0.45528123343568D-02 1 6 2 16 -0.21977909173430D+01 -0.11960701918879D-01 2 6 2 16 0.12873738576442D+01 -0.13769741829546D-02 3 6 2 16 -0.37607978775016D+00 0.65012570417141D-01 1 7 2 16 0.89171766890262D-01 -0.26609451199873D-01 2 7 2 16 -0.27797187308838D+00 -0.10193949992740D-01 3 7 2 16 0.20767249716439D+00 -0.94054658540133D-02 1 8 2 16 0.12608295382430D+01 0.12204994699754D-01 2 8 2 16 -0.23175373615651D+01 0.57779753515574D-02 3 8 2 16 -0.65422004179176D+00 0.85498412820499D-01 1 9 2 16 0.15289641943779D+01 -0.22584548497022D-01 2 9 2 16 0.15027919413291D+00 -0.23594633032802D-02 3 9 2 16 -0.21396494930190D+01 -0.94417468463857D-06 1 10 2 16 -0.67869591569543D+00 0.93344425159550D-02 2 10 2 16 -0.33478353757329D+00 -0.19639679643248D-02 3 10 2 16 -0.26016470698638D+01 0.82312268288987D-01 1 11 2 16 -0.40928988517289D+00 0.90318035260556D-02 2 11 2 16 -0.34620334871820D+00 0.69950907808249D-02 3 11 2 16 0.31960816568676D+01 0.14956826099440D-05 1 12 2 16 0.13787632836625D+01 -0.12509683799575D-01 2 12 2 16 0.65000998327061D+00 -0.12586852879376D-01 3 12 2 16 0.26120744864271D+01 0.55407714197684D-01 1 13 2 16 0.42416844527457D+00 -0.55006316855568D-06 2 13 2 16 0.84707703179603D+00 0.45047149551894D-16 3 13 2 16 0.14916776242601D+00 -0.30621673933086D-07 1 14 2 16 0.95303860896536D+00 0.60150321622907D-02 2 14 2 16 0.67736820099816D+00 -0.22450182719220D-15 3 14 2 16 0.18117068988275D+00 -0.92204988686866D-02 1 15 2 16 0.45407401985304D+01 -0.11004733036748D-01 2 15 2 16 0.42698097218778D+01 -0.74181966107354D-02 3 15 2 16 -0.20446992695352D+00 -0.36024759921540D-02 1 16 2 16 0.65413004175265D+01 -0.13867893823385D+00 2 16 2 16 0.15438927152218D+02 0.00000000000000D+00 3 16 2 16 -0.19966755567863D+01 -0.24576842909646D+00 1 17 2 16 -0.17425918532634D+00 0.67679638552004D-03 2 17 2 16 0.35895414866731D-14 0.55626929929109D-07 3 17 2 16 0.21238404067057D+00 -0.11160471241750D-02 1 18 2 16 -0.16402406394416D+00 0.13007313982929D-02 2 18 2 16 -0.23180533022016D-14 -0.41697473675397D-02 3 18 2 16 -0.84250477741821D-01 0.61727387437713D-02 1 19 2 16 -0.11972185995970D+01 -0.18151940233939D-07 2 19 2 16 -0.66249699924578D-14 0.81956010173521D-07 3 19 2 16 0.46319515530405D+00 -0.28298393597866D-06 1 20 2 16 -0.11328492275163D+01 -0.17771686275238D-02 2 20 2 16 0.32820005379261D-13 0.14887989700285D-02 3 20 2 16 -0.11586323857777D-01 0.28862187909306D-01 1 1 3 16 0.69570235660939D+00 -0.27898016116103D-02 2 1 3 16 -0.57473179760963D+00 0.59719574030920D-02 3 1 3 16 -0.44958523427863D-01 -0.12310374043769D-06 1 2 3 16 0.59817842655178D+00 0.88572067146617D-03 2 2 3 16 -0.62614459687667D+00 -0.14714487593227D-02 3 2 3 16 0.44381121288773D+00 0.16889012571152D-02 1 3 3 16 -0.38956142221445D+00 0.13481471670738D-01 2 3 3 16 0.70195143547442D+00 -0.15254249492249D-01 3 3 3 16 -0.20184457421974D+01 -0.33650333211986D-03 1 4 3 16 -0.95826380163167D+00 0.12094229383054D-01 2 4 3 16 0.84183351782030D+00 -0.70212322370555D-02 3 4 3 16 0.65032357226169D+00 0.35819906570914D-07 1 5 3 16 -0.49487343110543D-01 -0.14477814241089D-01 2 5 3 16 0.51299136639816D+00 -0.68963283496954D-02 3 5 3 16 -0.28377039333194D+01 -0.13288858565875D-01 1 6 3 16 0.90731475143180D+00 0.15657512190465D-01 2 6 3 16 0.13162303149503D+01 0.79750112227116D-02 3 6 3 16 0.32211215966646D+01 0.75223812782806D-02 1 7 3 16 -0.65422170228912D-01 -0.32433958052624D-01 2 7 3 16 0.29787887214579D+00 -0.29759813823277D-01 3 7 3 16 0.27182085584869D+01 0.31900596381035D-01 1 8 3 16 0.96407854234452D+00 0.86948716823744D-02 2 8 3 16 0.12447197071311D+01 0.19064598607904D-01 3 8 3 16 -0.29576833739170D+01 -0.87886963385079D-03 1 9 3 16 -0.20198802719665D+01 0.15121631187525D-01 2 9 3 16 -0.11306710335159D+01 0.24693145586138D-02 3 9 3 16 0.17035198209407D+01 -0.26680844392556D-05 1 10 3 16 -0.11813973042934D+01 -0.11645223633927D-01 2 10 3 16 -0.12227658592656D+01 -0.74414564454606D-02 3 10 3 16 -0.34057657659554D+01 -0.76311774053894D-01 1 11 3 16 0.87343912340423D+00 0.72677952405305D-04 2 11 3 16 0.16621987530293D+01 0.36014268524251D-02 3 11 3 16 -0.38509075865805D+01 -0.51020608759785D-06 1 12 3 16 0.12577055527437D+01 -0.79309320047603D-02 2 12 3 16 0.16372026278766D+01 -0.25871656357162D-02 3 12 3 16 0.15656387372481D+01 -0.11391631286563D-01 1 13 3 16 0.13494353405146D-01 -0.14591325901365D-06 2 13 3 16 -0.14916776242601D+00 -0.30621673933086D-07 3 13 3 16 -0.17429667864103D+01 -0.19788023486907D-15 1 14 3 16 -0.27845449107739D-01 0.31834257981196D-02 2 14 3 16 -0.18117068988275D+00 -0.92204988686866D-02 3 14 3 16 0.34417987723533D+00 0.60642834822139D-15 1 15 3 16 0.15890551258366D+00 -0.69581532588572D-03 2 15 3 16 -0.20446752567252D+00 -0.36016952142049D-02 3 15 3 16 0.12056623485435D+01 -0.99040090716819D-02 1 16 3 16 0.12533989959840D+01 -0.17847971290829D+00 2 16 3 16 -0.19967038258310D+01 0.24576823034110D+00 3 16 3 16 0.14944819687402D+02 0.00000000000000D+00 1 17 3 16 0.23410832737731D+00 -0.23050707619877D-02 2 17 3 16 0.21238464665665D+00 -0.11150492717764D-02 3 17 3 16 0.13529427884101D-13 0.89405305111735D-07 1 18 3 16 0.49779657171124D-01 0.76213733339871D-02 2 18 3 16 -0.84249717343216D-01 -0.61730325793650D-02 3 18 3 16 0.60809550556531D-14 -0.39435543142264D-03 1 19 3 16 0.17805383791154D+01 0.27936846766693D-06 2 19 3 16 -0.46319515530405D+00 -0.28298393592055D-06 3 19 3 16 -0.10327039002929D-13 -0.27808464500400D-07 1 20 3 16 0.31475421745964D+00 -0.23119860455358D-01 2 20 3 16 0.11586323857775D-01 0.28862187909306D-01 3 20 3 16 -0.13546725455146D-13 0.50784577220555D-02 1 1 1 17 -0.13160036258649D+01 0.39440115589894D-02 2 1 1 17 0.15794604274557D+00 0.19553670742051D-02 3 1 1 17 -0.69577824832151D+00 -0.49956770034411D-02 1 2 1 17 0.71675581434649D+00 0.64643204087180D-02 2 2 1 17 -0.81535905389242D+00 -0.28061440144157D-02 3 2 1 17 0.10601158843439D+01 0.13474040200727D-06 1 3 1 17 -0.10069046520912D+01 0.75801891297639D-02 2 3 1 17 0.98296591948539D+00 -0.11414437978488D-03 3 3 1 17 -0.44153365123538D+00 -0.32937484715592D-06 1 4 1 17 -0.55109143599849D+00 -0.16859470164460D-02 2 4 1 17 0.99309514956422D+00 0.22828829356255D-02 3 4 1 17 0.57842585428575D+00 -0.65392177609813D-03 1 5 1 17 0.10827856698304D+01 -0.98483646079533D-02 2 5 1 17 0.24617870014946D+01 0.81223136744643D-02 3 5 1 17 0.16328383843283D+00 -0.62236888688053D-01 1 6 1 17 0.11021003754773D+00 0.11188285938630D-01 2 6 1 17 0.35913873778795D+00 -0.20900740470025D-01 3 6 1 17 -0.37344062582968D+00 0.15954711032811D-01 1 7 1 17 0.23453182885645D+01 -0.16674234083555D-01 2 7 1 17 0.98466804978315D+00 0.58611420646934D-02 3 7 1 17 -0.11000385517927D+00 0.70037218515901D-01 1 8 1 17 0.39544003264494D+00 0.10151579064274D-01 2 8 1 17 0.14944663858131D+00 -0.46910145595024D-02 3 8 1 17 0.73236565614063D+00 -0.22460210510019D-02 1 9 1 17 0.51208103388208D+00 -0.73998515644722D-02 2 9 1 17 -0.15309479480782D+01 0.12027406262382D-01 3 9 1 17 0.23940770338269D+01 0.29573251647819D-01 1 10 1 17 0.28672537569087D+00 0.36001205228421D-02 2 10 1 17 0.63256779803009D+00 -0.81669387408801D-02 3 10 1 17 0.20382482901667D+01 0.92247872879158D-06 1 11 1 17 -0.12560827012671D+00 -0.12330983344349D-01 2 11 1 17 -0.71340983732439D+00 0.86869267897164D-02 3 11 1 17 0.23135068875126D+01 -0.94637920869662D-01 1 12 1 17 -0.11792543453489D+01 0.25928368317279D-01 2 12 1 17 0.96776936133487D+00 -0.15465194806863D-01 3 12 1 17 0.31924106243957D+01 0.25898796798333D-06 1 13 1 17 -0.90820801417698D-14 -0.27701138385525D-02 2 13 1 17 -0.11328492275163D+01 0.17771686275259D-02 3 13 1 17 -0.31475421745964D+00 -0.23119860455358D-01 1 14 1 17 -0.10475868386107D-13 0.14541766335727D-06 2 14 1 17 -0.11972185995970D+01 0.18151935576133D-07 3 14 1 17 -0.17805383791154D+01 0.27936845798027D-06 1 15 1 17 0.69656754602417D-14 0.17988293595836D-02 2 15 1 17 -0.16402152340575D+00 -0.13007202038274D-02 3 15 1 17 0.49779003552923D-01 -0.76211479211266D-02 1 16 1 17 -0.37134095965800D-15 0.63245001381313D-07 2 16 1 17 -0.17425885055314D+00 0.67634282606833D-03 3 16 1 17 0.23410909939360D+00 -0.23039730995280D-02 1 17 1 17 0.14018771555324D+02 0.00000000000000D+00 2 17 1 17 -0.65412930989866D+01 -0.13867832533663D+00 3 17 1 17 0.12534211744678D+01 0.17848228615364D+00 1 18 1 17 0.40053634807070D+01 -0.13755915305203D-01 2 18 1 17 -0.45407403845477D+01 0.11005341543039D-01 3 18 1 17 0.15890369664996D+00 -0.69597593046794D-03 1 19 1 17 0.55662578533547D+00 0.13443326796777D-15 2 19 1 17 -0.95303860896537D+00 0.60150321622906D-02 3 19 1 17 0.27845449107738D-01 0.31834257981199D-02 1 20 1 17 0.79957387128997D+00 -0.39273085784833D-15 2 20 1 17 -0.42416844527457D+00 -0.55006316866352D-06 3 20 1 17 -0.13494353405142D-01 -0.14591325895043D-06 1 1 2 17 0.24946234683046D+00 0.65656601002124D-02 2 1 2 17 -0.17254708423937D+01 0.11015428189470D-01 3 1 2 17 -0.37915633795141D+00 0.91334163740530D-04 1 2 2 17 -0.78575631330609D+00 -0.12548032918728D-02 2 2 2 17 0.85394703937671D+00 0.48041569582777D-02 3 2 2 17 0.69431667125021D+00 0.21940588786129D-07 1 3 2 17 0.11550840835894D+01 -0.16430291573585D-02 2 3 2 17 -0.10331870704528D+01 0.10190726007475D-01 3 3 2 17 -0.71922953309458D+00 0.71558839130609D-06 1 4 2 17 0.10457860794229D+01 0.21886711657089D-02 2 4 2 17 -0.44556139274741D+00 -0.17908386303745D-02 3 4 2 17 0.52686513852283D+00 -0.25246145760410D-03 1 5 2 17 0.12608295382431D+01 0.12204994699731D-01 2 5 2 17 0.23175373615651D+01 -0.57779753515384D-02 3 5 2 17 -0.65422004179177D+00 0.85498412820508D-01 1 6 2 17 0.89171766890273D-01 -0.26609451199874D-01 2 6 2 17 0.27797187308838D+00 0.10193949992739D-01 3 6 2 17 0.20767249716440D+00 -0.94054658540134D-02 1 7 2 17 0.21977909173430D+01 0.11960701918878D-01 2 7 2 17 0.12873738576441D+01 -0.13769741829541D-02 3 7 2 17 0.37607978775014D+00 -0.65012570417141D-01 1 8 2 17 0.38309205658961D+00 -0.35535921356560D-02 2 8 2 17 0.49139147588193D-01 -0.25472336714014D-02 3 8 2 17 -0.62837224393961D-02 0.45528123343570D-02 1 9 2 17 -0.13787632836625D+01 0.12509683799570D-01 2 9 2 17 0.65000998327061D+00 -0.12586852879374D-01 3 9 2 17 -0.26120744864271D+01 -0.55407714197692D-01 1 10 2 17 0.40928988517290D+00 -0.90318035260556D-02 2 10 2 17 -0.34620334871824D+00 0.69950907808238D-02 3 10 2 17 -0.31960816568676D+01 -0.14956826101997D-05 1 11 2 17 -0.67869591569543D+00 0.93344425159542D-02 2 11 2 17 0.33478353757332D+00 0.19639679643251D-02 3 11 2 17 -0.26016470698638D+01 0.82312268288983D-01 1 12 2 17 0.15289641943779D+01 -0.22584548497022D-01 2 12 2 17 -0.15027919413289D+00 0.23594633032794D-02 3 12 2 17 -0.21396494930190D+01 -0.94417468183378D-06 1 13 2 17 -0.11328492275163D+01 -0.17771686275261D-02 2 13 2 17 0.32820188338378D-13 -0.14887989700285D-02 3 13 2 17 -0.11586323857773D-01 0.28862187909305D-01 1 14 2 17 -0.11972185995970D+01 -0.18151939358734D-07 2 14 2 17 0.14603795158533D-13 -0.81956012768501D-07 3 14 2 17 0.46319515530405D+00 -0.28298393519432D-06 1 15 2 17 -0.16402406394416D+00 0.13007313982924D-02 2 15 2 17 0.93754086492157D-14 0.41697473675397D-02 3 15 2 17 -0.84250477741827D-01 0.61727387437712D-02 1 16 2 17 -0.17425918532634D+00 0.67679638551965D-03 2 16 2 17 0.35895414866731D-14 -0.55626929929109D-07 3 16 2 17 0.21238404067057D+00 -0.11160471241744D-02 1 17 2 17 -0.65413004175264D+01 0.13867893823385D+00 2 17 2 17 0.15438927152217D+02 0.00000000000000D+00 3 17 2 17 0.19966755567862D+01 0.24576842909646D+00 1 18 2 17 -0.45407401985304D+01 0.11004733036744D-01 2 18 2 17 0.42698097218778D+01 -0.74181966107367D-02 3 18 2 17 0.20446992695353D+00 0.36024759921557D-02 1 19 2 17 -0.95303860896537D+00 -0.60150321622911D-02 2 19 2 17 0.67736820099815D+00 0.11725665621035D-15 3 19 2 17 -0.18117068988275D+00 0.92204988686867D-02 1 20 2 17 -0.42416844527457D+00 0.55006316854882D-06 2 20 2 17 0.84707703179603D+00 0.12973870730074D-15 3 20 2 17 -0.14916776242600D+00 0.30621673572871D-07 1 1 3 17 -0.38956142221468D+00 0.13481471670719D-01 2 1 3 17 -0.70195143547449D+00 0.15254249492223D-01 3 1 3 17 -0.20184457421977D+01 -0.33650333214228D-03 1 2 3 17 0.95826380163157D+00 -0.12094229383061D-01 2 2 3 17 0.84183351782020D+00 -0.70212322370611D-02 3 2 3 17 -0.65032357226161D+00 -0.35819892962452D-07 1 3 3 17 -0.69570235660930D+00 0.27898016116011D-02 2 3 3 17 -0.57473179760965D+00 0.59719574030843D-02 3 3 3 17 0.44958523427770D-01 0.12310374548584D-06 1 4 3 17 0.59817842655179D+00 0.88572067146620D-03 2 4 3 17 0.62614459687668D+00 0.14714487593229D-02 3 4 3 17 0.44381121288779D+00 0.16889012571133D-02 1 5 3 17 -0.96407854234453D+00 -0.86948716823823D-02 2 5 3 17 0.12447197071311D+01 0.19064598607913D-01 3 5 3 17 0.29576833739170D+01 0.87886963382946D-03 1 6 3 17 0.65422170228907D-01 0.32433958052624D-01 2 6 3 17 0.29787887214580D+00 -0.29759813823277D-01 3 6 3 17 -0.27182085584869D+01 -0.31900596381032D-01 1 7 3 17 0.90731475143188D+00 0.15657512190465D-01 2 7 3 17 -0.13162303149503D+01 -0.79750112227116D-02 3 7 3 17 0.32211215966645D+01 0.75223812782813D-02 1 8 3 17 -0.49487343110528D-01 -0.14477814241087D-01 2 8 3 17 -0.51299136639818D+00 0.68963283496956D-02 3 8 3 17 -0.28377039333194D+01 -0.13288858565876D-01 1 9 3 17 0.12577055527437D+01 -0.79309320047547D-02 2 9 3 17 -0.16372026278765D+01 0.25871656357090D-02 3 9 3 17 0.15656387372481D+01 -0.11391631286558D-01 1 10 3 17 0.87343912340417D+00 0.72677952405233D-04 2 10 3 17 -0.16621987530293D+01 -0.36014268524253D-02 3 10 3 17 -0.38509075865803D+01 -0.51020608901390D-06 1 11 3 17 0.11813973042934D+01 0.11645223633930D-01 2 11 3 17 -0.12227658592657D+01 -0.74414564454641D-02 3 11 3 17 0.34057657659553D+01 0.76311774053900D-01 1 12 3 17 0.20198802719665D+01 -0.15121631187529D-01 2 12 3 17 -0.11306710335160D+01 0.24693145586166D-02 3 12 3 17 -0.17035198209407D+01 0.26680844407121D-05 1 13 3 17 -0.31475421745964D+00 0.23119860455358D-01 2 13 3 17 0.11586323857779D-01 0.28862187909305D-01 3 13 3 17 -0.17542906409855D-13 -0.50784577220555D-02 1 14 3 17 -0.17805383791154D+01 -0.27936846514181D-06 2 14 3 17 -0.46319515530406D+00 -0.28298393513447D-06 3 14 3 17 0.10323471197079D-13 0.27808461156050D-07 1 15 3 17 -0.49779657171123D-01 -0.76213733339868D-02 2 15 3 17 -0.84249717343222D-01 -0.61730325793651D-02 3 15 3 17 -0.60817888350996D-14 0.39435543142427D-03 1 16 3 17 -0.23410832737731D+00 0.23050707619877D-02 2 16 3 17 0.21238464665665D+00 -0.11150492717758D-02 3 16 3 17 0.13529427884101D-13 -0.89405305111735D-07 1 17 3 17 0.12533989959842D+01 -0.17847971290829D+00 2 17 3 17 0.19967038258309D+01 -0.24576823034110D+00 3 17 3 17 0.14944819687402D+02 0.00000000000000D+00 1 18 3 17 0.15890551258367D+00 -0.69581532588433D-03 2 18 3 17 0.20446752567252D+00 0.36016952142067D-02 3 18 3 17 0.12056623485435D+01 -0.99040090716803D-02 1 19 3 17 -0.27845449107740D-01 0.31834257981199D-02 2 19 3 17 0.18117068988275D+00 0.92204988686867D-02 3 19 3 17 0.34417987723532D+00 -0.28052837827918D-15 1 20 3 17 0.13494353405146D-01 -0.14591325895217D-06 2 20 3 17 0.14916776242601D+00 0.30621673572871D-07 3 20 3 17 -0.17429667864103D+01 -0.42365291068724D-15 1 1 1 18 -0.71675581434649D+00 -0.64643204087177D-02 2 1 1 18 0.81535905389243D+00 0.28061440144172D-02 3 1 1 18 -0.10601158843440D+01 -0.13474040882782D-06 1 2 1 18 0.13160036258649D+01 -0.39440115589865D-02 2 2 1 18 -0.15794604274555D+00 -0.19553670742223D-02 3 2 1 18 0.69577824832137D+00 0.49956770034128D-02 1 3 1 18 -0.55109143599850D+00 -0.16859470164466D-02 2 3 1 18 0.99309514956425D+00 0.22828829356266D-02 3 3 1 18 0.57842585428576D+00 -0.65392177609898D-03 1 4 1 18 -0.10069046520912D+01 0.75801891297621D-02 2 4 1 18 0.98296591948537D+00 -0.11414437978270D-03 3 4 1 18 -0.44153365123529D+00 -0.32937484775160D-06 1 5 1 18 -0.10827856698305D+01 0.98483646079582D-02 2 5 1 18 -0.24617870014943D+01 -0.81223136744886D-02 3 5 1 18 -0.16328383843289D+00 0.62236888688046D-01 1 6 1 18 -0.11021003754771D+00 -0.11188285938631D-01 2 6 1 18 -0.35913873778795D+00 0.20900740470024D-01 3 6 1 18 0.37344062582966D+00 -0.15954711032810D-01 1 7 1 18 -0.23453182885643D+01 0.16674234083568D-01 2 7 1 18 -0.98466804978318D+00 -0.58611420647175D-02 3 7 1 18 0.11000385517965D+00 -0.70037218515891D-01 1 8 1 18 -0.39544003264494D+00 -0.10151579064274D-01 2 8 1 18 -0.14944663858130D+00 0.46910145595011D-02 3 8 1 18 -0.73236565614060D+00 0.22460210510018D-02 1 9 1 18 0.28672537569089D+00 0.36001205228426D-02 2 9 1 18 0.63256779803005D+00 -0.81669387408802D-02 3 9 1 18 0.20382482901667D+01 0.92247872934603D-06 1 10 1 18 0.51208103388205D+00 -0.73998515644739D-02 2 10 1 18 -0.15309479480783D+01 0.12027406262388D-01 3 10 1 18 0.23940770338270D+01 0.29573251647813D-01 1 11 1 18 -0.11792543453489D+01 0.25928368317278D-01 2 11 1 18 0.96776936133485D+00 -0.15465194806865D-01 3 11 1 18 0.31924106243958D+01 0.25898796693098D-06 1 12 1 18 -0.12560827012671D+00 -0.12330983344347D-01 2 12 1 18 -0.71340983732440D+00 0.86869267897194D-02 3 12 1 18 0.23135068875126D+01 -0.94637920869669D-01 1 13 1 18 -0.55152217924512D-14 0.14541765375485D-06 2 13 1 18 -0.11972185995970D+01 0.18151936737424D-07 3 13 1 18 -0.17805383791154D+01 0.27936846168133D-06 1 14 1 18 0.11772171887084D-14 -0.27701138385504D-02 2 14 1 18 -0.11328492275163D+01 0.17771686275280D-02 3 14 1 18 -0.31475421745964D+00 -0.23119860455358D-01 1 15 1 18 -0.10300199825801D-14 0.63245002334032D-07 2 15 1 18 -0.17425885055315D+00 0.67634282606854D-03 3 15 1 18 0.23410909939360D+00 -0.23039730995280D-02 1 16 1 18 -0.23444850440090D-14 0.17988293595826D-02 2 16 1 18 -0.16402152340575D+00 -0.13007202038274D-02 3 16 1 18 0.49779003552917D-01 -0.76211479211268D-02 1 17 1 18 0.40053634807070D+01 -0.13755915305200D-01 2 17 1 18 -0.45407403845477D+01 0.11005341543047D-01 3 17 1 18 0.15890369664996D+00 -0.69597593047135D-03 1 18 1 18 0.14018771555323D+02 0.00000000000000D+00 2 18 1 18 -0.65412930989870D+01 -0.13867832533663D+00 3 18 1 18 0.12534211744676D+01 0.17848228615364D+00 1 19 1 18 0.79957387128999D+00 -0.89048479844230D-16 2 19 1 18 -0.42416844527457D+00 -0.55006316856634D-06 3 19 1 18 -0.13494353405146D-01 -0.14591325902604D-06 1 20 1 18 0.55662578533547D+00 0.28969074514522D-15 2 20 1 18 -0.95303860896536D+00 0.60150321622910D-02 3 20 1 18 0.27845449107738D-01 0.31834257981196D-02 1 1 2 18 0.78575631330611D+00 0.12548032918742D-02 2 1 2 18 -0.85394703937680D+00 -0.48041569582791D-02 3 1 2 18 -0.69431667125023D+00 -0.21940594227210D-07 1 2 2 18 -0.24946234683043D+00 -0.65656601002296D-02 2 2 2 18 0.17254708423938D+01 -0.11015428189478D-01 3 2 2 18 0.37915633795144D+00 -0.91334163778467D-04 1 3 2 18 0.10457860794230D+01 0.21886711657099D-02 2 3 2 18 -0.44556139274741D+00 -0.17908386303746D-02 3 3 2 18 0.52686513852284D+00 -0.25246145760384D-03 1 4 2 18 0.11550840835894D+01 -0.16430291573563D-02 2 4 2 18 -0.10331870704528D+01 0.10190726007474D-01 3 4 2 18 -0.71922953309453D+00 0.71558839133406D-06 1 5 2 18 -0.12608295382428D+01 -0.12204994699755D-01 2 5 2 18 -0.23175373615653D+01 0.57779753515545D-02 3 5 2 18 0.65422004179181D+00 -0.85498412820497D-01 1 6 2 18 -0.89171766890273D-01 0.26609451199874D-01 2 6 2 18 -0.27797187308837D+00 -0.10193949992740D-01 3 6 2 18 -0.20767249716437D+00 0.94054658540131D-02 1 7 2 18 -0.21977909173430D+01 -0.11960701918902D-01 2 7 2 18 -0.12873738576443D+01 0.13769741829587D-02 3 7 2 18 -0.37607978775034D+00 0.65012570417135D-01 1 8 2 18 -0.38309205658961D+00 0.35535921356547D-02 2 8 2 18 -0.49139147588201D-01 0.25472336714019D-02 3 8 2 18 0.62837224393668D-02 -0.45528123343562D-02 1 9 2 18 0.40928988517286D+00 -0.90318035260557D-02 2 9 2 18 -0.34620334871824D+00 0.69950907808253D-02 3 9 2 18 -0.31960816568676D+01 -0.14956826096216D-05 1 10 2 18 -0.13787632836625D+01 0.12509683799575D-01 2 10 2 18 0.65000998327061D+00 -0.12586852879375D-01 3 10 2 18 -0.26120744864272D+01 -0.55407714197684D-01 1 11 2 18 0.15289641943778D+01 -0.22584548497024D-01 2 11 2 18 -0.15027919413285D+00 0.23594633032798D-02 3 11 2 18 -0.21396494930190D+01 -0.94417468263501D-06 1 12 2 18 -0.67869591569544D+00 0.93344425159572D-02 2 12 2 18 0.33478353757330D+00 0.19639679643250D-02 3 12 2 18 -0.26016470698638D+01 0.82312268288990D-01 1 13 2 18 -0.11972185995970D+01 -0.18151938197442D-07 2 13 2 18 -0.86233742755156D-14 -0.81956009689501D-07 3 13 2 18 0.46319515530405D+00 -0.28298393584083D-06 1 14 2 18 -0.11328492275163D+01 -0.17771686275239D-02 2 14 2 18 -0.30235907363887D-13 -0.14887989700400D-02 3 14 2 18 -0.11586323857766D-01 0.28862187909308D-01 1 15 2 18 -0.17425918532636D+00 0.67679638551986D-03 2 15 2 18 0.55391001805019D-15 -0.55626930453773D-07 3 15 2 18 0.21238404067056D+00 -0.11160471241755D-02 1 16 2 18 -0.16402406394416D+00 0.13007313982924D-02 2 16 2 18 -0.23180533022016D-14 0.41697473675397D-02 3 16 2 18 -0.84250477741821D-01 0.61727387437712D-02 1 17 2 18 -0.45407401985304D+01 0.11004733036752D-01 2 17 2 18 0.42698097218778D+01 -0.74181966107333D-02 3 17 2 18 0.20446992695353D+00 0.36024759921527D-02 1 18 2 18 -0.65413004175267D+01 0.13867893823385D+00 2 18 2 18 0.15438927152218D+02 0.00000000000000D+00 3 18 2 18 0.19966755567863D+01 0.24576842909646D+00 1 19 2 18 -0.42416844527457D+00 0.55006316864599D-06 2 19 2 18 0.84707703179603D+00 0.29645728131156D-15 3 19 2 18 -0.14916776242601D+00 0.30621673608161D-07 1 20 2 18 -0.95303860896536D+00 -0.60150321622907D-02 2 20 2 18 0.67736820099816D+00 -0.94827090916110D-16 3 20 2 18 -0.18117068988275D+00 0.92204988686863D-02 1 1 3 18 -0.95826380163168D+00 0.12094229383055D-01 2 1 3 18 -0.84183351782022D+00 0.70212322370557D-02 3 1 3 18 0.65032357226175D+00 0.35819904084301D-07 1 2 3 18 0.38956142221453D+00 -0.13481471670747D-01 2 2 3 18 0.70195143547452D+00 -0.15254249492261D-01 3 2 3 18 0.20184457421975D+01 0.33650333211274D-03 1 3 3 18 0.59817842655181D+00 0.88572067146535D-03 2 3 3 18 0.62614459687669D+00 0.14714487593231D-02 3 3 3 18 0.44381121288777D+00 0.16889012571165D-02 1 4 3 18 -0.69570235660921D+00 0.27898016116005D-02 2 4 3 18 -0.57473179760961D+00 0.59719574030843D-02 3 4 3 18 0.44958523427806D-01 0.12310374408300D-06 1 5 3 18 0.96407854234447D+00 0.86948716823752D-02 2 5 3 18 -0.12447197071310D+01 -0.19064598607902D-01 3 5 3 18 -0.29576833739167D+01 -0.87886963385047D-03 1 6 3 18 -0.65422170228929D-01 -0.32433958052623D-01 2 6 3 18 -0.29787887214577D+00 0.29759813823277D-01 3 6 3 18 0.27182085584869D+01 0.31900596381037D-01 1 7 3 18 -0.90731475143150D+00 -0.15657512190454D-01 2 7 3 18 0.13162303149502D+01 0.79750112227052D-02 3 7 3 18 -0.32211215966645D+01 -0.75223812783030D-02 1 8 3 18 0.49487343110560D-01 0.14477814241087D-01 2 8 3 18 0.51299136639815D+00 -0.68963283496947D-02 3 8 3 18 0.28377039333194D+01 0.13288858565879D-01 1 9 3 18 0.87343912340415D+00 0.72677952405787D-04 2 9 3 18 -0.16621987530293D+01 -0.36014268524247D-02 3 9 3 18 -0.38509075865804D+01 -0.51020608879537D-06 1 10 3 18 0.12577055527437D+01 -0.79309320047604D-02 2 10 3 18 -0.16372026278766D+01 0.25871656357170D-02 3 10 3 18 0.15656387372481D+01 -0.11391631286563D-01 1 11 3 18 0.20198802719665D+01 -0.15121631187530D-01 2 11 3 18 -0.11306710335160D+01 0.24693145586158D-02 3 11 3 18 -0.17035198209407D+01 0.26680844404027D-05 1 12 3 18 0.11813973042934D+01 0.11645223633924D-01 2 12 3 18 -0.12227658592656D+01 -0.74414564454574D-02 3 12 3 18 0.34057657659554D+01 0.76311774053888D-01 1 13 3 18 -0.17805383791154D+01 -0.27936846144076D-06 2 13 3 18 -0.46319515530405D+00 -0.28298393578272D-06 3 13 3 18 -0.12325867550466D-13 0.27808464282407D-07 1 14 3 18 -0.31475421745964D+00 0.23119860455358D-01 2 14 3 18 0.11586323857787D-01 0.28862187909308D-01 3 14 3 18 0.16649045833703D-13 -0.50784577220494D-02 1 15 3 18 -0.23410832737730D+00 0.23050707619877D-02 2 15 3 18 0.21238464665665D+00 -0.11150492717769D-02 3 15 3 18 0.57904019005508D-14 -0.89405306693695D-07 1 16 3 18 -0.49779657171130D-01 -0.76213733339871D-02 2 16 3 18 -0.84249717343216D-01 -0.61730325793652D-02 3 16 3 18 0.60809550556531D-14 0.39435543142264D-03 1 17 3 18 0.15890551258367D+00 -0.69581532588775D-03 2 17 3 18 0.20446752567252D+00 0.36016952142036D-02 3 17 3 18 0.12056623485435D+01 -0.99040090716831D-02 1 18 3 18 0.12533989959839D+01 -0.17847971290829D+00 2 18 3 18 0.19967038258310D+01 -0.24576823034110D+00 3 18 3 18 0.14944819687401D+02 0.00000000000000D+00 1 19 3 18 0.13494353405142D-01 -0.14591325902778D-06 2 19 3 18 0.14916776242600D+00 0.30621673608161D-07 3 19 3 18 -0.17429667864102D+01 0.15424545380727D-14 1 20 3 18 -0.27845449107740D-01 0.31834257981196D-02 2 20 3 18 0.18117068988274D+00 0.92204988686863D-02 3 20 3 18 0.34417987723533D+00 0.37962172018961D-15 1 1 1 19 -0.71675581434649D+00 -0.64643204087180D-02 2 1 1 19 0.81535905389243D+00 0.28061440144175D-02 3 1 1 19 0.10601158843441D+01 0.13474040929707D-06 1 2 1 19 0.13160036258649D+01 -0.39440115589874D-02 2 2 1 19 -0.15794604274559D+00 -0.19553670742218D-02 3 2 1 19 -0.69577824832130D+00 -0.49956770034128D-02 1 3 1 19 -0.55109143599851D+00 -0.16859470164454D-02 2 3 1 19 0.99309514956424D+00 0.22828829356258D-02 3 3 1 19 -0.57842585428575D+00 0.65392177609790D-03 1 4 1 19 -0.10069046520912D+01 0.75801891297629D-02 2 4 1 19 0.98296591948542D+00 -0.11414437978378D-03 3 4 1 19 0.44153365123533D+00 0.32937484757797D-06 1 5 1 19 -0.11021003754771D+00 -0.11188285938631D-01 2 5 1 19 -0.35913873778796D+00 0.20900740470024D-01 3 5 1 19 -0.37344062582967D+00 0.15954711032811D-01 1 6 1 19 -0.10827856698304D+01 0.98483646079584D-02 2 6 1 19 -0.24617870014944D+01 -0.81223136744896D-02 3 6 1 19 0.16328383843290D+00 -0.62236888688048D-01 1 7 1 19 -0.39544003264493D+00 -0.10151579064274D-01 2 7 1 19 -0.14944663858130D+00 0.46910145595017D-02 3 7 1 19 0.73236565614060D+00 -0.22460210510010D-02 1 8 1 19 -0.23453182885643D+01 0.16674234083568D-01 2 8 1 19 -0.98466804978324D+00 -0.58611420647183D-02 3 8 1 19 -0.11000385517963D+00 0.70037218515892D-01 1 9 1 19 0.28672537569089D+00 0.36001205228415D-02 2 9 1 19 0.63256779803006D+00 -0.81669387408800D-02 3 9 1 19 -0.20382482901667D+01 -0.92247872911135D-06 1 10 1 19 0.51208103388207D+00 -0.73998515644727D-02 2 10 1 19 -0.15309479480783D+01 0.12027406262388D-01 3 10 1 19 -0.23940770338269D+01 -0.29573251647813D-01 1 11 1 19 -0.11792543453489D+01 0.25928368317278D-01 2 11 1 19 0.96776936133481D+00 -0.15465194806864D-01 3 11 1 19 -0.31924106243958D+01 -0.25898796650608D-06 1 12 1 19 -0.12560827012671D+00 -0.12330983344347D-01 2 12 1 19 -0.71340983732439D+00 0.86869267897188D-02 3 12 1 19 -0.23135068875126D+01 0.94637920869668D-01 1 13 1 19 -0.47098368995403D-15 0.17988293595823D-02 2 13 1 19 -0.16402152340575D+00 -0.13007202038262D-02 3 13 1 19 -0.49779003552910D-01 0.76211479211266D-02 1 14 1 19 -0.36558554319528D-14 0.63245000677012D-07 2 14 1 19 -0.17425885055315D+00 0.67634282606799D-03 3 14 1 19 -0.23410909939360D+00 0.23039730995281D-02 1 15 1 19 -0.68163885885927D-14 -0.27701138385510D-02 2 15 1 19 -0.11328492275163D+01 0.17771686275285D-02 3 15 1 19 0.31475421745964D+00 0.23119860455358D-01 1 16 1 19 -0.55152234286274D-14 0.14541765345512D-06 2 16 1 19 -0.11972185995970D+01 0.18151937787979D-07 3 16 1 19 0.17805383791154D+01 -0.27936846352441D-06 1 17 1 19 0.55662578533547D+00 -0.13443326796777D-15 2 17 1 19 -0.95303860896537D+00 0.60150321622911D-02 3 17 1 19 -0.27845449107740D-01 -0.31834257981199D-02 1 18 1 19 0.79957387128999D+00 0.89048479844230D-16 2 18 1 19 -0.42416844527457D+00 -0.55006316864599D-06 3 18 1 19 0.13494353405142D-01 0.14591325902778D-06 1 19 1 19 0.14018771555323D+02 0.00000000000000D+00 2 19 1 19 -0.65412930989869D+01 -0.13867832533663D+00 3 19 1 19 -0.12534211744676D+01 -0.17848228615364D+00 1 20 1 19 0.40053634807070D+01 -0.13755915305200D-01 2 20 1 19 -0.45407403845477D+01 0.11005341543047D-01 3 20 1 19 -0.15890369664997D+00 0.69597593047099D-03 1 1 2 19 0.78575631330610D+00 0.12548032918746D-02 2 1 2 19 -0.85394703937679D+00 -0.48041569582787D-02 3 1 2 19 0.69431667125025D+00 0.21940594395287D-07 1 2 2 19 -0.24946234683047D+00 -0.65656601002292D-02 2 2 2 19 0.17254708423938D+01 -0.11015428189477D-01 3 2 2 19 -0.37915633795141D+00 0.91334163778488D-04 1 3 2 19 0.10457860794229D+01 0.21886711657092D-02 2 3 2 19 -0.44556139274742D+00 -0.17908386303754D-02 3 3 2 19 -0.52686513852285D+00 0.25246145760382D-03 1 4 2 19 0.11550840835895D+01 -0.16430291573574D-02 2 4 2 19 -0.10331870704528D+01 0.10190726007476D-01 3 4 2 19 0.71922953309460D+00 -0.71558839161475D-06 1 5 2 19 -0.89171766890280D-01 0.26609451199873D-01 2 5 2 19 -0.27797187308837D+00 -0.10193949992741D-01 3 5 2 19 0.20767249716437D+00 -0.94054658540123D-02 1 6 2 19 -0.12608295382428D+01 -0.12204994699756D-01 2 6 2 19 -0.23175373615653D+01 0.57779753515536D-02 3 6 2 19 -0.65422004179184D+00 0.85498412820497D-01 1 7 2 19 -0.38309205658961D+00 0.35535921356553D-02 2 7 2 19 -0.49139147588201D-01 0.25472336714032D-02 3 7 2 19 -0.62837224393748D-02 0.45528123343574D-02 1 8 2 19 -0.21977909173431D+01 -0.11960701918903D-01 2 8 2 19 -0.12873738576443D+01 0.13769741829593D-02 3 8 2 19 0.37607978775036D+00 -0.65012570417134D-01 1 9 2 19 0.40928988517286D+00 -0.90318035260555D-02 2 9 2 19 -0.34620334871824D+00 0.69950907808249D-02 3 9 2 19 0.31960816568676D+01 0.14956826093713D-05 1 10 2 19 -0.13787632836625D+01 0.12509683799575D-01 2 10 2 19 0.65000998327061D+00 -0.12586852879375D-01 3 10 2 19 0.26120744864272D+01 0.55407714197684D-01 1 11 2 19 0.15289641943778D+01 -0.22584548497023D-01 2 11 2 19 -0.15027919413286D+00 0.23594633032802D-02 3 11 2 19 0.21396494930190D+01 0.94417468223115D-06 1 12 2 19 -0.67869591569542D+00 0.93344425159566D-02 2 12 2 19 0.33478353757330D+00 0.19639679643255D-02 3 12 2 19 0.26016470698638D+01 -0.82312268288990D-01 1 13 2 19 -0.16402406394416D+00 0.13007313982935D-02 2 13 2 19 -0.72557715125494D-15 0.41697473675394D-02 3 13 2 19 0.84250477741826D-01 -0.61727387437713D-02 1 14 2 19 -0.17425918532636D+00 0.67679638551931D-03 2 14 2 19 -0.15310374462656D-14 -0.55626931135157D-07 3 14 2 19 -0.21238404067057D+00 0.11160471241754D-02 1 15 2 19 -0.11328492275163D+01 -0.17771686275234D-02 2 15 2 19 -0.38229513141188D-13 -0.14887989700403D-02 3 15 2 19 0.11586323857777D-01 -0.28862187909307D-01 1 16 2 19 -0.11972185995970D+01 -0.18151937147755D-07 2 16 2 19 -0.66249699924578D-14 -0.81956010173521D-07 3 16 2 19 -0.46319515530405D+00 0.28298393597953D-06 1 17 2 19 -0.95303860896537D+00 -0.60150321622906D-02 2 17 2 19 0.67736820099815D+00 -0.11725665621035D-15 3 17 2 19 0.18117068988275D+00 -0.92204988686867D-02 1 18 2 19 -0.42416844527457D+00 0.55006316856634D-06 2 18 2 19 0.84707703179603D+00 -0.29645728131156D-15 3 18 2 19 0.14916776242600D+00 -0.30621673608161D-07 1 19 2 19 -0.65413004175267D+01 0.13867893823385D+00 2 19 2 19 0.15438927152218D+02 0.00000000000000D+00 3 19 2 19 -0.19966755567862D+01 -0.24576842909646D+00 1 20 2 19 -0.45407401985304D+01 0.11004733036752D-01 2 20 2 19 0.42698097218778D+01 -0.74181966107337D-02 3 20 2 19 -0.20446992695353D+00 -0.36024759921527D-02 1 1 3 19 0.95826380163169D+00 -0.12094229383054D-01 2 1 3 19 0.84183351782022D+00 -0.70212322370555D-02 3 1 3 19 0.65032357226186D+00 0.35819907301323D-07 1 2 3 19 -0.38956142221445D+00 0.13481471670747D-01 2 2 3 19 -0.70195143547449D+00 0.15254249492261D-01 3 2 3 19 0.20184457421975D+01 0.33650333210863D-03 1 3 3 19 -0.59817842655179D+00 -0.88572067146643D-03 2 3 3 19 -0.62614459687669D+00 -0.14714487593231D-02 3 3 3 19 0.44381121288777D+00 0.16889012571149D-02 1 4 3 19 0.69570235660927D+00 -0.27898016116007D-02 2 4 3 19 0.57473179760966D+00 -0.59719574030846D-02 3 4 3 19 0.44958523427707D-01 0.12310374548693D-06 1 5 3 19 0.65422170228921D-01 0.32433958052624D-01 2 5 3 19 0.29787887214576D+00 -0.29759813823276D-01 3 5 3 19 0.27182085584868D+01 0.31900596381035D-01 1 6 3 19 -0.96407854234447D+00 -0.86948716823772D-02 2 6 3 19 0.12447197071310D+01 0.19064598607902D-01 3 6 3 19 -0.29576833739166D+01 -0.87886963385058D-03 1 7 3 19 -0.49487343110555D-01 -0.14477814241087D-01 2 7 3 19 -0.51299136639816D+00 0.68963283496959D-02 3 7 3 19 0.28377039333194D+01 0.13288858565878D-01 1 8 3 19 0.90731475143151D+00 0.15657512190455D-01 2 8 3 19 -0.13162303149501D+01 -0.79750112227050D-02 3 8 3 19 -0.32211215966646D+01 -0.75223812783034D-02 1 9 3 19 -0.87343912340415D+00 -0.72677952405556D-04 2 9 3 19 0.16621987530294D+01 0.36014268524245D-02 3 9 3 19 -0.38509075865804D+01 -0.51020608859169D-06 1 10 3 19 -0.12577055527437D+01 0.79309320047605D-02 2 10 3 19 0.16372026278766D+01 -0.25871656357169D-02 3 10 3 19 0.15656387372481D+01 -0.11391631286562D-01 1 11 3 19 -0.20198802719665D+01 0.15121631187530D-01 2 11 3 19 0.11306710335159D+01 -0.24693145586162D-02 3 11 3 19 -0.17035198209408D+01 0.26680844418372D-05 1 12 3 19 -0.11813973042934D+01 -0.11645223633924D-01 2 12 3 19 0.12227658592656D+01 0.74414564454577D-02 3 12 3 19 0.34057657659554D+01 0.76311774053888D-01 1 13 3 19 0.49779657171136D-01 0.76213733339868D-02 2 13 3 19 0.84249717343221D-01 0.61730325793650D-02 3 13 3 19 0.12076159388629D-13 0.39435543142286D-03 1 14 3 19 0.23410832737730D+00 -0.23050707619876D-02 2 14 3 19 -0.21238464665665D+00 0.11150492717767D-02 3 14 3 19 -0.30771083728822D-14 -0.89405305320594D-07 1 15 3 19 0.31475421745964D+00 -0.23119860455358D-01 2 15 3 19 -0.11586323857776D-01 -0.28862187909307D-01 3 15 3 19 -0.11328573751576D-13 -0.50784577220504D-02 1 16 3 19 0.17805383791154D+01 0.27936845959680D-06 2 16 3 19 0.46319515530405D+00 0.28298393591795D-06 3 16 3 19 -0.10327039002929D-13 0.27808464500400D-07 1 17 3 19 0.27845449107738D-01 -0.31834257981199D-02 2 17 3 19 -0.18117068988275D+00 -0.92204988686867D-02 3 17 3 19 0.34417987723532D+00 0.28052837827918D-15 1 18 3 19 -0.13494353405146D-01 0.14591325902604D-06 2 18 3 19 -0.14916776242601D+00 -0.30621673608161D-07 3 18 3 19 -0.17429667864102D+01 -0.15424545380727D-14 1 19 3 19 -0.12533989959839D+01 0.17847971290829D+00 2 19 3 19 -0.19967038258310D+01 0.24576823034110D+00 3 19 3 19 0.14944819687401D+02 0.00000000000000D+00 1 20 3 19 -0.15890551258368D+00 0.69581532588738D-03 2 20 3 19 -0.20446752567252D+00 -0.36016952142037D-02 3 20 3 19 0.12056623485435D+01 -0.99040090716822D-02 1 1 1 20 -0.13160036258649D+01 0.39440115589883D-02 2 1 1 20 0.15794604274555D+00 0.19553670742045D-02 3 1 1 20 0.69577824832154D+00 0.49956770034411D-02 1 2 1 20 0.71675581434651D+00 0.64643204087172D-02 2 2 1 20 -0.81535905389246D+00 -0.28061440144148D-02 3 2 1 20 -0.10601158843441D+01 -0.13474040178195D-06 1 3 1 20 -0.10069046520912D+01 0.75801891297652D-02 2 3 1 20 0.98296591948538D+00 -0.11414437978449D-03 3 3 1 20 0.44153365123533D+00 0.32937484709504D-06 1 4 1 20 -0.55109143599850D+00 -0.16859470164449D-02 2 4 1 20 0.99309514956425D+00 0.22828829356239D-02 3 4 1 20 -0.57842585428576D+00 0.65392177609878D-03 1 5 1 20 0.11021003754773D+00 0.11188285938629D-01 2 5 1 20 0.35913873778794D+00 -0.20900740470025D-01 3 5 1 20 0.37344062582968D+00 -0.15954711032811D-01 1 6 1 20 0.10827856698304D+01 -0.98483646079538D-02 2 6 1 20 0.24617870014945D+01 0.81223136744646D-02 3 6 1 20 -0.16328383843285D+00 0.62236888688054D-01 1 7 1 20 0.39544003264493D+00 0.10151579064272D-01 2 7 1 20 0.14944663858130D+00 -0.46910145595033D-02 3 7 1 20 -0.73236565614063D+00 0.22460210510024D-02 1 8 1 20 0.23453182885645D+01 -0.16674234083554D-01 2 8 1 20 0.98466804978307D+00 0.58611420646933D-02 3 8 1 20 0.11000385517929D+00 -0.70037218515903D-01 1 9 1 20 0.51208103388208D+00 -0.73998515644720D-02 2 9 1 20 -0.15309479480782D+01 0.12027406262383D-01 3 9 1 20 -0.23940770338269D+01 -0.29573251647818D-01 1 10 1 20 0.28672537569085D+00 0.36001205228410D-02 2 10 1 20 0.63256779803007D+00 -0.81669387408799D-02 3 10 1 20 -0.20382482901667D+01 -0.92247872872600D-06 1 11 1 20 -0.12560827012670D+00 -0.12330983344349D-01 2 11 1 20 -0.71340983732439D+00 0.86869267897160D-02 3 11 1 20 -0.23135068875125D+01 0.94637920869662D-01 1 12 1 20 -0.11792543453489D+01 0.25928368317279D-01 2 12 1 20 0.96776936133488D+00 -0.15465194806862D-01 3 12 1 20 -0.31924106243957D+01 -0.25898796819903D-06 1 13 1 20 -0.18781594496572D-14 0.63244999801768D-07 2 13 1 20 -0.17425885055314D+00 0.67634282606854D-03 3 13 1 20 -0.23410909939360D+00 0.23039730995278D-02 1 14 1 20 0.90890382790055D-14 0.17988293595832D-02 2 14 1 20 -0.16402152340575D+00 -0.13007202038274D-02 3 14 1 20 -0.49779003552911D-01 0.76211479211258D-02 1 15 1 20 -0.10475649533341D-13 0.14541766393400D-06 2 15 1 20 -0.11972185995970D+01 0.18151936065336D-07 3 15 1 20 0.17805383791154D+01 -0.27936845760892D-06 1 16 1 20 -0.70836786974445D-14 -0.27701138385526D-02 2 16 1 20 -0.11328492275163D+01 0.17771686275264D-02 3 16 1 20 0.31475421745964D+00 0.23119860455358D-01 1 17 1 20 0.79957387128997D+00 0.39273085784833D-15 2 17 1 20 -0.42416844527457D+00 -0.55006316854882D-06 3 17 1 20 0.13494353405146D-01 0.14591325895217D-06 1 18 1 20 0.55662578533547D+00 -0.28969074514522D-15 2 18 1 20 -0.95303860896536D+00 0.60150321622907D-02 3 18 1 20 -0.27845449107740D-01 -0.31834257981196D-02 1 19 1 20 0.40053634807070D+01 -0.13755915305203D-01 2 19 1 20 -0.45407403845477D+01 0.11005341543039D-01 3 19 1 20 -0.15890369664997D+00 0.69597593046830D-03 1 20 1 20 0.14018771555323D+02 0.00000000000000D+00 2 20 1 20 -0.65412930989866D+01 -0.13867832533663D+00 3 20 1 20 -0.12534211744679D+01 -0.17848228615364D+00 1 1 2 20 0.24946234683043D+00 0.65656601002118D-02 2 1 2 20 -0.17254708423937D+01 0.11015428189467D-01 3 1 2 20 0.37915633795141D+00 -0.91334163740795D-04 1 2 2 20 -0.78575631330613D+00 -0.12548032918718D-02 2 2 2 20 0.85394703937677D+00 0.48041569582769D-02 3 2 2 20 -0.69431667125029D+00 -0.21940588601265D-07 1 3 2 20 0.11550840835894D+01 -0.16430291573581D-02 2 3 2 20 -0.10331870704528D+01 0.10190726007474D-01 3 3 2 20 0.71922953309458D+00 -0.71558839110799D-06 1 4 2 20 0.10457860794230D+01 0.21886711657072D-02 2 4 2 20 -0.44556139274742D+00 -0.17908386303741D-02 3 4 2 20 -0.52686513852283D+00 0.25246145760424D-03 1 5 2 20 0.89171766890258D-01 -0.26609451199875D-01 2 5 2 20 0.27797187308838D+00 0.10193949992741D-01 3 5 2 20 -0.20767249716440D+00 0.94054658540133D-02 1 6 2 20 0.12608295382429D+01 0.12204994699731D-01 2 6 2 20 0.23175373615651D+01 -0.57779753515374D-02 3 6 2 20 0.65422004179177D+00 -0.85498412820508D-01 1 7 2 20 0.38309205658961D+00 -0.35535921356569D-02 2 7 2 20 0.49139147588191D-01 -0.25472336714021D-02 3 7 2 20 0.62837224393899D-02 -0.45528123343571D-02 1 8 2 20 0.21977909173430D+01 0.11960701918878D-01 2 8 2 20 0.12873738576441D+01 -0.13769741829547D-02 3 8 2 20 -0.37607978775016D+00 0.65012570417141D-01 1 9 2 20 -0.13787632836625D+01 0.12509683799570D-01 2 9 2 20 0.65000998327061D+00 -0.12586852879374D-01 3 9 2 20 0.26120744864271D+01 0.55407714197691D-01 1 10 2 20 0.40928988517288D+00 -0.90318035260554D-02 2 10 2 20 -0.34620334871824D+00 0.69950907808254D-02 3 10 2 20 0.31960816568675D+01 0.14956826104499D-05 1 11 2 20 -0.67869591569542D+00 0.93344425159538D-02 2 11 2 20 0.33478353757333D+00 0.19639679643254D-02 3 11 2 20 0.26016470698638D+01 -0.82312268288983D-01 1 12 2 20 0.15289641943779D+01 -0.22584548497021D-01 2 12 2 20 -0.15027919413288D+00 0.23594633032794D-02 3 12 2 20 0.21396494930190D+01 0.94417468154578D-06 1 13 2 20 -0.17425918532635D+00 0.67679638551987D-03 2 13 2 20 0.23131123037650D-14 -0.55626929812878D-07 3 13 2 20 -0.21238404067058D+00 0.11160471241736D-02 1 14 2 20 -0.16402406394416D+00 0.13007313982924D-02 2 14 2 20 0.95627589521253D-14 0.41697473675394D-02 3 14 2 20 0.84250477741830D-01 -0.61727387437712D-02 1 15 2 20 -0.11972185995970D+01 -0.18151938870398D-07 2 15 2 20 0.16602252790088D-13 -0.81956012037514D-07 3 15 2 20 -0.46319515530405D+00 0.28298393521341D-06 1 16 2 20 -0.11328492275163D+01 -0.17771686275256D-02 2 16 2 20 0.32820188338378D-13 -0.14887989700285D-02 3 16 2 20 0.11586323857775D-01 -0.28862187909306D-01 1 17 2 20 -0.42416844527457D+00 0.55006316866352D-06 2 17 2 20 0.84707703179603D+00 -0.12973870730074D-15 3 17 2 20 0.14916776242601D+00 -0.30621673572871D-07 1 18 2 20 -0.95303860896536D+00 -0.60150321622910D-02 2 18 2 20 0.67736820099816D+00 0.94827090916110D-16 3 18 2 20 0.18117068988274D+00 -0.92204988686863D-02 1 19 2 20 -0.45407401985304D+01 0.11004733036744D-01 2 19 2 20 0.42698097218778D+01 -0.74181966107363D-02 3 19 2 20 -0.20446992695353D+00 -0.36024759921557D-02 1 20 2 20 -0.65413004175264D+01 0.13867893823385D+00 2 20 2 20 0.15438927152217D+02 0.00000000000000D+00 3 20 2 20 -0.19966755567864D+01 -0.24576842909646D+00 1 1 3 20 0.38956142221469D+00 -0.13481471670719D-01 2 1 3 20 0.70195143547449D+00 -0.15254249492223D-01 3 1 3 20 -0.20184457421977D+01 -0.33650333214056D-03 1 2 3 20 -0.95826380163168D+00 0.12094229383062D-01 2 2 3 20 -0.84183351782026D+00 0.70212322370613D-02 3 2 3 20 -0.65032357226175D+00 -0.35819893517031D-07 1 3 3 20 0.69570235660927D+00 -0.27898016116012D-02 2 3 3 20 0.57473179760963D+00 -0.59719574030841D-02 3 3 3 20 0.44958523427771D-01 0.12310374800410D-06 1 4 3 20 -0.59817842655181D+00 -0.88572067146555D-03 2 4 3 20 -0.62614459687668D+00 -0.14714487593227D-02 3 4 3 20 0.44381121288776D+00 0.16889012571153D-02 1 5 3 20 -0.65422170228906D-01 -0.32433958052623D-01 2 5 3 20 -0.29787887214580D+00 0.29759813823277D-01 3 5 3 20 -0.27182085584869D+01 -0.31900596381032D-01 1 6 3 20 0.96407854234451D+00 0.86948716823834D-02 2 6 3 20 -0.12447197071311D+01 -0.19064598607913D-01 3 6 3 20 0.29576833739171D+01 0.87886963382940D-03 1 7 3 20 0.49487343110530D-01 0.14477814241088D-01 2 7 3 20 0.51299136639817D+00 -0.68963283496957D-02 3 7 3 20 -0.28377039333194D+01 -0.13288858565876D-01 1 8 3 20 -0.90731475143185D+00 -0.15657512190466D-01 2 8 3 20 0.13162303149503D+01 0.79750112227119D-02 3 8 3 20 0.32211215966645D+01 0.75223812782811D-02 1 9 3 20 -0.12577055527437D+01 0.79309320047550D-02 2 9 3 20 0.16372026278765D+01 -0.25871656357093D-02 3 9 3 20 0.15656387372480D+01 -0.11391631286560D-01 1 10 3 20 -0.87343912340415D+00 -0.72677952405171D-04 2 10 3 20 0.16621987530293D+01 0.36014268524255D-02 3 10 3 20 -0.38509075865803D+01 -0.51020608976021D-06 1 11 3 20 -0.11813973042933D+01 -0.11645223633930D-01 2 11 3 20 0.12227658592656D+01 0.74414564454641D-02 3 11 3 20 0.34057657659553D+01 0.76311774053900D-01 1 12 3 20 -0.20198802719665D+01 0.15121631187528D-01 2 12 3 20 0.11306710335160D+01 -0.24693145586169D-02 3 12 3 20 -0.17035198209407D+01 0.26680844420943D-05 1 13 3 20 0.23410832737731D+00 -0.23050707619879D-02 2 13 3 20 -0.21238464665666D+00 0.11150492717749D-02 3 13 3 20 0.71555242791750D-14 -0.89405304253812D-07 1 14 3 20 0.49779657171135D-01 0.76213733339861D-02 2 14 3 20 0.84249717343225D-01 0.61730325793652D-02 3 14 3 20 0.29110177685894D-14 0.39435543142434D-03 1 15 3 20 0.17805383791154D+01 0.27936846550883D-06 2 15 3 20 0.46319515530406D+00 0.28298393515356D-06 3 15 3 20 0.20315565853314D-13 0.27808461071126D-07 1 16 3 20 0.31475421745964D+00 -0.23119860455358D-01 2 16 3 20 -0.11586323857777D-01 -0.28862187909306D-01 3 16 3 20 -0.13546103732962D-13 -0.50784577220555D-02 1 17 3 20 -0.13494353405142D-01 0.14591325895043D-06 2 17 3 20 -0.14916776242600D+00 -0.30621673572871D-07 3 17 3 20 -0.17429667864103D+01 0.42365291068724D-15 1 18 3 20 0.27845449107738D-01 -0.31834257981196D-02 2 18 3 20 -0.18117068988275D+00 -0.92204988686863D-02 3 18 3 20 0.34417987723533D+00 -0.37962172018961D-15 1 19 3 20 -0.15890551258368D+00 0.69581532588470D-03 2 19 3 20 -0.20446752567252D+00 -0.36016952142066D-02 3 19 3 20 0.12056623485435D+01 -0.99040090716811D-02 1 20 3 20 -0.12533989959842D+01 0.17847971290829D+00 2 20 3 20 -0.19967038258311D+01 0.24576823034110D+00 3 20 3 20 0.14944819687401D+02 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 3600 qpt 0.00000000E+00 0.00000000E+00 5.00000000E-01 1.0 1 1 1 1 0.81158056599706D+01 0.00000000000000D+00 2 1 1 1 0.12425079410484D+01 0.56527595965351D-06 3 1 1 1 -0.43274462731545D-13 -0.11102230246252D-15 1 2 1 1 -0.12299082979363D-13 -0.92499190759683D-15 2 2 1 1 0.21122624073297D-14 -0.22959217624927D-16 3 2 1 1 0.21187908855226D-01 -0.15151456242411D-07 1 3 1 1 -0.12235792755569D+01 0.37021528865367D-17 2 3 1 1 0.45025294740235D-01 -0.19636538421549D-09 3 3 1 1 -0.10476512820491D-15 -0.15205275863968D-15 1 4 1 1 -0.96390947014514D-14 0.15535245440770D-14 2 4 1 1 0.28428082883005D-14 0.13301770055413D-16 3 4 1 1 0.10469195529696D+00 0.16874976144604D-08 1 5 1 1 0.18263572863994D+01 -0.10463366534520D-01 2 5 1 1 -0.46856744436333D+00 -0.80924301391362D-03 3 5 1 1 0.14555098926400D-01 -0.25701753683843D-01 1 6 1 1 0.18263572863994D+01 -0.10463366534521D-01 2 6 1 1 -0.46856744436333D+00 -0.80924301391361D-03 3 6 1 1 -0.14555098926397D-01 0.25701753683843D-01 1 7 1 1 -0.34562685163368D+01 -0.23019407447613D-01 2 7 1 1 -0.18339418079305D+00 0.17890360038478D-02 3 7 1 1 0.16399621792101D+00 0.10845446110012D-01 1 8 1 1 -0.34562685163368D+01 -0.23019407447614D-01 2 8 1 1 -0.18339418079305D+00 0.17890360038479D-02 3 8 1 1 -0.16399621792102D+00 -0.10845446110012D-01 1 9 1 1 -0.76755469253953D+00 0.14826279891263D-07 2 9 1 1 -0.19313551784220D+00 0.19055500716071D-07 3 9 1 1 0.51409000856804D-16 0.80293788030953D-16 1 10 1 1 0.83120607043200D-14 0.10477725257320D-15 2 10 1 1 -0.12418427186188D-14 0.90273358663087D-17 3 10 1 1 -0.29268300004256D+00 0.67698843830787D-09 1 11 1 1 -0.84012011616232D-14 -0.11951492198691D-14 2 11 1 1 -0.56163417776507D-15 -0.76617967371197D-17 3 11 1 1 -0.14795965101577D-01 -0.30231350401810D-08 1 12 1 1 -0.11892115849383D+01 0.19615680584737D-07 2 12 1 1 0.46457196943739D+00 0.15522167509915D-07 3 12 1 1 -0.99392474653869D-16 -0.12093939348741D-15 1 13 1 1 -0.15288463293568D+00 -0.18495133994505D-08 2 13 1 1 -0.15279386361997D+00 0.28812252535948D-08 3 13 1 1 0.50339059316387D+00 0.18860126330409D-07 1 14 1 1 -0.35649811871904D-01 -0.22976920010702D-04 2 14 1 1 0.18553487339992D+00 0.23699499276419D-02 3 14 1 1 0.29484470087080D+00 -0.79704964006709D-02 1 15 1 1 0.35649811871902D-01 0.22976920009910D-04 2 15 1 1 -0.18553487339992D+00 -0.23699499276410D-02 3 15 1 1 0.29484470087082D+00 -0.79704964006734D-02 1 16 1 1 -0.15288463293569D+00 -0.18495129639201D-08 2 16 1 1 -0.15279386361995D+00 0.28812254658182D-08 3 16 1 1 -0.50339059316387D+00 -0.18860126499190D-07 1 17 1 1 -0.60909284293523D+00 -0.98141360211217D-02 2 17 1 1 -0.33776741098261D+00 -0.16831199647224D-01 3 17 1 1 -0.65607960698299D+00 -0.51932790800396D-02 1 18 1 1 0.11319999201775D+00 -0.15934551332230D-06 2 18 1 1 -0.43655032002932D+00 0.68847982421329D-07 3 18 1 1 0.71530282007185D+00 -0.24996742098557D-06 1 19 1 1 -0.11319999201775D+00 0.15934551342783D-06 2 19 1 1 0.43655032002932D+00 -0.68847984565514D-07 3 19 1 1 0.71530282007181D+00 -0.24996742841004D-06 1 20 1 1 -0.60909284293523D+00 -0.98141360211214D-02 2 20 1 1 -0.33776741098263D+00 -0.16831199647224D-01 3 20 1 1 0.65607960698300D+00 0.51932790800395D-02 1 1 2 1 0.12425044384668D+01 0.62896951241311D-06 2 1 2 1 0.80124818826371D+01 0.00000000000000D+00 3 1 2 1 -0.28603959322471D-13 -0.11102230246252D-15 1 2 2 1 0.21122624073039D-14 -0.22959217624927D-16 2 2 2 1 -0.60472418986678D-16 -0.50322539185304D-15 3 2 2 1 0.39711352324452D+00 0.76397089629301D-08 1 3 2 1 -0.45025294740247D-01 -0.19636538421549D-09 2 3 2 1 -0.13325896105438D+01 -0.80686683344946D-18 3 3 2 1 -0.27948668723051D-15 0.26529336640999D-17 1 4 2 1 0.28428082883005D-14 0.12000727448431D-16 2 4 2 1 0.82488655889723D-14 0.84327345000756D-15 3 4 2 1 -0.11681239788156D+00 0.50914751147095D-08 1 5 2 1 0.10243565881652D+00 0.10543373934863D-02 2 5 2 1 -0.35240726170191D+01 0.27589762282391D-01 3 5 2 1 0.19222618575798D+01 -0.12427612256765D-02 1 6 2 1 0.10243565881652D+00 0.10543373934863D-02 2 6 2 1 -0.35240726170191D+01 0.27589762282392D-01 3 6 2 1 -0.19222618575798D+01 0.12427612256773D-02 1 7 2 1 -0.46740396775780D+00 0.45331725949606D-02 2 7 2 1 0.17962833935334D+01 -0.33133797522056D-02 3 7 2 1 -0.85214487240036D+00 0.11842339030056D-01 1 8 2 1 -0.46740396775780D+00 0.45331725949606D-02 2 8 2 1 0.17962833935334D+01 -0.33133797522060D-02 3 8 2 1 0.85214487240036D+00 -0.11842339030056D-01 1 9 2 1 -0.35247003652189D+00 -0.27792333538141D-08 2 9 2 1 0.90289184219296D-01 0.31321176926496D-09 3 9 2 1 -0.96692846683775D-15 -0.30543483793846D-16 1 10 2 1 -0.12418844428238D-14 0.85936549973145D-17 2 10 2 1 0.89544433424382D-14 -0.12638620515966D-14 3 10 2 1 0.10078806932196D+00 -0.41034437445113D-08 1 11 2 1 -0.56163417771337D-15 -0.76617967371195D-17 2 11 2 1 -0.76612004798218D-14 0.12931222620741D-14 3 11 2 1 -0.10729816381845D+00 0.66063303210849D-09 1 12 2 1 0.55591842353409D+00 0.54455073680454D-08 2 12 2 1 -0.69995698096841D+00 0.68322125719267D-08 3 12 2 1 0.11305910062520D-14 0.12003141605639D-15 1 13 2 1 -0.28523624517146D+00 0.10409474773239D-07 2 13 2 1 -0.45120332247539D+00 0.49576435006825D-08 3 13 2 1 -0.39989241120040D+00 -0.22829861291827D-07 1 14 2 1 0.34323295459547D-01 -0.14054410318700D-02 2 14 2 1 -0.28218054671131D+00 -0.18748612809698D-02 3 14 2 1 -0.28412783100749D+00 0.25528681093146D-02 1 15 2 1 -0.34323295459550D-01 0.14054410318709D-02 2 15 2 1 0.28218054671132D+00 0.18748612809690D-02 3 15 2 1 -0.28412783100749D+00 0.25528681093169D-02 1 16 2 1 -0.28523624517143D+00 0.10409474985463D-07 2 16 2 1 -0.45120332247539D+00 0.49576435056172D-08 3 16 2 1 0.39989241120033D+00 0.22829860413774D-07 1 17 2 1 -0.45556429278286D+00 -0.22118327089461D-01 2 17 2 1 -0.84871976741020D+00 -0.13216417488587D-01 3 17 2 1 -0.86610704929422D+00 0.57210474409347D-02 1 18 2 1 -0.36430894697398D+00 0.48208171750847D-07 2 18 2 1 0.29421586446542D+00 -0.90674459663425D-07 3 18 2 1 0.51794483325804D+00 -0.10624453098218D-06 1 19 2 1 0.36430894697398D+00 -0.48208173895031D-07 2 19 2 1 -0.29421586446542D+00 0.90674460129711D-07 3 19 2 1 0.51794483325805D+00 -0.10624453635006D-06 1 20 2 1 -0.45556429278288D+00 -0.22118327089460D-01 2 20 2 1 -0.84871976741019D+00 -0.13216417488587D-01 3 20 2 1 0.86610704929423D+00 -0.57210474409353D-02 1 1 3 1 -0.43274462734854D-13 0.11102230246252D-15 2 1 3 1 -0.28603959309236D-13 0.00000000000000D+00 3 1 3 1 0.16991837925641D+02 0.00000000000000D+00 1 2 3 1 0.21184102996314D-01 0.16786813380189D-07 2 2 3 1 0.39711566111395D+00 -0.93305782194912D-08 3 2 3 1 0.34698883716413D-13 -0.13590809683826D-13 1 3 3 1 -0.10476512841170D-15 -0.15205275863968D-15 2 3 3 1 -0.27948668805769D-15 0.26529336640997D-17 3 3 3 1 0.40631824018541D+01 0.33616417185091D-18 1 4 3 1 -0.10469195529699D+00 0.16874976144604D-08 2 4 3 1 -0.11681239788157D+00 -0.50914749092855D-08 3 4 3 1 -0.19642695965852D-13 -0.11911170051970D-13 1 5 3 1 0.85450894627636D+00 0.26187666464878D-01 2 5 3 1 0.14775204471388D+01 -0.66069692373033D-02 3 5 3 1 0.27721741461292D+01 0.15542347152459D-01 1 6 3 1 -0.85450894627636D+00 -0.26187666464879D-01 2 6 3 1 -0.14775204471388D+01 0.66069692373042D-02 3 6 3 1 0.27721741461292D+01 0.15542347152455D-01 1 7 3 1 -0.78637741158040D+00 0.26696088749249D-01 2 7 3 1 -0.72999044866356D+00 0.16551315724606D-01 3 7 3 1 0.29269557900194D+01 -0.10026035311489D-01 1 8 3 1 0.78637741158040D+00 -0.26696088749249D-01 2 8 3 1 0.72999044866356D+00 -0.16551315724606D-01 3 8 3 1 0.29269557900194D+01 -0.10026035311487D-01 1 9 3 1 0.51409000856804D-16 0.80293788030953D-16 2 9 3 1 -0.96692846683775D-15 -0.30543483793847D-16 3 9 3 1 -0.76350971274507D+01 0.26017804865294D-07 1 10 3 1 0.18107892807839D+00 -0.29184833718983D-08 2 10 3 1 -0.34451018708669D-01 0.34097087154144D-08 3 10 3 1 0.18008226321129D-13 -0.20179737505015D-14 1 11 3 1 -0.22756514255047D+00 0.10531689492868D-07 2 11 3 1 -0.16289077714523D+00 0.69467132460601D-08 3 11 3 1 -0.12040375290666D-13 0.36917179253609D-14 1 12 3 1 -0.99392474653869D-16 -0.12093939348741D-15 2 12 3 1 0.11305910062520D-14 0.12003141605639D-15 3 12 3 1 -0.74626474160640D+01 0.11928904665887D-06 1 13 3 1 0.27355166152969D+00 -0.11581405486745D-07 2 13 3 1 -0.39677168349780D+00 0.10786792702180D-07 3 13 3 1 -0.16381316967650D+01 -0.10019959328018D-07 1 14 3 1 0.34363902348788D+00 -0.11830040968671D-02 2 14 3 1 -0.29814142361868D+00 0.37655918746181D-03 3 14 3 1 0.58931218389653D+00 0.16011952998745D-01 1 15 3 1 0.34363902348790D+00 -0.11830040968696D-02 2 15 3 1 -0.29814142361870D+00 0.37655918746415D-03 3 15 3 1 -0.58931218389646D+00 -0.16011952998750D-01 1 16 3 1 -0.27355166152969D+00 0.11581405316230D-07 2 16 3 1 0.39677168349776D+00 -0.10786793581099D-07 3 16 3 1 -0.16381316967651D+01 -0.10019956672028D-07 1 17 3 1 -0.77180569522044D+00 0.18709937733808D-02 2 17 3 1 -0.87601023640084D+00 -0.29483135551950D-02 3 17 3 1 -0.38720145901414D+01 0.56593951361140D-01 1 18 3 1 0.68280799992305D+00 -0.46232388920130D-06 2 18 3 1 0.58905314287557D+00 -0.66284182958296D-06 3 18 3 1 0.40245677350499D+00 0.63608096224688D-06 1 19 3 1 0.68280799992299D+00 -0.46232389662838D-06 2 19 3 1 0.58905314287557D+00 -0.66284183494911D-06 3 19 3 1 -0.40245677350494D+00 -0.63608096800457D-06 1 20 3 1 0.77180569522044D+00 -0.18709937733809D-02 2 20 3 1 0.87601023640088D+00 0.29483135551944D-02 3 20 3 1 -0.38720145901413D+01 0.56593951361144D-01 1 1 1 2 -0.12299082978950D-13 0.92499190759683D-15 2 1 1 2 0.21122624073297D-14 0.22959217624927D-16 3 1 1 2 0.21187908855226D-01 -0.15151455829763D-07 1 2 1 2 0.81158056599706D+01 0.00000000000000D+00 2 2 1 2 0.12425079410481D+01 0.56527595965351D-06 3 2 1 2 -0.64189858593891D-15 -0.11102230246252D-15 1 3 1 2 0.42539472666821D-14 -0.11416477705016D-14 2 3 1 2 0.10394096648390D-14 0.10668718119333D-16 3 3 1 2 0.10469195529697D+00 0.16874968729372D-08 1 4 1 2 -0.12235792755569D+01 0.19878320133070D-16 2 4 1 2 0.45025294740232D-01 -0.19636537409724D-09 3 4 1 2 0.13704736236524D-15 -0.90372723024762D-16 1 5 1 2 -0.18263572863994D+01 0.10463366534516D-01 2 5 1 2 0.46856744436333D+00 0.80924301391370D-03 3 5 1 2 -0.14555098926404D-01 0.25701753683843D-01 1 6 1 2 0.18263572863994D+01 -0.10463366534519D-01 2 6 1 2 -0.46856744436333D+00 -0.80924301391365D-03 3 6 1 2 -0.14555098926403D-01 0.25701753683843D-01 1 7 1 2 0.34562685163369D+01 0.23019407447628D-01 2 7 1 2 0.18339418079305D+00 -0.17890360038478D-02 3 7 1 2 -0.16399621792102D+00 -0.10845446110011D-01 1 8 1 2 -0.34562685163368D+01 -0.23019407447617D-01 2 8 1 2 -0.18339418079306D+00 0.17890360038478D-02 3 8 1 2 -0.16399621792100D+00 -0.10845446110012D-01 1 9 1 2 -0.33253521844294D-14 -0.71856894206794D-15 2 9 1 2 0.63490055593073D-15 0.37948387689606D-16 3 9 1 2 -0.29268300004255D+00 0.67698864680255D-09 1 10 1 2 -0.76755469253945D+00 0.14826279859409D-07 2 10 1 2 -0.19313551784223D+00 0.19055500752736D-07 3 10 1 2 -0.54502029089846D-14 0.82889094726516D-18 1 11 1 2 -0.11892115849380D+01 0.19615680603485D-07 2 11 1 2 0.46457196943756D+00 0.15522167519128D-07 3 11 1 2 -0.23290686783110D-14 0.14394574380797D-15 1 12 1 2 0.48229982388089D-14 -0.18686917471242D-15 2 12 1 2 -0.12290739035516D-14 -0.90808111663499D-17 3 12 1 2 -0.14795965101577D-01 -0.30231344198358D-08 1 13 1 2 -0.35649811871913D-01 -0.22976920009400D-04 2 13 1 2 0.18553487339993D+00 0.23699499276399D-02 3 13 1 2 0.29484470087084D+00 -0.79704964006756D-02 1 14 1 2 -0.15288463293576D+00 -0.18495125362428D-08 2 14 1 2 -0.15279386361993D+00 0.28812256357540D-08 3 14 1 2 0.50339059316381D+00 0.18860126757406D-07 1 15 1 2 -0.15288463293574D+00 -0.18495130135159D-08 2 15 1 2 -0.15279386362000D+00 0.28812253229491D-08 3 15 1 2 -0.50339059316381D+00 -0.18860126712095D-07 1 16 1 2 0.35649811871918D-01 0.22976920010060D-04 2 16 1 2 -0.18553487339994D+00 -0.23699499276409D-02 3 16 1 2 0.29484470087085D+00 -0.79704964006732D-02 1 17 1 2 0.11319999201776D+00 -0.15934551277428D-06 2 17 1 2 -0.43655032002930D+00 0.68847986322002D-07 3 17 1 2 0.71530282007164D+00 -0.24996743437843D-06 1 18 1 2 -0.60909284293518D+00 -0.98141360211208D-02 2 18 1 2 -0.33776741098257D+00 -0.16831199647224D-01 3 18 1 2 -0.65607960698287D+00 -0.51932790800398D-02 1 19 1 2 -0.60909284293518D+00 -0.98141360211213D-02 2 19 1 2 -0.33776741098251D+00 -0.16831199647224D-01 3 19 1 2 0.65607960698280D+00 0.51932790800398D-02 1 20 1 2 -0.11319999201777D+00 0.15934551188735D-06 2 20 1 2 0.43655032002933D+00 -0.68847984309018D-07 3 20 1 2 0.71530282007179D+00 -0.24996742772379D-06 1 1 2 2 0.21122624073039D-14 0.22959217624927D-16 2 1 2 2 -0.60472418986678D-16 0.50300855141854D-15 3 1 2 2 0.39711352324452D+00 0.76397108539538D-08 1 2 2 2 0.12425044384665D+01 0.62896951241311D-06 2 2 2 2 0.80124818826353D+01 0.00000000000000D+00 3 2 2 2 -0.35709386659392D-13 -0.11102230246252D-15 1 3 2 2 0.10394096648390D-14 0.93676755123504D-17 2 3 2 2 0.11751335051912D-13 0.76790007932071D-15 3 3 2 2 -0.11681239788157D+00 0.50914743722624D-08 1 4 2 2 -0.45025294740250D-01 -0.19636537409724D-09 2 4 2 2 -0.13325896105438D+01 0.18766718252071D-17 3 4 2 2 0.13155762095744D-14 0.85506615210084D-18 1 5 2 2 -0.10243565881652D+00 -0.10543373934862D-02 2 5 2 2 0.35240726170192D+01 -0.27589762282383D-01 3 5 2 2 -0.19222618575800D+01 0.12427612256717D-02 1 6 2 2 0.10243565881652D+00 0.10543373934862D-02 2 6 2 2 -0.35240726170191D+01 0.27589762282394D-01 3 6 2 2 -0.19222618575800D+01 0.12427612256772D-02 1 7 2 2 0.46740396775780D+00 -0.45331725949605D-02 2 7 2 2 -0.17962833935334D+01 0.33133797522017D-02 3 7 2 2 0.85214487240040D+00 -0.11842339030055D-01 1 8 2 2 -0.46740396775780D+00 0.45331725949605D-02 2 8 2 2 0.17962833935334D+01 -0.33133797522050D-02 3 8 2 2 0.85214487240039D+00 -0.11842339030056D-01 1 9 2 2 0.63485883162231D-15 0.37948387689606D-16 2 9 2 2 -0.10662427512620D-13 0.54429868712076D-15 3 9 2 2 0.10078806932194D+00 -0.41034437128745D-08 1 10 2 2 -0.35247003652192D+00 -0.27792333171487D-08 2 10 2 2 0.90289184219097D-01 0.31321189963797D-09 3 10 2 2 0.40380035784218D-15 0.74571703143875D-16 1 11 2 2 0.55591842353426D+00 0.54455073772579D-08 2 11 2 2 -0.69995698096862D+00 0.68322129386018D-08 3 11 2 2 -0.79474609385077D-15 0.14429581505675D-16 1 12 2 2 -0.12290739034999D-14 -0.90808111663498D-17 2 12 2 2 -0.51929900980447D-14 -0.41789593801265D-15 3 12 2 2 -0.10729816381841D+00 0.66063321779321D-09 1 13 2 2 0.34323295459559D-01 -0.14054410318720D-02 2 13 2 2 -0.28218054671127D+00 -0.18748612809672D-02 3 13 2 2 -0.28412783100751D+00 0.25528681093192D-02 1 14 2 2 -0.28523624517142D+00 0.10409475155399D-07 2 14 2 2 -0.45120332247529D+00 0.49576440394357D-08 3 14 2 2 -0.39989241120037D+00 -0.22829861339811D-07 1 15 2 2 -0.28523624517148D+00 0.10409474842594D-07 2 15 2 2 -0.45120332247527D+00 0.49576434705475D-08 3 15 2 2 0.39989241120043D+00 0.22829861282671D-07 1 16 2 2 -0.34323295459568D-01 0.14054410318710D-02 2 16 2 2 0.28218054671128D+00 0.18748612809689D-02 3 16 2 2 -0.28412783100754D+00 0.25528681093168D-02 1 17 2 2 -0.36430894697396D+00 0.48208175651520D-07 2 17 2 2 0.29421586446535D+00 -0.90674461416580D-07 3 17 2 2 0.51794483325803D+00 -0.10624454170314D-06 1 18 2 2 -0.45556429278283D+00 -0.22118327089461D-01 2 18 2 2 -0.84871976741032D+00 -0.13216417488587D-01 3 18 2 2 -0.86610704929416D+00 0.57210474409351D-02 1 19 2 2 -0.45556429278276D+00 -0.22118327089460D-01 2 19 2 2 -0.84871976741028D+00 -0.13216417488587D-01 3 19 2 2 0.86610704929405D+00 -0.57210474409353D-02 1 20 2 2 0.36430894697399D+00 -0.48208173638535D-07 2 20 2 2 -0.29421586446538D+00 0.90674460660598D-07 3 20 2 2 0.51794483325813D+00 -0.10624453639777D-06 1 1 3 2 0.21184102996314D-01 0.16786813792837D-07 2 1 3 2 0.39711566111395D+00 -0.93305763284676D-08 3 1 3 2 0.34698883716413D-13 0.13589074960350D-13 1 2 3 2 -0.64189858924764D-15 0.11102230246252D-15 2 2 3 2 -0.35709386646157D-13 0.00000000000000D+00 3 2 3 2 0.16991837925634D+02 0.00000000000000D+00 1 3 3 2 -0.10469195529697D+00 0.16874968729372D-08 2 3 3 2 -0.11681239788157D+00 -0.50914756517326D-08 3 3 3 2 -0.30290625708532D-14 0.13920049968895D-13 1 4 3 2 0.13704736215844D-15 -0.90372723024762D-16 2 4 3 2 0.13155762087472D-14 0.85506615210094D-18 3 4 3 2 0.40631824018540D+01 0.24049020337042D-16 1 5 3 2 -0.85450894627637D+00 -0.26187666464879D-01 2 5 3 2 -0.14775204471390D+01 0.66069692372985D-02 3 5 3 2 -0.27721741461295D+01 -0.15542347152451D-01 1 6 3 2 -0.85450894627637D+00 -0.26187666464879D-01 2 6 3 2 -0.14775204471390D+01 0.66069692373041D-02 3 6 3 2 0.27721741461293D+01 0.15542347152459D-01 1 7 3 2 0.78637741158039D+00 -0.26696088749248D-01 2 7 3 2 0.72999044866360D+00 -0.16551315724604D-01 3 7 3 2 -0.29269557900197D+01 0.10026035311482D-01 1 8 3 2 0.78637741158041D+00 -0.26696088749249D-01 2 8 3 2 0.72999044866360D+00 -0.16551315724606D-01 3 8 3 2 0.29269557900195D+01 -0.10026035311480D-01 1 9 3 2 0.18107892807840D+00 -0.29184831634036D-08 2 9 3 2 -0.34451018708689D-01 0.34097087470511D-08 3 9 3 2 -0.13005056168102D-13 0.20424496988876D-14 1 10 3 2 -0.54502029089846D-14 0.82889094726513D-18 2 10 3 2 0.40380035784218D-15 0.74571703143875D-16 3 10 3 2 -0.76350971274506D+01 0.26017804669709D-07 1 11 3 2 -0.23290686783110D-14 0.14394574380797D-15 2 11 3 2 -0.79474609385077D-15 0.14429581505675D-16 3 11 3 2 -0.74626474160641D+01 0.11928904669873D-06 1 12 3 2 -0.22756514255047D+00 0.10531690113213D-07 2 12 3 2 -0.16289077714518D+00 0.69467134317449D-08 3 12 3 2 -0.14781079204591D-13 0.69027374751092D-14 1 13 3 2 0.34363902348792D+00 -0.11830040968719D-02 2 13 3 2 -0.29814142361871D+00 0.37655918746641D-03 3 13 3 2 0.58931218389641D+00 0.16011952998743D-01 1 14 3 2 0.27355166152963D+00 -0.11581405059748D-07 2 14 3 2 -0.39677168349777D+00 0.10786792654195D-07 3 14 3 2 -0.16381316967650D+01 -0.10019955365272D-07 1 15 3 2 -0.27355166152963D+00 0.11581405103324D-07 2 15 3 2 0.39677168349786D+00 -0.10786792712203D-07 3 15 3 2 -0.16381316967652D+01 -0.10019961333055D-07 1 16 3 2 0.34363902348793D+00 -0.11830040968695D-02 2 16 3 2 -0.29814142361874D+00 0.37655918746408D-03 3 16 3 2 -0.58931218389648D+00 -0.16011952998750D-01 1 17 3 2 0.68280799992284D+00 -0.46232390260110D-06 2 17 3 2 0.58905314287556D+00 -0.66284184029698D-06 3 17 3 2 0.40245677350511D+00 0.63608098972905D-06 1 18 3 2 -0.77180569522031D+00 0.18709937733807D-02 2 18 3 2 -0.87601023640078D+00 -0.29483135551946D-02 3 18 3 2 -0.38720145901411D+01 0.56593951361141D-01 1 19 3 2 0.77180569522024D+00 -0.18709937733806D-02 2 19 3 2 0.87601023640070D+00 0.29483135551944D-02 3 19 3 2 -0.38720145901412D+01 0.56593951361141D-01 1 20 3 2 0.68280799992298D+00 -0.46232389594212D-06 2 20 3 2 0.58905314287565D+00 -0.66284183499682D-06 3 20 3 2 -0.40245677350506D+00 -0.63608097114271D-06 1 1 1 3 -0.12235792755569D+01 -0.37021528865367D-17 2 1 1 3 -0.45025294740247D-01 0.19636538421549D-09 3 1 1 3 -0.10476512841170D-15 0.15205275863968D-15 1 2 1 3 0.42539472666821D-14 0.11416477705016D-14 2 2 1 3 0.10394096648390D-14 -0.93676755123503D-17 3 2 1 3 -0.10469195529697D+00 -0.16874968729372D-08 1 3 1 3 0.81158056599706D+01 0.00000000000000D+00 2 3 1 3 -0.12425079410482D+01 -0.56527595965351D-06 3 3 1 3 -0.14852753301141D-13 -0.11102230246252D-15 1 4 1 3 -0.56212971869496D-14 0.17870460263114D-14 2 4 1 3 0.10400746603762D-14 -0.34711315727245D-16 3 4 1 3 -0.21187908855205D-01 0.15151455880572D-07 1 5 1 3 -0.34562685163368D+01 -0.23019407447616D-01 2 5 1 3 0.18339418079305D+00 -0.17890360038479D-02 3 5 1 3 -0.16399621792101D+00 -0.10845446110012D-01 1 6 1 3 -0.34562685163367D+01 -0.23019407447614D-01 2 6 1 3 0.18339418079306D+00 -0.17890360038479D-02 3 6 1 3 0.16399621792101D+00 0.10845446110012D-01 1 7 1 3 0.18263572863994D+01 -0.10463366534521D-01 2 7 1 3 0.46856744436333D+00 0.80924301391359D-03 3 7 1 3 -0.14555098926400D-01 0.25701753683843D-01 1 8 1 3 0.18263572863994D+01 -0.10463366534520D-01 2 8 1 3 0.46856744436334D+00 0.80924301391362D-03 3 8 1 3 0.14555098926398D-01 -0.25701753683843D-01 1 9 1 3 -0.11892115849382D+01 0.19615680802843D-07 2 9 1 3 -0.46457196943757D+00 -0.15522167519547D-07 3 9 1 3 0.16350093197402D-14 0.15099973544963D-15 1 10 1 3 -0.80128348242056D-14 -0.14383590357645D-14 2 10 1 3 -0.10420004634972D-15 0.21884912598100D-16 3 10 1 3 0.14795965101580D-01 0.30231350046825D-08 1 11 1 3 0.21251632420995D-15 -0.41596344223196D-15 2 11 1 3 -0.70381735150350D-16 -0.16320024117315D-16 3 11 1 3 0.29268300004257D+00 -0.67698854895275D-09 1 12 1 3 -0.76755469253945D+00 0.14826279863778D-07 2 12 1 3 0.19313551784229D+00 -0.19055500758212D-07 3 12 1 3 0.19372265038720D-14 -0.17922265283864D-16 1 13 1 3 -0.60909284293519D+00 -0.98141360211214D-02 2 13 1 3 0.33776741098255D+00 0.16831199647224D-01 3 13 1 3 0.65607960698278D+00 0.51932790800396D-02 1 14 1 3 0.11319999201774D+00 -0.15934551304816D-06 2 14 1 3 0.43655032002932D+00 -0.68847982776043D-07 3 14 1 3 -0.71530282007179D+00 0.24996742134922D-06 1 15 1 3 -0.11319999201774D+00 0.15934551310697D-06 2 15 1 3 -0.43655032002933D+00 0.68847984343723D-07 3 15 1 3 -0.71530282007175D+00 0.24996742823529D-06 1 16 1 3 -0.60909284293521D+00 -0.98141360211217D-02 2 16 1 3 0.33776741098253D+00 0.16831199647224D-01 3 16 1 3 -0.65607960698278D+00 -0.51932790800396D-02 1 17 1 3 -0.15288463293574D+00 -0.18495131321912D-08 2 17 1 3 0.15279386361997D+00 -0.28812252387616D-08 3 17 1 3 -0.50339059316377D+00 -0.18860126371284D-07 1 18 1 3 -0.35649811871917D-01 -0.22976920010910D-04 2 18 1 3 -0.18553487339994D+00 -0.23699499276418D-02 3 18 1 3 -0.29484470087087D+00 0.79704964006711D-02 1 19 1 3 0.35649811871922D-01 0.22976920009858D-04 2 19 1 3 0.18553487339995D+00 0.23699499276410D-02 3 19 1 3 -0.29484470087087D+00 0.79704964006733D-02 1 20 1 3 -0.15288463293573D+00 -0.18495135582203D-08 2 20 1 3 0.15279386361994D+00 -0.28812254085349D-08 3 20 1 3 0.50339059316377D+00 0.18860126751162D-07 1 1 2 3 0.45025294740235D-01 0.19636538421549D-09 2 1 2 3 -0.13325896105438D+01 0.80686683344946D-18 3 1 2 3 -0.27948668805769D-15 -0.26529336640998D-17 1 2 2 3 0.10394096648390D-14 -0.10668718119333D-16 2 2 2 3 0.11751335051912D-13 -0.76790007932071D-15 3 2 2 3 -0.11681239788157D+00 0.50914756517326D-08 1 3 2 3 -0.12425044384666D+01 -0.62896951241311D-06 2 3 2 3 0.80124818826371D+01 0.00000000000000D+00 3 3 2 3 -0.57025668705717D-13 0.11102230246252D-15 1 4 2 3 0.10400746604796D-14 -0.34711315727244D-16 2 4 2 3 -0.25576418495584D-13 0.73877978521300D-15 3 4 2 3 0.39711352324460D+00 0.76397096606480D-08 1 5 2 3 0.46740396775780D+00 -0.45331725949606D-02 2 5 2 3 0.17962833935334D+01 -0.33133797522039D-02 3 5 2 3 -0.85214487240046D+00 0.11842339030056D-01 1 6 2 3 0.46740396775780D+00 -0.45331725949607D-02 2 6 2 3 0.17962833935333D+01 -0.33133797522048D-02 3 6 2 3 0.85214487240047D+00 -0.11842339030056D-01 1 7 2 3 -0.10243565881652D+00 -0.10543373934863D-02 2 7 2 3 -0.35240726170190D+01 0.27589762282395D-01 3 7 2 3 0.19222618575801D+01 -0.12427612256764D-02 1 8 2 3 -0.10243565881652D+00 -0.10543373934863D-02 2 8 2 3 -0.35240726170190D+01 0.27589762282394D-01 3 8 2 3 -0.19222618575801D+01 0.12427612256777D-02 1 9 2 3 -0.55591842353427D+00 -0.54455073776766D-08 2 9 2 3 -0.69995698096851D+00 0.68322126462891D-08 3 9 2 3 0.38268037042616D-14 -0.34854859506895D-15 1 10 2 3 -0.10420004634972D-15 0.21884912598100D-16 2 10 2 3 -0.16887825474950D-13 -0.84821905243326D-15 3 10 2 3 -0.10729816381840D+00 0.66063303305972D-09 1 11 2 3 -0.70340010919482D-16 -0.16753704986309D-16 2 11 2 3 0.23082927961689D-13 -0.27945888977997D-15 3 11 2 3 0.10078806932196D+00 -0.41034437255903D-08 1 12 2 3 0.35247003652198D+00 0.27792333116730D-08 2 12 2 3 0.90289184219095D-01 0.31321192452316D-09 3 12 2 3 -0.31310984894821D-14 0.28168000493475D-16 1 13 2 3 0.45556429278280D+00 0.22118327089461D-01 2 13 2 3 -0.84871976741035D+00 -0.13216417488587D-01 3 13 2 3 -0.86610704929405D+00 0.57210474409350D-02 1 14 2 3 0.36430894697398D+00 -0.48208172105560D-07 2 14 2 3 0.29421586446535D+00 -0.90674459262164D-07 3 14 2 3 0.51794483325810D+00 -0.10624453099685D-06 1 15 2 3 -0.36430894697399D+00 0.48208173673240D-07 2 15 2 3 -0.29421586446536D+00 0.90674460443471D-07 3 15 2 3 0.51794483325807D+00 -0.10624453601416D-06 1 16 2 3 0.45556429278279D+00 0.22118327089460D-01 2 16 2 3 -0.84871976741036D+00 -0.13216417488586D-01 3 16 2 3 0.86610704929409D+00 -0.57210474409362D-02 1 17 2 3 0.28523624517145D+00 -0.10409474758406D-07 2 17 2 3 -0.45120332247529D+00 0.49576439930701D-08 3 17 2 3 -0.39989241120037D+00 -0.22829860497199D-07 1 18 2 3 -0.34323295459573D-01 0.14054410318701D-02 2 18 2 3 -0.28218054671126D+00 -0.18748612809697D-02 3 18 2 3 -0.28412783100756D+00 0.25528681093144D-02 1 19 2 3 0.34323295459579D-01 -0.14054410318709D-02 2 19 2 3 0.28218054671127D+00 0.18748612809688D-02 3 19 2 3 -0.28412783100756D+00 0.25528681093169D-02 1 20 2 3 0.28523624517143D+00 -0.10409474928180D-07 2 20 2 3 -0.45120332247528D+00 0.49576433217917D-08 3 20 2 3 0.39989241120036D+00 0.22829861143329D-07 1 1 3 3 -0.10476512820491D-15 0.15205275863968D-15 2 1 3 3 -0.27948668723051D-15 -0.26529336641000D-17 3 1 3 3 0.40631824018541D+01 -0.33616417185091D-18 1 2 3 3 0.10469195529697D+00 -0.16874968729372D-08 2 2 3 3 -0.11681239788157D+00 -0.50914743722624D-08 3 2 3 3 -0.30290625708532D-14 -0.13920049968895D-13 1 3 3 3 -0.14852753304450D-13 0.11102230246252D-15 2 3 3 3 -0.57025668718952D-13 0.00000000000000D+00 3 3 3 3 0.16991837925641D+02 0.00000000000000D+00 1 4 3 3 -0.21184102996292D-01 -0.16786813742028D-07 2 4 3 3 0.39711566111403D+00 -0.93305775217734D-08 3 4 3 3 0.16627054258686D-13 -0.81580656093270D-14 1 5 3 3 0.78637741158040D+00 -0.26696088749249D-01 2 5 3 3 -0.72999044866366D+00 0.16551315724606D-01 3 5 3 3 0.29269557900194D+01 -0.10026035311496D-01 1 6 3 3 -0.78637741158040D+00 0.26696088749249D-01 2 6 3 3 0.72999044866367D+00 -0.16551315724606D-01 3 6 3 3 0.29269557900194D+01 -0.10026035311442D-01 1 7 3 3 -0.85450894627636D+00 -0.26187666464879D-01 2 7 3 3 0.14775204471392D+01 -0.66069692373033D-02 3 7 3 3 0.27721741461292D+01 0.15542347152462D-01 1 8 3 3 0.85450894627636D+00 0.26187666464879D-01 2 8 3 3 -0.14775204471391D+01 0.66069692373045D-02 3 8 3 3 0.27721741461291D+01 0.15542347152462D-01 1 9 3 3 0.16350093197402D-14 0.15099973544963D-15 2 9 3 3 0.38268037042616D-14 -0.34854859506895D-15 3 9 3 3 -0.74626474160639D+01 0.11928904645746D-06 1 10 3 3 0.22756514255047D+00 -0.10531689528367D-07 2 10 3 3 -0.16289077714518D+00 0.69467132470114D-08 3 10 3 3 0.33142004799295D-14 -0.76729631397857D-14 1 11 3 3 -0.18107892807838D+00 0.29184832612534D-08 2 11 3 3 -0.34451018708672D-01 0.34097087343354D-08 3 11 3 3 0.14194545998254D-13 0.37506886365006D-15 1 12 3 3 0.19372265038720D-14 -0.17922265283864D-16 2 12 3 3 -0.31310984894821D-14 0.28168000493475D-16 3 12 3 3 -0.76350971274505D+01 0.26017804785487D-07 1 13 3 3 0.77180569522023D+00 -0.18709937733808D-02 2 13 3 3 -0.87601023640069D+00 -0.29483135551947D-02 3 13 3 3 -0.38720145901411D+01 0.56593951361141D-01 1 14 3 3 -0.68280799992298D+00 0.46232388956409D-06 2 14 3 3 0.58905314287562D+00 -0.66284182959417D-06 3 14 3 3 0.40245677350516D+00 0.63608096432086D-06 1 15 3 3 -0.68280799992297D+00 0.46232389645883D-06 2 15 3 3 0.58905314287560D+00 -0.66284183460973D-06 3 15 3 3 -0.40245677350504D+00 -0.63608096781650D-06 1 16 3 3 -0.77180569522023D+00 0.18709937733809D-02 2 16 3 3 0.87601023640071D+00 0.29483135551935D-02 3 16 3 3 -0.38720145901410D+01 0.56593951361142D-01 1 17 3 3 -0.27355166152959D+00 0.11581405444136D-07 2 17 3 3 -0.39677168349780D+00 0.10786793497675D-07 3 17 3 3 -0.16381316967651D+01 -0.10019956626997D-07 1 18 3 3 -0.34363902348795D+00 0.11830040968673D-02 2 18 3 3 -0.29814142361877D+00 0.37655918746162D-03 3 18 3 3 0.58931218389648D+00 0.16011952998745D-01 1 19 3 3 -0.34363902348796D+00 0.11830040968695D-02 2 19 3 3 -0.29814142361876D+00 0.37655918746411D-03 3 19 3 3 -0.58931218389638D+00 -0.16011952998745D-01 1 20 3 3 0.27355166152959D+00 -0.11581405065992D-07 2 20 3 3 0.39677168349776D+00 -0.10786792850677D-07 3 20 3 3 -0.16381316967651D+01 -0.10019952956954D-07 1 1 1 4 -0.96390947014514D-14 -0.15535245440770D-14 2 1 1 4 0.28428082883005D-14 -0.12000727448431D-16 3 1 1 4 -0.10469195529699D+00 -0.16874976144604D-08 1 2 1 4 -0.12235792755569D+01 -0.19878320133070D-16 2 2 1 4 -0.45025294740250D-01 0.19636537409724D-09 3 2 1 4 0.13704736215844D-15 0.90372723024762D-16 1 3 1 4 -0.56212971867428D-14 -0.17870460263114D-14 2 3 1 4 0.10400746602728D-14 0.34711315727244D-16 3 3 1 4 -0.21187908855205D-01 0.15151456191601D-07 1 4 1 4 0.81158056599706D+01 0.00000000000000D+00 2 4 1 4 -0.12425079410484D+01 -0.56527595965351D-06 3 4 1 4 -0.21958180658742D-13 -0.11102230246252D-15 1 5 1 4 0.34562685163369D+01 0.23019407447624D-01 2 5 1 4 -0.18339418079306D+00 0.17890360038477D-02 3 5 1 4 0.16399621792092D+00 0.10845446110011D-01 1 6 1 4 -0.34562685163369D+01 -0.23019407447617D-01 2 6 1 4 0.18339418079307D+00 -0.17890360038478D-02 3 6 1 4 0.16399621792086D+00 0.10845446110012D-01 1 7 1 4 -0.18263572863995D+01 0.10463366534517D-01 2 7 1 4 -0.46856744436334D+00 -0.80924301391369D-03 3 7 1 4 0.14555098926422D-01 -0.25701753683843D-01 1 8 1 4 0.18263572863994D+01 -0.10463366534522D-01 2 8 1 4 0.46856744436334D+00 0.80924301391356D-03 3 8 1 4 0.14555098926420D-01 -0.25701753683843D-01 1 9 1 4 0.33587795012534D-14 -0.58293525146595D-16 2 9 1 4 0.31551801045796D-16 0.69272189756708D-16 3 9 1 4 0.14795965101543D-01 0.30231344859217D-08 1 10 1 4 -0.11892115849381D+01 0.19615680763910D-07 2 10 1 4 -0.46457196943745D+00 -0.15522167533198D-07 3 10 1 4 0.26687924896856D-14 0.57605129316223D-15 1 11 1 4 -0.76755469253936D+00 0.14826279910353D-07 2 11 1 4 0.19313551784245D+00 -0.19055500778281D-07 3 11 1 4 0.30332913350766D-14 -0.49358579642063D-16 1 12 1 4 0.20809264799942D-14 0.45623855542252D-15 2 12 1 4 -0.13594329672662D-14 0.34978121590246D-16 3 12 1 4 0.29268300004257D+00 -0.67698856736323D-09 1 13 1 4 0.11319999201779D+00 -0.15934551321984D-06 2 13 1 4 0.43655032002930D+00 -0.68847986170499D-07 3 13 1 4 -0.71530282007164D+00 0.24996743431081D-06 1 14 1 4 -0.60909284293515D+00 -0.98141360211211D-02 2 14 1 4 0.33776741098258D+00 0.16831199647224D-01 3 14 1 4 0.65607960698281D+00 0.51932790800392D-02 1 15 1 4 -0.60909284293515D+00 -0.98141360211212D-02 2 15 1 4 0.33776741098246D+00 0.16831199647225D-01 3 15 1 4 -0.65607960698271D+00 -0.51932790800395D-02 1 16 1 4 -0.11319999201779D+00 0.15934551302161D-06 2 16 1 4 -0.43655032002933D+00 0.68847984235772D-07 3 16 1 4 -0.71530282007179D+00 0.24996742781829D-06 1 17 1 4 -0.35649811871919D-01 -0.22976920009330D-04 2 17 1 4 -0.18553487339996D+00 -0.23699499276398D-02 3 17 1 4 -0.29484470087088D+00 0.79704964006755D-02 1 18 1 4 -0.15288463293575D+00 -0.18495135916540D-08 2 18 1 4 0.15279386361990D+00 -0.28812253848394D-08 3 18 1 4 -0.50339059316378D+00 -0.18860126983778D-07 1 19 1 4 -0.15288463293572D+00 -0.18495131494526D-08 2 19 1 4 0.15279386361996D+00 -0.28812253573865D-08 3 19 1 4 0.50339059316379D+00 0.18860126610305D-07 1 20 1 4 0.35649811871913D-01 0.22976920010082D-04 2 20 1 4 0.18553487339995D+00 0.23699499276409D-02 3 20 1 4 -0.29484470087087D+00 0.79704964006735D-02 1 1 2 4 0.28428082883005D-14 -0.13301770055413D-16 2 1 2 4 0.82488655889723D-14 -0.84327345000756D-15 3 1 2 4 -0.11681239788157D+00 0.50914749092855D-08 1 2 2 4 0.45025294740232D-01 0.19636537409724D-09 2 2 2 4 -0.13325896105438D+01 -0.18766718252071D-17 3 2 2 4 0.13155762087472D-14 -0.85506615210123D-18 1 3 2 4 0.10400746604796D-14 0.34711315727245D-16 2 3 2 4 -0.25576418495584D-13 -0.73856294477850D-15 3 3 2 4 0.39711352324460D+00 0.76397101562359D-08 1 4 2 4 -0.12425044384668D+01 -0.62896951241311D-06 2 4 2 4 0.80124818826371D+01 0.00000000000000D+00 3 4 2 4 0.81530164767494D-13 0.11102230246252D-15 1 5 2 4 -0.46740396775781D+00 0.45331725949605D-02 2 5 2 4 -0.17962833935334D+01 0.33133797522023D-02 3 5 2 4 0.85214487240044D+00 -0.11842339030055D-01 1 6 2 4 0.46740396775782D+00 -0.45331725949605D-02 2 6 2 4 0.17962833935334D+01 -0.33133797522037D-02 3 6 2 4 0.85214487240044D+00 -0.11842339030056D-01 1 7 2 4 0.10243565881651D+00 0.10543373934862D-02 2 7 2 4 0.35240726170191D+01 -0.27589762282380D-01 3 7 2 4 -0.19222618575801D+01 0.12427612256720D-02 1 8 2 4 -0.10243565881652D+00 -0.10543373934863D-02 2 8 2 4 -0.35240726170191D+01 0.27589762282392D-01 3 8 2 4 -0.19222618575801D+01 0.12427612256771D-02 1 9 2 4 0.31551801045795D-16 0.69272189756708D-16 2 9 2 4 -0.12611501990055D-15 -0.95738036851606D-15 3 9 2 4 -0.10729816381840D+00 0.66063302394582D-09 1 10 2 4 -0.55591842353415D+00 -0.54455073913282D-08 2 10 2 4 -0.69995698096857D+00 0.68322128702619D-08 3 10 2 4 0.12152850419625D-15 0.18454511477395D-15 1 11 2 4 0.35247003652214D+00 0.27792332916045D-08 2 11 2 4 0.90289184218840D-01 0.31321203305381D-09 3 11 2 4 0.17399857572069D-17 0.20379701304317D-15 1 12 2 4 -0.13593912429319D-14 0.34978121590246D-16 2 12 2 4 0.11689254745973D-13 0.23810057845483D-15 3 12 2 4 0.10078806932192D+00 -0.41034439027250D-08 1 13 2 4 0.36430894697396D+00 -0.48208175500016D-07 2 13 2 4 0.29421586446533D+00 -0.90674461272966D-07 3 13 2 4 0.51794483325805D+00 -0.10624454157327D-06 1 14 2 4 0.45556429278284D+00 0.22118327089461D-01 2 14 2 4 -0.84871976741043D+00 -0.13216417488587D-01 3 14 2 4 -0.86610704929419D+00 0.57210474409351D-02 1 15 2 4 0.45556429278272D+00 0.22118327089461D-01 2 15 2 4 -0.84871976741038D+00 -0.13216417488586D-01 3 15 2 4 0.86610704929402D+00 -0.57210474409338D-02 1 16 2 4 -0.36430894697399D+00 0.48208173568759D-07 2 16 2 4 -0.29421586446536D+00 0.90674460865376D-07 3 16 2 4 0.51794483325812D+00 -0.10624453607599D-06 1 17 2 4 -0.34323295459582D-01 0.14054410318721D-02 2 17 2 4 -0.28218054671126D+00 -0.18748612809677D-02 3 17 2 4 -0.28412783100758D+00 0.25528681093189D-02 1 18 2 4 0.28523624517138D+00 -0.10409474904484D-07 2 18 2 4 -0.45120332247530D+00 0.49576434138154D-08 3 18 2 4 -0.39989241120027D+00 -0.22829860984621D-07 1 19 2 4 0.28523624517146D+00 -0.10409474877031D-07 2 19 2 4 -0.45120332247528D+00 0.49576433233205D-08 3 19 2 4 0.39989241120039D+00 0.22829860776993D-07 1 20 2 4 0.34323295459579D-01 -0.14054410318709D-02 2 20 2 4 0.28218054671126D+00 0.18748612809680D-02 3 20 2 4 -0.28412783100757D+00 0.25528681093167D-02 1 1 3 4 0.10469195529696D+00 -0.16874976144604D-08 2 1 3 4 -0.11681239788156D+00 -0.50914751147095D-08 3 1 3 4 -0.19642695965852D-13 0.11911170051970D-13 1 2 3 4 0.13704736236524D-15 0.90372723024762D-16 2 2 3 4 0.13155762095744D-14 -0.85506615210113D-18 3 2 3 4 0.40631824018540D+01 -0.24049020337042D-16 1 3 3 4 -0.21184102996292D-01 -0.16786813430998D-07 2 3 3 4 0.39711566111403D+00 -0.93305770261855D-08 3 3 3 4 0.16627054258686D-13 0.81598003328030D-14 1 4 3 4 -0.21958180662051D-13 0.11102230246252D-15 2 4 3 4 0.81530164754259D-13 0.00000000000000D+00 3 4 3 4 0.16991837925638D+02 0.00000000000000D+00 1 5 3 4 -0.78637741158049D+00 0.26696088749248D-01 2 5 3 4 0.72999044866364D+00 -0.16551315724604D-01 3 5 3 4 -0.29269557900197D+01 0.10026035311477D-01 1 6 3 4 -0.78637741158056D+00 0.26696088749249D-01 2 6 3 4 0.72999044866364D+00 -0.16551315724606D-01 3 6 3 4 0.29269557900195D+01 -0.10026035311528D-01 1 7 3 4 0.85450894627639D+00 0.26187666464879D-01 2 7 3 4 -0.14775204471390D+01 0.66069692372988D-02 3 7 3 4 -0.27721741461295D+01 -0.15542347152447D-01 1 8 3 4 0.85450894627638D+00 0.26187666464879D-01 2 8 3 4 -0.14775204471391D+01 0.66069692373040D-02 3 8 3 4 0.27721741461293D+01 0.15542347152458D-01 1 9 3 4 0.22756514255043D+00 -0.10531690047127D-07 2 9 3 4 -0.16289077714518D+00 0.69467132378975D-08 3 9 3 4 0.98972991372938D-14 0.10674709813928D-13 1 10 3 4 0.26687924896856D-14 0.57605129316223D-15 2 10 3 4 0.12152850419625D-15 0.18454511477395D-15 3 10 3 4 -0.74626474160641D+01 0.11928904664902D-06 1 11 3 4 0.30332913350766D-14 -0.49358579642063D-16 2 11 3 4 0.17399857572071D-17 0.20379701304317D-15 3 11 3 4 -0.76350971274503D+01 0.26017804819921D-07 1 12 3 4 -0.18107892807838D+00 0.29184832428430D-08 2 12 3 4 -0.34451018708707D-01 0.34097085572007D-08 3 12 3 4 0.63483053705103D-14 0.19637838664225D-14 1 13 3 4 -0.68280799992282D+00 0.46232390253262D-06 2 13 3 4 0.58905314287557D+00 -0.66284184017405D-06 3 13 3 4 0.40245677350513D+00 0.63608098857914D-06 1 14 3 4 0.77180569522025D+00 -0.18709937733813D-02 2 14 3 4 -0.87601023640084D+00 -0.29483135551946D-02 3 14 3 4 -0.38720145901411D+01 0.56593951361144D-01 1 15 3 4 -0.77180569522015D+00 0.18709937733810D-02 2 15 3 4 0.87601023640064D+00 0.29483135551959D-02 3 15 3 4 -0.38720145901411D+01 0.56593951361141D-01 1 16 3 4 -0.68280799992301D+00 0.46232389604183D-06 2 16 3 4 0.58905314287565D+00 -0.66284183467157D-06 3 16 3 4 -0.40245677350504D+00 -0.63608097039523D-06 1 17 3 4 -0.34363902348795D+00 0.11830040968718D-02 2 17 3 4 -0.29814142361878D+00 0.37655918746615D-03 3 17 3 4 0.58931218389636D+00 0.16011952998739D-01 1 18 3 4 -0.27355166152960D+00 0.11581404831641D-07 2 18 3 4 -0.39677168349770D+00 0.10786793010253D-07 3 18 3 4 -0.16381316967651D+01 -0.10019956779034D-07 1 19 3 4 0.27355166152960D+00 -0.11581405206849D-07 2 19 3 4 0.39677168349779D+00 -0.10786793217013D-07 3 19 3 4 -0.16381316967653D+01 -0.10019960456405D-07 1 20 3 4 -0.34363902348795D+00 0.11830040968697D-02 2 20 3 4 -0.29814142361876D+00 0.37655918746396D-03 3 20 3 4 -0.58931218389643D+00 -0.16011952998742D-01 1 1 1 5 0.18263575150759D+01 0.10463316046507D-01 2 1 1 5 0.10243458926398D+00 -0.10545846424687D-02 3 1 1 5 0.85451153995968D+00 -0.26188256688241D-01 1 2 1 5 -0.18263575150759D+01 -0.10463316046504D-01 2 2 1 5 -0.10243458926398D+00 0.10545846424686D-02 3 2 1 5 -0.85451153995969D+00 0.26188256688242D-01 1 3 1 5 -0.34562685163368D+01 0.23019407447616D-01 2 3 1 5 0.46740396775780D+00 0.45331725949606D-02 3 3 1 5 0.78637741158040D+00 0.26696088749249D-01 1 4 1 5 0.34562685163369D+01 -0.23019407447624D-01 2 4 1 5 -0.46740396775781D+00 -0.45331725949605D-02 3 4 1 5 -0.78637741158049D+00 -0.26696088749248D-01 1 5 1 5 0.17814804893075D+02 0.00000000000000D+00 2 5 1 5 0.42692573934765D+00 -0.80343366161171D-07 3 5 1 5 0.41640154347297D+00 -0.35551377622842D-07 1 6 1 5 -0.35726957487475D-13 0.17272825776976D-14 2 6 1 5 -0.19772103383834D-17 -0.20681475278021D-16 3 6 1 5 0.18422894893553D-16 0.37143205042801D-15 1 7 1 5 -0.13739810021253D+02 0.00000000000000D+00 2 7 1 5 -0.47449634027871D+01 0.30659550703948D-08 3 7 1 5 -0.39486275740516D+01 0.26286589376970D-07 1 8 1 5 0.11062767943869D-13 0.61839311525151D-15 2 8 1 5 -0.14893412137910D-14 0.43565291413662D-16 3 8 1 5 -0.87332300259269D-14 0.10919180550545D-15 1 9 1 5 -0.14609351257447D+01 0.99248007541050D+00 2 9 1 5 -0.11468517587729D+00 -0.33737731451701D-01 3 9 1 5 -0.59618987300065D+00 -0.31443463245434D+00 1 10 1 5 0.14609351257443D+01 -0.99248007541049D+00 2 10 1 5 0.11468517587727D+00 0.33737731451701D-01 3 10 1 5 0.59618987300061D+00 0.31443463245432D+00 1 11 1 5 -0.12029576947453D+01 0.26277579259031D-01 2 11 1 5 -0.35077330036195D+00 0.11376200440040D-01 3 11 1 5 0.54306240389876D-01 0.20505626814279D-01 1 12 1 5 0.12029576947453D+01 -0.26277579259032D-01 2 12 1 5 0.35077330036197D+00 -0.11376200440041D-01 3 12 1 5 -0.54306240389865D-01 -0.20505626814280D-01 1 13 1 5 -0.48396263283337D+00 0.16319570772128D-02 2 13 1 5 0.79319302849996D+00 0.48007065008383D-02 3 13 1 5 0.93573475454532D+00 -0.37582003428935D-01 1 14 1 5 0.48396263283308D+00 -0.16319570772340D-02 2 14 1 5 -0.79319302850008D+00 -0.48007065008609D-02 3 14 1 5 -0.93573475454500D+00 0.37582003428947D-01 1 15 1 5 0.37777211143034D+00 -0.46890990369810D-01 2 15 1 5 0.27843668475829D+00 -0.53936912421190D-01 3 15 1 5 0.24436588460005D+00 -0.29396970736664D-01 1 16 1 5 -0.37777211143033D+00 0.46890990369810D-01 2 16 1 5 -0.27843668475829D+00 0.53936912421190D-01 3 16 1 5 -0.24436588460004D+00 0.29396970736665D-01 1 17 1 5 0.13646047988225D+00 0.42100838790535D-02 2 17 1 5 0.57706589902637D+00 -0.12289748358360D-01 3 17 1 5 0.98353435861183D+00 -0.33940087545785D-01 1 18 1 5 -0.13646047988220D+00 -0.42100838790582D-02 2 18 1 5 -0.57706589902665D+00 0.12289748358382D-01 3 18 1 5 -0.98353435861179D+00 0.33940087545793D-01 1 19 1 5 0.25413208551327D+00 -0.88218531597782D-01 2 19 1 5 -0.41677659946974D+00 0.13267851192328D+00 3 19 1 5 0.20850660326205D+00 -0.65729194452606D-01 1 20 1 5 -0.25413208551328D+00 0.88218531597782D-01 2 20 1 5 0.41677659946974D+00 -0.13267851192328D+00 3 20 1 5 -0.20850660326205D+00 0.65729194452607D-01 1 1 2 5 -0.46856519757803D+00 0.80939902446521D-03 2 1 2 5 -0.35240698855760D+01 -0.27590164583609D-01 3 1 2 5 0.14775186762833D+01 0.66074084325936D-02 1 2 2 5 0.46856519757804D+00 -0.80939902446529D-03 2 2 2 5 0.35240698855761D+01 0.27590164583601D-01 3 2 2 5 -0.14775186762834D+01 -0.66074084325888D-02 1 3 2 5 0.18339418079305D+00 0.17890360038479D-02 2 3 2 5 0.17962833935334D+01 0.33133797522039D-02 3 3 2 5 -0.72999044866366D+00 -0.16551315724606D-01 1 4 2 5 -0.18339418079306D+00 -0.17890360038477D-02 2 4 2 5 -0.17962833935334D+01 -0.33133797522023D-02 3 4 2 5 0.72999044866364D+00 0.16551315724604D-01 1 5 2 5 0.42693515924402D+00 0.87974665184051D-07 2 5 2 5 0.18570594078078D+02 0.00000000000000D+00 3 5 2 5 -0.30503659827299D+01 0.27721419477738D-06 1 6 2 5 -0.19772103412106D-17 -0.20681475278021D-16 2 6 2 5 -0.23837672721954D-13 0.15580926143661D-14 3 6 2 5 0.78640671777130D-14 -0.28856110882903D-15 1 7 2 5 0.47449634027871D+01 0.30659550703948D-08 2 7 2 5 -0.14762433655738D+02 0.00000000000000D+00 3 7 2 5 0.37888229687980D+00 0.83145480447909D-08 1 8 2 5 -0.15011410810159D-14 0.43565291413662D-16 2 8 2 5 0.25062470248631D-13 0.14531695751469D-14 3 8 2 5 -0.10777181914535D-13 -0.35162514583521D-15 1 9 2 5 -0.53226088174312D-01 -0.21225596262135D-01 2 9 2 5 -0.14644458490857D+01 0.10202621373355D+01 3 9 2 5 0.15149923952850D+00 0.70592669203450D-01 1 10 2 5 0.53226088174290D-01 0.21225596262136D-01 2 10 2 5 0.14644458490853D+01 -0.10202621373355D+01 3 10 2 5 -0.15149923952867D+00 -0.70592669203446D-01 1 11 2 5 0.47379481343786D+00 -0.10765131700376D-01 2 11 2 5 -0.13287377129898D+01 0.26733383406706D-01 3 11 2 5 -0.26021371927452D+00 -0.17342934288836D-01 1 12 2 5 -0.47379481343784D+00 0.10765131700376D-01 2 12 2 5 0.13287377129898D+01 -0.26733383406706D-01 3 12 2 5 0.26021371927461D+00 0.17342934288836D-01 1 13 2 5 -0.75629175951968D+00 -0.77991850861340D-02 2 13 2 5 -0.30875624439428D-01 -0.46336606044468D-03 3 13 2 5 0.79230353471466D+00 -0.17900070251474D-01 1 14 2 5 0.75629175951957D+00 0.77991850861113D-02 2 14 2 5 0.30875624439624D-01 0.46336606044002D-03 3 14 2 5 -0.79230353471445D+00 0.17900070251481D-01 1 15 2 5 -0.14158513548062D+00 -0.32825000619358D-01 2 15 2 5 -0.88549792089430D-01 -0.28832767553978D-01 3 15 2 5 0.76798941795577D-01 0.16238853335857D-02 1 16 2 5 0.14158513548062D+00 0.32825000619358D-01 2 16 2 5 0.88549792089432D-01 0.28832767553978D-01 3 16 2 5 -0.76798941795584D-01 -0.16238853335853D-02 1 17 2 5 -0.10201618763046D+01 -0.33250236328525D-02 2 17 2 5 -0.14783112415731D+00 0.52523946663003D-02 3 17 2 5 -0.78284481223617D+00 0.45147056285257D-01 1 18 2 5 0.10201618763043D+01 0.33250236328744D-02 2 18 2 5 0.14783112415745D+00 -0.52523946663226D-02 3 18 2 5 0.78284481223608D+00 -0.45147056285265D-01 1 19 2 5 -0.56239408163787D-01 0.13810226758316D+00 2 19 2 5 0.55606464042187D-01 -0.17124834068808D+00 3 19 2 5 -0.82729911584853D-01 0.44821577622643D-01 1 20 2 5 0.56239408163779D-01 -0.13810226758316D+00 2 20 2 5 -0.55606464042191D-01 0.17124834068808D+00 3 20 2 5 0.82729911584874D-01 -0.44821577622644D-01 1 1 3 5 0.14552923027610D-01 0.25702590298476D-01 2 1 3 5 0.19222625175942D+01 0.12428092140348D-02 3 1 3 5 0.27721804615839D+01 -0.15539713737764D-01 1 2 3 5 -0.14552923027613D-01 -0.25702590298475D-01 2 2 3 5 -0.19222625175943D+01 -0.12428092140300D-02 3 2 3 5 -0.27721804615842D+01 0.15539713737755D-01 1 3 3 5 -0.16399621792101D+00 0.10845446110012D-01 2 3 3 5 -0.85214487240046D+00 -0.11842339030056D-01 3 3 3 5 0.29269557900194D+01 0.10026035311496D-01 1 4 3 5 0.16399621792092D+00 -0.10845446110011D-01 2 4 3 5 0.85214487240044D+00 0.11842339030055D-01 3 4 3 5 -0.29269557900197D+01 -0.10026035311477D-01 1 5 3 5 0.41639356531766D+00 0.67121813308893D-07 2 5 3 5 -0.30503750119135D+01 -0.30863071093042D-06 3 5 3 5 0.55145407904738D+02 0.00000000000000D+00 1 6 3 5 -0.31535357084226D-16 0.37143205042801D-15 2 6 3 5 0.78776473380782D-14 -0.28856110882903D-15 3 6 3 5 0.24500035949608D-12 -0.24440418740424D-13 1 7 3 5 0.39486275740516D+01 0.26286589376970D-07 2 7 3 5 0.37888229687980D+00 -0.83145480447909D-08 3 7 3 5 0.16955906091858D+02 0.00000000000000D+00 1 8 3 5 -0.87332300259269D-14 0.10919180550545D-15 2 8 3 5 -0.10772759109667D-13 -0.35162514583521D-15 3 8 3 5 -0.47189364974516D-13 0.13422018782584D-14 1 9 3 5 -0.19437877341003D+01 -0.46587979889756D+00 2 9 3 5 0.39232003853720D+00 0.10632735356758D+00 3 9 3 5 -0.13229070618331D+02 -0.26203554511113D+01 1 10 3 5 0.19437877341003D+01 0.46587979889754D+00 2 10 3 5 -0.39232003853737D+00 -0.10632735356758D+00 3 10 3 5 0.13229070618332D+02 0.26203554511113D+01 1 11 3 5 -0.41945609494044D+00 -0.10639367904397D-01 2 11 3 5 -0.18717592153538D+00 -0.32243574706698D-02 3 11 3 5 0.89881011904707D+01 -0.24041959735202D+00 1 12 3 5 0.41945609494045D+00 0.10639367904396D-01 2 12 3 5 0.18717592153547D+00 0.32243574706695D-02 3 12 3 5 -0.89881011904708D+01 0.24041959735202D+00 1 13 3 5 -0.65238296326373D+00 -0.33397516841104D-01 2 13 3 5 -0.28586002827539D+00 -0.40320476730401D-01 3 13 3 5 -0.81225047683413D+01 0.26875960527009D-01 1 14 3 5 0.65238296326404D+00 0.33397516841115D-01 2 14 3 5 0.28586002827559D+00 0.40320476730408D-01 3 14 3 5 0.81225047683412D+01 -0.26875960526987D-01 1 15 3 5 0.22174517997335D+01 0.11338761750796D-02 2 15 3 5 0.19766674239629D+01 0.80777843326801D-02 3 15 3 5 0.29125009571178D+00 -0.16060897962065D-02 1 16 3 5 -0.22174517997335D+01 -0.11338761750788D-02 2 16 3 5 -0.19766674239629D+01 -0.80777843326796D-02 3 16 3 5 -0.29125009571179D+00 0.16060897961964D-02 1 17 3 5 -0.59001136683451D+00 -0.32308394610656D-01 2 17 3 5 -0.95059776604209D-01 0.54538587718519D-01 3 17 3 5 -0.81322331927145D+01 0.28941632785684D-01 1 18 3 5 0.59001136683456D+00 0.32308394610663D-01 2 18 3 5 0.95059776604124D-01 -0.54538587718528D-01 3 18 3 5 0.81322331927143D+01 -0.28941632785659D-01 1 19 3 5 0.18250739261309D+01 0.22972407861432D-01 2 19 3 5 -0.23864544706738D+01 -0.24997903745377D-01 3 19 3 5 0.47060275579350D+00 0.17445600285657D-01 1 20 3 5 -0.18250739261309D+01 -0.22972407861432D-01 2 20 3 5 0.23864544706739D+01 0.24997903745376D-01 3 20 3 5 -0.47060275579346D+00 -0.17445600285651D-01 1 1 1 6 0.18263575150759D+01 0.10463316046508D-01 2 1 1 6 0.10243458926398D+00 -0.10545846424687D-02 3 1 1 6 -0.85451153995968D+00 0.26188256688241D-01 1 2 1 6 0.18263575150759D+01 0.10463316046506D-01 2 2 1 6 0.10243458926398D+00 -0.10545846424687D-02 3 2 1 6 -0.85451153995969D+00 0.26188256688241D-01 1 3 1 6 -0.34562685163367D+01 0.23019407447614D-01 2 3 1 6 0.46740396775780D+00 0.45331725949607D-02 3 3 1 6 -0.78637741158040D+00 -0.26696088749249D-01 1 4 1 6 -0.34562685163369D+01 0.23019407447617D-01 2 4 1 6 0.46740396775782D+00 0.45331725949605D-02 3 4 1 6 -0.78637741158056D+00 -0.26696088749249D-01 1 5 1 6 -0.35726957487475D-13 -0.17272825776976D-14 2 5 1 6 -0.19772103412106D-17 0.20681475278021D-16 3 5 1 6 -0.31535357084226D-16 -0.37143205042801D-15 1 6 1 6 0.17814804893076D+02 0.00000000000000D+00 2 6 1 6 0.42692573934770D+00 -0.80343366161171D-07 3 6 1 6 -0.41640154347276D+00 0.35551377622842D-07 1 7 1 6 0.10324715421871D-13 -0.61839311525151D-15 2 7 1 6 -0.12466570893605D-14 -0.43565291413662D-16 3 7 1 6 0.77340216828524D-14 -0.10919180550545D-15 1 8 1 6 -0.13739810021253D+02 0.00000000000000D+00 2 8 1 6 -0.47449634027871D+01 0.30659550703948D-08 3 8 1 6 0.39486275740516D+01 -0.26286589376970D-07 1 9 1 6 -0.14609351257446D+01 0.99248007541050D+00 2 9 1 6 -0.11468517587729D+00 -0.33737731451701D-01 3 9 1 6 0.59618987300067D+00 0.31443463245434D+00 1 10 1 6 -0.14609351257444D+01 0.99248007541050D+00 2 10 1 6 -0.11468517587728D+00 -0.33737731451701D-01 3 10 1 6 0.59618987300050D+00 0.31443463245434D+00 1 11 1 6 0.12029576947453D+01 -0.26277579259033D-01 2 11 1 6 0.35077330036195D+00 -0.11376200440041D-01 3 11 1 6 0.54306240389860D-01 0.20505626814280D-01 1 12 1 6 0.12029576947453D+01 -0.26277579259033D-01 2 12 1 6 0.35077330036197D+00 -0.11376200440041D-01 3 12 1 6 0.54306240389864D-01 0.20505626814281D-01 1 13 1 6 -0.37777211143034D+00 0.46890990369810D-01 2 13 1 6 -0.27843668475829D+00 0.53936912421190D-01 3 13 1 6 0.24436588460006D+00 -0.29396970736665D-01 1 14 1 6 -0.37777211143034D+00 0.46890990369810D-01 2 14 1 6 -0.27843668475829D+00 0.53936912421190D-01 3 14 1 6 0.24436588460007D+00 -0.29396970736665D-01 1 15 1 6 -0.48396263283308D+00 0.16319570772130D-02 2 15 1 6 0.79319302850001D+00 0.48007065008382D-02 3 15 1 6 -0.93573475454499D+00 0.37582003428936D-01 1 16 1 6 -0.48396263283335D+00 0.16319570772127D-02 2 16 1 6 0.79319302849994D+00 0.48007065008382D-02 3 16 1 6 -0.93573475454532D+00 0.37582003428936D-01 1 17 1 6 -0.25413208551327D+00 0.88218531597782D-01 2 17 1 6 0.41677659946974D+00 -0.13267851192328D+00 3 17 1 6 0.20850660326205D+00 -0.65729194452607D-01 1 18 1 6 -0.25413208551327D+00 0.88218531597783D-01 2 18 1 6 0.41677659946974D+00 -0.13267851192328D+00 3 18 1 6 0.20850660326204D+00 -0.65729194452606D-01 1 19 1 6 0.13646047988220D+00 0.42100838790545D-02 2 19 1 6 0.57706589902662D+00 -0.12289748358360D-01 3 19 1 6 -0.98353435861180D+00 0.33940087545786D-01 1 20 1 6 0.13646047988226D+00 0.42100838790540D-02 2 20 1 6 0.57706589902639D+00 -0.12289748358360D-01 3 20 1 6 -0.98353435861184D+00 0.33940087545785D-01 1 1 2 6 -0.46856519757803D+00 0.80939902446520D-03 2 1 2 6 -0.35240698855760D+01 -0.27590164583610D-01 3 1 2 6 -0.14775186762833D+01 -0.66074084325945D-02 1 2 2 6 -0.46856519757804D+00 0.80939902446524D-03 2 2 2 6 -0.35240698855760D+01 -0.27590164583612D-01 3 2 2 6 -0.14775186762834D+01 -0.66074084325944D-02 1 3 2 6 0.18339418079306D+00 0.17890360038479D-02 2 3 2 6 0.17962833935333D+01 0.33133797522048D-02 3 3 2 6 0.72999044866367D+00 0.16551315724606D-01 1 4 2 6 0.18339418079307D+00 0.17890360038478D-02 2 4 2 6 0.17962833935334D+01 0.33133797522037D-02 3 4 2 6 0.72999044866364D+00 0.16551315724606D-01 1 5 2 6 -0.19772103383834D-17 0.20681475278022D-16 2 5 2 6 -0.23837672721954D-13 -0.15580926143661D-14 3 5 2 6 0.78776473380782D-14 0.28856110882903D-15 1 6 2 6 0.42693515924407D+00 0.87974665184051D-07 2 6 2 6 0.18570594078078D+02 0.00000000000000D+00 3 6 2 6 0.30503659827299D+01 -0.27721419477738D-06 1 7 2 6 -0.12584569566371D-14 -0.43565291413662D-16 2 7 2 6 0.66876797532456D-14 -0.14531695751469D-14 3 7 2 6 -0.82076508622372D-14 0.35162514583521D-15 1 8 2 6 0.47449634027871D+01 0.30659550703948D-08 2 8 2 6 -0.14762433655738D+02 0.00000000000000D+00 3 8 2 6 -0.37888229687980D+00 -0.83145480447909D-08 1 9 2 6 -0.53226088174310D-01 -0.21225596262136D-01 2 9 2 6 -0.14644458490856D+01 0.10202621373355D+01 3 9 2 6 -0.15149923952849D+00 -0.70592669203450D-01 1 10 2 6 -0.53226088174304D-01 -0.21225596262135D-01 2 10 2 6 -0.14644458490855D+01 0.10202621373355D+01 3 10 2 6 -0.15149923952866D+00 -0.70592669203450D-01 1 11 2 6 -0.47379481343785D+00 0.10765131700376D-01 2 11 2 6 0.13287377129898D+01 -0.26733383406707D-01 3 11 2 6 -0.26021371927452D+00 -0.17342934288836D-01 1 12 2 6 -0.47379481343784D+00 0.10765131700376D-01 2 12 2 6 0.13287377129898D+01 -0.26733383406707D-01 3 12 2 6 -0.26021371927461D+00 -0.17342934288836D-01 1 13 2 6 0.14158513548062D+00 0.32825000619359D-01 2 13 2 6 0.88549792089436D-01 0.28832767553978D-01 3 13 2 6 0.76798941795584D-01 0.16238853335849D-02 1 14 2 6 0.14158513548062D+00 0.32825000619358D-01 2 14 2 6 0.88549792089423D-01 0.28832767553978D-01 3 14 2 6 0.76798941795573D-01 0.16238853335855D-02 1 15 2 6 -0.75629175951961D+00 -0.77991850861340D-02 2 15 2 6 -0.30875624439638D-01 -0.46336606044465D-03 3 15 2 6 -0.79230353471445D+00 0.17900070251474D-01 1 16 2 6 -0.75629175951968D+00 -0.77991850861340D-02 2 16 2 6 -0.30875624439432D-01 -0.46336606044429D-03 3 16 2 6 -0.79230353471464D+00 0.17900070251474D-01 1 17 2 6 0.56239408163783D-01 -0.13810226758316D+00 2 17 2 6 -0.55606464042188D-01 0.17124834068808D+00 3 17 2 6 -0.82729911584879D-01 0.44821577622645D-01 1 18 2 6 0.56239408163785D-01 -0.13810226758316D+00 2 18 2 6 -0.55606464042189D-01 0.17124834068808D+00 3 18 2 6 -0.82729911584851D-01 0.44821577622644D-01 1 19 2 6 -0.10201618763044D+01 -0.33250236328524D-02 2 19 2 6 -0.14783112415751D+00 0.52523946663015D-02 3 19 2 6 0.78284481223608D+00 -0.45147056285258D-01 1 20 2 6 -0.10201618763046D+01 -0.33250236328524D-02 2 20 2 6 -0.14783112415719D+00 0.52523946663003D-02 3 20 2 6 0.78284481223614D+00 -0.45147056285256D-01 1 1 3 6 -0.14552923027606D-01 -0.25702590298476D-01 2 1 3 6 -0.19222625175942D+01 -0.12428092140357D-02 3 1 3 6 0.27721804615839D+01 -0.15539713737760D-01 1 2 3 6 -0.14552923027613D-01 -0.25702590298476D-01 2 2 3 6 -0.19222625175943D+01 -0.12428092140356D-02 3 2 3 6 0.27721804615840D+01 -0.15539713737763D-01 1 3 3 6 0.16399621792101D+00 -0.10845446110012D-01 2 3 3 6 0.85214487240047D+00 0.11842339030056D-01 3 3 3 6 0.29269557900194D+01 0.10026035311442D-01 1 4 3 6 0.16399621792086D+00 -0.10845446110012D-01 2 4 3 6 0.85214487240044D+00 0.11842339030056D-01 3 4 3 6 0.29269557900195D+01 0.10026035311528D-01 1 5 3 6 0.18422894893553D-16 -0.37143205042801D-15 2 5 3 6 0.78640671777130D-14 0.28856110882903D-15 3 5 3 6 0.24500035949608D-12 0.24440418740424D-13 1 6 3 6 -0.41639356531745D+00 -0.67121813308893D-07 2 6 3 6 0.30503750119135D+01 0.30863071093042D-06 3 6 3 6 0.55145407904738D+02 0.00000000000000D+00 1 7 3 6 0.77340216828524D-14 -0.10919180550545D-15 2 7 3 6 -0.82120736671051D-14 0.35162514583521D-15 3 7 3 6 -0.50752983777903D-13 -0.13422018782584D-14 1 8 3 6 -0.39486275740516D+01 -0.26286589376970D-07 2 8 3 6 -0.37888229687980D+00 0.83145480447909D-08 3 8 3 6 0.16955906091858D+02 0.00000000000000D+00 1 9 3 6 0.19437877341004D+01 0.46587979889756D+00 2 9 3 6 -0.39232003853719D+00 -0.10632735356758D+00 3 9 3 6 -0.13229070618331D+02 -0.26203554511113D+01 1 10 3 6 0.19437877341002D+01 0.46587979889756D+00 2 10 3 6 -0.39232003853736D+00 -0.10632735356758D+00 3 10 3 6 -0.13229070618332D+02 -0.26203554511113D+01 1 11 3 6 -0.41945609494045D+00 -0.10639367904396D-01 2 11 3 6 -0.18717592153538D+00 -0.32243574706696D-02 3 11 3 6 -0.89881011904708D+01 0.24041959735202D+00 1 12 3 6 -0.41945609494045D+00 -0.10639367904395D-01 2 12 3 6 -0.18717592153547D+00 -0.32243574706700D-02 3 12 3 6 -0.89881011904709D+01 0.24041959735203D+00 1 13 3 6 0.22174517997335D+01 0.11338761750786D-02 2 13 3 6 0.19766674239629D+01 0.80777843326793D-02 3 13 3 6 -0.29125009571181D+00 0.16060897962002D-02 1 14 3 6 0.22174517997335D+01 0.11338761750787D-02 2 14 3 6 0.19766674239629D+01 0.80777843326799D-02 3 14 3 6 -0.29125009571174D+00 0.16060897962091D-02 1 15 3 6 0.65238296326405D+00 0.33397516841104D-01 2 15 3 6 0.28586002827560D+00 0.40320476730401D-01 3 15 3 6 -0.81225047683411D+01 0.26875960527011D-01 1 16 3 6 0.65238296326373D+00 0.33397516841104D-01 2 16 3 6 0.28586002827541D+00 0.40320476730400D-01 3 16 3 6 -0.81225047683411D+01 0.26875960527008D-01 1 17 3 6 0.18250739261309D+01 0.22972407861431D-01 2 17 3 6 -0.23864544706739D+01 -0.24997903745376D-01 3 17 3 6 -0.47060275579352D+00 -0.17445600285650D-01 1 18 3 6 0.18250739261309D+01 0.22972407861432D-01 2 18 3 6 -0.23864544706738D+01 -0.24997903745376D-01 3 18 3 6 -0.47060275579348D+00 -0.17445600285648D-01 1 19 3 6 0.59001136683455D+00 0.32308394610657D-01 2 19 3 6 0.95059776604117D-01 -0.54538587718520D-01 3 19 3 6 -0.81322331927143D+01 0.28941632785683D-01 1 20 3 6 0.59001136683451D+00 0.32308394610656D-01 2 20 3 6 0.95059776604181D-01 -0.54538587718518D-01 3 20 3 6 -0.81322331927146D+01 0.28941632785681D-01 1 1 1 7 -0.34562685163368D+01 0.23019407447613D-01 2 1 1 7 -0.46740396775780D+00 -0.45331725949606D-02 3 1 1 7 -0.78637741158040D+00 -0.26696088749249D-01 1 2 1 7 0.34562685163369D+01 -0.23019407447628D-01 2 2 1 7 0.46740396775780D+00 0.45331725949605D-02 3 2 1 7 0.78637741158039D+00 0.26696088749248D-01 1 3 1 7 0.18263575150759D+01 0.10463316046508D-01 2 3 1 7 -0.10243458926398D+00 0.10545846424687D-02 3 3 1 7 -0.85451153995968D+00 0.26188256688241D-01 1 4 1 7 -0.18263575150759D+01 -0.10463316046504D-01 2 4 1 7 0.10243458926397D+00 -0.10545846424686D-02 3 4 1 7 0.85451153995971D+00 -0.26188256688241D-01 1 5 1 7 -0.13739810021253D+02 0.00000000000000D+00 2 5 1 7 0.47449634027871D+01 -0.30659550703948D-08 3 5 1 7 0.39486275740516D+01 -0.26286589376970D-07 1 6 1 7 0.10324715421871D-13 0.61839311525151D-15 2 6 1 7 -0.12584569566371D-14 0.43565291413662D-16 3 6 1 7 0.77340216828524D-14 0.10919180550545D-15 1 7 1 7 0.17814804893076D+02 0.00000000000000D+00 2 7 1 7 -0.42692573934759D+00 0.80343366161171D-07 3 7 1 7 -0.41640154347260D+00 0.35551377622842D-07 1 8 1 7 -0.24735749543686D-13 0.17272825776976D-14 2 8 1 7 -0.54253952256620D-15 -0.20681475278021D-16 3 8 1 7 0.62915317128512D-14 0.37143205042801D-15 1 9 1 7 0.12029576947453D+01 -0.26277579259035D-01 2 9 1 7 -0.35077330036197D+00 0.11376200440041D-01 3 9 1 7 0.54306240389882D-01 0.20505626814280D-01 1 10 1 7 -0.12029576947453D+01 0.26277579259031D-01 2 10 1 7 0.35077330036197D+00 -0.11376200440040D-01 3 10 1 7 -0.54306240389882D-01 -0.20505626814279D-01 1 11 1 7 0.14609351257443D+01 -0.99248007541049D+00 2 11 1 7 -0.11468517587717D+00 -0.33737731451701D-01 3 11 1 7 -0.59618987300061D+00 -0.31443463245432D+00 1 12 1 7 -0.14609351257445D+01 0.99248007541050D+00 2 12 1 7 0.11468517587732D+00 0.33737731451701D-01 3 12 1 7 0.59618987300044D+00 0.31443463245434D+00 1 13 1 7 0.13646047988226D+00 0.42100838790544D-02 2 13 1 7 -0.57706589902637D+00 0.12289748358360D-01 3 13 1 7 -0.98353435861184D+00 0.33940087545786D-01 1 14 1 7 -0.13646047988213D+00 -0.42100838790579D-02 2 14 1 7 0.57706589902689D+00 -0.12289748358382D-01 3 14 1 7 0.98353435861188D+00 -0.33940087545792D-01 1 15 1 7 0.25413208551327D+00 -0.88218531597782D-01 2 15 1 7 0.41677659946974D+00 -0.13267851192328D+00 3 15 1 7 -0.20850660326203D+00 0.65729194452606D-01 1 16 1 7 -0.25413208551328D+00 0.88218531597782D-01 2 16 1 7 -0.41677659946974D+00 0.13267851192328D+00 3 16 1 7 0.20850660326205D+00 -0.65729194452607D-01 1 17 1 7 -0.48396263283354D+00 0.16319570772135D-02 2 17 1 7 -0.79319302849989D+00 -0.48007065008382D-02 3 17 1 7 -0.93573475454541D+00 0.37582003428936D-01 1 18 1 7 0.48396263283321D+00 -0.16319570772342D-02 2 18 1 7 0.79319302849997D+00 0.48007065008608D-02 3 18 1 7 0.93573475454506D+00 -0.37582003428945D-01 1 19 1 7 0.37777211143034D+00 -0.46890990369810D-01 2 19 1 7 -0.27843668475829D+00 0.53936912421190D-01 3 19 1 7 -0.24436588460006D+00 0.29396970736664D-01 1 20 1 7 -0.37777211143033D+00 0.46890990369810D-01 2 20 1 7 0.27843668475829D+00 -0.53936912421190D-01 3 20 1 7 0.24436588460005D+00 -0.29396970736665D-01 1 1 2 7 -0.18339418079305D+00 -0.17890360038478D-02 2 1 2 7 0.17962833935334D+01 0.33133797522056D-02 3 1 2 7 -0.72999044866356D+00 -0.16551315724606D-01 1 2 2 7 0.18339418079305D+00 0.17890360038478D-02 2 2 2 7 -0.17962833935334D+01 -0.33133797522017D-02 3 2 2 7 0.72999044866360D+00 0.16551315724604D-01 1 3 2 7 0.46856519757804D+00 -0.80939902446518D-03 2 3 2 7 -0.35240698855760D+01 -0.27590164583613D-01 3 3 2 7 0.14775186762836D+01 0.66074084325936D-02 1 4 2 7 -0.46856519757805D+00 0.80939902446528D-03 2 4 2 7 0.35240698855761D+01 0.27590164583598D-01 3 4 2 7 -0.14775186762835D+01 -0.66074084325891D-02 1 5 2 7 -0.47449634027871D+01 -0.30659550703948D-08 2 5 2 7 -0.14762433655738D+02 0.00000000000000D+00 3 5 2 7 0.37888229687980D+00 0.83145480447909D-08 1 6 2 7 -0.12466570893605D-14 0.43565291413662D-16 2 6 2 7 0.66876797532456D-14 0.14531695751469D-14 3 6 2 7 -0.82120736671051D-14 -0.35162514583521D-15 1 7 2 7 -0.42693515924397D+00 -0.87974665184051D-07 2 7 2 7 0.18570594078077D+02 0.00000000000000D+00 3 7 2 7 -0.30503659827308D+01 0.27721419477738D-06 1 8 2 7 -0.54253952256903D-15 -0.20681475278021D-16 2 8 2 7 -0.31831278499255D-13 0.15580926143661D-14 3 8 2 7 0.26026508750753D-14 -0.28856110882903D-15 1 9 2 7 0.47379481343783D+00 -0.10765131700376D-01 2 9 2 7 0.13287377129898D+01 -0.26733383406706D-01 3 9 2 7 0.26021371927460D+00 0.17342934288836D-01 1 10 2 7 -0.47379481343784D+00 0.10765131700376D-01 2 10 2 7 -0.13287377129897D+01 0.26733383406706D-01 3 10 2 7 -0.26021371927458D+00 -0.17342934288836D-01 1 11 2 7 -0.53226088174195D-01 -0.21225596262136D-01 2 11 2 7 0.14644458490854D+01 -0.10202621373355D+01 3 11 2 7 -0.15149923952928D+00 -0.70592669203446D-01 1 12 2 7 0.53226088174347D-01 0.21225596262135D-01 2 12 2 7 -0.14644458490855D+01 0.10202621373355D+01 3 12 2 7 0.15149923952837D+00 0.70592669203450D-01 1 13 2 7 0.10201618763046D+01 0.33250236328524D-02 2 13 2 7 -0.14783112415735D+00 0.52523946662995D-02 3 13 2 7 -0.78284481223615D+00 0.45147056285258D-01 1 14 2 7 -0.10201618763041D+01 -0.33250236328745D-02 2 14 2 7 0.14783112415748D+00 -0.52523946663219D-02 3 14 2 7 0.78284481223617D+00 -0.45147056285267D-01 1 15 2 7 0.56239408163784D-01 -0.13810226758316D+00 2 15 2 7 0.55606464042180D-01 -0.17124834068808D+00 3 15 2 7 -0.82729911584847D-01 0.44821577622644D-01 1 16 2 7 -0.56239408163779D-01 0.13810226758316D+00 2 16 2 7 -0.55606464042187D-01 0.17124834068808D+00 3 16 2 7 0.82729911584870D-01 -0.44821577622644D-01 1 17 2 7 0.75629175951973D+00 0.77991850861340D-02 2 17 2 7 -0.30875624439343D-01 -0.46336606044423D-03 3 17 2 7 0.79230353471468D+00 -0.17900070251475D-01 1 18 2 7 -0.75629175951967D+00 -0.77991850861114D-02 2 18 2 7 0.30875624439531D-01 0.46336606043915D-03 3 18 2 7 -0.79230353471448D+00 0.17900070251481D-01 1 19 2 7 0.14158513548062D+00 0.32825000619358D-01 2 19 2 7 -0.88549792089430D-01 -0.28832767553978D-01 3 19 2 7 0.76798941795586D-01 0.16238853335860D-02 1 20 2 7 -0.14158513548062D+00 -0.32825000619358D-01 2 20 2 7 0.88549792089430D-01 0.28832767553978D-01 3 20 2 7 -0.76798941795584D-01 -0.16238853335855D-02 1 1 3 7 0.16399621792101D+00 -0.10845446110012D-01 2 1 3 7 -0.85214487240036D+00 -0.11842339030056D-01 3 1 3 7 0.29269557900194D+01 0.10026035311489D-01 1 2 3 7 -0.16399621792102D+00 0.10845446110011D-01 2 2 3 7 0.85214487240040D+00 0.11842339030055D-01 3 2 3 7 -0.29269557900197D+01 -0.10026035311482D-01 1 3 3 7 -0.14552923027609D-01 -0.25702590298476D-01 2 3 3 7 0.19222625175945D+01 0.12428092140348D-02 3 3 3 7 0.27721804615839D+01 -0.15539713737766D-01 1 4 3 7 0.14552923027632D-01 0.25702590298476D-01 2 4 3 7 -0.19222625175944D+01 -0.12428092140303D-02 3 4 3 7 -0.27721804615842D+01 0.15539713737751D-01 1 5 3 7 -0.39486275740516D+01 -0.26286589376970D-07 2 5 3 7 0.37888229687980D+00 -0.83145480447909D-08 3 5 3 7 0.16955906091858D+02 0.00000000000000D+00 1 6 3 7 0.77340216828524D-14 0.10919180550545D-15 2 6 3 7 -0.82076508622372D-14 -0.35162514583521D-15 3 6 3 7 -0.50752983777903D-13 0.13422018782584D-14 1 7 3 7 -0.41639356531729D+00 -0.67121813308893D-07 2 7 3 7 -0.30503750119145D+01 -0.30863071093042D-06 3 7 3 7 0.55145407904737D+02 0.00000000000000D+00 1 8 3 7 0.63414899648290D-14 0.37143205042801D-15 2 8 3 7 0.26162310354405D-14 -0.28856110882903D-15 3 8 3 7 0.24500035949608D-12 -0.24440418740424D-13 1 9 3 7 -0.41945609494043D+00 -0.10639367904396D-01 2 9 3 7 0.18717592153546D+00 0.32243574706694D-02 3 9 3 7 -0.89881011904707D+01 0.24041959735203D+00 1 10 3 7 0.41945609494043D+00 0.10639367904397D-01 2 10 3 7 -0.18717592153544D+00 -0.32243574706700D-02 3 10 3 7 0.89881011904706D+01 -0.24041959735202D+00 1 11 3 7 -0.19437877341003D+01 -0.46587979889754D+00 2 11 3 7 -0.39232003853798D+00 -0.10632735356758D+00 3 11 3 7 0.13229070618332D+02 0.26203554511113D+01 1 12 3 7 0.19437877341001D+01 0.46587979889756D+00 2 12 3 7 0.39232003853708D+00 0.10632735356758D+00 3 12 3 7 -0.13229070618332D+02 -0.26203554511113D+01 1 13 3 7 0.59001136683450D+00 0.32308394610656D-01 2 13 3 7 -0.95059776604188D-01 0.54538587718520D-01 3 13 3 7 -0.81322331927146D+01 0.28941632785684D-01 1 14 3 7 -0.59001136683446D+00 -0.32308394610663D-01 2 14 3 7 0.95059776604202D-01 -0.54538587718529D-01 3 14 3 7 0.81322331927140D+01 -0.28941632785661D-01 1 15 3 7 -0.18250739261309D+01 -0.22972407861432D-01 2 15 3 7 -0.23864544706738D+01 -0.24997903745377D-01 3 15 3 7 0.47060275579350D+00 0.17445600285676D-01 1 16 3 7 0.18250739261309D+01 0.22972407861432D-01 2 16 3 7 0.23864544706739D+01 0.24997903745376D-01 3 16 3 7 -0.47060275579347D+00 -0.17445600285651D-01 1 17 3 7 0.65238296326363D+00 0.33397516841105D-01 2 17 3 7 -0.28586002827537D+00 -0.40320476730402D-01 3 17 3 7 -0.81225047683410D+01 0.26875960527008D-01 1 18 3 7 -0.65238296326398D+00 -0.33397516841113D-01 2 18 3 7 0.28586002827556D+00 0.40320476730408D-01 3 18 3 7 0.81225047683410D+01 -0.26875960526985D-01 1 19 3 7 -0.22174517997335D+01 -0.11338761750796D-02 2 19 3 7 0.19766674239629D+01 0.80777843326803D-02 3 19 3 7 0.29125009571178D+00 -0.16060897962143D-02 1 20 3 7 0.22174517997335D+01 0.11338761750789D-02 2 20 3 7 -0.19766674239629D+01 -0.80777843326799D-02 3 20 3 7 -0.29125009571178D+00 0.16060897962089D-02 1 1 1 8 -0.34562685163368D+01 0.23019407447614D-01 2 1 1 8 -0.46740396775780D+00 -0.45331725949606D-02 3 1 1 8 0.78637741158040D+00 0.26696088749249D-01 1 2 1 8 -0.34562685163368D+01 0.23019407447617D-01 2 2 1 8 -0.46740396775780D+00 -0.45331725949605D-02 3 2 1 8 0.78637741158041D+00 0.26696088749249D-01 1 3 1 8 0.18263575150759D+01 0.10463316046507D-01 2 3 1 8 -0.10243458926397D+00 0.10545846424687D-02 3 3 1 8 0.85451153995968D+00 -0.26188256688241D-01 1 4 1 8 0.18263575150759D+01 0.10463316046509D-01 2 4 1 8 -0.10243458926397D+00 0.10545846424688D-02 3 4 1 8 0.85451153995970D+00 -0.26188256688241D-01 1 5 1 8 0.11062767943869D-13 -0.61839311525151D-15 2 5 1 8 -0.15011410810159D-14 -0.43565291413662D-16 3 5 1 8 -0.87332300259269D-14 -0.10919180550545D-15 1 6 1 8 -0.13739810021253D+02 0.00000000000000D+00 2 6 1 8 0.47449634027871D+01 -0.30659550703948D-08 3 6 1 8 -0.39486275740516D+01 0.26286589376970D-07 1 7 1 8 -0.24735749543686D-13 -0.17272825776976D-14 2 7 1 8 -0.54253952256903D-15 0.20681475278022D-16 3 7 1 8 0.63414899648290D-14 -0.37143205042801D-15 1 8 1 8 0.17814804893076D+02 0.00000000000000D+00 2 8 1 8 -0.42692573934750D+00 0.80343366161171D-07 3 8 1 8 0.41640154347239D+00 -0.35551377622842D-07 1 9 1 8 0.12029576947454D+01 -0.26277579259032D-01 2 9 1 8 -0.35077330036197D+00 0.11376200440041D-01 3 9 1 8 -0.54306240389885D-01 -0.20505626814280D-01 1 10 1 8 0.12029576947453D+01 -0.26277579259033D-01 2 10 1 8 -0.35077330036197D+00 0.11376200440041D-01 3 10 1 8 -0.54306240389862D-01 -0.20505626814280D-01 1 11 1 8 -0.14609351257444D+01 0.99248007541050D+00 2 11 1 8 0.11468517587719D+00 0.33737731451701D-01 3 11 1 8 -0.59618987300043D+00 -0.31443463245434D+00 1 12 1 8 -0.14609351257445D+01 0.99248007541050D+00 2 12 1 8 0.11468517587732D+00 0.33737731451701D-01 3 12 1 8 -0.59618987300043D+00 -0.31443463245434D+00 1 13 1 8 -0.25413208551327D+00 0.88218531597782D-01 2 13 1 8 -0.41677659946974D+00 0.13267851192328D+00 3 13 1 8 -0.20850660326206D+00 0.65729194452607D-01 1 14 1 8 -0.25413208551327D+00 0.88218531597783D-01 2 14 1 8 -0.41677659946974D+00 0.13267851192328D+00 3 14 1 8 -0.20850660326204D+00 0.65729194452607D-01 1 15 1 8 0.13646047988214D+00 0.42100838790544D-02 2 15 1 8 -0.57706589902682D+00 0.12289748358360D-01 3 15 1 8 0.98353435861188D+00 -0.33940087545786D-01 1 16 1 8 0.13646047988225D+00 0.42100838790540D-02 2 16 1 8 -0.57706589902639D+00 0.12289748358360D-01 3 16 1 8 0.98353435861183D+00 -0.33940087545786D-01 1 17 1 8 -0.37777211143033D+00 0.46890990369810D-01 2 17 1 8 0.27843668475829D+00 -0.53936912421190D-01 3 17 1 8 -0.24436588460006D+00 0.29396970736665D-01 1 18 1 8 -0.37777211143034D+00 0.46890990369810D-01 2 18 1 8 0.27843668475829D+00 -0.53936912421190D-01 3 18 1 8 -0.24436588460006D+00 0.29396970736665D-01 1 19 1 8 -0.48396263283321D+00 0.16319570772136D-02 2 19 1 8 -0.79319302849989D+00 -0.48007065008382D-02 3 19 1 8 0.93573475454506D+00 -0.37582003428935D-01 1 20 1 8 -0.48396263283351D+00 0.16319570772134D-02 2 20 1 8 -0.79319302849996D+00 -0.48007065008383D-02 3 20 1 8 0.93573475454540D+00 -0.37582003428937D-01 1 1 2 8 -0.18339418079305D+00 -0.17890360038479D-02 2 1 2 8 0.17962833935334D+01 0.33133797522060D-02 3 1 2 8 0.72999044866356D+00 0.16551315724606D-01 1 2 2 8 -0.18339418079306D+00 -0.17890360038478D-02 2 2 2 8 0.17962833935334D+01 0.33133797522050D-02 3 2 2 8 0.72999044866360D+00 0.16551315724606D-01 1 3 2 8 0.46856519757804D+00 -0.80939902446521D-03 2 3 2 8 -0.35240698855759D+01 -0.27590164583612D-01 3 3 2 8 -0.14775186762836D+01 -0.66074084325948D-02 1 4 2 8 0.46856519757804D+00 -0.80939902446515D-03 2 4 2 8 -0.35240698855760D+01 -0.27590164583610D-01 3 4 2 8 -0.14775186762836D+01 -0.66074084325943D-02 1 5 2 8 -0.14893412137910D-14 -0.43565291413662D-16 2 5 2 8 0.25062470248631D-13 -0.14531695751469D-14 3 5 2 8 -0.10772759109667D-13 0.35162514583521D-15 1 6 2 8 -0.47449634027871D+01 -0.30659550703948D-08 2 6 2 8 -0.14762433655738D+02 0.00000000000000D+00 3 6 2 8 -0.37888229687980D+00 -0.83145480447909D-08 1 7 2 8 -0.54253952256620D-15 0.20681475278021D-16 2 7 2 8 -0.31831278499255D-13 -0.15580926143661D-14 3 7 2 8 0.26162310354405D-14 0.28856110882903D-15 1 8 2 8 -0.42693515924387D+00 -0.87974665184051D-07 2 8 2 8 0.18570594078077D+02 0.00000000000000D+00 3 8 2 8 0.30503659827308D+01 -0.27721419477738D-06 1 9 2 8 0.47379481343783D+00 -0.10765131700376D-01 2 9 2 8 0.13287377129898D+01 -0.26733383406709D-01 3 9 2 8 -0.26021371927460D+00 -0.17342934288836D-01 1 10 2 8 0.47379481343784D+00 -0.10765131700376D-01 2 10 2 8 0.13287377129898D+01 -0.26733383406706D-01 3 10 2 8 -0.26021371927459D+00 -0.17342934288836D-01 1 11 2 8 0.53226088174210D-01 0.21225596262135D-01 2 11 2 8 -0.14644458490856D+01 0.10202621373355D+01 3 11 2 8 -0.15149923952924D+00 -0.70592669203450D-01 1 12 2 8 0.53226088174342D-01 0.21225596262135D-01 2 12 2 8 -0.14644458490855D+01 0.10202621373355D+01 3 12 2 8 -0.15149923952835D+00 -0.70592669203450D-01 1 13 2 8 -0.56239408163781D-01 0.13810226758316D+00 2 13 2 8 -0.55606464042189D-01 0.17124834068808D+00 3 13 2 8 -0.82729911584877D-01 0.44821577622645D-01 1 14 2 8 -0.56239408163786D-01 0.13810226758316D+00 2 14 2 8 -0.55606464042180D-01 0.17124834068808D+00 3 14 2 8 -0.82729911584831D-01 0.44821577622644D-01 1 15 2 8 0.10201618763042D+01 0.33250236328524D-02 2 15 2 8 -0.14783112415751D+00 0.52523946662996D-02 3 15 2 8 0.78284481223620D+00 -0.45147056285257D-01 1 16 2 8 0.10201618763046D+01 0.33250236328524D-02 2 16 2 8 -0.14783112415719D+00 0.52523946663005D-02 3 16 2 8 0.78284481223614D+00 -0.45147056285257D-01 1 17 2 8 -0.14158513548062D+00 -0.32825000619358D-01 2 17 2 8 0.88549792089433D-01 0.28832767553978D-01 3 17 2 8 0.76798941795580D-01 0.16238853335848D-02 1 18 2 8 -0.14158513548062D+00 -0.32825000619358D-01 2 18 2 8 0.88549792089434D-01 0.28832767553978D-01 3 18 2 8 0.76798941795582D-01 0.16238853335852D-02 1 19 2 8 0.75629175951973D+00 0.77991850861340D-02 2 19 2 8 -0.30875624439542D-01 -0.46336606044443D-03 3 19 2 8 -0.79230353471446D+00 0.17900070251473D-01 1 20 2 8 0.75629175951968D+00 0.77991850861340D-02 2 20 2 8 -0.30875624439343D-01 -0.46336606044466D-03 3 20 2 8 -0.79230353471466D+00 0.17900070251474D-01 1 1 3 8 -0.16399621792102D+00 0.10845446110012D-01 2 1 3 8 0.85214487240036D+00 0.11842339030056D-01 3 1 3 8 0.29269557900194D+01 0.10026035311487D-01 1 2 3 8 -0.16399621792100D+00 0.10845446110012D-01 2 2 3 8 0.85214487240039D+00 0.11842339030056D-01 3 2 3 8 0.29269557900195D+01 0.10026035311480D-01 1 3 3 8 0.14552923027608D-01 0.25702590298476D-01 2 3 3 8 -0.19222625175945D+01 -0.12428092140360D-02 3 3 3 8 0.27721804615838D+01 -0.15539713737767D-01 1 4 3 8 0.14552923027630D-01 0.25702590298476D-01 2 4 3 8 -0.19222625175944D+01 -0.12428092140355D-02 3 4 3 8 0.27721804615840D+01 -0.15539713737762D-01 1 5 3 8 -0.87332300259269D-14 -0.10919180550545D-15 2 5 3 8 -0.10777181914535D-13 0.35162514583521D-15 3 5 3 8 -0.47189364974516D-13 -0.13422018782584D-14 1 6 3 8 0.39486275740516D+01 0.26286589376970D-07 2 6 3 8 -0.37888229687980D+00 0.83145480447909D-08 3 6 3 8 0.16955906091858D+02 0.00000000000000D+00 1 7 3 8 0.62915317128512D-14 -0.37143205042801D-15 2 7 3 8 0.26026508750753D-14 0.28856110882903D-15 3 7 3 8 0.24500035949608D-12 0.24440418740424D-13 1 8 3 8 0.41639356531708D+00 0.67121813308893D-07 2 8 3 8 0.30503750119145D+01 0.30863071093042D-06 3 8 3 8 0.55145407904737D+02 0.00000000000000D+00 1 9 3 8 0.41945609494043D+00 0.10639367904396D-01 2 9 3 8 -0.18717592153546D+00 -0.32243574706695D-02 3 9 3 8 -0.89881011904709D+01 0.24041959735202D+00 1 10 3 8 0.41945609494045D+00 0.10639367904396D-01 2 10 3 8 -0.18717592153544D+00 -0.32243574706697D-02 3 10 3 8 -0.89881011904708D+01 0.24041959735203D+00 1 11 3 8 -0.19437877341001D+01 -0.46587979889756D+00 2 11 3 8 -0.39232003853794D+00 -0.10632735356758D+00 3 11 3 8 -0.13229070618331D+02 -0.26203554511113D+01 1 12 3 8 -0.19437877341001D+01 -0.46587979889756D+00 2 12 3 8 -0.39232003853705D+00 -0.10632735356758D+00 3 12 3 8 -0.13229070618332D+02 -0.26203554511113D+01 1 13 3 8 -0.18250739261309D+01 -0.22972407861431D-01 2 13 3 8 -0.23864544706739D+01 -0.24997903745376D-01 3 13 3 8 -0.47060275579351D+00 -0.17445600285665D-01 1 14 3 8 -0.18250739261309D+01 -0.22972407861432D-01 2 14 3 8 -0.23864544706738D+01 -0.24997903745376D-01 3 14 3 8 -0.47060275579347D+00 -0.17445600285666D-01 1 15 3 8 -0.59001136683447D+00 -0.32308394610656D-01 2 15 3 8 0.95059776604238D-01 -0.54538587718520D-01 3 15 3 8 -0.81322331927140D+01 0.28941632785681D-01 1 16 3 8 -0.59001136683451D+00 -0.32308394610656D-01 2 16 3 8 0.95059776604174D-01 -0.54538587718519D-01 3 16 3 8 -0.81322331927146D+01 0.28941632785684D-01 1 17 3 8 -0.22174517997335D+01 -0.11338761750785D-02 2 17 3 8 0.19766674239629D+01 0.80777843326792D-02 3 17 3 8 -0.29125009571181D+00 0.16060897961967D-02 1 18 3 8 -0.22174517997335D+01 -0.11338761750790D-02 2 18 3 8 0.19766674239629D+01 0.80777843326796D-02 3 18 3 8 -0.29125009571175D+00 0.16060897961966D-02 1 19 3 8 -0.65238296326398D+00 -0.33397516841103D-01 2 19 3 8 0.28586002827558D+00 0.40320476730400D-01 3 19 3 8 -0.81225047683411D+01 0.26875960527010D-01 1 20 3 8 -0.65238296326364D+00 -0.33397516841105D-01 2 20 3 8 0.28586002827539D+00 0.40320476730401D-01 3 20 3 8 -0.81225047683409D+01 0.26875960527008D-01 1 1 1 9 -0.76755231806590D+00 -0.15052829439622D-07 2 1 1 9 -0.35247618671949D+00 -0.10292247576552D-07 3 1 1 9 0.51409000856804D-16 -0.80293788030953D-16 1 2 1 9 -0.33253521844294D-14 0.71856894206794D-15 2 2 1 9 0.63485883162231D-15 -0.37948387689606D-16 3 2 1 9 0.18107892807840D+00 0.29184831634036D-08 1 3 1 9 -0.11892115849382D+01 -0.19615680802843D-07 2 3 1 9 -0.55591842353427D+00 0.54455073776766D-08 3 3 1 9 0.16350093197402D-14 -0.15099973544963D-15 1 4 1 9 0.33587795012534D-14 0.58293525146595D-16 2 4 1 9 0.31551801045796D-16 -0.69272189756708D-16 3 4 1 9 0.22756514255043D+00 0.10531690047127D-07 1 5 1 9 -0.14609342511780D+01 -0.99248034875254D+00 2 5 1 9 -0.53226250046685D-01 0.21225465655935D-01 3 5 1 9 -0.19437883501975D+01 0.46587973269807D+00 1 6 1 9 -0.14609342511780D+01 -0.99248034875254D+00 2 6 1 9 -0.53226250046683D-01 0.21225465655935D-01 3 6 1 9 0.19437883501976D+01 -0.46587973269807D+00 1 7 1 9 0.12029576947453D+01 0.26277579259036D-01 2 7 1 9 0.47379481343783D+00 0.10765131700376D-01 3 7 1 9 -0.41945609494043D+00 0.10639367904395D-01 1 8 1 9 0.12029576947454D+01 0.26277579259033D-01 2 8 1 9 0.47379481343783D+00 0.10765131700376D-01 3 8 1 9 0.41945609494043D+00 -0.10639367904396D-01 1 9 1 9 0.89482831938517D+01 0.00000000000000D+00 2 9 1 9 0.88319108041419D+00 0.61803623979336D-07 3 9 1 9 -0.73365108485390D-14 0.00000000000000D+00 1 10 1 9 0.22039576395432D-14 -0.24555423411607D-15 2 10 1 9 -0.26953166464592D-15 0.97510105853185D-17 3 10 1 9 0.11575019172018D+01 -0.31392872280383D-08 1 11 1 9 -0.22029354180394D-14 -0.31493986771507D-15 2 11 1 9 0.64626419117177D-16 0.72310004384957D-17 3 11 1 9 -0.78669168399801D-01 -0.38850246636673D-08 1 12 1 9 -0.45771581749922D+00 -0.16060037603958D-15 2 12 1 9 -0.17904437952974D+00 -0.76339836172642D-09 3 12 1 9 0.17562955177485D-15 -0.10306832242023D-15 1 13 1 9 -0.15843846343864D+01 -0.23607683596060D-08 2 13 1 9 -0.86498807698320D+00 0.17148043118694D-08 3 13 1 9 -0.12779867517876D+01 -0.61693062665934D-08 1 14 1 9 0.15265269930115D+00 -0.24036828917296D-01 2 14 1 9 0.59321503213183D+00 -0.23378399653819D-01 3 14 1 9 -0.12573991981888D+01 -0.55477043253233D-02 1 15 1 9 -0.15265269930115D+00 0.24036828917297D-01 2 15 1 9 -0.59321503213184D+00 0.23378399653818D-01 3 15 1 9 -0.12573991981888D+01 -0.55477043253263D-02 1 16 1 9 -0.15843846343864D+01 -0.23607682684291D-08 2 16 1 9 -0.86498807698319D+00 0.17148042274727D-08 3 16 1 9 0.12779867517876D+01 0.61693062237296D-08 1 17 1 9 -0.74239324152537D+00 -0.11585687028954D-01 2 17 1 9 0.76177137240512D+00 0.26446894859379D-01 3 17 1 9 -0.74344148718083D+00 0.32574386823827D-01 1 18 1 9 -0.18323066985082D-02 -0.26881542083723D-06 2 18 1 9 -0.44113266732785D+00 -0.46049440822324D-06 3 18 1 9 -0.10062446340674D+01 -0.21762410118023D-06 1 19 1 9 0.18323066985060D-02 0.26881542165742D-06 2 19 1 9 0.44113266732786D+00 0.46049440907654D-06 3 19 1 9 -0.10062446340674D+01 -0.21762410329366D-06 1 20 1 9 -0.74239324152536D+00 -0.11585687028954D-01 2 20 1 9 0.76177137240511D+00 0.26446894859379D-01 3 20 1 9 0.74344148718084D+00 -0.32574386823827D-01 1 1 2 9 -0.19313490578631D+00 -0.14357171429734D-07 2 1 2 9 0.90293952823197D-01 0.89828899698915D-09 3 1 2 9 -0.96692846683775D-15 0.30543483793846D-16 1 2 2 9 0.63490055593073D-15 -0.37948387689606D-16 2 2 2 9 -0.10662427512620D-13 -0.54429868712076D-15 3 2 2 9 -0.34451018708689D-01 -0.34097087470511D-08 1 3 2 9 -0.46457196943757D+00 0.15522167519547D-07 2 3 2 9 -0.69995698096851D+00 -0.68322126462891D-08 3 3 2 9 0.38268037042616D-14 0.34854859506895D-15 1 4 2 9 0.31551801045796D-16 -0.69272189756708D-16 2 4 2 9 -0.12611501990055D-15 0.95738036851606D-15 3 4 2 9 -0.16289077714518D+00 -0.69467132378975D-08 1 5 2 9 -0.11468597402095D+00 0.33737496751837D-01 2 5 2 9 -0.14644451270106D+01 -0.10202619431083D+01 3 5 2 9 0.39231822155082D+00 -0.10632777307956D+00 1 6 2 9 -0.11468597402095D+00 0.33737496751837D-01 2 6 2 9 -0.14644451270106D+01 -0.10202619431083D+01 3 6 2 9 -0.39231822155080D+00 0.10632777307956D+00 1 7 2 9 -0.35077330036197D+00 -0.11376200440041D-01 2 7 2 9 0.13287377129898D+01 0.26733383406707D-01 3 7 2 9 0.18717592153546D+00 -0.32243574706693D-02 1 8 2 9 -0.35077330036197D+00 -0.11376200440041D-01 2 8 2 9 0.13287377129898D+01 0.26733383406710D-01 3 8 2 9 -0.18717592153546D+00 0.32243574706694D-02 1 9 2 9 0.88318995446957D+00 -0.49315267996994D-07 2 9 2 9 0.67660750150380D+01 0.00000000000000D+00 3 9 2 9 -0.42698174091229D-13 -0.69388939039072D-17 1 10 2 9 -0.26953166464592D-15 0.97510105853187D-17 2 10 2 9 -0.33251240160318D-15 0.21691341657732D-15 3 10 2 9 -0.34836129512968D+00 0.20972835654317D-07 1 11 2 9 0.64626419013780D-16 0.74478408729929D-17 2 11 2 9 0.25098233349790D-14 0.88531527795707D-15 3 11 2 9 0.67960099383585D-01 -0.64136780222997D-08 1 12 2 9 0.17904437952976D+00 -0.76339836172642D-09 2 12 2 9 -0.62015464892372D+00 -0.17485440325654D-16 3 12 2 9 0.24035696371546D-15 -0.10070642532565D-17 1 13 2 9 -0.83505610438401D+00 -0.71429918477670D-08 2 13 2 9 -0.18067321176108D+00 0.22588309578200D-09 3 13 2 9 -0.99186727998493D+00 -0.93216519724894D-08 1 14 2 9 0.52178585841405D+00 -0.49392494826821D-02 2 14 2 9 0.41162146845689D+00 -0.26224677299956D-02 3 14 2 9 -0.12461235163825D+01 0.84584109992135D-03 1 15 2 9 -0.52178585841405D+00 0.49392494826808D-02 2 15 2 9 -0.41162146845688D+00 0.26224677299960D-02 3 15 2 9 -0.12461235163825D+01 0.84584109991793D-03 1 16 2 9 -0.83505610438400D+00 -0.71429919321638D-08 2 16 2 9 -0.18067321176109D+00 0.22588304382074D-09 3 16 2 9 0.99186727998493D+00 0.93216518328454D-08 1 17 2 9 0.96285669216839D+00 0.47341334967090D-01 2 17 2 9 -0.10469420610392D+01 -0.45916799788300D-01 3 17 2 9 0.10037781864827D+01 -0.45031915050346D-01 1 18 2 9 -0.49085820329485D+00 0.14012253974319D-06 2 18 2 9 0.60600698876671D+00 -0.42409423446658D-07 3 18 2 9 0.16991444083957D+01 0.64620988973805D-06 1 19 2 9 0.49085820329485D+00 -0.14012253888122D-06 2 19 2 9 -0.60600698876671D+00 0.42409422338281D-07 3 19 2 9 0.16991444083956D+01 0.64620989396117D-06 1 20 2 9 0.96285669216838D+00 0.47341334967089D-01 2 20 2 9 -0.10469420610392D+01 -0.45916799788300D-01 3 20 2 9 -0.10037781864828D+01 0.45031915050346D-01 1 1 3 9 0.51409000856804D-16 -0.80293788030953D-16 2 1 3 9 -0.96692846683775D-15 0.30543483793846D-16 3 1 3 9 -0.76351195447636D+01 -0.54207221439892D-07 1 2 3 9 -0.29268300004255D+00 -0.67698864680255D-09 2 2 3 9 0.10078806932194D+00 0.41034437128745D-08 3 2 3 9 -0.13005056168102D-13 -0.20424496988876D-14 1 3 3 9 0.16350093197402D-14 -0.15099973544963D-15 2 3 3 9 0.38268037042616D-14 0.34854859506895D-15 3 3 3 9 -0.74626474160639D+01 -0.11928904645746D-06 1 4 3 9 0.14795965101543D-01 -0.30231344859217D-08 2 4 3 9 -0.10729816381840D+00 -0.66063302394582D-09 3 4 3 9 0.98972991372938D-14 -0.10674709813928D-13 1 5 3 9 -0.59618921838893D+00 0.31443500464895D+00 2 5 3 9 0.15149986541090D+00 -0.70591888157526D-01 3 5 3 9 -0.13229065770009D+02 0.26203564013998D+01 1 6 3 9 0.59618921838893D+00 -0.31443500464895D+00 2 6 3 9 -0.15149986541089D+00 0.70591888157526D-01 3 6 3 9 -0.13229065770009D+02 0.26203564013998D+01 1 7 3 9 0.54306240389881D-01 -0.20505626814280D-01 2 7 3 9 0.26021371927460D+00 -0.17342934288836D-01 3 7 3 9 -0.89881011904707D+01 -0.24041959735203D+00 1 8 3 9 -0.54306240389885D-01 0.20505626814280D-01 2 8 3 9 -0.26021371927460D+00 0.17342934288836D-01 3 8 3 9 -0.89881011904709D+01 -0.24041959735202D+00 1 9 3 9 -0.73365108485390D-14 0.13877787807815D-16 2 9 3 9 -0.42698174094538D-13 0.00000000000000D+00 3 9 3 9 0.51966795352957D+02 0.00000000000000D+00 1 10 3 9 0.11574941593644D+01 0.27101591156648D-08 2 10 3 9 -0.34834994385852D+00 -0.21576015057184D-07 3 10 3 9 0.17634314025750D-13 -0.24851772393200D-14 1 11 3 9 0.78669168399783D-01 -0.38850246636673D-08 2 11 3 9 0.67960099383585D-01 0.64136778085614D-08 3 11 3 9 -0.43030592753885D-14 -0.16199002637100D-14 1 12 3 9 0.17562955177485D-15 -0.10306832242023D-15 2 12 3 9 0.24035696371546D-15 -0.10070642532565D-17 3 12 3 9 0.11356062695460D+02 0.19656999700137D-16 1 13 3 9 -0.28622929406996D+01 0.95779726774515D-09 2 13 3 9 -0.18179060547875D+01 0.11332619573499D-07 3 13 3 9 0.15157278350334D+01 -0.71463970589355D-08 1 14 3 9 -0.21994584043566D+01 -0.23967446206660D-01 2 14 3 9 -0.23509712146944D+01 -0.38786575229658D-01 3 14 3 9 0.77577005757850D+00 0.98657686511048D-01 1 15 3 9 -0.21994584043566D+01 -0.23967446206663D-01 2 15 3 9 -0.23509712146944D+01 -0.38786575229662D-01 3 15 3 9 -0.77577005757840D+00 -0.98657686511055D-01 1 16 3 9 0.28622929406997D+01 -0.95779731407841D-09 2 16 3 9 0.18179060547875D+01 -0.11332619720082D-07 3 16 3 9 0.15157278350333D+01 -0.71463963318649D-08 1 17 3 9 -0.19890755571761D+01 0.68886348381706D-01 2 17 3 9 0.25308862285828D+01 -0.78720112808229D-01 3 17 3 9 0.19085745169969D+01 0.17173873451275D+00 1 18 3 9 -0.16760073288540D+01 0.15008876229064D-06 2 18 3 9 0.29444700367643D+01 -0.60948104746174D-06 3 18 3 9 0.12629097866750D+01 -0.69783901733837D-06 1 19 3 9 -0.16760073288540D+01 0.15008876018155D-06 2 19 3 9 0.29444700367643D+01 -0.60948104323861D-06 3 19 3 9 -0.12629097866749D+01 0.69783900974972D-06 1 20 3 9 0.19890755571761D+01 -0.68886348381706D-01 2 20 3 9 -0.25308862285828D+01 0.78720112808229D-01 3 20 3 9 0.19085745169969D+01 0.17173873451275D+00 1 1 1 10 0.83120607043200D-14 -0.10477725257320D-15 2 1 1 10 -0.12418844428238D-14 -0.85936549973145D-17 3 1 1 10 0.18107892807839D+00 0.29184833718983D-08 1 2 1 10 -0.76755231806582D+00 -0.15052829407768D-07 2 2 1 10 -0.35247618671953D+00 -0.10292247613217D-07 3 2 1 10 -0.54502029089846D-14 -0.82889094726513D-18 1 3 1 10 -0.80128348242056D-14 0.14383590357645D-14 2 3 1 10 -0.10420004634972D-15 -0.21884912598100D-16 3 3 1 10 0.22756514255047D+00 0.10531689528367D-07 1 4 1 10 -0.11892115849381D+01 -0.19615680763910D-07 2 4 1 10 -0.55591842353415D+00 0.54455073913282D-08 3 4 1 10 0.26687924896856D-14 -0.57605129316223D-15 1 5 1 10 0.14609342511777D+01 0.99248034875253D+00 2 5 1 10 0.53226250046663D-01 -0.21225465655936D-01 3 5 1 10 0.19437883501975D+01 -0.46587973269805D+00 1 6 1 10 -0.14609342511777D+01 -0.99248034875254D+00 2 6 1 10 -0.53226250046677D-01 0.21225465655935D-01 3 6 1 10 0.19437883501974D+01 -0.46587973269807D+00 1 7 1 10 -0.12029576947453D+01 -0.26277579259032D-01 2 7 1 10 -0.47379481343784D+00 -0.10765131700376D-01 3 7 1 10 0.41945609494043D+00 -0.10639367904396D-01 1 8 1 10 0.12029576947453D+01 0.26277579259034D-01 2 8 1 10 0.47379481343784D+00 0.10765131700376D-01 3 8 1 10 0.41945609494045D+00 -0.10639367904395D-01 1 9 1 10 0.22039576395432D-14 0.27330980973170D-15 2 9 1 10 -0.26953166454252D-15 -0.97510105853186D-17 3 9 1 10 0.11575019172018D+01 -0.31392865771034D-08 1 10 1 10 0.89482831938510D+01 0.00000000000000D+00 2 10 1 10 0.88319108041415D+00 0.61803623979336D-07 3 10 1 10 0.13477203630348D-12 0.00000000000000D+00 1 11 1 10 -0.45771581749926D+00 0.13420938077933D-15 2 11 1 10 -0.17904437952982D+00 -0.76339836190527D-09 3 11 1 10 0.10800140959146D-14 0.76382015858435D-16 1 12 1 10 -0.31333971710787D-14 -0.60292557084145D-16 2 12 1 10 0.10606432641353D-14 0.69709793242239D-17 3 12 1 10 -0.78669168399791D-01 -0.38850246065726D-08 1 13 1 10 0.15265269930118D+00 -0.24036828917296D-01 2 13 1 10 0.59321503213185D+00 -0.23378399653816D-01 3 13 1 10 -0.12573991981889D+01 -0.55477043253289D-02 1 14 1 10 -0.15843846343864D+01 -0.23607684726796D-08 2 14 1 10 -0.86498807698324D+00 0.17148043273567D-08 3 14 1 10 -0.12779867517876D+01 -0.61693061738765D-08 1 15 1 10 -0.15843846343864D+01 -0.23607691681250D-08 2 15 1 10 -0.86498807698322D+00 0.17148043211699D-08 3 15 1 10 0.12779867517876D+01 0.61693062857112D-08 1 16 1 10 -0.15265269930117D+00 0.24036828917296D-01 2 16 1 10 -0.59321503213184D+00 0.23378399653818D-01 3 16 1 10 -0.12573991981888D+01 -0.55477043253262D-02 1 17 1 10 -0.18323066984745D-02 -0.26881542249784D-06 2 17 1 10 -0.44113266732787D+00 -0.46049440999467D-06 3 17 1 10 -0.10062446340674D+01 -0.21762410511071D-06 1 18 1 10 -0.74239324152534D+00 -0.11585687028954D-01 2 18 1 10 0.76177137240514D+00 0.26446894859379D-01 3 18 1 10 -0.74344148718089D+00 0.32574386823827D-01 1 19 1 10 -0.74239324152534D+00 -0.11585687028953D-01 2 19 1 10 0.76177137240514D+00 0.26446894859379D-01 3 19 1 10 0.74344148718086D+00 -0.32574386823827D-01 1 20 1 10 0.18323066984651D-02 0.26881542161798D-06 2 20 1 10 0.44113266732785D+00 0.46049440912018D-06 3 20 1 10 -0.10062446340674D+01 -0.21762410319482D-06 1 1 2 10 -0.12418427186188D-14 -0.90273358663088D-17 2 1 2 10 0.89544433424382D-14 0.12638620515966D-14 3 1 2 10 -0.34451018708669D-01 -0.34097087154144D-08 1 2 2 10 -0.19313490578635D+00 -0.14357171466400D-07 2 2 2 10 0.90293952822998D-01 0.89828886661614D-09 3 2 2 10 0.40380035784218D-15 -0.74571703143876D-16 1 3 2 10 -0.10420004634972D-15 -0.21884912598100D-16 2 3 2 10 -0.16887825474950D-13 0.84821905243326D-15 3 3 2 10 -0.16289077714518D+00 -0.69467132470114D-08 1 4 2 10 -0.46457196943745D+00 0.15522167533198D-07 2 4 2 10 -0.69995698096857D+00 -0.68322128702619D-08 3 4 2 10 0.12152850419625D-15 -0.18454511477395D-15 1 5 2 10 0.11468597402093D+00 -0.33737496751838D-01 2 5 2 10 0.14644451270103D+01 0.10202619431082D+01 3 5 2 10 -0.39231822155099D+00 0.10632777307956D+00 1 6 2 10 -0.11468597402095D+00 0.33737496751837D-01 2 6 2 10 -0.14644451270105D+01 -0.10202619431083D+01 3 6 2 10 -0.39231822155097D+00 0.10632777307956D+00 1 7 2 10 0.35077330036197D+00 0.11376200440040D-01 2 7 2 10 -0.13287377129897D+01 -0.26733383406707D-01 3 7 2 10 -0.18717592153544D+00 0.32243574706699D-02 1 8 2 10 -0.35077330036197D+00 -0.11376200440041D-01 2 8 2 10 0.13287377129898D+01 0.26733383406707D-01 3 8 2 10 -0.18717592153544D+00 0.32243574706697D-02 1 9 2 10 -0.26953166474931D-15 -0.97510105853185D-17 2 9 2 10 -0.33251240160318D-15 -0.18915784096169D-15 3 9 2 10 -0.34836129512968D+00 0.20972835281062D-07 1 10 2 10 0.88318995446954D+00 -0.49315267996994D-07 2 10 2 10 0.67660750150378D+01 0.00000000000000D+00 3 10 2 10 -0.21381892018429D-13 -0.69388939039072D-17 1 11 2 10 0.17904437952969D+00 -0.76339836190527D-09 2 11 2 10 -0.62015464892368D+00 -0.92074505072873D-17 3 11 2 10 0.16124444288844D-15 0.13910528606085D-17 1 12 2 10 0.10606432640319D-14 0.71878197587211D-17 2 12 2 10 0.76502686344100D-14 -0.40870399945966D-15 3 12 2 10 0.67960099383576D-01 -0.64136779205969D-08 1 13 2 10 0.52178585841406D+00 -0.49392494826796D-02 2 13 2 10 0.41162146845687D+00 -0.26224677299953D-02 3 13 2 10 -0.12461235163825D+01 0.84584109991445D-03 1 14 2 10 -0.83505610438405D+00 -0.71429918322798D-08 2 14 2 10 -0.18067321176109D+00 0.22588272701199D-09 3 14 2 10 -0.99186727998498D+00 -0.93216518840101D-08 1 15 2 10 -0.83505610438403D+00 -0.71429918384665D-08 2 15 2 10 -0.18067321176110D+00 0.22588301769164D-09 3 15 2 10 0.99186727998497D+00 0.93216517565461D-08 1 16 2 10 -0.52178585841406D+00 0.49392494826808D-02 2 16 2 10 -0.41162146845687D+00 0.26224677299957D-02 3 16 2 10 -0.12461235163825D+01 0.84584109991806D-03 1 17 2 10 -0.49085820329486D+00 0.14012253797177D-06 2 17 2 10 0.60600698876671D+00 -0.42409421599734D-07 3 17 2 10 0.16991444083956D+01 0.64620989788590D-06 1 18 2 10 0.96285669216841D+00 0.47341334967089D-01 2 18 2 10 -0.10469420610392D+01 -0.45916799788300D-01 3 18 2 10 0.10037781864828D+01 -0.45031915050346D-01 1 19 2 10 0.96285669216841D+00 0.47341334967089D-01 2 19 2 10 -0.10469420610392D+01 -0.45916799788300D-01 3 19 2 10 -0.10037781864828D+01 0.45031915050346D-01 1 20 2 10 0.49085820329484D+00 -0.14012253884452D-06 2 20 2 10 -0.60600698876671D+00 0.42409422545390D-07 3 20 2 10 0.16991444083956D+01 0.64620989392872D-06 1 1 3 10 -0.29268300004256D+00 -0.67698843830787D-09 2 1 3 10 0.10078806932196D+00 0.41034437445113D-08 3 1 3 10 0.18008226321129D-13 0.20179737505015D-14 1 2 3 10 -0.54502029089846D-14 -0.82889094726496D-18 2 2 3 10 0.40380035784218D-15 -0.74571703143875D-16 3 2 3 10 -0.76351195447636D+01 -0.54207221244307D-07 1 3 3 10 0.14795965101580D-01 -0.30231350046825D-08 2 3 3 10 -0.10729816381840D+00 -0.66063303305972D-09 3 3 3 10 0.33142004799295D-14 0.76729631397857D-14 1 4 3 10 0.26687924896856D-14 -0.57605129316223D-15 2 4 3 10 0.12152850419625D-15 -0.18454511477395D-15 3 4 3 10 -0.74626474160641D+01 -0.11928904664902D-06 1 5 3 10 0.59618921838889D+00 -0.31443500464894D+00 2 5 3 10 -0.15149986541108D+00 0.70591888157522D-01 3 5 3 10 0.13229065770010D+02 -0.26203564013998D+01 1 6 3 10 0.59618921838876D+00 -0.31443500464895D+00 2 6 3 10 -0.15149986541106D+00 0.70591888157526D-01 3 6 3 10 -0.13229065770010D+02 0.26203564013998D+01 1 7 3 10 -0.54306240389882D-01 0.20505626814280D-01 2 7 3 10 -0.26021371927458D+00 0.17342934288836D-01 3 7 3 10 0.89881011904706D+01 0.24041959735203D+00 1 8 3 10 -0.54306240389862D-01 0.20505626814280D-01 2 8 3 10 -0.26021371927459D+00 0.17342934288836D-01 3 8 3 10 -0.89881011904708D+01 -0.24041959735203D+00 1 9 3 10 0.11574941593644D+01 0.27101597665997D-08 2 9 3 10 -0.34834994385852D+00 -0.21576015430439D-07 3 9 3 10 0.17634314025750D-13 0.24851772393200D-14 1 10 3 10 0.13477203630348D-12 0.13877787807815D-16 2 10 3 10 -0.21381892021738D-13 0.00000000000000D+00 3 10 3 10 0.51966795352956D+02 0.00000000000000D+00 1 11 3 10 0.10800140959146D-14 0.76382015858435D-16 2 11 3 10 0.16124444288844D-15 0.13910528606085D-17 3 11 3 10 0.11356062695460D+02 0.37719985866814D-16 1 12 3 10 0.78669168399793D-01 -0.38850246065726D-08 2 12 3 10 0.67960099383576D-01 0.64136779102643D-08 3 12 3 10 -0.11304957802972D-14 0.20980916555579D-14 1 13 3 10 -0.21994584043566D+01 -0.23967446206666D-01 2 13 3 10 -0.23509712146944D+01 -0.38786575229665D-01 3 13 3 10 0.77577005757845D+00 0.98657686511060D-01 1 14 3 10 -0.28622929406997D+01 0.95779736046209D-09 2 14 3 10 -0.18179060547876D+01 0.11332619661978D-07 3 14 3 10 0.15157278350334D+01 -0.71463950318974D-08 1 15 3 10 0.28622929406997D+01 -0.95779725209677D-09 2 15 3 10 0.18179060547876D+01 -0.11332619796381D-07 3 15 3 10 0.15157278350333D+01 -0.71463946959215D-08 1 16 3 10 -0.21994584043566D+01 -0.23967446206663D-01 2 16 3 10 -0.23509712146944D+01 -0.38786575229662D-01 3 16 3 10 -0.77577005757847D+00 -0.98657686511057D-01 1 17 3 10 -0.16760073288540D+01 0.15008875836363D-06 2 17 3 10 0.29444700367643D+01 -0.60948103931389D-06 3 17 3 10 0.12629097866748D+01 -0.69783900047232D-06 1 18 3 10 -0.19890755571761D+01 0.68886348381706D-01 2 18 3 10 0.25308862285828D+01 -0.78720112808229D-01 3 18 3 10 0.19085745169970D+01 0.17173873451275D+00 1 19 3 10 0.19890755571761D+01 -0.68886348381705D-01 2 19 3 10 -0.25308862285828D+01 0.78720112808229D-01 3 19 3 10 0.19085745169968D+01 0.17173873451275D+00 1 20 3 10 -0.16760073288540D+01 0.15008876027692D-06 2 20 3 10 0.29444700367643D+01 -0.60948104327106D-06 3 20 3 10 -0.12629097866748D+01 0.69783901558750D-06 1 1 1 11 -0.84012011616232D-14 0.11951492198691D-14 2 1 1 11 -0.56163417771337D-15 0.76617967371195D-17 3 1 1 11 -0.22756514255047D+00 -0.10531689492868D-07 1 2 1 11 -0.11892115849380D+01 -0.19615680603485D-07 2 2 1 11 0.55591842353426D+00 -0.54455073772579D-08 3 2 1 11 -0.23290686783110D-14 -0.14394574380797D-15 1 3 1 11 0.21251632420995D-15 0.41596344223196D-15 2 3 1 11 -0.70340010919482D-16 0.16753704986309D-16 3 3 1 11 -0.18107892807838D+00 -0.29184832612534D-08 1 4 1 11 -0.76755231806573D+00 -0.15052829458712D-07 2 4 1 11 0.35247618671975D+00 0.10292247638761D-07 3 4 1 11 0.30332913350766D-14 0.49358579642063D-16 1 5 1 11 -0.12029576947453D+01 -0.26277579259032D-01 2 5 1 11 0.47379481343786D+00 0.10765131700376D-01 3 5 1 11 -0.41945609494044D+00 0.10639367904396D-01 1 6 1 11 0.12029576947453D+01 0.26277579259034D-01 2 6 1 11 -0.47379481343785D+00 -0.10765131700376D-01 3 6 1 11 -0.41945609494045D+00 0.10639367904395D-01 1 7 1 11 0.14609342511777D+01 0.99248034875254D+00 2 7 1 11 -0.53226250046568D-01 0.21225465655936D-01 3 7 1 11 -0.19437883501975D+01 0.46587973269805D+00 1 8 1 11 -0.14609342511777D+01 -0.99248034875255D+00 2 8 1 11 0.53226250046583D-01 -0.21225465655935D-01 3 8 1 11 -0.19437883501974D+01 0.46587973269807D+00 1 9 1 11 -0.22029354180394D-14 0.31493986771507D-15 2 9 1 11 0.64626419013780D-16 -0.74478408729929D-17 3 9 1 11 0.78669168399783D-01 0.38850246636673D-08 1 10 1 11 -0.45771581749926D+00 -0.13420938077933D-15 2 10 1 11 0.17904437952969D+00 0.76339836190527D-09 3 10 1 11 0.10800140959146D-14 -0.76382015858435D-16 1 11 1 11 0.89482831938508D+01 0.00000000000000D+00 2 11 1 11 -0.88319108041407D+00 -0.61803623979336D-07 3 11 1 11 -0.12812877592776D-12 0.00000000000000D+00 1 12 1 11 0.18536596288818D-14 -0.32222398782293D-15 2 12 1 11 0.22491514848798D-15 0.19633970640727D-16 3 12 1 11 -0.11575019172018D+01 0.31392865958813D-08 1 13 1 11 -0.18323066984971D-02 -0.26881542290383D-06 2 13 1 11 0.44113266732788D+00 0.46049440996181D-06 3 13 1 11 0.10062446340675D+01 0.21762410514853D-06 1 14 1 11 -0.74239324152531D+00 -0.11585687028954D-01 2 14 1 11 -0.76177137240513D+00 -0.26446894859379D-01 3 14 1 11 0.74344148718086D+00 -0.32574386823827D-01 1 15 1 11 -0.74239324152531D+00 -0.11585687028954D-01 2 15 1 11 -0.76177137240513D+00 -0.26446894859379D-01 3 15 1 11 -0.74344148718085D+00 0.32574386823827D-01 1 16 1 11 0.18323066984904D-02 0.26881542200500D-06 2 16 1 11 -0.44113266732787D+00 -0.46049440901804D-06 3 16 1 11 0.10062446340675D+01 0.21762410317228D-06 1 17 1 11 0.15265269930118D+00 -0.24036828917296D-01 2 17 1 11 -0.59321503213185D+00 0.23378399653816D-01 3 17 1 11 0.12573991981888D+01 0.55477043253292D-02 1 18 1 11 -0.15843846343864D+01 -0.23607684571511D-08 2 18 1 11 0.86498807698322D+00 -0.17148043200452D-08 3 18 1 11 0.12779867517877D+01 0.61693060672405D-08 1 19 1 11 -0.15843846343864D+01 -0.23607687881863D-08 2 19 1 11 0.86498807698321D+00 -0.17148043542612D-08 3 19 1 11 -0.12779867517876D+01 -0.61693061722945D-08 1 20 1 11 -0.15265269930118D+00 0.24036828917296D-01 2 20 1 11 0.59321503213183D+00 -0.23378399653818D-01 3 20 1 11 0.12573991981888D+01 0.55477043253263D-02 1 1 2 11 -0.56163417776507D-15 0.76617967371196D-17 2 1 2 11 -0.76612004798218D-14 -0.12931222620741D-14 3 1 2 11 -0.16289077714523D+00 -0.69467132460601D-08 1 2 2 11 0.46457196943756D+00 -0.15522167519128D-07 2 2 2 11 -0.69995698096862D+00 -0.68322129386018D-08 3 2 2 11 -0.79474609385077D-15 -0.14429581505675D-16 1 3 2 11 -0.70381735150350D-16 0.16320024117315D-16 2 3 2 11 0.23082927961689D-13 0.27945888977997D-15 3 3 2 11 -0.34451018708672D-01 -0.34097087343354D-08 1 4 2 11 0.19313490578657D+00 0.14357171491944D-07 2 4 2 11 0.90293952822741D-01 0.89828873320030D-09 3 4 2 11 0.17399857572070D-17 -0.20379701304317D-15 1 5 2 11 -0.35077330036195D+00 -0.11376200440040D-01 2 5 2 11 -0.13287377129898D+01 -0.26733383406706D-01 3 5 2 11 -0.18717592153538D+00 0.32243574706697D-02 1 6 2 11 0.35077330036195D+00 0.11376200440041D-01 2 6 2 11 0.13287377129898D+01 0.26733383406708D-01 3 6 2 11 -0.18717592153538D+00 0.32243574706695D-02 1 7 2 11 -0.11468597402084D+00 0.33737496751838D-01 2 7 2 11 0.14644451270104D+01 0.10202619431082D+01 3 7 2 11 -0.39231822155159D+00 0.10632777307956D+00 1 8 2 11 0.11468597402085D+00 -0.33737496751837D-01 2 8 2 11 -0.14644451270106D+01 -0.10202619431083D+01 3 8 2 11 -0.39231822155156D+00 0.10632777307956D+00 1 9 2 11 0.64626419117177D-16 -0.72310004384957D-17 2 9 2 11 0.25098233349790D-14 -0.88531527795707D-15 3 9 2 11 0.67960099383585D-01 -0.64136778085614D-08 1 10 2 11 -0.17904437952982D+00 0.76339836190527D-09 2 10 2 11 -0.62015464892368D+00 0.92074505072873D-17 3 10 2 11 0.16124444288844D-15 -0.13910528606086D-17 1 11 2 11 -0.88318995446946D+00 0.49315267996994D-07 2 11 2 11 0.67660750150380D+01 0.00000000000000D+00 3 11 2 11 -0.42698174097847D-13 0.69388939039073D-17 1 12 2 11 0.22491514859138D-15 0.19633970640727D-16 2 12 2 11 -0.72996043355558D-14 0.12270230850924D-15 3 12 2 11 -0.34836129512970D+00 0.20972835419067D-07 1 13 2 11 0.49085820329487D+00 -0.14012253800289D-06 2 13 2 11 0.60600698876666D+00 -0.42409421481053D-07 3 13 2 11 0.16991444083957D+01 0.64620989789228D-06 1 14 2 11 -0.96285669216839D+00 -0.47341334967089D-01 2 14 2 11 -0.10469420610393D+01 -0.45916799788300D-01 3 14 2 11 0.10037781864828D+01 -0.45031915050345D-01 1 15 2 11 -0.96285669216840D+00 -0.47341334967090D-01 2 15 2 11 -0.10469420610393D+01 -0.45916799788300D-01 3 15 2 11 -0.10037781864828D+01 0.45031915050346D-01 1 16 2 11 -0.49085820329486D+00 0.14012253894840D-06 2 16 2 11 -0.60600698876665D+00 0.42409422523108D-07 3 16 2 11 0.16991444083956D+01 0.64620989376240D-06 1 17 2 11 -0.52178585841406D+00 0.49392494826797D-02 2 17 2 11 0.41162146845691D+00 -0.26224677299954D-02 3 17 2 11 -0.12461235163825D+01 0.84584109991451D-03 1 18 2 11 0.83505610438403D+00 0.71429918395912D-08 2 18 2 11 -0.18067321176101D+00 0.22588234789834D-09 3 18 2 11 -0.99186727998495D+00 -0.93216519094574D-08 1 19 2 11 0.83505610438402D+00 0.71429918053752D-08 2 19 2 11 -0.18067321176102D+00 0.22588292193367D-09 3 19 2 11 0.99186727998494D+00 0.93216518996167D-08 1 20 2 11 0.52178585841404D+00 -0.49392494826809D-02 2 20 2 11 -0.41162146845691D+00 0.26224677299952D-02 3 20 2 11 -0.12461235163824D+01 0.84584109991806D-03 1 1 3 11 -0.14795965101577D-01 0.30231350401810D-08 2 1 3 11 -0.10729816381845D+00 -0.66063303210849D-09 3 1 3 11 -0.12040375290666D-13 -0.36917179253609D-14 1 2 3 11 -0.23290686783110D-14 -0.14394574380797D-15 2 2 3 11 -0.79474609385077D-15 -0.14429581505675D-16 3 2 3 11 -0.74626474160641D+01 -0.11928904669873D-06 1 3 3 11 0.29268300004257D+00 0.67698854895275D-09 2 3 3 11 0.10078806932196D+00 0.41034437255903D-08 3 3 3 11 0.14194545998254D-13 -0.37506886365006D-15 1 4 3 11 0.30332913350766D-14 0.49358579642063D-16 2 4 3 11 0.17399857572073D-17 -0.20379701304317D-15 3 4 3 11 -0.76351195447633D+01 -0.54207221394520D-07 1 5 3 11 0.54306240389875D-01 -0.20505626814280D-01 2 5 3 11 -0.26021371927452D+00 0.17342934288836D-01 3 5 3 11 0.89881011904707D+01 0.24041959735203D+00 1 6 3 11 0.54306240389860D-01 -0.20505626814280D-01 2 6 3 11 -0.26021371927452D+00 0.17342934288836D-01 3 6 3 11 -0.89881011904708D+01 -0.24041959735203D+00 1 7 3 11 -0.59618921838887D+00 0.31443500464894D+00 2 7 3 11 -0.15149986541168D+00 0.70591888157522D-01 3 7 3 11 0.13229065770010D+02 -0.26203564013997D+01 1 8 3 11 -0.59618921838872D+00 0.31443500464895D+00 2 8 3 11 -0.15149986541165D+00 0.70591888157526D-01 3 8 3 11 -0.13229065770009D+02 0.26203564013998D+01 1 9 3 11 -0.78669168399801D-01 0.38850246636673D-08 2 9 3 11 0.67960099383585D-01 0.64136780222997D-08 3 9 3 11 -0.43030592753885D-14 0.16199002637100D-14 1 10 3 11 0.10800140959146D-14 -0.76382015858435D-16 2 10 3 11 0.16124444288844D-15 -0.13910528606085D-17 3 10 3 11 0.11356062695460D+02 -0.37719985866814D-16 1 11 3 11 -0.12812877592776D-12 0.13877787807814D-16 2 11 3 11 -0.42698174094538D-13 0.00000000000000D+00 3 11 3 11 0.51966795352957D+02 0.00000000000000D+00 1 12 3 11 -0.11574941593644D+01 -0.27101597478218D-08 2 12 3 11 -0.34834994385853D+00 -0.21576015292434D-07 3 12 3 11 0.11484866897188D-13 0.20999197380983D-14 1 13 3 11 0.16760073288540D+01 -0.15008875832408D-06 2 13 3 11 0.29444700367644D+01 -0.60948103930750D-06 3 13 3 11 0.12629097866750D+01 -0.69783900630277D-06 1 14 3 11 0.19890755571761D+01 -0.68886348381706D-01 2 14 3 11 0.25308862285828D+01 -0.78720112808228D-01 3 14 3 11 0.19085745169970D+01 0.17173873451275D+00 1 15 3 11 -0.19890755571761D+01 0.68886348381706D-01 2 15 3 11 -0.25308862285828D+01 0.78720112808229D-01 3 15 3 11 0.19085745169968D+01 0.17173873451275D+00 1 16 3 11 0.16760073288540D+01 -0.15008876030380D-06 2 16 3 11 0.29444700367643D+01 -0.60948104343739D-06 3 16 3 11 -0.12629097866750D+01 0.69783901503646D-06 1 17 3 11 0.21994584043566D+01 0.23967446206666D-01 2 17 3 11 -0.23509712146944D+01 -0.38786575229665D-01 3 17 3 11 0.77577005757841D+00 0.98657686511055D-01 1 18 3 11 0.28622929406997D+01 -0.95779747056747D-09 2 18 3 11 -0.18179060547875D+01 0.11332619643470D-07 3 18 3 11 0.15157278350333D+01 -0.71463961618997D-08 1 19 3 11 -0.28622929406997D+01 0.95779736204402D-09 2 19 3 11 0.18179060547875D+01 -0.11332619646371D-07 3 19 3 11 0.15157278350333D+01 -0.71463972025651D-08 1 20 3 11 0.21994584043565D+01 0.23967446206663D-01 2 20 3 11 -0.23509712146944D+01 -0.38786575229662D-01 3 20 3 11 -0.77577005757835D+00 -0.98657686511054D-01 1 1 1 12 -0.11892115849383D+01 -0.19615680584737D-07 2 1 1 12 0.55591842353409D+00 -0.54455073680454D-08 3 1 1 12 -0.99392474653869D-16 0.12093939348741D-15 1 2 1 12 0.48229982388089D-14 0.18686917471242D-15 2 2 1 12 -0.12290739034999D-14 0.90808111663498D-17 3 2 1 12 -0.22756514255047D+00 -0.10531690113213D-07 1 3 1 12 -0.76755231806582D+00 -0.15052829412138D-07 2 3 1 12 0.35247618671959D+00 0.10292247618693D-07 3 3 1 12 0.19372265038720D-14 0.17922265283864D-16 1 4 1 12 0.20809264799942D-14 -0.45623855542252D-15 2 4 1 12 -0.13593912429319D-14 -0.34978121590246D-16 3 4 1 12 -0.18107892807838D+00 -0.29184832428430D-08 1 5 1 12 0.12029576947453D+01 0.26277579259033D-01 2 5 1 12 -0.47379481343784D+00 -0.10765131700376D-01 3 5 1 12 0.41945609494045D+00 -0.10639367904396D-01 1 6 1 12 0.12029576947453D+01 0.26277579259033D-01 2 6 1 12 -0.47379481343784D+00 -0.10765131700376D-01 3 6 1 12 -0.41945609494045D+00 0.10639367904395D-01 1 7 1 12 -0.14609342511778D+01 -0.99248034875254D+00 2 7 1 12 0.53226250046720D-01 -0.21225465655935D-01 3 7 1 12 0.19437883501973D+01 -0.46587973269807D+00 1 8 1 12 -0.14609342511778D+01 -0.99248034875255D+00 2 8 1 12 0.53226250046715D-01 -0.21225465655935D-01 3 8 1 12 -0.19437883501973D+01 0.46587973269807D+00 1 9 1 12 -0.45771581749922D+00 0.16060037603958D-15 2 9 1 12 0.17904437952976D+00 0.76339836172642D-09 3 9 1 12 0.17562955177485D-15 0.10306832242023D-15 1 10 1 12 -0.31333971710787D-14 0.60292557084145D-16 2 10 1 12 0.10606432640319D-14 -0.71878197587210D-17 3 10 1 12 0.78669168399793D-01 0.38850246065726D-08 1 11 1 12 0.18536596288689D-14 0.29446841220730D-15 2 11 1 12 0.22491514869478D-15 -0.19633970640727D-16 3 11 1 12 -0.11575019172018D+01 0.31392872092603D-08 1 12 1 12 0.89482831938515D+01 0.00000000000000D+00 2 12 1 12 -0.88319108041411D+00 -0.61803623979336D-07 3 12 1 12 -0.23108349093801D-15 0.00000000000000D+00 1 13 1 12 -0.74239324152535D+00 -0.11585687028954D-01 2 13 1 12 -0.76177137240516D+00 -0.26446894859379D-01 3 13 1 12 0.74344148718087D+00 -0.32574386823827D-01 1 14 1 12 -0.18323066984935D-02 -0.26881542110663D-06 2 14 1 12 0.44113266732786D+00 0.46049440821874D-06 3 14 1 12 0.10062446340674D+01 0.21762410124834D-06 1 15 1 12 0.18323066984869D-02 0.26881542177086D-06 2 15 1 12 -0.44113266732787D+00 -0.46049440905103D-06 3 15 1 12 0.10062446340674D+01 0.21762410309342D-06 1 16 1 12 -0.74239324152535D+00 -0.11585687028954D-01 2 16 1 12 -0.76177137240515D+00 -0.26446894859379D-01 3 16 1 12 -0.74344148718088D+00 0.32574386823827D-01 1 17 1 12 -0.15843846343864D+01 -0.23607687158339D-08 2 17 1 12 0.86498807698322D+00 -0.17148043100133D-08 3 17 1 12 0.12779867517876D+01 0.61693062455709D-08 1 18 1 12 0.15265269930118D+00 -0.24036828917296D-01 2 18 1 12 -0.59321503213184D+00 0.23378399653819D-01 3 18 1 12 0.12573991981888D+01 0.55477043253231D-02 1 19 1 12 -0.15265269930117D+00 0.24036828917296D-01 2 19 1 12 0.59321503213184D+00 -0.23378399653818D-01 3 19 1 12 0.12573991981888D+01 0.55477043253262D-02 1 20 1 12 -0.15843846343864D+01 -0.23607689965039D-08 2 20 1 12 0.86498807698321D+00 -0.17148043567721D-08 3 20 1 12 -0.12779867517876D+01 -0.61693061060455D-08 1 1 2 12 0.46457196943739D+00 -0.15522167509915D-07 2 1 2 12 -0.69995698096841D+00 -0.68322125719267D-08 3 1 2 12 0.11305910062520D-14 -0.12003141605639D-15 1 2 2 12 -0.12290739035516D-14 0.90808111663499D-17 2 2 2 12 -0.51929900980447D-14 0.41789593801265D-15 3 2 2 12 -0.16289077714518D+00 -0.69467134317449D-08 1 3 2 12 0.19313490578641D+00 0.14357171471875D-07 2 3 2 12 0.90293952822996D-01 0.89828884173095D-09 3 3 2 12 -0.31310984894821D-14 -0.28168000493475D-16 1 4 2 12 -0.13594329672662D-14 -0.34978121590246D-16 2 4 2 12 0.11689254745973D-13 -0.23810057845483D-15 3 4 2 12 -0.34451018708707D-01 -0.34097085572007D-08 1 5 2 12 0.35077330036197D+00 0.11376200440041D-01 2 5 2 12 0.13287377129898D+01 0.26733383406707D-01 3 5 2 12 0.18717592153547D+00 -0.32243574706694D-02 1 6 2 12 0.35077330036197D+00 0.11376200440041D-01 2 6 2 12 0.13287377129898D+01 0.26733383406708D-01 3 6 2 12 -0.18717592153547D+00 0.32243574706699D-02 1 7 2 12 0.11468597402099D+00 -0.33737496751837D-01 2 7 2 12 -0.14644451270105D+01 -0.10202619431083D+01 3 7 2 12 0.39231822155069D+00 -0.10632777307956D+00 1 8 2 12 0.11468597402098D+00 -0.33737496751837D-01 2 8 2 12 -0.14644451270105D+01 -0.10202619431083D+01 3 8 2 12 -0.39231822155066D+00 0.10632777307956D+00 1 9 2 12 -0.17904437952974D+00 0.76339836172642D-09 2 9 2 12 -0.62015464892372D+00 0.17485440325654D-16 3 9 2 12 0.24035696371546D-15 0.10070642532565D-17 1 10 2 12 0.10606432641353D-14 -0.69709793242239D-17 2 10 2 12 0.76502686344100D-14 0.40870399945966D-15 3 10 2 12 0.67960099383576D-01 -0.64136779102643D-08 1 11 2 12 0.22491514838458D-15 -0.19633970640727D-16 2 11 2 12 -0.72996043355558D-14 -0.15045788412487D-15 3 11 2 12 -0.34836129512970D+00 0.20972835516313D-07 1 12 2 12 -0.88318995446950D+00 0.49315267996994D-07 2 12 2 12 0.67660750150376D+01 0.00000000000000D+00 3 12 2 12 -0.21381892025044D-13 0.69388939039072D-17 1 13 2 12 -0.96285669216842D+00 -0.47341334967089D-01 2 13 2 12 -0.10469420610392D+01 -0.45916799788300D-01 3 13 2 12 0.10037781864828D+01 -0.45031915050345D-01 1 14 2 12 0.49085820329486D+00 -0.14012253974597D-06 2 14 2 12 0.60600698876670D+00 -0.42409423395183D-07 3 14 2 12 0.16991444083956D+01 0.64620988964478D-06 1 15 2 12 -0.49085820329486D+00 0.14012253890847D-06 2 15 2 12 -0.60600698876670D+00 0.42409422594054D-07 3 15 2 12 0.16991444083956D+01 0.64620989367554D-06 1 16 2 12 -0.96285669216842D+00 -0.47341334967089D-01 2 16 2 12 -0.10469420610392D+01 -0.45916799788300D-01 3 16 2 12 -0.10037781864828D+01 0.45031915050346D-01 1 17 2 12 0.83505610438403D+00 0.71429918496231D-08 2 17 2 12 -0.18067321176108D+00 0.22588335996938D-09 3 17 2 12 -0.99186727998495D+00 -0.93216515650226D-08 1 18 2 12 -0.52178585841405D+00 0.49392494826820D-02 2 18 2 12 0.41162146845686D+00 -0.26224677299958D-02 3 18 2 12 -0.12461235163825D+01 0.84584109992121D-03 1 19 2 12 0.52178585841405D+00 -0.49392494826808D-02 2 19 2 12 -0.41162146845686D+00 0.26224677299957D-02 3 19 2 12 -0.12461235163825D+01 0.84584109991787D-03 1 20 2 12 0.83505610438402D+00 0.71429918028644D-08 2 20 2 12 -0.18067321176109D+00 0.22588279873615D-09 3 20 2 12 0.99186727998495D+00 0.93216517264030D-08 1 1 3 12 -0.99392474653869D-16 0.12093939348741D-15 2 1 3 12 0.11305910062520D-14 -0.12003141605639D-15 3 1 3 12 -0.74626474160640D+01 -0.11928904665887D-06 1 2 3 12 -0.14795965101577D-01 0.30231344198358D-08 2 2 3 12 -0.10729816381841D+00 -0.66063321779321D-09 3 2 3 12 -0.14781079204591D-13 -0.69027374751092D-14 1 3 3 12 0.19372265038720D-14 0.17922265283864D-16 2 3 3 12 -0.31310984894821D-14 -0.28168000493475D-16 3 3 3 12 -0.76351195447634D+01 -0.54207221360086D-07 1 4 3 12 0.29268300004257D+00 0.67698856736323D-09 2 4 3 12 0.10078806932192D+00 0.41034439027250D-08 3 4 3 12 0.63483053705103D-14 -0.19637838664225D-14 1 5 3 12 -0.54306240389864D-01 0.20505626814280D-01 2 5 3 12 0.26021371927461D+00 -0.17342934288836D-01 3 5 3 12 -0.89881011904708D+01 -0.24041959735202D+00 1 6 3 12 0.54306240389863D-01 -0.20505626814281D-01 2 6 3 12 -0.26021371927461D+00 0.17342934288836D-01 3 6 3 12 -0.89881011904709D+01 -0.24041959735203D+00 1 7 3 12 0.59618921838870D+00 -0.31443500464895D+00 2 7 3 12 0.15149986541078D+00 -0.70591888157526D-01 3 7 3 12 -0.13229065770009D+02 0.26203564013998D+01 1 8 3 12 -0.59618921838870D+00 0.31443500464895D+00 2 8 3 12 -0.15149986541075D+00 0.70591888157526D-01 3 8 3 12 -0.13229065770009D+02 0.26203564013998D+01 1 9 3 12 0.17562955177485D-15 0.10306832242023D-15 2 9 3 12 0.24035696371546D-15 0.10070642532565D-17 3 9 3 12 0.11356062695460D+02 -0.19656999700137D-16 1 10 3 12 -0.78669168399791D-01 0.38850246065726D-08 2 10 3 12 0.67960099383576D-01 0.64136779205969D-08 3 10 3 12 -0.11304957802972D-14 -0.20980916555579D-14 1 11 3 12 -0.11574941593644D+01 -0.27101591344427D-08 2 11 3 12 -0.34834994385853D+00 -0.21576015195188D-07 3 11 3 12 0.11484866897188D-13 -0.20999197380983D-14 1 12 3 12 -0.23108349093801D-15 0.13877787807814D-16 2 12 3 12 -0.21381892021735D-13 0.00000000000000D+00 3 12 3 12 0.51966795352957D+02 0.00000000000000D+00 1 13 3 12 0.19890755571761D+01 -0.68886348381706D-01 2 13 3 12 0.25308862285828D+01 -0.78720112808228D-01 3 13 3 12 0.19085745169969D+01 0.17173873451275D+00 1 14 3 12 0.16760073288540D+01 -0.15008876222254D-06 2 14 3 12 0.29444700367643D+01 -0.60948104755500D-06 3 14 3 12 0.12629097866750D+01 -0.69783901483666D-06 1 15 3 12 0.16760073288540D+01 -0.15008876037572D-06 2 15 3 12 0.29444700367643D+01 -0.60948104352425D-06 3 15 3 12 -0.12629097866749D+01 0.69783900914290D-06 1 16 3 12 -0.19890755571761D+01 0.68886348381706D-01 2 16 3 12 -0.25308862285828D+01 0.78720112808229D-01 3 16 3 12 0.19085745169969D+01 0.17173873451275D+00 1 17 3 12 0.28622929406997D+01 -0.95779729223715D-09 2 17 3 12 -0.18179060547875D+01 0.11332619987904D-07 3 17 3 12 0.15157278350334D+01 -0.71463974725612D-08 1 18 3 12 0.21994584043566D+01 0.23967446206660D-01 2 18 3 12 -0.23509712146944D+01 -0.38786575229658D-01 3 18 3 12 0.77577005757849D+00 0.98657686511042D-01 1 19 3 12 0.21994584043566D+01 0.23967446206663D-01 2 19 3 12 -0.23509712146944D+01 -0.38786575229662D-01 3 19 3 12 -0.77577005757839D+00 -0.98657686511052D-01 1 20 3 12 -0.28622929406997D+01 0.95779742829301D-09 2 20 3 12 0.18179060547875D+01 -0.11332619819585D-07 3 20 3 12 0.15157278350333D+01 -0.71463945923847D-08 1 1 1 13 -0.15288541954487D+00 -0.74179412901036D-07 2 1 1 13 -0.28523776767467D+00 0.81435523219151D-07 3 1 1 13 0.27354924894103D+00 0.16530707453864D-06 1 2 1 13 -0.35649811871913D-01 0.22976920010006D-04 2 2 1 13 0.34323295459559D-01 0.14054410318713D-02 3 2 1 13 0.34363902348792D+00 0.11830040968701D-02 1 3 1 13 -0.60909284293519D+00 0.98141360211214D-02 2 3 1 13 0.45556429278280D+00 -0.22118327089461D-01 3 3 1 13 0.77180569522023D+00 0.18709937733808D-02 1 4 1 13 0.11319999201779D+00 0.15934551321984D-06 2 4 1 13 0.36430894697396D+00 0.48208175500016D-07 3 4 1 13 -0.68280799992282D+00 -0.46232390253262D-06 1 5 1 13 -0.48396428542291D+00 -0.16319914985138D-02 2 5 1 13 -0.75629071487943D+00 0.78015039093783D-02 3 5 1 13 -0.65238380414922D+00 0.33400063853366D-01 1 6 1 13 -0.37777211143034D+00 -0.46890990369810D-01 2 6 1 13 0.14158513548062D+00 -0.32825000619359D-01 3 6 1 13 0.22174517997335D+01 -0.11338761750786D-02 1 7 1 13 0.13646047988226D+00 -0.42100838790538D-02 2 7 1 13 0.10201618763046D+01 -0.33250236328472D-02 3 7 1 13 0.59001136683450D+00 -0.32308394610655D-01 1 8 1 13 -0.25413098103869D+00 -0.88218626130818D-01 2 8 1 13 -0.56236868110947D-01 -0.13810217998739D+00 3 8 1 13 -0.18250727146300D+01 0.22972871185770D-01 1 9 1 13 -0.15843853485635D+01 0.75467703125018D-06 2 9 1 13 -0.83505586236789D+00 -0.44334549348681D-06 3 9 1 13 -0.28623021674884D+01 -0.99588238256912D-06 1 10 1 13 0.15265303959880D+00 0.72110512408721D-01 2 10 1 13 0.52178561066734D+00 0.14817750461864D-01 3 10 1 13 -0.21994628736096D+01 0.71902339905678D-01 1 11 1 13 -0.18323066984971D-02 0.26881542349364D-06 2 11 1 13 0.49085820329487D+00 0.14012253764207D-06 3 11 1 13 0.16760073288540D+01 0.15008875741509D-06 1 12 1 13 -0.74239324152535D+00 0.11585687028954D-01 2 12 1 13 -0.96285669216842D+00 0.47341334967089D-01 3 12 1 13 0.19890755571761D+01 0.68886348381706D-01 1 13 1 13 0.12520191818080D+02 0.00000000000000D+00 2 13 1 13 0.58185532262867D+01 0.20370962133179D+00 3 13 1 13 -0.12619568631377D+01 -0.16681885451866D+00 1 14 1 13 0.38501409953344D+01 -0.18355876600556D-02 2 14 1 13 0.28256148935147D+01 -0.48860234700130D-02 3 14 1 13 -0.16793740323249D+00 0.32475725493910D-03 1 15 1 13 -0.33519375200848D-14 0.11721002366909D+00 2 15 1 13 -0.14587929325478D+00 0.11165341930050D+00 3 15 1 13 0.15379355314301D+00 -0.70023280371413D-03 1 16 1 13 0.19478205682408D+00 0.32735916118210D-15 2 16 1 13 -0.53824066490421D-01 -0.20296063019519D-06 3 16 1 13 0.85418311256751D-01 0.10629427249070D-06 1 17 1 13 0.93881008275057D+00 0.19216755888230D-16 2 17 1 13 -0.10479016972652D+01 0.22136055575462D-01 3 17 1 13 0.39051230720331D-01 0.63531479365454D-02 1 18 1 13 0.57169838216393D+01 -0.14096505951707D-13 2 18 1 13 -0.93083969808799D+00 0.25243339442627D-06 3 18 1 13 0.53487764930099D-02 -0.46179843798512D-06 1 19 1 13 -0.43459039905274D-14 -0.12744696070424D-01 2 19 1 13 0.36193148615834D-01 0.26981141758843D-01 3 19 1 13 -0.58426994074742D-01 -0.22476716037368D-02 1 20 1 13 0.18500269963520D+00 -0.11607586027923D-01 2 20 1 13 0.47278071650213D-01 0.16508978366318D-01 3 20 1 13 -0.56319555519058D-01 0.32112442240880D-02 1 1 2 13 -0.15279480153779D+00 -0.19371876362706D-06 2 1 2 13 -0.45120418987762D+00 0.88025875729932D-07 3 1 2 13 -0.39677128756520D+00 -0.16957807149818D-05 1 2 2 13 0.18553487339993D+00 -0.23699499276406D-02 2 2 2 13 -0.28218054671127D+00 0.18748612809683D-02 3 2 2 13 -0.29814142361871D+00 -0.37655918746450D-03 1 3 2 13 0.33776741098255D+00 -0.16831199647224D-01 2 3 2 13 -0.84871976741035D+00 0.13216417488587D-01 3 3 2 13 -0.87601023640069D+00 0.29483135551947D-02 1 4 2 13 0.43655032002930D+00 0.68847986170499D-07 2 4 2 13 0.29421586446533D+00 0.90674461272966D-07 3 4 2 13 0.58905314287557D+00 0.66284184017405D-06 1 5 2 13 0.79318326597436D+00 -0.47977922943873D-02 2 5 2 13 -0.30874624286692D-01 0.46348542474629D-03 3 5 2 13 -0.28585800908282D+00 0.40316759174324D-01 1 6 2 13 -0.27843668475829D+00 -0.53936912421190D-01 2 6 2 13 0.88549792089436D-01 -0.28832767553978D-01 3 6 2 13 0.19766674239629D+01 -0.80777843326793D-02 1 7 2 13 -0.57706589902637D+00 -0.12289748358355D-01 2 7 2 13 -0.14783112415735D+00 -0.52523946662943D-02 3 7 2 13 -0.95059776604188D-01 -0.54538587718518D-01 1 8 2 13 -0.41677828610136D+00 -0.13267869402024D+00 2 8 2 13 -0.55607803036372D-01 -0.17124846105233D+00 3 8 2 13 -0.23864525531633D+01 0.24998031974807D-01 1 9 2 13 -0.86498691456238D+00 -0.62461559712594D-06 2 9 2 13 -0.18067071117330D+00 0.31089459501024D-06 3 9 2 13 -0.18179129312139D+01 -0.14425826973754D-05 1 10 2 13 0.59321479850324D+00 0.70135200294598D-01 2 10 2 13 0.41162189561845D+00 0.78674046189827D-02 3 10 2 13 -0.23509757886370D+01 0.11635973491769D+00 1 11 2 13 0.44113266732788D+00 -0.46049441032957D-06 2 11 2 13 0.60600698876666D+00 0.42409421099413D-07 3 11 2 13 0.29444700367644D+01 0.60948103747564D-06 1 12 2 13 -0.76177137240516D+00 0.26446894859379D-01 2 12 2 13 -0.10469420610392D+01 0.45916799788300D-01 3 12 2 13 0.25308862285828D+01 0.78720112808228D-01 1 13 2 13 0.58185567758218D+01 -0.20371021439641D+00 2 13 2 13 0.13731883222882D+02 0.00000000000000D+00 3 13 2 13 0.20787092960345D+01 0.19185204557219D+00 1 14 2 13 0.28256158045279D+01 -0.48863057830681D-02 2 14 2 13 0.41682457591848D+01 -0.26710682798443D-02 3 14 2 13 0.27459926317735D-01 0.21428220518210D-02 1 15 2 13 0.14587929325478D+00 0.11165341930050D+00 2 15 2 13 -0.18758295073244D-14 0.14993874537244D+00 3 15 2 13 -0.16118901074331D+00 -0.39653957860840D-02 1 16 2 13 -0.53824066490421D-01 0.20296063018208D-06 2 16 2 13 0.83471335358974D-01 0.17668878533999D-15 3 16 2 13 -0.87932415540537D-01 0.64602065281075D-07 1 17 2 13 0.10479016972652D+01 0.22136055575462D-01 2 17 2 13 -0.64393653654150D+01 -0.14256034861921D-16 3 17 2 13 0.18134901390989D+00 0.11544913539420D-01 1 18 2 13 0.93083969808799D+00 0.25243339454879D-06 2 18 2 13 -0.86159019638052D+00 0.34119878693126D-14 3 18 2 13 0.26679586968602D+00 0.10024764427177D-05 1 19 2 13 0.36193545926835D-01 -0.26981111142863D-01 2 19 2 13 -0.30349016256779D-15 0.14044334778164D-01 3 19 2 13 0.28569069696729D-01 -0.48119547178875D-02 1 20 2 13 -0.47277664526166D-01 -0.16508898655494D-01 2 20 2 13 -0.14281461824262D+00 0.20448212100466D-01 3 20 2 13 0.14250039598138D-01 -0.38130937328808D-03 1 1 3 13 0.50339059700791D+00 0.76624322715909D-06 2 1 3 13 -0.39989247456720D+00 -0.95934758128376D-07 3 1 3 13 -0.16381327018093D+01 0.30592576135600D-06 1 2 3 13 0.29484470087084D+00 0.79704964006739D-02 2 2 3 13 -0.28412783100751D+00 -0.25528681093172D-02 3 2 3 13 0.58931218389641D+00 -0.16011952998747D-01 1 3 3 13 0.65607960698278D+00 -0.51932790800396D-02 2 3 3 13 -0.86610704929405D+00 -0.57210474409350D-02 3 3 3 13 -0.38720145901411D+01 -0.56593951361141D-01 1 4 3 13 -0.71530282007164D+00 -0.24996743431081D-06 2 4 3 13 0.51794483325805D+00 0.10624454157327D-06 3 4 3 13 0.40245677350513D+00 -0.63608098857914D-06 1 5 3 13 0.93572737633787D+00 0.37579462405121D-01 2 5 3 13 0.79229774483731D+00 0.17897778936933D-01 3 5 3 13 -0.81224984678901D+01 -0.26874692129969D-01 1 6 3 13 0.24436588460006D+00 0.29396970736665D-01 2 6 3 13 0.76798941795582D-01 -0.16238853335849D-02 3 6 3 13 -0.29125009571181D+00 -0.16060897962002D-02 1 7 3 13 -0.98353435861184D+00 -0.33940087545784D-01 2 7 3 13 -0.78284481223616D+00 -0.45147056285256D-01 3 7 3 13 -0.81322331927146D+01 -0.28941632785696D-01 1 8 3 13 -0.20850745211573D+00 -0.65729656124460D-01 2 8 3 13 -0.82729805709343D-01 -0.44822502987789D-01 3 8 3 13 -0.47060580026553D+00 0.17445021945166D-01 1 9 3 13 -0.12779869366894D+01 0.13694471896260D-05 2 9 3 13 -0.99186826058953D+00 0.80057566016890D-06 3 9 3 13 0.15157351949622D+01 0.56607467166662D-06 1 10 3 13 -0.12573982645369D+01 0.16643125022086D-01 2 10 3 13 -0.12461223281264D+01 -0.25375252784138D-02 3 10 3 13 0.77577045673885D+00 -0.29597302715578D+00 1 11 3 13 0.10062446340675D+01 -0.21762410610783D-06 2 11 3 13 0.16991444083957D+01 -0.64620989980048D-06 3 11 3 13 0.12629097866750D+01 0.69783900602521D-06 1 12 3 13 0.74344148718087D+00 0.32574386823827D-01 2 12 3 13 0.10037781864828D+01 0.45031915050345D-01 3 12 3 13 0.19085745169969D+01 -0.17173873451275D+00 1 13 3 13 -0.12619333890139D+01 0.16682055028654D+00 2 13 3 13 0.20787346150450D+01 -0.19185415816596D+00 3 13 3 13 0.16435630284476D+02 0.00000000000000D+00 1 14 3 13 -0.16793934489498D+00 0.32541325510196D-03 2 14 3 13 0.27457478724115D-01 0.21405129243713D-02 3 14 3 13 -0.73618058473113D+00 0.77640860358512D-02 1 15 3 13 0.15379355314301D+00 0.70023280371412D-03 2 15 3 13 -0.16118901074331D+00 0.39653957860839D-02 3 15 3 13 0.19231820816635D-14 0.41737250275797D-01 1 16 3 13 -0.85418311256752D-01 0.10629427249070D-06 2 16 3 13 0.87932415540539D-01 0.64602065282810D-07 3 16 3 13 -0.69322977755906D+00 -0.24347583623150D-14 1 17 3 13 -0.39051230720330D-01 0.63531479365454D-02 2 17 3 13 0.18134901390989D+00 -0.11544913539420D-01 3 17 3 13 0.29161152602151D+01 0.81122906455807D-16 1 18 3 13 -0.53487764930095D-02 -0.46179843796171D-06 2 18 3 13 0.26679586968602D+00 -0.10024764441690D-05 3 18 3 13 -0.21639835254678D+01 0.10775661289071D-13 1 19 3 13 0.58425409200677D-01 -0.22476609889910D-02 2 19 3 13 0.28570349578279D-01 0.48121967695516D-02 3 19 3 13 -0.16277555915659D-14 0.37413913772884D-01 1 20 3 13 -0.56316791822393D-01 0.32119232228888D-02 2 20 3 13 -0.14251317612225D-01 0.38046285316885D-03 3 20 3 13 0.26987263189449D-01 -0.48193293616582D-01 1 1 1 14 -0.35649811871904D-01 0.22976920011309D-04 2 1 1 14 0.34323295459547D-01 0.14054410318693D-02 3 1 1 14 0.34363902348788D+00 0.11830040968654D-02 1 2 1 14 -0.15288541954495D+00 -0.74179413764244D-07 2 2 1 14 -0.28523776767462D+00 0.81435522836992D-07 3 2 1 14 0.27354924894098D+00 0.16530707411164D-06 1 3 1 14 0.11319999201774D+00 0.15934551304816D-06 2 3 1 14 0.36430894697398D+00 0.48208172105560D-07 3 3 1 14 -0.68280799992298D+00 -0.46232388956409D-06 1 4 1 14 -0.60909284293515D+00 0.98141360211211D-02 2 4 1 14 0.45556429278284D+00 -0.22118327089461D-01 3 4 1 14 0.77180569522025D+00 0.18709937733813D-02 1 5 1 14 0.48396428542263D+00 0.16319914985351D-02 2 5 1 14 0.75629071487931D+00 -0.78015039093557D-02 3 5 1 14 0.65238380414954D+00 -0.33400063853377D-01 1 6 1 14 -0.37777211143034D+00 -0.46890990369810D-01 2 6 1 14 0.14158513548062D+00 -0.32825000619358D-01 3 6 1 14 0.22174517997335D+01 -0.11338761750787D-02 1 7 1 14 -0.13646047988213D+00 0.42100838790572D-02 2 7 1 14 -0.10201618763041D+01 0.33250236328693D-02 3 7 1 14 -0.59001136683446D+00 0.32308394610661D-01 1 8 1 14 -0.25413098103869D+00 -0.88218626130819D-01 2 8 1 14 -0.56236868110951D-01 -0.13810217998739D+00 3 8 1 14 -0.18250727146300D+01 0.22972871185771D-01 1 9 1 14 0.15265303959878D+00 0.72110512408721D-01 2 9 1 14 0.52178561066732D+00 0.14817750461867D-01 3 9 1 14 -0.21994628736096D+01 0.71902339905672D-01 1 10 1 14 -0.15843853485635D+01 0.75467703136325D-06 2 10 1 14 -0.83505586236793D+00 -0.44334549350230D-06 3 10 1 14 -0.28623021674884D+01 -0.99588238266183D-06 1 11 1 14 -0.74239324152531D+00 0.11585687028954D-01 2 11 1 14 -0.96285669216839D+00 0.47341334967089D-01 3 11 1 14 0.19890755571761D+01 0.68886348381706D-01 1 12 1 14 -0.18323066984935D-02 0.26881542169643D-06 2 12 1 14 0.49085820329486D+00 0.14012253938514D-06 3 12 1 14 0.16760073288540D+01 0.15008876131354D-06 1 13 1 14 0.38501409953344D+01 -0.18355876600519D-02 2 13 1 14 0.28256148935147D+01 -0.48860234700146D-02 3 13 1 14 -0.16793740323249D+00 0.32475725494017D-03 1 14 1 14 0.12520191818080D+02 0.00000000000000D+00 2 14 1 14 0.58185532262871D+01 0.20370962133179D+00 3 14 1 14 -0.12619568631373D+01 -0.16681885451866D+00 1 15 1 14 0.19478205682407D+00 -0.14615718460997D-15 2 15 1 14 -0.53824066490422D-01 -0.20296063017354D-06 3 15 1 14 0.85418311256752D-01 0.10629427232019D-06 1 16 1 14 -0.49485333778939D-15 0.11721002366909D+00 2 16 1 14 -0.14587929325478D+00 0.11165341930050D+00 3 16 1 14 0.15379355314301D+00 -0.70023280371405D-03 1 17 1 14 0.57169838216393D+01 0.55106272530207D-14 2 17 1 14 -0.93083969808799D+00 0.25243339440620D-06 3 17 1 14 0.53487764930215D-02 -0.46179843794259D-06 1 18 1 14 0.93881008275053D+00 0.14275729683866D-15 2 18 1 14 -0.10479016972652D+01 0.22136055575462D-01 3 18 1 14 0.39051230720331D-01 0.63531479365453D-02 1 19 1 14 0.18500269963520D+00 -0.11607586027923D-01 2 19 1 14 0.47278071650212D-01 0.16508978366318D-01 3 19 1 14 -0.56319555519061D-01 0.32112442240880D-02 1 20 1 14 -0.76797998446432D-14 -0.12744696070424D-01 2 20 1 14 0.36193148615834D-01 0.26981141758843D-01 3 20 1 14 -0.58426994074737D-01 -0.22476716037368D-02 1 1 2 14 0.18553487339992D+00 -0.23699499276426D-02 2 1 2 14 -0.28218054671131D+00 0.18748612809709D-02 3 1 2 14 -0.29814142361868D+00 -0.37655918745990D-03 1 2 2 14 -0.15279480153774D+00 -0.19371876400922D-06 2 2 2 14 -0.45120418987752D+00 0.88025875191179D-07 3 2 2 14 -0.39677128756517D+00 -0.16957807149338D-05 1 3 2 14 0.43655032002932D+00 0.68847982776043D-07 2 3 2 14 0.29421586446535D+00 0.90674459262164D-07 3 3 2 14 0.58905314287562D+00 0.66284182959417D-06 1 4 2 14 0.33776741098258D+00 -0.16831199647224D-01 2 4 2 14 -0.84871976741043D+00 0.13216417488587D-01 3 4 2 14 -0.87601023640084D+00 0.29483135551946D-02 1 5 2 14 -0.79318326597449D+00 0.47977922944099D-02 2 5 2 14 0.30874624286888D-01 -0.46348542474164D-03 3 5 2 14 0.28585800908302D+00 -0.40316759174331D-01 1 6 2 14 -0.27843668475829D+00 -0.53936912421190D-01 2 6 2 14 0.88549792089423D-01 -0.28832767553978D-01 3 6 2 14 0.19766674239629D+01 -0.80777843326799D-02 1 7 2 14 0.57706589902688D+00 0.12289748358377D-01 2 7 2 14 0.14783112415748D+00 0.52523946663167D-02 3 7 2 14 0.95059776604202D-01 0.54538587718527D-01 1 8 2 14 -0.41677828610136D+00 -0.13267869402024D+00 2 8 2 14 -0.55607803036362D-01 -0.17124846105233D+00 3 8 2 14 -0.23864525531632D+01 0.24998031974807D-01 1 9 2 14 0.59321479850322D+00 0.70135200294601D-01 2 9 2 14 0.41162189561847D+00 0.78674046189830D-02 3 9 2 14 -0.23509757886370D+01 0.11635973491768D+00 1 10 2 14 -0.86498691456241D+00 -0.62461559714143D-06 2 10 2 14 -0.18067071117331D+00 0.31089459537901D-06 3 10 2 14 -0.18179129312139D+01 -0.14425826974638D-05 1 11 2 14 -0.76177137240513D+00 0.26446894859379D-01 2 11 2 14 -0.10469420610393D+01 0.45916799788300D-01 3 11 2 14 0.25308862285828D+01 0.78720112808228D-01 1 12 2 14 0.44113266732786D+00 -0.46049440858650D-06 2 12 2 14 0.60600698876670D+00 0.42409423013544D-07 3 12 2 14 0.29444700367643D+01 0.60948104572313D-06 1 13 2 14 0.28256158045279D+01 -0.48863057830697D-02 2 13 2 14 0.41682457591848D+01 -0.26710682798395D-02 3 13 2 14 0.27459926317735D-01 0.21428220518199D-02 1 14 2 14 0.58185567758222D+01 -0.20371021439641D+00 2 14 2 14 0.13731883222882D+02 0.00000000000000D+00 3 14 2 14 0.20787092960349D+01 0.19185204557219D+00 1 15 2 14 -0.53824066490422D-01 0.20296063020373D-06 2 15 2 14 0.83471335358964D-01 -0.76929324713139D-15 3 15 2 14 -0.87932415540540D-01 0.64602065243662D-07 1 16 2 14 0.14587929325478D+00 0.11165341930050D+00 2 16 2 14 0.64969472750679D-14 0.14993874537244D+00 3 16 2 14 -0.16118901074331D+00 -0.39653957860839D-02 1 17 2 14 0.93083969808800D+00 0.25243339452871D-06 2 17 2 14 -0.86159019638056D+00 -0.83724865192893D-15 3 17 2 14 0.26679586968601D+00 0.10024764436550D-05 1 18 2 14 0.10479016972652D+01 0.22136055575462D-01 2 18 2 14 -0.64393653654149D+01 -0.78075874248333D-17 3 18 2 14 0.18134901390989D+00 0.11544913539420D-01 1 19 2 14 -0.47277664526166D-01 -0.16508898655494D-01 2 19 2 14 -0.14281461824261D+00 0.20448212100466D-01 3 19 2 14 0.14250039598143D-01 -0.38130937328817D-03 1 20 2 14 0.36193545926834D-01 -0.26981111142863D-01 2 20 2 14 -0.87196549118242D-15 0.14044334778164D-01 3 20 2 14 0.28569069696724D-01 -0.48119547178875D-02 1 1 3 14 0.29484470087080D+00 0.79704964006691D-02 2 1 3 14 -0.28412783100749D+00 -0.25528681093126D-02 3 1 3 14 0.58931218389653D+00 -0.16011952998749D-01 1 2 3 14 0.50339059700785D+00 0.76624322673210D-06 2 2 3 14 -0.39989247456717D+00 -0.95934758080392D-07 3 2 3 14 -0.16381327018094D+01 0.30592575739326D-06 1 3 3 14 -0.71530282007179D+00 -0.24996742134922D-06 2 3 3 14 0.51794483325810D+00 0.10624453099685D-06 3 3 3 14 0.40245677350516D+00 -0.63608096432086D-06 1 4 3 14 0.65607960698281D+00 -0.51932790800392D-02 2 4 3 14 -0.86610704929419D+00 -0.57210474409351D-02 3 4 3 14 -0.38720145901411D+01 -0.56593951361144D-01 1 5 3 14 -0.93572737633756D+00 -0.37579462405132D-01 2 5 3 14 -0.79229774483710D+00 -0.17897778936940D-01 3 5 3 14 0.81224984678900D+01 0.26874692129946D-01 1 6 3 14 0.24436588460007D+00 0.29396970736665D-01 2 6 3 14 0.76798941795573D-01 -0.16238853335855D-02 3 6 3 14 -0.29125009571174D+00 -0.16060897962091D-02 1 7 3 14 0.98353435861188D+00 0.33940087545791D-01 2 7 3 14 0.78284481223617D+00 0.45147056285265D-01 3 7 3 14 0.81322331927140D+01 0.28941632785673D-01 1 8 3 14 -0.20850745211571D+00 -0.65729656124459D-01 2 8 3 14 -0.82729805709297D-01 -0.44822502987789D-01 3 8 3 14 -0.47060580026549D+00 0.17445021945168D-01 1 9 3 14 -0.12573982645368D+01 0.16643125022080D-01 2 9 3 14 -0.12461223281264D+01 -0.25375252784207D-02 3 9 3 14 0.77577045673891D+00 -0.29597302715577D+00 1 10 3 14 -0.12779869366894D+01 0.13694471895333D-05 2 10 3 14 -0.99186826058958D+00 0.80057566008042D-06 3 10 3 14 0.15157351949622D+01 0.56607466963958D-06 1 11 3 14 0.74344148718086D+00 0.32574386823827D-01 2 11 3 14 0.10037781864828D+01 0.45031915050345D-01 3 11 3 14 0.19085745169970D+01 -0.17173873451275D+00 1 12 3 14 0.10062446340674D+01 -0.21762410221111D-06 2 12 3 14 0.16991444083956D+01 -0.64620989155298D-06 3 12 3 14 0.12629097866750D+01 0.69783901455910D-06 1 13 3 14 -0.16793934489498D+00 0.32541325510304D-03 2 13 3 14 0.27457478724115D-01 0.21405129243702D-02 3 13 3 14 -0.73618058473113D+00 0.77640860358475D-02 1 14 3 14 -0.12619333890136D+01 0.16682055028654D+00 2 14 3 14 0.20787346150454D+01 -0.19185415816596D+00 3 14 3 14 0.16435630284475D+02 0.00000000000000D+00 1 15 3 14 -0.85418311256751D-01 0.10629427232019D-06 2 15 3 14 0.87932415540536D-01 0.64602065245396D-07 3 15 3 14 -0.69322977755903D+00 0.55957939680329D-14 1 16 3 14 0.15379355314301D+00 0.70023280371420D-03 2 16 3 14 -0.16118901074331D+00 0.39653957860840D-02 3 16 3 14 0.24350813001181D-13 0.41737250275799D-01 1 17 3 14 -0.53487764929979D-02 -0.46179843791960D-06 2 17 3 14 0.26679586968601D+00 -0.10024764432318D-05 3 17 3 14 -0.21639835254678D+01 0.32890943479230D-14 1 18 3 14 -0.39051230720331D-01 0.63531479365453D-02 2 18 3 14 0.18134901390989D+00 -0.11544913539420D-01 3 18 3 14 0.29161152602150D+01 0.12531630057890D-16 1 19 3 14 -0.56316791822397D-01 0.32119232228888D-02 2 19 3 14 -0.14251317612220D-01 0.38046285316876D-03 3 19 3 14 0.26987263189468D-01 -0.48193293616581D-01 1 20 3 14 0.58425409200683D-01 -0.22476609889910D-02 2 20 3 14 0.28570349578274D-01 0.48121967695515D-02 3 20 3 14 0.63791849976081D-14 0.37413913772888D-01 1 1 1 15 0.35649811871902D-01 -0.22976920010516D-04 2 1 1 15 -0.34323295459550D-01 -0.14054410318702D-02 3 1 1 15 0.34363902348790D+00 0.11830040968679D-02 1 2 1 15 -0.15288541954492D+00 -0.74179413290440D-07 2 2 1 15 -0.28523776767470D+00 0.81435523151532D-07 3 2 1 15 -0.27354924894098D+00 -0.16530707415695D-06 1 3 1 15 -0.11319999201774D+00 -0.15934551310697D-06 2 3 1 15 -0.36430894697399D+00 -0.48208173673240D-07 3 3 1 15 -0.68280799992297D+00 -0.46232389645883D-06 1 4 1 15 -0.60909284293515D+00 0.98141360211212D-02 2 4 1 15 0.45556429278272D+00 -0.22118327089461D-01 3 4 1 15 -0.77180569522015D+00 -0.18709937733810D-02 1 5 1 15 0.37777211143034D+00 0.46890990369810D-01 2 5 1 15 -0.14158513548062D+00 0.32825000619358D-01 3 5 1 15 0.22174517997335D+01 -0.11338761750796D-02 1 6 1 15 -0.48396428542264D+00 -0.16319914985141D-02 2 6 1 15 -0.75629071487934D+00 0.78015039093783D-02 3 6 1 15 0.65238380414955D+00 -0.33400063853367D-01 1 7 1 15 0.25413098103868D+00 0.88218626130818D-01 2 7 1 15 0.56236868110950D-01 0.13810217998739D+00 3 7 1 15 -0.18250727146300D+01 0.22972871185771D-01 1 8 1 15 0.13646047988214D+00 -0.42100838790537D-02 2 8 1 15 0.10201618763042D+01 -0.33250236328473D-02 3 8 1 15 -0.59001136683446D+00 0.32308394610655D-01 1 9 1 15 -0.15265303959877D+00 -0.72110512408721D-01 2 9 1 15 -0.52178561066733D+00 -0.14817750461866D-01 3 9 1 15 -0.21994628736096D+01 0.71902339905675D-01 1 10 1 15 -0.15843853485635D+01 0.75467703206217D-06 2 10 1 15 -0.83505586236791D+00 -0.44334549349611D-06 3 10 1 15 0.28623021674884D+01 0.99588238254653D-06 1 11 1 15 -0.74239324152531D+00 0.11585687028954D-01 2 11 1 15 -0.96285669216840D+00 0.47341334967090D-01 3 11 1 15 -0.19890755571761D+01 -0.68886348381706D-01 1 12 1 15 0.18323066984869D-02 -0.26881542236761D-06 2 12 1 15 -0.49085820329486D+00 -0.14012253854765D-06 3 12 1 15 0.16760073288540D+01 0.15008875947366D-06 1 13 1 15 -0.33519375200848D-14 -0.11721002366909D+00 2 13 1 15 0.14587929325478D+00 -0.11165341930050D+00 3 13 1 15 0.15379355314301D+00 -0.70023280371412D-03 1 14 1 15 0.19478205682407D+00 0.14615718460997D-15 2 14 1 15 -0.53824066490422D-01 -0.20296063020373D-06 3 14 1 15 -0.85418311256751D-01 -0.10629427232019D-06 1 15 1 15 0.12520191818080D+02 0.00000000000000D+00 2 15 1 15 0.58185532262872D+01 0.20370962133179D+00 3 15 1 15 0.12619568631373D+01 0.16681885451866D+00 1 16 1 15 -0.38501409953344D+01 0.18355876600536D-02 2 16 1 15 -0.28256148935147D+01 0.48860234700138D-02 3 16 1 15 -0.16793740323249D+00 0.32475725493967D-03 1 17 1 15 -0.53049292262538D-14 0.12744696070424D-01 2 17 1 15 -0.36193148615835D-01 -0.26981141758843D-01 3 17 1 15 -0.58426994074733D-01 -0.22476716037369D-02 1 18 1 15 0.18500269963520D+00 -0.11607586027923D-01 2 18 1 15 0.47278071650212D-01 0.16508978366318D-01 3 18 1 15 0.56319555519064D-01 -0.32112442240881D-02 1 19 1 15 0.93881008275053D+00 0.11088915726302D-15 2 19 1 15 -0.10479016972652D+01 0.22136055575462D-01 3 19 1 15 -0.39051230720331D-01 -0.63531479365454D-02 1 20 1 15 -0.57169838216393D+01 0.41142949497634D-14 2 20 1 15 0.93083969808799D+00 -0.25243339440366D-06 3 20 1 15 0.53487764930215D-02 -0.46179843794397D-06 1 1 2 15 -0.18553487339992D+00 0.23699499276417D-02 2 1 2 15 0.28218054671132D+00 -0.18748612809701D-02 3 1 2 15 -0.29814142361870D+00 -0.37655918746224D-03 1 2 2 15 -0.15279480153781D+00 -0.19371876369641D-06 2 2 2 15 -0.45120418987750D+00 0.88025875760501D-07 3 2 2 15 0.39677128756526D+00 0.16957807149918D-05 1 3 2 15 -0.43655032002933D+00 -0.68847984343723D-07 2 3 2 15 -0.29421586446536D+00 -0.90674460443471D-07 3 3 2 15 0.58905314287560D+00 0.66284183460973D-06 1 4 2 15 0.33776741098246D+00 -0.16831199647225D-01 2 4 2 15 -0.84871976741038D+00 0.13216417488586D-01 3 4 2 15 0.87601023640064D+00 -0.29483135551959D-02 1 5 2 15 0.27843668475829D+00 0.53936912421190D-01 2 5 2 15 -0.88549792089430D-01 0.28832767553978D-01 3 5 2 15 0.19766674239629D+01 -0.80777843326801D-02 1 6 2 15 0.79318326597439D+00 -0.47977922943872D-02 2 6 2 15 -0.30874624286902D-01 0.46348542474626D-03 3 6 2 15 0.28585800908303D+00 -0.40316759174324D-01 1 7 2 15 0.41677828610136D+00 0.13267869402024D+00 2 7 2 15 0.55607803036362D-01 0.17124846105233D+00 3 7 2 15 -0.23864525531632D+01 0.24998031974808D-01 1 8 2 15 -0.57706589902682D+00 -0.12289748358355D-01 2 8 2 15 -0.14783112415751D+00 -0.52523946662944D-02 3 8 2 15 0.95059776604238D-01 0.54538587718517D-01 1 9 2 15 -0.59321479850323D+00 -0.70135200294600D-01 2 9 2 15 -0.41162189561847D+00 -0.78674046189834D-02 3 9 2 15 -0.23509757886370D+01 0.11635973491769D+00 1 10 2 15 -0.86498691456240D+00 -0.62461559713177D-06 2 10 2 15 -0.18067071117332D+00 0.31089459509180D-06 3 10 2 15 0.18179129312139D+01 0.14425826975913D-05 1 11 2 15 -0.76177137240513D+00 0.26446894859379D-01 2 11 2 15 -0.10469420610393D+01 0.45916799788300D-01 3 11 2 15 -0.25308862285828D+01 -0.78720112808229D-01 1 12 2 15 -0.44113266732787D+00 0.46049440941879D-06 2 12 2 15 -0.60600698876670D+00 -0.42409422219353D-07 3 12 2 15 0.29444700367643D+01 0.60948104169238D-06 1 13 2 15 -0.14587929325478D+00 -0.11165341930050D+00 2 13 2 15 -0.18758295073244D-14 -0.14993874537244D+00 3 13 2 15 -0.16118901074331D+00 -0.39653957860839D-02 1 14 2 15 -0.53824066490422D-01 0.20296063017354D-06 2 14 2 15 0.83471335358964D-01 0.76929324713139D-15 3 14 2 15 0.87932415540536D-01 -0.64602065245396D-07 1 15 2 15 0.58185567758223D+01 -0.20371021439641D+00 2 15 2 15 0.13731883222882D+02 0.00000000000000D+00 3 15 2 15 -0.20787092960347D+01 -0.19185204557219D+00 1 16 2 15 -0.28256158045279D+01 0.48863057830689D-02 2 16 2 15 -0.41682457591848D+01 0.26710682798418D-02 3 16 2 15 0.27459926317740D-01 0.21428220518204D-02 1 17 2 15 -0.36193545926836D-01 0.26981111142863D-01 2 17 2 15 -0.39803187424295D-14 -0.14044334778164D-01 3 17 2 15 0.28569069696728D-01 -0.48119547178873D-02 1 18 2 15 -0.47277664526167D-01 -0.16508898655494D-01 2 18 2 15 -0.14281461824262D+00 0.20448212100466D-01 3 18 2 15 -0.14250039598143D-01 0.38130937328824D-03 1 19 2 15 0.10479016972652D+01 0.22136055575462D-01 2 19 2 15 -0.64393653654149D+01 -0.29063836106099D-17 3 19 2 15 -0.18134901390989D+00 -0.11544913539420D-01 1 20 2 15 -0.93083969808800D+00 -0.25243339452619D-06 2 20 2 15 0.86159019638056D+00 -0.15615355478321D-14 3 20 2 15 0.26679586968601D+00 0.10024764430285D-05 1 1 3 15 0.29484470087082D+00 0.79704964006716D-02 2 1 3 15 -0.28412783100749D+00 -0.25528681093150D-02 3 1 3 15 -0.58931218389646D+00 0.16011952998754D-01 1 2 3 15 -0.50339059700785D+00 -0.76624322677741D-06 2 2 3 15 0.39989247456726D+00 0.95934758138400D-07 3 2 3 15 -0.16381327018095D+01 0.30592576336104D-06 1 3 3 15 -0.71530282007175D+00 -0.24996742823529D-06 2 3 3 15 0.51794483325807D+00 0.10624453601416D-06 3 3 3 15 -0.40245677350504D+00 0.63608096781650D-06 1 4 3 15 -0.65607960698271D+00 0.51932790800395D-02 2 4 3 15 0.86610704929402D+00 0.57210474409338D-02 3 4 3 15 -0.38720145901411D+01 -0.56593951361141D-01 1 5 3 15 0.24436588460005D+00 0.29396970736664D-01 2 5 3 15 0.76798941795579D-01 -0.16238853335857D-02 3 5 3 15 0.29125009571178D+00 0.16060897962065D-02 1 6 3 15 -0.93572737633754D+00 -0.37579462405122D-01 2 6 3 15 -0.79229774483710D+00 -0.17897778936933D-01 3 6 3 15 -0.81224984678899D+01 -0.26874692129970D-01 1 7 3 15 -0.20850745211571D+00 -0.65729656124459D-01 2 7 3 15 -0.82729805709315D-01 -0.44822502987788D-01 3 7 3 15 0.47060580026552D+00 -0.17445021945177D-01 1 8 3 15 0.98353435861188D+00 0.33940087545784D-01 2 8 3 15 0.78284481223619D+00 0.45147056285255D-01 3 8 3 15 -0.81322331927140D+01 -0.28941632785693D-01 1 9 3 15 -0.12573982645368D+01 0.16643125022083D-01 2 9 3 15 -0.12461223281264D+01 -0.25375252784173D-02 3 9 3 15 -0.77577045673880D+00 0.29597302715578D+00 1 10 3 15 0.12779869366894D+01 -0.13694471896451D-05 2 10 3 15 0.99186826058956D+00 -0.80057565995122D-06 3 10 3 15 0.15157351949621D+01 0.56607466930361D-06 1 11 3 15 -0.74344148718085D+00 -0.32574386823827D-01 2 11 3 15 -0.10037781864828D+01 -0.45031915050346D-01 3 11 3 15 0.19085745169968D+01 -0.17173873451275D+00 1 12 3 15 0.10062446340674D+01 -0.21762410405446D-06 2 12 3 15 0.16991444083956D+01 -0.64620989558373D-06 3 12 3 15 -0.12629097866749D+01 -0.69783900886535D-06 1 13 3 15 0.15379355314301D+00 0.70023280371413D-03 2 13 3 15 -0.16118901074331D+00 0.39653957860840D-02 3 13 3 15 0.19231820816635D-14 -0.41737250275797D-01 1 14 3 15 0.85418311256752D-01 -0.10629427232019D-06 2 14 3 15 -0.87932415540540D-01 -0.64602065243662D-07 3 14 3 15 -0.69322977755903D+00 -0.55957939680329D-14 1 15 3 15 0.12619333890135D+01 -0.16682055028654D+00 2 15 3 15 -0.20787346150452D+01 0.19185415816596D+00 3 15 3 15 0.16435630284476D+02 0.00000000000000D+00 1 16 3 15 -0.16793934489499D+00 0.32541325510253D-03 2 16 3 15 0.27457478724121D-01 0.21405129243707D-02 3 16 3 15 0.73618058473118D+00 -0.77640860358478D-02 1 17 3 15 0.58425409200686D-01 -0.22476609889911D-02 2 17 3 15 0.28570349578278D-01 0.48121967695517D-02 3 17 3 15 -0.60692576937032D-15 -0.37413913772884D-01 1 18 3 15 0.56316791822400D-01 -0.32119232228889D-02 2 18 3 15 0.14251317612221D-01 -0.38046285316869D-03 3 18 3 15 0.26987263189482D-01 -0.48193293616582D-01 1 19 3 15 0.39051230720331D-01 -0.63531479365454D-02 2 19 3 15 -0.18134901390989D+00 0.11544913539420D-01 3 19 3 15 0.29161152602150D+01 -0.19791761908771D-16 1 20 3 15 -0.53487764929979D-02 -0.46179843792098D-06 2 20 3 15 0.26679586968601D+00 -0.10024764438582D-05 3 20 3 15 0.21639835254679D+01 -0.77106952499933D-14 1 1 1 16 -0.15288541954487D+00 -0.74179413340036D-07 2 1 1 16 -0.28523776767465D+00 0.81435523008663D-07 3 1 1 16 -0.27354924894103D+00 -0.16530707436985D-06 1 2 1 16 0.35649811871918D-01 -0.22976920010666D-04 2 2 1 16 -0.34323295459568D-01 -0.14054410318703D-02 3 2 1 16 0.34363902348793D+00 0.11830040968677D-02 1 3 1 16 -0.60909284293521D+00 0.98141360211217D-02 2 3 1 16 0.45556429278279D+00 -0.22118327089460D-01 3 3 1 16 -0.77180569522023D+00 -0.18709937733809D-02 1 4 1 16 -0.11319999201779D+00 -0.15934551302161D-06 2 4 1 16 -0.36430894697399D+00 -0.48208173568759D-07 3 4 1 16 -0.68280799992301D+00 -0.46232389604183D-06 1 5 1 16 -0.37777211143033D+00 -0.46890990369810D-01 2 5 1 16 0.14158513548062D+00 -0.32825000619358D-01 3 5 1 16 -0.22174517997335D+01 0.11338761750788D-02 1 6 1 16 -0.48396428542293D+00 -0.16319914985138D-02 2 6 1 16 -0.75629071487941D+00 0.78015039093783D-02 3 6 1 16 0.65238380414923D+00 -0.33400063853367D-01 1 7 1 16 -0.25413098103869D+00 -0.88218626130819D-01 2 7 1 16 -0.56236868110944D-01 -0.13810217998739D+00 3 7 1 16 0.18250727146300D+01 -0.22972871185771D-01 1 8 1 16 0.13646047988225D+00 -0.42100838790533D-02 2 8 1 16 0.10201618763046D+01 -0.33250236328473D-02 3 8 1 16 -0.59001136683451D+00 0.32308394610655D-01 1 9 1 16 -0.15843853485635D+01 0.75467703116247D-06 2 9 1 16 -0.83505586236788D+00 -0.44334549340241D-06 3 9 1 16 0.28623021674884D+01 0.99588238260851D-06 1 10 1 16 -0.15265303959879D+00 -0.72110512408721D-01 2 10 1 16 -0.52178561066734D+00 -0.14817750461866D-01 3 10 1 16 -0.21994628736096D+01 0.71902339905675D-01 1 11 1 16 0.18323066984904D-02 -0.26881542260174D-06 2 11 1 16 -0.49085820329486D+00 -0.14012253858757D-06 3 11 1 16 0.16760073288540D+01 0.15008875938786D-06 1 12 1 16 -0.74239324152535D+00 0.11585687028954D-01 2 12 1 16 -0.96285669216842D+00 0.47341334967089D-01 3 12 1 16 -0.19890755571761D+01 -0.68886348381706D-01 1 13 1 16 0.19478205682408D+00 -0.32735916118210D-15 2 13 1 16 -0.53824066490421D-01 -0.20296063018208D-06 3 13 1 16 -0.85418311256752D-01 -0.10629427249070D-06 1 14 1 16 -0.49485333778939D-15 -0.11721002366909D+00 2 14 1 16 0.14587929325478D+00 -0.11165341930050D+00 3 14 1 16 0.15379355314301D+00 -0.70023280371420D-03 1 15 1 16 -0.38501409953344D+01 0.18355876600540D-02 2 15 1 16 -0.28256148935147D+01 0.48860234700138D-02 3 15 1 16 -0.16793740323249D+00 0.32475725493960D-03 1 16 1 16 0.12520191818080D+02 0.00000000000000D+00 2 16 1 16 0.58185532262868D+01 0.20370962133179D+00 3 16 1 16 0.12619568631377D+01 0.16681885451866D+00 1 17 1 16 0.18500269963520D+00 -0.11607586027923D-01 2 17 1 16 0.47278071650212D-01 0.16508978366318D-01 3 17 1 16 0.56319555519057D-01 -0.32112442240881D-02 1 18 1 16 -0.63443054348527D-14 0.12744696070424D-01 2 18 1 16 -0.36193148615835D-01 -0.26981141758843D-01 3 18 1 16 -0.58426994074745D-01 -0.22476716037370D-02 1 19 1 16 -0.57169838216393D+01 0.45787370619917D-14 2 19 1 16 0.93083969808799D+00 -0.25243339441068D-06 3 19 1 16 0.53487764930079D-02 -0.46179843800533D-06 1 20 1 16 0.93881008275057D+00 -0.19651695094723D-16 2 20 1 16 -0.10479016972652D+01 0.22136055575462D-01 3 20 1 16 -0.39051230720332D-01 -0.63531479365455D-02 1 1 2 16 -0.15279480153777D+00 -0.19371876383928D-06 2 1 2 16 -0.45120418987762D+00 0.88025875725431D-07 3 1 2 16 0.39677128756516D+00 0.16957807158607D-05 1 2 2 16 -0.18553487339994D+00 0.23699499276416D-02 2 2 2 16 0.28218054671128D+00 -0.18748612809700D-02 3 2 2 16 -0.29814142361874D+00 -0.37655918746217D-03 1 3 2 16 0.33776741098253D+00 -0.16831199647224D-01 2 3 2 16 -0.84871976741036D+00 0.13216417488586D-01 3 3 2 16 0.87601023640071D+00 -0.29483135551935D-02 1 4 2 16 -0.43655032002933D+00 -0.68847984235772D-07 2 4 2 16 -0.29421586446536D+00 -0.90674460865376D-07 3 4 2 16 0.58905314287565D+00 0.66284183467157D-06 1 5 2 16 -0.27843668475829D+00 -0.53936912421190D-01 2 5 2 16 0.88549792089432D-01 -0.28832767553978D-01 3 5 2 16 -0.19766674239629D+01 0.80777843326796D-02 1 6 2 16 0.79318326597435D+00 -0.47977922943872D-02 2 6 2 16 -0.30874624286692D-01 0.46348542474590D-03 3 6 2 16 0.28585800908284D+00 -0.40316759174323D-01 1 7 2 16 -0.41677828610136D+00 -0.13267869402024D+00 2 7 2 16 -0.55607803036370D-01 -0.17124846105233D+00 3 7 2 16 0.23864525531633D+01 -0.24998031974808D-01 1 8 2 16 -0.57706589902639D+00 -0.12289748358355D-01 2 8 2 16 -0.14783112415719D+00 -0.52523946662953D-02 3 8 2 16 0.95059776604174D-01 0.54538587718517D-01 1 9 2 16 -0.86498691456237D+00 -0.62461559703808D-06 2 9 2 16 -0.18067071117330D+00 0.31089459506567D-06 3 9 2 16 0.18179129312139D+01 0.14425826975150D-05 1 10 2 16 -0.59321479850323D+00 -0.70135200294600D-01 2 10 2 16 -0.41162189561845D+00 -0.78674046189831D-02 3 10 2 16 -0.23509757886370D+01 0.11635973491769D+00 1 11 2 16 -0.44113266732787D+00 0.46049440938580D-06 2 11 2 16 -0.60600698876665D+00 -0.42409422148407D-07 3 11 2 16 0.29444700367643D+01 0.60948104160552D-06 1 12 2 16 -0.76177137240515D+00 0.26446894859379D-01 2 12 2 16 -0.10469420610392D+01 0.45916799788300D-01 3 12 2 16 -0.25308862285828D+01 -0.78720112808229D-01 1 13 2 16 -0.53824066490421D-01 0.20296063019519D-06 2 13 2 16 0.83471335358974D-01 -0.17668878533999D-15 3 13 2 16 0.87932415540539D-01 -0.64602065282810D-07 1 14 2 16 -0.14587929325478D+00 -0.11165341930050D+00 2 14 2 16 0.64969472750679D-14 -0.14993874537244D+00 3 14 2 16 -0.16118901074331D+00 -0.39653957860840D-02 1 15 2 16 -0.28256158045279D+01 0.48863057830689D-02 2 15 2 16 -0.41682457591848D+01 0.26710682798419D-02 3 15 2 16 0.27459926317740D-01 0.21428220518206D-02 1 16 2 16 0.58185567758219D+01 -0.20371021439641D+00 2 16 2 16 0.13731883222882D+02 0.00000000000000D+00 3 16 2 16 -0.20787092960346D+01 -0.19185204557219D+00 1 17 2 16 -0.47277664526167D-01 -0.16508898655494D-01 2 17 2 16 -0.14281461824261D+00 0.20448212100466D-01 3 17 2 16 -0.14250039598143D-01 0.38130937328805D-03 1 18 2 16 -0.36193545926836D-01 0.26981111142863D-01 2 18 2 16 0.25067618685146D-14 -0.14044334778164D-01 3 18 2 16 0.28569069696730D-01 -0.48119547178876D-02 1 19 2 16 -0.93083969808799D+00 -0.25243339453323D-06 2 19 2 16 0.86159019638052D+00 -0.14061968380354D-14 3 19 2 16 0.26679586968602D+00 0.10024764433053D-05 1 20 2 16 0.10479016972652D+01 0.22136055575462D-01 2 20 2 16 -0.64393653654150D+01 -0.13551665114436D-16 3 20 2 16 -0.18134901390989D+00 -0.11544913539420D-01 1 1 3 16 -0.50339059700791D+00 -0.76624322699031D-06 2 1 3 16 0.39989247456716D+00 0.95934759007296D-07 3 1 3 16 -0.16381327018094D+01 0.30592575870001D-06 1 2 3 16 0.29484470087085D+00 0.79704964006715D-02 2 2 3 16 -0.28412783100754D+00 -0.25528681093149D-02 3 2 3 16 -0.58931218389648D+00 0.16011952998753D-01 1 3 3 16 -0.65607960698278D+00 0.51932790800396D-02 2 3 3 16 0.86610704929409D+00 0.57210474409362D-02 3 3 3 16 -0.38720145901410D+01 -0.56593951361142D-01 1 4 3 16 -0.71530282007179D+00 -0.24996742781829D-06 2 4 3 16 0.51794483325812D+00 0.10624453607599D-06 3 4 3 16 -0.40245677350504D+00 0.63608097039523D-06 1 5 3 16 -0.24436588460004D+00 -0.29396970736665D-01 2 5 3 16 -0.76798941795584D-01 0.16238853335853D-02 3 5 3 16 -0.29125009571179D+00 -0.16060897961964D-02 1 6 3 16 -0.93572737633787D+00 -0.37579462405121D-01 2 6 3 16 -0.79229774483729D+00 -0.17897778936932D-01 3 6 3 16 -0.81224984678899D+01 -0.26874692129967D-01 1 7 3 16 0.20850745211572D+00 0.65729656124459D-01 2 7 3 16 0.82729805709334D-01 0.44822502987788D-01 3 7 3 16 -0.47060580026549D+00 0.17445021945153D-01 1 8 3 16 0.98353435861183D+00 0.33940087545784D-01 2 8 3 16 0.78284481223614D+00 0.45147056285255D-01 3 8 3 16 -0.81322331927146D+01 -0.28941632785696D-01 1 9 3 16 0.12779869366894D+01 -0.13694471895832D-05 2 9 3 16 0.99186826058953D+00 -0.80057566002752D-06 3 9 3 16 0.15157351949622D+01 0.56607467093955D-06 1 10 3 16 -0.12573982645368D+01 0.16643125022083D-01 2 10 3 16 -0.12461223281264D+01 -0.25375252784174D-02 3 10 3 16 -0.77577045673888D+00 0.29597302715578D+00 1 11 3 16 0.10062446340675D+01 -0.21762410413332D-06 2 11 3 16 0.16991444083956D+01 -0.64620989567060D-06 3 11 3 16 -0.12629097866750D+01 -0.69783901475890D-06 1 12 3 16 -0.74344148718088D+00 -0.32574386823827D-01 2 12 3 16 -0.10037781864828D+01 -0.45031915050346D-01 3 12 3 16 0.19085745169969D+01 -0.17173873451275D+00 1 13 3 16 0.85418311256751D-01 -0.10629427249070D-06 2 13 3 16 -0.87932415540537D-01 -0.64602065281075D-07 3 13 3 16 -0.69322977755906D+00 0.24347583623150D-14 1 14 3 16 0.15379355314301D+00 0.70023280371405D-03 2 14 3 16 -0.16118901074331D+00 0.39653957860839D-02 3 14 3 16 0.24350813001181D-13 -0.41737250275799D-01 1 15 3 16 -0.16793934489499D+00 0.32541325510247D-03 2 15 3 16 0.27457478724121D-01 0.21405129243709D-02 3 15 3 16 0.73618058473118D+00 -0.77640860358510D-02 1 16 3 16 0.12619333890139D+01 -0.16682055028654D+00 2 16 3 16 -0.20787346150451D+01 0.19185415816596D+00 3 16 3 16 0.16435630284476D+02 0.00000000000000D+00 1 17 3 16 0.56316791822393D-01 -0.32119232228889D-02 2 17 3 16 0.14251317612220D-01 -0.38046285316888D-03 3 17 3 16 0.26987263189448D-01 -0.48193293616577D-01 1 18 3 16 0.58425409200674D-01 -0.22476609889912D-02 2 18 3 16 0.28570349578281D-01 0.48121967695514D-02 3 18 3 16 0.12361054518711D-13 -0.37413913772888D-01 1 19 3 16 -0.53487764930115D-02 -0.46179843798148D-06 2 19 3 16 0.26679586968602D+00 -0.10024764435814D-05 3 19 3 16 0.21639835254679D+01 -0.72551296387972D-14 1 20 3 16 0.39051230720330D-01 -0.63531479365455D-02 2 20 3 16 -0.18134901390989D+00 0.11544913539420D-01 3 20 3 16 0.29161152602151D+01 -0.20799195292530D-16 1 1 1 17 -0.60909284293523D+00 0.98141360211217D-02 2 1 1 17 -0.45556429278286D+00 0.22118327089461D-01 3 1 1 17 -0.77180569522044D+00 -0.18709937733808D-02 1 2 1 17 0.11319999201776D+00 0.15934551277428D-06 2 2 1 17 -0.36430894697396D+00 -0.48208175651520D-07 3 2 1 17 0.68280799992284D+00 0.46232390260110D-06 1 3 1 17 -0.15288541954492D+00 -0.74179413171765D-07 2 3 1 17 0.28523776767467D+00 -0.81435523235719D-07 3 3 1 17 -0.27354924894093D+00 -0.16530707449776D-06 1 4 1 17 -0.35649811871919D-01 0.22976920009936D-04 2 4 1 17 -0.34323295459582D-01 -0.14054410318714D-02 3 4 1 17 -0.34363902348795D+00 -0.11830040968701D-02 1 5 1 17 0.13646047988225D+00 -0.42100838790529D-02 2 5 1 17 -0.10201618763046D+01 0.33250236328473D-02 3 5 1 17 -0.59001136683451D+00 0.32308394610654D-01 1 6 1 17 -0.25413098103869D+00 -0.88218626130818D-01 2 6 1 17 0.56236868110949D-01 0.13810217998739D+00 3 6 1 17 0.18250727146300D+01 -0.22972871185770D-01 1 7 1 17 -0.48396428542310D+00 -0.16319914985146D-02 2 7 1 17 0.75629071487947D+00 -0.78015039093784D-02 3 7 1 17 0.65238380414914D+00 -0.33400063853367D-01 1 8 1 17 -0.37777211143033D+00 -0.46890990369810D-01 2 8 1 17 -0.14158513548062D+00 0.32825000619358D-01 3 8 1 17 -0.22174517997335D+01 0.11338761750785D-02 1 9 1 17 -0.74239324152537D+00 0.11585687028954D-01 2 9 1 17 0.96285669216839D+00 -0.47341334967090D-01 3 9 1 17 -0.19890755571761D+01 -0.68886348381706D-01 1 10 1 17 -0.18323066984745D-02 0.26881542309459D-06 2 10 1 17 -0.49085820329486D+00 -0.14012253761095D-06 3 10 1 17 -0.16760073288540D+01 -0.15008875744770D-06 1 11 1 17 0.15265303959880D+00 0.72110512408721D-01 2 11 1 17 -0.52178561066734D+00 -0.14817750461864D-01 3 11 1 17 0.21994628736096D+01 -0.71902339905678D-01 1 12 1 17 -0.15843853485635D+01 0.75467703160988D-06 2 12 1 17 0.83505586236791D+00 0.44334549348495D-06 3 12 1 17 0.28623021674884D+01 0.99588238258667D-06 1 13 1 17 0.93881008275057D+00 -0.19216755888230D-16 2 13 1 17 0.10479016972652D+01 -0.22136055575462D-01 3 13 1 17 -0.39051230720330D-01 -0.63531479365454D-02 1 14 1 17 0.57169838216393D+01 -0.14062813989586D-13 2 14 1 17 0.93083969808800D+00 -0.25243339440619D-06 3 14 1 17 -0.53487764929979D-02 0.46179843794324D-06 1 15 1 17 -0.53049292262538D-14 -0.12744696070424D-01 2 15 1 17 -0.36193148615835D-01 -0.26981141758843D-01 3 15 1 17 0.58426994074752D-01 0.22476716037369D-02 1 16 1 17 0.18500269963520D+00 -0.11607586027923D-01 2 16 1 17 -0.47278071650212D-01 -0.16508978366318D-01 3 16 1 17 0.56319555519057D-01 -0.32112442240880D-02 1 17 1 17 0.12520191818080D+02 0.00000000000000D+00 2 17 1 17 -0.58185532262866D+01 -0.20370962133179D+00 3 17 1 17 0.12619568631378D+01 0.16681885451866D+00 1 18 1 17 0.38501409953344D+01 -0.18355876600557D-02 2 18 1 17 -0.28256148935147D+01 0.48860234700130D-02 3 18 1 17 0.16793740323249D+00 -0.32475725493915D-03 1 19 1 17 -0.31161326071751D-14 0.11721002366909D+00 2 19 1 17 0.14587929325478D+00 -0.11165341930050D+00 3 19 1 17 -0.15379355314301D+00 0.70023280371427D-03 1 20 1 17 0.19478205682408D+00 -0.25979381432415D-15 2 20 1 17 0.53824066490422D-01 0.20296063018630D-06 3 20 1 17 -0.85418311256751D-01 -0.10629427242986D-06 1 1 2 17 -0.33776741098261D+00 0.16831199647224D-01 2 1 2 17 -0.84871976741020D+00 0.13216417488587D-01 3 1 2 17 -0.87601023640084D+00 0.29483135551950D-02 1 2 2 17 -0.43655032002930D+00 -0.68847986322002D-07 2 2 2 17 0.29421586446535D+00 0.90674461416580D-07 3 2 2 17 0.58905314287556D+00 0.66284184029698D-06 1 3 2 17 0.15279480153778D+00 0.19371876361222D-06 2 3 2 17 -0.45120418987752D+00 0.88025875237978D-07 3 3 2 17 -0.39677128756520D+00 -0.16957807157773D-05 1 4 2 17 -0.18553487339996D+00 0.23699499276405D-02 2 4 2 17 -0.28218054671126D+00 0.18748612809688D-02 3 4 2 17 -0.29814142361878D+00 -0.37655918746424D-03 1 5 2 17 0.57706589902637D+00 0.12289748358355D-01 2 5 2 17 -0.14783112415731D+00 -0.52523946662952D-02 3 5 2 17 -0.95059776604209D-01 -0.54538587718517D-01 1 6 2 17 0.41677828610136D+00 0.13267869402024D+00 2 6 2 17 -0.55607803036371D-01 -0.17124846105233D+00 3 6 2 17 -0.23864525531633D+01 0.24998031974807D-01 1 7 2 17 -0.79318326597428D+00 0.47977922943872D-02 2 7 2 17 -0.30874624286607D-01 0.46348542474585D-03 3 7 2 17 -0.28585800908279D+00 0.40316759174325D-01 1 8 2 17 0.27843668475829D+00 0.53936912421190D-01 2 8 2 17 0.88549792089433D-01 -0.28832767553978D-01 3 8 2 17 0.19766674239629D+01 -0.80777843326792D-02 1 9 2 17 0.76177137240512D+00 -0.26446894859379D-01 2 9 2 17 -0.10469420610392D+01 0.45916799788300D-01 3 9 2 17 0.25308862285828D+01 0.78720112808229D-01 1 10 2 17 -0.44113266732786D+00 0.46049441035549D-06 2 10 2 17 0.60600698876671D+00 0.42409421225034D-07 3 10 2 17 0.29444700367643D+01 0.60948103748202D-06 1 11 2 17 -0.59321479850324D+00 -0.70135200294598D-01 2 11 2 17 0.41162189561849D+00 0.78674046189828D-02 3 11 2 17 -0.23509757886370D+01 0.11635973491769D+00 1 12 2 17 0.86498691456239D+00 0.62461559712062D-06 2 12 2 17 -0.18067071117330D+00 0.31089459474953D-06 3 12 2 17 -0.18179129312139D+01 -0.14425826977828D-05 1 13 2 17 -0.10479016972652D+01 -0.22136055575462D-01 2 13 2 17 -0.64393653654150D+01 0.14256034861921D-16 3 13 2 17 0.18134901390989D+00 0.11544913539420D-01 1 14 2 17 -0.93083969808799D+00 -0.25243339452872D-06 2 14 2 17 -0.86159019638056D+00 0.35841832761382D-14 3 14 2 17 0.26679586968601D+00 0.10024764425622D-05 1 15 2 17 -0.36193545926836D-01 0.26981111142863D-01 2 15 2 17 -0.39803187424295D-14 0.14044334778164D-01 3 15 2 17 0.28569069696728D-01 -0.48119547178876D-02 1 16 2 17 0.47277664526167D-01 0.16508898655494D-01 2 16 2 17 -0.14281461824261D+00 0.20448212100465D-01 3 16 2 17 0.14250039598125D-01 -0.38130937328805D-03 1 17 2 17 -0.58185567758217D+01 0.20371021439641D+00 2 17 2 17 0.13731883222881D+02 0.00000000000000D+00 3 17 2 17 0.20787092960345D+01 0.19185204557219D+00 1 18 2 17 -0.28256158045279D+01 0.48863057830681D-02 2 18 2 17 0.41682457591847D+01 -0.26710682798439D-02 3 18 2 17 0.27459926317732D-01 0.21428220518211D-02 1 19 2 17 -0.14587929325478D+00 -0.11165341930050D+00 2 19 2 17 -0.46170685069206D-15 0.14993874537244D+00 3 19 2 17 -0.16118901074332D+00 -0.39653957860838D-02 1 20 2 17 0.53824066490422D-01 -0.20296063019097D-06 2 20 2 17 0.83471335358967D-01 0.29246124284710D-15 3 20 2 17 -0.87932415540536D-01 0.64602065306886D-07 1 1 3 17 -0.65607960698300D+00 0.51932790800396D-02 2 1 3 17 -0.86610704929422D+00 -0.57210474409347D-02 3 1 3 17 -0.38720145901414D+01 -0.56593951361140D-01 1 2 3 17 0.71530282007164D+00 0.24996743437843D-06 2 2 3 17 0.51794483325803D+00 0.10624454170314D-06 3 2 3 17 0.40245677350511D+00 -0.63608098972905D-06 1 3 3 17 -0.50339059700781D+00 -0.76624322711822D-06 2 3 3 17 -0.39989247456720D+00 -0.95934758923871D-07 3 3 3 17 -0.16381327018094D+01 0.30592575865498D-06 1 4 3 17 -0.29484470087088D+00 -0.79704964006738D-02 2 4 3 17 -0.28412783100758D+00 -0.25528681093170D-02 3 4 3 17 0.58931218389636D+00 -0.16011952998743D-01 1 5 3 17 0.98353435861183D+00 0.33940087545784D-01 2 5 3 17 -0.78284481223617D+00 -0.45147056285255D-01 3 5 3 17 -0.81322331927145D+01 -0.28941632785696D-01 1 6 3 17 0.20850745211572D+00 0.65729656124460D-01 2 6 3 17 -0.82729805709345D-01 -0.44822502987789D-01 3 6 3 17 -0.47060580026554D+00 0.17445021945151D-01 1 7 3 17 -0.93572737633795D+00 -0.37579462405122D-01 2 7 3 17 0.79229774483733D+00 0.17897778936934D-01 3 7 3 17 -0.81224984678898D+01 -0.26874692129968D-01 1 8 3 17 -0.24436588460005D+00 -0.29396970736665D-01 2 8 3 17 0.76798941795580D-01 -0.16238853335848D-02 3 8 3 17 -0.29125009571181D+00 -0.16060897961967D-02 1 9 3 17 -0.74344148718083D+00 -0.32574386823827D-01 2 9 3 17 0.10037781864827D+01 0.45031915050346D-01 3 9 3 17 0.19085745169969D+01 -0.17173873451275D+00 1 10 3 17 -0.10062446340674D+01 0.21762410607522D-06 2 10 3 17 0.16991444083956D+01 -0.64620989979409D-06 3 10 3 17 0.12629097866748D+01 0.69783900019477D-06 1 11 3 17 0.12573982645368D+01 -0.16643125022086D-01 2 11 3 17 -0.12461223281264D+01 -0.25375252784138D-02 3 11 3 17 0.77577045673882D+00 -0.29597302715578D+00 1 12 3 17 0.12779869366894D+01 -0.13694471896050D-05 2 12 3 17 -0.99186826058955D+00 0.80057565975969D-06 3 12 3 17 0.15157351949622D+01 0.56607467208025D-06 1 13 3 17 0.39051230720331D-01 -0.63531479365454D-02 2 13 3 17 0.18134901390989D+00 -0.11544913539420D-01 3 13 3 17 0.29161152602151D+01 -0.81122906455807D-16 1 14 3 17 0.53487764930215D-02 0.46179843791895D-06 2 14 3 17 0.26679586968601D+00 -0.10024764443246D-05 3 14 3 17 -0.21639835254678D+01 0.97334747862349D-14 1 15 3 17 -0.58425409200667D-01 0.22476609889911D-02 2 15 3 17 0.28570349578278D-01 0.48121967695514D-02 3 15 3 17 -0.60692576937032D-15 0.37413913772884D-01 1 16 3 17 0.56316791822393D-01 -0.32119232228888D-02 2 16 3 17 -0.14251317612238D-01 0.38046285316888D-03 3 16 3 17 0.26987263189448D-01 -0.48193293616585D-01 1 17 3 17 0.12619333890140D+01 -0.16682055028654D+00 2 17 3 17 0.20787346150450D+01 -0.19185415816596D+00 3 17 3 17 0.16435630284476D+02 0.00000000000000D+00 1 18 3 17 0.16793934489499D+00 -0.32541325510202D-03 2 18 3 17 0.27457478724113D-01 0.21405129243714D-02 3 18 3 17 -0.73618058473114D+00 0.77640860358510D-02 1 19 3 17 -0.15379355314301D+00 -0.70023280371398D-03 2 19 3 17 -0.16118901074332D+00 0.39653957860841D-02 3 19 3 17 0.18688982910746D-14 0.41737250275797D-01 1 20 3 17 0.85418311256752D-01 -0.10629427242986D-06 2 20 3 17 0.87932415540540D-01 0.64602065305152D-07 3 20 3 17 -0.69322977755907D+00 -0.10102711231000D-14 1 1 1 18 0.11319999201775D+00 0.15934551332230D-06 2 1 1 18 -0.36430894697398D+00 -0.48208171750847D-07 3 1 1 18 0.68280799992305D+00 0.46232388920130D-06 1 2 1 18 -0.60909284293518D+00 0.98141360211208D-02 2 2 1 18 -0.45556429278283D+00 0.22118327089461D-01 3 2 1 18 -0.77180569522031D+00 -0.18709937733807D-02 1 3 1 18 -0.35649811871917D-01 0.22976920011516D-04 2 3 1 18 -0.34323295459573D-01 -0.14054410318694D-02 3 3 1 18 -0.34363902348795D+00 -0.11830040968656D-02 1 4 1 18 -0.15288541954493D+00 -0.74179412712302D-07 2 4 1 18 0.28523776767460D+00 -0.81435523089641D-07 3 4 1 18 -0.27354924894095D+00 -0.16530707388527D-06 1 5 1 18 -0.13646047988220D+00 0.42100838790576D-02 2 5 1 18 0.10201618763043D+01 -0.33250236328693D-02 3 5 1 18 0.59001136683455D+00 -0.32308394610662D-01 1 6 1 18 -0.25413098103868D+00 -0.88218626130819D-01 2 6 1 18 0.56236868110950D-01 0.13810217998739D+00 3 6 1 18 0.18250727146300D+01 -0.22972871185771D-01 1 7 1 18 0.48396428542277D+00 0.16319914985353D-02 2 7 1 18 -0.75629071487941D+00 0.78015039093557D-02 3 7 1 18 -0.65238380414948D+00 0.33400063853375D-01 1 8 1 18 -0.37777211143034D+00 -0.46890990369810D-01 2 8 1 18 -0.14158513548062D+00 0.32825000619358D-01 3 8 1 18 -0.22174517997335D+01 0.11338761750790D-02 1 9 1 18 -0.18323066985082D-02 0.26881542142010D-06 2 9 1 18 -0.49085820329485D+00 -0.14012253938237D-06 3 9 1 18 -0.16760073288540D+01 -0.15008876138858D-06 1 10 1 18 -0.74239324152534D+00 0.11585687028954D-01 2 10 1 18 0.96285669216841D+00 -0.47341334967089D-01 3 10 1 18 -0.19890755571761D+01 -0.68886348381706D-01 1 11 1 18 -0.15843853485636D+01 0.75467703135119D-06 2 11 1 18 0.83505586236791D+00 0.44334549349499D-06 3 11 1 18 0.28623021674884D+01 0.99588238276500D-06 1 12 1 18 0.15265303959880D+00 0.72110512408721D-01 2 12 1 18 -0.52178561066733D+00 -0.14817750461867D-01 3 12 1 18 0.21994628736096D+01 -0.71902339905672D-01 1 13 1 18 0.57169838216393D+01 0.55443192151410D-14 2 13 1 18 0.93083969808799D+00 -0.25243339442627D-06 3 13 1 18 -0.53487764930095D-02 0.46179843798534D-06 1 14 1 18 0.93881008275053D+00 -0.14275729683866D-15 2 14 1 18 0.10479016972652D+01 -0.22136055575462D-01 3 14 1 18 -0.39051230720331D-01 -0.63531479365453D-02 1 15 1 18 0.18500269963520D+00 -0.11607586027923D-01 2 15 1 18 -0.47278071650212D-01 -0.16508978366318D-01 3 15 1 18 0.56319555519064D-01 -0.32112442240880D-02 1 16 1 18 -0.63443054348527D-14 -0.12744696070424D-01 2 16 1 18 -0.36193148615835D-01 -0.26981141758843D-01 3 16 1 18 0.58426994074740D-01 0.22476716037370D-02 1 17 1 18 0.38501409953344D+01 -0.18355876600519D-02 2 17 1 18 -0.28256148935147D+01 0.48860234700146D-02 3 17 1 18 0.16793740323249D+00 -0.32475725494012D-03 1 18 1 18 0.12520191818080D+02 0.00000000000000D+00 2 18 1 18 -0.58185532262870D+01 -0.20370962133179D+00 3 18 1 18 0.12619568631375D+01 0.16681885451866D+00 1 19 1 18 0.19478205682408D+00 -0.11088311807635D-15 2 19 1 18 0.53824066490422D-01 0.20296063020286D-06 3 19 1 18 -0.85418311256750D-01 -0.10629427253480D-06 1 20 1 18 -0.60410325829510D-14 0.11721002366909D+00 2 20 1 18 0.14587929325478D+00 -0.11165341930050D+00 3 20 1 18 -0.15379355314301D+00 0.70023280371417D-03 1 1 2 18 -0.43655032002932D+00 -0.68847982421329D-07 2 1 2 18 0.29421586446542D+00 0.90674459663425D-07 3 1 2 18 0.58905314287557D+00 0.66284182958296D-06 1 2 2 18 -0.33776741098257D+00 0.16831199647224D-01 2 2 2 18 -0.84871976741032D+00 0.13216417488587D-01 3 2 2 18 -0.87601023640078D+00 0.29483135551946D-02 1 3 2 18 -0.18553487339994D+00 0.23699499276425D-02 2 3 2 18 -0.28218054671126D+00 0.18748612809708D-02 3 3 2 18 -0.29814142361877D+00 -0.37655918745971D-03 1 4 2 18 0.15279480153772D+00 0.19371876375830D-06 2 4 2 18 -0.45120418987753D+00 0.88025875817233D-07 3 4 2 18 -0.39677128756510D+00 -0.16957807152899D-05 1 5 2 18 -0.57706589902665D+00 -0.12289748358377D-01 2 5 2 18 0.14783112415745D+00 0.52523946663174D-02 3 5 2 18 0.95059776604124D-01 0.54538587718525D-01 1 6 2 18 0.41677828610136D+00 0.13267869402024D+00 2 6 2 18 -0.55607803036372D-01 -0.17124846105233D+00 3 6 2 18 -0.23864525531632D+01 0.24998031974807D-01 1 7 2 18 0.79318326597436D+00 -0.47977922944098D-02 2 7 2 18 0.30874624286795D-01 -0.46348542474076D-03 3 7 2 18 0.28585800908299D+00 -0.40316759174331D-01 1 8 2 18 0.27843668475829D+00 0.53936912421190D-01 2 8 2 18 0.88549792089434D-01 -0.28832767553978D-01 3 8 2 18 0.19766674239629D+01 -0.80777843326796D-02 1 9 2 18 -0.44113266732785D+00 0.46049440858407D-06 2 9 2 18 0.60600698876671D+00 0.42409423058080D-07 3 9 2 18 0.29444700367643D+01 0.60948104562987D-06 1 10 2 18 0.76177137240514D+00 -0.26446894859379D-01 2 10 2 18 -0.10469420610392D+01 0.45916799788300D-01 3 10 2 18 0.25308862285828D+01 0.78720112808229D-01 1 11 2 18 0.86498691456240D+00 0.62461559713065D-06 2 11 2 18 -0.18067071117323D+00 0.31089459576160D-06 3 11 2 18 -0.18179129312139D+01 -0.14425826974384D-05 1 12 2 18 -0.59321479850323D+00 -0.70135200294601D-01 2 12 2 18 0.41162189561845D+00 0.78674046189832D-02 3 12 2 18 -0.23509757886370D+01 0.11635973491768D+00 1 13 2 18 -0.93083969808799D+00 -0.25243339454879D-06 2 13 2 18 -0.86159019638052D+00 -0.66505324510335D-15 3 13 2 18 0.26679586968602D+00 0.10024764434994D-05 1 14 2 18 -0.10479016972652D+01 -0.22136055575462D-01 2 14 2 18 -0.64393653654149D+01 0.78075874248333D-17 3 14 2 18 0.18134901390989D+00 0.11544913539420D-01 1 15 2 18 0.47277664526167D-01 0.16508898655494D-01 2 15 2 18 -0.14281461824262D+00 0.20448212100465D-01 3 15 2 18 0.14250039598126D-01 -0.38130937328824D-03 1 16 2 18 -0.36193545926836D-01 0.26981111142863D-01 2 16 2 18 0.25067618685146D-14 0.14044334778164D-01 3 16 2 18 0.28569069696730D-01 -0.48119547178873D-02 1 17 2 18 -0.28256158045279D+01 0.48863057830697D-02 2 17 2 18 0.41682457591847D+01 -0.26710682798399D-02 3 17 2 18 0.27459926317732D-01 0.21428220518199D-02 1 18 2 18 -0.58185567758221D+01 0.20371021439641D+00 2 18 2 18 0.13731883222882D+02 0.00000000000000D+00 3 18 2 18 0.20787092960346D+01 0.19185204557219D+00 1 19 2 18 0.53824066490422D-01 -0.20296063017441D-06 2 19 2 18 0.83471335358974D-01 0.57635700295339D-16 3 19 2 18 -0.87932415540537D-01 0.64602065110601D-07 1 20 2 18 -0.14587929325478D+00 -0.11165341930050D+00 2 20 2 18 -0.68404431069445D-14 0.14993874537244D+00 3 20 2 18 -0.16118901074332D+00 -0.39653957860839D-02 1 1 3 18 0.71530282007185D+00 0.24996742098557D-06 2 1 3 18 0.51794483325804D+00 0.10624453098218D-06 3 1 3 18 0.40245677350499D+00 -0.63608096224688D-06 1 2 3 18 -0.65607960698287D+00 0.51932790800398D-02 2 2 3 18 -0.86610704929416D+00 -0.57210474409351D-02 3 2 3 18 -0.38720145901411D+01 -0.56593951361141D-01 1 3 3 18 -0.29484470087087D+00 -0.79704964006693D-02 2 3 3 18 -0.28412783100756D+00 -0.25528681093124D-02 3 3 3 18 0.58931218389648D+00 -0.16011952998748D-01 1 4 3 18 -0.50339059700782D+00 -0.76624322650573D-06 2 4 3 18 -0.39989247456710D+00 -0.95934758436450D-07 3 4 3 18 -0.16381327018094D+01 0.30592575880702D-06 1 5 3 18 -0.98353435861179D+00 -0.33940087545791D-01 2 5 3 18 0.78284481223608D+00 0.45147056285263D-01 3 5 3 18 0.81322331927143D+01 0.28941632785671D-01 1 6 3 18 0.20850745211571D+00 0.65729656124459D-01 2 6 3 18 -0.82729805709317D-01 -0.44822502987789D-01 3 6 3 18 -0.47060580026550D+00 0.17445021945149D-01 1 7 3 18 0.93572737633761D+00 0.37579462405130D-01 2 7 3 18 -0.79229774483713D+00 -0.17897778936940D-01 3 7 3 18 0.81224984678898D+01 0.26874692129945D-01 1 8 3 18 -0.24436588460006D+00 -0.29396970736665D-01 2 8 3 18 0.76798941795580D-01 -0.16238853335852D-02 3 8 3 18 -0.29125009571175D+00 -0.16060897961966D-02 1 9 3 18 -0.10062446340674D+01 0.21762410213780D-06 2 9 3 18 0.16991444083957D+01 -0.64620989164624D-06 3 9 3 18 0.12629097866750D+01 0.69783901706081D-06 1 10 3 18 -0.74344148718089D+00 -0.32574386823827D-01 2 10 3 18 0.10037781864828D+01 0.45031915050346D-01 3 10 3 18 0.19085745169970D+01 -0.17173873451275D+00 1 11 3 18 0.12779869366895D+01 -0.13694471894267D-05 2 11 3 18 -0.99186826058955D+00 0.80057566010413D-06 3 11 3 18 0.15157351949622D+01 0.56607467076958D-06 1 12 3 18 0.12573982645368D+01 -0.16643125022080D-01 2 12 3 18 -0.12461223281263D+01 -0.25375252784206D-02 3 12 3 18 0.77577045673890D+00 -0.29597302715577D+00 1 13 3 18 0.53487764930099D-02 0.46179843796149D-06 2 13 3 18 0.26679586968602D+00 -0.10024764433873D-05 3 13 3 18 -0.21639835254678D+01 0.22434383981353D-14 1 14 3 18 0.39051230720331D-01 -0.63531479365453D-02 2 14 3 18 0.18134901390989D+00 -0.11544913539420D-01 3 14 3 18 0.29161152602150D+01 -0.12531630057890D-16 1 15 3 18 0.56316791822400D-01 -0.32119232228888D-02 2 15 3 18 -0.14251317612238D-01 0.38046285316869D-03 3 15 3 18 0.26987263189482D-01 -0.48193293616579D-01 1 16 3 18 -0.58425409200679D-01 0.22476609889912D-02 2 16 3 18 0.28570349578281D-01 0.48121967695517D-02 3 16 3 18 0.12361054518711D-13 0.37413913772888D-01 1 17 3 18 0.16793934489499D+00 -0.32541325510298D-03 2 17 3 18 0.27457478724113D-01 0.21405129243702D-02 3 17 3 18 -0.73618058473114D+00 0.77640860358478D-02 1 18 3 18 0.12619333890138D+01 -0.16682055028654D+00 2 18 3 18 0.20787346150451D+01 -0.19185415816596D+00 3 18 3 18 0.16435630284476D+02 0.00000000000000D+00 1 19 3 18 0.85418311256754D-01 -0.10629427253480D-06 2 19 3 18 0.87932415540539D-01 0.64602065108866D-07 3 19 3 18 -0.69322977755903D+00 -0.82758498936050D-15 1 20 3 18 -0.15379355314301D+00 -0.70023280371408D-03 2 20 3 18 -0.16118901074332D+00 0.39653957860841D-02 3 20 3 18 0.13121755436972D-13 0.41737250275799D-01 1 1 1 19 -0.11319999201775D+00 -0.15934551342783D-06 2 1 1 19 0.36430894697398D+00 0.48208173895031D-07 3 1 1 19 0.68280799992299D+00 0.46232389662838D-06 1 2 1 19 -0.60909284293518D+00 0.98141360211213D-02 2 2 1 19 -0.45556429278277D+00 0.22118327089460D-01 3 2 1 19 0.77180569522024D+00 0.18709937733806D-02 1 3 1 19 0.35649811871922D-01 -0.22976920010464D-04 2 3 1 19 0.34323295459579D-01 0.14054410318702D-02 3 3 1 19 -0.34363902348796D+00 -0.11830040968678D-02 1 4 1 19 -0.15288541954491D+00 -0.74179413151034D-07 2 4 1 19 0.28523776767466D+00 -0.81435523115360D-07 3 4 1 19 0.27354924894095D+00 0.16530707425874D-06 1 5 1 19 0.25413098103869D+00 0.88218626130818D-01 2 5 1 19 -0.56236868110952D-01 -0.13810217998739D+00 3 5 1 19 0.18250727146300D+01 -0.22972871185771D-01 1 6 1 19 0.13646047988220D+00 -0.42100838790539D-02 2 6 1 19 -0.10201618763044D+01 0.33250236328472D-02 3 6 1 19 0.59001136683455D+00 -0.32308394610655D-01 1 7 1 19 0.37777211143034D+00 0.46890990369810D-01 2 7 1 19 0.14158513548062D+00 -0.32825000619358D-01 3 7 1 19 -0.22174517997335D+01 0.11338761750796D-02 1 8 1 19 -0.48396428542276D+00 -0.16319914985147D-02 2 8 1 19 0.75629071487948D+00 -0.78015039093783D-02 3 8 1 19 -0.65238380414948D+00 0.33400063853366D-01 1 9 1 19 0.18323066985060D-02 -0.26881542224722D-06 2 9 1 19 0.49085820329485D+00 0.14012253852040D-06 3 9 1 19 -0.16760073288540D+01 -0.15008875927255D-06 1 10 1 19 -0.74239324152534D+00 0.11585687028953D-01 2 10 1 19 0.96285669216841D+00 -0.47341334967089D-01 3 10 1 19 0.19890755571761D+01 0.68886348381705D-01 1 11 1 19 -0.15843853485635D+01 0.75467703167876D-06 2 11 1 19 0.83505586236791D+00 0.44334549352920D-06 3 11 1 19 -0.28623021674884D+01 -0.99588238266341D-06 1 12 1 19 -0.15265303959880D+00 -0.72110512408721D-01 2 12 1 19 0.52178561066733D+00 0.14817750461865D-01 3 12 1 19 0.21994628736096D+01 -0.71902339905675D-01 1 13 1 19 -0.43459039905274D-14 0.12744696070424D-01 2 13 1 19 0.36193148615834D-01 0.26981141758843D-01 3 13 1 19 0.58426994074743D-01 0.22476716037368D-02 1 14 1 19 0.18500269963520D+00 -0.11607586027923D-01 2 14 1 19 -0.47278071650212D-01 -0.16508978366318D-01 3 14 1 19 -0.56319555519061D-01 0.32112442240882D-02 1 15 1 19 0.93881008275053D+00 -0.11088915726302D-15 2 15 1 19 0.10479016972652D+01 -0.22136055575462D-01 3 15 1 19 0.39051230720331D-01 0.63531479365454D-02 1 16 1 19 -0.57169838216393D+01 0.39734496745739D-14 2 16 1 19 -0.93083969808799D+00 0.25243339441069D-06 3 16 1 19 -0.53487764930115D-02 0.46179843800490D-06 1 17 1 19 -0.31161326071751D-14 -0.11721002366909D+00 2 17 1 19 -0.14587929325478D+00 0.11165341930050D+00 3 17 1 19 -0.15379355314301D+00 0.70023280371398D-03 1 18 1 19 0.19478205682408D+00 0.11088311807635D-15 2 18 1 19 0.53824066490422D-01 0.20296063017441D-06 3 18 1 19 0.85418311256754D-01 0.10629427253480D-06 1 19 1 19 0.12520191818080D+02 0.00000000000000D+00 2 19 1 19 -0.58185532262870D+01 -0.20370962133179D+00 3 19 1 19 -0.12619568631376D+01 -0.16681885451866D+00 1 20 1 19 -0.38501409953344D+01 0.18355876600538D-02 2 20 1 19 0.28256148935147D+01 -0.48860234700138D-02 3 20 1 19 0.16793740323249D+00 -0.32475725493963D-03 1 1 2 19 0.43655032002932D+00 0.68847984565514D-07 2 1 2 19 -0.29421586446542D+00 -0.90674460129711D-07 3 1 2 19 0.58905314287557D+00 0.66284183494911D-06 1 2 2 19 -0.33776741098251D+00 0.16831199647224D-01 2 2 2 19 -0.84871976741028D+00 0.13216417488587D-01 3 2 2 19 0.87601023640069D+00 -0.29483135551944D-02 1 3 2 19 0.18553487339995D+00 -0.23699499276417D-02 2 3 2 19 0.28218054671127D+00 -0.18748612809699D-02 3 3 2 19 -0.29814142361876D+00 -0.37655918746220D-03 1 4 2 19 0.15279480153778D+00 0.19371876373085D-06 2 4 2 19 -0.45120418987751D+00 0.88025875907294D-07 3 4 2 19 0.39677128756519D+00 0.16957807154966D-05 1 5 2 19 -0.41677828610137D+00 -0.13267869402024D+00 2 5 2 19 0.55607803036370D-01 0.17124846105233D+00 3 5 2 19 -0.23864525531632D+01 0.24998031974808D-01 1 6 2 19 0.57706589902659D+00 0.12289748358355D-01 2 6 2 19 -0.14783112415751D+00 -0.52523946662963D-02 3 6 2 19 0.95059776604117D-01 0.54538587718518D-01 1 7 2 19 -0.27843668475829D+00 -0.53936912421190D-01 2 7 2 19 -0.88549792089430D-01 0.28832767553978D-01 3 7 2 19 0.19766674239629D+01 -0.80777843326803D-02 1 8 2 19 -0.79318326597426D+00 0.47977922943872D-02 2 8 2 19 -0.30874624286803D-01 0.46348542474605D-03 3 8 2 19 0.28585800908301D+00 -0.40316759174323D-01 1 9 2 19 0.44113266732786D+00 -0.46049440944430D-06 2 9 2 19 -0.60600698876671D+00 -0.42409421956642D-07 3 9 2 19 0.29444700367643D+01 0.60948104140674D-06 1 10 2 19 0.76177137240514D+00 -0.26446894859379D-01 2 10 2 19 -0.10469420610392D+01 0.45916799788300D-01 3 10 2 19 -0.25308862285828D+01 -0.78720112808229D-01 1 11 2 19 0.86498691456239D+00 0.62461559716834D-06 2 11 2 19 -0.18067071117324D+00 0.31089459518409D-06 3 11 2 19 0.18179129312139D+01 0.14425826974482D-05 1 12 2 19 0.59321479850323D+00 0.70135200294599D-01 2 12 2 19 -0.41162189561845D+00 -0.78674046189830D-02 3 12 2 19 -0.23509757886370D+01 0.11635973491769D+00 1 13 2 19 0.36193545926835D-01 -0.26981111142863D-01 2 13 2 19 -0.30349016256779D-15 -0.14044334778164D-01 3 13 2 19 0.28569069696729D-01 -0.48119547178875D-02 1 14 2 19 0.47277664526167D-01 0.16508898655494D-01 2 14 2 19 -0.14281461824261D+00 0.20448212100465D-01 3 14 2 19 -0.14250039598125D-01 0.38130937328817D-03 1 15 2 19 -0.10479016972652D+01 -0.22136055575462D-01 2 15 2 19 -0.64393653654149D+01 0.29063836106099D-17 3 15 2 19 -0.18134901390989D+00 -0.11544913539420D-01 1 16 2 19 0.93083969808799D+00 0.25243339453322D-06 2 16 2 19 0.86159019638052D+00 -0.13398704244359D-14 3 16 2 19 0.26679586968602D+00 0.10024764429118D-05 1 17 2 19 0.14587929325478D+00 0.11165341930050D+00 2 17 2 19 -0.46170685069206D-15 -0.14993874537244D+00 3 17 2 19 -0.16118901074332D+00 -0.39653957860841D-02 1 18 2 19 0.53824066490422D-01 -0.20296063020286D-06 2 18 2 19 0.83471335358974D-01 -0.57635700295339D-16 3 18 2 19 0.87932415540539D-01 -0.64602065108866D-07 1 19 2 19 -0.58185567758221D+01 0.20371021439641D+00 2 19 2 19 0.13731883222882D+02 0.00000000000000D+00 3 19 2 19 -0.20787092960345D+01 -0.19185204557219D+00 1 20 2 19 0.28256158045279D+01 -0.48863057830689D-02 2 20 2 19 -0.41682457591848D+01 0.26710682798419D-02 3 20 2 19 0.27459926317726D-01 0.21428220518206D-02 1 1 3 19 0.71530282007181D+00 0.24996742841004D-06 2 1 3 19 0.51794483325805D+00 0.10624453635006D-06 3 1 3 19 -0.40245677350494D+00 0.63608096800457D-06 1 2 3 19 0.65607960698280D+00 -0.51932790800398D-02 2 2 3 19 0.86610704929405D+00 0.57210474409353D-02 3 2 3 19 -0.38720145901412D+01 -0.56593951361141D-01 1 3 3 19 -0.29484470087087D+00 -0.79704964006715D-02 2 3 3 19 -0.28412783100756D+00 -0.25528681093149D-02 3 3 3 19 -0.58931218389638D+00 0.16011952998748D-01 1 4 3 19 0.50339059700782D+00 0.76624322687920D-06 2 4 3 19 0.39989247456718D+00 0.95934758643210D-07 3 4 3 19 -0.16381327018096D+01 0.30592576248439D-06 1 5 3 19 0.20850745211572D+00 0.65729656124459D-01 2 5 3 19 -0.82729805709320D-01 -0.44822502987788D-01 3 5 3 19 0.47060580026552D+00 -0.17445021945159D-01 1 6 3 19 -0.98353435861180D+00 -0.33940087545785D-01 2 6 3 19 0.78284481223608D+00 0.45147056285256D-01 3 6 3 19 -0.81322331927143D+01 -0.28941632785695D-01 1 7 3 19 -0.24436588460006D+00 -0.29396970736664D-01 2 7 3 19 0.76798941795586D-01 -0.16238853335860D-02 3 7 3 19 0.29125009571178D+00 0.16060897962143D-02 1 8 3 19 0.93572737633762D+00 0.37579462405121D-01 2 8 3 19 -0.79229774483711D+00 -0.17897778936932D-01 3 8 3 19 -0.81224984678899D+01 -0.26874692129970D-01 1 9 3 19 -0.10062446340674D+01 0.21762410425470D-06 2 9 3 19 0.16991444083956D+01 -0.64620989586937D-06 3 9 3 19 -0.12629097866749D+01 -0.69783900947217D-06 1 10 3 19 0.74344148718086D+00 0.32574386823827D-01 2 10 3 19 -0.10037781864828D+01 -0.45031915050346D-01 3 10 3 19 0.19085745169968D+01 -0.17173873451275D+00 1 11 3 19 -0.12779869366895D+01 0.13694471895317D-05 2 11 3 19 0.99186826058953D+00 -0.80057566009602D-06 3 11 3 19 0.15157351949621D+01 0.56607467181025D-06 1 12 3 19 0.12573982645368D+01 -0.16643125022083D-01 2 12 3 19 -0.12461223281264D+01 -0.25375252784172D-02 3 12 3 19 -0.77577045673880D+00 0.29597302715578D+00 1 13 3 19 -0.58425409200676D-01 0.22476609889910D-02 2 13 3 19 0.28570349578279D-01 0.48121967695516D-02 3 13 3 19 -0.16277555915659D-14 -0.37413913772884D-01 1 14 3 19 -0.56316791822398D-01 0.32119232228890D-02 2 14 3 19 0.14251317612238D-01 -0.38046285316876D-03 3 14 3 19 0.26987263189468D-01 -0.48193293616580D-01 1 15 3 19 -0.39051230720331D-01 0.63531479365454D-02 2 15 3 19 -0.18134901390989D+00 0.11544913539420D-01 3 15 3 19 0.29161152602150D+01 0.19791761908771D-16 1 16 3 19 0.53487764930078D-02 0.46179843798192D-06 2 16 3 19 0.26679586968602D+00 -0.10024764439749D-05 3 16 3 19 0.21639835254679D+01 -0.57674394953607D-14 1 17 3 19 -0.15379355314301D+00 -0.70023280371427D-03 2 17 3 19 -0.16118901074332D+00 0.39653957860838D-02 3 17 3 19 0.18688982910746D-14 -0.41737250275797D-01 1 18 3 19 -0.85418311256750D-01 0.10629427253480D-06 2 18 3 19 -0.87932415540537D-01 -0.64602065110601D-07 3 18 3 19 -0.69322977755903D+00 0.82758498936050D-15 1 19 3 19 -0.12619333890138D+01 0.16682055028654D+00 2 19 3 19 -0.20787346150450D+01 0.19185415816596D+00 3 19 3 19 0.16435630284476D+02 0.00000000000000D+00 1 20 3 19 0.16793934489498D+00 -0.32541325510249D-03 2 20 3 19 0.27457478724106D-01 0.21405129243709D-02 3 20 3 19 0.73618058473118D+00 -0.77640860358493D-02 1 1 1 20 -0.60909284293523D+00 0.98141360211214D-02 2 1 1 20 -0.45556429278288D+00 0.22118327089460D-01 3 1 1 20 0.77180569522044D+00 0.18709937733809D-02 1 2 1 20 -0.11319999201777D+00 -0.15934551188735D-06 2 2 1 20 0.36430894697399D+00 0.48208173638535D-07 3 2 1 20 0.68280799992298D+00 0.46232389594212D-06 1 3 1 20 -0.15288541954492D+00 -0.74179412742266D-07 2 3 1 20 0.28523776767464D+00 -0.81435523064211D-07 3 3 1 20 0.27354924894093D+00 0.16530707411788D-06 1 4 1 20 0.35649811871913D-01 -0.22976920010688D-04 2 4 1 20 0.34323295459579D-01 0.14054410318702D-02 3 4 1 20 -0.34363902348795D+00 -0.11830040968680D-02 1 5 1 20 -0.25413098103870D+00 -0.88218626130818D-01 2 5 1 20 0.56236868110945D-01 0.13810217998739D+00 3 5 1 20 -0.18250727146300D+01 0.22972871185771D-01 1 6 1 20 0.13646047988226D+00 -0.42100838790533D-02 2 6 1 20 -0.10201618763046D+01 0.33250236328473D-02 3 6 1 20 0.59001136683451D+00 -0.32308394610654D-01 1 7 1 20 -0.37777211143033D+00 -0.46890990369810D-01 2 7 1 20 -0.14158513548062D+00 0.32825000619358D-01 3 7 1 20 0.22174517997335D+01 -0.11338761750789D-02 1 8 1 20 -0.48396428542306D+00 -0.16319914985144D-02 2 8 1 20 0.75629071487943D+00 -0.78015039093783D-02 3 8 1 20 -0.65238380414914D+00 0.33400063853368D-01 1 9 1 20 -0.74239324152536D+00 0.11585687028954D-01 2 9 1 20 0.96285669216838D+00 -0.47341334967089D-01 3 9 1 20 0.19890755571761D+01 0.68886348381706D-01 1 10 1 20 0.18323066984651D-02 -0.26881542220778D-06 2 10 1 20 0.49085820329484D+00 0.14012253848370D-06 3 10 1 20 -0.16760073288540D+01 -0.15008875936793D-06 1 11 1 20 -0.15265303959880D+00 -0.72110512408721D-01 2 11 1 20 0.52178561066732D+00 0.14817750461866D-01 3 11 1 20 0.21994628736095D+01 -0.71902339905675D-01 1 12 1 20 -0.15843853485635D+01 0.75467703188708D-06 2 12 1 20 0.83505586236791D+00 0.44334549353171D-06 3 12 1 20 -0.28623021674884D+01 -0.99588238272966D-06 1 13 1 20 0.18500269963520D+00 -0.11607586027923D-01 2 13 1 20 -0.47278071650212D-01 -0.16508978366318D-01 3 13 1 20 -0.56319555519058D-01 0.32112442240881D-02 1 14 1 20 -0.76797998446432D-14 0.12744696070424D-01 2 14 1 20 0.36193148615834D-01 0.26981141758843D-01 3 14 1 20 0.58426994074748D-01 0.22476716037368D-02 1 15 1 20 -0.57169838216393D+01 0.44378917868023D-14 2 15 1 20 -0.93083969808800D+00 0.25243339440365D-06 3 15 1 20 -0.53487764929979D-02 0.46179843794440D-06 1 16 1 20 0.93881008275057D+00 0.19651695094723D-16 2 16 1 20 0.10479016972652D+01 -0.22136055575462D-01 3 16 1 20 0.39051230720330D-01 0.63531479365455D-02 1 17 1 20 0.19478205682408D+00 0.25979381432415D-15 2 17 1 20 0.53824066490422D-01 0.20296063019097D-06 3 17 1 20 0.85418311256752D-01 0.10629427242986D-06 1 18 1 20 -0.60410325829510D-14 -0.11721002366909D+00 2 18 1 20 -0.14587929325478D+00 0.11165341930050D+00 3 18 1 20 -0.15379355314301D+00 0.70023280371408D-03 1 19 1 20 -0.38501409953344D+01 0.18355876600537D-02 2 19 1 20 0.28256148935147D+01 -0.48860234700138D-02 3 19 1 20 0.16793740323249D+00 -0.32475725493964D-03 1 20 1 20 0.12520191818080D+02 0.00000000000000D+00 2 20 1 20 -0.58185532262866D+01 -0.20370962133179D+00 3 20 1 20 -0.12619568631378D+01 -0.16681885451866D+00 1 1 2 20 -0.33776741098263D+00 0.16831199647224D-01 2 1 2 20 -0.84871976741019D+00 0.13216417488587D-01 3 1 2 20 0.87601023640088D+00 -0.29483135551944D-02 1 2 2 20 0.43655032002933D+00 0.68847984309018D-07 2 2 2 20 -0.29421586446538D+00 -0.90674460660598D-07 3 2 2 20 0.58905314287565D+00 0.66284183499682D-06 1 3 2 20 0.15279480153776D+00 0.19371876378200D-06 2 3 2 20 -0.45120418987751D+00 0.88025875908823D-07 3 3 2 20 0.39677128756516D+00 0.16957807151303D-05 1 4 2 20 0.18553487339995D+00 -0.23699499276416D-02 2 4 2 20 0.28218054671126D+00 -0.18748612809691D-02 3 4 2 20 -0.29814142361876D+00 -0.37655918746205D-03 1 5 2 20 0.41677828610136D+00 0.13267869402024D+00 2 5 2 20 -0.55607803036374D-01 -0.17124846105233D+00 3 5 2 20 0.23864525531633D+01 -0.24998031974808D-01 1 6 2 20 0.57706589902639D+00 0.12289748358355D-01 2 6 2 20 -0.14783112415719D+00 -0.52523946662951D-02 3 6 2 20 0.95059776604181D-01 0.54538587718516D-01 1 7 2 20 0.27843668475829D+00 0.53936912421190D-01 2 7 2 20 0.88549792089430D-01 -0.28832767553978D-01 3 7 2 20 -0.19766674239629D+01 0.80777843326799D-02 1 8 2 20 -0.79318326597433D+00 0.47977922943873D-02 2 8 2 20 -0.30874624286607D-01 0.46348542474627D-03 3 8 2 20 0.28585800908281D+00 -0.40316759174324D-01 1 9 2 20 0.76177137240511D+00 -0.26446894859379D-01 2 9 2 20 -0.10469420610392D+01 0.45916799788300D-01 3 9 2 20 -0.25308862285828D+01 -0.78720112808229D-01 1 10 2 20 0.44113266732785D+00 -0.46049440948794D-06 2 10 2 20 -0.60600698876671D+00 -0.42409422163751D-07 3 10 2 20 0.29444700367642D+01 0.60948104143919D-06 1 11 2 20 0.59321479850322D+00 0.70135200294600D-01 2 11 2 20 -0.41162189561849D+00 -0.78674046189826D-02 3 11 2 20 -0.23509757886370D+01 0.11635973491769D+00 1 12 2 20 0.86498691456239D+00 0.62461559717085D-06 2 12 2 20 -0.18067071117330D+00 0.31089459530729D-06 3 12 2 20 0.18179129312139D+01 0.14425826976215D-05 1 13 2 20 0.47277664526167D-01 0.16508898655494D-01 2 13 2 20 -0.14281461824262D+00 0.20448212100465D-01 3 13 2 20 -0.14250039598130D-01 0.38130937328808D-03 1 14 2 20 0.36193545926834D-01 -0.26981111142863D-01 2 14 2 20 -0.87196549118242D-15 -0.14044334778164D-01 3 14 2 20 0.28569069696724D-01 -0.48119547178874D-02 1 15 2 20 0.93083969808799D+00 0.25243339452621D-06 2 15 2 20 0.86159019638056D+00 -0.11845317146392D-14 3 15 2 20 0.26679586968601D+00 0.10024764431886D-05 1 16 2 20 -0.10479016972652D+01 -0.22136055575462D-01 2 16 2 20 -0.64393653654150D+01 0.13551665114436D-16 3 16 2 20 -0.18134901390989D+00 -0.11544913539420D-01 1 17 2 20 0.53824066490422D-01 -0.20296063018630D-06 2 17 2 20 0.83471335358967D-01 -0.29246124284710D-15 3 17 2 20 0.87932415540540D-01 -0.64602065305152D-07 1 18 2 20 0.14587929325478D+00 0.11165341930050D+00 2 18 2 20 -0.68404431069445D-14 -0.14993874537244D+00 3 18 2 20 -0.16118901074332D+00 -0.39653957860841D-02 1 19 2 20 0.28256158045279D+01 -0.48863057830689D-02 2 19 2 20 -0.41682457591848D+01 0.26710682798419D-02 3 19 2 20 0.27459926317726D-01 0.21428220518203D-02 1 20 2 20 -0.58185567758217D+01 0.20371021439641D+00 2 20 2 20 0.13731883222881D+02 0.00000000000000D+00 3 20 2 20 -0.20787092960347D+01 -0.19185204557219D+00 1 1 3 20 0.65607960698300D+00 -0.51932790800395D-02 2 1 3 20 0.86610704929423D+00 0.57210474409353D-02 3 1 3 20 -0.38720145901413D+01 -0.56593951361144D-01 1 2 3 20 0.71530282007179D+00 0.24996742772379D-06 2 2 3 20 0.51794483325813D+00 0.10624453639777D-06 3 2 3 20 -0.40245677350506D+00 0.63608097114271D-06 1 3 3 20 0.50339059700781D+00 0.76624322673834D-06 2 3 3 20 0.39989247456716D+00 0.95934758276874D-07 3 3 3 20 -0.16381327018094D+01 0.30592575498494D-06 1 4 3 20 -0.29484470087087D+00 -0.79704964006717D-02 2 4 3 20 -0.28412783100757D+00 -0.25528681093148D-02 3 4 3 20 -0.58931218389643D+00 0.16011952998745D-01 1 5 3 20 -0.20850745211572D+00 -0.65729656124459D-01 2 5 3 20 0.82729805709342D-01 0.44822502987788D-01 3 5 3 20 -0.47060580026548D+00 0.17445021945153D-01 1 6 3 20 -0.98353435861183D+00 -0.33940087545784D-01 2 6 3 20 0.78284481223614D+00 0.45147056285254D-01 3 6 3 20 -0.81322331927146D+01 -0.28941632785693D-01 1 7 3 20 0.24436588460005D+00 0.29396970736665D-01 2 7 3 20 -0.76798941795582D-01 0.16238853335855D-02 3 7 3 20 -0.29125009571178D+00 -0.16060897962089D-02 1 8 3 20 0.93572737633796D+00 0.37579462405123D-01 2 8 3 20 -0.79229774483731D+00 -0.17897778936933D-01 3 8 3 20 -0.81224984678897D+01 -0.26874692129967D-01 1 9 3 20 0.74344148718084D+00 0.32574386823827D-01 2 9 3 20 -0.10037781864828D+01 -0.45031915050346D-01 3 9 3 20 0.19085745169969D+01 -0.17173873451275D+00 1 10 3 20 -0.10062446340674D+01 0.21762410415586D-06 2 10 3 20 0.16991444083956D+01 -0.64620989583692D-06 3 10 3 20 -0.12629097866748D+01 -0.69783901530994D-06 1 11 3 20 0.12573982645368D+01 -0.16643125022083D-01 2 11 3 20 -0.12461223281263D+01 -0.25375252784174D-02 3 11 3 20 -0.77577045673876D+00 0.29597302715578D+00 1 12 3 20 -0.12779869366894D+01 0.13694471894655D-05 2 12 3 20 0.99186826058954D+00 -0.80057565992281D-06 3 12 3 20 0.15157351949622D+01 0.56607466920007D-06 1 13 3 20 -0.56316791822394D-01 0.32119232228889D-02 2 13 3 20 0.14251317612233D-01 -0.38046285316885D-03 3 13 3 20 0.26987263189449D-01 -0.48193293616580D-01 1 14 3 20 -0.58425409200671D-01 0.22476609889910D-02 2 14 3 20 0.28570349578274D-01 0.48121967695516D-02 3 14 3 20 0.63791849976081D-14 -0.37413913772888D-01 1 15 3 20 0.53487764930214D-02 0.46179843792055D-06 2 15 3 20 0.26679586968601D+00 -0.10024764436981D-05 3 15 3 20 0.21639835254679D+01 -0.53118738841646D-14 1 16 3 20 -0.39051230720332D-01 0.63531479365455D-02 2 16 3 20 -0.18134901390989D+00 0.11544913539420D-01 3 16 3 20 0.29161152602151D+01 0.20799195292530D-16 1 17 3 20 -0.85418311256751D-01 0.10629427242986D-06 2 17 3 20 -0.87932415540536D-01 -0.64602065306886D-07 3 17 3 20 -0.69322977755907D+00 0.10102711231000D-14 1 18 3 20 -0.15379355314301D+00 -0.70023280371417D-03 2 18 3 20 -0.16118901074332D+00 0.39653957860839D-02 3 18 3 20 0.13121755436972D-13 -0.41737250275799D-01 1 19 3 20 0.16793934489498D+00 -0.32541325510251D-03 2 19 3 20 0.27457478724106D-01 0.21405129243706D-02 3 19 3 20 0.73618058473118D+00 -0.77640860358494D-02 1 20 3 20 -0.12619333890141D+01 0.16682055028654D+00 2 20 3 20 -0.20787346150452D+01 0.19185415816596D+00 3 20 3 20 0.16435630284475D+02 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 0.00000000E+00 5.00000000E-01 1.0 1 1 1 1 0.91767034962249D+01 0.00000000000000D+00 2 1 1 1 0.12531398040088D+01 0.56687726263018D-06 3 1 1 1 -0.43641791814408D-13 0.11102230246252D-15 1 2 1 1 0.14750190458057D-13 -0.24346685599698D-14 2 2 1 1 0.28435010364622D-15 -0.55794016602881D-16 3 2 1 1 -0.46543269579149D-01 -0.12413924064927D-07 1 3 1 1 0.79792467307875D-01 -0.12247162637992D-14 2 3 1 1 0.40744203558300D-01 -0.95371562376899D-09 3 3 1 1 0.16344383944713D-14 0.81191439531329D-15 1 4 1 1 0.49356013477347D-14 0.36011595342229D-16 2 4 1 1 0.42963835382655D-14 -0.69068750267548D-16 3 4 1 1 -0.10961377319982D+01 -0.52693661264073D-08 1 5 1 1 0.33543616728584D+01 0.61640066908408D-02 2 5 1 1 -0.61161739452681D+00 0.32014046312442D-03 3 5 1 1 -0.24458727958744D+00 -0.16465306599682D-01 1 6 1 1 0.33543616728583D+01 0.61640066908428D-02 2 6 1 1 -0.61161739452681D+00 0.32014046312400D-03 3 6 1 1 0.24458727958744D+00 0.16465306599681D-01 1 7 1 1 -0.12798186148450D-01 -0.20891510903254D-01 2 7 1 1 0.34587762083187D+00 0.29972506986920D-02 3 7 1 1 0.68301135923742D+01 -0.11263961782755D-02 1 8 1 1 -0.12798186148432D-01 -0.20891510903252D-01 2 8 1 1 0.34587762083186D+00 0.29972506986922D-02 3 8 1 1 -0.68301135923743D+01 0.11263961782691D-02 1 9 1 1 -0.13601470966758D+01 0.18283276260787D-07 2 9 1 1 -0.18412219540148D+00 0.17480483349703D-07 3 9 1 1 0.34625277607665D-15 -0.11069740067251D-15 1 10 1 1 0.26092995753065D-13 0.16993464479755D-14 2 10 1 1 0.19432365449786D-14 -0.84105489238480D-16 3 10 1 1 0.41289204564323D+00 0.71724842448312D-08 1 11 1 1 0.70958520822952D-14 0.63220806651172D-15 2 11 1 1 -0.67735916100682D-15 -0.99752640989078D-16 3 11 1 1 0.26506167626628D+01 -0.11469790962541D-07 1 12 1 1 -0.32901829520358D+01 0.72003782375135D-08 2 12 1 1 0.25502894899883D+00 0.36554647805310D-08 3 12 1 1 0.34472534203354D-14 0.55350675762674D-14 1 13 1 1 0.10668546520188D+01 0.19841926923918D-08 2 13 1 1 0.62660610534657D+00 -0.22871375720938D-08 3 13 1 1 -0.10785556802538D+01 -0.19449713013608D-07 1 14 1 1 0.66066883358690D+00 0.58092146726291D-02 2 14 1 1 0.67176802529486D+00 0.52547534079837D-02 3 14 1 1 0.80663723739242D+00 -0.65285290862613D-02 1 15 1 1 -0.66066883358686D+00 -0.58092146726301D-02 2 15 1 1 -0.67176802529486D+00 -0.52547534079832D-02 3 15 1 1 0.80663723739248D+00 -0.65285290862646D-02 1 16 1 1 0.10668546520188D+01 0.19841917497711D-08 2 16 1 1 0.62660610534655D+00 -0.22871378254525D-08 3 16 1 1 0.10785556802538D+01 0.19449715145818D-07 1 17 1 1 0.15275697490881D+01 -0.64572596198195D-02 2 17 1 1 -0.11310439235655D+00 0.27092240302342D-01 3 17 1 1 0.25142281874055D+00 -0.69760145231625D-02 1 18 1 1 0.83722932351963D+00 -0.63653622376613D-06 2 18 1 1 -0.86353847218527D+00 0.22690739439507D-06 3 18 1 1 0.11093678603690D+01 -0.28405313526652D-06 1 19 1 1 -0.83722932351961D+00 0.63653622369531D-06 2 19 1 1 0.86353847218527D+00 -0.22690739623192D-06 3 19 1 1 0.11093678603690D+01 -0.28405313952331D-06 1 20 1 1 0.15275697490882D+01 -0.64572596198202D-02 2 20 1 1 -0.11310439235656D+00 0.27092240302342D-01 3 20 1 1 -0.25142281874053D+00 0.69760145231656D-02 1 1 2 1 0.12531378256454D+01 0.62939489387228D-06 2 1 2 1 0.79896825300129D+01 0.00000000000000D+00 3 1 2 1 -0.28136526312962D-13 0.00000000000000D+00 1 2 2 1 0.28435010364622D-15 -0.55794016602881D-16 2 2 2 1 0.18940715873910D-13 0.96013562039078D-15 3 2 2 1 0.32777068616145D+00 0.60956055725576D-08 1 3 2 1 -0.40744203557956D-01 -0.95371562376899D-09 2 3 2 1 0.37261554587703D+00 -0.33999266560255D-14 3 3 2 1 -0.87478955638920D-14 0.53382358850539D-16 1 4 2 1 0.42963835390927D-14 -0.70803473743525D-16 2 4 2 1 0.20235621669531D-14 0.20381685200383D-15 3 4 2 1 0.47979162914170D-01 -0.29035711258190D-08 1 5 2 1 0.22164045386791D+00 -0.15659011129084D-02 2 5 2 1 -0.34356370384059D+01 0.30086279326465D-01 3 5 2 1 0.19740883652859D+01 0.19116697511382D-02 1 6 2 1 0.22164045386790D+00 -0.15659011129088D-02 2 6 2 1 -0.34356370384059D+01 0.30086279326461D-01 3 6 2 1 -0.19740883652859D+01 -0.19116697511375D-02 1 7 2 1 0.40942422053712D+00 0.80965316320255D-02 2 7 2 1 -0.64248236354105D+00 0.39529224498704D-02 3 7 2 1 -0.22612074747947D-01 0.42968796516401D-02 1 8 2 1 0.40942422053712D+00 0.80965316320257D-02 2 8 2 1 -0.64248236354104D+00 0.39529224498707D-02 3 8 2 1 0.22612074747950D-01 -0.42968796516398D-02 1 9 2 1 -0.37924151268480D+00 -0.40782198315036D-08 2 9 2 1 0.92924610258308D-01 0.68640094744443D-09 3 9 2 1 0.49394068986470D-15 0.15516367704496D-15 1 10 2 1 0.19431586793656D-14 -0.83671808369485D-16 2 10 2 1 -0.44282855286124D-14 0.50573816733092D-15 3 10 2 1 -0.22854053578514D+00 0.41213474332516D-08 1 11 2 1 -0.67735916095512D-15 -0.99318960120084D-16 2 11 2 1 -0.33230995208309D-16 -0.16671883387190D-16 3 11 2 1 0.21683191281970D+00 0.24383217614415D-08 1 12 2 1 0.21474564783803D+00 0.47484901311467D-08 2 12 2 1 -0.25132987898845D+00 -0.17101883416923D-08 3 12 2 1 0.45233782443037D-14 0.63856442403685D-16 1 13 2 1 0.36123461004001D+00 -0.89515344295455D-08 2 13 2 1 0.37565111373290D+00 -0.64859607831757D-09 3 13 2 1 0.46771173421883D+00 0.16008556999999D-07 1 14 2 1 0.23438760987990D+00 -0.19385491922700D-02 2 14 2 1 -0.26721322086050D+00 -0.67301329828311D-03 3 14 2 1 -0.24739921605504D+00 0.21134327938201D-02 1 15 2 1 -0.23438760987989D+00 0.19385491922706D-02 2 15 2 1 0.26721322086049D+00 0.67301329828239D-03 3 15 2 1 -0.24739921605504D+00 0.21134327938223D-02 1 16 2 1 0.36123461004002D+00 -0.89515346811695D-08 2 16 2 1 0.37565111373290D+00 -0.64859620538438D-09 3 16 2 1 -0.46771173421881D+00 -0.16008557426047D-07 1 17 2 1 0.49549009324293D+00 0.24006154107437D-01 2 17 2 1 0.83235442486972D+00 0.12606854493728D-01 3 17 2 1 0.86237266963285D+00 -0.10810685967275D-01 1 18 2 1 -0.34428420488003D+00 0.37372532496878D-06 2 18 2 1 0.12389191950378D+00 0.16777393989141D-07 3 18 2 1 0.61624736641728D+00 -0.73002882458510D-07 1 19 2 1 0.34428420488003D+00 -0.37372532680389D-06 2 19 2 1 -0.12389191950378D+00 -0.16777395084060D-07 3 19 2 1 0.61624736641727D+00 -0.73002887971685D-07 1 20 2 1 0.49549009324294D+00 0.24006154107437D-01 2 20 2 1 0.83235442486972D+00 0.12606854493728D-01 3 20 2 1 -0.86237266963282D+00 0.10810685967275D-01 1 1 3 1 -0.43641791814408D-13 0.11102230246252D-15 2 1 3 1 -0.28136526312962D-13 0.00000000000000D+00 3 1 3 1 0.14867105049052D+02 0.00000000000000D+00 1 2 3 1 -0.46547308502683D-01 0.17651322655910D-07 2 2 3 1 0.32776984814127D+00 -0.49739330149072D-08 3 2 3 1 0.74194077319951D-13 -0.65885658448095D-14 1 3 3 1 0.16344383944713D-14 0.81191439531329D-15 2 3 3 1 -0.87478955651328D-14 0.53382358850538D-16 3 3 3 1 -0.70526463535709D+00 0.39988058505127D-14 1 4 3 1 -0.10961377319982D+01 0.52693682479087D-08 2 4 3 1 -0.47979162914179D-01 -0.29035711258190D-08 3 4 3 1 0.71970343856284D-14 0.49053747047667D-16 1 5 3 1 0.91957137112215D+00 0.10141322121641D-01 2 5 3 1 0.14077544617297D+01 0.27386350849675D-02 3 5 3 1 -0.33718112333226D+00 -0.22845026214971D-02 1 6 3 1 -0.91957137112216D+00 -0.10141322121641D-01 2 6 3 1 -0.14077544617297D+01 -0.27386350849669D-02 3 6 3 1 -0.33718112333229D+00 -0.22845026215024D-02 1 7 3 1 0.64607748118075D+01 -0.14372675444771D-01 2 7 3 1 -0.14596092989901D+00 0.46235710956260D-02 3 7 3 1 0.15081770436805D+01 -0.65515176709630D-02 1 8 3 1 -0.64607748118076D+01 0.14372675444765D-01 2 8 3 1 0.14596092989901D+00 -0.46235710956257D-02 3 8 3 1 0.15081770436805D+01 -0.65515176709640D-02 1 9 3 1 0.34625277607665D-15 -0.11069740067251D-15 2 9 3 1 0.49394069275983D-15 0.16253625181786D-15 3 9 3 1 -0.38255091315882D+01 0.27557862703776D-07 1 10 3 1 0.12972833328334D+00 0.97144962057492D-08 2 10 3 1 0.22769931938097D-01 -0.35771731824572D-08 3 10 3 1 0.38087868836112D-14 0.26161909103170D-14 1 11 3 1 0.90846730455016D+00 -0.17265956918256D-07 2 11 3 1 -0.10613762213917D+00 0.62670758546944D-08 3 11 3 1 0.79397812249970D-14 0.18474367630210D-14 1 12 3 1 0.34472534203354D-14 0.55350675762674D-14 2 12 3 1 0.45233782443037D-14 0.63856442403685D-16 3 12 3 1 -0.64698506258255D+00 0.67594556891292D-07 1 13 3 1 -0.10142403148698D+01 0.12347779804538D-07 2 13 3 1 -0.74400833557133D-02 -0.15182183648152D-07 3 13 3 1 0.17515667442613D+00 0.10496312808441D-07 1 14 3 1 0.13585071658990D+01 -0.74788430588034D-03 2 14 3 1 0.16166081741408D+00 -0.99471786066901D-03 3 14 3 1 -0.21372329087670D+00 0.37789498105809D-02 1 15 3 1 0.13585071658990D+01 -0.74788430588366D-03 2 15 3 1 0.16166081741409D+00 -0.99471786066685D-03 3 15 3 1 0.21372329087674D+00 -0.37789498105840D-02 1 16 3 1 0.10142403148699D+01 -0.12347777668858D-07 2 16 3 1 0.74400833557275D-02 0.15182183222538D-07 3 16 3 1 0.17515667442610D+00 0.10496314282995D-07 1 17 3 1 0.19271974120576D+00 0.13899459436928D-01 2 17 3 1 0.10948572598823D+01 -0.12558143074985D-01 3 17 3 1 0.23982246383879D+01 -0.24477481513512D-01 1 18 3 1 0.17584629655882D+01 0.13190429903560D-06 2 18 3 1 0.16706368605351D+00 -0.20213449796757D-06 3 18 3 1 -0.30191144601155D+00 0.48429957243655D-06 1 19 3 1 0.17584629655882D+01 0.13190429477968D-06 2 19 3 1 0.16706368605349D+00 -0.20213450347727D-06 3 19 3 1 0.30191144601155D+00 -0.48429958789456D-06 1 20 3 1 -0.19271974120576D+00 -0.13899459436925D-01 2 20 3 1 -0.10948572598823D+01 0.12558143074984D-01 3 20 3 1 0.23982246383879D+01 -0.24477481513514D-01 1 1 1 2 0.14750190458057D-13 0.24338011982318D-14 2 1 1 2 0.28435010323263D-15 0.55794016602881D-16 3 1 1 2 -0.46543269579149D-01 -0.12413923614323D-07 1 2 1 2 0.91767034962249D+01 0.00000000000000D+00 2 2 1 2 0.12531398040085D+01 0.56687726263018D-06 3 2 1 2 -0.10092276688023D-14 0.11102230246252D-15 1 3 1 2 -0.39922742905444D-14 0.10873752317695D-16 2 3 1 2 0.14316431121270D-14 0.39496714589651D-15 3 3 1 2 0.10961377319982D+01 0.52693672208851D-08 1 4 1 2 -0.79792467307858D-01 -0.14238535102920D-14 2 4 1 2 -0.40744203558148D-01 0.95371580377885D-09 3 4 1 2 -0.20406395509345D-13 0.85946364797072D-16 1 5 1 2 -0.33543616728584D+01 -0.61640066908453D-02 2 5 1 2 0.61161739452682D+00 -0.32014046312423D-03 3 5 1 2 0.24458727958744D+00 0.16465306599683D-01 1 6 1 2 0.33543616728584D+01 0.61640066908437D-02 2 6 1 2 -0.61161739452681D+00 0.32014046312428D-03 3 6 1 2 0.24458727958745D+00 0.16465306599684D-01 1 7 1 2 -0.12798186148427D-01 -0.20891510903242D-01 2 7 1 2 0.34587762083191D+00 0.29972506986937D-02 3 7 1 2 0.68301135923744D+01 -0.11263961782543D-02 1 8 1 2 0.12798186148458D-01 0.20891510903245D-01 2 8 1 2 -0.34587762083190D+00 -0.29972506986919D-02 3 8 1 2 0.68301135923743D+01 -0.11263961782728D-02 1 9 1 2 -0.28887805409521D-14 0.21639285347739D-14 2 9 1 2 0.32656245506598D-14 0.66396704872647D-16 3 9 1 2 -0.41289204564316D+00 -0.71724844129880D-08 1 10 1 2 0.13601470966757D+01 -0.18283272264001D-07 2 10 1 2 0.18412219540152D+00 -0.17480486311098D-07 3 10 1 2 -0.54279459024548D-14 -0.49881539597266D-15 1 11 1 2 0.32901829520357D+01 -0.72004002872136D-08 2 11 1 2 -0.25502894899915D+00 -0.36554620898718D-08 3 11 1 2 -0.31446858903255D-13 -0.26291784226690D-14 1 12 1 2 -0.73453326743327D-17 0.95659039590586D-15 2 12 1 2 -0.16726053255356D-14 0.24431570919719D-16 3 12 1 2 -0.26506167626628D+01 0.11469793354771D-07 1 13 1 2 -0.66066883358689D+00 -0.58092146726287D-02 2 13 1 2 -0.67176802529488D+00 -0.52547534079835D-02 3 13 1 2 -0.80663723739248D+00 0.65285290862640D-02 1 14 1 2 -0.10668546520188D+01 -0.19841949872492D-08 2 14 1 2 -0.62660610534656D+00 0.22871426629517D-08 3 14 1 2 0.10785556802537D+01 0.19449709500206D-07 1 15 1 2 -0.10668546520188D+01 -0.19841921245347D-08 2 15 1 2 -0.62660610534660D+00 0.22871422885006D-08 3 15 1 2 -0.10785556802538D+01 -0.19449705596872D-07 1 16 1 2 0.66066883358685D+00 0.58092146726285D-02 2 16 1 2 0.67176802529490D+00 0.52547534079844D-02 3 16 1 2 -0.80663723739252D+00 0.65285290862605D-02 1 17 1 2 -0.83722932351965D+00 0.63653622347648D-06 2 17 1 2 0.86353847218525D+00 -0.22690739649995D-06 3 17 1 2 -0.11093678603688D+01 0.28405314335517D-06 1 18 1 2 -0.15275697490881D+01 0.64572596198174D-02 2 18 1 2 0.11310439235659D+00 -0.27092240302348D-01 3 18 1 2 -0.25142281874041D+00 0.69760145231563D-02 1 19 1 2 -0.15275697490881D+01 0.64572596198175D-02 2 19 1 2 0.11310439235667D+00 -0.27092240302347D-01 3 19 1 2 0.25142281874033D+00 -0.69760145231567D-02 1 20 1 2 0.83722932351961D+00 -0.63653622059669D-06 2 20 1 2 -0.86353847218528D+00 0.22690739479055D-06 3 20 1 2 -0.11093678603689D+01 0.28405313514252D-06 1 1 2 2 0.28435010364622D-15 0.55794016602881D-16 2 1 2 2 0.18940715873910D-13 -0.96056930125977D-15 3 1 2 2 0.32777068616145D+00 0.60956060146388D-08 1 2 2 2 0.12531378256451D+01 0.62939489387228D-06 2 2 2 2 0.79896825300129D+01 0.00000000000000D+00 3 2 2 2 -0.35241953691242D-13 0.00000000000000D+00 1 3 2 2 0.14316431129542D-14 0.39670186937248D-15 2 3 2 2 -0.39599946711585D-14 0.12192355533221D-15 3 3 2 2 -0.47979162914177D-01 0.29035706448336D-08 1 4 2 2 0.40744203558108D-01 0.95371580377885D-09 2 4 2 2 -0.37261554587709D+00 -0.22954667435828D-14 3 4 2 2 0.40518496310173D-14 -0.14273701576780D-15 1 5 2 2 -0.22164045386790D+00 0.15659011129086D-02 2 5 2 2 0.34356370384060D+01 -0.30086279326455D-01 3 5 2 2 -0.19740883652860D+01 -0.19116697511427D-02 1 6 2 2 0.22164045386790D+00 -0.15659011129086D-02 2 6 2 2 -0.34356370384059D+01 0.30086279326462D-01 3 6 2 2 -0.19740883652860D+01 -0.19116697511378D-02 1 7 2 2 0.40942422053716D+00 0.80965316320272D-02 2 7 2 2 -0.64248236354108D+00 0.39529224498671D-02 3 7 2 2 -0.22612074747944D-01 0.42968796516415D-02 1 8 2 2 -0.40942422053715D+00 -0.80965316320254D-02 2 8 2 2 0.64248236354108D+00 -0.39529224498675D-02 3 8 2 2 -0.22612074747940D-01 0.42968796516413D-02 1 9 2 2 0.32657024162728D-14 0.66396704872647D-16 2 9 2 2 -0.47081948433809D-14 -0.10689955559177D-14 3 9 2 2 0.22854053578512D+00 -0.41213474333467D-08 1 10 2 2 0.37924151268483D+00 0.40782168701085D-08 2 10 2 2 -0.92924610258082D-01 -0.68642185139101D-09 3 10 2 2 -0.41145951442353D-14 0.21429895091999D-17 1 11 2 2 -0.21474564783835D+00 -0.47484874404875D-08 2 11 2 2 0.25132987898859D+00 0.17101941985569D-08 3 11 2 2 0.24024880685432D-14 -0.98130468217683D-16 1 12 2 2 -0.16726053255356D-14 0.23997890050725D-16 2 12 2 2 0.31703659452563D-14 -0.25112429686895D-15 3 12 2 2 -0.21683191281968D+00 -0.24383216982534D-08 1 13 2 2 -0.23438760987992D+00 0.19385491922702D-02 2 13 2 2 0.26721322086045D+00 0.67301329828254D-03 3 13 2 2 0.24739921605507D+00 -0.21134327938221D-02 1 14 2 2 -0.36123461004000D+00 0.89515395151993D-08 2 14 2 2 -0.37565111373280D+00 0.64859446310332D-09 3 14 2 2 -0.46771173421879D+00 -0.16008549979356D-07 1 15 2 2 -0.36123461004006D+00 0.89515391424829D-08 2 15 2 2 -0.37565111373277D+00 0.64859472501989D-09 3 15 2 2 0.46771173421886D+00 0.16008550108591D-07 1 16 2 2 0.23438760987994D+00 -0.19385491922693D-02 2 16 2 2 -0.26721322086046D+00 -0.67301329828411D-03 3 16 2 2 0.24739921605509D+00 -0.21134327938200D-02 1 17 2 2 0.34428420488001D+00 -0.37372532707192D-06 2 17 2 2 -0.12389191950372D+00 -0.16777393759868D-07 3 17 2 2 -0.61624736641726D+00 0.73002888118514D-07 1 18 2 2 -0.49549009324290D+00 -0.24006154107443D-01 2 18 2 2 -0.83235442486986D+00 -0.12606854493732D-01 3 18 2 2 -0.86237266963278D+00 0.10810685967263D-01 1 19 2 2 -0.49549009324282D+00 -0.24006154107443D-01 2 19 2 2 -0.83235442486980D+00 -0.12606854493732D-01 3 19 2 2 0.86237266963271D+00 -0.10810685967263D-01 1 20 2 2 -0.34428420488005D+00 0.37372532536252D-06 2 20 2 2 0.12389191950373D+00 0.16777394210876D-07 3 20 2 2 -0.61624736641738D+00 0.73002882396234D-07 1 1 3 2 -0.46547308502683D-01 0.17651323106513D-07 2 1 3 2 0.32776984814127D+00 -0.49739325728261D-08 3 1 3 2 0.74194077318297D-13 0.65894332065475D-14 1 2 3 2 -0.10092276688023D-14 0.11102230246252D-15 2 2 3 2 -0.35241953691242D-13 0.00000000000000D+00 3 2 3 2 0.14867105049052D+02 0.00000000000000D+00 1 3 3 2 0.10961377319982D+01 -0.52693671534309D-08 2 3 3 2 0.47979162914172D-01 0.29035706448336D-08 3 3 3 2 -0.62680075725062D-15 -0.10299177806896D-16 1 4 3 2 -0.20406395509345D-13 0.85946364797072D-16 2 4 3 2 0.40518496297765D-14 -0.14273701576780D-15 3 4 3 2 0.70526463535718D+00 0.35879683966497D-14 1 5 3 2 -0.91957137112215D+00 -0.10141322121640D-01 2 5 3 2 -0.14077544617299D+01 -0.27386350849721D-02 3 5 3 2 0.33718112333215D+00 0.22845026215073D-02 1 6 3 2 -0.91957137112214D+00 -0.10141322121639D-01 2 6 3 2 -0.14077544617299D+01 -0.27386350849672D-02 3 6 3 2 -0.33718112333220D+00 -0.22845026214964D-02 1 7 3 2 0.64607748118077D+01 -0.14372675444750D-01 2 7 3 2 -0.14596092989901D+00 0.46235710956274D-02 3 7 3 2 0.15081770436805D+01 -0.65515176709542D-02 1 8 3 2 0.64607748118076D+01 -0.14372675444768D-01 2 8 3 2 -0.14596092989900D+00 0.46235710956272D-02 3 8 3 2 -0.15081770436805D+01 0.65515176709543D-02 1 9 3 2 -0.12972833328327D+00 -0.97144963739059D-08 2 9 3 2 -0.22769931938120D-01 0.35771731823619D-08 3 9 3 2 -0.12198038638383D-14 -0.19227716117300D-14 1 10 3 2 -0.54279459016276D-14 -0.49881539597266D-15 2 10 3 2 -0.41145951442353D-14 -0.52295852637013D-17 3 10 3 2 0.38255091315881D+01 -0.27557851684439D-07 1 11 3 2 -0.31446858903255D-13 -0.26291784226690D-14 2 11 3 2 0.24024880685432D-14 -0.98130468217683D-16 3 11 3 2 0.64698506258264D+00 -0.67594544271706D-07 1 12 3 2 -0.90846730455017D+00 0.17265959310487D-07 2 12 3 2 0.10613762213919D+00 -0.62670757915063D-08 3 12 3 2 -0.72517773127350D-16 0.16652828872896D-14 1 13 3 2 -0.13585071658991D+01 0.74788430588298D-03 2 13 3 2 -0.16166081741405D+00 0.99471786066703D-03 3 13 3 2 0.21372329087677D+00 -0.37789498105824D-02 1 14 3 2 0.10142403148697D+01 -0.12347783314904D-07 2 14 3 2 0.74400833557551D-02 0.15182190669229D-07 3 14 3 2 -0.17515667442613D+00 -0.10496319420720D-07 1 15 3 2 -0.10142403148698D+01 0.12347787220840D-07 2 15 3 2 -0.74400833556849D-02 -0.15182190539126D-07 3 15 3 2 -0.17515667442623D+00 -0.10496319195399D-07 1 16 3 2 -0.13585071658991D+01 0.74788430587949D-03 2 16 3 2 -0.16166081741404D+00 0.99471786066912D-03 3 16 3 2 -0.21372329087679D+00 0.37789498105808D-02 1 17 3 2 -0.17584629655880D+01 -0.13190429094695D-06 2 17 3 2 -0.16706368605348D+00 0.20213450362757D-06 3 17 3 2 0.30191144601133D+00 -0.48429958564836D-06 1 18 3 2 -0.19271974120562D+00 -0.13899459436934D-01 2 18 3 2 -0.10948572598823D+01 0.12558143074972D-01 3 18 3 2 -0.23982246383876D+01 0.24477481513503D-01 1 19 3 2 0.19271974120556D+00 0.13899459436934D-01 2 19 3 2 0.10948572598822D+01 -0.12558143074973D-01 3 19 3 2 -0.23982246383877D+01 0.24477481513501D-01 1 20 3 2 -0.17584629655882D+01 -0.13190429916133D-06 2 20 3 2 -0.16706368605361D+00 0.20213449790529D-06 3 20 3 2 -0.30191144601152D+00 0.48429957173785D-06 1 1 1 3 0.79792467307875D-01 0.12247162637992D-14 2 1 1 3 -0.40744203557956D-01 0.95371562376899D-09 3 1 1 3 0.16344383944713D-14 -0.81191439531329D-15 1 2 1 3 -0.39922742905444D-14 -0.10873752317695D-16 2 2 1 3 0.14316431129542D-14 -0.39670186937248D-15 3 2 1 3 0.10961377319982D+01 0.52693671534309D-08 1 3 1 3 0.91767034962249D+01 0.00000000000000D+00 2 3 1 3 -0.12531398040086D+01 -0.56687726263018D-06 3 3 1 3 -0.15220082384004D-13 0.11102230246252D-15 1 4 1 3 -0.20825160071597D-13 0.69063136708876D-14 2 4 1 3 -0.62920808125059D-14 -0.18583610323951D-16 3 4 1 3 0.46543269579173D-01 0.12413924290126D-07 1 5 1 3 -0.12798186148453D-01 -0.20891510903242D-01 2 5 1 3 -0.34587762083197D+00 -0.29972506986933D-02 3 5 1 3 -0.68301135923742D+01 0.11263961782594D-02 1 6 1 3 -0.12798186148448D-01 -0.20891510903241D-01 2 6 1 3 -0.34587762083197D+00 -0.29972506986933D-02 3 6 1 3 0.68301135923743D+01 -0.11263961782654D-02 1 7 1 3 0.33543616728584D+01 0.61640066908453D-02 2 7 1 3 0.61161739452682D+00 -0.32014046312435D-03 3 7 1 3 0.24458727958745D+00 0.16465306599683D-01 1 8 1 3 0.33543616728585D+01 0.61640066908423D-02 2 8 1 3 0.61161739452682D+00 -0.32014046312417D-03 3 8 1 3 -0.24458727958744D+00 -0.16465306599683D-01 1 9 1 3 -0.32901829520359D+01 0.72003893468381D-08 2 9 1 3 -0.25502894899908D+00 -0.36554667418686D-08 3 9 1 3 0.13184989953747D-14 0.34369479863956D-14 1 10 1 3 -0.63647133902148D-14 0.12011573580321D-15 2 10 1 3 -0.10788504826081D-14 0.54831451963299D-16 3 10 1 3 0.26506167626628D+01 -0.11469791548904D-07 1 11 1 3 -0.22527190515601D-13 0.10591090309319D-14 2 11 1 3 0.49935882030029D-14 -0.13448788743999D-15 3 11 1 3 0.41289204564321D+00 0.71724834906001D-08 1 12 1 3 -0.13601470966757D+01 0.18283276636190D-07 2 12 1 3 0.18412219540159D+00 -0.17480483209318D-07 3 12 1 3 0.53916139976595D-14 0.61953963228450D-15 1 13 1 3 -0.15275697490881D+01 0.64572596198172D-02 2 13 1 3 -0.11310439235665D+00 0.27092240302348D-01 3 13 1 3 0.25142281874029D+00 -0.69760145231565D-02 1 14 1 3 0.83722932351963D+00 -0.63653622092170D-06 2 14 1 3 0.86353847218527D+00 -0.22690739475855D-06 3 14 1 3 -0.11093678603689D+01 0.28405313636617D-06 1 15 1 3 -0.83722932351959D+00 0.63653622056587D-06 2 15 1 3 -0.86353847218528D+00 0.22690739639850D-06 3 15 1 3 -0.11093678603690D+01 0.28405314319352D-06 1 16 1 3 -0.15275697490882D+01 0.64572596198224D-02 2 16 1 3 -0.11310439235661D+00 0.27092240302348D-01 3 16 1 3 -0.25142281874032D+00 0.69760145231552D-02 1 17 1 3 -0.10668546520188D+01 -0.19841936476932D-08 2 17 1 3 0.62660610534655D+00 -0.22871420617552D-08 3 17 1 3 -0.10785556802537D+01 -0.19449707432838D-07 1 18 1 3 0.66066883358689D+00 0.58092146726282D-02 2 18 1 3 -0.67176802529491D+00 -0.52547534079834D-02 3 18 1 3 -0.80663723739251D+00 0.65285290862625D-02 1 19 1 3 -0.66066883358686D+00 -0.58092146726289D-02 2 19 1 3 0.67176802529489D+00 0.52547534079826D-02 3 19 1 3 -0.80663723739254D+00 0.65285290862636D-02 1 20 1 3 -0.10668546520188D+01 -0.19841934483617D-08 2 20 1 3 0.62660610534656D+00 -0.22871422255868D-08 3 20 1 3 0.10785556802538D+01 0.19449707157508D-07 1 1 2 3 0.40744203558300D-01 0.95371562376899D-09 2 1 2 3 0.37261554587703D+00 0.33999266560255D-14 3 1 2 3 -0.87478955651328D-14 -0.53382358850538D-16 1 2 2 3 0.14316431121270D-14 -0.39496714589651D-15 2 2 2 3 -0.39599946711585D-14 -0.12192355533221D-15 3 2 2 3 0.47979162914172D-01 -0.29035706448336D-08 1 3 2 3 -0.12531378256452D+01 -0.62939489387228D-06 2 3 2 3 0.79896825300148D+01 0.00000000000000D+00 3 3 2 3 -0.56558235764037D-13 0.00000000000000D+00 1 4 2 3 -0.62920808125059D-14 -0.18583610323950D-16 2 4 2 3 -0.79770696192747D-14 -0.88303352593457D-15 3 4 2 3 0.32777068616153D+00 0.60956052606693D-08 1 5 2 3 -0.40942422053722D+00 -0.80965316320268D-02 2 5 2 3 -0.64248236354105D+00 0.39529224498673D-02 3 5 2 3 -0.22612074747940D-01 0.42968796516414D-02 1 6 2 3 -0.40942422053722D+00 -0.80965316320268D-02 2 6 2 3 -0.64248236354105D+00 0.39529224498676D-02 3 6 2 3 0.22612074747945D-01 -0.42968796516413D-02 1 7 2 3 -0.22164045386790D+00 0.15659011129085D-02 2 7 2 3 -0.34356370384058D+01 0.30086279326462D-01 3 7 2 3 0.19740883652862D+01 0.19116697511383D-02 1 8 2 3 -0.22164045386789D+00 0.15659011129087D-02 2 8 2 3 -0.34356370384058D+01 0.30086279326463D-01 3 8 2 3 -0.19740883652862D+01 -0.19116697511380D-02 1 9 2 3 -0.21474564783828D+00 -0.47484920924843D-08 2 9 2 3 -0.25132987898843D+00 -0.17101903477353D-08 3 9 2 3 -0.66081767419820D-15 -0.10594011177242D-15 1 10 2 3 -0.10788504821945D-14 0.56132494570282D-16 2 10 2 3 -0.38931707560140D-14 0.25730489654246D-15 3 10 2 3 -0.21683191281968D+00 -0.24383217497395D-08 1 11 2 3 0.49935103372865D-14 -0.13492156830898D-15 2 11 2 3 0.14789246552123D-13 0.86517812465597D-15 3 11 2 3 0.22854053578514D+00 -0.41213476182782D-08 1 12 2 3 0.37924151268490D+00 0.40782199718882D-08 2 12 2 3 0.92924610258166D-01 0.68640086584035D-09 3 12 2 3 0.21833617236094D-14 0.12799936515614D-15 1 13 2 3 0.49549009324285D+00 0.24006154107443D-01 2 13 2 3 -0.83235442486988D+00 -0.12606854493732D-01 3 13 2 3 -0.86237266963271D+00 0.10810685967263D-01 1 14 2 3 0.34428420488003D+00 -0.37372532533053D-06 2 14 2 3 0.12389191950372D+00 0.16777394971728D-07 3 14 2 3 0.61624736641733D+00 -0.73002882338838D-07 1 15 2 3 -0.34428420488004D+00 0.37372532696700D-06 2 15 2 3 -0.12389191950372D+00 -0.16777393966671D-07 3 15 2 3 0.61624736641730D+00 -0.73002887859725D-07 1 16 2 3 0.49549009324287D+00 0.24006154107443D-01 2 16 2 3 -0.83235442486988D+00 -0.12606854493732D-01 3 16 2 3 0.86237266963271D+00 -0.10810685967263D-01 1 17 2 3 0.36123461004001D+00 -0.89515389157375D-08 2 17 2 3 -0.37565111373281D+00 0.64859472495081D-09 3 17 2 3 -0.46771173421883D+00 -0.16008549872465D-07 1 18 2 3 -0.23438760987995D+00 0.19385491922703D-02 2 18 2 3 -0.26721322086047D+00 -0.67301329828329D-03 3 18 2 3 -0.24739921605511D+00 0.21134327938200D-02 1 19 2 3 0.23438760987993D+00 -0.19385491922711D-02 2 19 2 3 0.26721322086046D+00 0.67301329828225D-03 3 19 2 3 -0.24739921605511D+00 0.21134327938222D-02 1 20 2 3 0.36123461004000D+00 -0.89515390778343D-08 2 20 2 3 -0.37565111373280D+00 0.64859468240187D-09 3 20 2 3 0.46771173421880D+00 0.16008549686772D-07 1 1 3 3 0.16344383944713D-14 -0.81191439531329D-15 2 1 3 3 -0.87478955638920D-14 -0.53382358850538D-16 3 1 3 3 -0.70526463535709D+00 -0.39988058505127D-14 1 2 3 3 0.10961377319982D+01 -0.52693672208851D-08 2 2 3 3 -0.47979162914177D-01 -0.29035706448336D-08 3 2 3 3 -0.62680075725062D-15 0.10299177806896D-16 1 3 3 3 -0.15220082384004D-13 0.11102230246252D-15 2 3 3 3 -0.56558235764037D-13 0.00000000000000D+00 3 3 3 3 0.14867105049052D+02 0.00000000000000D+00 1 4 3 3 0.46547308502706D-01 -0.17651322430711D-07 2 4 3 3 0.32776984814136D+00 -0.49739333267956D-08 3 4 3 3 0.34684521704899D-13 -0.12393493322623D-13 1 5 3 3 -0.64607748118075D+01 0.14372675444755D-01 2 5 3 3 -0.14596092989900D+00 0.46235710956273D-02 3 5 3 3 0.15081770436805D+01 -0.65515176709517D-02 1 6 3 3 0.64607748118076D+01 -0.14372675444761D-01 2 6 3 3 0.14596092989901D+00 -0.46235710956272D-02 3 6 3 3 0.15081770436805D+01 -0.65515176709539D-02 1 7 3 3 -0.91957137112215D+00 -0.10141322121640D-01 2 7 3 3 0.14077544617300D+01 0.27386350849677D-02 3 7 3 3 -0.33718112333236D+00 -0.22845026214857D-02 1 8 3 3 0.91957137112216D+00 0.10141322121640D-01 2 8 3 3 -0.14077544617300D+01 -0.27386350849673D-02 3 8 3 3 -0.33718112333233D+00 -0.22845026214900D-02 1 9 3 3 0.13184989953747D-14 0.34369479863956D-14 2 9 3 3 -0.66081767502538D-15 -0.10594011177242D-15 3 9 3 3 -0.64698506258237D+00 0.67594554071680D-07 1 10 3 3 0.90846730455020D+00 -0.17265957504619D-07 2 10 3 3 0.10613762213919D+00 -0.62670758429924D-08 3 10 3 3 0.21302207907539D-13 -0.12002745031396D-14 1 11 3 3 0.12972833328332D+00 0.97144954515180D-08 2 11 3 3 -0.22769931938100D-01 0.35771729974305D-08 3 11 3 3 0.10886474844336D-13 -0.17208416827371D-14 1 12 3 3 0.53916139976595D-14 0.61953963228450D-15 2 12 3 3 0.21833617207142D-14 0.12062679038324D-15 3 12 3 3 -0.38255091315880D+01 0.27557863511247D-07 1 13 3 3 0.19271974120552D+00 0.13899459436934D-01 2 13 3 3 -0.10948572598822D+01 0.12558143074972D-01 3 13 3 3 -0.23982246383876D+01 0.24477481513504D-01 1 14 3 3 -0.17584629655881D+01 -0.13190429793942D-06 2 14 3 3 0.16706368605354D+00 -0.20213449784616D-06 3 14 3 3 -0.30191144601141D+00 0.48429957261514D-06 1 15 3 3 -0.17584629655882D+01 -0.13190429111033D-06 2 15 3 3 0.16706368605352D+00 -0.20213450336705D-06 3 15 3 3 0.30191144601141D+00 -0.48429958462757D-06 1 16 3 3 -0.19271974120553D+00 -0.13899459436936D-01 2 16 3 3 0.10948572598822D+01 -0.12558143074972D-01 3 16 3 3 -0.23982246383876D+01 0.24477481513503D-01 1 17 3 3 -0.10142403148697D+01 0.12347785384874D-07 2 17 3 3 0.74400833557133D-02 0.15182190775253D-07 3 17 3 3 -0.17515667442618D+00 -0.10496317091143D-07 1 18 3 3 -0.13585071658991D+01 0.74788430588153D-03 2 18 3 3 0.16166081741401D+00 -0.99471786066918D-03 3 18 3 3 -0.21372329087677D+00 0.37789498105771D-02 1 19 3 3 -0.13585071658991D+01 0.74788430588267D-03 2 19 3 3 0.16166081741401D+00 -0.99471786066692D-03 3 19 3 3 0.21372329087681D+00 -0.37789498105838D-02 1 20 3 3 0.10142403148698D+01 -0.12347785657602D-07 2 20 3 3 -0.74400833557409D-02 -0.15182190961813D-07 3 20 3 3 -0.17515667442619D+00 -0.10496318065875D-07 1 1 1 4 0.49356013477347D-14 -0.36011595342229D-16 2 1 1 4 0.42963835390927D-14 0.70803473743525D-16 3 1 1 4 -0.10961377319982D+01 -0.52693682479087D-08 1 2 1 4 -0.79792467307858D-01 0.14238535102920D-14 2 2 1 4 0.40744203558108D-01 -0.95371580377885D-09 3 2 1 4 -0.20406395509345D-13 -0.85946364797072D-16 1 3 1 4 -0.20825160071545D-13 -0.69054463091496D-14 2 3 1 4 -0.62920808129195D-14 0.18583610323950D-16 3 3 1 4 0.46543269579173D-01 0.12413923389125D-07 1 4 1 4 0.91767034962249D+01 0.00000000000000D+00 2 4 1 4 -0.12531398040088D+01 -0.56687726263018D-06 3 4 1 4 -0.22325509741605D-13 0.11102230246252D-15 1 5 1 4 -0.12798186148417D-01 -0.20891510903254D-01 2 5 1 4 -0.34587762083194D+00 -0.29972506986945D-02 3 5 1 4 -0.68301135923743D+01 0.11263961782478D-02 1 6 1 4 0.12798186148382D-01 0.20891510903252D-01 2 6 1 4 0.34587762083193D+00 0.29972506986927D-02 3 6 1 4 -0.68301135923743D+01 0.11263961782604D-02 1 7 1 4 -0.33543616728584D+01 -0.61640066908421D-02 2 7 1 4 -0.61161739452682D+00 0.32014046312428D-03 3 7 1 4 -0.24458727958741D+00 -0.16465306599681D-01 1 8 1 4 0.33543616728584D+01 0.61640066908358D-02 2 8 1 4 0.61161739452682D+00 -0.32014046312434D-03 3 8 1 4 -0.24458727958742D+00 -0.16465306599681D-01 1 9 1 4 -0.22951993546343D-14 -0.58254517231871D-15 2 9 1 4 -0.28664440083696D-14 -0.30632263198980D-16 3 9 1 4 0.26506167626628D+01 -0.11469794547727D-07 1 10 1 4 -0.32901829520357D+01 0.72003780813798D-08 2 10 1 4 -0.25502894899901D+00 -0.36554649035413D-08 3 10 1 4 -0.15736440797375D-13 0.63758046449103D-15 1 11 1 4 -0.13601470966757D+01 0.18283276155813D-07 2 11 1 4 0.18412219540174D+00 -0.17480483297134D-07 3 11 1 4 -0.40921129048382D-14 0.12470532856663D-14 1 12 1 4 -0.63361902729571D-14 0.21393717055070D-14 2 12 1 4 0.61750361084490D-14 -0.43916642443632D-16 3 12 1 4 0.41289204564321D+00 0.71724847336016D-08 1 13 1 4 0.83722932351964D+00 -0.63653622607135D-06 2 13 1 4 0.86353847218524D+00 -0.22690739862683D-06 3 13 1 4 -0.11093678603688D+01 0.28405314997881D-06 1 14 1 4 -0.15275697490880D+01 0.64572596198214D-02 2 14 1 4 -0.11310439235659D+00 0.27092240302348D-01 3 14 1 4 0.25142281874035D+00 -0.69760145231549D-02 1 15 1 4 -0.15275697490881D+01 0.64572596198174D-02 2 15 1 4 -0.11310439235671D+00 0.27092240302348D-01 3 15 1 4 -0.25142281874029D+00 0.69760145231563D-02 1 16 1 4 -0.83722932351963D+00 0.63653622281854D-06 2 16 1 4 -0.86353847218530D+00 0.22690739634226D-06 3 16 1 4 -0.11093678603689D+01 0.28405314305627D-06 1 17 1 4 0.66066883358687D+00 0.58092146726304D-02 2 17 1 4 -0.67176802529491D+00 -0.52547534079819D-02 3 17 1 4 -0.80663723739254D+00 0.65285290862657D-02 1 18 1 4 -0.10668546520188D+01 -0.19841928713043D-08 2 18 1 4 0.62660610534651D+00 -0.22871427140193D-08 3 18 1 4 -0.10785556802537D+01 -0.19449708311280D-07 1 19 1 4 -0.10668546520188D+01 -0.19841935642511D-08 2 19 1 4 0.62660610534657D+00 -0.22871426411723D-08 3 19 1 4 0.10785556802537D+01 0.19449705339428D-07 1 20 1 4 -0.66066883358687D+00 -0.58092146726290D-02 2 20 1 4 0.67176802529491D+00 0.52547534079833D-02 3 20 1 4 -0.80663723739252D+00 0.65285290862628D-02 1 1 2 4 0.42963835382655D-14 0.69068750267548D-16 2 1 2 4 0.20235621669531D-14 -0.20381685200383D-15 3 1 2 4 -0.47979162914179D-01 0.29035711258190D-08 1 2 2 4 -0.40744203558148D-01 -0.95371580377885D-09 2 2 2 4 -0.37261554587709D+00 0.22954667435828D-14 3 2 2 4 0.40518496297765D-14 0.14273701576780D-15 1 3 2 4 -0.62920808125059D-14 0.18583610323951D-16 2 3 2 4 -0.79770696192747D-14 0.88346720680356D-15 3 3 2 4 0.32777068616153D+00 0.60956063265271D-08 1 4 2 4 -0.12531378256455D+01 -0.62939489387228D-06 2 4 2 4 0.79896825300148D+01 0.00000000000000D+00 3 4 2 4 0.81997597709174D-13 0.00000000000000D+00 1 5 2 4 -0.40942422053719D+00 -0.80965316320280D-02 2 5 2 4 -0.64248236354107D+00 0.39529224498700D-02 3 5 2 4 -0.22612074747935D-01 0.42968796516403D-02 1 6 2 4 0.40942422053718D+00 0.80965316320262D-02 2 6 2 4 0.64248236354109D+00 -0.39529224498709D-02 3 6 2 4 -0.22612074747928D-01 0.42968796516402D-02 1 7 2 4 0.22164045386790D+00 -0.15659011129086D-02 2 7 2 4 0.34356370384060D+01 -0.30086279326454D-01 3 7 2 4 -0.19740883652861D+01 -0.19116697511432D-02 1 8 2 4 -0.22164045386789D+00 0.15659011129085D-02 2 8 2 4 -0.34356370384059D+01 0.30086279326462D-01 3 8 2 4 -0.19740883652861D+01 -0.19116697511385D-02 1 9 2 4 -0.28664440079560D-14 -0.29331220591997D-16 2 9 2 4 -0.62948263564015D-14 0.25672667919329D-15 3 9 2 4 -0.21683191281967D+00 -0.24383217810423D-08 1 10 2 4 -0.21474564783821D+00 -0.47484902541570D-08 2 10 2 4 -0.25132987898857D+00 -0.17101881229518D-08 3 10 2 4 0.42408843537406D-14 0.82426745566736D-16 1 11 2 4 0.37924151268506D+00 0.40782198840727D-08 2 11 2 4 0.92924610257853D-01 0.68640103721148D-09 3 11 2 4 -0.18174883957910D-14 -0.21815450868830D-15 1 12 2 4 0.61749582429395D-14 -0.43916642443632D-16 2 12 2 4 0.20458013182142D-13 0.63228865952766D-15 3 12 2 4 0.22854053578510D+00 -0.41213476158576D-08 1 13 2 4 0.34428420488000D+00 -0.37372532919880D-06 2 13 2 4 0.12389191950369D+00 0.16777393022930D-07 3 13 2 4 0.61624736641726D+00 -0.73002893090891D-07 1 14 2 4 0.49549009324290D+00 0.24006154107443D-01 2 14 2 4 -0.83235442486996D+00 -0.12606854493732D-01 3 14 2 4 -0.86237266963281D+00 0.10810685967263D-01 1 15 2 4 0.49549009324277D+00 0.24006154107443D-01 2 15 2 4 -0.83235442486991D+00 -0.12606854493732D-01 3 15 2 4 0.86237266963265D+00 -0.10810685967263D-01 1 16 2 4 -0.34428420488006D+00 0.37372532691077D-06 2 16 2 4 -0.12389191950372D+00 -0.16777392391038D-07 3 16 2 4 0.61624736641738D+00 -0.73002887815823D-07 1 17 2 4 -0.23438760987995D+00 0.19385491922718D-02 2 17 2 4 -0.26721322086045D+00 -0.67301329828096D-03 3 17 2 4 -0.24739921605512D+00 0.21134327938247D-02 1 18 2 4 0.36123461003998D+00 -0.89515395680016D-08 2 18 2 4 -0.37565111373282D+00 0.64859480067568D-09 3 18 2 4 -0.46771173421874D+00 -0.16008550178575D-07 1 19 2 4 0.36123461004001D+00 -0.89515394934198D-08 2 19 2 4 -0.37565111373279D+00 0.64859460150449D-09 3 19 2 4 0.46771173421880D+00 0.16008549906206D-07 1 20 2 4 0.23438760987996D+00 -0.19385491922704D-02 2 20 2 4 0.26721322086048D+00 0.67301329828208D-03 3 20 2 4 -0.24739921605510D+00 0.21134327938221D-02 1 1 3 4 -0.10961377319982D+01 0.52693661264073D-08 2 1 3 4 0.47979162914170D-01 0.29035711258190D-08 3 1 3 4 0.71970343856284D-14 -0.49053747047667D-16 1 2 3 4 -0.20406395509345D-13 -0.85946364797072D-16 2 2 3 4 0.40518496310173D-14 0.14273701576780D-15 3 2 3 4 0.70526463535718D+00 -0.35879683966497D-14 1 3 3 4 0.46547308502706D-01 -0.17651323331712D-07 2 3 3 4 0.32776984814135D+00 -0.49739322609377D-08 3 3 3 4 0.34684521704899D-13 0.12392625960885D-13 1 4 3 4 -0.22325509741605D-13 0.11102230246252D-15 2 4 3 4 0.81997597709174D-13 0.00000000000000D+00 3 4 3 4 0.14867105049052D+02 0.00000000000000D+00 1 5 3 4 -0.64607748118077D+01 0.14372675444743D-01 2 5 3 4 -0.14596092989900D+00 0.46235710956262D-02 3 5 3 4 0.15081770436805D+01 -0.65515176709594D-02 1 6 3 4 -0.64607748118076D+01 0.14372675444756D-01 2 6 3 4 -0.14596092989899D+00 0.46235710956261D-02 3 6 3 4 -0.15081770436806D+01 0.65515176709629D-02 1 7 3 4 0.91957137112218D+00 0.10141322121641D-01 2 7 3 4 -0.14077544617299D+01 -0.27386350849726D-02 3 7 3 4 0.33718112333215D+00 0.22845026215060D-02 1 8 3 4 0.91957137112217D+00 0.10141322121641D-01 2 8 3 4 -0.14077544617300D+01 -0.27386350849679D-02 3 8 3 4 -0.33718112333224D+00 -0.22845026215031D-02 1 9 3 4 0.90846730455020D+00 -0.17265960503443D-07 2 9 3 4 0.10613762213919D+00 -0.62670758742952D-08 3 9 3 4 0.14270743538244D-13 0.88236325091029D-15 1 10 3 4 -0.15736440797375D-13 0.63758046449103D-15 2 10 3 4 0.42408843537406D-14 0.82426745566736D-16 3 10 3 4 -0.64698506258274D+00 0.67594556878523D-07 1 11 3 4 -0.40921129048382D-14 0.12470532856663D-14 2 11 3 4 -0.18174884003405D-14 -0.22552708346120D-15 3 11 3 4 -0.38255091315878D+01 0.27557862603231D-07 1 12 3 4 0.12972833328332D+00 0.97144966945195D-08 2 12 3 4 -0.22769931938134D-01 0.35771729998511D-08 3 12 3 4 0.24714361946420D-14 0.18768375064151D-14 1 13 3 4 -0.17584629655880D+01 -0.13190428432330D-06 2 13 3 4 0.16706368605347D+00 -0.20213450859821D-06 3 13 3 4 -0.30191144601133D+00 0.48429959661434D-06 1 14 3 4 0.19271974120558D+00 0.13899459436936D-01 2 14 3 4 -0.10948572598823D+01 0.12558143074973D-01 3 14 3 4 -0.23982246383876D+01 0.24477481513504D-01 1 15 3 4 -0.19271974120550D+00 -0.13899459436935D-01 2 15 3 4 0.10948572598821D+01 -0.12558143074972D-01 3 15 3 4 -0.23982246383877D+01 0.24477481513505D-01 1 16 3 4 -0.17584629655881D+01 -0.13190429124758D-06 2 16 3 4 0.16706368605360D+00 -0.20213450332315D-06 3 16 3 4 0.30191144601152D+00 -0.48429958888994D-06 1 17 3 4 -0.13585071658991D+01 0.74788430588470D-03 2 17 3 4 0.16166081741401D+00 -0.99471786066447D-03 3 17 3 4 -0.21372329087681D+00 0.37789498105875D-02 1 18 3 4 -0.10142403148697D+01 0.12347784506432D-07 2 18 3 4 0.74400833557986D-02 0.15182190469143D-07 3 18 3 4 -0.17515667442617D+00 -0.10496318979689D-07 1 19 3 4 0.10142403148697D+01 -0.12347787475682D-07 2 19 3 4 -0.74400833557409D-02 -0.15182190742379D-07 3 19 3 4 -0.17515667442625D+00 -0.10496319381798D-07 1 20 3 4 -0.13585071658991D+01 0.74788430588178D-03 2 20 3 4 0.16166081741401D+00 -0.99471786066701D-03 3 20 3 4 0.21372329087680D+00 -0.37789498105818D-02 1 1 1 5 0.33543626171697D+01 -0.61631118258643D-02 2 1 1 5 0.22163936393642D+00 0.15650509672711D-02 3 1 1 5 0.91957351167256D+00 -0.10142032844979D-01 1 2 1 5 -0.33543626171698D+01 0.61631118258688D-02 2 2 1 5 -0.22163936393640D+00 -0.15650509672713D-02 3 2 1 5 -0.91957351167256D+00 0.10142032844978D-01 1 3 1 5 -0.12798186148453D-01 0.20891510903242D-01 2 3 1 5 -0.40942422053722D+00 0.80965316320268D-02 3 3 1 5 -0.64607748118075D+01 -0.14372675444755D-01 1 4 1 5 -0.12798186148417D-01 0.20891510903254D-01 2 4 1 5 -0.40942422053719D+00 0.80965316320280D-02 3 4 1 5 -0.64607748118077D+01 -0.14372675444743D-01 1 5 1 5 0.25854593827377D+02 0.00000000000000D+00 2 5 1 5 -0.51875643189908D+00 -0.70447379816915D-07 3 5 1 5 -0.17386615460774D+01 -0.34462456922810D-07 1 6 1 5 -0.76974651472566D-13 -0.26797765493737D-14 2 6 1 5 -0.17375529140859D-17 -0.15954928323413D-15 3 6 1 5 0.10121082778377D-16 -0.18159229443740D-14 1 7 1 5 0.48819177293273D-14 -0.22448155728790D-15 2 7 1 5 -0.16456043337165D-14 0.93089458287226D-15 3 7 1 5 0.36226197631479D-19 -0.39892330160386D-14 1 8 1 5 -0.17299159085149D+01 0.32249771395310D-09 2 8 1 5 -0.39502714767077D+00 0.22773438928422D-08 3 8 1 5 -0.88371231839109D+01 0.63278688119106D-09 1 9 1 5 -0.27925764469562D+01 0.97198643229883D+00 2 9 1 5 -0.11197478486125D+00 -0.24155486835260D-01 3 9 1 5 -0.17498303511795D+00 -0.44483826156623D+00 1 10 1 5 -0.27925764469558D+01 0.97198643229881D+00 2 10 1 5 -0.11197478486124D+00 -0.24155486835261D-01 3 10 1 5 -0.17498303511783D+00 -0.44483826156620D+00 1 11 1 5 -0.36134755383845D+00 -0.14193648446026D-01 2 11 1 5 0.19019581456350D+00 -0.15482127518059D-02 3 11 1 5 0.68906983096762D+01 0.18296233989491D+00 1 12 1 5 -0.36134755383845D+00 -0.14193648446027D-01 2 12 1 5 0.19019581456357D+00 -0.15482127518063D-02 3 12 1 5 0.68906983096762D+01 0.18296233989490D+00 1 13 1 5 0.51358465400043D+01 -0.13475394102436D-01 2 13 1 5 0.14573935793101D+01 -0.13077479710832D-01 3 13 1 5 -0.55414460510230D+00 0.45931930924360D-01 1 14 1 5 0.51358465400042D+01 -0.13475394102433D-01 2 14 1 5 0.14573935793100D+01 -0.13077479710833D-01 3 14 1 5 -0.55414460510188D+00 0.45931930924362D-01 1 15 1 5 0.73418429166608D+00 -0.27675484520819D-01 2 15 1 5 0.20463990501138D+00 -0.34349079966531D-01 3 15 1 5 0.18464602830797D+01 -0.13801012644521D-01 1 16 1 5 0.73418429166610D+00 -0.27675484520816D-01 2 16 1 5 0.20463990501136D+00 -0.34349079966531D-01 3 16 1 5 0.18464602830797D+01 -0.13801012644520D-01 1 17 1 5 0.46510512037135D+01 -0.15901986239630D-01 2 17 1 5 -0.24317149100596D+01 0.21193322633168D-01 3 17 1 5 -0.54457476066144D+00 0.32243085944312D-01 1 18 1 5 0.46510512037136D+01 -0.15901986239629D-01 2 18 1 5 -0.24317149100598D+01 0.21193322633168D-01 3 18 1 5 -0.54457476066137D+00 0.32243085944316D-01 1 19 1 5 0.64261459815117D+00 -0.39033970235500D-01 2 19 1 5 -0.40576584135339D+00 0.10221387364992D+00 3 19 1 5 0.11749799206645D+01 -0.16783113070778D-01 1 20 1 5 0.64261459815121D+00 -0.39033970235501D-01 2 20 1 5 -0.40576584135338D+00 0.10221387364992D+00 3 20 1 5 0.11749799206645D+01 -0.16783113070779D-01 1 1 2 5 -0.61161652853125D+00 -0.31960623911220D-03 2 1 2 5 -0.34356341081678D+01 -0.30086513295990D-01 3 1 2 5 0.14077523970497D+01 -0.27382922036715D-02 1 2 2 5 0.61161652853126D+00 0.31960623911201D-03 2 2 2 5 0.34356341081678D+01 0.30086513295980D-01 3 2 2 5 -0.14077523970499D+01 0.27382922036760D-02 1 3 2 5 -0.34587762083197D+00 0.29972506986933D-02 2 3 2 5 -0.64248236354105D+00 -0.39529224498673D-02 3 3 2 5 -0.14596092989900D+00 -0.46235710956273D-02 1 4 2 5 -0.34587762083194D+00 0.29972506986945D-02 2 4 2 5 -0.64248236354107D+00 -0.39529224498700D-02 3 4 2 5 -0.14596092989900D+00 -0.46235710956262D-02 1 5 2 5 -0.51874875056767D+00 0.75153692136189D-07 2 5 2 5 0.17749688782662D+02 0.00000000000000D+00 3 5 2 5 -0.26437063705518D+01 0.27852658405213D-06 1 6 2 5 -0.17375529140859D-17 -0.15954928323413D-15 2 6 2 5 -0.23241732853137D-13 0.17997235496011D-14 3 6 2 5 0.69705558204505D-14 0.42806344822323D-15 1 7 2 5 -0.16456045730301D-14 0.93089458287226D-15 2 7 2 5 -0.19283011950047D-13 -0.47527134207975D-14 3 7 2 5 0.17526000489566D-19 -0.26729417526995D-15 1 8 2 5 0.39503222974707D+00 0.21700655604290D-08 2 8 2 5 0.40361010132440D+00 -0.26596227849753D-10 3 8 2 5 0.11692820874661D+01 -0.81244195761089D-08 1 9 2 5 0.51572162110190D-01 -0.20203243078611D-01 2 9 2 5 -0.14158884176234D+01 0.10221399323969D+01 3 9 2 5 0.11342645015602D+00 0.94682794168435D-01 1 10 2 5 0.51572162110203D-01 -0.20203243078612D-01 2 10 2 5 -0.14158884176231D+01 0.10221399323969D+01 3 10 2 5 0.11342645015620D+00 0.94682794168426D-01 1 11 2 5 0.13656873541772D+00 0.32873551971116D-02 2 11 2 5 0.15321258205104D+00 0.26097329654379D-02 3 11 2 5 -0.10794854753982D+01 -0.29037904891686D-01 1 12 2 5 0.13656873541779D+00 0.32873551971112D-02 2 12 2 5 0.15321258205105D+00 0.26097329654351D-02 3 12 2 5 -0.10794854753981D+01 -0.29037904891687D-01 1 13 2 5 -0.53369586582183D+00 0.96338579716757D-02 2 13 2 5 0.91069035316952D-01 0.22412026742566D-02 3 13 2 5 -0.95921967565682D+00 0.36210872683385D-01 1 14 2 5 -0.53369586582193D+00 0.96338579716746D-02 2 14 2 5 0.91069035317130D-01 0.22412026742581D-02 3 14 2 5 -0.95921967565661D+00 0.36210872683386D-01 1 15 2 5 -0.15938290873738D+00 -0.20789309500503D-01 2 15 2 5 -0.16252001627054D+00 -0.11416271009605D-01 3 15 2 5 0.25795522233826D+00 -0.51648474989793D-02 1 16 2 5 -0.15938290873740D+00 -0.20789309500504D-01 2 16 2 5 -0.16252001627054D+00 -0.11416271009604D-01 3 16 2 5 0.25795522233825D+00 -0.51648474989787D-02 1 17 2 5 0.68345312777832D+00 0.97797549474612D-02 2 17 2 5 0.12131103227846D+01 -0.78851080443718D-02 3 17 2 5 0.83142332788891D+00 -0.63777950819961D-01 1 18 2 5 0.68345312777808D+00 0.97797549474616D-02 2 18 2 5 0.12131103227848D+01 -0.78851080443711D-02 3 18 2 5 0.83142332788884D+00 -0.63777950819960D-01 1 19 2 5 -0.15300585868729D+00 0.77026585835272D-01 2 19 2 5 0.24422371225416D-01 -0.10412436341650D+00 3 19 2 5 -0.39263801672989D+00 0.36582536478171D-01 1 20 2 5 -0.15300585868729D+00 0.77026585835272D-01 2 20 2 5 0.24422371225418D-01 -0.10412436341650D+00 3 20 2 5 -0.39263801672990D+00 0.36582536478170D-01 1 1 3 5 -0.24458784879502D+00 0.16466022068859D-01 2 1 3 5 0.19740873466911D+01 -0.19120570588220D-02 3 1 3 5 -0.33717690951946D+00 0.22842629006431D-02 1 2 3 5 0.24458784879502D+00 -0.16466022068859D-01 2 2 3 5 -0.19740873466913D+01 0.19120570588265D-02 3 2 3 5 0.33717690951936D+00 -0.22842629006532D-02 1 3 3 5 -0.68301135923742D+01 -0.11263961782594D-02 2 3 3 5 -0.22612074747940D-01 -0.42968796516414D-02 3 3 3 5 0.15081770436805D+01 0.65515176709517D-02 1 4 3 5 -0.68301135923743D+01 -0.11263961782478D-02 2 4 3 5 -0.22612074747935D-01 -0.42968796516403D-02 3 4 3 5 0.15081770436805D+01 0.65515176709594D-02 1 5 3 5 -0.17386556980803D+01 0.67741031509177D-07 2 5 3 5 -0.26437231096067D+01 -0.31039695107410D-06 3 5 3 5 0.46577374571396D+02 0.00000000000000D+00 1 6 3 5 -0.23172268514947D-16 -0.18159229443740D-14 2 6 3 5 0.69801441511090D-14 0.42806344822323D-15 3 6 3 5 0.33446938637314D-12 -0.10643224439598D-13 1 7 3 5 0.36425031170828D-19 -0.39892330160386D-14 2 7 3 5 0.17525987564868D-19 -0.26729417526995D-15 3 7 3 5 0.61873397449803D-14 0.28116003165862D-14 1 8 3 5 -0.88371213354321D+01 0.26774342346765D-09 2 8 3 5 -0.11692768811688D+01 -0.89404802564830D-08 3 8 3 5 0.35642461447620D+01 0.28963997077231D-09 1 9 3 5 -0.10852882265972D+01 -0.44291984871116D+00 2 9 3 5 0.38823622062824D+00 0.10808312793810D+00 3 9 3 5 -0.78131065789739D+01 -0.22829416715194D+01 1 10 3 5 -0.10852882265971D+01 -0.44291984871113D+00 2 10 3 5 0.38823622062842D+00 0.10808312793810D+00 3 10 3 5 -0.78131065789748D+01 -0.22829416715192D+01 1 11 3 5 0.18848320615518D+01 0.30947067888418D-01 2 11 3 5 0.58900100571392D-01 0.73454160392630D-02 3 11 3 5 -0.22077548035897D+01 0.98614898976904D-02 1 12 3 5 0.18848320615518D+01 0.30947067888414D-01 2 12 3 5 0.58900100571425D-01 0.73454160392627D-02 3 12 3 5 -0.22077548035897D+01 0.98614898976870D-02 1 13 3 5 -0.49749725110218D+00 0.40968419484890D-01 2 13 3 5 -0.78860554444012D+00 0.48876454191928D-01 3 13 3 5 0.38543560558657D+01 -0.24962800375827D-01 1 14 3 5 -0.49749725110176D+00 0.40968419484892D-01 2 14 3 5 -0.78860554443992D+00 0.48876454191928D-01 3 14 3 5 0.38543560558659D+01 -0.24962800375829D-01 1 15 3 5 0.42221527349252D+01 -0.10684640142366D-01 2 15 3 5 0.28426666852924D+01 -0.45046507557076D-02 3 15 3 5 -0.30555578378940D+00 0.15861160436607D-01 1 16 3 5 0.42221527349252D+01 -0.10684640142365D-01 2 16 3 5 0.28426666852924D+01 -0.45046507557070D-02 3 16 3 5 -0.30555578378939D+00 0.15861160436609D-01 1 17 3 5 -0.62141502835395D+00 0.50205480190904D-01 2 17 3 5 0.77267282968485D+00 -0.64486680591534D-01 3 17 3 5 0.43358483535489D+01 -0.26942192371730D-01 1 18 3 5 -0.62141502835388D+00 0.50205480190907D-01 2 18 3 5 0.77267282968477D+00 -0.64486680591534D-01 3 18 3 5 0.43358483535486D+01 -0.26942192371729D-01 1 19 3 5 0.38966689520463D+01 -0.11517327971764D-01 2 19 3 5 -0.30359965124749D+01 0.79445211495148D-02 3 19 3 5 -0.20019502751876D+00 0.74632616766795D-01 1 20 3 5 0.38966689520464D+01 -0.11517327971764D-01 2 20 3 5 -0.30359965124750D+01 0.79445211495140D-02 3 20 3 5 -0.20019502751878D+00 0.74632616766796D-01 1 1 1 6 0.33543626171697D+01 -0.61631118258663D-02 2 1 1 6 0.22163936393641D+00 0.15650509672715D-02 3 1 1 6 -0.91957351167257D+00 0.10142032844979D-01 1 2 1 6 0.33543626171698D+01 -0.61631118258673D-02 2 2 1 6 0.22163936393641D+00 0.15650509672713D-02 3 2 1 6 -0.91957351167255D+00 0.10142032844977D-01 1 3 1 6 -0.12798186148448D-01 0.20891510903241D-01 2 3 1 6 -0.40942422053722D+00 0.80965316320268D-02 3 3 1 6 0.64607748118076D+01 0.14372675444761D-01 1 4 1 6 0.12798186148382D-01 -0.20891510903252D-01 2 4 1 6 0.40942422053718D+00 -0.80965316320262D-02 3 4 1 6 -0.64607748118076D+01 -0.14372675444756D-01 1 5 1 6 -0.76974651472566D-13 0.26797765493737D-14 2 5 1 6 -0.17375529140857D-17 0.15954928323413D-15 3 5 1 6 -0.23172268514947D-16 0.18159229443740D-14 1 6 1 6 0.25854593827376D+02 0.00000000000000D+00 2 6 1 6 -0.51875643189903D+00 -0.70447379816915D-07 3 6 1 6 0.17386615460776D+01 0.34462456922810D-07 1 7 1 6 -0.17299159085149D+01 0.32249771395310D-09 2 7 1 6 -0.39502714767077D+00 0.22773438928422D-08 3 7 1 6 0.88371231839109D+01 -0.63278571745126D-09 1 8 1 6 0.42851545084963D-13 -0.22448155728790D-15 2 8 1 6 -0.16456043634446D-14 0.93089458287226D-15 3 8 1 6 0.42593284572103D-13 -0.39892330160386D-14 1 9 1 6 -0.27925764469562D+01 0.97198643229884D+00 2 9 1 6 -0.11197478486126D+00 -0.24155486835259D-01 3 9 1 6 0.17498303511793D+00 0.44483826156623D+00 1 10 1 6 0.27925764469559D+01 -0.97198643229882D+00 2 10 1 6 0.11197478486124D+00 0.24155486835260D-01 3 10 1 6 -0.17498303511773D+00 -0.44483826156622D+00 1 11 1 6 0.36134755383845D+00 0.14193648446025D-01 2 11 1 6 -0.19019581456349D+00 0.15482127518061D-02 3 11 1 6 0.68906983096763D+01 0.18296233989490D+00 1 12 1 6 -0.36134755383845D+00 -0.14193648446026D-01 2 12 1 6 0.19019581456357D+00 -0.15482127518064D-02 3 12 1 6 -0.68906983096763D+01 -0.18296233989490D+00 1 13 1 6 0.73418429166609D+00 -0.27675484520820D-01 2 13 1 6 0.20463990501137D+00 -0.34349079966531D-01 3 13 1 6 -0.18464602830797D+01 0.13801012644521D-01 1 14 1 6 -0.73418429166607D+00 0.27675484520820D-01 2 14 1 6 -0.20463990501137D+00 0.34349079966532D-01 3 14 1 6 0.18464602830797D+01 -0.13801012644522D-01 1 15 1 6 -0.51358465400042D+01 0.13475394102414D-01 2 15 1 6 -0.14573935793099D+01 0.13077479710809D-01 3 15 1 6 -0.55414460510186D+00 0.45931930924343D-01 1 16 1 6 0.51358465400043D+01 -0.13475394102435D-01 2 16 1 6 0.14573935793101D+01 -0.13077479710832D-01 3 16 1 6 0.55414460510228D+00 -0.45931930924365D-01 1 17 1 6 0.64261459815120D+00 -0.39033970235498D-01 2 17 1 6 -0.40576584135339D+00 0.10221387364992D+00 3 17 1 6 -0.11749799206646D+01 0.16783113070779D-01 1 18 1 6 -0.64261459815117D+00 0.39033970235501D-01 2 18 1 6 0.40576584135339D+00 -0.10221387364992D+00 3 18 1 6 0.11749799206646D+01 -0.16783113070780D-01 1 19 1 6 -0.46510512037136D+01 0.15901986239626D-01 2 19 1 6 0.24317149100597D+01 -0.21193322633146D-01 3 19 1 6 -0.54457476066135D+00 0.32243085944308D-01 1 20 1 6 0.46510512037136D+01 -0.15901986239630D-01 2 20 1 6 -0.24317149100597D+01 0.21193322633168D-01 3 20 1 6 0.54457476066144D+00 -0.32243085944313D-01 1 1 2 6 -0.61161652853126D+00 -0.31960623911178D-03 2 1 2 6 -0.34356341081677D+01 -0.30086513295986D-01 3 1 2 6 -0.14077523970497D+01 0.27382922036708D-02 1 2 2 6 -0.61161652853126D+00 -0.31960623911206D-03 2 2 2 6 -0.34356341081678D+01 -0.30086513295988D-01 3 2 2 6 -0.14077523970499D+01 0.27382922036711D-02 1 3 2 6 -0.34587762083197D+00 0.29972506986933D-02 2 3 2 6 -0.64248236354105D+00 -0.39529224498676D-02 3 3 2 6 0.14596092989901D+00 0.46235710956272D-02 1 4 2 6 0.34587762083193D+00 -0.29972506986927D-02 2 4 2 6 0.64248236354109D+00 0.39529224498709D-02 3 4 2 6 -0.14596092989899D+00 -0.46235710956261D-02 1 5 2 6 -0.17375529140859D-17 0.15954928323413D-15 2 5 2 6 -0.23241732853137D-13 -0.17997235496011D-14 3 5 2 6 0.69801441511090D-14 -0.42806344822323D-15 1 6 2 6 -0.51874875056762D+00 0.75153692136189D-07 2 6 2 6 0.17749688782662D+02 0.00000000000000D+00 3 6 2 6 0.26437063705518D+01 -0.27852658405213D-06 1 7 2 6 0.39503222974707D+00 0.21700655604290D-08 2 7 2 6 0.40361010132440D+00 -0.26596227849753D-10 3 7 2 6 -0.11692820874661D+01 0.81244195761089D-08 1 8 2 6 -0.16456046027583D-14 0.93089458287226D-15 2 8 2 6 -0.72926032915415D-14 -0.47527134207975D-14 3 8 2 6 0.17469721128464D-14 -0.26729417526995D-15 1 9 2 6 0.51572162110184D-01 -0.20203243078611D-01 2 9 2 6 -0.14158884176234D+01 0.10221399323969D+01 3 9 2 6 -0.11342645015603D+00 -0.94682794168434D-01 1 10 2 6 -0.51572162110197D-01 0.20203243078611D-01 2 10 2 6 0.14158884176232D+01 -0.10221399323969D+01 3 10 2 6 0.11342645015617D+00 0.94682794168430D-01 1 11 2 6 -0.13656873541771D+00 -0.32873551971114D-02 2 11 2 6 -0.15321258205105D+00 -0.26097329654372D-02 3 11 2 6 -0.10794854753982D+01 -0.29037904891686D-01 1 12 2 6 0.13656873541779D+00 0.32873551971111D-02 2 12 2 6 0.15321258205105D+00 0.26097329654356D-02 3 12 2 6 0.10794854753981D+01 0.29037904891687D-01 1 13 2 6 -0.15938290873739D+00 -0.20789309500504D-01 2 13 2 6 -0.16252001627054D+00 -0.11416271009605D-01 3 13 2 6 -0.25795522233825D+00 0.51648474989791D-02 1 14 2 6 0.15938290873739D+00 0.20789309500504D-01 2 14 2 6 0.16252001627054D+00 0.11416271009605D-01 3 14 2 6 0.25795522233826D+00 -0.51648474989799D-02 1 15 2 6 0.53369586582198D+00 -0.96338579716982D-02 2 15 2 6 -0.91069035317151D-01 -0.22412026742627D-02 3 15 2 6 -0.95921967565661D+00 0.36210872683379D-01 1 16 2 6 -0.53369586582173D+00 0.96338579716756D-02 2 16 2 6 0.91069035316952D-01 0.22412026742579D-02 3 16 2 6 0.95921967565681D+00 -0.36210872683385D-01 1 17 2 6 -0.15300585868729D+00 0.77026585835272D-01 2 17 2 6 0.24422371225423D-01 -0.10412436341650D+00 3 17 2 6 0.39263801672990D+00 -0.36582536478170D-01 1 18 2 6 0.15300585868730D+00 -0.77026585835272D-01 2 18 2 6 -0.24422371225416D-01 0.10412436341650D+00 3 18 2 6 -0.39263801672987D+00 0.36582536478171D-01 1 19 2 6 -0.68345312777819D+00 -0.97797549474392D-02 2 19 2 6 -0.12131103227848D+01 0.78851080443494D-02 3 19 2 6 0.83142332788881D+00 -0.63777950819951D-01 1 20 2 6 0.68345312777825D+00 0.97797549474613D-02 2 20 2 6 0.12131103227846D+01 -0.78851080443709D-02 3 20 2 6 -0.83142332788890D+00 0.63777950819962D-01 1 1 3 6 0.24458784879502D+00 -0.16466022068858D-01 2 1 3 6 -0.19740873466911D+01 0.19120570588214D-02 3 1 3 6 -0.33717690951949D+00 0.22842629006484D-02 1 2 3 6 0.24458784879504D+00 -0.16466022068861D-01 2 2 3 6 -0.19740873466913D+01 0.19120570588216D-02 3 2 3 6 -0.33717690951941D+00 0.22842629006424D-02 1 3 3 6 0.68301135923743D+01 0.11263961782654D-02 2 3 3 6 0.22612074747945D-01 0.42968796516413D-02 3 3 3 6 0.15081770436805D+01 0.65515176709539D-02 1 4 3 6 -0.68301135923743D+01 -0.11263961782604D-02 2 4 3 6 -0.22612074747928D-01 -0.42968796516402D-02 3 4 3 6 -0.15081770436806D+01 -0.65515176709629D-02 1 5 3 6 0.10121082778376D-16 0.18159229443740D-14 2 5 3 6 0.69705558204505D-14 -0.42806344822323D-15 3 5 3 6 0.33446938637314D-12 0.10643224439598D-13 1 6 3 6 0.17386556980805D+01 -0.67741031509177D-07 2 6 3 6 0.26437231096067D+01 0.31039695107410D-06 3 6 3 6 0.46577374571396D+02 0.00000000000000D+00 1 7 3 6 0.88371213354321D+01 -0.26774225972786D-09 2 7 3 6 0.11692768811688D+01 0.89404802564830D-08 3 7 3 6 0.35642461447620D+01 0.28963997077231D-09 1 8 3 6 0.42593284373269D-13 -0.39892330160386D-14 2 8 3 6 0.17469721128335D-14 -0.26729417526995D-15 3 8 3 6 0.34164959814778D-13 0.28116003165862D-14 1 9 3 6 0.10852882265972D+01 0.44291984871117D+00 2 9 3 6 -0.38823622062825D+00 -0.10808312793810D+00 3 9 3 6 -0.78131065789739D+01 -0.22829416715194D+01 1 10 3 6 -0.10852882265970D+01 -0.44291984871115D+00 2 10 3 6 0.38823622062838D+00 0.10808312793810D+00 3 10 3 6 0.78131065789743D+01 0.22829416715193D+01 1 11 3 6 0.18848320615519D+01 0.30947067888415D-01 2 11 3 6 0.58900100571404D-01 0.73454160392630D-02 3 11 3 6 0.22077548035897D+01 -0.98614898976874D-02 1 12 3 6 -0.18848320615519D+01 -0.30947067888417D-01 2 12 3 6 -0.58900100571430D-01 -0.73454160392626D-02 3 12 3 6 -0.22077548035897D+01 0.98614898976893D-02 1 13 3 6 -0.42221527349252D+01 0.10684640142366D-01 2 13 3 6 -0.28426666852924D+01 0.45046507557074D-02 3 13 3 6 -0.30555578378943D+00 0.15861160436610D-01 1 14 3 6 0.42221527349251D+01 -0.10684640142367D-01 2 14 3 6 0.28426666852924D+01 -0.45046507557082D-02 3 14 3 6 0.30555578378938D+00 -0.15861160436613D-01 1 15 3 6 -0.49749725110175D+00 0.40968419484873D-01 2 15 3 6 -0.78860554443992D+00 0.48876454191921D-01 3 15 3 6 -0.38543560558658D+01 0.24962800375850D-01 1 16 3 6 0.49749725110215D+00 -0.40968419484895D-01 2 16 3 6 0.78860554444012D+00 -0.48876454191927D-01 3 16 3 6 0.38543560558657D+01 -0.24962800375831D-01 1 17 3 6 -0.38966689520464D+01 0.11517327971764D-01 2 17 3 6 0.30359965124750D+01 -0.79445211495144D-02 3 17 3 6 -0.20019502751882D+00 0.74632616766796D-01 1 18 3 6 0.38966689520464D+01 -0.11517327971765D-01 2 18 3 6 -0.30359965124749D+01 0.79445211495152D-02 3 18 3 6 0.20019502751872D+00 -0.74632616766801D-01 1 19 3 6 -0.62141502835387D+00 0.50205480190900D-01 2 19 3 6 0.77267282968477D+00 -0.64486680591525D-01 3 19 3 6 -0.43358483535486D+01 0.26942192371753D-01 1 20 3 6 0.62141502835397D+00 -0.50205480190904D-01 2 20 3 6 -0.77267282968484D+00 0.64486680591536D-01 3 20 3 6 0.43358483535488D+01 -0.26942192371728D-01 1 1 1 7 -0.12798186148450D-01 0.20891510903254D-01 2 1 1 7 0.40942422053712D+00 -0.80965316320255D-02 3 1 1 7 0.64607748118075D+01 0.14372675444771D-01 1 2 1 7 -0.12798186148427D-01 0.20891510903242D-01 2 2 1 7 0.40942422053716D+00 -0.80965316320272D-02 3 2 1 7 0.64607748118077D+01 0.14372675444750D-01 1 3 1 7 0.33543626171697D+01 -0.61631118258688D-02 2 3 1 7 -0.22163936393641D+00 -0.15650509672712D-02 3 3 1 7 -0.91957351167256D+00 0.10142032844978D-01 1 4 1 7 -0.33543626171698D+01 0.61631118258656D-02 2 4 1 7 0.22163936393641D+00 0.15650509672713D-02 3 4 1 7 0.91957351167260D+00 -0.10142032844979D-01 1 5 1 7 0.48819177293273D-14 0.22448155728790D-15 2 5 1 7 -0.16456045730301D-14 -0.93089458287226D-15 3 5 1 7 0.36425031170828D-19 0.39892330160386D-14 1 6 1 7 -0.17299159085149D+01 0.32249771395310D-09 2 6 1 7 0.39502714767077D+00 -0.22773438928422D-08 3 6 1 7 0.88371231839109D+01 -0.63278571745126D-09 1 7 1 7 0.25854593827376D+02 0.00000000000000D+00 2 7 1 7 0.51875643189914D+00 0.70447379816915D-07 3 7 1 7 0.17386615460778D+01 0.34462456922810D-07 1 8 1 7 -0.42002626196873D-13 -0.26797765493737D-14 2 8 1 7 0.11010477949288D-14 -0.15954928323413D-15 3 8 1 7 0.37524917369003D-13 -0.18159229443740D-14 1 9 1 7 -0.36134755383841D+00 -0.14193648446026D-01 2 9 1 7 -0.19019581456357D+00 0.15482127518063D-02 3 9 1 7 -0.68906983096762D+01 -0.18296233989490D+00 1 10 1 7 0.36134755383847D+00 0.14193648446025D-01 2 10 1 7 0.19019581456355D+00 -0.15482127518061D-02 3 10 1 7 0.68906983096762D+01 0.18296233989490D+00 1 11 1 7 0.27925764469559D+01 -0.97198643229882D+00 2 11 1 7 -0.11197478486114D+00 -0.24155486835260D-01 3 11 1 7 -0.17498303511792D+00 -0.44483826156621D+00 1 12 1 7 -0.27925764469561D+01 0.97198643229884D+00 2 12 1 7 0.11197478486129D+00 0.24155486835259D-01 3 12 1 7 0.17498303511773D+00 0.44483826156623D+00 1 13 1 7 -0.46510512037135D+01 0.15901986239626D-01 2 13 1 7 -0.24317149100595D+01 0.21193322633146D-01 3 13 1 7 -0.54457476066144D+00 0.32243085944306D-01 1 14 1 7 0.46510512037136D+01 -0.15901986239631D-01 2 14 1 7 0.24317149100601D+01 -0.21193322633168D-01 3 14 1 7 0.54457476066148D+00 -0.32243085944311D-01 1 15 1 7 0.64261459815119D+00 -0.39033970235500D-01 2 15 1 7 0.40576584135339D+00 -0.10221387364992D+00 3 15 1 7 -0.11749799206645D+01 0.16783113070781D-01 1 16 1 7 -0.64261459815121D+00 0.39033970235498D-01 2 16 1 7 -0.40576584135338D+00 0.10221387364992D+00 3 16 1 7 0.11749799206645D+01 -0.16783113070781D-01 1 17 1 7 -0.51358465400045D+01 0.13475394102415D-01 2 17 1 7 0.14573935793101D+01 -0.13077479710809D-01 3 17 1 7 -0.55414460510237D+00 0.45931930924349D-01 1 18 1 7 0.51358465400043D+01 -0.13475394102436D-01 2 18 1 7 -0.14573935793101D+01 0.13077479710832D-01 3 18 1 7 0.55414460510193D+00 -0.45931930924361D-01 1 19 1 7 0.73418429166607D+00 -0.27675484520819D-01 2 19 1 7 -0.20463990501137D+00 0.34349079966531D-01 3 19 1 7 -0.18464602830797D+01 0.13801012644522D-01 1 20 1 7 -0.73418429166609D+00 0.27675484520816D-01 2 20 1 7 0.20463990501137D+00 -0.34349079966531D-01 3 20 1 7 0.18464602830797D+01 -0.13801012644522D-01 1 1 2 7 0.34587762083187D+00 -0.29972506986920D-02 2 1 2 7 -0.64248236354105D+00 -0.39529224498704D-02 3 1 2 7 -0.14596092989901D+00 -0.46235710956260D-02 1 2 2 7 0.34587762083191D+00 -0.29972506986937D-02 2 2 2 7 -0.64248236354108D+00 -0.39529224498671D-02 3 2 2 7 -0.14596092989901D+00 -0.46235710956274D-02 1 3 2 7 0.61161652853126D+00 0.31960623911213D-03 2 3 2 7 -0.34356341081677D+01 -0.30086513295988D-01 3 3 2 7 0.14077523970500D+01 -0.27382922036716D-02 1 4 2 7 -0.61161652853126D+00 -0.31960623911206D-03 2 4 2 7 0.34356341081679D+01 0.30086513295979D-01 3 4 2 7 -0.14077523970499D+01 0.27382922036765D-02 1 5 2 7 -0.16456043337165D-14 -0.93089458287226D-15 2 5 2 7 -0.19283011950047D-13 0.47527134207975D-14 3 5 2 7 0.17525987564868D-19 0.26729417526995D-15 1 6 2 7 -0.39503222974707D+00 -0.21700655604290D-08 2 6 2 7 0.40361010132440D+00 -0.26596227849753D-10 3 6 2 7 0.11692820874661D+01 -0.81244195761089D-08 1 7 2 7 0.51874875056772D+00 -0.75153692136189D-07 2 7 2 7 0.17749688782660D+02 0.00000000000000D+00 3 7 2 7 -0.26437063705528D+01 0.27852658405213D-06 1 8 2 7 0.11010477949288D-14 -0.15954928323413D-15 2 8 2 7 -0.35232141519089D-13 0.17997235496011D-14 3 8 2 7 0.16350090071755D-15 0.42806344822323D-15 1 9 2 7 -0.13656873541779D+00 -0.32873551971112D-02 2 9 2 7 0.15321258205104D+00 0.26097329654360D-02 3 9 2 7 -0.10794854753981D+01 -0.29037904891687D-01 1 10 2 7 0.13656873541777D+00 0.32873551971114D-02 2 10 2 7 -0.15321258205105D+00 -0.26097329654364D-02 3 10 2 7 0.10794854753981D+01 0.29037904891687D-01 1 11 2 7 0.51572162110304D-01 -0.20203243078612D-01 2 11 2 7 0.14158884176232D+01 -0.10221399323969D+01 3 11 2 7 -0.11342645015682D+00 -0.94682794168430D-01 1 12 2 7 -0.51572162110152D-01 0.20203243078611D-01 2 12 2 7 -0.14158884176234D+01 0.10221399323969D+01 3 12 2 7 0.11342645015589D+00 0.94682794168434D-01 1 13 2 7 0.68345312777839D+00 0.97797549474392D-02 2 13 2 7 -0.12131103227847D+01 0.78851080443485D-02 3 13 2 7 -0.83142332788890D+00 0.63777950819952D-01 1 14 2 7 -0.68345312777787D+00 -0.97797549474614D-02 2 14 2 7 0.12131103227848D+01 -0.78851080443716D-02 3 14 2 7 0.83142332788892D+00 -0.63777950819960D-01 1 15 2 7 0.15300585868730D+00 -0.77026585835272D-01 2 15 2 7 0.24422371225421D-01 -0.10412436341650D+00 3 15 2 7 -0.39263801672987D+00 0.36582536478171D-01 1 16 2 7 -0.15300585868729D+00 0.77026585835271D-01 2 16 2 7 -0.24422371225417D-01 0.10412436341650D+00 3 16 2 7 0.39263801672990D+00 -0.36582536478171D-01 1 17 2 7 -0.53369586582173D+00 0.96338579716982D-02 2 17 2 7 -0.91069035316867D-01 -0.22412026742621D-02 3 17 2 7 0.95921967565684D+00 -0.36210872683379D-01 1 18 2 7 0.53369586582180D+00 -0.96338579716755D-02 2 18 2 7 0.91069035317069D-01 0.22412026742572D-02 3 18 2 7 -0.95921967565665D+00 0.36210872683386D-01 1 19 2 7 0.15938290873739D+00 0.20789309500503D-01 2 19 2 7 -0.16252001627054D+00 -0.11416271009605D-01 3 19 2 7 0.25795522233826D+00 -0.51648474989793D-02 1 20 2 7 -0.15938290873739D+00 -0.20789309500503D-01 2 20 2 7 0.16252001627055D+00 0.11416271009605D-01 3 20 2 7 -0.25795522233825D+00 0.51648474989800D-02 1 1 3 7 0.68301135923742D+01 0.11263961782755D-02 2 1 3 7 -0.22612074747947D-01 -0.42968796516401D-02 3 1 3 7 0.15081770436805D+01 0.65515176709630D-02 1 2 3 7 0.68301135923744D+01 0.11263961782543D-02 2 2 3 7 -0.22612074747944D-01 -0.42968796516415D-02 3 2 3 7 0.15081770436805D+01 0.65515176709542D-02 1 3 3 7 0.24458784879503D+00 -0.16466022068859D-01 2 3 3 7 0.19740873466915D+01 -0.19120570588221D-02 3 3 3 7 -0.33717690951956D+00 0.22842629006317D-02 1 4 3 7 -0.24458784879499D+00 0.16466022068858D-01 2 4 3 7 -0.19740873466913D+01 0.19120570588270D-02 3 4 3 7 0.33717690951936D+00 -0.22842629006519D-02 1 5 3 7 0.36226197631479D-19 0.39892330160386D-14 2 5 3 7 0.17526000489566D-19 0.26729417526995D-15 3 5 3 7 0.61873397449803D-14 -0.28116003165862D-14 1 6 3 7 0.88371213354321D+01 -0.26774225972786D-09 2 6 3 7 -0.11692768811688D+01 -0.89404802564830D-08 3 6 3 7 0.35642461447620D+01 0.28963997077231D-09 1 7 3 7 0.17386556980807D+01 -0.67741031509177D-07 2 7 3 7 -0.26437231096077D+01 -0.31039695107410D-06 3 7 3 7 0.46577374571395D+02 0.00000000000000D+00 1 8 3 7 0.37558210720296D-13 -0.18159229443740D-14 2 8 3 7 0.17308923137600D-15 0.42806344822323D-15 3 8 3 7 0.36644380948235D-12 -0.10643224439598D-13 1 9 3 7 -0.18848320615518D+01 -0.30947067888416D-01 2 9 3 7 0.58900100571438D-01 0.73454160392628D-02 3 9 3 7 -0.22077548035897D+01 0.98614898976887D-02 1 10 3 7 0.18848320615518D+01 0.30947067888417D-01 2 10 3 7 -0.58900100571429D-01 -0.73454160392627D-02 3 10 3 7 0.22077548035897D+01 -0.98614898976899D-02 1 11 3 7 -0.10852882265972D+01 -0.44291984871115D+00 2 11 3 7 -0.38823622062904D+00 -0.10808312793810D+00 3 11 3 7 0.78131065789748D+01 0.22829416715193D+01 1 12 3 7 0.10852882265970D+01 0.44291984871117D+00 2 12 3 7 0.38823622062811D+00 0.10808312793810D+00 3 12 3 7 -0.78131065789743D+01 -0.22829416715194D+01 1 13 3 7 -0.62141502835397D+00 0.50205480190898D-01 2 13 3 7 -0.77267282968484D+00 0.64486680591525D-01 3 13 3 7 -0.43358483535489D+01 0.26942192371753D-01 1 14 3 7 0.62141502835400D+00 -0.50205480190902D-01 2 14 3 7 0.77267282968486D+00 -0.64486680591533D-01 3 14 3 7 0.43358483535483D+01 -0.26942192371726D-01 1 15 3 7 -0.38966689520463D+01 0.11517327971766D-01 2 15 3 7 -0.30359965124749D+01 0.79445211495148D-02 3 15 3 7 -0.20019502751874D+00 0.74632616766798D-01 1 16 3 7 0.38966689520463D+01 -0.11517327971767D-01 2 16 3 7 0.30359965124750D+01 -0.79445211495153D-02 3 16 3 7 0.20019502751877D+00 -0.74632616766801D-01 1 17 3 7 -0.49749725110223D+00 0.40968419484880D-01 2 17 3 7 0.78860554444014D+00 -0.48876454191921D-01 3 17 3 7 -0.38543560558655D+01 0.24962800375849D-01 1 18 3 7 0.49749725110181D+00 -0.40968419484891D-01 2 18 3 7 -0.78860554443996D+00 0.48876454191928D-01 3 18 3 7 0.38543560558658D+01 -0.24962800375829D-01 1 19 3 7 -0.42221527349252D+01 0.10684640142367D-01 2 19 3 7 0.28426666852924D+01 -0.45046507557076D-02 3 19 3 7 -0.30555578378941D+00 0.15861160436606D-01 1 20 3 7 0.42221527349251D+01 -0.10684640142367D-01 2 20 3 7 -0.28426666852924D+01 0.45046507557083D-02 3 20 3 7 0.30555578378940D+00 -0.15861160436612D-01 1 1 1 8 -0.12798186148432D-01 0.20891510903252D-01 2 1 1 8 0.40942422053712D+00 -0.80965316320257D-02 3 1 1 8 -0.64607748118076D+01 -0.14372675444765D-01 1 2 1 8 0.12798186148458D-01 -0.20891510903245D-01 2 2 1 8 -0.40942422053715D+00 0.80965316320254D-02 3 2 1 8 0.64607748118076D+01 0.14372675444768D-01 1 3 1 8 0.33543626171698D+01 -0.61631118258658D-02 2 3 1 8 -0.22163936393640D+00 -0.15650509672714D-02 3 3 1 8 0.91957351167257D+00 -0.10142032844978D-01 1 4 1 8 0.33543626171698D+01 -0.61631118258593D-02 2 4 1 8 -0.22163936393640D+00 -0.15650509672712D-02 3 4 1 8 0.91957351167258D+00 -0.10142032844979D-01 1 5 1 8 -0.17299159085149D+01 0.32249771395310D-09 2 5 1 8 0.39502714767077D+00 -0.22773438928422D-08 3 5 1 8 -0.88371231839109D+01 0.63278455371147D-09 1 6 1 8 0.42851545084963D-13 0.22448155728790D-15 2 6 1 8 -0.16456046027583D-14 -0.93089458287226D-15 3 6 1 8 0.42593284373269D-13 0.39892330160386D-14 1 7 1 8 -0.42002626196873D-13 0.26797765493737D-14 2 7 1 8 0.11010477949288D-14 0.15954928323413D-15 3 7 1 8 0.37558210720296D-13 0.18159229443740D-14 1 8 1 8 0.25854593827377D+02 0.00000000000000D+00 2 8 1 8 0.51875643189923D+00 0.70447379816915D-07 3 8 1 8 -0.17386615460780D+01 -0.34462456922810D-07 1 9 1 8 -0.36134755383841D+00 -0.14193648446025D-01 2 9 1 8 -0.19019581456357D+00 0.15482127518066D-02 3 9 1 8 0.68906983096763D+01 0.18296233989490D+00 1 10 1 8 -0.36134755383849D+00 -0.14193648446026D-01 2 10 1 8 -0.19019581456355D+00 0.15482127518062D-02 3 10 1 8 0.68906983096762D+01 0.18296233989490D+00 1 11 1 8 -0.27925764469559D+01 0.97198643229884D+00 2 11 1 8 0.11197478486114D+00 0.24155486835260D-01 3 11 1 8 -0.17498303511773D+00 -0.44483826156623D+00 1 12 1 8 -0.27925764469561D+01 0.97198643229883D+00 2 12 1 8 0.11197478486129D+00 0.24155486835260D-01 3 12 1 8 -0.17498303511769D+00 -0.44483826156623D+00 1 13 1 8 -0.64261459815119D+00 0.39033970235507D-01 2 13 1 8 -0.40576584135338D+00 0.10221387364992D+00 3 13 1 8 -0.11749799206646D+01 0.16783113070781D-01 1 14 1 8 -0.64261459815118D+00 0.39033970235496D-01 2 14 1 8 -0.40576584135339D+00 0.10221387364992D+00 3 14 1 8 -0.11749799206646D+01 0.16783113070779D-01 1 15 1 8 -0.46510512037137D+01 0.15901986239629D-01 2 15 1 8 -0.24317149100600D+01 0.21193322633146D-01 3 15 1 8 0.54457476066144D+00 -0.32243085944306D-01 1 16 1 8 -0.46510512037136D+01 0.15901986239627D-01 2 16 1 8 -0.24317149100596D+01 0.21193322633146D-01 3 16 1 8 0.54457476066143D+00 -0.32243085944305D-01 1 17 1 8 -0.73418429166607D+00 0.27675484520815D-01 2 17 1 8 0.20463990501137D+00 -0.34349079966532D-01 3 17 1 8 -0.18464602830797D+01 0.13801012644522D-01 1 18 1 8 -0.73418429166608D+00 0.27675484520818D-01 2 18 1 8 0.20463990501138D+00 -0.34349079966531D-01 3 18 1 8 -0.18464602830797D+01 0.13801012644523D-01 1 19 1 8 -0.51358465400043D+01 0.13475394102419D-01 2 19 1 8 0.14573935793100D+01 -0.13077479710808D-01 3 19 1 8 0.55414460510195D+00 -0.45931930924354D-01 1 20 1 8 -0.51358465400045D+01 0.13475394102414D-01 2 20 1 8 0.14573935793102D+01 -0.13077479710809D-01 3 20 1 8 0.55414460510231D+00 -0.45931930924356D-01 1 1 2 8 0.34587762083186D+00 -0.29972506986922D-02 2 1 2 8 -0.64248236354104D+00 -0.39529224498707D-02 3 1 2 8 0.14596092989901D+00 0.46235710956257D-02 1 2 2 8 -0.34587762083190D+00 0.29972506986919D-02 2 2 2 8 0.64248236354108D+00 0.39529224498675D-02 3 2 2 8 -0.14596092989900D+00 -0.46235710956272D-02 1 3 2 8 0.61161652853126D+00 0.31960623911195D-03 2 3 2 8 -0.34356341081677D+01 -0.30086513295988D-01 3 3 2 8 -0.14077523970500D+01 0.27382922036713D-02 1 4 2 8 0.61161652853127D+00 0.31960623911212D-03 2 4 2 8 -0.34356341081678D+01 -0.30086513295987D-01 3 4 2 8 -0.14077523970500D+01 0.27382922036718D-02 1 5 2 8 -0.39503222974707D+00 -0.21700655604290D-08 2 5 2 8 0.40361010132440D+00 -0.26596227849753D-10 3 5 2 8 -0.11692820874661D+01 0.81244195761089D-08 1 6 2 8 -0.16456043634446D-14 -0.93089458287226D-15 2 6 2 8 -0.72926032915415D-14 0.47527134207975D-14 3 6 2 8 0.17469721128335D-14 0.26729417526995D-15 1 7 2 8 0.11010477949288D-14 0.15954928323413D-15 2 7 2 8 -0.35232141519089D-13 -0.17997235496011D-14 3 7 2 8 0.17308923137600D-15 -0.42806344822323D-15 1 8 2 8 0.51874875056782D+00 -0.75153692136189D-07 2 8 2 8 0.17749688782662D+02 0.00000000000000D+00 3 8 2 8 0.26437063705527D+01 -0.27852658405213D-06 1 9 2 8 -0.13656873541779D+00 -0.32873551971109D-02 2 9 2 8 0.15321258205103D+00 0.26097329654365D-02 3 9 2 8 0.10794854753981D+01 0.29037904891687D-01 1 10 2 8 -0.13656873541777D+00 -0.32873551971113D-02 2 10 2 8 0.15321258205106D+00 0.26097329654348D-02 3 10 2 8 0.10794854753981D+01 0.29037904891687D-01 1 11 2 8 -0.51572162110296D-01 0.20203243078611D-01 2 11 2 8 -0.14158884176234D+01 0.10221399323969D+01 3 11 2 8 -0.11342645015675D+00 -0.94682794168434D-01 1 12 2 8 -0.51572162110154D-01 0.20203243078611D-01 2 12 2 8 -0.14158884176234D+01 0.10221399323969D+01 3 12 2 8 -0.11342645015589D+00 -0.94682794168434D-01 1 13 2 8 -0.15300585868729D+00 0.77026585835272D-01 2 13 2 8 -0.24422371225419D-01 0.10412436341650D+00 3 13 2 8 -0.39263801672990D+00 0.36582536478171D-01 1 14 2 8 -0.15300585868729D+00 0.77026585835272D-01 2 14 2 8 -0.24422371225406D-01 0.10412436341650D+00 3 14 2 8 -0.39263801672986D+00 0.36582536478171D-01 1 15 2 8 0.68345312777792D+00 0.97797549474390D-02 2 15 2 8 -0.12131103227848D+01 0.78851080443488D-02 3 15 2 8 0.83142332788892D+00 -0.63777950819952D-01 1 16 2 8 0.68345312777832D+00 0.97797549474394D-02 2 16 2 8 -0.12131103227846D+01 0.78851080443494D-02 3 16 2 8 0.83142332788891D+00 -0.63777950819952D-01 1 17 2 8 -0.15938290873739D+00 -0.20789309500504D-01 2 17 2 8 0.16252001627055D+00 0.11416271009605D-01 3 17 2 8 0.25795522233825D+00 -0.51648474989803D-02 1 18 2 8 -0.15938290873738D+00 -0.20789309500503D-01 2 18 2 8 0.16252001627055D+00 0.11416271009605D-01 3 18 2 8 0.25795522233826D+00 -0.51648474989799D-02 1 19 2 8 -0.53369586582193D+00 0.96338579716992D-02 2 19 2 8 -0.91069035317069D-01 -0.22412026742621D-02 3 19 2 8 -0.95921967565665D+00 0.36210872683379D-01 1 20 2 8 -0.53369586582166D+00 0.96338579716981D-02 2 20 2 8 -0.91069035316856D-01 -0.22412026742621D-02 3 20 2 8 -0.95921967565683D+00 0.36210872683379D-01 1 1 3 8 -0.68301135923743D+01 -0.11263961782691D-02 2 1 3 8 0.22612074747950D-01 0.42968796516398D-02 3 1 3 8 0.15081770436805D+01 0.65515176709640D-02 1 2 3 8 0.68301135923743D+01 0.11263961782728D-02 2 2 3 8 -0.22612074747940D-01 -0.42968796516413D-02 3 2 3 8 -0.15081770436805D+01 -0.65515176709543D-02 1 3 3 8 -0.24458784879502D+00 0.16466022068859D-01 2 3 3 8 -0.19740873466914D+01 0.19120570588218D-02 3 3 3 8 -0.33717690951954D+00 0.22842629006359D-02 1 4 3 8 -0.24458784879501D+00 0.16466022068858D-01 2 4 3 8 -0.19740873466914D+01 0.19120570588223D-02 3 4 3 8 -0.33717690951944D+00 0.22842629006490D-02 1 5 3 8 -0.88371213354321D+01 0.26774109598806D-09 2 5 3 8 0.11692768811688D+01 0.89404802564830D-08 3 5 3 8 0.35642461447620D+01 0.28963997077231D-09 1 6 3 8 0.42593284572103D-13 0.39892330160386D-14 2 6 3 8 0.17469721128464D-14 0.26729417526995D-15 3 6 3 8 0.34164959814778D-13 -0.28116003165862D-14 1 7 3 8 0.37524917369003D-13 0.18159229443740D-14 2 7 3 8 0.16350090071755D-15 -0.42806344822323D-15 3 7 3 8 0.36644380948235D-12 0.10643224439598D-13 1 8 3 8 -0.17386556980809D+01 0.67741031509177D-07 2 8 3 8 0.26437231096077D+01 0.31039695107410D-06 3 8 3 8 0.46577374571395D+02 0.00000000000000D+00 1 9 3 8 0.18848320615519D+01 0.30947067888415D-01 2 9 3 8 -0.58900100571434D-01 -0.73454160392628D-02 3 9 3 8 -0.22077548035897D+01 0.98614898976884D-02 1 10 3 8 0.18848320615518D+01 0.30947067888413D-01 2 10 3 8 -0.58900100571430D-01 -0.73454160392627D-02 3 10 3 8 -0.22077548035897D+01 0.98614898976867D-02 1 11 3 8 -0.10852882265970D+01 -0.44291984871116D+00 2 11 3 8 -0.38823622062897D+00 -0.10808312793810D+00 3 11 3 8 -0.78131065789740D+01 -0.22829416715194D+01 1 12 3 8 -0.10852882265970D+01 -0.44291984871116D+00 2 12 3 8 -0.38823622062811D+00 -0.10808312793810D+00 3 12 3 8 -0.78131065789744D+01 -0.22829416715194D+01 1 13 3 8 -0.38966689520464D+01 0.11517327971767D-01 2 13 3 8 -0.30359965124750D+01 0.79445211495156D-02 3 13 3 8 0.20019502751882D+00 -0.74632616766795D-01 1 14 3 8 -0.38966689520464D+01 0.11517327971765D-01 2 14 3 8 -0.30359965124749D+01 0.79445211495151D-02 3 14 3 8 0.20019502751870D+00 -0.74632616766799D-01 1 15 3 8 0.62141502835396D+00 -0.50205480190898D-01 2 15 3 8 0.77267282968486D+00 -0.64486680591525D-01 3 15 3 8 -0.43358483535482D+01 0.26942192371752D-01 1 16 3 8 0.62141502835394D+00 -0.50205480190897D-01 2 16 3 8 0.77267282968485D+00 -0.64486680591525D-01 3 16 3 8 -0.43358483535488D+01 0.26942192371753D-01 1 17 3 8 -0.42221527349252D+01 0.10684640142367D-01 2 17 3 8 0.28426666852924D+01 -0.45046507557085D-02 3 17 3 8 0.30555578378945D+00 -0.15861160436610D-01 1 18 3 8 -0.42221527349252D+01 0.10684640142368D-01 2 18 3 8 0.28426666852924D+01 -0.45046507557082D-02 3 18 3 8 0.30555578378937D+00 -0.15861160436614D-01 1 19 3 8 0.49749725110183D+00 -0.40968419484884D-01 2 19 3 8 -0.78860554443995D+00 0.48876454191921D-01 3 19 3 8 -0.38543560558657D+01 0.24962800375852D-01 1 20 3 8 0.49749725110218D+00 -0.40968419484886D-01 2 20 3 8 -0.78860554444013D+00 0.48876454191921D-01 3 20 3 8 -0.38543560558655D+01 0.24962800375852D-01 1 1 1 9 -0.13601446467444D+01 -0.22995527372673D-07 2 1 1 9 -0.37924436509455D+00 -0.10690203410886D-07 3 1 1 9 0.34625277442229D-15 0.11069740067251D-15 1 2 1 9 -0.28887805409521D-14 -0.21639285347739D-14 2 2 1 9 0.32657024162728D-14 -0.66396704872647D-16 3 2 1 9 -0.12972833328327D+00 0.97144963739059D-08 1 3 1 9 -0.32901829520359D+01 -0.72003893468381D-08 2 3 1 9 -0.21474564783828D+00 0.47484920924843D-08 3 3 1 9 0.13184989953747D-14 -0.34369479863956D-14 1 4 1 9 -0.22951993546343D-14 0.58254517231871D-15 2 4 1 9 -0.28664440079560D-14 0.29331220591997D-16 3 4 1 9 0.90846730455020D+00 0.17265960503443D-07 1 5 1 9 -0.27925756026444D+01 -0.97198684567999D+00 2 5 1 9 0.51572366326949D-01 0.20203100763490D-01 3 5 1 9 -0.10852874883878D+01 0.44291949282744D+00 1 6 1 9 -0.27925756026444D+01 -0.97198684568000D+00 2 6 1 9 0.51572366326942D-01 0.20203100763490D-01 3 6 1 9 0.10852874883878D+01 -0.44291949282744D+00 1 7 1 9 -0.36134755383841D+00 0.14193648446025D-01 2 7 1 9 -0.13656873541779D+00 0.32873551971110D-02 3 7 1 9 -0.18848320615518D+01 0.30947067888411D-01 1 8 1 9 -0.36134755383841D+00 0.14193648446024D-01 2 8 1 9 -0.13656873541779D+00 0.32873551971107D-02 3 8 1 9 0.18848320615519D+01 -0.30947067888411D-01 1 9 1 9 0.95330703484917D+01 0.00000000000000D+00 2 9 1 9 0.88947217536786D+00 0.58242133947695D-07 3 9 1 9 -0.74687493183699D-14 0.13877787807815D-16 1 10 1 9 0.19240140770276D-13 0.61531880653971D-16 2 10 1 9 0.21757099407563D-14 -0.75566755162824D-16 3 10 1 9 -0.18113509150141D+01 -0.72003978808674D-08 1 11 1 9 0.11753788541606D-14 -0.70489285814994D-17 2 11 1 9 -0.10993320285440D-14 -0.71079278212916D-16 3 11 1 9 -0.20606573664554D+01 -0.64057402011684D-08 1 12 1 9 0.69090348926738D-01 -0.16382280544849D-15 2 12 1 9 -0.17034232713893D+00 -0.42669545453283D-08 3 12 1 9 -0.53761715406099D-14 0.21592056029315D-14 1 13 1 9 0.79845910098695D+00 0.33932205755569D-09 2 13 1 9 0.10478578443022D+01 0.48356111447593D-09 3 13 1 9 0.23102472143651D+01 0.18413163978509D-07 1 14 1 9 -0.40134067340285D+00 -0.17834422106551D-01 2 14 1 9 0.26089825287153D+00 -0.18487522871309D-01 3 14 1 9 -0.14460629600099D+01 -0.12006358334136D-01 1 15 1 9 0.40134067340286D+00 0.17834422106552D-01 2 15 1 9 -0.26089825287153D+00 0.18487522871308D-01 3 15 1 9 -0.14460629600099D+01 -0.12006358334141D-01 1 16 1 9 0.79845910098695D+00 0.33932261259747D-09 2 16 1 9 0.10478578443022D+01 0.48356126710093D-09 3 16 1 9 -0.23102472143651D+01 -0.18413164767203D-07 1 17 1 9 0.64942645387029D-01 0.36633641645379D-02 2 17 1 9 -0.80935195239606D+00 -0.29507372588114D-01 3 17 1 9 0.15212693177318D+01 -0.29378448157187D-01 1 18 1 9 -0.63306122767651D+00 -0.23395148364602D-06 2 18 1 9 -0.15520533430960D+00 -0.11134938503178D-06 3 18 1 9 -0.10691410880597D+01 -0.50385591651901D-06 1 19 1 9 0.63306122767647D+00 0.23395148459139D-06 2 19 1 9 0.15520533430961D+00 0.11134938595898D-06 3 19 1 9 -0.10691410880597D+01 -0.50385591908633D-06 1 20 1 9 0.64942645387028D-01 0.36633641645376D-02 2 20 1 9 -0.80935195239606D+00 -0.29507372588114D-01 3 20 1 9 -0.15212693177318D+01 0.29378448157186D-01 1 1 2 9 -0.18412347215818D+00 -0.10766057268489D-07 2 1 2 9 0.92923385120542D-01 -0.13093648729134D-08 3 1 2 9 0.49394068945111D-15 -0.16210257094887D-15 1 2 2 9 0.32656245506598D-14 -0.66396704872647D-16 2 2 2 9 -0.47081948433809D-14 0.10689955559177D-14 3 2 2 9 -0.22769931938120D-01 -0.35771731823619D-08 1 3 2 9 -0.25502894899908D+00 0.36554667418686D-08 2 3 2 9 -0.25132987898843D+00 0.17101903477353D-08 3 3 2 9 -0.66081767502538D-15 0.10594011177242D-15 1 4 2 9 -0.28664440083696D-14 0.30632263198980D-16 2 4 2 9 -0.62948263564015D-14 -0.25672667919329D-15 3 4 2 9 0.10613762213919D+00 0.62670758742952D-08 1 5 2 9 -0.11197596840009D+00 0.24155456528833D-01 2 5 2 9 -0.14158881793438D+01 -0.10221397795320D+01 3 5 2 9 0.38823464913708D+00 -0.10808318930333D+00 1 6 2 9 -0.11197596840009D+00 0.24155456528833D-01 2 6 2 9 -0.14158881793438D+01 -0.10221397795320D+01 3 6 2 9 -0.38823464913709D+00 0.10808318930333D+00 1 7 2 9 -0.19019581456357D+00 -0.15482127518065D-02 2 7 2 9 0.15321258205104D+00 -0.26097329654353D-02 3 7 2 9 0.58900100571438D-01 -0.73454160392627D-02 1 8 2 9 -0.19019581456357D+00 -0.15482127518067D-02 2 8 2 9 0.15321258205103D+00 -0.26097329654358D-02 3 8 2 9 -0.58900100571434D-01 0.73454160392627D-02 1 9 2 9 0.88947355820457D+00 -0.45753696801657D-07 2 9 2 9 0.67571270235592D+01 0.00000000000000D+00 3 9 2 9 -0.42529898227460D-13 0.00000000000000D+00 1 10 2 9 0.21757099405495D-14 -0.74699393424836D-16 2 10 2 9 0.64072830298679D-14 0.50774630308006D-15 3 10 2 9 0.38116860928560D+00 -0.23451668981055D-07 1 11 2 9 -0.10993320285440D-14 -0.71133488321540D-16 2 11 2 9 -0.10179887448946D-14 0.34744987144163D-16 3 11 2 9 0.17403278626412D+00 -0.87082646786680D-08 1 12 2 9 0.17034232713894D+00 -0.42669545453283D-08 2 12 2 9 -0.46572736058257D+00 -0.11489915743977D-15 3 12 2 9 0.57612210419001D-15 0.81652653640183D-16 1 13 2 9 0.86617686171477D+00 0.67154469902951D-08 2 13 2 9 0.20412482979856D+00 0.26603683426511D-08 3 13 2 9 0.10915064791448D+01 0.16027645108824D-07 1 14 2 9 0.55778781506927D+00 -0.36358835157208D-02 2 14 2 9 0.39716448006902D+00 -0.80859148335081D-03 3 14 2 9 -0.12976196960095D+01 -0.12426146858368D-02 1 15 2 9 -0.55778781506927D+00 0.36358835157195D-02 2 15 2 9 -0.39716448006901D+00 0.80859148335045D-03 3 15 2 9 -0.12976196960095D+01 -0.12426146858402D-02 1 16 2 9 0.86617686171477D+00 0.67154471394506D-08 2 16 2 9 0.20412482979855D+00 0.26603682532990D-08 3 16 2 9 -0.10915064791448D+01 -0.16027645050029D-07 1 17 2 9 -0.90819511059348D+00 -0.44958752794669D-01 2 17 2 9 0.93502320659135D+00 0.41300989148832D-01 3 17 2 9 -0.10273560672803D+01 0.56343722398490D-01 1 18 2 9 -0.52364748639403D+00 0.25801219322390D-06 2 18 2 9 0.53388500064516D+00 -0.27426758257088D-06 3 18 2 9 0.17446300102037D+01 0.59352764518031D-06 1 19 2 9 0.52364748639404D+00 -0.25801219230364D-06 2 19 2 9 -0.53388500064516D+00 0.27426758131270D-06 3 19 2 9 0.17446300102037D+01 0.59352764941303D-06 1 20 2 9 -0.90819511059349D+00 -0.44958752794669D-01 2 20 2 9 0.93502320659137D+00 0.41300989148832D-01 3 20 2 9 0.10273560672803D+01 -0.56343722398490D-01 1 1 3 9 0.34625277607665D-15 0.10722795372055D-15 2 1 3 9 0.49394068779675D-15 -0.16904146485278D-15 3 1 3 9 -0.38255253036799D+01 -0.46427711839585D-07 1 2 3 9 -0.41289204564316D+00 0.71724844129880D-08 2 2 3 9 0.22854053578512D+00 0.41213474333467D-08 3 2 3 9 -0.12198038638383D-14 0.19227716117300D-14 1 3 3 9 0.13184989953747D-14 -0.34369479863956D-14 2 3 3 9 -0.66081767419820D-15 0.10594011177242D-15 3 3 3 9 -0.64698506258237D+00 -0.67594554071680D-07 1 4 3 9 0.26506167626628D+01 0.11469794547727D-07 2 4 3 9 -0.21683191281967D+00 0.24383217810423D-08 3 4 3 9 0.14270743538244D-13 -0.88236325091029D-15 1 5 3 9 -0.17498372172130D+00 0.44483839413103D+00 2 5 3 9 0.11342713471798D+00 -0.94681802555721D-01 3 5 3 9 -0.78131019418244D+01 0.22829431552101D+01 1 6 3 9 0.17498372172129D+00 -0.44483839413103D+00 2 6 3 9 -0.11342713471799D+00 0.94681802555721D-01 3 6 3 9 -0.78131019418244D+01 0.22829431552101D+01 1 7 3 9 -0.68906983096762D+01 0.18296233989490D+00 2 7 3 9 -0.10794854753981D+01 0.29037904891687D-01 3 7 3 9 -0.22077548035897D+01 -0.98614898976891D-02 1 8 3 9 0.68906983096763D+01 -0.18296233989490D+00 2 8 3 9 0.10794854753981D+01 -0.29037904891687D-01 3 8 3 9 -0.22077548035897D+01 -0.98614898976888D-02 1 9 3 9 -0.74687493183699D-14 -0.13877787807815D-16 2 9 3 9 -0.42529898230768D-13 0.69388939039070D-17 3 9 3 9 0.45156705309127D+02 0.00000000000000D+00 1 10 3 9 -0.18113377482113D+01 0.74958103762337D-08 2 10 3 9 0.38115544765785D+00 0.24071869554822D-07 3 10 3 9 -0.13319629828517D-13 0.30324107696114D-15 1 11 3 9 -0.20606573664554D+01 0.64057408328389D-08 2 11 3 9 -0.17403278626412D+00 -0.87082646786680D-08 3 11 3 9 -0.19603106763673D-14 -0.19867222832537D-17 1 12 3 9 -0.53761715406099D-14 0.21592056029315D-14 2 12 3 9 0.57612210419001D-15 0.81652653640183D-16 3 12 3 9 0.67541894467108D+00 0.20915786943188D-16 1 13 3 9 0.42098203200070D+01 -0.16310428669550D-07 2 13 3 9 0.27702610682966D+01 -0.15214179199431D-07 3 13 3 9 0.11148623500516D+01 0.29365148586870D-07 1 14 3 9 -0.34985424832815D+01 -0.46949611660843D-01 2 14 3 9 -0.29534036729796D+01 -0.57447006603537D-01 3 14 3 9 0.23985564715927D+01 0.55815870487233D-01 1 15 3 9 -0.34985424832815D+01 -0.46949611660847D-01 2 15 3 9 -0.29534036729796D+01 -0.57447006603540D-01 3 15 3 9 -0.23985564715927D+01 -0.55815870487242D-01 1 16 3 9 -0.42098203200070D+01 0.16310427894734D-07 2 16 3 9 -0.27702610682966D+01 0.15214179258226D-07 3 16 3 9 0.11148623500516D+01 0.29365149600380D-07 1 17 3 9 0.34417030988129D+01 -0.17217352796030D+00 2 17 3 9 -0.31649972223185D+01 0.10999950761532D+00 3 17 3 9 0.67939509470963D+00 -0.11016207830167D+00 1 18 3 9 -0.32019615082073D+01 0.37732334366176D-06 2 18 3 9 0.34957157651689D+01 -0.71307482361919D-06 3 18 3 9 0.26654984393297D+01 -0.10056049488220D-06 1 19 3 9 -0.32019615082073D+01 0.37732334108924D-06 2 19 3 9 0.34957157651689D+01 -0.71307481940381D-06 3 19 3 9 -0.26654984393297D+01 0.10056048768905D-06 1 20 3 9 -0.34417030988130D+01 0.17217352796030D+00 2 20 3 9 0.31649972223185D+01 -0.10999950761532D+00 3 20 3 9 0.67939509470963D+00 -0.11016207830167D+00 1 1 1 10 0.26092995753065D-13 -0.16993464479755D-14 2 1 1 10 0.19431586793656D-14 0.83671808369485D-16 3 1 1 10 0.12972833328334D+00 -0.97144962057492D-08 1 2 1 10 0.13601446467444D+01 0.22995523375886D-07 2 2 1 10 0.37924436509459D+00 0.10690206372281D-07 3 2 1 10 -0.54279459008004D-14 0.49881539597266D-15 1 3 1 10 -0.63647133902148D-14 -0.12011573580321D-15 2 3 1 10 -0.10788504821945D-14 -0.56132494570282D-16 3 3 1 10 0.90846730455020D+00 0.17265957504619D-07 1 4 1 10 -0.32901829520357D+01 -0.72003780813798D-08 2 4 1 10 -0.21474564783821D+00 0.47484902541570D-08 3 4 1 10 -0.15736440797375D-13 -0.63758046449102D-15 1 5 1 10 -0.27925756026439D+01 -0.97198684567998D+00 2 5 1 10 0.51572366326962D-01 0.20203100763492D-01 3 5 1 10 -0.10852874883877D+01 0.44291949282741D+00 1 6 1 10 0.27925756026441D+01 0.97198684567998D+00 2 6 1 10 -0.51572366326956D-01 -0.20203100763491D-01 3 6 1 10 -0.10852874883876D+01 0.44291949282742D+00 1 7 1 10 0.36134755383847D+00 -0.14193648446024D-01 2 7 1 10 0.13656873541777D+00 -0.32873551971112D-02 3 7 1 10 0.18848320615518D+01 -0.30947067888413D-01 1 8 1 10 -0.36134755383849D+00 0.14193648446026D-01 2 8 1 10 -0.13656873541777D+00 0.32873551971111D-02 3 8 1 10 0.18848320615518D+01 -0.30947067888409D-01 1 9 1 10 0.19240140770276D-13 -0.61531880653971D-16 2 9 1 10 0.21757099403427D-14 0.73832031686848D-16 3 9 1 10 -0.18113509150141D+01 -0.72004007624609D-08 1 10 1 10 0.95330703484910D+01 0.00000000000000D+00 2 10 1 10 0.88947217536782D+00 0.58242133947695D-07 3 10 1 10 0.13463979783365D-12 0.13877787807815D-16 1 11 1 10 0.69090348926710D-01 0.39284865015120D-15 2 11 1 10 -0.17034232713902D+00 -0.42669546665963D-08 3 11 1 10 -0.36946569662604D-14 -0.35483597743481D-15 1 12 1 10 -0.11799188844598D-14 0.15227910941481D-17 2 12 1 10 -0.22541850778660D-14 -0.10023399814316D-15 3 12 1 10 -0.20606573664554D+01 -0.64057408075027D-08 1 13 1 10 -0.40134067340285D+00 -0.17834422106553D-01 2 13 1 10 0.26089825287155D+00 -0.18487522871307D-01 3 13 1 10 -0.14460629600100D+01 -0.12006358334144D-01 1 14 1 10 0.79845910098693D+00 0.33932696537957D-09 2 14 1 10 0.10478578443022D+01 0.48356520439254D-09 3 14 1 10 0.23102472143651D+01 0.18413170721752D-07 1 15 1 10 0.79845910098691D+00 0.33932710385980D-09 2 15 1 10 0.10478578443022D+01 0.48356468694562D-09 3 15 1 10 -0.23102472143651D+01 -0.18413171409769D-07 1 16 1 10 0.40134067340284D+00 0.17834422106551D-01 2 16 1 10 -0.26089825287154D+00 0.18487522871308D-01 3 16 1 10 -0.14460629600099D+01 -0.12006358334142D-01 1 17 1 10 -0.63306122767649D+00 -0.23395148710717D-06 2 17 1 10 -0.15520533430962D+00 -0.11134938668174D-06 3 17 1 10 -0.10691410880597D+01 -0.50385592149150D-06 1 18 1 10 0.64942645386986D-01 0.36633641645393D-02 2 18 1 10 -0.80935195239608D+00 -0.29507372588118D-01 3 18 1 10 0.15212693177318D+01 -0.29378448157181D-01 1 19 1 10 0.64942645387004D-01 0.36633641645388D-02 2 19 1 10 -0.80935195239606D+00 -0.29507372588118D-01 3 19 1 10 -0.15212693177318D+01 0.29378448157180D-01 1 20 1 10 0.63306122767643D+00 0.23395148480566D-06 2 20 1 10 0.15520533430961D+00 0.11134938600553D-06 3 20 1 10 -0.10691410880597D+01 -0.50385591880233D-06 1 1 2 10 0.19432365449786D-14 0.84105489238480D-16 2 1 2 10 -0.44282855286124D-14 -0.50573816733092D-15 3 1 2 10 0.22769931938097D-01 0.35771731824572D-08 1 2 2 10 0.18412347215822D+00 0.10766060229884D-07 2 2 2 10 -0.92923385120317D-01 0.13093857768600D-08 3 2 2 10 -0.41145951541614D-14 0.47959043947071D-17 1 3 2 10 -0.10788504826081D-14 -0.54831451963299D-16 2 3 2 10 -0.38931707560140D-14 -0.25730489654246D-15 3 3 2 10 0.10613762213919D+00 0.62670758429924D-08 1 4 2 10 -0.25502894899901D+00 0.36554649035413D-08 2 4 2 10 -0.25132987898857D+00 0.17101881229518D-08 3 4 2 10 0.42408843537406D-14 -0.82426745566736D-16 1 5 2 10 -0.11197596840007D+00 0.24155456528834D-01 2 5 2 10 -0.14158881793436D+01 -0.10221397795320D+01 3 5 2 10 0.38823464913727D+00 -0.10808318930332D+00 1 6 2 10 0.11197596840008D+00 -0.24155456528834D-01 2 6 2 10 0.14158881793437D+01 0.10221397795320D+01 3 6 2 10 0.38823464913723D+00 -0.10808318930333D+00 1 7 2 10 0.19019581456355D+00 0.15482127518063D-02 2 7 2 10 -0.15321258205105D+00 0.26097329654357D-02 3 7 2 10 -0.58900100571429D-01 0.73454160392626D-02 1 8 2 10 -0.19019581456355D+00 -0.15482127518064D-02 2 8 2 10 0.15321258205106D+00 -0.26097329654340D-02 3 8 2 10 -0.58900100571430D-01 0.73454160392626D-02 1 9 2 10 0.21757099405495D-14 0.74699393424836D-16 2 9 2 10 0.64072830298679D-14 -0.53550187869569D-15 3 9 2 10 0.38116860928560D+00 -0.23451668113572D-07 1 10 2 10 0.88947355820454D+00 -0.45753696801657D-07 2 10 2 10 0.67571270235592D+01 0.00000000000000D+00 3 10 2 10 -0.21213616154660D-13 0.00000000000000D+00 1 11 2 10 0.17034232713885D+00 -0.42669546665963D-08 2 11 2 10 -0.46572736058250D+00 0.33461367655510D-15 3 11 2 10 -0.15676970818884D-14 -0.19549068614946D-16 1 12 2 10 -0.22541850778660D-14 -0.10028820825179D-15 2 12 2 10 -0.98169096551502D-15 -0.18591655716692D-16 3 12 2 10 0.17403278626412D+00 -0.87082646988567D-08 1 13 2 10 0.55778781506929D+00 -0.36358835157184D-02 2 13 2 10 0.39716448006900D+00 -0.80859148335031D-03 3 13 2 10 -0.12976196960095D+01 -0.12426146858432D-02 1 14 2 10 0.86617686171481D+00 0.67154510802117D-08 2 14 2 10 0.20412482979856D+00 0.26603671853599D-08 3 14 2 10 0.10915064791449D+01 0.16027649397554D-07 1 15 2 10 0.86617686171478D+00 0.67154505592953D-08 2 15 2 10 0.20412482979856D+00 0.26603675198453D-08 3 15 2 10 -0.10915064791448D+01 -0.16027649360812D-07 1 16 2 10 -0.55778781506927D+00 0.36358835157195D-02 2 16 2 10 -0.39716448006900D+00 0.80859148335053D-03 3 16 2 10 -0.12976196960094D+01 -0.12426146858399D-02 1 17 2 10 -0.52364748639405D+00 0.25801219157741D-06 2 17 2 10 0.53388500064517D+00 -0.27426758071660D-06 3 17 2 10 0.17446300102037D+01 0.59352765346112D-06 1 18 2 10 -0.90819511059350D+00 -0.44958752794674D-01 2 18 2 10 0.93502320659138D+00 0.41300989148835D-01 3 18 2 10 -0.10273560672803D+01 0.56343722398483D-01 1 19 2 10 -0.90819511059349D+00 -0.44958752794674D-01 2 19 2 10 0.93502320659138D+00 0.41300989148836D-01 3 19 2 10 0.10273560672804D+01 -0.56343722398483D-01 1 20 2 10 0.52364748639404D+00 -0.25801219225536D-06 2 20 2 10 -0.53388500064516D+00 0.27426758185651D-06 3 20 2 10 0.17446300102037D+01 0.59352764946130D-06 1 1 3 10 0.41289204564323D+00 -0.71724842448312D-08 2 1 3 10 -0.22854053578514D+00 -0.41213474332516D-08 3 1 3 10 0.38087868836112D-14 -0.26161909103170D-14 1 2 3 10 -0.54279459024548D-14 0.50228484292461D-15 2 2 3 10 -0.41145951425809D-14 0.11734798298615D-16 3 2 3 10 0.38255253036798D+01 0.46427700820247D-07 1 3 3 10 0.26506167626628D+01 0.11469791548904D-07 2 3 3 10 -0.21683191281968D+00 0.24383217497395D-08 3 3 3 10 0.21302207907539D-13 0.12002745031396D-14 1 4 3 10 -0.15736440797375D-13 -0.63758046449103D-15 2 4 3 10 0.42408843537406D-14 -0.82426745566736D-16 3 4 3 10 -0.64698506258274D+00 -0.67594556878523D-07 1 5 3 10 -0.17498372172119D+00 0.44483839413100D+00 2 5 3 10 0.11342713471817D+00 -0.94681802555712D-01 3 5 3 10 -0.78131019418253D+01 0.22829431552099D+01 1 6 3 10 -0.17498372172109D+00 0.44483839413101D+00 2 6 3 10 0.11342713471813D+00 -0.94681802555716D-01 3 6 3 10 0.78131019418248D+01 -0.22829431552100D+01 1 7 3 10 0.68906983096762D+01 -0.18296233989490D+00 2 7 3 10 0.10794854753981D+01 -0.29037904891687D-01 3 7 3 10 0.22077548035897D+01 0.98614898976904D-02 1 8 3 10 0.68906983096762D+01 -0.18296233989490D+00 2 8 3 10 0.10794854753981D+01 -0.29037904891687D-01 3 8 3 10 -0.22077548035897D+01 -0.98614898976872D-02 1 9 3 10 -0.18113377482113D+01 0.74958074946402D-08 2 9 3 10 0.38115544765785D+00 0.24071870422305D-07 3 9 3 10 -0.13319629828517D-13 -0.30324107696114D-15 1 10 3 10 0.13463979783365D-12 -0.13877787807815D-16 2 10 3 10 -0.21213616157968D-13 0.69388939039070D-17 3 10 3 10 0.45156705309128D+02 0.00000000000000D+00 1 11 3 10 -0.36946569662604D-14 -0.35483597743481D-15 2 11 3 10 -0.15676970818884D-14 -0.19549068614946D-16 3 11 3 10 0.67541894467105D+00 -0.81973478188852D-16 1 12 3 10 -0.20606573664554D+01 0.64057402265046D-08 2 12 3 10 -0.17403278626412D+00 -0.87082646988567D-08 3 12 3 10 0.86964464215889D-16 -0.33938488086233D-17 1 13 3 10 -0.34985424832816D+01 -0.46949611660851D-01 2 13 3 10 -0.29534036729796D+01 -0.57447006603543D-01 3 13 3 10 0.23985564715927D+01 0.55815870487247D-01 1 14 3 10 0.42098203200070D+01 -0.16310421926306D-07 2 14 3 10 0.27702610682966D+01 -0.15214174910700D-07 3 14 3 10 0.11148623500516D+01 0.29365155690104D-07 1 15 3 10 -0.42098203200070D+01 0.16310421224412D-07 2 15 3 10 -0.27702610682966D+01 0.15214174947443D-07 3 15 3 10 0.11148623500517D+01 0.29365153637352D-07 1 16 3 10 -0.34985424832815D+01 -0.46949611660848D-01 2 16 3 10 -0.29534036729796D+01 -0.57447006603540D-01 3 16 3 10 -0.23985564715927D+01 -0.55815870487241D-01 1 17 3 10 -0.32019615082073D+01 0.37732333867713D-06 2 17 3 10 0.34957157651689D+01 -0.71307481536266D-06 3 17 3 10 0.26654984393296D+01 -0.10056048227564D-06 1 18 3 10 0.34417030988130D+01 -0.17217352796030D+00 2 18 3 10 -0.31649972223185D+01 0.10999950761531D+00 3 18 3 10 0.67939509470960D+00 -0.11016207830166D+00 1 19 3 10 -0.34417030988130D+01 0.17217352796029D+00 2 19 3 10 0.31649972223185D+01 -0.10999950761531D+00 3 19 3 10 0.67939509470968D+00 -0.11016207830167D+00 1 20 3 10 -0.32019615082073D+01 0.37732334136977D-06 2 20 3 10 0.34957157651689D+01 -0.71307481935555D-06 3 20 3 10 -0.26654984393296D+01 0.10056048801485D-06 1 1 1 11 0.70958520822952D-14 -0.63220806651172D-15 2 1 1 11 -0.67735916095512D-15 0.99318960120084D-16 3 1 1 11 0.90846730455016D+00 0.17265956918256D-07 1 2 1 11 0.32901829520357D+01 0.72004002872136D-08 2 2 1 11 -0.21474564783835D+00 0.47484874404875D-08 3 2 1 11 -0.31446858903255D-13 0.26291784226690D-14 1 3 1 11 -0.22527190515601D-13 -0.10591090309319D-14 2 3 1 11 0.49935103372865D-14 0.13492156830898D-15 3 3 1 11 0.12972833328332D+00 -0.97144954515180D-08 1 4 1 11 -0.13601446467443D+01 -0.22995527267699D-07 2 4 1 11 0.37924436509481D+00 0.10690203358317D-07 3 4 1 11 -0.40921129064925D-14 -0.12470532856663D-14 1 5 1 11 -0.36134755383845D+00 0.14193648446025D-01 2 5 1 11 0.13656873541772D+00 -0.32873551971114D-02 3 5 1 11 0.18848320615518D+01 -0.30947067888414D-01 1 6 1 11 0.36134755383845D+00 -0.14193648446024D-01 2 6 1 11 -0.13656873541771D+00 0.32873551971112D-02 3 6 1 11 0.18848320615519D+01 -0.30947067888411D-01 1 7 1 11 0.27925756026440D+01 0.97198684567998D+00 2 7 1 11 0.51572366327063D-01 0.20203100763491D-01 3 7 1 11 -0.10852874883877D+01 0.44291949282742D+00 1 8 1 11 -0.27925756026441D+01 -0.97198684568000D+00 2 8 1 11 -0.51572366327055D-01 -0.20203100763490D-01 3 8 1 11 -0.10852874883876D+01 0.44291949282744D+00 1 9 1 11 0.11753788541606D-14 0.70489285814994D-17 2 9 1 11 -0.10993320285440D-14 0.71133488321540D-16 3 9 1 11 -0.20606573664554D+01 -0.64057408328389D-08 1 10 1 11 0.69090348926710D-01 -0.39284865015120D-15 2 10 1 11 0.17034232713885D+00 0.42669546665963D-08 3 10 1 11 -0.36946569662604D-14 0.35483597743481D-15 1 11 1 11 0.95330703484904D+01 0.00000000000000D+00 2 11 1 11 -0.88947217536775D+00 -0.58242133947695D-07 3 11 1 11 -0.12826101439759D-12 0.13877787807815D-16 1 12 1 11 -0.99584634344910D-14 -0.88778845763452D-15 2 12 1 11 -0.35310747004814D-14 -0.78494788195344D-17 3 12 1 11 -0.18113509150141D+01 -0.72003992417535D-08 1 13 1 11 -0.63306122767650D+00 -0.23395148584476D-06 2 13 1 11 0.15520533430964D+00 0.11134938683658D-06 3 13 1 11 0.10691410880598D+01 0.50385592051523D-06 1 14 1 11 -0.64942645386992D-01 -0.36633641645378D-02 2 14 1 11 -0.80935195239606D+00 -0.29507372588116D-01 3 14 1 11 0.15212693177318D+01 -0.29378448157184D-01 1 15 1 11 -0.64942645386988D-01 -0.36633641645373D-02 2 15 1 11 -0.80935195239605D+00 -0.29507372588117D-01 3 15 1 11 -0.15212693177318D+01 0.29378448157184D-01 1 16 1 11 0.63306122767647D+00 0.23395148541671D-06 2 16 1 11 -0.15520533430962D+00 -0.11134938639998D-06 3 16 1 11 0.10691410880598D+01 0.50385591910319D-06 1 17 1 11 -0.40134067340285D+00 -0.17834422106554D-01 2 17 1 11 -0.26089825287155D+00 0.18487522871307D-01 3 17 1 11 0.14460629600099D+01 0.12006358334144D-01 1 18 1 11 -0.79845910098697D+00 -0.33932458031557D-09 2 18 1 11 0.10478578443022D+01 0.48356344485008D-09 3 18 1 11 0.23102472143652D+01 0.18413167566994D-07 1 19 1 11 -0.79845910098695D+00 -0.33932384929945D-09 2 19 1 11 0.10478578443021D+01 0.48356342335184D-09 3 19 1 11 -0.23102472143651D+01 -0.18413167107947D-07 1 20 1 11 0.40134067340283D+00 0.17834422106552D-01 2 20 1 11 0.26089825287153D+00 -0.18487522871308D-01 3 20 1 11 0.14460629600099D+01 0.12006358334140D-01 1 1 2 11 -0.67735916100682D-15 0.99752640989078D-16 2 1 2 11 -0.33230995208309D-16 0.16671883387190D-16 3 1 2 11 -0.10613762213917D+00 -0.62670758546944D-08 1 2 2 11 -0.25502894899915D+00 0.36554620898718D-08 2 2 2 11 0.25132987898859D+00 -0.17101941985569D-08 3 2 2 11 0.24024880685432D-14 0.98130468217683D-16 1 3 2 11 0.49935882030029D-14 0.13448788743999D-15 2 3 2 11 0.14789246552123D-13 -0.86517812465597D-15 3 3 2 11 -0.22769931938100D-01 -0.35771729974305D-08 1 4 2 11 0.18412347215845D+00 0.10766057215919D-07 2 4 2 11 0.92923385120088D-01 -0.13093649626805D-08 3 4 2 11 -0.18174883970317D-14 0.22509340259220D-15 1 5 2 11 0.19019581456350D+00 0.15482127518061D-02 2 5 2 11 0.15321258205104D+00 -0.26097329654372D-02 3 5 2 11 0.58900100571392D-01 -0.73454160392629D-02 1 6 2 11 -0.19019581456349D+00 -0.15482127518063D-02 2 6 2 11 -0.15321258205105D+00 0.26097329654365D-02 3 6 2 11 0.58900100571404D-01 -0.73454160392629D-02 1 7 2 11 -0.11197596839997D+00 0.24155456528834D-01 2 7 2 11 0.14158881793436D+01 0.10221397795320D+01 3 7 2 11 -0.38823464913788D+00 0.10808318930333D+00 1 8 2 11 0.11197596839998D+00 -0.24155456528833D-01 2 8 2 11 -0.14158881793438D+01 -0.10221397795320D+01 3 8 2 11 -0.38823464913781D+00 0.10808318930333D+00 1 9 2 11 -0.10993320285440D-14 0.71079278212916D-16 2 9 2 11 -0.10179887448946D-14 -0.34744987144163D-16 3 9 2 11 -0.17403278626412D+00 0.87082646786680D-08 1 10 2 11 -0.17034232713902D+00 0.42669546665963D-08 2 10 2 11 -0.46572736058250D+00 -0.33461367655510D-15 3 10 2 11 -0.15676970818884D-14 0.19549068614946D-16 1 11 2 11 -0.88947355820446D+00 0.45753696801657D-07 2 11 2 11 0.67571270235596D+01 0.00000000000000D+00 3 11 2 11 -0.42529898234077D-13 0.00000000000000D+00 1 12 2 11 -0.35310747001712D-14 -0.78494788195343D-17 2 12 2 11 -0.74478038344678D-14 0.45772965588921D-15 3 12 2 11 -0.38116860928562D+00 0.23451668448087D-07 1 13 2 11 0.52364748639407D+00 -0.25801219142257D-06 2 13 2 11 0.53388500064512D+00 -0.27426758059270D-06 3 13 2 11 0.17446300102037D+01 0.59352765360765D-06 1 14 2 11 -0.90819511059349D+00 -0.44958752794671D-01 2 14 2 11 -0.93502320659142D+00 -0.41300989148834D-01 3 14 2 11 0.10273560672803D+01 -0.56343722398487D-01 1 15 2 11 -0.90819511059348D+00 -0.44958752794672D-01 2 15 2 11 -0.93502320659140D+00 -0.41300989148834D-01 3 15 2 11 -0.10273560672804D+01 0.56343722398487D-01 1 16 2 11 -0.52364748639405D+00 0.25801219186264D-06 2 16 2 11 -0.53388500064511D+00 0.27426758184694D-06 3 16 2 11 0.17446300102037D+01 0.59352764947985D-06 1 17 2 11 -0.55778781506929D+00 0.36358835157183D-02 2 17 2 11 0.39716448006904D+00 -0.80859148335032D-03 3 17 2 11 -0.12976196960095D+01 -0.12426146858433D-02 1 18 2 11 0.86617686171479D+00 0.67154493171998D-08 2 18 2 11 -0.20412482979850D+00 -0.26603677537996D-08 3 18 2 11 -0.10915064791448D+01 -0.16027647111618D-07 1 19 2 11 0.86617686171475D+00 0.67154493061099D-08 2 19 2 11 -0.20412482979851D+00 -0.26603675733986D-08 3 19 2 11 0.10915064791448D+01 0.16027647059000D-07 1 20 2 11 0.55778781506926D+00 -0.36358835157192D-02 2 20 2 11 -0.39716448006904D+00 0.80859148335048D-03 3 20 2 11 -0.12976196960094D+01 -0.12426146858401D-02 1 1 3 11 0.26506167626628D+01 0.11469790962541D-07 2 1 3 11 0.21683191281970D+00 -0.24383217614415D-08 3 1 3 11 0.79397812249970D-14 -0.18474367630210D-14 1 2 3 11 -0.31446858903255D-13 0.26291784226690D-14 2 2 3 11 0.24024880685432D-14 0.98130468217683D-16 3 2 3 11 0.64698506258264D+00 0.67594544271706D-07 1 3 3 11 0.41289204564321D+00 -0.71724834906001D-08 2 3 3 11 0.22854053578514D+00 0.41213476182782D-08 3 3 3 11 0.10886474844336D-13 0.17208416827371D-14 1 4 3 11 -0.40921129048382D-14 -0.12505227326183D-14 2 4 3 11 -0.18174883962046D-14 0.23203229649611D-15 3 4 3 11 -0.38255253036795D+01 -0.46427711739040D-07 1 5 3 11 0.68906983096762D+01 -0.18296233989490D+00 2 5 3 11 -0.10794854753982D+01 0.29037904891686D-01 3 5 3 11 -0.22077548035897D+01 -0.98614898976909D-02 1 6 3 11 0.68906983096763D+01 -0.18296233989490D+00 2 6 3 11 -0.10794854753982D+01 0.29037904891686D-01 3 6 3 11 0.22077548035897D+01 0.98614898976879D-02 1 7 3 11 -0.17498372172128D+00 0.44483839413101D+00 2 7 3 11 -0.11342713471878D+00 0.94681802555717D-01 3 7 3 11 0.78131019418253D+01 -0.22829431552100D+01 1 8 3 11 -0.17498372172109D+00 0.44483839413103D+00 2 8 3 11 -0.11342713471871D+00 0.94681802555721D-01 3 8 3 11 -0.78131019418245D+01 0.22829431552101D+01 1 9 3 11 -0.20606573664554D+01 0.64057402011684D-08 2 9 3 11 0.17403278626412D+00 0.87082646786680D-08 3 9 3 11 -0.19603106763673D-14 0.19867222832537D-17 1 10 3 11 -0.36946569662604D-14 0.35483597743481D-15 2 10 3 11 -0.15676970818884D-14 0.19549068614946D-16 3 10 3 11 0.67541894467105D+00 0.81973478188852D-16 1 11 3 11 -0.12826101439759D-12 -0.13877787807815D-16 2 11 3 11 -0.42529898230768D-13 -0.69388939039072D-17 3 11 3 11 0.45156705309128D+02 0.00000000000000D+00 1 12 3 11 -0.18113377482113D+01 0.74958090153492D-08 2 12 3 11 -0.38115544765787D+00 -0.24071870087788D-07 3 12 3 11 0.15965043831260D-13 0.12319370380802D-14 1 13 3 11 0.32019615082074D+01 -0.37732333964820D-06 2 13 3 11 0.34957157651689D+01 -0.71307481521960D-06 3 13 3 11 0.26654984393297D+01 -0.10056048101643D-06 1 14 3 11 0.34417030988129D+01 -0.17217352796030D+00 2 14 3 11 0.31649972223185D+01 -0.10999950761531D+00 3 14 3 11 -0.67939509470961D+00 0.11016207830167D+00 1 15 3 11 -0.34417030988130D+01 0.17217352796030D+00 2 15 3 11 -0.31649972223185D+01 0.10999950761531D+00 3 15 3 11 -0.67939509470969D+00 0.11016207830167D+00 1 16 3 11 0.32019615082073D+01 -0.37732334106544D-06 2 16 3 11 0.34957157651689D+01 -0.71307481934047D-06 3 16 3 11 -0.26654984393298D+01 0.10056048890446D-06 1 17 3 11 0.34985424832815D+01 0.46949611660851D-01 2 17 3 11 -0.29534036729796D+01 -0.57447006603543D-01 3 17 3 11 0.23985564715927D+01 0.55815870487244D-01 1 18 3 11 0.42098203200071D+01 -0.16310425053309D-07 2 18 3 11 -0.27702610682966D+01 0.15214177198372D-07 3 18 3 11 -0.11148623500517D+01 -0.29365152158219D-07 1 19 3 11 -0.42098203200071D+01 0.16310425540112D-07 2 19 3 11 0.27702610682966D+01 -0.15214177254458D-07 3 19 3 11 -0.11148623500517D+01 -0.29365150811873D-07 1 20 3 11 0.34985424832814D+01 0.46949611660847D-01 2 20 3 11 -0.29534036729795D+01 -0.57447006603540D-01 3 20 3 11 -0.23985564715926D+01 -0.55815870487239D-01 1 1 1 12 -0.32901829520358D+01 -0.72003782375135D-08 2 1 1 12 0.21474564783803D+00 -0.47484901311467D-08 3 1 1 12 0.34472534203354D-14 -0.55350675762674D-14 1 2 1 12 -0.73453326743327D-17 -0.95659039590586D-15 2 2 1 12 -0.16726053255356D-14 -0.23997890050725D-16 3 2 1 12 -0.90846730455017D+00 -0.17265959310487D-07 1 3 1 12 -0.13601446467444D+01 -0.22995527748075D-07 2 3 1 12 0.37924436509465D+00 0.10690203270501D-07 3 3 1 12 0.53916139960052D-14 -0.61953963228450D-15 1 4 1 12 -0.63361902729571D-14 -0.21393717055070D-14 2 4 1 12 0.61749582429395D-14 0.43916642443632D-16 3 4 1 12 0.12972833328332D+00 -0.97144966945195D-08 1 5 1 12 -0.36134755383845D+00 0.14193648446027D-01 2 5 1 12 0.13656873541779D+00 -0.32873551971110D-02 3 5 1 12 0.18848320615518D+01 -0.30947067888409D-01 1 6 1 12 -0.36134755383845D+00 0.14193648446026D-01 2 6 1 12 0.13656873541779D+00 -0.32873551971109D-02 3 6 1 12 -0.18848320615519D+01 0.30947067888412D-01 1 7 1 12 -0.27925756026442D+01 -0.97198684568000D+00 2 7 1 12 -0.51572366326910D-01 -0.20203100763490D-01 3 7 1 12 0.10852874883876D+01 -0.44291949282744D+00 1 8 1 12 -0.27925756026442D+01 -0.97198684567999D+00 2 8 1 12 -0.51572366326913D-01 -0.20203100763490D-01 3 8 1 12 -0.10852874883875D+01 0.44291949282743D+00 1 9 1 12 0.69090348926738D-01 0.16382280544849D-15 2 9 1 12 0.17034232713894D+00 0.42669545453283D-08 3 9 1 12 -0.53761715406099D-14 -0.21592056029315D-14 1 10 1 12 -0.11799188844598D-14 -0.15227910941481D-17 2 10 1 12 -0.22541850778660D-14 0.10028820825179D-15 3 10 1 12 -0.20606573664554D+01 -0.64057402265046D-08 1 11 1 12 -0.99584634344910D-14 0.88778845763452D-15 2 11 1 12 -0.35310747001712D-14 0.87168405575227D-17 3 11 1 12 -0.18113509150141D+01 -0.72003994015764D-08 1 12 1 12 0.95330703484915D+01 0.00000000000000D+00 2 12 1 12 -0.88947217536779D+00 -0.58242133947695D-07 3 12 1 12 -0.36332196076885D-15 0.13877787807814D-16 1 13 1 12 -0.64942645387024D-01 -0.36633641645386D-02 2 13 1 12 -0.80935195239609D+00 -0.29507372588116D-01 3 13 1 12 0.15212693177318D+01 -0.29378448157184D-01 1 14 1 12 -0.63306122767650D+00 -0.23395148541087D-06 2 14 1 12 0.15520533430962D+00 0.11134938495755D-06 3 14 1 12 0.10691410880597D+01 0.50385591612073D-06 1 15 1 12 0.63306122767648D+00 0.23395148483519D-06 2 15 1 12 -0.15520533430962D+00 -0.11134938593159D-06 3 15 1 12 0.10691410880597D+01 0.50385591851297D-06 1 16 1 12 -0.64942645387016D-01 -0.36633641645378D-02 2 16 1 12 -0.80935195239608D+00 -0.29507372588116D-01 3 16 1 12 -0.15212693177318D+01 0.29378448157183D-01 1 17 1 12 -0.79845910098693D+00 -0.33932740740946D-09 2 17 1 12 0.10478578443022D+01 0.48356296444225D-09 3 17 1 12 0.23102472143651D+01 0.18413167623786D-07 1 18 1 12 -0.40134067340283D+00 -0.17834422106552D-01 2 18 1 12 -0.26089825287154D+00 0.18487522871309D-01 3 18 1 12 0.14460629600100D+01 0.12006358334137D-01 1 19 1 12 0.40134067340284D+00 0.17834422106553D-01 2 19 1 12 0.26089825287154D+00 -0.18487522871308D-01 3 19 1 12 0.14460629600100D+01 0.12006358334140D-01 1 20 1 12 -0.79845910098694D+00 -0.33932535320978D-09 2 20 1 12 0.10478578443022D+01 0.48356310067483D-09 3 20 1 12 -0.23102472143651D+01 -0.18413167510225D-07 1 1 2 12 0.25502894899883D+00 -0.36554647805310D-08 2 1 2 12 -0.25132987898845D+00 0.17101883416923D-08 3 1 2 12 0.45233782443037D-14 -0.63856442403685D-16 1 2 2 12 -0.16726053255356D-14 -0.24431570919719D-16 2 2 2 12 0.31703659452563D-14 0.25112429686895D-15 3 2 2 12 0.10613762213919D+00 0.62670757915063D-08 1 3 2 12 0.18412347215829D+00 0.10766057128104D-07 2 3 2 12 0.92923385120400D-01 -0.13093647913093D-08 3 3 2 12 0.21833617240230D-14 -0.12106047125223D-15 1 4 2 12 0.61750361084490D-14 0.43916642443632D-16 2 4 2 12 0.20458013182142D-13 -0.63228865952766D-15 3 4 2 12 -0.22769931938134D-01 -0.35771729998511D-08 1 5 2 12 0.19019581456357D+00 0.15482127518065D-02 2 5 2 12 0.15321258205105D+00 -0.26097329654344D-02 3 5 2 12 0.58900100571425D-01 -0.73454160392626D-02 1 6 2 12 0.19019581456357D+00 0.15482127518066D-02 2 6 2 12 0.15321258205105D+00 -0.26097329654348D-02 3 6 2 12 -0.58900100571430D-01 0.73454160392625D-02 1 7 2 12 0.11197596840013D+00 -0.24155456528833D-01 2 7 2 12 -0.14158881793438D+01 -0.10221397795320D+01 3 7 2 12 0.38823464913695D+00 -0.10808318930333D+00 1 8 2 12 0.11197596840012D+00 -0.24155456528833D-01 2 8 2 12 -0.14158881793438D+01 -0.10221397795320D+01 3 8 2 12 -0.38823464913695D+00 0.10808318930333D+00 1 9 2 12 -0.17034232713893D+00 0.42669545453283D-08 2 9 2 12 -0.46572736058257D+00 0.11489915743977D-15 3 9 2 12 0.57612210419001D-15 -0.81652653640183D-16 1 10 2 12 -0.22541850778660D-14 0.10023399814316D-15 2 10 2 12 -0.98169096551502D-15 0.18591655716692D-16 3 10 2 12 -0.17403278626412D+00 0.87082646988567D-08 1 11 2 12 -0.35310747000678D-14 0.87168405575228D-17 2 11 2 12 -0.74478038344678D-14 -0.48548523150483D-15 3 11 2 12 -0.38116860928562D+00 0.23451668646538D-07 1 12 2 12 -0.88947355820450D+00 0.45753696801657D-07 2 12 2 12 0.67571270235594D+01 0.00000000000000D+00 3 12 2 12 -0.21213616161274D-13 0.00000000000000D+00 1 13 2 12 -0.90819511059352D+00 -0.44958752794671D-01 2 13 2 12 -0.93502320659138D+00 -0.41300989148834D-01 3 13 2 12 0.10273560672804D+01 -0.56343722398486D-01 1 14 2 12 0.52364748639405D+00 -0.25801219329813D-06 2 14 2 12 0.53388500064515D+00 -0.27426758237648D-06 3 14 2 12 0.17446300102037D+01 0.59352764494530D-06 1 15 2 12 -0.52364748639404D+00 0.25801219233276D-06 2 15 2 12 -0.53388500064515D+00 0.27426758153221D-06 3 15 2 12 0.17446300102037D+01 0.59352764929800D-06 1 16 2 12 -0.90819511059351D+00 -0.44958752794671D-01 2 16 2 12 -0.93502320659138D+00 -0.41300989148834D-01 3 16 2 12 -0.10273560672803D+01 0.56343722398486D-01 1 17 2 12 0.86617686171478D+00 0.67154488298531D-08 2 17 2 12 -0.20412482979854D+00 -0.26603676614639D-08 3 17 2 12 -0.10915064791448D+01 -0.16027647282005D-07 1 18 2 12 -0.55778781506927D+00 0.36358835157207D-02 2 18 2 12 0.39716448006900D+00 -0.80859148335077D-03 3 18 2 12 -0.12976196960094D+01 -0.12426146858367D-02 1 19 2 12 0.55778781506927D+00 -0.36358835157195D-02 2 19 2 12 -0.39716448006900D+00 0.80859148335036D-03 3 19 2 12 -0.12976196960095D+01 -0.12426146858401D-02 1 20 2 12 0.86617686171477D+00 0.67154489695551D-08 2 20 2 12 -0.20412482979855D+00 -0.26603676878135D-08 3 20 2 12 0.10915064791448D+01 0.16027647475865D-07 1 1 3 12 0.34472534203354D-14 -0.55350675762674D-14 2 1 3 12 0.45233782443037D-14 -0.63856442403685D-16 3 1 3 12 -0.64698506258255D+00 -0.67594556891292D-07 1 2 3 12 -0.26506167626628D+01 -0.11469793354771D-07 2 2 3 12 -0.21683191281968D+00 0.24383216982534D-08 3 2 3 12 -0.72517773127350D-16 -0.16652828872896D-14 1 3 3 12 0.53916139976595D-14 -0.62300907923645D-15 2 3 3 12 0.21833617231958D-14 -0.11412157734832D-15 3 3 3 12 -0.38255253036797D+01 -0.46427712647055D-07 1 4 3 12 0.41289204564321D+00 -0.71724847336016D-08 2 4 3 12 0.22854053578510D+00 0.41213476158576D-08 3 4 3 12 0.24714361946420D-14 -0.18768375064151D-14 1 5 3 12 0.68906983096762D+01 -0.18296233989490D+00 2 5 3 12 -0.10794854753981D+01 0.29037904891687D-01 3 5 3 12 -0.22077548035897D+01 -0.98614898976875D-02 1 6 3 12 -0.68906983096763D+01 0.18296233989490D+00 2 6 3 12 0.10794854753981D+01 -0.29037904891687D-01 3 6 3 12 -0.22077548035897D+01 -0.98614898976898D-02 1 7 3 12 0.17498372172109D+00 -0.44483839413103D+00 2 7 3 12 0.11342713471785D+00 -0.94681802555721D-01 3 7 3 12 -0.78131019418248D+01 0.22829431552101D+01 1 8 3 12 -0.17498372172105D+00 0.44483839413102D+00 2 8 3 12 -0.11342713471785D+00 0.94681802555720D-01 3 8 3 12 -0.78131019418249D+01 0.22829431552101D+01 1 9 3 12 -0.53761715406099D-14 -0.21592056029315D-14 2 9 3 12 0.57612210419001D-15 -0.81652653640183D-16 3 9 3 12 0.67541894467108D+00 -0.20915786943188D-16 1 10 3 12 -0.20606573664554D+01 0.64057408075027D-08 2 10 3 12 0.17403278626412D+00 0.87082646988567D-08 3 10 3 12 0.86964464215889D-16 0.33938488086233D-17 1 11 3 12 -0.18113377482113D+01 0.74958088555263D-08 2 11 3 12 -0.38115544765787D+00 -0.24071869889337D-07 3 11 3 12 0.15965043831260D-13 -0.12319370380802D-14 1 12 3 12 -0.36332196076884D-15 -0.13877787807814D-16 2 12 3 12 -0.21213616157965D-13 -0.69388939039072D-17 3 12 3 12 0.45156705309128D+02 0.00000000000000D+00 1 13 3 12 0.34417030988130D+01 -0.17217352796030D+00 2 13 3 12 0.31649972223185D+01 -0.10999950761531D+00 3 13 3 12 -0.67939509470965D+00 0.11016207830167D+00 1 14 3 12 0.32019615082073D+01 -0.37732334405485D-06 2 14 3 12 0.34957157651689D+01 -0.71307482386808D-06 3 14 3 12 0.26654984393297D+01 -0.10056049528361D-06 1 15 3 12 0.32019615082073D+01 -0.37732334166780D-06 2 15 3 12 0.34957157651689D+01 -0.71307481951884D-06 3 15 3 12 -0.26654984393297D+01 0.10056048745395D-06 1 16 3 12 -0.34417030988130D+01 0.17217352796030D+00 2 16 3 12 -0.31649972223185D+01 0.10999950761531D+00 3 16 3 12 -0.67939509470965D+00 0.11016207830167D+00 1 17 3 12 0.42098203200070D+01 -0.16310425024273D-07 2 17 3 12 -0.27702610682966D+01 0.15214177021045D-07 3 17 3 12 -0.11148623500516D+01 -0.29365151918631D-07 1 18 3 12 0.34985424832815D+01 0.46949611660844D-01 2 18 3 12 -0.29534036729796D+01 -0.57447006603537D-01 3 18 3 12 0.23985564715927D+01 0.55815870487235D-01 1 19 3 12 0.34985424832815D+01 0.46949611660847D-01 2 19 3 12 -0.29534036729796D+01 -0.57447006603540D-01 3 19 3 12 -0.23985564715927D+01 -0.55815870487240D-01 1 20 3 12 -0.42098203200070D+01 0.16310425110078D-07 2 20 3 12 0.27702610682966D+01 -0.15214176830655D-07 3 20 3 12 -0.11148623500516D+01 -0.29365150948988D-07 1 1 1 13 0.10668548975768D+01 -0.63037185960043D-06 2 1 1 13 0.36123798914906D+00 0.60182699063078D-06 3 1 1 13 -0.10142356701901D+01 -0.73102491277601D-06 1 2 1 13 -0.66066883358689D+00 0.58092146726287D-02 2 2 1 13 -0.23438760987992D+00 -0.19385491922702D-02 3 2 1 13 -0.13585071658991D+01 -0.74788430588298D-03 1 3 1 13 -0.15275697490881D+01 -0.64572596198172D-02 2 3 1 13 0.49549009324285D+00 -0.24006154107443D-01 3 3 1 13 0.19271974120552D+00 -0.13899459436934D-01 1 4 1 13 0.83722932351964D+00 0.63653622607135D-06 2 4 1 13 0.34428420488000D+00 0.37372532919880D-06 3 4 1 13 -0.17584629655880D+01 0.13190428432330D-06 1 5 1 13 0.51358504712510D+01 0.13474928096314D-01 2 5 1 13 -0.53370378876704D+00 -0.96362797232677D-02 3 5 1 13 -0.49749972773592D+00 -0.40974196505354D-01 1 6 1 13 0.73418429166609D+00 0.27675484520820D-01 2 6 1 13 -0.15938290873739D+00 0.20789309500504D-01 3 6 1 13 -0.42221527349252D+01 -0.10684640142366D-01 1 7 1 13 -0.46510512037135D+01 -0.15901986239627D-01 2 7 1 13 0.68345312777839D+00 -0.97797549474339D-02 3 7 1 13 -0.62141502835397D+00 -0.50205480190897D-01 1 8 1 13 -0.64261471368817D+00 -0.39035000447825D-01 2 8 1 13 -0.15300371689550D+00 -0.77025902269862D-01 3 8 1 13 -0.38966692907452D+01 -0.11517268690804D-01 1 9 1 13 0.79845861100862D+00 -0.72611612290693D-06 2 9 1 13 0.86617816800294D+00 0.31855261411321D-06 3 9 1 13 0.42098323762825D+01 0.18699115756590D-05 1 10 1 13 -0.40134067866259D+00 0.53503290406861D-01 2 10 1 13 0.55778767451164D+00 0.10907649972752D-01 3 10 1 13 -0.34985486325795D+01 0.14084884797158D+00 1 11 1 13 -0.63306122767650D+00 0.23395148724294D-06 2 11 1 13 0.52364748639407D+00 0.25801219101664D-06 3 11 1 13 0.32019615082074D+01 0.37732333836451D-06 1 12 1 13 -0.64942645387024D-01 0.36633641645379D-02 2 12 1 13 -0.90819511059352D+00 0.44958752794672D-01 3 12 1 13 0.34417030988130D+01 0.17217352796030D+00 1 13 1 13 0.15006438807181D+02 0.00000000000000D+00 2 13 1 13 0.68864760119759D+01 0.18971069931448D+00 3 13 1 13 -0.12907953016802D+01 -0.16577648637509D+00 1 14 1 13 -0.67478870946504D+00 0.30054587356225D-02 2 14 1 13 -0.36442224451329D+00 0.13700804630378D-02 3 14 1 13 0.81563602512016D+00 0.93795643715308D-02 1 15 1 13 0.34820445651950D-14 -0.14972163595795D-01 2 15 1 13 -0.42015320180647D-01 -0.24734312916945D-02 3 15 1 13 0.14086396224381D+01 -0.12527673441751D-01 1 16 1 13 0.36179266440758D+00 -0.67505641235514D-16 2 16 1 13 -0.68287835135632D-01 -0.11803477806568D-05 3 16 1 13 0.22178120985564D+00 -0.20237112453163D-06 1 17 1 13 0.29394031008974D+01 0.99115321008070D-16 2 17 1 13 -0.19436888327661D+01 0.38948290896356D-01 3 17 1 13 0.46819130833404D-01 0.91282937840375D-02 1 18 1 13 0.13508623170114D-13 0.19408568722634D-06 2 18 1 13 0.92517370870155D+00 -0.44206987265906D-06 3 18 1 13 0.17538159518834D+01 0.60820574656837D-06 1 19 1 13 0.20020795220701D-01 -0.10028013879135D-06 2 19 1 13 -0.19009642624043D-01 -0.53128080730073D-02 3 19 1 13 0.93322813237245D+00 -0.12406512192839D-02 1 20 1 13 0.33116110735534D+00 -0.13483226342345D-01 2 20 1 13 0.64995108599878D-01 0.17700200239526D-01 3 20 1 13 -0.15997970813980D+00 0.31200264480519D-02 1 1 2 13 0.62660586630814D+00 -0.44614389839883D-06 2 1 2 13 0.37565393369078D+00 0.18546162993240D-06 3 1 2 13 -0.74414560792020D-02 -0.41294039798182D-06 1 2 2 13 -0.67176802529488D+00 0.52547534079835D-02 2 2 2 13 0.26721322086045D+00 -0.67301329828254D-03 3 2 2 13 -0.16166081741405D+00 -0.99471786066703D-03 1 3 2 13 -0.11310439235665D+00 -0.27092240302348D-01 2 3 2 13 -0.83235442486988D+00 0.12606854493732D-01 3 3 2 13 -0.10948572598822D+01 -0.12558143074972D-01 1 4 2 13 0.86353847218524D+00 0.22690739862683D-06 2 4 2 13 0.12389191950369D+00 -0.16777393022930D-07 3 4 2 13 0.16706368605347D+00 0.20213450859821D-06 1 5 2 13 0.14573982766881D+01 0.13075103789416D-01 2 5 2 13 0.91062083360317D-01 -0.22416544868934D-02 3 5 2 13 -0.78861004528221D+00 -0.48875958825168D-01 1 6 2 13 0.20463990501137D+00 0.34349079966531D-01 2 6 2 13 -0.16252001627054D+00 0.11416271009605D-01 3 6 2 13 -0.28426666852924D+01 -0.45046507557074D-02 1 7 2 13 -0.24317149100595D+01 -0.21193322633141D-01 2 7 2 13 -0.12131103227847D+01 -0.78851080443435D-02 3 7 2 13 -0.77267282968484D+00 -0.64486680591523D-01 1 8 2 13 -0.40576931150239D+00 -0.10221440279522D+00 2 8 2 13 -0.24423588943716D-01 -0.10412357639943D+00 3 8 2 13 -0.30359982702477D+01 -0.79447551651899D-02 1 9 2 13 0.10478562970400D+01 0.33718615556650D-06 2 9 2 13 0.20412257977079D+00 -0.38833377350738D-08 3 9 2 13 0.27702728437013D+01 0.61738257851014D-06 1 10 2 13 0.26089769289023D+00 0.55462572263883D-01 2 10 2 13 0.39716460783178D+00 0.24257768962601D-02 3 10 2 13 -0.29534081319711D+01 0.17234104266561D+00 1 11 2 13 0.15520533430964D+00 -0.11134938726679D-06 2 11 2 13 0.53388500064512D+00 0.27426758021800D-06 3 11 2 13 0.34957157651689D+01 0.71307481345712D-06 1 12 2 13 -0.80935195239609D+00 0.29507372588117D-01 2 12 2 13 -0.93502320659138D+00 0.41300989148834D-01 3 12 2 13 0.31649972223185D+01 0.10999950761531D+00 1 13 2 13 0.68864779151044D+01 -0.18971120964227D+00 2 13 2 13 0.14365659165686D+02 0.00000000000000D+00 3 13 2 13 0.19885876466293D+01 0.19398185013989D+00 1 14 2 13 -0.36442300744289D+00 0.13691846451493D-02 2 14 2 13 0.88768276842115D+00 0.56518251296560D-03 3 14 2 13 0.61484961140266D+00 0.19261466535199D-01 1 15 2 13 0.42015320180646D-01 -0.24734312916945D-02 2 15 2 13 -0.82111061247810D-15 0.46464540167991D-01 3 15 2 13 0.63675814312606D+00 -0.18902846730645D-01 1 16 2 13 -0.68287835135632D-01 0.11803477806323D-05 2 16 2 13 -0.24051314802434D-01 -0.11293486094590D-14 3 16 2 13 -0.43610611744183D-01 -0.17347005596275D-06 1 17 2 13 0.19436888327661D+01 0.38948290896356D-01 2 17 2 13 -0.67630302568860D+01 0.19527433334913D-17 3 17 2 13 0.14443674954483D+00 0.11416482061087D-01 1 18 2 13 0.92517370870155D+00 0.44206987050103D-06 2 18 2 13 0.46160340852430D-14 0.43762548185386D-06 3 18 2 13 0.20212138681151D+00 0.29871211834697D-06 1 19 2 13 0.19009638188727D-01 -0.53125567924776D-02 2 19 2 13 -0.58986358954180D-01 0.14350436274848D-06 3 19 2 13 0.41405230449544D+00 0.84084633348851D-02 1 20 2 13 -0.64993224846046D-01 -0.17697402654779D-01 2 20 2 13 -0.56647615393749D-01 0.19282002014646D-01 3 20 2 13 -0.86378308593939D-01 0.17418634182744D-02 1 1 3 13 -0.10785564770849D+01 0.33993420580828D-06 2 1 3 13 0.46771224625458D+00 0.77575138909562D-06 3 1 3 13 0.17515671466157D+00 0.67991553915492D-06 1 2 3 13 -0.80663723739248D+00 -0.65285290862640D-02 2 2 3 13 0.24739921605507D+00 0.21134327938221D-02 3 2 3 13 0.21372329087677D+00 0.37789498105824D-02 1 3 3 13 0.25142281874029D+00 0.69760145231565D-02 2 3 3 13 -0.86237266963271D+00 -0.10810685967263D-01 3 3 3 13 -0.23982246383876D+01 -0.24477481513504D-01 1 4 3 13 -0.11093678603688D+01 -0.28405314997881D-06 2 4 3 13 0.61624736641726D+00 0.73002893090891D-07 3 4 3 13 -0.30191144601133D+00 -0.48429959661434D-06 1 5 3 13 -0.55412559341254D+00 -0.45925951970454D-01 2 5 3 13 -0.95920887648790D+00 -0.36209539711455D-01 3 5 3 13 0.38543492098478D+01 0.24961300556862D-01 1 6 3 13 -0.18464602830797D+01 -0.13801012644521D-01 2 6 3 13 -0.25795522233825D+00 -0.51648474989791D-02 3 6 3 13 -0.30555578378943D+00 -0.15861160436610D-01 1 7 3 13 -0.54457476066143D+00 -0.32243085944305D-01 2 7 3 13 -0.83142332788890D+00 -0.63777950819950D-01 3 7 3 13 -0.43358483535489D+01 -0.26942192371761D-01 1 8 3 13 -0.11749824647070D+01 -0.16782858801057D-01 2 8 3 13 -0.39263645059178D+00 -0.36584022370916D-01 3 8 3 13 0.20019335293066D+00 0.74632070191073D-01 1 9 3 13 0.23102469375356D+01 0.16841861482629D-06 2 9 3 13 0.10915050290647D+01 -0.97442887094145D-06 3 9 3 13 0.11148553456062D+01 0.50408510292676D-06 1 10 3 13 -0.14460635025581D+01 0.36019086614240D-01 2 10 3 13 -0.12976185230743D+01 0.37278351710205D-02 3 10 3 13 0.23985556697210D+01 -0.16744757717882D+00 1 11 3 13 0.10691410880598D+01 -0.50385592193596D-06 2 11 3 13 0.17446300102037D+01 -0.59352765546034D-06 3 11 3 13 0.26654984393297D+01 0.10056047907353D-06 1 12 3 13 0.15212693177318D+01 0.29378448157181D-01 2 12 3 13 0.10273560672804D+01 0.56343722398485D-01 3 12 3 13 -0.67939509470965D+00 -0.11016207830167D+00 1 13 3 13 -0.12907705592794D+01 0.16577756281318D+00 2 13 3 13 0.19886166343829D+01 -0.19398128188652D+00 3 13 3 13 0.15247819034118D+02 0.00000000000000D+00 1 14 3 13 0.81563612093760D+00 0.93784244454300D-02 2 14 3 13 0.61484764818829D+00 0.19261892934483D-01 3 14 3 13 -0.39852344590290D+00 0.22487926582551D-02 1 15 3 13 0.14086396224381D+01 0.12527673441752D-01 2 15 3 13 0.63675814312606D+00 0.18902846730645D-01 3 15 3 13 0.34190820673392D-14 0.92826278285585D-02 1 16 3 13 -0.22178120985566D+00 -0.20237112452990D-06 2 16 3 13 0.43610611744182D-01 -0.17347005596275D-06 3 16 3 13 -0.10161085321636D+01 -0.24240369269476D-17 1 17 3 13 -0.46819130833405D-01 0.91282937840375D-02 2 17 3 13 0.14443674954483D+00 -0.11416482061087D-01 3 17 3 13 0.17321575636989D+01 0.15214864500241D-15 1 18 3 13 0.17538159518834D+01 -0.60820575075610D-06 2 18 3 13 -0.20212138681150D+00 0.29871211834610D-06 3 18 3 13 0.16315291088080D-13 0.54291375846955D-06 1 19 3 13 0.93322963471947D+00 0.12403348810597D-02 2 19 3 13 -0.41405356045998D+00 0.84096525770970D-02 3 19 3 13 0.86695235884171D-01 -0.89247515056943D-08 1 20 3 13 -0.15997690726364D+00 0.31207405124738D-02 2 20 3 13 0.86377337554126D-01 -0.17427755476425D-02 3 20 3 13 -0.24682108153475D+00 -0.17144360058820D-01 1 1 1 14 0.66066883358690D+00 -0.58092146726291D-02 2 1 1 14 0.23438760987990D+00 0.19385491922700D-02 3 1 1 14 0.13585071658990D+01 0.74788430588034D-03 1 2 1 14 -0.10668548975769D+01 0.63037186189355D-06 2 2 1 14 -0.36123798914905D+00 -0.60182699571644D-06 3 2 1 14 0.10142356701900D+01 0.73102491628637D-06 1 3 1 14 0.83722932351963D+00 0.63653622092170D-06 2 3 1 14 0.34428420488003D+00 0.37372532533053D-06 3 3 1 14 -0.17584629655881D+01 0.13190429793942D-06 1 4 1 14 -0.15275697490880D+01 -0.64572596198214D-02 2 4 1 14 0.49549009324290D+00 -0.24006154107443D-01 3 4 1 14 0.19271974120558D+00 -0.13899459436936D-01 1 5 1 14 0.51358504712508D+01 0.13474928096312D-01 2 5 1 14 -0.53370378876714D+00 -0.96362797232665D-02 3 5 1 14 -0.49749972773550D+00 -0.40974196505355D-01 1 6 1 14 -0.73418429166607D+00 -0.27675484520820D-01 2 6 1 14 0.15938290873739D+00 -0.20789309500504D-01 3 6 1 14 0.42221527349251D+01 0.10684640142367D-01 1 7 1 14 0.46510512037136D+01 0.15901986239633D-01 2 7 1 14 -0.68345312777788D+00 0.97797549474560D-02 3 7 1 14 0.62141502835400D+00 0.50205480190901D-01 1 8 1 14 -0.64261471368817D+00 -0.39035000447814D-01 2 8 1 14 -0.15300371689550D+00 -0.77025902269862D-01 3 8 1 14 -0.38966692907452D+01 -0.11517268690801D-01 1 9 1 14 -0.40134067866259D+00 0.53503290406859D-01 2 9 1 14 0.55778767451162D+00 0.10907649972754D-01 3 9 1 14 -0.34985486325795D+01 0.14084884797157D+00 1 10 1 14 0.79845861100860D+00 -0.72611612781475D-06 2 10 1 14 0.86617816800298D+00 0.31855261002329D-06 3 10 1 14 0.42098323762825D+01 0.18699115688602D-05 1 11 1 14 -0.64942645386992D-01 0.36633641645371D-02 2 11 1 14 -0.90819511059349D+00 0.44958752794672D-01 3 11 1 14 0.34417030988129D+01 0.17217352796030D+00 1 12 1 14 -0.63306122767650D+00 0.23395148680906D-06 2 12 1 14 0.52364748639405D+00 0.25801219289221D-06 3 12 1 14 0.32019615082073D+01 0.37732334277115D-06 1 13 1 14 -0.67478870946504D+00 0.30054587356253D-02 2 13 1 14 -0.36442224451329D+00 0.13700804630355D-02 3 13 1 14 0.81563602512016D+00 0.93795643715263D-02 1 14 1 14 0.15006438807181D+02 0.00000000000000D+00 2 14 1 14 0.68864760119764D+01 0.18971069931448D+00 3 14 1 14 -0.12907953016798D+01 -0.16577648637509D+00 1 15 1 14 0.36179266440758D+00 0.31027177623688D-15 2 15 1 14 -0.68287835135632D-01 -0.11803477806966D-05 3 15 1 14 0.22178120985564D+00 -0.20237112341084D-06 1 16 1 14 0.34030378788029D-14 -0.14972163595794D-01 2 16 1 14 -0.42015320180648D-01 -0.24734312916946D-02 3 16 1 14 0.14086396224381D+01 -0.12527673441751D-01 1 17 1 14 -0.55179202615609D-14 0.19408569639398D-06 2 17 1 14 0.92517370870153D+00 -0.44206987052279D-06 3 17 1 14 0.17538159518834D+01 0.60820574946410D-06 1 18 1 14 0.29394031008973D+01 -0.27659277224051D-16 2 18 1 14 -0.19436888327661D+01 0.38948290896356D-01 3 18 1 14 0.46819130833406D-01 0.91282937840370D-02 1 19 1 14 0.33116110735535D+00 -0.13483226342344D-01 2 19 1 14 0.64995108599880D-01 0.17700200239526D-01 3 19 1 14 -0.15997970813981D+00 0.31200264480518D-02 1 20 1 14 0.20020795220702D-01 -0.10028013876332D-06 2 20 1 14 -0.19009642624042D-01 -0.53128080730072D-02 3 20 1 14 0.93322813237245D+00 -0.12406512192839D-02 1 1 2 14 0.67176802529486D+00 -0.52547534079837D-02 2 1 2 14 -0.26721322086050D+00 0.67301329828311D-03 3 1 2 14 0.16166081741408D+00 0.99471786066901D-03 1 2 2 14 -0.62660586630813D+00 0.44614389330450D-06 2 2 2 14 -0.37565393369068D+00 -0.18546162831718D-06 3 2 2 14 0.74414560792437D-02 0.41294039096162D-06 1 3 2 14 0.86353847218527D+00 0.22690739475855D-06 2 3 2 14 0.12389191950372D+00 -0.16777394971728D-07 3 3 2 14 0.16706368605354D+00 0.20213449784616D-06 1 4 2 14 -0.11310439235659D+00 -0.27092240302348D-01 2 4 2 14 -0.83235442486996D+00 0.12606854493732D-01 3 4 2 14 -0.10948572598823D+01 -0.12558143074973D-01 1 5 2 14 0.14573982766880D+01 0.13075103789417D-01 2 5 2 14 0.91062083360494D-01 -0.22416544868948D-02 3 5 2 14 -0.78861004528200D+00 -0.48875958825168D-01 1 6 2 14 -0.20463990501137D+00 -0.34349079966532D-01 2 6 2 14 0.16252001627054D+00 -0.11416271009605D-01 3 6 2 14 0.28426666852924D+01 0.45046507557082D-02 1 7 2 14 0.24317149100601D+01 0.21193322633163D-01 2 7 2 14 0.12131103227848D+01 0.78851080443665D-02 3 7 2 14 0.77267282968486D+00 0.64486680591531D-01 1 8 2 14 -0.40576931150239D+00 -0.10221440279522D+00 2 8 2 14 -0.24423588943704D-01 -0.10412357639943D+00 3 8 2 14 -0.30359982702477D+01 -0.79447551651893D-02 1 9 2 14 0.26089769289022D+00 0.55462572263886D-01 2 9 2 14 0.39716460783179D+00 0.24257768962606D-02 3 9 2 14 -0.29534081319711D+01 0.17234104266560D+00 1 10 2 14 0.10478562970400D+01 0.33718615147658D-06 2 10 2 14 0.20412257977079D+00 -0.38833365847214D-08 3 10 2 14 0.27702728437014D+01 0.61738257422141D-06 1 11 2 14 -0.80935195239606D+00 0.29507372588117D-01 2 11 2 14 -0.93502320659142D+00 0.41300989148835D-01 3 11 2 14 0.31649972223185D+01 0.10999950761531D+00 1 12 2 14 0.15520533430962D+00 -0.11134938538776D-06 2 12 2 14 0.53388500064515D+00 0.27426758200178D-06 3 12 2 14 0.34957157651689D+01 0.71307482210560D-06 1 13 2 14 -0.36442300744289D+00 0.13691846451470D-02 2 13 2 14 0.88768276842115D+00 0.56518251296936D-03 3 13 2 14 0.61484961140266D+00 0.19261466535198D-01 1 14 2 14 0.68864779151048D+01 -0.18971120964227D+00 2 14 2 14 0.14365659165686D+02 0.00000000000000D+00 3 14 2 14 0.19885876466297D+01 0.19398185013989D+00 1 15 2 14 -0.68287835135632D-01 0.11803477805926D-05 2 15 2 14 -0.24051314802437D-01 -0.57866455103657D-15 3 15 2 14 -0.43610611744181D-01 -0.17347005593167D-06 1 16 2 14 0.42015320180645D-01 -0.24734312916946D-02 2 16 2 14 -0.92508327641555D-15 0.46464540167991D-01 3 16 2 14 0.63675814312606D+00 -0.18902846730645D-01 1 17 2 14 0.92517370870153D+00 0.44206987263731D-06 2 17 2 14 -0.86120091221411D-14 0.43762547958400D-06 3 17 2 14 0.20212138681151D+00 0.29871211898064D-06 1 18 2 14 0.19436888327661D+01 0.38948290896356D-01 2 18 2 14 -0.67630302568858D+01 0.17619068779888D-16 3 18 2 14 0.14443674954483D+00 0.11416482061087D-01 1 19 2 14 -0.64993224846044D-01 -0.17697402654779D-01 2 19 2 14 -0.56647615393739D-01 0.19282002014645D-01 3 19 2 14 -0.86378308593938D-01 0.17418634182743D-02 1 20 2 14 0.19009638188729D-01 -0.53125567924775D-02 2 20 2 14 -0.58986358954178D-01 0.14350436275827D-06 3 20 2 14 0.41405230449544D+00 0.84084633348852D-02 1 1 3 14 0.80663723739242D+00 0.65285290862613D-02 2 1 3 14 -0.24739921605504D+00 -0.21134327938201D-02 3 1 3 14 -0.21372329087670D+00 -0.37789498105809D-02 1 2 3 14 0.10785564770849D+01 -0.33993420229488D-06 2 2 3 14 -0.46771224625454D+00 -0.77575139611627D-06 3 2 3 14 -0.17515671466158D+00 -0.67991553254264D-06 1 3 3 14 -0.11093678603689D+01 -0.28405313636617D-06 2 3 3 14 0.61624736641733D+00 0.73002882338838D-07 3 3 3 14 -0.30191144601141D+00 -0.48429957261514D-06 1 4 3 14 0.25142281874035D+00 0.69760145231549D-02 2 4 3 14 -0.86237266963280D+00 -0.10810685967263D-01 3 4 3 14 -0.23982246383876D+01 -0.24477481513504D-01 1 5 3 14 -0.55412559341211D+00 -0.45925951970455D-01 2 5 3 14 -0.95920887648769D+00 -0.36209539711455D-01 3 5 3 14 0.38543492098480D+01 0.24961300556863D-01 1 6 3 14 0.18464602830797D+01 0.13801012644522D-01 2 6 3 14 0.25795522233826D+00 0.51648474989799D-02 3 6 3 14 0.30555578378938D+00 0.15861160436613D-01 1 7 3 14 0.54457476066148D+00 0.32243085944309D-01 2 7 3 14 0.83142332788892D+00 0.63777950819958D-01 3 7 3 14 0.43358483535483D+01 0.26942192371734D-01 1 8 3 14 -0.11749824647070D+01 -0.16782858801055D-01 2 8 3 14 -0.39263645059175D+00 -0.36584022370915D-01 3 8 3 14 0.20019335293054D+00 0.74632070191078D-01 1 9 3 14 -0.14460635025580D+01 0.36019086614232D-01 2 9 3 14 -0.12976185230743D+01 0.37278351710141D-02 3 9 3 14 0.23985556697210D+01 -0.16744757717880D+00 1 10 3 14 0.23102469375356D+01 0.16841860806917D-06 2 10 3 14 0.10915050290647D+01 -0.97442887523018D-06 3 10 3 14 0.11148553456062D+01 0.50408509582353D-06 1 11 3 14 0.15212693177318D+01 0.29378448157182D-01 2 11 3 14 0.10273560672803D+01 0.56343722398486D-01 3 11 3 14 -0.67939509470961D+00 -0.11016207830167D+00 1 12 3 14 0.10691410880597D+01 -0.50385591753800D-06 2 12 3 14 0.17446300102037D+01 -0.59352764679798D-06 3 12 3 14 0.26654984393297D+01 0.10056049334072D-06 1 13 3 14 0.81563612093760D+00 0.93784244454256D-02 2 13 3 14 0.61484764818829D+00 0.19261892934482D-01 3 13 3 14 -0.39852344590290D+00 0.22487926582523D-02 1 14 3 14 -0.12907705592791D+01 0.16577756281318D+00 2 14 3 14 0.19886166343832D+01 -0.19398128188652D+00 3 14 3 14 0.15247819034117D+02 0.00000000000000D+00 1 15 3 14 -0.22178120985566D+00 -0.20237112340911D-06 2 15 3 14 0.43610611744184D-01 -0.17347005593167D-06 3 15 3 14 -0.10161085321636D+01 0.17284015172984D-15 1 16 3 14 0.14086396224381D+01 0.12527673441751D-01 2 16 3 14 0.63675814312606D+00 0.18902846730645D-01 3 16 3 14 0.47906314417847D-14 0.92826278285592D-02 1 17 3 14 0.17538159518834D+01 -0.60820574786038D-06 2 17 3 14 -0.20212138681150D+00 0.29871211897977D-06 3 17 3 14 -0.34303946999342D-13 0.54291375536107D-06 1 18 3 14 -0.46819130833404D-01 0.91282937840370D-02 2 18 3 14 0.14443674954483D+00 -0.11416482061087D-01 3 18 3 14 0.17321575636988D+01 0.66092214381381D-16 1 19 3 14 -0.15997690726365D+00 0.31207405124737D-02 2 19 3 14 0.86377337554128D-01 -0.17427755476426D-02 3 19 3 14 -0.24682108153473D+00 -0.17144360058820D-01 1 20 3 14 0.93322963471947D+00 0.12403348810597D-02 2 20 3 14 -0.41405356045998D+00 0.84096525770971D-02 3 20 3 14 0.86695235884166D-01 -0.89247515172814D-08 1 1 1 15 -0.66066883358686D+00 0.58092146726301D-02 2 1 1 15 -0.23438760987989D+00 -0.19385491922706D-02 3 1 1 15 0.13585071658990D+01 0.74788430588366D-03 1 2 1 15 -0.10668548975769D+01 0.63037185903170D-06 2 2 1 15 -0.36123798914911D+00 -0.60182699534372D-06 3 2 1 15 -0.10142356701901D+01 -0.73102492019231D-06 1 3 1 15 -0.83722932351959D+00 -0.63653622056587D-06 2 3 1 15 -0.34428420488004D+00 -0.37372532696700D-06 3 3 1 15 -0.17584629655882D+01 0.13190429111033D-06 1 4 1 15 -0.15275697490881D+01 -0.64572596198174D-02 2 4 1 15 0.49549009324277D+00 -0.24006154107443D-01 3 4 1 15 -0.19271974120550D+00 0.13899459436935D-01 1 5 1 15 0.73418429166608D+00 0.27675484520819D-01 2 5 1 15 -0.15938290873738D+00 0.20789309500503D-01 3 5 1 15 0.42221527349252D+01 0.10684640142366D-01 1 6 1 15 -0.51358504712508D+01 -0.13474928096293D-01 2 6 1 15 0.53370378876723D+00 0.96362797232901D-02 3 6 1 15 -0.49749972773548D+00 -0.40974196505337D-01 1 7 1 15 0.64261471368817D+00 0.39035000447818D-01 2 7 1 15 0.15300371689551D+00 0.77025902269862D-01 3 7 1 15 -0.38966692907451D+01 -0.11517268690803D-01 1 8 1 15 -0.46510512037137D+01 -0.15901986239630D-01 2 8 1 15 0.68345312777792D+00 -0.97797549474336D-02 3 8 1 15 0.62141502835397D+00 0.50205480190896D-01 1 9 1 15 0.40134067866261D+00 -0.53503290406860D-01 2 9 1 15 -0.55778767451162D+00 -0.10907649972753D-01 3 9 1 15 -0.34985486325794D+01 0.14084884797158D+00 1 10 1 15 0.79845861100858D+00 -0.72611612795843D-06 2 10 1 15 0.86617816800296D+00 0.31855261054767D-06 3 10 1 15 -0.42098323762825D+01 -0.18699115681722D-05 1 11 1 15 -0.64942645386988D-01 0.36633641645365D-02 2 11 1 15 -0.90819511059348D+00 0.44958752794673D-01 3 11 1 15 -0.34417030988130D+01 -0.17217352796030D+00 1 12 1 15 0.63306122767648D+00 -0.23395148623338D-06 2 12 1 15 -0.52364748639404D+00 -0.25801219192337D-06 3 12 1 15 0.32019615082073D+01 0.37732334037717D-06 1 13 1 15 0.34820445651950D-14 0.14972163595795D-01 2 13 1 15 0.42015320180646D-01 0.24734312916945D-02 3 13 1 15 0.14086396224381D+01 -0.12527673441752D-01 1 14 1 15 0.36179266440758D+00 -0.31027177623688D-15 2 14 1 15 -0.68287835135632D-01 -0.11803477805926D-05 3 14 1 15 -0.22178120985566D+00 0.20237112340911D-06 1 15 1 15 0.15006438807181D+02 0.00000000000000D+00 2 15 1 15 0.68864760119764D+01 0.18971069931448D+00 3 15 1 15 0.12907953016798D+01 0.16577648637509D+00 1 16 1 15 0.67478870946501D+00 -0.30054587356248D-02 2 16 1 15 0.36442224451329D+00 -0.13700804630370D-02 3 16 1 15 0.81563602512013D+00 0.93795643715270D-02 1 17 1 15 -0.20020795220703D-01 0.10028013878796D-06 2 17 1 15 0.19009642624042D-01 0.53128080730072D-02 3 17 1 15 0.93322813237244D+00 -0.12406512192839D-02 1 18 1 15 0.33116110735534D+00 -0.13483226342345D-01 2 18 1 15 0.64995108599877D-01 0.17700200239526D-01 3 18 1 15 0.15997970813982D+00 -0.31200264480517D-02 1 19 1 15 0.29394031008974D+01 0.13118784182002D-15 2 19 1 15 -0.19436888327661D+01 0.38948290896356D-01 3 19 1 15 -0.46819130833403D-01 -0.91282937840373D-02 1 20 1 15 -0.10469449470543D-13 -0.19408569634642D-06 2 20 1 15 -0.92517370870153D+00 0.44206987256041D-06 3 20 1 15 0.17538159518834D+01 0.60820574625932D-06 1 1 2 15 -0.67176802529486D+00 0.52547534079832D-02 2 1 2 15 0.26721322086049D+00 -0.67301329828239D-03 3 1 2 15 0.16166081741409D+00 0.99471786066685D-03 1 2 2 15 -0.62660586630817D+00 0.44614389368068D-06 2 2 2 15 -0.37565393369065D+00 -0.18546162857823D-06 3 2 2 15 -0.74414560791718D-02 -0.41294039109085D-06 1 3 2 15 -0.86353847218528D+00 -0.22690739639850D-06 2 3 2 15 -0.12389191950372D+00 0.16777393966671D-07 3 3 2 15 0.16706368605352D+00 0.20213450336705D-06 1 4 2 15 -0.11310439235671D+00 -0.27092240302348D-01 2 4 2 15 -0.83235442486991D+00 0.12606854493732D-01 3 4 2 15 0.10948572598821D+01 0.12558143074972D-01 1 5 2 15 0.20463990501138D+00 0.34349079966531D-01 2 5 2 15 -0.16252001627054D+00 0.11416271009605D-01 3 5 2 15 0.28426666852924D+01 0.45046507557076D-02 1 6 2 15 -0.14573982766879D+01 -0.13075103789393D-01 2 6 2 15 -0.91062083360516D-01 0.22416544868994D-02 3 6 2 15 -0.78861004528200D+00 -0.48875958825161D-01 1 7 2 15 0.40576931150240D+00 0.10221440279522D+00 2 7 2 15 0.24423588943719D-01 0.10412357639943D+00 3 7 2 15 -0.30359982702477D+01 -0.79447551651891D-02 1 8 2 15 -0.24317149100600D+01 -0.21193322633141D-01 2 8 2 15 -0.12131103227848D+01 -0.78851080443437D-02 3 8 2 15 0.77267282968486D+00 0.64486680591523D-01 1 9 2 15 -0.26089769289022D+00 -0.55462572263884D-01 2 9 2 15 -0.39716460783179D+00 -0.24257768962602D-02 3 9 2 15 -0.29534081319711D+01 0.17234104266561D+00 1 10 2 15 0.10478562970400D+01 0.33718615200097D-06 2 10 2 15 0.20412257977080D+00 -0.38833369192068D-08 3 10 2 15 -0.27702728437014D+01 -0.61738257425815D-06 1 11 2 15 -0.80935195239605D+00 0.29507372588118D-01 2 11 2 15 -0.93502320659140D+00 0.41300989148835D-01 3 11 2 15 -0.31649972223185D+01 -0.10999950761531D+00 1 12 2 15 -0.15520533430962D+00 0.11134938636180D-06 2 12 2 15 -0.53388500064515D+00 -0.27426758115751D-06 3 12 2 15 0.34957157651689D+01 0.71307481777024D-06 1 13 2 15 -0.42015320180647D-01 0.24734312916945D-02 2 13 2 15 -0.82111061247810D-15 -0.46464540167991D-01 3 13 2 15 0.63675814312606D+00 -0.18902846730645D-01 1 14 2 15 -0.68287835135632D-01 0.11803477806966D-05 2 14 2 15 -0.24051314802437D-01 0.57866455103657D-15 3 14 2 15 0.43610611744184D-01 0.17347005593167D-06 1 15 2 15 0.68864779151049D+01 -0.18971120964227D+00 2 15 2 15 0.14365659165686D+02 0.00000000000000D+00 3 15 2 15 -0.19885876466295D+01 -0.19398185013989D+00 1 16 2 15 0.36442300744289D+00 -0.13691846451485D-02 2 16 2 15 -0.88768276842115D+00 -0.56518251296786D-03 3 16 2 15 0.61484961140265D+00 0.19261466535199D-01 1 17 2 15 -0.19009638188728D-01 0.53125567924774D-02 2 17 2 15 0.58986358954179D-01 -0.14350436270817D-06 3 17 2 15 0.41405230449544D+00 0.84084633348852D-02 1 18 2 15 -0.64993224846047D-01 -0.17697402654779D-01 2 18 2 15 -0.56647615393757D-01 0.19282002014645D-01 3 18 2 15 0.86378308593936D-01 -0.17418634182744D-02 1 19 2 15 0.19436888327661D+01 0.38948290896356D-01 2 19 2 15 -0.67630302568859D+01 0.11543556742304D-16 3 19 2 15 -0.14443674954483D+00 -0.11416482061087D-01 1 20 2 15 -0.92517370870153D+00 -0.44206987059969D-06 2 20 2 15 0.12608878002594D-13 -0.43762547964053D-06 3 20 2 15 0.20212138681151D+00 0.29871211898969D-06 1 1 3 15 0.80663723739248D+00 0.65285290862646D-02 2 1 3 15 -0.24739921605504D+00 -0.21134327938223D-02 3 1 3 15 0.21372329087674D+00 0.37789498105840D-02 1 2 3 15 -0.10785564770849D+01 0.33993419838981D-06 2 2 3 15 0.46771224625460D+00 0.77575139598703D-06 3 2 3 15 -0.17515671466166D+00 -0.67991553276623D-06 1 3 3 15 -0.11093678603690D+01 -0.28405314319352D-06 2 3 3 15 0.61624736641730D+00 0.73002887859725D-07 3 3 3 15 0.30191144601141D+00 0.48429958462757D-06 1 4 3 15 -0.25142281874029D+00 -0.69760145231563D-02 2 4 3 15 0.86237266963265D+00 0.10810685967263D-01 3 4 3 15 -0.23982246383877D+01 -0.24477481513505D-01 1 5 3 15 0.18464602830797D+01 0.13801012644521D-01 2 5 3 15 0.25795522233826D+00 0.51648474989793D-02 3 5 3 15 -0.30555578378940D+00 -0.15861160436607D-01 1 6 3 15 -0.55412559341209D+00 -0.45925951970437D-01 2 6 3 15 -0.95920887648769D+00 -0.36209539711448D-01 3 6 3 15 -0.38543492098479D+01 -0.24961300556884D-01 1 7 3 15 -0.11749824647070D+01 -0.16782858801056D-01 2 7 3 15 -0.39263645059176D+00 -0.36584022370915D-01 3 7 3 15 -0.20019335293059D+00 -0.74632070191077D-01 1 8 3 15 0.54457476066143D+00 0.32243085944304D-01 2 8 3 15 0.83142332788892D+00 0.63777950819950D-01 3 8 3 15 -0.43358483535482D+01 -0.26942192371760D-01 1 9 3 15 -0.14460635025580D+01 0.36019086614237D-01 2 9 3 15 -0.12976185230743D+01 0.37278351710175D-02 3 9 3 15 -0.23985556697210D+01 0.16744757717881D+00 1 10 3 15 -0.23102469375356D+01 -0.16841860739156D-06 2 10 3 15 -0.10915050290647D+01 0.97442887519344D-06 3 10 3 15 0.11148553456063D+01 0.50408509789016D-06 1 11 3 15 -0.15212693177318D+01 -0.29378448157181D-01 2 11 3 15 -0.10273560672804D+01 -0.56343722398485D-01 3 11 3 15 -0.67939509470969D+00 -0.11016207830167D+00 1 12 3 15 0.10691410880597D+01 -0.50385591993198D-06 2 12 3 15 0.17446300102037D+01 -0.59352765115069D-06 3 12 3 15 -0.26654984393297D+01 -0.10056048551106D-06 1 13 3 15 0.14086396224381D+01 0.12527673441751D-01 2 13 3 15 0.63675814312606D+00 0.18902846730645D-01 3 13 3 15 0.34190820673392D-14 -0.92826278285585D-02 1 14 3 15 0.22178120985564D+00 0.20237112341084D-06 2 14 3 15 -0.43610611744181D-01 0.17347005593167D-06 3 14 3 15 -0.10161085321636D+01 -0.17284015172984D-15 1 15 3 15 0.12907705592790D+01 -0.16577756281318D+00 2 15 3 15 -0.19886166343831D+01 0.19398128188652D+00 3 15 3 15 0.15247819034118D+02 0.00000000000000D+00 1 16 3 15 0.81563612093758D+00 0.93784244454263D-02 2 16 3 15 0.61484764818829D+00 0.19261892934482D-01 3 16 3 15 0.39852344590289D+00 -0.22487926582540D-02 1 17 3 15 0.93322963471947D+00 0.12403348810596D-02 2 17 3 15 -0.41405356045998D+00 0.84096525770971D-02 3 17 3 15 -0.86695235884170D-01 0.89247515320280D-08 1 18 3 15 0.15997690726366D+00 -0.31207405124736D-02 2 18 3 15 -0.86377337554130D-01 0.17427755476425D-02 3 18 3 15 -0.24682108153475D+00 -0.17144360058818D-01 1 19 3 15 0.46819130833407D-01 -0.91282937840373D-02 2 19 3 15 -0.14443674954483D+00 0.11416482061087D-01 3 19 3 15 0.17321575636988D+01 -0.14749791465939D-15 1 20 3 15 0.17538159518834D+01 -0.60820575106516D-06 2 20 3 15 -0.20212138681150D+00 0.29871211899056D-06 3 20 3 15 0.20315018881788D-13 -0.54291375589894D-06 1 1 1 16 0.10668548975768D+01 -0.63037185865607D-06 2 1 1 16 0.36123798914907D+00 0.60182699088241D-06 3 1 1 16 0.10142356701902D+01 0.73102491064033D-06 1 2 1 16 0.66066883358685D+00 -0.58092146726285D-02 2 2 1 16 0.23438760987994D+00 0.19385491922693D-02 3 2 1 16 -0.13585071658991D+01 -0.74788430587949D-03 1 3 1 16 -0.15275697490882D+01 -0.64572596198224D-02 2 3 1 16 0.49549009324287D+00 -0.24006154107443D-01 3 3 1 16 -0.19271974120553D+00 0.13899459436936D-01 1 4 1 16 -0.83722932351963D+00 -0.63653622281854D-06 2 4 1 16 -0.34428420488006D+00 -0.37372532691077D-06 3 4 1 16 -0.17584629655881D+01 0.13190429124758D-06 1 5 1 16 0.73418429166610D+00 0.27675484520816D-01 2 5 1 16 -0.15938290873740D+00 0.20789309500504D-01 3 5 1 16 0.42221527349252D+01 0.10684640142365D-01 1 6 1 16 0.51358504712509D+01 0.13474928096314D-01 2 6 1 16 -0.53370378876697D+00 -0.96362797232675D-02 3 6 1 16 0.49749972773589D+00 0.40974196505358D-01 1 7 1 16 -0.64261471368819D+00 -0.39035000447816D-01 2 7 1 16 -0.15300371689550D+00 -0.77025902269862D-01 3 7 1 16 0.38966692907452D+01 0.11517268690803D-01 1 8 1 16 -0.46510512037136D+01 -0.15901986239629D-01 2 8 1 16 0.68345312777832D+00 -0.97797549474340D-02 3 8 1 16 0.62141502835394D+00 0.50205480190895D-01 1 9 1 16 0.79845861100862D+00 -0.72611612345676D-06 2 9 1 16 0.86617816800294D+00 0.31855261396058D-06 3 9 1 16 -0.42098323762825D+01 -0.18699115748147D-05 1 10 1 16 0.40134067866258D+00 -0.53503290406860D-01 2 10 1 16 -0.55778767451163D+00 -0.10907649972753D-01 3 10 1 16 -0.34985486325794D+01 0.14084884797158D+00 1 11 1 16 0.63306122767647D+00 -0.23395148681490D-06 2 11 1 16 -0.52364748639405D+00 -0.25801219145325D-06 3 11 1 16 0.32019615082073D+01 0.37732333977481D-06 1 12 1 16 -0.64942645387016D-01 0.36633641645371D-02 2 12 1 16 -0.90819511059351D+00 0.44958752794672D-01 3 12 1 16 -0.34417030988130D+01 -0.17217352796030D+00 1 13 1 16 0.36179266440758D+00 0.67505641235514D-16 2 13 1 16 -0.68287835135632D-01 -0.11803477806323D-05 3 13 1 16 -0.22178120985566D+00 0.20237112452990D-06 1 14 1 16 0.34030378788029D-14 0.14972163595794D-01 2 14 1 16 0.42015320180645D-01 0.24734312916946D-02 3 14 1 16 0.14086396224381D+01 -0.12527673441751D-01 1 15 1 16 0.67478870946501D+00 -0.30054587356231D-02 2 15 1 16 0.36442224451329D+00 -0.13700804630363D-02 3 15 1 16 0.81563602512013D+00 0.93795643715301D-02 1 16 1 16 0.15006438807181D+02 0.00000000000000D+00 2 16 1 16 0.68864760119760D+01 0.18971069931448D+00 3 16 1 16 0.12907953016802D+01 0.16577648637509D+00 1 17 1 16 0.33116110735534D+00 -0.13483226342345D-01 2 17 1 16 0.64995108599878D-01 0.17700200239526D-01 3 17 1 16 0.15997970813979D+00 -0.31200264480515D-02 1 18 1 16 -0.20020795220703D-01 0.10028013878198D-06 2 18 1 16 0.19009642624041D-01 0.53128080730072D-02 3 18 1 16 0.93322813237244D+00 -0.12406512192839D-02 1 19 1 16 -0.55150157905772D-14 -0.19408568715890D-06 2 19 1 16 -0.92517370870155D+00 0.44206987050720D-06 3 19 1 16 0.17538159518834D+01 0.60820575088331D-06 1 20 1 16 0.29394031008974D+01 0.42301672733414D-16 2 20 1 16 -0.19436888327661D+01 0.38948290896356D-01 3 20 1 16 -0.46819130833403D-01 -0.91282937840377D-02 1 1 2 16 0.62660586630813D+00 -0.44614389814200D-06 2 1 2 16 0.37565393369078D+00 0.18546163005990D-06 3 1 2 16 0.74414560792162D-02 0.41294039840787D-06 1 2 2 16 0.67176802529490D+00 -0.52547534079844D-02 2 2 2 16 -0.26721322086046D+00 0.67301329828411D-03 3 2 2 16 -0.16166081741404D+00 -0.99471786066912D-03 1 3 2 16 -0.11310439235661D+00 -0.27092240302348D-01 2 3 2 16 -0.83235442486988D+00 0.12606854493732D-01 3 3 2 16 0.10948572598822D+01 0.12558143074972D-01 1 4 2 16 -0.86353847218530D+00 -0.22690739634226D-06 2 4 2 16 -0.12389191950372D+00 0.16777392391038D-07 3 4 2 16 0.16706368605360D+00 0.20213450332315D-06 1 5 2 16 0.20463990501136D+00 0.34349079966531D-01 2 5 2 16 -0.16252001627054D+00 0.11416271009604D-01 3 5 2 16 0.28426666852924D+01 0.45046507557070D-02 1 6 2 16 0.14573982766881D+01 0.13075103789416D-01 2 6 2 16 0.91062083360317D-01 -0.22416544868947D-02 3 6 2 16 0.78861004528221D+00 0.48875958825168D-01 1 7 2 16 -0.40576931150239D+00 -0.10221440279522D+00 2 7 2 16 -0.24423588943715D-01 -0.10412357639943D+00 3 7 2 16 0.30359982702477D+01 0.79447551651896D-02 1 8 2 16 -0.24317149100596D+01 -0.21193322633141D-01 2 8 2 16 -0.12131103227846D+01 -0.78851080443443D-02 3 8 2 16 0.77267282968485D+00 0.64486680591523D-01 1 9 2 16 0.10478562970400D+01 0.33718615540694D-06 2 9 2 16 0.20412257977079D+00 -0.38833376526606D-08 3 9 2 16 -0.27702728437013D+01 -0.61738257856894D-06 1 10 2 16 -0.26089769289022D+00 -0.55462572263884D-01 2 10 2 16 -0.39716460783177D+00 -0.24257768962603D-02 3 10 2 16 -0.29534081319711D+01 0.17234104266560D+00 1 11 2 16 -0.15520533430962D+00 0.11134938683019D-06 2 11 2 16 -0.53388500064511D+00 -0.27426758147224D-06 3 11 2 16 0.34957157651689D+01 0.71307481759187D-06 1 12 2 16 -0.80935195239608D+00 0.29507372588117D-01 2 12 2 16 -0.93502320659138D+00 0.41300989148835D-01 3 12 2 16 -0.31649972223185D+01 -0.10999950761531D+00 1 13 2 16 -0.68287835135632D-01 0.11803477806568D-05 2 13 2 16 -0.24051314802434D-01 0.11293486094590D-14 3 13 2 16 0.43610611744182D-01 0.17347005596275D-06 1 14 2 16 -0.42015320180648D-01 0.24734312916946D-02 2 14 2 16 -0.92508327641555D-15 -0.46464540167991D-01 3 14 2 16 0.63675814312606D+00 -0.18902846730645D-01 1 15 2 16 0.36442300744289D+00 -0.13691846451478D-02 2 15 2 16 -0.88768276842115D+00 -0.56518251296709D-03 3 15 2 16 0.61484961140265D+00 0.19261466535199D-01 1 16 2 16 0.68864779151045D+01 -0.18971120964227D+00 2 16 2 16 0.14365659165686D+02 0.00000000000000D+00 3 16 2 16 -0.19885876466294D+01 -0.19398185013989D+00 1 17 2 16 -0.64993224846046D-01 -0.17697402654779D-01 2 17 2 16 -0.56647615393752D-01 0.19282002014645D-01 3 17 2 16 0.86378308593942D-01 -0.17418634182742D-02 1 18 2 16 -0.19009638188729D-01 0.53125567924774D-02 2 18 2 16 0.58986358954178D-01 -0.14350436268158D-06 3 18 2 16 0.41405230449544D+00 0.84084633348851D-02 1 19 2 16 -0.92517370870155D+00 -0.44206987265290D-06 2 19 2 16 -0.61923523669386D-15 -0.43762548201937D-06 3 19 2 16 0.20212138681150D+00 0.29871211824179D-06 1 20 2 16 0.19436888327661D+01 0.38948290896356D-01 2 20 2 16 -0.67630302568860D+01 -0.65074664339319D-17 3 20 2 16 -0.14443674954483D+00 -0.11416482061087D-01 1 1 3 16 0.10785564770850D+01 -0.33993420794223D-06 2 1 3 16 -0.46771224625455D+00 -0.77575138866957D-06 3 1 3 16 0.17515671466154D+00 0.67991553768037D-06 1 2 3 16 -0.80663723739252D+00 -0.65285290862605D-02 2 2 3 16 0.24739921605509D+00 0.21134327938200D-02 3 2 3 16 -0.21372329087679D+00 -0.37789498105808D-02 1 3 3 16 -0.25142281874032D+00 -0.69760145231552D-02 2 3 3 16 0.86237266963271D+00 0.10810685967263D-01 3 3 3 16 -0.23982246383876D+01 -0.24477481513503D-01 1 4 3 16 -0.11093678603689D+01 -0.28405314305627D-06 2 4 3 16 0.61624736641738D+00 0.73002887815823D-07 3 4 3 16 0.30191144601152D+00 0.48429958888994D-06 1 5 3 16 0.18464602830797D+01 0.13801012644520D-01 2 5 3 16 0.25795522233825D+00 0.51648474989787D-02 3 5 3 16 -0.30555578378939D+00 -0.15861160436609D-01 1 6 3 16 0.55412559341250D+00 0.45925951970458D-01 2 6 3 16 0.95920887648789D+00 0.36209539711455D-01 3 6 3 16 0.38543492098478D+01 0.24961300556866D-01 1 7 3 16 0.11749824647070D+01 0.16782858801057D-01 2 7 3 16 0.39263645059179D+00 0.36584022370915D-01 3 7 3 16 0.20019335293062D+00 0.74632070191079D-01 1 8 3 16 0.54457476066142D+00 0.32243085944304D-01 2 8 3 16 0.83142332788891D+00 0.63777950819950D-01 3 8 3 16 -0.43358483535488D+01 -0.26942192371761D-01 1 9 3 16 -0.23102469375356D+01 -0.16841861402719D-06 2 9 3 16 -0.10915050290647D+01 0.97442887088266D-06 3 9 3 16 0.11148553456062D+01 0.50408510192713D-06 1 10 3 16 -0.14460635025580D+01 0.36019086614238D-01 2 10 3 16 -0.12976185230743D+01 0.37278351710172D-02 3 10 3 16 -0.23985556697210D+01 0.16744757717881D+00 1 11 3 16 0.10691410880598D+01 -0.50385592052566D-06 2 11 3 16 0.17446300102037D+01 -0.59352765133253D-06 3 11 3 16 -0.26654984393298D+01 -0.10056048696157D-06 1 12 3 16 -0.15212693177318D+01 -0.29378448157181D-01 2 12 3 16 -0.10273560672803D+01 -0.56343722398485D-01 3 12 3 16 -0.67939509470965D+00 -0.11016207830167D+00 1 13 3 16 0.22178120985564D+00 0.20237112453163D-06 2 13 3 16 -0.43610611744183D-01 0.17347005596275D-06 3 13 3 16 -0.10161085321636D+01 0.24240369269476D-17 1 14 3 16 0.14086396224381D+01 0.12527673441751D-01 2 14 3 16 0.63675814312606D+00 0.18902846730645D-01 3 14 3 16 0.47906314417847D-14 -0.92826278285592D-02 1 15 3 16 0.81563612093758D+00 0.93784244454293D-02 2 15 3 16 0.61484764818829D+00 0.19261892934482D-01 3 15 3 16 0.39852344590289D+00 -0.22487926582535D-02 1 16 3 16 0.12907705592794D+01 -0.16577756281318D+00 2 16 3 16 -0.19886166343830D+01 0.19398128188652D+00 3 16 3 16 0.15247819034118D+02 0.00000000000000D+00 1 17 3 16 0.15997690726363D+00 -0.31207405124734D-02 2 17 3 16 -0.86377337554124D-01 0.17427755476427D-02 3 17 3 16 -0.24682108153475D+00 -0.17144360058817D-01 1 18 3 16 0.93322963471947D+00 0.12403348810596D-02 2 18 3 16 -0.41405356045998D+00 0.84096525770970D-02 3 18 3 16 -0.86695235884171D-01 0.89247515290002D-08 1 19 3 16 0.17538159518834D+01 -0.60820574644117D-06 2 19 3 16 -0.20212138681150D+00 0.29871211824266D-06 3 19 3 16 -0.23269014898736D-14 -0.54291375923575D-06 1 20 3 16 0.46819130833407D-01 -0.91282937840377D-02 2 20 3 16 -0.14443674954483D+00 0.11416482061087D-01 3 20 3 16 0.17321575636988D+01 0.30811844581359D-15 1 1 1 17 0.15275697490881D+01 0.64572596198195D-02 2 1 1 17 0.49549009324293D+00 -0.24006154107437D-01 3 1 1 17 0.19271974120576D+00 -0.13899459436928D-01 1 2 1 17 -0.83722932351965D+00 -0.63653622347648D-06 2 2 1 17 0.34428420488001D+00 0.37372532707192D-06 3 2 1 17 -0.17584629655880D+01 0.13190429094695D-06 1 3 1 17 -0.10668548975768D+01 0.63037186055486D-06 2 3 1 17 0.36123798914906D+00 0.60182699511697D-06 3 3 1 17 -0.10142356701900D+01 -0.73102491835634D-06 1 4 1 17 0.66066883358687D+00 -0.58092146726304D-02 2 4 1 17 -0.23438760987995D+00 -0.19385491922718D-02 3 4 1 17 -0.13585071658991D+01 -0.74788430588470D-03 1 5 1 17 0.46510512037135D+01 0.15901986239632D-01 2 5 1 17 0.68345312777832D+00 -0.97797549474559D-02 3 5 1 17 -0.62141502835395D+00 -0.50205480190902D-01 1 6 1 17 0.64261471368818D+00 0.39035000447817D-01 2 6 1 17 -0.15300371689550D+00 -0.77025902269862D-01 3 6 1 17 -0.38966692907452D+01 -0.11517268690801D-01 1 7 1 17 -0.51358504712511D+01 -0.13474928096294D-01 2 7 1 17 -0.53370378876697D+00 -0.96362797232901D-02 3 7 1 17 -0.49749972773598D+00 -0.40974196505343D-01 1 8 1 17 -0.73418429166607D+00 -0.27675484520815D-01 2 8 1 17 -0.15938290873739D+00 0.20789309500504D-01 3 8 1 17 -0.42221527349252D+01 -0.10684640142367D-01 1 9 1 17 0.64942645387029D-01 -0.36633641645372D-02 2 9 1 17 -0.90819511059348D+00 0.44958752794670D-01 3 9 1 17 0.34417030988129D+01 0.17217352796030D+00 1 10 1 17 -0.63306122767649D+00 0.23395148850883D-06 2 10 1 17 -0.52364748639405D+00 -0.25801219116801D-06 3 10 1 17 -0.32019615082073D+01 -0.37732333738650D-06 1 11 1 17 -0.40134067866259D+00 0.53503290406862D-01 2 11 1 17 -0.55778767451164D+00 -0.10907649972752D-01 3 11 1 17 0.34985486325794D+01 -0.14084884797158D+00 1 12 1 17 -0.79845861100860D+00 0.72611612825678D-06 2 12 1 17 0.86617816800296D+00 0.31855261226671D-06 3 12 1 17 0.42098323762825D+01 0.18699115719859D-05 1 13 1 17 0.29394031008974D+01 -0.99115321008070D-16 2 13 1 17 0.19436888327661D+01 -0.38948290896356D-01 3 13 1 17 -0.46819130833405D-01 -0.91282937840375D-02 1 14 1 17 -0.55179202615609D-14 -0.19408569639398D-06 2 14 1 17 0.92517370870153D+00 -0.44206987263731D-06 3 14 1 17 0.17538159518834D+01 0.60820574786038D-06 1 15 1 17 -0.20020795220703D-01 0.10028013876536D-06 2 15 1 17 -0.19009642624043D-01 -0.53128080730072D-02 3 15 1 17 0.93322813237244D+00 -0.12406512192839D-02 1 16 1 17 0.33116110735534D+00 -0.13483226342345D-01 2 16 1 17 -0.64995108599880D-01 -0.17700200239526D-01 3 16 1 17 0.15997970813979D+00 -0.31200264480519D-02 1 17 1 17 0.15006438807182D+02 0.00000000000000D+00 2 17 1 17 -0.68864760119758D+01 -0.18971069931448D+00 3 17 1 17 0.12907953016803D+01 0.16577648637509D+00 1 18 1 17 0.67478870946502D+00 -0.30054587356250D-02 2 18 1 17 -0.36442224451330D+00 0.13700804630371D-02 3 18 1 17 0.81563602512015D+00 0.93795643715281D-02 1 19 1 17 0.89171461111833D-15 0.14972163595795D-01 2 19 1 17 -0.42015320180645D-01 -0.24734312916944D-02 3 19 1 17 0.14086396224381D+01 -0.12527673441751D-01 1 20 1 17 0.36179266440758D+00 -0.31648318022769D-15 2 20 1 17 0.68287835135634D-01 0.11803477805882D-05 3 20 1 17 -0.22178120985566D+00 0.20237112367416D-06 1 1 2 17 -0.11310439235655D+00 -0.27092240302342D-01 2 1 2 17 0.83235442486972D+00 -0.12606854493728D-01 3 1 2 17 0.10948572598823D+01 0.12558143074985D-01 1 2 2 17 0.86353847218525D+00 0.22690739649995D-06 2 2 2 17 -0.12389191950372D+00 0.16777393759868D-07 3 2 2 17 -0.16706368605348D+00 -0.20213450362757D-06 1 3 2 17 0.62660586630812D+00 -0.44614389390743D-06 2 3 2 17 -0.37565393369069D+00 -0.18546162857816D-06 3 3 2 17 0.74414560792020D-02 0.41294039085472D-06 1 4 2 17 -0.67176802529491D+00 0.52547534079819D-02 2 4 2 17 -0.26721322086045D+00 0.67301329828096D-03 3 4 2 17 0.16166081741401D+00 0.99471786066447D-03 1 5 2 17 -0.24317149100596D+01 -0.21193322633163D-01 2 5 2 17 0.12131103227846D+01 0.78851080443668D-02 3 5 2 17 0.77267282968485D+00 0.64486680591532D-01 1 6 2 17 -0.40576931150239D+00 -0.10221440279522D+00 2 6 2 17 0.24423588943720D-01 0.10412357639943D+00 3 6 2 17 0.30359982702477D+01 0.79447551651886D-02 1 7 2 17 0.14573982766881D+01 0.13075103789393D-01 2 7 2 17 -0.91062083360232D-01 0.22416544868989D-02 3 7 2 17 0.78861004528222D+00 0.48875958825161D-01 1 8 2 17 0.20463990501137D+00 0.34349079966532D-01 2 8 2 17 0.16252001627055D+00 -0.11416271009605D-01 3 8 2 17 0.28426666852924D+01 0.45046507557085D-02 1 9 2 17 -0.80935195239606D+00 0.29507372588115D-01 2 9 2 17 0.93502320659135D+00 -0.41300989148833D-01 3 9 2 17 -0.31649972223185D+01 -0.10999950761531D+00 1 10 2 17 -0.15520533430962D+00 0.11134938711195D-06 2 10 2 17 0.53388500064517D+00 0.27426758034190D-06 3 10 2 17 0.34957157651689D+01 0.71307481358631D-06 1 11 2 17 -0.26089769289024D+00 -0.55462572263883D-01 2 11 2 17 0.39716460783181D+00 0.24257768962601D-02 3 11 2 17 -0.29534081319711D+01 0.17234104266561D+00 1 12 2 17 0.10478562970400D+01 0.33718615370960D-06 2 12 2 17 -0.20412257977077D+00 0.38833370590907D-08 3 12 2 17 -0.27702728437013D+01 -0.61738257633175D-06 1 13 2 17 -0.19436888327661D+01 -0.38948290896356D-01 2 13 2 17 -0.67630302568860D+01 -0.19527433334913D-17 3 13 2 17 0.14443674954483D+00 0.11416482061087D-01 1 14 2 17 0.92517370870153D+00 0.44206987052279D-06 2 14 2 17 -0.86120091221411D-14 -0.43762547958400D-06 3 14 2 17 -0.20212138681150D+00 -0.29871211897977D-06 1 15 2 17 0.19009638188728D-01 -0.53125567924774D-02 2 15 2 17 0.58986358954179D-01 -0.14350436274004D-06 3 15 2 17 -0.41405230449544D+00 -0.84084633348852D-02 1 16 2 17 0.64993224846044D-01 0.17697402654779D-01 2 16 2 17 -0.56647615393752D-01 0.19282002014646D-01 3 16 2 17 -0.86378308593949D-01 0.17418634182742D-02 1 17 2 17 -0.68864779151043D+01 0.18971120964227D+00 2 17 2 17 0.14365659165685D+02 0.00000000000000D+00 3 17 2 17 0.19885876466293D+01 0.19398185013989D+00 1 18 2 17 -0.36442300744290D+00 0.13691846451486D-02 2 18 2 17 -0.88768276842114D+00 -0.56518251296796D-03 3 18 2 17 -0.61484961140266D+00 -0.19261466535199D-01 1 19 2 17 0.42015320180648D-01 -0.24734312916944D-02 2 19 2 17 0.19997205635530D-14 -0.46464540167991D-01 3 19 2 17 -0.63675814312606D+00 0.18902846730645D-01 1 20 2 17 0.68287835135634D-01 -0.11803477807010D-05 2 20 2 17 -0.24051314802430D-01 -0.34002143330241D-15 3 20 2 17 -0.43610611744183D-01 -0.17347005584703D-06 1 1 3 17 0.25142281874055D+00 0.69760145231625D-02 2 1 3 17 0.86237266963285D+00 0.10810685967275D-01 3 1 3 17 0.23982246383879D+01 0.24477481513512D-01 1 2 3 17 -0.11093678603688D+01 -0.28405314335517D-06 2 2 3 17 -0.61624736641726D+00 -0.73002888118514D-07 3 2 3 17 0.30191144601133D+00 0.48429958564836D-06 1 3 3 17 -0.10785564770848D+01 0.33993420022578D-06 2 3 3 17 -0.46771224625457D+00 -0.77575139622316D-06 3 3 3 17 -0.17515671466161D+00 -0.67991553487048D-06 1 4 3 17 -0.80663723739254D+00 -0.65285290862657D-02 2 4 3 17 -0.24739921605512D+00 -0.21134327938247D-02 3 4 3 17 -0.21372329087681D+00 -0.37789498105875D-02 1 5 3 17 -0.54457476066143D+00 -0.32243085944310D-01 2 5 3 17 0.83142332788890D+00 0.63777950819959D-01 3 5 3 17 0.43358483535489D+01 0.26942192371738D-01 1 6 3 17 -0.11749824647070D+01 -0.16782858801055D-01 2 6 3 17 0.39263645059178D+00 0.36584022370914D-01 3 6 3 17 -0.20019335293066D+00 -0.74632070191075D-01 1 7 3 17 -0.55412559341259D+00 -0.45925951970443D-01 2 7 3 17 0.95920887648792D+00 0.36209539711448D-01 3 7 3 17 -0.38543492098477D+01 -0.24961300556884D-01 1 8 3 17 -0.18464602830797D+01 -0.13801012644522D-01 2 8 3 17 0.25795522233825D+00 0.51648474989803D-02 3 8 3 17 0.30555578378945D+00 0.15861160436610D-01 1 9 3 17 0.15212693177318D+01 0.29378448157185D-01 2 9 3 17 -0.10273560672803D+01 -0.56343722398488D-01 3 9 3 17 0.67939509470963D+00 0.11016207830167D+00 1 10 3 17 -0.10691410880597D+01 0.50385592291397D-06 2 10 3 17 0.17446300102037D+01 -0.59352765531380D-06 3 10 3 17 0.26654984393296D+01 0.10056048033275D-06 1 11 3 17 0.14460635025580D+01 -0.36019086614240D-01 2 11 3 17 -0.12976185230743D+01 0.37278351710206D-02 3 11 3 17 0.23985556697210D+01 -0.16744757717881D+00 1 12 3 17 0.23102469375356D+01 0.16841861117407D-06 2 12 3 17 -0.10915050290647D+01 0.97442887311810D-06 3 12 3 17 -0.11148553456062D+01 -0.50408509959500D-06 1 13 3 17 0.46819130833404D-01 -0.91282937840375D-02 2 13 3 17 0.14443674954483D+00 -0.11416482061087D-01 3 13 3 17 0.17321575636989D+01 -0.15214864500241D-15 1 14 3 17 0.17538159518834D+01 -0.60820574946410D-06 2 14 3 17 0.20212138681151D+00 -0.29871211898064D-06 3 14 3 17 -0.34303946999342D-13 -0.54291375536107D-06 1 15 3 17 0.93322963471947D+00 0.12403348810596D-02 2 15 3 17 0.41405356045998D+00 -0.84096525770971D-02 3 15 3 17 -0.86695235884170D-01 0.89247515033372D-08 1 16 3 17 0.15997690726363D+00 -0.31207405124738D-02 2 16 3 17 0.86377337554116D-01 -0.17427755476427D-02 3 16 3 17 -0.24682108153475D+00 -0.17144360058819D-01 1 17 3 17 0.12907705592796D+01 -0.16577756281318D+00 2 17 3 17 0.19886166343829D+01 -0.19398128188652D+00 3 17 3 17 0.15247819034118D+02 0.00000000000000D+00 1 18 3 17 0.81563612093760D+00 0.93784244454273D-02 2 18 3 17 -0.61484764818829D+00 -0.19261892934482D-01 3 18 3 17 0.39852344590289D+00 -0.22487926582538D-02 1 19 3 17 0.14086396224381D+01 0.12527673441752D-01 2 19 3 17 -0.63675814312606D+00 -0.18902846730645D-01 3 19 3 17 0.10521815539166D-14 -0.92826278285592D-02 1 20 3 17 0.22178120985564D+00 0.20237112367589D-06 2 20 3 17 0.43610611744182D-01 -0.17347005584703D-06 3 20 3 17 -0.10161085321636D+01 -0.78732595685601D-15 1 1 1 18 0.83722932351963D+00 0.63653622376613D-06 2 1 1 18 -0.34428420488003D+00 -0.37372532496878D-06 3 1 1 18 0.17584629655882D+01 -0.13190429903560D-06 1 2 1 18 -0.15275697490881D+01 -0.64572596198174D-02 2 2 1 18 -0.49549009324290D+00 0.24006154107443D-01 3 2 1 18 -0.19271974120562D+00 0.13899459436934D-01 1 3 1 18 0.66066883358689D+00 -0.58092146726282D-02 2 3 1 18 -0.23438760987995D+00 -0.19385491922703D-02 3 3 1 18 -0.13585071658991D+01 -0.74788430588153D-03 1 4 1 18 -0.10668548975768D+01 0.63037185977847D-06 2 4 1 18 0.36123798914902D+00 0.60182699576924D-06 3 4 1 18 -0.10142356701900D+01 -0.73102491747790D-06 1 5 1 18 0.46510512037136D+01 0.15901986239631D-01 2 5 1 18 0.68345312777808D+00 -0.97797549474563D-02 3 5 1 18 -0.62141502835389D+00 -0.50205480190906D-01 1 6 1 18 -0.64261471368816D+00 -0.39035000447820D-01 2 6 1 18 0.15300371689551D+00 0.77025902269862D-01 3 6 1 18 0.38966692907452D+01 0.11517268690802D-01 1 7 1 18 0.51358504712509D+01 0.13474928096314D-01 2 7 1 18 0.53370378876703D+00 0.96362797232674D-02 3 7 1 18 0.49749972773554D+00 0.40974196505355D-01 1 8 1 18 -0.73418429166608D+00 -0.27675484520818D-01 2 8 1 18 -0.15938290873738D+00 0.20789309500503D-01 3 8 1 18 -0.42221527349252D+01 -0.10684640142368D-01 1 9 1 18 -0.63306122767651D+00 0.23395148504767D-06 2 9 1 18 -0.52364748639403D+00 -0.25801219282144D-06 3 9 1 18 -0.32019615082073D+01 -0.37732334237113D-06 1 10 1 18 0.64942645386986D-01 -0.36633641645386D-02 2 10 1 18 -0.90819511059350D+00 0.44958752794675D-01 3 10 1 18 0.34417030988130D+01 0.17217352796029D+00 1 11 1 18 -0.79845861100863D+00 0.72611612543662D-06 2 11 1 18 0.86617816800296D+00 0.31855261177936D-06 3 11 1 18 0.42098323762826D+01 0.18699115720427D-05 1 12 1 18 -0.40134067866257D+00 0.53503290406860D-01 2 12 1 18 -0.55778767451163D+00 -0.10907649972754D-01 3 12 1 18 0.34985486325795D+01 -0.14084884797158D+00 1 13 1 18 0.13508623170114D-13 -0.19408568722634D-06 2 13 1 18 0.92517370870155D+00 -0.44206987050103D-06 3 13 1 18 0.17538159518834D+01 0.60820575075610D-06 1 14 1 18 0.29394031008973D+01 0.27659277224051D-16 2 14 1 18 0.19436888327661D+01 -0.38948290896356D-01 3 14 1 18 -0.46819130833404D-01 -0.91282937840370D-02 1 15 1 18 0.33116110735534D+00 -0.13483226342345D-01 2 15 1 18 -0.64995108599881D-01 -0.17700200239526D-01 3 15 1 18 0.15997970813982D+00 -0.31200264480517D-02 1 16 1 18 -0.20020795220703D-01 0.10028013877134D-06 2 16 1 18 -0.19009642624044D-01 -0.53128080730072D-02 3 16 1 18 0.93322813237244D+00 -0.12406512192839D-02 1 17 1 18 0.67478870946502D+00 -0.30054587356229D-02 2 17 1 18 -0.36442224451330D+00 0.13700804630363D-02 3 17 1 18 0.81563602512015D+00 0.93795643715291D-02 1 18 1 18 0.15006438807181D+02 0.00000000000000D+00 2 18 1 18 -0.68864760119762D+01 -0.18971069931448D+00 3 18 1 18 0.12907953016800D+01 0.16577648637509D+00 1 19 1 18 0.36179266440759D+00 -0.81378854505298D-15 2 19 1 18 0.68287835135634D-01 0.11803477806768D-05 3 19 1 18 -0.22178120985563D+00 0.20237112433332D-06 1 20 1 18 -0.20172472936118D-14 0.14972163595795D-01 2 20 1 18 -0.42015320180645D-01 -0.24734312916943D-02 3 20 1 18 0.14086396224381D+01 -0.12527673441751D-01 1 1 2 18 -0.86353847218527D+00 -0.22690739439507D-06 2 1 2 18 0.12389191950378D+00 -0.16777393989141D-07 3 1 2 18 0.16706368605351D+00 0.20213449796757D-06 1 2 2 18 0.11310439235659D+00 0.27092240302348D-01 2 2 2 18 -0.83235442486986D+00 0.12606854493732D-01 3 2 2 18 -0.10948572598823D+01 -0.12558143074972D-01 1 3 2 18 -0.67176802529491D+00 0.52547534079834D-02 2 3 2 18 -0.26721322086047D+00 0.67301329828329D-03 3 3 2 18 0.16166081741401D+00 0.99471786066918D-03 1 4 2 18 0.62660586630808D+00 -0.44614389325517D-06 2 4 2 18 -0.37565393369070D+00 -0.18546162865389D-06 3 4 2 18 0.74414560792873D-02 0.41294039116083D-06 1 5 2 18 -0.24317149100598D+01 -0.21193322633163D-01 2 5 2 18 0.12131103227848D+01 0.78851080443661D-02 3 5 2 18 0.77267282968479D+00 0.64486680591532D-01 1 6 2 18 0.40576931150239D+00 0.10221440279522D+00 2 6 2 18 -0.24423588943713D-01 -0.10412357639943D+00 3 6 2 18 -0.30359982702477D+01 -0.79447551651895D-02 1 7 2 18 -0.14573982766881D+01 -0.13075103789416D-01 2 7 2 18 0.91062083360434D-01 -0.22416544868940D-02 3 7 2 18 -0.78861004528204D+00 -0.48875958825168D-01 1 8 2 18 0.20463990501138D+00 0.34349079966531D-01 2 8 2 18 0.16252001627055D+00 -0.11416271009605D-01 3 8 2 18 0.28426666852924D+01 0.45046507557082D-02 1 9 2 18 -0.15520533430960D+00 0.11134938546199D-06 2 9 2 18 0.53388500064516D+00 0.27426758219618D-06 3 9 2 18 0.34957157651689D+01 0.71307482189835D-06 1 10 2 18 -0.80935195239608D+00 0.29507372588119D-01 2 10 2 18 0.93502320659138D+00 -0.41300989148836D-01 3 10 2 18 -0.31649972223185D+01 -0.10999950761531D+00 1 11 2 18 0.10478562970400D+01 0.33718615322919D-06 2 11 2 18 -0.20412257977074D+00 0.38833371479570D-08 3 11 2 18 -0.27702728437013D+01 -0.61738257650908D-06 1 12 2 18 -0.26089769289022D+00 -0.55462572263886D-01 2 12 2 18 0.39716460783177D+00 0.24257768962605D-02 3 12 2 18 -0.29534081319711D+01 0.17234104266560D+00 1 13 2 18 0.92517370870155D+00 0.44206987265906D-06 2 13 2 18 0.46160340852430D-14 -0.43762548185386D-06 3 13 2 18 -0.20212138681150D+00 -0.29871211834610D-06 1 14 2 18 -0.19436888327661D+01 -0.38948290896356D-01 2 14 2 18 -0.67630302568858D+01 -0.17619068779888D-16 3 14 2 18 0.14443674954483D+00 0.11416482061087D-01 1 15 2 18 0.64993224846043D-01 0.17697402654779D-01 2 15 2 18 -0.56647615393757D-01 0.19282002014646D-01 3 15 2 18 -0.86378308593955D-01 0.17418634182744D-02 1 16 2 18 0.19009638188727D-01 -0.53125567924774D-02 2 16 2 18 0.58986358954178D-01 -0.14350436276662D-06 3 16 2 18 -0.41405230449544D+00 -0.84084633348851D-02 1 17 2 18 -0.36442300744290D+00 0.13691846451477D-02 2 17 2 18 -0.88768276842114D+00 -0.56518251296699D-03 3 17 2 18 -0.61484961140266D+00 -0.19261466535199D-01 1 18 2 18 -0.68864779151046D+01 0.18971120964227D+00 2 18 2 18 0.14365659165686D+02 0.00000000000000D+00 3 18 2 18 0.19885876466294D+01 0.19398185013989D+00 1 19 2 18 0.68287835135634D-01 -0.11803477806123D-05 2 19 2 18 -0.24051314802435D-01 -0.70098020806373D-15 3 19 2 18 -0.43610611744181D-01 -0.17347005573689D-06 1 20 2 18 0.42015320180648D-01 -0.24734312916943D-02 2 20 2 18 0.37584259624929D-14 -0.46464540167991D-01 3 20 2 18 -0.63675814312606D+00 0.18902846730645D-01 1 1 3 18 0.11093678603690D+01 0.28405313526652D-06 2 1 3 18 0.61624736641728D+00 0.73002882458510D-07 3 1 3 18 -0.30191144601155D+00 -0.48429957243655D-06 1 2 3 18 -0.25142281874041D+00 -0.69760145231563D-02 2 2 3 18 -0.86237266963278D+00 -0.10810685967263D-01 3 2 3 18 -0.23982246383876D+01 -0.24477481513503D-01 1 3 3 18 -0.80663723739251D+00 -0.65285290862625D-02 2 3 3 18 -0.24739921605511D+00 -0.21134327938200D-02 3 3 3 18 -0.21372329087677D+00 -0.37789498105771D-02 1 4 3 18 -0.10785564770849D+01 0.33993420110422D-06 2 4 3 18 -0.46771224625448D+00 -0.77575139591705D-06 3 4 3 18 -0.17515671466161D+00 -0.67991553298194D-06 1 5 3 18 -0.54457476066136D+00 -0.32243085944314D-01 2 5 3 18 0.83142332788883D+00 0.63777950819958D-01 3 5 3 18 0.43358483535486D+01 0.26942192371736D-01 1 6 3 18 0.11749824647070D+01 0.16782858801055D-01 2 6 3 18 -0.39263645059176D+00 -0.36584022370915D-01 3 6 3 18 0.20019335293057D+00 0.74632070191079D-01 1 7 3 18 0.55412559341216D+00 0.45925951970455D-01 2 7 3 18 -0.95920887648773D+00 -0.36209539711455D-01 3 7 3 18 0.38543492098479D+01 0.24961300556863D-01 1 8 3 18 -0.18464602830797D+01 -0.13801012644523D-01 2 8 3 18 0.25795522233827D+00 0.51648474989799D-02 3 8 3 18 0.30555578378937D+00 0.15861160436614D-01 1 9 3 18 -0.10691410880597D+01 0.50385591793802D-06 2 9 3 18 0.17446300102037D+01 -0.59352764703299D-06 3 9 3 18 0.26654984393297D+01 0.10056049293931D-06 1 10 3 18 0.15212693177318D+01 0.29378448157178D-01 2 10 3 18 -0.10273560672803D+01 -0.56343722398482D-01 3 10 3 18 0.67939509470960D+00 0.11016207830166D+00 1 11 3 18 0.23102469375357D+01 0.16841861123780D-06 2 11 3 18 -0.10915050290647D+01 0.97442887294772D-06 3 11 3 18 -0.11148553456062D+01 -0.50408509935541D-06 1 12 3 18 0.14460635025581D+01 -0.36019086614234D-01 2 12 3 18 -0.12976185230743D+01 0.37278351710140D-02 3 12 3 18 0.23985556697210D+01 -0.16744757717881D+00 1 13 3 18 0.17538159518834D+01 -0.60820574656837D-06 2 13 3 18 0.20212138681151D+00 -0.29871211834697D-06 3 13 3 18 0.16315291088080D-13 -0.54291375846955D-06 1 14 3 18 0.46819130833406D-01 -0.91282937840370D-02 2 14 3 18 0.14443674954483D+00 -0.11416482061087D-01 3 14 3 18 0.17321575636988D+01 -0.66092214381381D-16 1 15 3 18 0.15997690726366D+00 -0.31207405124736D-02 2 15 3 18 0.86377337554110D-01 -0.17427755476425D-02 3 15 3 18 -0.24682108153475D+00 -0.17144360058819D-01 1 16 3 18 0.93322963471947D+00 0.12403348810596D-02 2 16 3 18 0.41405356045998D+00 -0.84096525770970D-02 3 16 3 18 -0.86695235884171D-01 0.89247515063650D-08 1 17 3 18 0.81563612093760D+00 0.93784244454283D-02 2 17 3 18 -0.61484764818829D+00 -0.19261892934482D-01 3 17 3 18 0.39852344590289D+00 -0.22487926582536D-02 1 18 3 18 0.12907705592793D+01 -0.16577756281318D+00 2 18 3 18 0.19886166343830D+01 -0.19398128188652D+00 3 18 3 18 0.15247819034117D+02 0.00000000000000D+00 1 19 3 18 0.22178120985567D+00 0.20237112433505D-06 2 19 3 18 0.43610611744183D-01 -0.17347005573689D-06 3 19 3 18 -0.10161085321636D+01 -0.38799796375037D-15 1 20 3 18 0.14086396224381D+01 0.12527673441751D-01 2 20 3 18 -0.63675814312606D+00 -0.18902846730645D-01 3 20 3 18 0.91704948476063D-15 -0.92826278285592D-02 1 1 1 19 -0.83722932351961D+00 -0.63653622369531D-06 2 1 1 19 0.34428420488003D+00 0.37372532680389D-06 3 1 1 19 0.17584629655882D+01 -0.13190429477968D-06 1 2 1 19 -0.15275697490881D+01 -0.64572596198175D-02 2 2 1 19 -0.49549009324282D+00 0.24006154107443D-01 3 2 1 19 0.19271974120556D+00 -0.13899459436934D-01 1 3 1 19 -0.66066883358686D+00 0.58092146726289D-02 2 3 1 19 0.23438760987993D+00 0.19385491922711D-02 3 3 1 19 -0.13585071658991D+01 -0.74788430588267D-03 1 4 1 19 -0.10668548975768D+01 0.63037186047055D-06 2 4 1 19 0.36123798914906D+00 0.60182699569466D-06 3 4 1 19 0.10142356701900D+01 0.73102492044715D-06 1 5 1 19 0.64261471368816D+00 0.39035000447819D-01 2 5 1 19 -0.15300371689550D+00 -0.77025902269862D-01 3 5 1 19 0.38966692907452D+01 0.11517268690800D-01 1 6 1 19 -0.46510512037136D+01 -0.15901986239628D-01 2 6 1 19 -0.68345312777821D+00 0.97797549474338D-02 3 6 1 19 -0.62141502835388D+00 -0.50205480190898D-01 1 7 1 19 0.73418429166607D+00 0.27675484520819D-01 2 7 1 19 0.15938290873739D+00 -0.20789309500503D-01 3 7 1 19 -0.42221527349252D+01 -0.10684640142367D-01 1 8 1 19 -0.51358504712509D+01 -0.13474928096297D-01 2 8 1 19 -0.53370378876716D+00 -0.96362797232912D-02 3 8 1 19 0.49749972773557D+00 0.40974196505348D-01 1 9 1 19 0.63306122767647D+00 -0.23395148598957D-06 2 9 1 19 0.52364748639404D+00 0.25801219189772D-06 3 9 1 19 -0.32019615082073D+01 -0.37732333979861D-06 1 10 1 19 0.64942645387004D-01 -0.36633641645381D-02 2 10 1 19 -0.90819511059349D+00 0.44958752794675D-01 3 10 1 19 -0.34417030988130D+01 -0.17217352796029D+00 1 11 1 19 -0.79845861100862D+00 0.72611612469347D-06 2 11 1 19 0.86617816800293D+00 0.31855261181127D-06 3 11 1 19 -0.42098323762825D+01 -0.18699115725018D-05 1 12 1 19 0.40134067866258D+00 -0.53503290406861D-01 2 12 1 19 0.55778767451163D+00 0.10907649972753D-01 3 12 1 19 0.34985486325795D+01 -0.14084884797158D+00 1 13 1 19 0.20020795220701D-01 -0.10028013876196D-06 2 13 1 19 0.19009642624041D-01 0.53128080730073D-02 3 13 1 19 0.93322813237245D+00 -0.12406512192840D-02 1 14 1 19 0.33116110735535D+00 -0.13483226342345D-01 2 14 1 19 -0.64995108599878D-01 -0.17700200239526D-01 3 14 1 19 -0.15997970813981D+00 0.31200264480516D-02 1 15 1 19 0.29394031008974D+01 -0.13118784182002D-15 2 15 1 19 0.19436888327661D+01 -0.38948290896356D-01 3 15 1 19 0.46819130833407D-01 0.91282937840373D-02 1 16 1 19 -0.55150157905772D-14 0.19408568715890D-06 2 16 1 19 -0.92517370870155D+00 0.44206987265290D-06 3 16 1 19 0.17538159518834D+01 0.60820574644117D-06 1 17 1 19 0.89171461111833D-15 -0.14972163595795D-01 2 17 1 19 0.42015320180648D-01 0.24734312916944D-02 3 17 1 19 0.14086396224381D+01 -0.12527673441752D-01 1 18 1 19 0.36179266440759D+00 0.81378854505298D-15 2 18 1 19 0.68287835135634D-01 0.11803477806123D-05 3 18 1 19 0.22178120985567D+00 -0.20237112433505D-06 1 19 1 19 0.15006438807181D+02 0.00000000000000D+00 2 19 1 19 -0.68864760119761D+01 -0.18971069931448D+00 3 19 1 19 -0.12907953016800D+01 -0.16577648637509D+00 1 20 1 19 -0.67478870946501D+00 0.30054587356236D-02 2 20 1 19 0.36442224451333D+00 -0.13700804630379D-02 3 20 1 19 0.81563602512014D+00 0.93795643715276D-02 1 1 2 19 0.86353847218527D+00 0.22690739623192D-06 2 1 2 19 -0.12389191950378D+00 0.16777395084060D-07 3 1 2 19 0.16706368605349D+00 0.20213450347727D-06 1 2 2 19 0.11310439235667D+00 0.27092240302347D-01 2 2 2 19 -0.83235442486980D+00 0.12606854493732D-01 3 2 2 19 0.10948572598822D+01 0.12558143074973D-01 1 3 2 19 0.67176802529489D+00 -0.52547534079826D-02 2 3 2 19 0.26721322086046D+00 -0.67301329828225D-03 3 3 2 19 0.16166081741401D+00 0.99471786066692D-03 1 4 2 19 0.62660586630814D+00 -0.44614389332628D-06 2 4 2 19 -0.37565393369067D+00 -0.18546162845558D-06 3 4 2 19 -0.74414560792295D-02 -0.41294039088846D-06 1 5 2 19 -0.40576931150239D+00 -0.10221440279522D+00 2 5 2 19 0.24423588943714D-01 0.10412357639943D+00 3 5 2 19 -0.30359982702477D+01 -0.79447551651891D-02 1 6 2 19 0.24317149100597D+01 0.21193322633141D-01 2 6 2 19 -0.12131103227848D+01 -0.78851080443444D-02 3 6 2 19 0.77267282968477D+00 0.64486680591523D-01 1 7 2 19 -0.20463990501137D+00 -0.34349079966531D-01 2 7 2 19 -0.16252001627054D+00 0.11416271009605D-01 3 7 2 19 0.28426666852924D+01 0.45046507557076D-02 1 8 2 19 0.14573982766880D+01 0.13075103789392D-01 2 8 2 19 -0.91062083360431D-01 0.22416544868989D-02 3 8 2 19 -0.78861004528204D+00 -0.48875958825162D-01 1 9 2 19 0.15520533430961D+00 -0.11134938638919D-06 2 9 2 19 -0.53388500064516D+00 -0.27426758093800D-06 3 9 2 19 0.34957157651689D+01 0.71307481765521D-06 1 10 2 19 -0.80935195239606D+00 0.29507372588119D-01 2 10 2 19 0.93502320659138D+00 -0.41300989148836D-01 3 10 2 19 0.31649972223185D+01 0.10999950761531D+00 1 11 2 19 0.10478562970400D+01 0.33718615325763D-06 2 11 2 19 -0.20412257977074D+00 0.38833369727601D-08 3 11 2 19 0.27702728437013D+01 0.61738257656517D-06 1 12 2 19 0.26089769289022D+00 0.55462572263884D-01 2 12 2 19 -0.39716460783178D+00 -0.24257768962601D-02 3 12 2 19 -0.29534081319711D+01 0.17234104266561D+00 1 13 2 19 -0.19009638188729D-01 0.53125567924776D-02 2 13 2 19 -0.58986358954180D-01 0.14350436269973D-06 3 13 2 19 -0.41405230449544D+00 -0.84084633348851D-02 1 14 2 19 0.64993224846046D-01 0.17697402654779D-01 2 14 2 19 -0.56647615393739D-01 0.19282002014646D-01 3 14 2 19 0.86378308593953D-01 -0.17418634182743D-02 1 15 2 19 -0.19436888327661D+01 -0.38948290896356D-01 2 15 2 19 -0.67630302568859D+01 -0.11543556742304D-16 3 15 2 19 -0.14443674954483D+00 -0.11416482061087D-01 1 16 2 19 -0.92517370870155D+00 -0.44206987050720D-06 2 16 2 19 -0.61923523669386D-15 0.43762548201937D-06 3 16 2 19 -0.20212138681150D+00 -0.29871211824266D-06 1 17 2 19 -0.42015320180645D-01 0.24734312916944D-02 2 17 2 19 0.19997205635530D-14 0.46464540167991D-01 3 17 2 19 -0.63675814312606D+00 0.18902846730645D-01 1 18 2 19 0.68287835135634D-01 -0.11803477806768D-05 2 18 2 19 -0.24051314802435D-01 0.70098020806373D-15 3 18 2 19 0.43610611744183D-01 0.17347005573689D-06 1 19 2 19 -0.68864779151046D+01 0.18971120964227D+00 2 19 2 19 0.14365659165686D+02 0.00000000000000D+00 3 19 2 19 -0.19885876466293D+01 -0.19398185013989D+00 1 20 2 19 0.36442300744293D+00 -0.13691846451494D-02 2 20 2 19 0.88768276842115D+00 0.56518251296548D-03 3 20 2 19 -0.61484961140265D+00 -0.19261466535199D-01 1 1 3 19 0.11093678603690D+01 0.28405313952331D-06 2 1 3 19 0.61624736641727D+00 0.73002887971685D-07 3 1 3 19 0.30191144601155D+00 0.48429958789456D-06 1 2 3 19 0.25142281874033D+00 0.69760145231567D-02 2 2 3 19 0.86237266963271D+00 0.10810685967263D-01 3 2 3 19 -0.23982246383877D+01 -0.24477481513501D-01 1 3 3 19 -0.80663723739254D+00 -0.65285290862636D-02 2 3 3 19 -0.24739921605511D+00 -0.21134327938222D-02 3 3 3 19 0.21372329087681D+00 0.37789498105838D-02 1 4 3 19 0.10785564770849D+01 -0.33993419813410D-06 2 4 3 19 0.46771224625455D+00 0.77575139618942D-06 3 4 3 19 -0.17515671466169D+00 -0.67991553258157D-06 1 5 3 19 0.11749824647070D+01 0.16782858801054D-01 2 5 3 19 -0.39263645059177D+00 -0.36584022370915D-01 3 5 3 19 -0.20019335293061D+00 -0.74632070191073D-01 1 6 3 19 -0.54457476066135D+00 -0.32243085944306D-01 2 6 3 19 0.83142332788881D+00 0.63777950819949D-01 3 6 3 19 -0.43358483535486D+01 -0.26942192371761D-01 1 7 3 19 -0.18464602830797D+01 -0.13801012644522D-01 2 7 3 19 0.25795522233825D+00 0.51648474989793D-02 3 7 3 19 -0.30555578378941D+00 -0.15861160436606D-01 1 8 3 19 0.55412559341218D+00 0.45925951970448D-01 2 8 3 19 -0.95920887648773D+00 -0.36209539711449D-01 3 8 3 19 -0.38543492098478D+01 -0.24961300556886D-01 1 9 3 19 -0.10691410880597D+01 0.50385592050534D-06 2 9 3 19 0.17446300102037D+01 -0.59352765126572D-06 3 9 3 19 -0.26654984393297D+01 -0.10056048574616D-06 1 10 3 19 -0.15212693177318D+01 -0.29378448157178D-01 2 10 3 19 0.10273560672804D+01 0.56343722398482D-01 3 10 3 19 0.67939509470968D+00 0.11016207830167D+00 1 11 3 19 -0.23102469375356D+01 -0.16841861168297D-06 2 11 3 19 0.10915050290647D+01 -0.97442887288122D-06 3 11 3 19 -0.11148553456063D+01 -0.50408510071564D-06 1 12 3 19 0.14460635025581D+01 -0.36019086614236D-01 2 12 3 19 -0.12976185230743D+01 0.37278351710173D-02 3 12 3 19 -0.23985556697210D+01 0.16744757717881D+00 1 13 3 19 0.93322963471947D+00 0.12403348810596D-02 2 13 3 19 0.41405356045998D+00 -0.84096525770970D-02 3 13 3 19 0.86695235884171D-01 -0.89247515296709D-08 1 14 3 19 -0.15997690726365D+00 0.31207405124735D-02 2 14 3 19 -0.86377337554112D-01 0.17427755476426D-02 3 14 3 19 -0.24682108153473D+00 -0.17144360058817D-01 1 15 3 19 -0.46819130833403D-01 0.91282937840373D-02 2 15 3 19 -0.14443674954483D+00 0.11416482061087D-01 3 15 3 19 0.17321575636988D+01 0.14749791465939D-15 1 16 3 19 0.17538159518834D+01 -0.60820575088331D-06 2 16 3 19 0.20212138681150D+00 -0.29871211824179D-06 3 16 3 19 -0.23269014898736D-14 0.54291375923575D-06 1 17 3 19 0.14086396224381D+01 0.12527673441751D-01 2 17 3 19 -0.63675814312606D+00 -0.18902846730645D-01 3 17 3 19 0.10521815539166D-14 0.92826278285592D-02 1 18 3 19 -0.22178120985563D+00 -0.20237112433332D-06 2 18 3 19 -0.43610611744181D-01 0.17347005573689D-06 3 18 3 19 -0.10161085321636D+01 0.38799796375037D-15 1 19 3 19 -0.12907705592793D+01 0.16577756281318D+00 2 19 3 19 -0.19886166343829D+01 0.19398128188652D+00 3 19 3 19 0.15247819034117D+02 0.00000000000000D+00 1 20 3 19 0.81563612093758D+00 0.93784244454269D-02 2 20 3 19 -0.61484764818829D+00 -0.19261892934483D-01 3 20 3 19 -0.39852344590289D+00 0.22487926582545D-02 1 1 1 20 0.15275697490882D+01 0.64572596198202D-02 2 1 1 20 0.49549009324294D+00 -0.24006154107437D-01 3 1 1 20 -0.19271974120576D+00 0.13899459436925D-01 1 2 1 20 0.83722932351961D+00 0.63653622059669D-06 2 2 1 20 -0.34428420488005D+00 -0.37372532536252D-06 3 2 1 20 -0.17584629655882D+01 0.13190429916133D-06 1 3 1 20 -0.10668548975769D+01 0.63037186035466D-06 2 3 1 20 0.36123798914905D+00 0.60182699527907D-06 3 3 1 20 0.10142356701901D+01 0.73102491862907D-06 1 4 1 20 -0.66066883358687D+00 0.58092146726290D-02 2 4 1 20 0.23438760987996D+00 0.19385491922704D-02 3 4 1 20 -0.13585071658991D+01 -0.74788430588178D-03 1 5 1 20 0.64261471368819D+00 0.39035000447820D-01 2 5 1 20 -0.15300371689550D+00 -0.77025902269862D-01 3 5 1 20 0.38966692907452D+01 0.11517268690801D-01 1 6 1 20 0.46510512037136D+01 0.15901986239632D-01 2 6 1 20 0.68345312777826D+00 -0.97797549474559D-02 3 6 1 20 0.62141502835397D+00 0.50205480190903D-01 1 7 1 20 -0.73418429166609D+00 -0.27675484520816D-01 2 7 1 20 -0.15938290873739D+00 0.20789309500503D-01 3 7 1 20 0.42221527349251D+01 0.10684640142367D-01 1 8 1 20 -0.51358504712511D+01 -0.13474928096293D-01 2 8 1 20 -0.53370378876689D+00 -0.96362797232900D-02 3 8 1 20 0.49749972773592D+00 0.40974196505349D-01 1 9 1 20 0.64942645387028D-01 -0.36633641645369D-02 2 9 1 20 -0.90819511059349D+00 0.44958752794671D-01 3 9 1 20 -0.34417030988130D+01 -0.17217352796030D+00 1 10 1 20 0.63306122767643D+00 -0.23395148620385D-06 2 10 1 20 0.52364748639404D+00 0.25801219184943D-06 3 10 1 20 -0.32019615082073D+01 -0.37732334007914D-06 1 11 1 20 0.40134067866257D+00 -0.53503290406860D-01 2 11 1 20 0.55778767451162D+00 0.10907649972752D-01 3 11 1 20 0.34985486325794D+01 -0.14084884797158D+00 1 12 1 20 -0.79845861100861D+00 0.72611612620778D-06 2 12 1 20 0.86617816800295D+00 0.31855261213395D-06 3 12 1 20 -0.42098323762825D+01 -0.18699115721272D-05 1 13 1 20 0.33116110735534D+00 -0.13483226342344D-01 2 13 1 20 -0.64995108599880D-01 -0.17700200239526D-01 3 13 1 20 -0.15997970813980D+00 0.31200264480515D-02 1 14 1 20 0.20020795220702D-01 -0.10028013879000D-06 2 14 1 20 0.19009642624043D-01 0.53128080730072D-02 3 14 1 20 0.93322813237245D+00 -0.12406512192840D-02 1 15 1 20 -0.10469449470543D-13 0.19408569634642D-06 2 15 1 20 -0.92517370870153D+00 0.44206987059969D-06 3 15 1 20 0.17538159518834D+01 0.60820575106516D-06 1 16 1 20 0.29394031008974D+01 -0.42301672733414D-16 2 16 1 20 0.19436888327661D+01 -0.38948290896356D-01 3 16 1 20 0.46819130833407D-01 0.91282937840377D-02 1 17 1 20 0.36179266440758D+00 0.31648318022769D-15 2 17 1 20 0.68287835135634D-01 0.11803477807010D-05 3 17 1 20 0.22178120985564D+00 -0.20237112367589D-06 1 18 1 20 -0.20172472936118D-14 -0.14972163595795D-01 2 18 1 20 0.42015320180648D-01 0.24734312916943D-02 3 18 1 20 0.14086396224381D+01 -0.12527673441751D-01 1 19 1 20 -0.67478870946501D+00 0.30054587356243D-02 2 19 1 20 0.36442224451333D+00 -0.13700804630355D-02 3 19 1 20 0.81563602512014D+00 0.93795643715295D-02 1 20 1 20 0.15006438807181D+02 0.00000000000000D+00 2 20 1 20 -0.68864760119758D+01 -0.18971069931448D+00 3 20 1 20 -0.12907953016803D+01 -0.16577648637509D+00 1 1 2 20 -0.11310439235656D+00 -0.27092240302342D-01 2 1 2 20 0.83235442486972D+00 -0.12606854493728D-01 3 1 2 20 -0.10948572598823D+01 -0.12558143074984D-01 1 2 2 20 -0.86353847218528D+00 -0.22690739479055D-06 2 2 2 20 0.12389191950373D+00 -0.16777394210876D-07 3 2 2 20 -0.16706368605361D+00 -0.20213449790529D-06 1 3 2 20 0.62660586630813D+00 -0.44614389374186D-06 2 3 2 20 -0.37565393369068D+00 -0.18546162853648D-06 3 3 2 20 -0.74414560792295D-02 -0.41294039066903D-06 1 4 2 20 0.67176802529491D+00 -0.52547534079833D-02 2 4 2 20 0.26721322086048D+00 -0.67301329828208D-03 3 4 2 20 0.16166081741401D+00 0.99471786066701D-03 1 5 2 20 -0.40576931150239D+00 -0.10221440279522D+00 2 5 2 20 0.24423588943715D-01 0.10412357639943D+00 3 5 2 20 -0.30359982702477D+01 -0.79447551651883D-02 1 6 2 20 -0.24317149100597D+01 -0.21193322633163D-01 2 6 2 20 0.12131103227846D+01 0.78851080443659D-02 3 6 2 20 -0.77267282968484D+00 -0.64486680591533D-01 1 7 2 20 0.20463990501137D+00 0.34349079966531D-01 2 7 2 20 0.16252001627055D+00 -0.11416271009605D-01 3 7 2 20 -0.28426666852924D+01 -0.45046507557083D-02 1 8 2 20 0.14573982766882D+01 0.13075103789394D-01 2 8 2 20 -0.91062083360221D-01 0.22416544868989D-02 3 8 2 20 -0.78861004528221D+00 -0.48875958825162D-01 1 9 2 20 -0.80935195239606D+00 0.29507372588115D-01 2 9 2 20 0.93502320659137D+00 -0.41300989148833D-01 3 9 2 20 0.31649972223185D+01 0.10999950761531D+00 1 10 2 20 0.15520533430961D+00 -0.11134938643574D-06 2 10 2 20 -0.53388500064516D+00 -0.27426758148181D-06 3 10 2 20 0.34957157651689D+01 0.71307481760695D-06 1 11 2 20 0.26089769289021D+00 0.55462572263884D-01 2 11 2 20 -0.39716460783181D+00 -0.24257768962603D-02 3 11 2 20 -0.29534081319711D+01 0.17234104266561D+00 1 12 2 20 0.10478562970400D+01 0.33718615358030D-06 2 12 2 20 -0.20412257977078D+00 0.38833370837055D-08 3 12 2 20 0.27702728437013D+01 0.61738257614136D-06 1 13 2 20 0.64993224846044D-01 0.17697402654779D-01 2 13 2 20 -0.56647615393749D-01 0.19282002014645D-01 3 13 2 20 0.86378308593952D-01 -0.17418634182744D-02 1 14 2 20 -0.19009638188727D-01 0.53125567924775D-02 2 14 2 20 -0.58986358954178D-01 0.14350436268993D-06 3 14 2 20 -0.41405230449544D+00 -0.84084633348852D-02 1 15 2 20 -0.92517370870153D+00 -0.44206987256041D-06 2 15 2 20 0.12608878002594D-13 0.43762547964053D-06 3 15 2 20 -0.20212138681150D+00 -0.29871211899056D-06 1 16 2 20 -0.19436888327661D+01 -0.38948290896356D-01 2 16 2 20 -0.67630302568860D+01 0.65074664339319D-17 3 16 2 20 -0.14443674954483D+00 -0.11416482061087D-01 1 17 2 20 0.68287835135634D-01 -0.11803477805882D-05 2 17 2 20 -0.24051314802430D-01 0.34002143330241D-15 3 17 2 20 0.43610611744182D-01 0.17347005584703D-06 1 18 2 20 -0.42015320180645D-01 0.24734312916943D-02 2 18 2 20 0.37584259624929D-14 0.46464540167991D-01 3 18 2 20 -0.63675814312606D+00 0.18902846730645D-01 1 19 2 20 0.36442300744293D+00 -0.13691846451469D-02 2 19 2 20 0.88768276842115D+00 0.56518251296947D-03 3 19 2 20 -0.61484961140265D+00 -0.19261466535198D-01 1 20 2 20 -0.68864779151043D+01 0.18971120964227D+00 2 20 2 20 0.14365659165685D+02 0.00000000000000D+00 3 20 2 20 -0.19885876466295D+01 -0.19398185013989D+00 1 1 3 20 -0.25142281874053D+00 -0.69760145231656D-02 2 1 3 20 -0.86237266963282D+00 -0.10810685967275D-01 3 1 3 20 0.23982246383879D+01 0.24477481513514D-01 1 2 3 20 -0.11093678603689D+01 -0.28405313514252D-06 2 2 3 20 -0.61624736641738D+00 -0.73002882396234D-07 3 2 3 20 -0.30191144601152D+00 -0.48429957173785D-06 1 3 3 20 0.10785564770849D+01 -0.33993419995218D-06 2 3 3 20 0.46771224625455D+00 0.77575139640885D-06 3 3 3 20 -0.17515671466163D+00 -0.67991553389749D-06 1 4 3 20 -0.80663723739252D+00 -0.65285290862628D-02 2 4 3 20 -0.24739921605510D+00 -0.21134327938221D-02 3 4 3 20 0.21372329087680D+00 0.37789498105818D-02 1 5 3 20 0.11749824647070D+01 0.16782858801055D-01 2 5 3 20 -0.39263645059179D+00 -0.36584022370914D-01 3 5 3 20 -0.20019335293063D+00 -0.74632070191075D-01 1 6 3 20 0.54457476066143D+00 0.32243085944311D-01 2 6 3 20 -0.83142332788888D+00 -0.63777950819960D-01 3 6 3 20 0.43358483535488D+01 0.26942192371735D-01 1 7 3 20 0.18464602830797D+01 0.13801012644522D-01 2 7 3 20 -0.25795522233825D+00 -0.51648474989800D-02 3 7 3 20 0.30555578378940D+00 0.15861160436612D-01 1 8 3 20 0.55412559341254D+00 0.45925951970449D-01 2 8 3 20 -0.95920887648790D+00 -0.36209539711449D-01 3 8 3 20 -0.38543492098477D+01 -0.24961300556887D-01 1 9 3 20 -0.15212693177318D+01 -0.29378448157184D-01 2 9 3 20 0.10273560672803D+01 0.56343722398488D-01 3 9 3 20 0.67939509470963D+00 0.11016207830167D+00 1 10 3 20 -0.10691410880597D+01 0.50385592022133D-06 2 10 3 20 0.17446300102037D+01 -0.59352765131398D-06 3 10 3 20 -0.26654984393296D+01 -0.10056048607196D-06 1 11 3 20 0.14460635025580D+01 -0.36019086614237D-01 2 11 3 20 -0.12976185230742D+01 0.37278351710174D-02 3 11 3 20 -0.23985556697209D+01 0.16744757717881D+00 1 12 3 20 -0.23102469375356D+01 -0.16841861128763D-06 2 12 3 20 0.10915050290647D+01 -0.97442887331196D-06 3 12 3 20 -0.11148553456062D+01 -0.50408510057852D-06 1 13 3 20 -0.15997690726364D+00 0.31207405124734D-02 2 13 3 20 -0.86377337554114D-01 0.17427755476425D-02 3 13 3 20 -0.24682108153475D+00 -0.17144360058817D-01 1 14 3 20 0.93322963471947D+00 0.12403348810596D-02 2 14 3 20 0.41405356045998D+00 -0.84096525770971D-02 3 14 3 20 0.86695235884166D-01 -0.89247515180838D-08 1 15 3 20 0.17538159518834D+01 -0.60820574625932D-06 2 15 3 20 0.20212138681151D+00 -0.29871211898969D-06 3 15 3 20 0.20315018881788D-13 0.54291375589894D-06 1 16 3 20 -0.46819130833403D-01 0.91282937840377D-02 2 16 3 20 -0.14443674954483D+00 0.11416482061087D-01 3 16 3 20 0.17321575636988D+01 -0.30811844581359D-15 1 17 3 20 -0.22178120985566D+00 -0.20237112367416D-06 2 17 3 20 -0.43610611744183D-01 0.17347005584703D-06 3 17 3 20 -0.10161085321636D+01 0.78732595685601D-15 1 18 3 20 0.14086396224381D+01 0.12527673441751D-01 2 18 3 20 -0.63675814312606D+00 -0.18902846730645D-01 3 18 3 20 0.91704948476063D-15 0.92826278285592D-02 1 19 3 20 0.81563612093758D+00 0.93784244454287D-02 2 19 3 20 -0.61484764818829D+00 -0.19261892934482D-01 3 19 3 20 -0.39852344590289D+00 0.22487926582530D-02 1 20 3 20 -0.12907705592796D+01 0.16577756281318D+00 2 20 3 20 -0.19886166343830D+01 0.19398128188652D+00 3 20 3 20 0.15247819034117D+02 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 3600 qpt 0.00000000E+00 5.00000000E-01 5.00000000E-01 1.0 1 1 1 1 0.80943217583681D+01 0.00000000000000D+00 2 1 1 1 0.13186135840081D+01 0.57296114286964D-06 3 1 1 1 -0.42646596956478D-13 0.00000000000000D+00 1 2 1 1 0.95142489520177D-14 -0.27334138856404D-15 2 2 1 1 -0.97402180069091D-15 -0.94726716963915D-16 3 2 1 1 0.25427140732212D-01 0.84774281023530D-08 1 3 1 1 0.15051021470047D-12 0.49881189984900D-08 2 3 1 1 0.10158903207779D+00 0.37759552788041D-08 3 3 1 1 0.13745148677290D-15 0.23979773728661D-16 1 4 1 1 -0.86800489883308D-15 -0.10026883031610D-14 2 4 1 1 0.84824365843741D-15 0.11965937642150D-16 3 4 1 1 0.40926675664256D-01 0.64650026361458D-08 1 5 1 1 0.55811863381891D+00 -0.88024739414606D-02 2 5 1 1 0.19958250941004D+00 -0.86434670879928D-02 3 5 1 1 0.39059267555499D+00 0.75696288097516D-03 1 6 1 1 0.55811863381892D+00 -0.88024739414606D-02 2 6 1 1 0.19958250941004D+00 -0.86434670879929D-02 3 6 1 1 -0.39059267555498D+00 -0.75696288097489D-03 1 7 1 1 -0.34119545832177D+01 -0.24534919728119D-01 2 7 1 1 -0.69558746439050D-01 -0.33519815380904D-02 3 7 1 1 0.26816151616295D+00 -0.51820868099591D-02 1 8 1 1 -0.34119545832177D+01 -0.24534919728117D-01 2 8 1 1 -0.69558746439051D-01 -0.33519815380908D-02 3 8 1 1 -0.26816151616296D+00 0.51820868099592D-02 1 9 1 1 -0.34656041519058D+00 0.11443052896922D-07 2 9 1 1 0.53615338254875D-01 0.20378772842160D-07 3 9 1 1 0.19715070492573D-14 0.61419302266506D-16 1 10 1 1 -0.28523351763842D-14 0.76920041112006D-16 2 10 1 1 -0.14385465772217D-14 -0.30432064542246D-15 3 10 1 1 0.33766389153619D+00 -0.10623606788790D-08 1 11 1 1 0.64589903821403D-14 -0.19258816618414D-14 2 11 1 1 -0.13259624379736D-14 0.90962563803894D-16 3 11 1 1 0.63017924966148D-01 -0.13109017868255D-07 1 12 1 1 0.11950148942892D+01 -0.18785284889324D-07 2 12 1 1 -0.46523303941539D+00 -0.15398837769661D-07 3 12 1 1 0.10064345225366D-14 0.98794097085265D-16 1 13 1 1 -0.18060809380495D+00 -0.79003607450267D-08 2 13 1 1 -0.31573517581627D+00 0.11350789185959D-08 3 13 1 1 0.52399729090690D+00 0.19408705840164D-07 1 14 1 1 0.34159599944569D-01 -0.10186584683516D-01 2 14 1 1 -0.29645719455466D+00 -0.10397496925168D-01 3 14 1 1 -0.32589235607614D+00 0.53961947241053D-03 1 15 1 1 -0.34159599944575D-01 0.10186584683516D-01 2 15 1 1 0.29645719455465D+00 0.10397496925167D-01 3 15 1 1 -0.32589235607614D+00 0.53961947241247D-03 1 16 1 1 -0.18060809380495D+00 -0.79003614460328D-08 2 16 1 1 -0.31573517581627D+00 0.11350790134656D-08 3 16 1 1 -0.52399729090687D+00 -0.19408705740624D-07 1 17 1 1 0.43486473279458D+00 0.15350506746489D-01 2 17 1 1 0.34479890278878D+00 0.54361281411015D-02 3 17 1 1 0.56626506089967D+00 -0.48887486834291D-02 1 18 1 1 0.92518036333799D-02 -0.30638200021204D-07 2 18 1 1 -0.30490190754154D+00 -0.68056519823792D-07 3 18 1 1 0.81823224224857D+00 -0.30844529748223D-06 1 19 1 1 -0.92518036333788D-02 0.30638199284225D-07 2 19 1 1 0.30490190754154D+00 0.68056517977089D-07 3 19 1 1 0.81823224224859D+00 -0.30844530402627D-06 1 20 1 1 0.43486473279457D+00 0.15350506746488D-01 2 20 1 1 0.34479890278876D+00 0.54361281411016D-02 3 20 1 1 -0.56626506089964D+00 0.48887486834285D-02 1 1 2 1 0.13186082980879D+01 0.62285906677980D-06 2 1 2 1 0.90519195953002D+01 0.00000000000000D+00 3 1 2 1 -0.32489664425812D-13 0.11102230246252D-15 1 2 2 1 -0.97402180069091D-15 -0.94726716963915D-16 2 2 2 1 -0.25647873873354D-13 -0.54814827485121D-14 3 2 2 1 -0.52911342726239D+00 0.55963899602601D-09 1 3 2 1 0.10158903207780D+00 -0.37759560669383D-08 2 3 2 1 -0.54130519899930D-13 -0.11817477907232D-07 3 3 2 1 0.20431055034664D-13 -0.72605979750786D-15 1 4 2 1 0.84824365843741D-15 0.11098575904161D-16 2 4 2 1 -0.27331563067263D-14 0.16021848643006D-15 3 4 2 1 -0.10396587672362D+01 0.79499785473515D-09 1 5 2 1 0.18400059467742D+00 0.96692812179009D-03 2 5 2 1 -0.57686684450242D+00 0.14826831048324D-01 3 5 2 1 0.67534143987683D+01 0.12288835753295D-01 1 6 2 1 0.18400059467742D+00 0.96692812179006D-03 2 6 2 1 -0.57686684450238D+00 0.14826831048335D-01 3 6 2 1 -0.67534143987683D+01 -0.12288835753302D-01 1 7 2 1 -0.60931119429412D+00 0.62667131860606D-02 2 7 2 1 0.33480134856161D+01 -0.12065918392820D-01 3 7 2 1 -0.99228147842170D+00 0.69398204166024D-02 1 8 2 1 -0.60931119429412D+00 0.62667131860602D-02 2 8 2 1 0.33480134856160D+01 -0.12065918392822D-01 3 8 2 1 0.99228147842167D+00 -0.69398204166009D-02 1 9 2 1 -0.47604055640837D+00 0.34260406355456D-08 2 9 2 1 -0.21724557850265D+01 0.10840747472141D-07 3 9 2 1 -0.14073438967469D-13 -0.15125693860538D-14 1 10 2 1 -0.14396083189590D-14 -0.30432064542246D-15 2 10 2 1 0.70226490399803D-15 0.15424656650652D-15 3 10 2 1 0.26303757206776D+01 0.18228245885590D-07 1 11 2 1 -0.13259624381804D-14 0.90962563803894D-16 2 11 2 1 -0.15658494438417D-14 0.43004396343367D-14 3 11 2 1 -0.25794895146209D+00 0.11773231049548D-07 1 12 2 1 -0.60939674657526D+00 -0.74825776906182D-08 2 12 2 1 0.12368887393920D+01 -0.11244907752492D-07 3 12 2 1 0.38476324321452D-15 0.52893186208015D-16 1 13 2 1 -0.72301312555332D+00 0.78458255071622D-08 2 13 2 1 -0.13059172872157D+01 -0.44285432992814D-08 3 13 2 1 -0.79397209156001D+00 -0.27923318309302D-07 1 14 2 1 -0.50608893451166D+00 -0.25217175319899D-02 2 14 2 1 -0.42669990022289D+00 -0.40911720073808D-02 3 14 2 1 0.98454495694062D+00 -0.63353830294851D-02 1 15 2 1 0.50608893451165D+00 0.25217175319881D-02 2 15 2 1 0.42669990022291D+00 0.40911720073820D-02 3 15 2 1 0.98454495694062D+00 -0.63353830294886D-02 1 16 2 1 -0.72301312555334D+00 0.78458256055013D-08 2 16 2 1 -0.13059172872157D+01 -0.44285472808934D-08 3 16 2 1 0.79397209156001D+00 0.27923319448804D-07 1 17 2 1 -0.16761329463243D-01 0.31249629992591D-01 2 17 2 1 0.17851870533801D+01 -0.22602251736435D-02 3 17 2 1 0.40625835904015D+00 -0.84648125232288D-02 1 18 2 1 -0.80259503795468D+00 -0.99245325663730D-07 2 18 2 1 0.10669534109938D+01 0.20708555513325D-06 3 18 2 1 0.92567424803793D+00 -0.81584868760726D-07 1 19 2 1 0.80259503795468D+00 0.99245323813558D-07 2 19 2 1 -0.10669534109938D+01 -0.20708555150975D-06 3 19 2 1 0.92567424803794D+00 -0.81584872601130D-07 1 20 2 1 -0.16761329463243D-01 0.31249629992591D-01 2 20 2 1 0.17851870533801D+01 -0.22602251736433D-02 3 20 2 1 -0.40625835904024D+00 0.84648125232295D-02 1 1 3 1 -0.42646596906847D-13 0.11102230246252D-15 2 1 3 1 -0.32489664439047D-13 0.11102230246252D-15 3 1 3 1 0.14810453964154D+02 0.00000000000000D+00 1 2 3 1 0.25427663988177D-01 -0.96968383752569D-08 2 2 3 1 -0.52911283615963D+00 -0.64224766070019D-09 3 2 3 1 -0.62611623752404D-13 0.12068576776255D-13 1 3 3 1 0.13745148677290D-15 0.23979773728660D-16 2 3 3 1 0.20431055034664D-13 -0.72605979750786D-15 3 3 3 1 -0.21372364450924D-12 -0.11626153452631D-07 1 4 3 1 -0.40926675664263D-01 0.64650026361458D-08 2 4 3 1 -0.10396587672362D+01 -0.79499768349999D-09 3 4 3 1 -0.67601296156300D-14 -0.78288234321485D-15 1 5 3 1 -0.78683661998381D-02 -0.31391281372027D-02 2 5 3 1 0.67961458154964D+01 0.15400178195876D-01 3 5 3 1 -0.41581799573405D+00 0.46382264600095D-02 1 6 3 1 0.78683661998411D-02 0.31391281372030D-02 2 6 3 1 -0.67961458154964D+01 -0.15400178195883D-01 3 6 3 1 -0.41581799573399D+00 0.46382264600100D-02 1 7 3 1 -0.58627756627625D+00 0.10593882194419D-01 2 7 3 1 -0.86899923548528D+00 0.12757658958083D-01 3 7 3 1 -0.11086389653709D-01 0.10217755955325D-01 1 8 3 1 0.58627756627624D+00 -0.10593882194419D-01 2 8 3 1 0.86899923548525D+00 -0.12757658958081D-01 3 8 3 1 -0.11086389653690D-01 0.10217755955318D-01 1 9 3 1 0.19715070492573D-14 0.60985621397511D-16 2 9 3 1 -0.14073438965814D-13 -0.15125693860538D-14 3 9 3 1 -0.12782401410138D+01 0.31764003270884D-07 1 10 3 1 0.21247939582633D-01 -0.46867255583688D-08 2 10 3 1 0.87852324247809D+00 -0.12183567861399D-07 3 10 3 1 0.47360697445233D-14 0.80575063714527D-16 1 11 3 1 -0.10381392416551D+00 0.11582382677622D-07 2 11 3 1 -0.86709724151753D-01 0.41128706196451D-08 3 11 3 1 0.15119053361585D-13 -0.62676994131194D-15 1 12 3 1 0.10064345225366D-14 0.98794097085265D-16 2 12 3 1 0.38476324321452D-15 0.52893186208015D-16 3 12 3 1 0.37027410533118D+01 -0.12589757952881D-06 1 13 3 1 -0.14815034947978D+00 -0.16133284155834D-07 2 13 3 1 -0.12016508029001D+01 0.11998678656501D-07 3 13 3 1 -0.31623890243690D+00 -0.21372883372406D-08 1 14 3 1 0.12198240512238D+00 0.15071331504316D-02 2 14 3 1 0.14104596669028D+01 -0.24786916402034D-03 3 14 3 1 0.45332216840792D+00 -0.33781122828537D-02 1 15 3 1 0.12198240512237D+00 0.15071331504335D-02 2 15 3 1 0.14104596669028D+01 -0.24786916402379D-03 3 15 3 1 -0.45332216840789D+00 0.33781122828562D-02 1 16 3 1 0.14815034947978D+00 0.16133284253639D-07 2 16 3 1 0.12016508029001D+01 -0.11998677517000D-07 3 16 3 1 -0.31623890243690D+00 -0.21372942946055D-08 1 17 3 1 0.11152602876194D+01 -0.62582020916374D-02 2 17 3 1 -0.13647920929397D+00 0.13824023979004D-01 3 17 3 1 0.24683163743510D+01 -0.24138185634093D-01 1 18 3 1 0.35195673198046D+00 -0.59913862342212D-07 2 18 3 1 0.13109063117039D+01 -0.47398371213707D-07 3 18 3 1 -0.40516331287124D+00 0.30872765706028D-06 1 19 3 1 0.35195673198045D+00 -0.59913868885384D-07 2 19 3 1 0.13109063117039D+01 -0.47398375054110D-07 3 19 3 1 0.40516331287125D+00 -0.30872767449097D-06 1 20 3 1 -0.11152602876193D+01 0.62582020916367D-02 2 20 3 1 0.13647920929385D+00 -0.13824023979003D-01 3 20 3 1 0.24683163743510D+01 -0.24138185634092D-01 1 1 1 2 0.95142489520177D-14 0.27334138856404D-15 2 1 1 2 -0.97402180069091D-15 0.94726716963915D-16 3 1 1 2 0.25427140732212D-01 0.84774285910790D-08 1 2 1 2 0.80943217583681D+01 0.00000000000000D+00 2 2 1 2 0.13186135840078D+01 0.57296114286964D-06 3 2 1 2 -0.14032810871502D-16 0.00000000000000D+00 1 3 1 2 0.67918679767932D-14 -0.10044386879934D-15 2 3 1 2 0.10422584748696D-14 -0.42458674578996D-16 3 3 1 2 0.40926675664260D-01 0.64650026781081D-08 1 4 1 2 0.24560592253757D-13 0.49881240740645D-08 2 4 1 2 0.10158903207784D+00 0.37759561133169D-08 3 4 1 2 -0.13176978595680D-14 0.17826099351762D-15 1 5 1 2 -0.55811863381897D+00 0.88024739414616D-02 2 5 1 2 -0.19958250941004D+00 0.86434670879930D-02 3 5 1 2 -0.39059267555499D+00 -0.75696288097482D-03 1 6 1 2 0.55811863381895D+00 -0.88024739414628D-02 2 6 1 2 0.19958250941004D+00 -0.86434670879929D-02 3 6 1 2 -0.39059267555499D+00 -0.75696288097463D-03 1 7 1 2 -0.34119545832178D+01 -0.24534919728139D-01 2 7 1 2 -0.69558746439051D-01 -0.33519815380905D-02 3 7 1 2 0.26816151616297D+00 -0.51820868099612D-02 1 8 1 2 0.34119545832178D+01 0.24534919728129D-01 2 8 1 2 0.69558746439058D-01 0.33519815380906D-02 3 8 1 2 0.26816151616295D+00 -0.51820868099601D-02 1 9 1 2 -0.31636351237506D-14 -0.65365886362255D-16 2 9 1 2 -0.15267433586726D-14 -0.17648994741536D-15 3 9 1 2 0.33766389153620D+00 -0.10623609630858D-08 1 10 1 2 -0.34656041519045D+00 0.11443051884465D-07 2 10 1 2 0.53615338254925D-01 0.20378770789568D-07 3 10 1 2 0.10423214802204D-14 0.32931860340359D-16 1 11 1 2 0.11950148942890D+01 -0.18785238670539D-07 2 11 1 2 -0.46523303941556D+00 -0.15398843276732D-07 3 11 1 2 -0.15335580028914D-14 -0.20480793753418D-15 1 12 1 2 0.70985113073084D-14 0.15579476266956D-14 2 12 1 2 0.11494264876207D-14 0.96409830206399D-16 3 12 1 2 0.63017924966153D-01 -0.13109017250006D-07 1 13 1 2 0.34159599944584D-01 -0.10186584683518D-01 2 13 1 2 -0.29645719455466D+00 -0.10397496925163D-01 3 13 1 2 -0.32589235607619D+00 0.53961947241873D-03 1 14 1 2 -0.18060809380502D+00 -0.79003606441698D-08 2 14 1 2 -0.31573517581627D+00 0.11350790041727D-08 3 14 1 2 0.52399729090680D+00 0.19408706009754D-07 1 15 1 2 -0.18060809380499D+00 -0.79003605968977D-08 2 15 1 2 -0.31573517581630D+00 0.11350796844820D-08 3 15 1 2 -0.52399729090682D+00 -0.19408706430496D-07 1 16 1 2 -0.34159599944587D-01 0.10186584683518D-01 2 16 1 2 0.29645719455467D+00 0.10397496925165D-01 3 16 1 2 -0.32589235607617D+00 0.53961947241700D-03 1 17 1 2 0.92518036333994D-02 -0.30638199694113D-07 2 17 1 2 -0.30490190754152D+00 -0.68056516041297D-07 3 17 1 2 0.81823224224843D+00 -0.30844531089644D-06 1 18 1 2 0.43486473279453D+00 0.15350506746488D-01 2 18 1 2 0.34479890278873D+00 0.54361281411131D-02 3 18 1 2 0.56626506089950D+00 -0.48887486834106D-02 1 19 1 2 0.43486473279452D+00 0.15350506746488D-01 2 19 1 2 0.34479890278867D+00 0.54361281411128D-02 3 19 1 2 -0.56626506089947D+00 0.48887486834107D-02 1 20 1 2 -0.92518036334017D-02 0.30638199337122D-07 2 20 1 2 0.30490190754157D+00 0.68056517666289D-07 3 20 1 2 0.81823224224854D+00 -0.30844530430314D-06 1 1 2 2 -0.97402180069091D-15 0.94509876529418D-16 2 1 2 2 -0.25647873873354D-13 0.54823501102501D-14 3 1 2 2 -0.52911342726238D+00 0.55964039858357D-09 1 2 2 2 0.13186082980876D+01 0.62285906677980D-06 2 2 2 2 0.90519195953020D+01 0.00000000000000D+00 3 2 2 2 -0.39595091804093D-13 0.11102230246252D-15 1 3 2 2 0.10422584748696D-14 -0.43326036316985D-16 2 3 2 2 0.57861399460735D-14 0.61367958676606D-15 3 3 2 2 -0.10396587672363D+01 0.79499687194217D-09 1 4 2 2 0.10158903207784D+00 -0.37759552324255D-08 2 4 2 2 -0.18536756471870D-13 -0.11817471393708D-07 3 4 2 2 0.25534358893769D-13 0.83814494815845D-15 1 5 2 2 -0.18400059467742D+00 -0.96692812178989D-03 2 5 2 2 0.57686684450241D+00 -0.14826831048341D-01 3 5 2 2 -0.67534143987684D+01 -0.12288835753328D-01 1 6 2 2 0.18400059467742D+00 0.96692812179000D-03 2 6 2 2 -0.57686684450244D+00 0.14826831048339D-01 3 6 2 2 -0.67534143987684D+01 -0.12288835753305D-01 1 7 2 2 -0.60931119429412D+00 0.62667131860604D-02 2 7 2 2 0.33480134856161D+01 -0.12065918392816D-01 3 7 2 2 -0.99228147842180D+00 0.69398204166017D-02 1 8 2 2 0.60931119429413D+00 -0.62667131860604D-02 2 8 2 2 -0.33480134856161D+01 0.12065918392819D-01 3 8 2 2 -0.99228147842178D+00 0.69398204166008D-02 1 9 2 2 -0.15278051004100D-14 -0.17648994741536D-15 2 9 2 2 -0.14713473634173D-14 0.14785960961616D-15 3 9 2 2 0.26303757206776D+01 0.18228243090913D-07 1 10 2 2 -0.47604055640832D+00 0.34260385829530D-08 2 10 2 2 -0.21724557850268D+01 0.10840755691156D-07 3 10 2 2 0.23364814344297D-13 0.13736569185865D-15 1 11 2 2 -0.60939674657544D+00 -0.74825831976890D-08 2 11 2 2 0.12368887393921D+01 -0.11244919877852D-07 3 11 2 2 0.81120952228998D-14 -0.13703891844895D-14 1 12 2 2 0.11494264874139D-14 0.96409830206399D-16 2 12 2 2 -0.41532836700164D-14 -0.74256017354325D-14 3 12 2 2 -0.25794895146192D+00 0.11773231699160D-07 1 13 2 2 -0.50608893451166D+00 -0.25217175319844D-02 2 13 2 2 -0.42669990022297D+00 -0.40911720073848D-02 3 13 2 2 0.98454495694056D+00 -0.63353830294970D-02 1 14 2 2 -0.72301312555332D+00 0.78458255927390D-08 2 14 2 2 -0.13059172872156D+01 -0.44285424931560D-08 3 14 2 2 -0.79397209156003D+00 -0.27923318547498D-07 1 15 2 2 -0.72301312555336D+00 0.78458262765178D-08 2 15 2 2 -0.13059172872156D+01 -0.44285427474033D-08 3 15 2 2 0.79397209156007D+00 0.27923320612766D-07 1 16 2 2 0.50608893451168D+00 0.25217175319861D-02 2 16 2 2 0.42669990022294D+00 0.40911720073844D-02 3 16 2 2 0.98454495694063D+00 -0.63353830294943D-02 1 17 2 2 -0.80259503795466D+00 -0.99245321884704D-07 2 17 2 2 0.10669534109937D+01 0.20708555026117D-06 3 17 2 2 0.92567424803794D+00 -0.81584878475079D-07 1 18 2 2 -0.16761329463293D-01 0.31249629992602D-01 2 18 2 2 0.17851870533802D+01 -0.22602251736406D-02 3 18 2 2 0.40625835904024D+00 -0.84648125232017D-02 1 19 2 2 -0.16761329463336D-01 0.31249629992602D-01 2 19 2 2 0.17851870533802D+01 -0.22602251736390D-02 3 19 2 2 -0.40625835904010D+00 0.84648125232020D-02 1 20 2 2 0.80259503795470D+00 0.99245323504493D-07 2 20 2 2 -0.10669534109937D+01 -0.20708555195190D-06 3 20 2 2 0.92567424803803D+00 -0.81584872658294D-07 1 1 3 2 0.25427663988177D-01 -0.96968378865310D-08 2 1 3 2 -0.52911283615963D+00 -0.64224625814263D-09 3 1 3 2 -0.62611623752404D-13 -0.12068576776255D-13 1 2 3 2 -0.14032761240665D-16 0.11102230246252D-15 2 2 3 2 -0.39595091817328D-13 0.11102230246252D-15 3 2 3 2 0.14810453964154D+02 0.00000000000000D+00 1 3 3 2 -0.40926675664259D-01 0.64650026781081D-08 2 3 3 2 -0.10396587672363D+01 -0.79499866629297D-09 3 3 3 2 0.18560226960074D-13 0.38717400808732D-15 1 4 3 2 -0.13176978595680D-14 0.17826099351762D-15 2 4 3 2 0.25534358893769D-13 0.83814494815845D-15 3 4 3 2 -0.14103289845163D-13 -0.11626151542268D-07 1 5 3 2 0.78683661998368D-02 0.31391281372031D-02 2 5 3 2 -0.67961458154965D+01 -0.15400178195909D-01 3 5 3 2 0.41581799573401D+00 -0.46382264600089D-02 1 6 3 2 0.78683661998344D-02 0.31391281372033D-02 2 6 3 2 -0.67961458154964D+01 -0.15400178195886D-01 3 6 3 2 -0.41581799573409D+00 0.46382264600173D-02 1 7 3 2 -0.58627756627623D+00 0.10593882194417D-01 2 7 3 2 -0.86899923548539D+00 0.12757658958082D-01 3 7 3 2 -0.11086389653640D-01 0.10217755955319D-01 1 8 3 2 -0.58627756627625D+00 0.10593882194418D-01 2 8 3 2 -0.86899923548536D+00 0.12757658958081D-01 3 8 3 2 0.11086389653526D-01 -0.10217755955312D-01 1 9 3 2 0.21247939582640D-01 -0.46867258425756D-08 2 9 3 2 0.87852324247815D+00 -0.12183570656076D-07 3 9 3 2 0.14581776438464D-14 0.22400689348726D-15 1 10 3 2 0.10423214802204D-14 0.32498179471365D-16 2 10 3 2 0.23364814345951D-13 0.13736569185865D-15 3 10 3 2 -0.12782401410135D+01 0.31763996113051D-07 1 11 3 2 -0.15335580028914D-14 -0.20480793753418D-15 2 11 3 2 0.81120952228998D-14 -0.13703891844895D-14 3 11 3 2 0.37027410533120D+01 -0.12589760590738D-06 1 12 3 2 -0.10381392416551D+00 0.11582383295871D-07 2 12 3 2 -0.86709724151587D-01 0.41128712692572D-08 3 12 3 2 -0.79974437964016D-14 0.62639722887399D-15 1 13 3 2 0.12198240512232D+00 0.15071331504398D-02 2 13 3 2 0.14104596669027D+01 -0.24786916403220D-03 3 13 3 2 0.45332216840792D+00 -0.33781122828657D-02 1 14 3 2 -0.14815034947988D+00 -0.16133283986243D-07 2 14 3 2 -0.12016508029001D+01 0.11998678418305D-07 3 14 3 2 -0.31623890243688D+00 -0.21372887290576D-08 1 15 3 2 0.14815034947984D+00 0.16133283563767D-07 2 15 3 2 0.12016508029001D+01 -0.11998676353038D-07 3 15 3 2 -0.31623890243691D+00 -0.21372904197442D-08 1 16 3 2 0.12198240512233D+00 0.15071331504380D-02 2 16 3 2 0.14104596669028D+01 -0.24786916402949D-03 3 16 3 2 -0.45332216840794D+00 0.33781122828635D-02 1 17 3 2 0.35195673198032D+00 -0.59913875758156D-07 2 17 3 2 0.13109063117039D+01 -0.47398380924590D-07 3 17 3 2 -0.40516331287108D+00 0.30872768524387D-06 1 18 3 2 0.11152602876192D+01 -0.62582020916189D-02 2 18 3 2 -0.13647920929388D+00 0.13824023979031D-01 3 18 3 2 0.24683163743508D+01 -0.24138185634072D-01 1 19 3 2 -0.11152602876192D+01 0.62582020916189D-02 2 19 3 2 0.13647920929400D+00 -0.13824023979031D-01 3 19 3 2 0.24683163743509D+01 -0.24138185634074D-01 1 20 3 2 0.35195673198040D+00 -0.59913869158788D-07 2 20 3 2 0.13109063117039D+01 -0.47398375109540D-07 3 20 3 2 0.40516331287122D+00 -0.30872767432246D-06 1 1 1 3 0.15051021470047D-12 -0.49881189984900D-08 2 1 1 3 0.10158903207780D+00 0.37759560669383D-08 3 1 1 3 0.13745148677290D-15 -0.23979773728660D-16 1 2 1 3 0.67918679767932D-14 0.10044386879934D-15 2 2 1 3 0.10422584748696D-14 0.43326036316985D-16 3 2 1 3 -0.40926675664259D-01 -0.64650026781081D-08 1 3 1 3 0.80943217583681D+01 0.00000000000000D+00 2 3 1 3 -0.13186135840079D+01 -0.57296114286964D-06 3 3 1 3 -0.14224887526073D-13 0.00000000000000D+00 1 4 1 3 -0.12717166785137D-13 0.35268812787605D-14 2 4 1 3 0.33844516804365D-14 -0.84212611147785D-16 3 4 1 3 0.25427140732220D-01 0.84774283596714D-08 1 5 1 3 -0.34119545832177D+01 -0.24534919728117D-01 2 5 1 3 0.69558746439059D-01 0.33519815380904D-02 3 5 1 3 -0.26816151616296D+00 0.51820868099588D-02 1 6 1 3 -0.34119545832177D+01 -0.24534919728115D-01 2 6 1 3 0.69558746439058D-01 0.33519815380904D-02 3 6 1 3 0.26816151616296D+00 -0.51820868099592D-02 1 7 1 3 -0.55811863381900D+00 0.88024739414595D-02 2 7 1 3 0.19958250941004D+00 -0.86434670879932D-02 3 7 1 3 0.39059267555499D+00 0.75696288097492D-03 1 8 1 3 -0.55811863381901D+00 0.88024739414608D-02 2 8 1 3 0.19958250941004D+00 -0.86434670879931D-02 3 8 1 3 -0.39059267555499D+00 -0.75696288097510D-03 1 9 1 3 -0.11950148942890D+01 0.18785261918410D-07 2 9 1 3 -0.46523303941558D+00 -0.15398840518021D-07 3 9 1 3 0.16347834067064D-15 0.23664779489892D-15 1 10 1 3 0.52322647135963D-14 -0.69368443056041D-15 2 10 1 3 0.20698592035674D-14 0.23478247875564D-16 3 10 1 3 -0.63017924966139D-01 0.13109018004590D-07 1 11 1 3 0.16364465052166D-14 -0.96884868636642D-16 2 11 1 3 -0.33009038430781D-14 0.12908736386201D-15 3 11 1 3 0.33766389153619D+00 -0.10623608383051D-08 1 12 1 3 -0.34656041519043D+00 0.11443054021275D-07 2 12 1 3 -0.53615338254897D-01 -0.20378772773102D-07 3 12 1 3 -0.42986351633347D-15 -0.54472349405837D-16 1 13 1 3 -0.43486473279454D+00 -0.15350506746488D-01 2 13 1 3 0.34479890278870D+00 0.54361281411069D-02 3 13 1 3 0.56626506089943D+00 -0.48887486834200D-02 1 14 1 3 0.92518036333728D-02 -0.30638199855187D-07 2 14 1 3 0.30490190754155D+00 0.68056519613296D-07 3 14 1 3 -0.81823224224853D+00 0.30844529756899D-06 1 15 1 3 -0.92518036333797D-02 0.30638199750964D-07 2 15 1 3 -0.30490190754155D+00 -0.68056517886256D-07 3 15 1 3 -0.81823224224852D+00 0.30844530443479D-06 1 16 1 3 -0.43486473279454D+00 -0.15350506746488D-01 2 16 1 3 0.34479890278870D+00 0.54361281411072D-02 3 16 1 3 -0.56626506089940D+00 0.48887486834203D-02 1 17 1 3 -0.18060809380500D+00 -0.79003609834913D-08 2 17 1 3 0.31573517581629D+00 -0.11350792483918D-08 3 17 1 3 -0.52399729090678D+00 -0.19408705790098D-07 1 18 1 3 -0.34159599944594D-01 0.10186584683517D-01 2 18 1 3 -0.29645719455468D+00 -0.10397496925166D-01 3 18 1 3 -0.32589235607620D+00 0.53961947241255D-03 1 19 1 3 0.34159599944593D-01 -0.10186584683517D-01 2 19 1 3 0.29645719455468D+00 0.10397496925166D-01 3 19 1 3 -0.32589235607622D+00 0.53961947241465D-03 1 20 1 3 -0.18060809380498D+00 -0.79003610131045D-08 2 20 1 3 0.31573517581629D+00 -0.11350787669626D-08 3 20 1 3 0.52399729090680D+00 0.19408706506171D-07 1 1 2 3 0.10158903207779D+00 -0.37759552788041D-08 2 1 2 3 -0.54130519899930D-13 0.11817477907232D-07 3 1 2 3 0.20431055034664D-13 0.72605979750786D-15 1 2 2 3 0.10422584748696D-14 0.42458674578996D-16 2 2 2 3 0.57861399460735D-14 -0.61367958676606D-15 3 2 2 3 -0.10396587672363D+01 0.79499866629297D-09 1 3 2 3 -0.13186082980876D+01 -0.62285906677980D-06 2 3 2 3 0.90519195953002D+01 0.00000000000000D+00 3 3 2 3 -0.60911373903358D-13 -0.11102230246252D-15 1 4 2 3 0.33844516807467D-14 -0.84212611147785D-16 2 4 2 3 -0.21954774581223D-13 -0.25207944817521D-14 3 4 2 3 0.52911342726252D+00 -0.55963871911644D-09 1 5 2 3 0.60931119429413D+00 -0.62667131860606D-02 2 5 2 3 0.33480134856161D+01 -0.12065918392824D-01 3 5 2 3 -0.99228147842185D+00 0.69398204166017D-02 1 6 2 3 0.60931119429413D+00 -0.62667131860605D-02 2 6 2 3 0.33480134856160D+01 -0.12065918392824D-01 3 6 2 3 0.99228147842188D+00 -0.69398204166036D-02 1 7 2 3 0.18400059467742D+00 0.96692812178978D-03 2 7 2 3 0.57686684450240D+00 -0.14826831048329D-01 3 7 2 3 -0.67534143987684D+01 -0.12288835753310D-01 1 8 2 3 0.18400059467742D+00 0.96692812178987D-03 2 8 2 3 0.57686684450242D+00 -0.14826831048328D-01 3 8 2 3 0.67534143987684D+01 0.12288835753310D-01 1 9 2 3 -0.60939674657545D+00 -0.74825804389780D-08 2 9 2 3 -0.12368887393920D+01 0.11244913726051D-07 3 9 2 3 0.28670423730404D-15 -0.12757344866727D-15 1 10 2 3 0.20698592035674D-14 0.23478247875564D-16 2 10 2 3 -0.17364779066401D-13 0.26422545367606D-14 3 10 2 3 -0.25794895146193D+00 0.11773230071313D-07 1 11 2 3 -0.33019655841950D-14 0.12908736386201D-15 2 11 2 3 -0.67624358188686D-15 -0.57609950110114D-16 3 11 2 3 -0.26303757206776D+01 -0.18228244434121D-07 1 12 2 3 0.47604055640835D+00 -0.34260405664876D-08 2 12 2 3 -0.21724557850269D+01 0.10840748027118D-07 3 12 2 3 -0.28587241037126D-14 0.42195733223013D-14 1 13 2 3 -0.16761329463301D-01 0.31249629992596D-01 2 13 2 3 -0.17851870533803D+01 0.22602251736466D-02 3 13 2 3 -0.40625835904004D+00 0.84648125232138D-02 1 14 2 3 0.80259503795468D+00 0.99245325454969D-07 2 14 2 3 0.10669534109937D+01 0.20708555399422D-06 3 14 2 3 0.92567424803796D+00 -0.81584867603806D-07 1 15 2 3 -0.80259503795468D+00 -0.99245323722725D-07 2 15 2 3 -0.10669534109937D+01 -0.20708555362728D-06 3 15 2 3 0.92567424803800D+00 -0.81584875360290D-07 1 16 2 3 -0.16761329463314D-01 0.31249629992596D-01 2 16 2 3 -0.17851870533803D+01 0.22602251736416D-02 3 16 2 3 0.40625835904024D+00 -0.84648125232146D-02 1 17 2 3 0.72301312555335D+00 -0.78458258404276D-08 2 17 2 3 -0.13059172872156D+01 -0.44285438496743D-08 3 17 2 3 -0.79397209156006D+00 -0.27923318599388D-07 1 18 2 3 -0.50608893451168D+00 -0.25217175319879D-02 2 18 2 3 0.42669990022297D+00 0.40911720073804D-02 3 18 2 3 -0.98454495694060D+00 0.63353830294893D-02 1 19 2 3 0.50608893451168D+00 0.25217175319873D-02 2 19 2 3 -0.42669990022294D+00 -0.40911720073816D-02 3 19 2 3 -0.98454495694062D+00 0.63353830294921D-02 1 20 2 3 0.72301312555334D+00 -0.78458253555290D-08 2 20 2 3 -0.13059172872156D+01 -0.44285447451491D-08 3 20 2 3 0.79397209156006D+00 0.27923319801349D-07 1 1 3 3 0.13745148677290D-15 -0.23979773728661D-16 2 1 3 3 0.20431055034664D-13 0.72605979750786D-15 3 1 3 3 -0.21372364450924D-12 0.11626153452631D-07 1 2 3 3 0.40926675664260D-01 -0.64650026781081D-08 2 2 3 3 -0.10396587672363D+01 -0.79499687194217D-09 3 2 3 3 0.18560226960074D-13 -0.38717400808732D-15 1 3 3 3 -0.14224887476443D-13 0.11102230246252D-15 2 3 3 3 -0.60911373890123D-13 -0.11102230246252D-15 3 3 3 3 0.14810453964154D+02 0.00000000000000D+00 1 4 3 3 0.25427663988186D-01 -0.96968381179386D-08 2 4 3 3 0.52911283615975D+00 0.64224793760983D-09 3 4 3 3 0.35233698125566D-13 -0.10878928284857D-13 1 5 3 3 0.58627756627624D+00 -0.10593882194419D-01 2 5 3 3 -0.86899923548543D+00 0.12757658958082D-01 3 5 3 3 -0.11086389653598D-01 0.10217755955324D-01 1 6 3 3 -0.58627756627623D+00 0.10593882194419D-01 2 6 3 3 0.86899923548546D+00 -0.12757658958084D-01 3 6 3 3 -0.11086389653711D-01 0.10217755955325D-01 1 7 3 3 -0.78683661998318D-02 -0.31391281372030D-02 2 7 3 3 -0.67961458154964D+01 -0.15400178195891D-01 3 7 3 3 0.41581799573417D+00 -0.46382264600096D-02 1 8 3 3 0.78683661998312D-02 0.31391281372028D-02 2 8 3 3 0.67961458154964D+01 0.15400178195891D-01 3 8 3 3 0.41581799573417D+00 -0.46382264600104D-02 1 9 3 3 0.16347834067064D-15 0.23664779489892D-15 2 9 3 3 0.28670423730404D-15 -0.12757344866727D-15 3 9 3 3 -0.37027410533118D+01 0.12589759285420D-06 1 10 3 3 0.10381392416552D+00 -0.11582382541287D-07 2 10 3 3 -0.86709724151600D-01 0.41128696414103D-08 3 10 3 3 0.30813859392647D-13 -0.29281187335941D-15 1 11 3 3 0.21247939582636D-01 -0.46867257177949D-08 2 11 3 3 -0.87852324247811D+00 0.12183569312868D-07 3 11 3 3 -0.34207389922651D-14 0.34346855293386D-15 1 12 3 3 -0.42986351633347D-15 -0.54906030274831D-16 2 12 3 3 -0.28587241053670D-14 0.42195733223013D-14 3 12 3 3 -0.12782401410135D+01 0.31764000157385D-07 1 13 3 3 0.11152602876191D+01 -0.62582020916283D-02 2 13 3 3 0.13647920929405D+00 -0.13824023979019D-01 3 13 3 3 -0.24683163743508D+01 0.24138185634086D-01 1 14 3 3 -0.35195673198039D+00 0.59913862424637D-07 2 14 3 3 0.13109063117039D+01 -0.47398370056786D-07 3 14 3 3 -0.40516331287114D+00 0.30872766025512D-06 1 15 3 3 -0.35195673198040D+00 0.59913869294776D-07 2 15 3 3 0.13109063117039D+01 -0.47398377815005D-07 3 15 3 3 0.40516331287115D+00 -0.30872767565670D-06 1 16 3 3 -0.11152602876191D+01 0.62582020916285D-02 2 16 3 3 -0.13647920929385D+00 0.13824023979018D-01 3 16 3 3 -0.24683163743508D+01 0.24138185634084D-01 1 17 3 3 0.14815034947988D+00 0.16133284204164D-07 2 17 3 3 -0.12016508029001D+01 0.11998678366416D-07 3 17 3 3 -0.31623890243694D+00 -0.21372907151000D-08 1 18 3 3 0.12198240512231D+00 0.15071331504336D-02 2 18 3 3 -0.14104596669028D+01 0.24786916402451D-03 3 18 3 3 -0.45332216840795D+00 0.33781122828558D-02 1 19 3 3 0.12198240512230D+00 0.15071331504357D-02 2 19 3 3 -0.14104596669028D+01 0.24786916402734D-03 3 19 3 3 0.45332216840797D+00 -0.33781122828586D-02 1 20 3 3 -0.14815034947988D+00 -0.16133283489826D-07 2 20 3 3 0.12016508029001D+01 -0.11998677164455D-07 3 20 3 3 -0.31623890243695D+00 -0.21372891840324D-08 1 1 1 4 -0.86800489883308D-15 0.10026883031610D-14 2 1 1 4 0.84824365843741D-15 -0.11098575904161D-16 3 1 1 4 -0.40926675664263D-01 -0.64650026361458D-08 1 2 1 4 0.24560592253757D-13 -0.49881240740645D-08 2 2 1 4 0.10158903207784D+00 0.37759552324255D-08 3 2 1 4 -0.13176978595680D-14 -0.17826099351762D-15 1 3 1 4 -0.12717166785137D-13 -0.35268812787605D-14 2 3 1 4 0.33844516804365D-14 0.84212611147785D-16 3 3 1 4 0.25427140732220D-01 0.84774283337606D-08 1 4 1 4 0.80943217583663D+01 0.00000000000000D+00 2 4 1 4 -0.13186135840081D+01 -0.57296114286964D-06 3 4 1 4 -0.21330314883675D-13 0.00000000000000D+00 1 5 1 4 0.34119545832178D+01 0.24534919728128D-01 2 5 1 4 -0.69558746439069D-01 -0.33519815380906D-02 3 5 1 4 0.26816151616288D+00 -0.51820868099601D-02 1 6 1 4 -0.34119545832178D+01 -0.24534919728115D-01 2 6 1 4 0.69558746439071D-01 0.33519815380902D-02 3 6 1 4 0.26816151616280D+00 -0.51820868099590D-02 1 7 1 4 -0.55811863381899D+00 0.88024739414617D-02 2 7 1 4 0.19958250941002D+00 -0.86434670879930D-02 3 7 1 4 0.39059267555499D+00 0.75696288097480D-03 1 8 1 4 0.55811863381900D+00 -0.88024739414616D-02 2 8 1 4 -0.19958250941003D+00 0.86434670879931D-02 3 8 1 4 0.39059267555500D+00 0.75696288097445D-03 1 9 1 4 0.64725237817426D-14 -0.25955594387181D-15 2 9 1 4 -0.56258126035917D-15 -0.13085092419596D-15 3 9 1 4 -0.63017924966180D-01 0.13109017245930D-07 1 10 1 4 -0.11950148942890D+01 0.18785261752927D-07 2 10 1 4 -0.46523303941547D+00 -0.15398840535791D-07 3 10 1 4 0.75081765364939D-15 0.13180075199546D-15 1 11 1 4 -0.34656041519030D+00 0.11443051551535D-07 2 11 1 4 -0.53615338254769D-01 -0.20378770960232D-07 3 11 1 4 -0.23766816600936D-14 0.14242597525520D-15 1 12 1 4 0.20126327357192D-14 0.59933812700298D-16 2 12 1 4 -0.17569224290876D-14 -0.96679726316260D-16 3 12 1 4 0.33766389153620D+00 -0.10623610288756D-08 1 13 1 4 0.92518036334154D-02 -0.30638199655596D-07 2 13 1 4 0.30490190754153D+00 0.68056515857598D-07 3 13 1 4 -0.81823224224843D+00 0.30844531107131D-06 1 14 1 4 -0.43486473279451D+00 -0.15350506746489D-01 2 14 1 4 0.34479890278873D+00 0.54361281411068D-02 3 14 1 4 0.56626506089947D+00 -0.48887486834199D-02 1 15 1 4 -0.43486473279450D+00 -0.15350506746489D-01 2 15 1 4 0.34479890278865D+00 0.54361281411070D-02 3 15 1 4 -0.56626506089939D+00 0.48887486834202D-02 1 16 1 4 -0.92518036334092D-02 0.30638199696969D-07 2 16 1 4 -0.30490190754157D+00 -0.68056517638356D-07 3 16 1 4 -0.81823224224853D+00 0.30844530426557D-06 1 17 1 4 -0.34159599944601D-01 0.10186584683518D-01 2 17 1 4 -0.29645719455467D+00 -0.10397496925164D-01 3 17 1 4 -0.32589235607621D+00 0.53961947241700D-03 1 18 1 4 -0.18060809380500D+00 -0.79003606805376D-08 2 18 1 4 0.31573517581623D+00 -0.11350793776114D-08 3 18 1 4 -0.52399729090676D+00 -0.19408705915243D-07 1 19 1 4 -0.18060809380498D+00 -0.79003606966231D-08 2 19 1 4 0.31573517581628D+00 -0.11350794759794D-08 3 19 1 4 0.52399729090682D+00 0.19408706069708D-07 1 20 1 4 0.34159599944591D-01 -0.10186584683517D-01 2 20 1 4 0.29645719455468D+00 0.10397496925166D-01 3 20 1 4 -0.32589235607620D+00 0.53961947241472D-03 1 1 2 4 0.84824365843741D-15 -0.11965937642150D-16 2 1 2 4 -0.27331563067263D-14 -0.16021848643006D-15 3 1 2 4 -0.10396587672362D+01 0.79499768349999D-09 1 2 2 4 0.10158903207784D+00 -0.37759561133169D-08 2 2 2 4 -0.18536756471870D-13 0.11817471393708D-07 3 2 2 4 0.25534358893769D-13 -0.83814494815845D-15 1 3 2 4 0.33844516805399D-14 0.84429451582282D-16 2 3 2 4 -0.21954774581223D-13 0.25216618434901D-14 3 3 2 4 0.52911342726252D+00 -0.55964067549321D-09 1 4 2 4 -0.13186082980879D+01 -0.62285906677980D-06 2 4 2 4 0.90519195953020D+01 0.00000000000000D+00 3 4 2 4 0.77644459569854D-13 -0.11102230246252D-15 1 5 2 4 -0.60931119429414D+00 0.62667131860604D-02 2 5 2 4 -0.33480134856161D+01 0.12065918392814D-01 3 5 2 4 0.99228147842182D+00 -0.69398204166020D-02 1 6 2 4 0.60931119429414D+00 -0.62667131860607D-02 2 6 2 4 0.33480134856161D+01 -0.12065918392819D-01 3 6 2 4 0.99228147842180D+00 -0.69398204166014D-02 1 7 2 4 0.18400059467740D+00 0.96692812178993D-03 2 7 2 4 0.57686684450244D+00 -0.14826831048336D-01 3 7 2 4 -0.67534143987684D+01 -0.12288835753325D-01 1 8 2 4 -0.18400059467741D+00 -0.96692812178986D-03 2 8 2 4 -0.57686684450243D+00 0.14826831048337D-01 3 8 2 4 -0.67534143987684D+01 -0.12288835753309D-01 1 9 2 4 -0.56258126035917D-15 -0.13085092419596D-15 2 9 2 4 0.19720602877222D-14 0.39239851220577D-14 3 9 2 4 -0.25794895146193D+00 0.11773231496637D-07 1 10 2 4 -0.60939674657534D+00 -0.74825804567487D-08 2 10 2 4 -0.12368887393921D+01 0.11244913477704D-07 3 10 2 4 -0.11890949818827D-14 -0.66731582791945D-15 1 11 2 4 0.47604055640848D+00 -0.34260387536177D-08 2 11 2 4 -0.21724557850273D+01 0.10840758192818D-07 3 11 2 4 0.31916482173574D-14 -0.59358477815908D-14 1 12 2 4 -0.17579841704114D-14 -0.96679726316260D-16 2 12 2 4 -0.14684742672215D-14 0.23122495208358D-16 3 12 2 4 -0.26303757206776D+01 -0.18228244473452D-07 1 13 2 4 0.80259503795466D+00 0.99245321699271D-07 2 13 2 4 0.10669534109937D+01 0.20708554993139D-06 3 13 2 4 0.92567424803798D+00 -0.81584878502837D-07 1 14 2 4 -0.16761329463272D-01 0.31249629992596D-01 2 14 2 4 -0.17851870533804D+01 0.22602251736405D-02 3 14 2 4 -0.40625835904033D+00 0.84648125232145D-02 1 15 2 4 -0.16761329463365D-01 0.31249629992596D-01 2 15 2 4 -0.17851870533803D+01 0.22602251736407D-02 3 15 2 4 0.40625835904012D+00 -0.84648125232170D-02 1 16 2 4 -0.80259503795470D+00 -0.99245323481764D-07 2 16 2 4 -0.10669534109937D+01 -0.20708555297149D-06 3 16 2 4 0.92567424803804D+00 -0.81584871299335D-07 1 17 2 4 -0.50608893451168D+00 -0.25217175319857D-02 2 17 2 4 0.42669990022295D+00 0.40911720073848D-02 3 17 2 4 -0.98454495694060D+00 0.63353830294927D-02 1 18 2 4 0.72301312555329D+00 -0.78458259696472D-08 2 18 2 4 -0.13059172872156D+01 -0.44285427038562D-08 3 18 2 4 -0.79397209155997D+00 -0.27923320661305D-07 1 19 2 4 0.72301312555333D+00 -0.78458260645457D-08 2 19 2 4 -0.13059172872156D+01 -0.44285430822843D-08 3 19 2 4 0.79397209156001D+00 0.27923319305573D-07 1 20 2 4 0.50608893451168D+00 0.25217175319877D-02 2 20 2 4 -0.42669990022294D+00 -0.40911720073828D-02 3 20 2 4 -0.98454495694062D+00 0.63353830294924D-02 1 1 3 4 0.40926675664256D-01 -0.64650026361458D-08 2 1 3 4 -0.10396587672362D+01 -0.79499785473515D-09 3 1 3 4 -0.67601296156300D-14 0.78288234321485D-15 1 2 3 4 -0.13176978595680D-14 -0.17826099351762D-15 2 2 3 4 0.25534358893769D-13 -0.83814494815845D-15 3 2 3 4 -0.14103289845163D-13 0.11626151542268D-07 1 3 3 4 0.25427663988185D-01 -0.96968381438493D-08 2 3 3 4 0.52911283615975D+00 0.64224598123306D-09 3 3 3 4 0.35233698125566D-13 0.10878928284857D-13 1 4 3 4 -0.21330314834044D-13 0.11102230246252D-15 2 4 3 4 0.77644459583088D-13 -0.11102230246252D-15 3 4 3 4 0.14810453964150D+02 0.00000000000000D+00 1 5 3 4 -0.58627756627632D+00 0.10593882194418D-01 2 5 3 4 0.86899923548540D+00 -0.12757658958082D-01 3 5 3 4 0.11086389653522D-01 -0.10217755955309D-01 1 6 3 4 -0.58627756627639D+00 0.10593882194419D-01 2 6 3 4 0.86899923548538D+00 -0.12757658958082D-01 3 6 3 4 -0.11086389653568D-01 0.10217755955313D-01 1 7 3 4 -0.78683661998318D-02 -0.31391281372031D-02 2 7 3 4 -0.67961458154964D+01 -0.15400178195906D-01 3 7 3 4 0.41581799573404D+00 -0.46382264600114D-02 1 8 3 4 -0.78683661998245D-02 -0.31391281372034D-02 2 8 3 4 -0.67961458154964D+01 -0.15400178195890D-01 3 8 3 4 -0.41581799573408D+00 0.46382264600081D-02 1 9 3 4 0.10381392416548D+00 -0.11582383299947D-07 2 9 3 4 -0.86709724151597D-01 0.41128710667338D-08 3 9 3 4 0.20029413871686D-13 0.26623959152347D-14 1 10 3 4 0.75081765364939D-15 0.13180075199546D-15 2 10 3 4 -0.11890949818827D-14 -0.66731582791945D-15 3 10 3 4 -0.37027410533119D+01 0.12589759289543D-06 1 11 3 4 -0.23766816600936D-14 0.14199229438620D-15 2 11 3 4 0.31916482157030D-14 -0.59358477815908D-14 3 11 3 4 -0.12782401410131D+01 0.31763997354699D-07 1 12 3 4 0.21247939582642D-01 -0.46867259083654D-08 2 12 3 4 -0.87852324247811D+00 0.12183569273537D-07 3 12 3 4 -0.79172190961627D-14 0.17075117947562D-15 1 13 3 4 -0.35195673198029D+00 0.59913875928694D-07 2 13 3 4 0.13109063117039D+01 -0.47398380955818D-07 3 13 3 4 -0.40516331287107D+00 0.30872768920502D-06 1 14 3 4 0.11152602876192D+01 -0.62582020916281D-02 2 14 3 4 0.13647920929377D+00 -0.13824023979018D-01 3 14 3 4 -0.24683163743508D+01 0.24138185634083D-01 1 15 3 4 -0.11152602876191D+01 0.62582020916284D-02 2 15 3 4 -0.13647920929397D+00 0.13824023979016D-01 3 15 3 4 -0.24683163743508D+01 0.24138185634085D-01 1 16 3 4 -0.35195673198042D+00 0.59913869122081D-07 2 16 3 4 0.13109063117040D+01 -0.47398373750581D-07 3 16 3 4 0.40516331287124D+00 -0.30872767202694D-06 1 17 3 4 0.12198240512229D+00 0.15071331504380D-02 2 17 3 4 -0.14104596669028D+01 0.24786916402794D-03 3 17 3 4 -0.45332216840798D+00 0.33781122828636D-02 1 18 3 4 0.14815034947990D+00 0.16133284079020D-07 2 18 3 4 -0.12016508029000D+01 0.11998676304498D-07 3 18 3 4 -0.31623890243692D+00 -0.21372862735812D-08 1 19 3 4 -0.14815034947987D+00 -0.16133283926290D-07 2 19 3 4 0.12016508029001D+01 -0.11998677660230D-07 3 19 3 4 -0.31623890243699D+00 -0.21372870436579D-08 1 20 3 4 0.12198240512231D+00 0.15071331504357D-02 2 20 3 4 -0.14104596669028D+01 0.24786916402764D-03 3 20 3 4 0.45332216840794D+00 -0.33781122828588D-02 1 1 1 5 0.55811917905529D+00 0.88032337559073D-02 2 1 1 5 0.18400242893230D+00 -0.96791005009883D-03 3 1 1 5 -0.78662503091604D-02 0.31381182230548D-02 1 2 1 5 -0.55811917905534D+00 -0.88032337559083D-02 2 2 1 5 -0.18400242893230D+00 0.96791005009863D-03 3 2 1 5 0.78662503091591D-02 -0.31381182230551D-02 1 3 1 5 -0.34119545832177D+01 0.24534919728117D-01 2 3 1 5 0.60931119429413D+00 0.62667131860606D-02 3 3 1 5 0.58627756627624D+00 0.10593882194419D-01 1 4 1 5 0.34119545832178D+01 -0.24534919728128D-01 2 4 1 5 -0.60931119429414D+00 -0.62667131860604D-02 3 4 1 5 -0.58627756627632D+00 -0.10593882194418D-01 1 5 1 5 0.17103127485998D+02 0.00000000000000D+00 2 5 1 5 0.11964608912776D+01 -0.85435484783889D-07 3 5 1 5 0.66152489404008D+00 -0.39296266395809D-07 1 6 1 5 -0.23455477709814D-13 0.27733383209635D-14 2 6 1 5 -0.14880708736022D-17 -0.15242600558486D-16 3 6 1 5 0.11208283184136D-16 0.23272156852883D-16 1 7 1 5 -0.59218563921815D-14 0.25835601485383D-14 2 7 1 5 0.21893369071828D-14 0.18835480714282D-15 3 7 1 5 -0.38069026595396D-17 -0.33716473831139D-15 1 8 1 5 -0.29842419140116D-14 -0.20738425384214D-08 2 8 1 5 0.89105395026049D+00 -0.31128250375007D-08 3 8 1 5 0.11584755732354D+01 0.81578008764159D-08 1 9 1 5 -0.14348998472425D+01 0.99561485241658D+00 2 9 1 5 -0.89837415147509D-01 -0.28434571662258D-01 3 9 1 5 -0.43958843349088D+00 -0.38432929013885D+00 1 10 1 5 0.14348998472422D+01 -0.99561485241657D+00 2 10 1 5 0.89837415147488D-01 0.28434571662259D-01 3 10 1 5 0.43958843349087D+00 0.38432929013884D+00 1 11 1 5 -0.66260619793180D-01 0.19008188054164D-02 2 11 1 5 -0.20231996251957D+00 0.74936408584535D-03 3 11 1 5 -0.10833421476976D+01 -0.24669330446019D-01 1 12 1 5 0.66260619793231D-01 -0.19008188054176D-02 2 12 1 5 0.20231996251958D+00 -0.74936408584530D-03 3 12 1 5 0.10833421476976D+01 0.24669330446018D-01 1 13 1 5 -0.13845730161114D+01 0.72380285350871D-02 2 13 1 5 0.47626471351755D+00 0.15005981134197D-01 3 13 1 5 0.65731579623203D+00 -0.56732508242438D-01 1 14 1 5 0.13845730161113D+01 -0.72380285351077D-02 2 14 1 5 -0.47626471351781D+00 -0.15005981134219D-01 3 14 1 5 -0.65731579623171D+00 0.56732508242447D-01 1 15 1 5 0.53668345860630D+00 -0.28185231299410D-01 2 15 1 5 0.44045047321920D+00 -0.31562444327087D-01 3 15 1 5 0.43515068697145D+00 -0.16001986766968D-01 1 16 1 5 -0.53668345860631D+00 0.28185231299410D-01 2 16 1 5 -0.44045047321919D+00 0.31562444327086D-01 3 16 1 5 -0.43515068697145D+00 0.16001986766969D-01 1 17 1 5 0.10161148680498D+00 0.12921154873963D-01 2 17 1 5 -0.68146394044034D+00 -0.19992458410019D-01 3 17 1 5 0.89708384060989D+00 -0.45108112857921D-01 1 18 1 5 -0.10161148680494D+00 -0.12921154873967D-01 2 18 1 5 0.68146394044011D+00 0.19992458410041D-01 3 18 1 5 -0.89708384060985D+00 0.45108112857928D-01 1 19 1 5 0.42653587354495D+00 -0.40733070771101D-01 2 19 1 5 -0.57101547054755D+00 0.86049765744084D-01 3 19 1 5 0.31176258682280D+00 -0.24129461132842D-01 1 20 1 5 -0.42653587354496D+00 0.40733070771101D-01 2 20 1 5 0.57101547054754D+00 -0.86049765744083D-01 3 20 1 5 -0.31176258682280D+00 0.24129461132842D-01 1 1 2 5 0.19958313727998D+00 0.86442319679255D-02 2 1 2 5 -0.57686310444302D+00 -0.14826965851511D-01 3 1 2 5 0.67961455079363D+01 -0.15399510733535D-01 1 2 2 5 -0.19958313727998D+00 -0.86442319679257D-02 2 2 2 5 0.57686310444302D+00 0.14826965851528D-01 3 2 2 5 -0.67961455079364D+01 0.15399510733568D-01 1 3 2 5 0.69558746439059D-01 -0.33519815380904D-02 2 3 2 5 0.33480134856161D+01 0.12065918392824D-01 3 3 2 5 -0.86899923548543D+00 -0.12757658958082D-01 1 4 2 5 -0.69558746439069D-01 0.33519815380906D-02 2 4 2 5 -0.33480134856161D+01 -0.12065918392814D-01 3 4 2 5 0.86899923548540D+00 0.12757658958082D-01 1 5 2 5 0.11964495053950D+01 0.92801755418816D-07 2 5 2 5 0.27171439032596D+02 0.00000000000000D+00 3 5 2 5 -0.30621762849944D+01 0.29683733849656D-06 1 6 2 5 -0.14880708703711D-17 -0.15242600558486D-16 2 6 2 5 -0.41485329109855D-13 0.18200673636163D-14 3 6 2 5 0.42552101166062D-13 0.25695478992455D-14 1 7 2 5 0.21842079885805D-14 0.18835480714282D-15 2 7 2 5 -0.31840078666837D-13 0.66084816315254D-14 3 7 2 5 -0.16616400979042D-16 -0.93652744686248D-15 1 8 2 5 0.89105691456755D+00 0.36445128936373D-08 2 8 2 5 0.62349256668420D-14 -0.13037060676157D-08 3 8 2 5 0.95967947517878D+01 -0.22470642305522D-08 1 9 2 5 -0.17280737966038D+00 -0.26919297650924D-01 2 9 2 5 -0.26386513098339D+01 0.10039895553932D+01 3 9 2 5 0.11665557843305D-01 0.12240381992961D+00 1 10 2 5 0.17280737966036D+00 0.26919297650924D-01 2 10 2 5 0.26386513098335D+01 -0.10039895553932D+01 3 10 2 5 -0.11665557843497D-01 -0.12240381992960D+00 1 11 2 5 -0.10715354635021D+00 0.14813378605735D-01 2 11 2 5 0.31159283523964D+00 0.78900338346492D-02 3 11 2 5 -0.71913698842732D+01 -0.19030339771505D+00 1 12 2 5 0.10715354635022D+00 -0.14813378605735D-01 2 12 2 5 -0.31159283523971D+00 -0.78900338346510D-02 3 12 2 5 0.71913698842732D+01 0.19030339771505D+00 1 13 2 5 -0.26678709400265D+01 -0.10444277046125D-01 2 13 2 5 -0.50877705951579D+01 -0.39081011523109D-02 3 13 2 5 0.43996757603053D+00 -0.21416164457979D-01 1 14 2 5 0.26678709400263D+01 0.10444277046102D-01 2 14 2 5 0.50877705951581D+01 0.39081011523078D-02 3 14 2 5 -0.43996757603031D+00 0.21416164457984D-01 1 15 2 5 -0.25621508332100D+00 -0.25622006102618D-01 2 15 2 5 0.45311663921894D-01 -0.16202328843039D-01 3 15 2 5 0.12163822420998D+01 -0.57385749439743D-02 1 16 2 5 0.25621508332101D+00 0.25622006102616D-01 2 16 2 5 -0.45311663921905D-01 0.16202328843040D-01 3 16 2 5 -0.12163822420998D+01 0.57385749439746D-02 1 17 2 5 0.13720704530734D+01 -0.93931795399761D-02 2 17 2 5 -0.52675461638689D+01 0.14939669842365D-01 3 17 2 5 -0.37668213502734D+00 0.52669567900922D-01 1 18 2 5 -0.13720704530736D+01 0.93931795399980D-02 2 18 2 5 0.52675461638691D+01 -0.14939669842388D-01 3 18 2 5 0.37668213502732D+00 -0.52669567900934D-01 1 19 2 5 -0.10236940830580D+00 0.80797613398194D-01 2 19 2 5 0.39314106725630D+00 -0.10539800877488D+00 3 19 2 5 -0.18790885120283D+01 0.37555646432894D-01 1 20 2 5 0.10236940830580D+00 -0.80797613398192D-01 2 20 2 5 -0.39314106725633D+00 0.10539800877488D+00 3 20 2 5 0.18790885120284D+01 -0.37555646432896D-01 1 1 3 5 0.39059135541117D+00 -0.75688831137670D-03 2 1 3 5 0.67534155778311D+01 -0.12288078113762D-01 3 1 3 5 -0.41581645217128D+00 -0.46388928904217D-02 1 2 3 5 -0.39059135541117D+00 0.75688831137636D-03 2 2 3 5 -0.67534155778312D+01 0.12288078113795D-01 3 2 3 5 0.41581645217125D+00 0.46388928904212D-02 1 3 3 5 -0.26816151616296D+00 -0.51820868099588D-02 2 3 3 5 -0.99228147842185D+00 -0.69398204166017D-02 3 3 3 5 -0.11086389653598D-01 -0.10217755955324D-01 1 4 3 5 0.26816151616287D+00 0.51820868099601D-02 2 4 3 5 0.99228147842182D+00 0.69398204166020D-02 3 4 3 5 0.11086389653522D-01 0.10217755955309D-01 1 5 3 5 0.66152888511880D+00 0.71029185551163D-07 2 5 3 5 -0.30621819332284D+01 -0.33115259129583D-06 3 5 3 5 0.46292281750279D+02 0.00000000000000D+00 1 6 3 5 -0.24319961025001D-16 0.23272156852883D-16 2 6 3 5 0.42560961253940D-13 0.25695478992455D-14 3 6 3 5 0.36798306176172D-12 -0.96861999945378D-14 1 7 3 5 0.37936111467927D-17 -0.33716473831139D-15 2 7 3 5 -0.16616400979042D-16 -0.93652744686250D-15 3 7 3 5 -0.43441896447452D-13 -0.49131896751974D-14 1 8 3 5 -0.11584876421650D+01 0.87376214958480D-08 2 8 3 5 0.95967892222620D+01 0.27820480570544D-08 3 8 3 5 0.18382853548248D-14 -0.12714943158531D-07 1 9 3 5 -0.18172566497776D+01 -0.44826001288329D+00 2 9 3 5 0.10071192072824D+00 0.11100264511879D+00 3 9 3 5 -0.79046572296047D+01 -0.23201526240615D+01 1 10 3 5 0.18172566497776D+01 0.44826001288327D+00 2 10 3 5 -0.10071192072844D+00 -0.11100264511879D+00 3 10 3 5 0.79046572296053D+01 0.23201526240614D+01 1 11 3 5 0.25055805143925D+00 0.78027860827715D-02 2 11 3 5 -0.17926419446748D+01 -0.28819059804326D-01 3 11 3 5 0.16044242939860D+00 -0.11914068240677D-01 1 12 3 5 -0.25055805143922D+00 -0.78027860827726D-02 2 12 3 5 0.17926419446749D+01 0.28819059804329D-01 3 12 3 5 -0.16044242939865D+00 0.11914068240677D-01 1 13 3 5 -0.44484082043110D+00 -0.39226475628244D-01 2 13 3 5 -0.48293872093478D+00 -0.50087726758091D-01 3 13 3 5 -0.47413405231887D+01 0.29166084374177D-01 1 14 3 5 0.44484082043142D+00 0.39226475628253D-01 2 14 3 5 0.48293872093500D+00 0.50087726758096D-01 3 14 3 5 0.47413405231889D+01 -0.29166084374154D-01 1 15 3 5 0.30154452868179D+01 -0.61764351561418D-02 2 15 3 5 0.39939332590606D+01 -0.54859697995831D-02 3 15 3 5 -0.29639836161840D+00 0.16795988062122D-01 1 16 3 5 -0.30154452868179D+01 0.61764351561425D-02 2 16 3 5 -0.39939332590606D+01 0.54859697995835D-02 3 16 3 5 0.29639836161842D+00 -0.16795988062126D-01 1 17 3 5 -0.21687698938736D+00 -0.45240790056758D-01 2 17 3 5 0.61828817619141D+00 0.66510466617491D-01 3 17 3 5 -0.40120124420439D+01 0.33325999191647D-01 1 18 3 5 0.21687698938740D+00 0.45240790056765D-01 2 18 3 5 -0.61828817619144D+00 -0.66510466617503D-01 3 18 3 5 0.40120124420436D+01 -0.33325999191624D-01 1 19 3 5 0.27364761524283D+01 -0.35602897432222D-02 2 19 3 5 -0.46274354307469D+01 0.12249582240389D-01 3 19 3 5 0.16730730623443D+00 0.76010911761058D-01 1 20 3 5 -0.27364761524283D+01 0.35602897432224D-02 2 20 3 5 0.46274354307470D+01 -0.12249582240391D-01 3 20 3 5 -0.16730730623438D+00 -0.76010911761063D-01 1 1 1 6 0.55811917905529D+00 0.88032337559073D-02 2 1 1 6 0.18400242893230D+00 -0.96791005009880D-03 3 1 1 6 0.78662503091638D-02 -0.31381182230550D-02 1 2 1 6 0.55811917905532D+00 0.88032337559095D-02 2 2 1 6 0.18400242893230D+00 -0.96791005009873D-03 3 2 1 6 0.78662503091571D-02 -0.31381182230553D-02 1 3 1 6 -0.34119545832177D+01 0.24534919728115D-01 2 3 1 6 0.60931119429413D+00 0.62667131860605D-02 3 3 1 6 -0.58627756627623D+00 -0.10593882194419D-01 1 4 1 6 -0.34119545832178D+01 0.24534919728115D-01 2 4 1 6 0.60931119429414D+00 0.62667131860607D-02 3 4 1 6 -0.58627756627639D+00 -0.10593882194419D-01 1 5 1 6 -0.23455477709814D-13 -0.27733383209635D-14 2 5 1 6 -0.14880708703711D-17 0.15242600558486D-16 3 5 1 6 -0.24319961025001D-16 -0.23272156852883D-16 1 6 1 6 0.17103127485998D+02 0.00000000000000D+00 2 6 1 6 0.11964608912777D+01 -0.85435484783889D-07 3 6 1 6 -0.66152489403986D+00 0.39296266395809D-07 1 7 1 6 0.28593275336663D-14 -0.20738425384214D-08 2 7 1 6 0.89105395026049D+00 -0.31128250375007D-08 3 7 1 6 -0.11584755732354D+01 -0.81578008764159D-08 1 8 1 6 -0.59218717249681D-14 0.25835601485383D-14 2 8 1 6 0.21893368764751D-14 0.18835480714282D-15 3 8 1 6 -0.11229406559144D-15 -0.33716473831139D-15 1 9 1 6 -0.14348998472425D+01 0.99561485241658D+00 2 9 1 6 -0.89837415147513D-01 -0.28434571662258D-01 3 9 1 6 0.43958843349094D+00 0.38432929013885D+00 1 10 1 6 -0.14348998472423D+01 0.99561485241658D+00 2 10 1 6 -0.89837415147497D-01 -0.28434571662258D-01 3 10 1 6 0.43958843349070D+00 0.38432929013885D+00 1 11 1 6 0.66260619793175D-01 -0.19008188054166D-02 2 11 1 6 0.20231996251958D+00 -0.74936408584574D-03 3 11 1 6 -0.10833421476976D+01 -0.24669330446018D-01 1 12 1 6 0.66260619793234D-01 -0.19008188054177D-02 2 12 1 6 0.20231996251958D+00 -0.74936408584513D-03 3 12 1 6 -0.10833421476976D+01 -0.24669330446018D-01 1 13 1 6 -0.53668345860631D+00 0.28185231299411D-01 2 13 1 6 -0.44045047321920D+00 0.31562444327087D-01 3 13 1 6 0.43515068697146D+00 -0.16001986766970D-01 1 14 1 6 -0.53668345860630D+00 0.28185231299410D-01 2 14 1 6 -0.44045047321919D+00 0.31562444327087D-01 3 14 1 6 0.43515068697147D+00 -0.16001986766969D-01 1 15 1 6 -0.13845730161112D+01 0.72380285350868D-02 2 15 1 6 0.47626471351779D+00 0.15005981134197D-01 3 15 1 6 -0.65731579623171D+00 0.56732508242438D-01 1 16 1 6 -0.13845730161115D+01 0.72380285350868D-02 2 16 1 6 0.47626471351754D+00 0.15005981134196D-01 3 16 1 6 -0.65731579623203D+00 0.56732508242439D-01 1 17 1 6 -0.42653587354495D+00 0.40733070771102D-01 2 17 1 6 0.57101547054755D+00 -0.86049765744083D-01 3 17 1 6 0.31176258682280D+00 -0.24129461132843D-01 1 18 1 6 -0.42653587354495D+00 0.40733070771101D-01 2 18 1 6 0.57101547054755D+00 -0.86049765744083D-01 3 18 1 6 0.31176258682279D+00 -0.24129461132842D-01 1 19 1 6 0.10161148680495D+00 0.12921154873964D-01 2 19 1 6 -0.68146394044004D+00 -0.19992458410018D-01 3 19 1 6 -0.89708384060983D+00 0.45108112857922D-01 1 20 1 6 0.10161148680499D+00 0.12921154873964D-01 2 20 1 6 -0.68146394044037D+00 -0.19992458410019D-01 3 20 1 6 -0.89708384060991D+00 0.45108112857921D-01 1 1 2 6 0.19958313727998D+00 0.86442319679255D-02 2 1 2 6 -0.57686310444299D+00 -0.14826965851521D-01 3 1 2 6 -0.67961455079363D+01 0.15399510733542D-01 1 2 2 6 0.19958313727998D+00 0.86442319679256D-02 2 2 2 6 -0.57686310444305D+00 -0.14826965851526D-01 3 2 2 6 -0.67961455079364D+01 0.15399510733545D-01 1 3 2 6 0.69558746439058D-01 -0.33519815380904D-02 2 3 2 6 0.33480134856160D+01 0.12065918392824D-01 3 3 2 6 0.86899923548546D+00 0.12757658958084D-01 1 4 2 6 0.69558746439071D-01 -0.33519815380902D-02 2 4 2 6 0.33480134856161D+01 0.12065918392819D-01 3 4 2 6 0.86899923548538D+00 0.12757658958082D-01 1 5 2 6 -0.14880708736022D-17 0.15242600558486D-16 2 5 2 6 -0.41485329109855D-13 -0.18200673636163D-14 3 5 2 6 0.42560961253940D-13 -0.25695478992455D-14 1 6 2 6 0.11964495053951D+01 0.92801755418816D-07 2 6 2 6 0.27171439032596D+02 0.00000000000000D+00 3 6 2 6 0.30621762849943D+01 -0.29683733849656D-06 1 7 2 6 0.89105691456754D+00 0.36445128936373D-08 2 7 2 6 -0.62349256628870D-14 -0.13037060676157D-08 3 7 2 6 -0.95967947517878D+01 0.22470630167812D-08 1 8 2 6 0.21842079578728D-14 0.18835480714282D-15 2 8 2 6 0.48095979102454D-13 0.66084816315254D-14 3 8 2 6 0.44283015971067D-13 -0.93652744686250D-15 1 9 2 6 -0.17280737966039D+00 -0.26919297650924D-01 2 9 2 6 -0.26386513098339D+01 0.10039895553932D+01 3 9 2 6 -0.11665557843290D-01 -0.12240381992961D+00 1 10 2 6 -0.17280737966037D+00 -0.26919297650924D-01 2 10 2 6 -0.26386513098338D+01 0.10039895553932D+01 3 10 2 6 -0.11665557843468D-01 -0.12240381992961D+00 1 11 2 6 0.10715354635022D+00 -0.14813378605736D-01 2 11 2 6 -0.31159283523963D+00 -0.78900338346496D-02 3 11 2 6 -0.71913698842732D+01 -0.19030339771505D+00 1 12 2 6 0.10715354635022D+00 -0.14813378605735D-01 2 12 2 6 -0.31159283523972D+00 -0.78900338346514D-02 3 12 2 6 -0.71913698842732D+01 -0.19030339771505D+00 1 13 2 6 0.25621508332100D+00 0.25622006102618D-01 2 13 2 6 -0.45311663921885D-01 0.16202328843040D-01 3 13 2 6 0.12163822420998D+01 -0.57385749439763D-02 1 14 2 6 0.25621508332101D+00 0.25622006102617D-01 2 14 2 6 -0.45311663921933D-01 0.16202328843039D-01 3 14 2 6 0.12163822420997D+01 -0.57385749439751D-02 1 15 2 6 -0.26678709400263D+01 -0.10444277046125D-01 2 15 2 6 -0.50877705951580D+01 -0.39081011523136D-02 3 15 2 6 -0.43996757603033D+00 0.21416164457982D-01 1 16 2 6 -0.26678709400265D+01 -0.10444277046125D-01 2 16 2 6 -0.50877705951578D+01 -0.39081011523107D-02 3 16 2 6 -0.43996757603053D+00 0.21416164457978D-01 1 17 2 6 0.10236940830580D+00 -0.80797613398192D-01 2 17 2 6 -0.39314106725631D+00 0.10539800877489D+00 3 17 2 6 -0.18790885120284D+01 0.37555646432896D-01 1 18 2 6 0.10236940830580D+00 -0.80797613398192D-01 2 18 2 6 -0.39314106725631D+00 0.10539800877489D+00 3 18 2 6 -0.18790885120283D+01 0.37555646432895D-01 1 19 2 6 0.13720704530737D+01 -0.93931795399754D-02 2 19 2 6 -0.52675461638692D+01 0.14939669842367D-01 3 19 2 6 0.37668213502725D+00 -0.52669567900923D-01 1 20 2 6 0.13720704530733D+01 -0.93931795399762D-02 2 20 2 6 -0.52675461638689D+01 0.14939669842366D-01 3 20 2 6 0.37668213502738D+00 -0.52669567900919D-01 1 1 3 6 -0.39059135541116D+00 0.75688831137643D-03 2 1 3 6 -0.67534155778311D+01 0.12288078113769D-01 3 1 3 6 -0.41581645217123D+00 -0.46388928904222D-02 1 2 3 6 -0.39059135541117D+00 0.75688831137617D-03 2 2 3 6 -0.67534155778312D+01 0.12288078113772D-01 3 2 3 6 -0.41581645217133D+00 -0.46388928904296D-02 1 3 3 6 0.26816151616296D+00 0.51820868099592D-02 2 3 3 6 0.99228147842188D+00 0.69398204166036D-02 3 3 3 6 -0.11086389653711D-01 -0.10217755955325D-01 1 4 3 6 0.26816151616280D+00 0.51820868099590D-02 2 4 3 6 0.99228147842180D+00 0.69398204166014D-02 3 4 3 6 -0.11086389653568D-01 -0.10217755955313D-01 1 5 3 6 0.11208283184136D-16 -0.23272156852883D-16 2 5 3 6 0.42552101166062D-13 -0.25695478992455D-14 3 5 3 6 0.36798306176172D-12 0.96861999945378D-14 1 6 3 6 -0.66152888511859D+00 -0.71029185551163D-07 2 6 3 6 0.30621819332284D+01 0.33115259129583D-06 3 6 3 6 0.46292281750279D+02 0.00000000000000D+00 1 7 3 6 0.11584876421650D+01 -0.87376214958480D-08 2 7 3 6 -0.95967892222620D+01 -0.27820492708253D-08 3 7 3 6 -0.18382891655425D-14 -0.12714943158531D-07 1 8 3 6 -0.11989457939777D-15 -0.33716473831139D-15 2 8 3 6 0.44283015971067D-13 -0.93652744686248D-15 3 8 3 6 0.36494161172947D-13 -0.49131896751974D-14 1 9 3 6 0.18172566497777D+01 0.44826001288329D+00 2 9 3 6 -0.10071192072822D+00 -0.11100264511879D+00 3 9 3 6 -0.79046572296046D+01 -0.23201526240615D+01 1 10 3 6 0.18172566497774D+01 0.44826001288329D+00 2 10 3 6 -0.10071192072839D+00 -0.11100264511879D+00 3 10 3 6 -0.79046572296050D+01 -0.23201526240615D+01 1 11 3 6 0.25055805143924D+00 0.78027860827718D-02 2 11 3 6 -0.17926419446749D+01 -0.28819059804327D-01 3 11 3 6 -0.16044242939859D+00 0.11914068240678D-01 1 12 3 6 0.25055805143922D+00 0.78027860827727D-02 2 12 3 6 -0.17926419446749D+01 -0.28819059804330D-01 3 12 3 6 -0.16044242939867D+00 0.11914068240676D-01 1 13 3 6 0.30154452868180D+01 -0.61764351561429D-02 2 13 3 6 0.39939332590607D+01 -0.54859697995852D-02 3 13 3 6 0.29639836161845D+00 -0.16795988062123D-01 1 14 3 6 0.30154452868180D+01 -0.61764351561422D-02 2 14 3 6 0.39939332590606D+01 -0.54859697995840D-02 3 14 3 6 0.29639836161834D+00 -0.16795988062125D-01 1 15 3 6 0.44484082043142D+00 0.39226475628243D-01 2 15 3 6 0.48293872093498D+00 0.50087726758094D-01 3 15 3 6 -0.47413405231889D+01 0.29166084374176D-01 1 16 3 6 0.44484082043110D+00 0.39226475628245D-01 2 16 3 6 0.48293872093478D+00 0.50087726758090D-01 3 16 3 6 -0.47413405231887D+01 0.29166084374175D-01 1 17 3 6 0.27364761524283D+01 -0.35602897432235D-02 2 17 3 6 -0.46274354307469D+01 0.12249582240391D-01 3 17 3 6 -0.16730730623437D+00 -0.76010911761059D-01 1 18 3 6 0.27364761524283D+01 -0.35602897432231D-02 2 18 3 6 -0.46274354307469D+01 0.12249582240390D-01 3 18 3 6 -0.16730730623448D+00 -0.76010911761061D-01 1 19 3 6 0.21687698938742D+00 0.45240790056759D-01 2 19 3 6 -0.61828817619151D+00 -0.66510466617491D-01 3 19 3 6 -0.40120124420436D+01 0.33325999191645D-01 1 20 3 6 0.21687698938734D+00 0.45240790056758D-01 2 20 3 6 -0.61828817619138D+00 -0.66510466617487D-01 3 20 3 6 -0.40120124420440D+01 0.33325999191646D-01 1 1 1 7 -0.34119545832177D+01 0.24534919728119D-01 2 1 1 7 -0.60931119429412D+00 -0.62667131860606D-02 3 1 1 7 -0.58627756627625D+00 -0.10593882194419D-01 1 2 1 7 -0.34119545832178D+01 0.24534919728139D-01 2 2 1 7 -0.60931119429412D+00 -0.62667131860604D-02 3 2 1 7 -0.58627756627623D+00 -0.10593882194417D-01 1 3 1 7 -0.55811917905537D+00 -0.88032337559061D-02 2 3 1 7 0.18400242893230D+00 -0.96791005009852D-03 3 3 1 7 -0.78662503091544D-02 0.31381182230550D-02 1 4 1 7 -0.55811917905536D+00 -0.88032337559084D-02 2 4 1 7 0.18400242893228D+00 -0.96791005009867D-03 3 4 1 7 -0.78662503091544D-02 0.31381182230551D-02 1 5 1 7 -0.59218563921815D-14 -0.25835601485383D-14 2 5 1 7 0.21842079885805D-14 -0.18835480714282D-15 3 5 1 7 0.37936111467927D-17 0.33716473831139D-15 1 6 1 7 0.28593275336663D-14 0.20738425384214D-08 2 6 1 7 0.89105395026049D+00 -0.31128250375007D-08 3 6 1 7 0.11584755732354D+01 0.81578008764159D-08 1 7 1 7 0.17103127485998D+02 0.00000000000000D+00 2 7 1 7 -0.11964608912776D+01 0.85435484783889D-07 3 7 1 7 -0.66152489403970D+00 0.39296266395809D-07 1 8 1 7 -0.23455477709814D-13 0.27733383209635D-14 2 8 1 7 0.16575477309767D-15 -0.15242600558486D-16 3 8 1 7 0.62987471089105D-14 0.23272156852883D-16 1 9 1 7 0.66260619793235D-01 -0.19008188054176D-02 2 9 1 7 -0.20231996251957D+00 0.74936408584558D-03 3 9 1 7 -0.10833421476976D+01 -0.24669330446018D-01 1 10 1 7 0.66260619793209D-01 -0.19008188054163D-02 2 10 1 7 -0.20231996251956D+00 0.74936408584435D-03 3 10 1 7 -0.10833421476976D+01 -0.24669330446019D-01 1 11 1 7 0.14348998472422D+01 -0.99561485241657D+00 2 11 1 7 -0.89837415147388D-01 -0.28434571662259D-01 3 11 1 7 -0.43958843349087D+00 -0.38432929013884D+00 1 12 1 7 0.14348998472424D+01 -0.99561485241657D+00 2 12 1 7 -0.89837415147540D-01 -0.28434571662259D-01 3 12 1 7 -0.43958843349067D+00 -0.38432929013883D+00 1 13 1 7 0.10161148680499D+00 0.12921154873964D-01 2 13 1 7 0.68146394044034D+00 0.19992458410019D-01 3 13 1 7 -0.89708384060989D+00 0.45108112857921D-01 1 14 1 7 0.10161148680487D+00 0.12921154873971D-01 2 14 1 7 0.68146394043985D+00 0.19992458410064D-01 3 14 1 7 -0.89708384060995D+00 0.45108112857935D-01 1 15 1 7 -0.42653587354495D+00 0.40733070771101D-01 2 15 1 7 -0.57101547054755D+00 0.86049765744084D-01 3 15 1 7 0.31176258682278D+00 -0.24129461132841D-01 1 16 1 7 -0.42653587354496D+00 0.40733070771101D-01 2 16 1 7 -0.57101547054755D+00 0.86049765744083D-01 3 16 1 7 0.31176258682281D+00 -0.24129461132842D-01 1 17 1 7 0.13845730161115D+01 -0.72380285351074D-02 2 17 1 7 0.47626471351752D+00 0.15005981134219D-01 3 17 1 7 0.65731579623210D+00 -0.56732508242447D-01 1 18 1 7 0.13845730161114D+01 -0.72380285351076D-02 2 18 1 7 0.47626471351769D+00 0.15005981134220D-01 3 18 1 7 0.65731579623177D+00 -0.56732508242447D-01 1 19 1 7 0.53668345860631D+00 -0.28185231299411D-01 2 19 1 7 -0.44045047321920D+00 0.31562444327087D-01 3 19 1 7 -0.43515068697145D+00 0.16001986766968D-01 1 20 1 7 0.53668345860631D+00 -0.28185231299410D-01 2 20 1 7 -0.44045047321919D+00 0.31562444327087D-01 3 20 1 7 -0.43515068697144D+00 0.16001986766968D-01 1 1 2 7 -0.69558746439050D-01 0.33519815380904D-02 2 1 2 7 0.33480134856161D+01 0.12065918392820D-01 3 1 2 7 -0.86899923548528D+00 -0.12757658958083D-01 1 2 2 7 -0.69558746439051D-01 0.33519815380905D-02 2 2 2 7 0.33480134856161D+01 0.12065918392816D-01 3 2 2 7 -0.86899923548539D+00 -0.12757658958082D-01 1 3 2 7 0.19958313727998D+00 0.86442319679258D-02 2 3 2 7 0.57686310444300D+00 0.14826965851516D-01 3 3 2 7 -0.67961455079363D+01 0.15399510733551D-01 1 4 2 7 0.19958313727996D+00 0.86442319679256D-02 2 4 2 7 0.57686310444304D+00 0.14826965851522D-01 3 4 2 7 -0.67961455079363D+01 0.15399510733566D-01 1 5 2 7 0.21893369071828D-14 -0.18835480714282D-15 2 5 2 7 -0.31840078666837D-13 -0.66084816315254D-14 3 5 2 7 -0.16616400979042D-16 0.93652744686250D-15 1 6 2 7 0.89105691456754D+00 0.36445128936373D-08 2 6 2 7 -0.62349256628870D-14 0.13037060676157D-08 3 6 2 7 -0.95967947517878D+01 0.22470654443232D-08 1 7 2 7 -0.11964495053950D+01 -0.92801755418816D-07 2 7 2 7 0.27171439032595D+02 0.00000000000000D+00 3 7 2 7 -0.30621762849953D+01 0.29683733849656D-06 1 8 2 7 0.16575477310091D-15 -0.15242600558486D-16 2 8 2 7 -0.82452558718524D-13 0.18200673636163D-14 3 8 2 7 -0.39304295494856D-13 0.25695478992455D-14 1 9 2 7 -0.10715354635021D+00 0.14813378605735D-01 2 9 2 7 -0.31159283523970D+00 -0.78900338346503D-02 3 9 2 7 0.71913698842732D+01 0.19030339771505D+00 1 10 2 7 -0.10715354635020D+00 0.14813378605734D-01 2 10 2 7 -0.31159283523968D+00 -0.78900338346488D-02 3 10 2 7 0.71913698842732D+01 0.19030339771505D+00 1 11 2 7 -0.17280737966026D+00 -0.26919297650924D-01 2 11 2 7 0.26386513098336D+01 -0.10039895553932D+01 3 11 2 7 -0.11665557844150D-01 -0.12240381992960D+00 1 12 2 7 -0.17280737966041D+00 -0.26919297650924D-01 2 12 2 7 0.26386513098338D+01 -0.10039895553932D+01 3 12 2 7 -0.11665557843166D-01 -0.12240381992960D+00 1 13 2 7 -0.13720704530734D+01 0.93931795399760D-02 2 13 2 7 -0.52675461638689D+01 0.14939669842364D-01 3 13 2 7 -0.37668213502734D+00 0.52669567900925D-01 1 14 2 7 -0.13720704530738D+01 0.93931795400212D-02 2 14 2 7 -0.52675461638691D+01 0.14939669842408D-01 3 14 2 7 -0.37668213502739D+00 0.52669567900948D-01 1 15 2 7 -0.10236940830580D+00 0.80797613398194D-01 2 15 2 7 -0.39314106725631D+00 0.10539800877489D+00 3 15 2 7 0.18790885120284D+01 -0.37555646432893D-01 1 16 2 7 -0.10236940830580D+00 0.80797613398193D-01 2 16 2 7 -0.39314106725633D+00 0.10539800877488D+00 3 16 2 7 0.18790885120283D+01 -0.37555646432895D-01 1 17 2 7 -0.26678709400266D+01 -0.10444277046102D-01 2 17 2 7 0.50877705951578D+01 0.39081011523073D-02 3 17 2 7 -0.43996757603056D+00 0.21416164457987D-01 1 18 2 7 -0.26678709400264D+01 -0.10444277046102D-01 2 18 2 7 0.50877705951579D+01 0.39081011523093D-02 3 18 2 7 -0.43996757603035D+00 0.21416164457986D-01 1 19 2 7 0.25621508332100D+00 0.25622006102618D-01 2 19 2 7 0.45311663921905D-01 -0.16202328843040D-01 3 19 2 7 0.12163822420998D+01 -0.57385749439757D-02 1 20 2 7 0.25621508332101D+00 0.25622006102618D-01 2 20 2 7 0.45311663921887D-01 -0.16202328843042D-01 3 20 2 7 0.12163822420998D+01 -0.57385749439736D-02 1 1 3 7 0.26816151616295D+00 0.51820868099591D-02 2 1 3 7 -0.99228147842170D+00 -0.69398204166024D-02 3 1 3 7 -0.11086389653709D-01 -0.10217755955325D-01 1 2 3 7 0.26816151616297D+00 0.51820868099612D-02 2 2 3 7 -0.99228147842180D+00 -0.69398204166017D-02 3 2 3 7 -0.11086389653640D-01 -0.10217755955319D-01 1 3 3 7 0.39059135541117D+00 -0.75688831137646D-03 2 3 3 7 -0.67534155778312D+01 0.12288078113778D-01 3 3 3 7 0.41581645217141D+00 0.46388928904219D-02 1 4 3 7 0.39059135541117D+00 -0.75688831137634D-03 2 4 3 7 -0.67534155778312D+01 0.12288078113793D-01 3 4 3 7 0.41581645217128D+00 0.46388928904237D-02 1 5 3 7 -0.38069026595396D-17 0.33716473831139D-15 2 5 3 7 -0.16616400979042D-16 0.93652744686248D-15 3 5 3 7 -0.43441896447452D-13 0.49131896751974D-14 1 6 3 7 -0.11584876421650D+01 0.87376214958480D-08 2 6 3 7 -0.95967892222620D+01 -0.27820468432834D-08 3 6 3 7 -0.18382891655425D-14 0.12714943158531D-07 1 7 3 7 -0.66152888511842D+00 -0.71029185551163D-07 2 7 3 7 -0.30621819332294D+01 -0.33115259129583D-06 3 7 3 7 0.46292281750279D+02 0.00000000000000D+00 1 8 3 7 0.63342753531196D-14 0.23272156852883D-16 2 8 3 7 -0.39295435406978D-13 0.25695478992455D-14 3 8 3 7 0.32002142709791D-12 -0.96861999945378D-14 1 9 3 7 0.25055805143921D+00 0.78027860827726D-02 2 9 3 7 0.17926419446749D+01 0.28819059804329D-01 3 9 3 7 -0.16044242939864D+00 0.11914068240676D-01 1 10 3 7 0.25055805143922D+00 0.78027860827716D-02 2 10 3 7 0.17926419446749D+01 0.28819059804330D-01 3 10 3 7 -0.16044242939865D+00 0.11914068240678D-01 1 11 3 7 -0.18172566497776D+01 -0.44826001288328D+00 2 11 3 7 -0.10071192072908D+00 -0.11100264511879D+00 3 11 3 7 0.79046572296053D+01 0.23201526240614D+01 1 12 3 7 -0.18172566497774D+01 -0.44826001288327D+00 2 12 3 7 -0.10071192072810D+00 -0.11100264511879D+00 3 12 3 7 0.79046572296050D+01 0.23201526240614D+01 1 13 3 7 0.21687698938736D+00 0.45240790056758D-01 2 13 3 7 0.61828817619142D+00 0.66510466617494D-01 3 13 3 7 -0.40120124420439D+01 0.33325999191643D-01 1 14 3 7 0.21687698938730D+00 0.45240790056772D-01 2 14 3 7 0.61828817619137D+00 0.66510466617517D-01 3 14 3 7 -0.40120124420432D+01 0.33325999191601D-01 1 15 3 7 0.27364761524283D+01 -0.35602897432216D-02 2 15 3 7 0.46274354307469D+01 -0.12249582240388D-01 3 15 3 7 -0.16730730623447D+00 -0.76010911761057D-01 1 16 3 7 0.27364761524283D+01 -0.35602897432230D-02 2 16 3 7 0.46274354307469D+01 -0.12249582240390D-01 3 16 3 7 -0.16730730623438D+00 -0.76010911761063D-01 1 17 3 7 -0.44484082043105D+00 -0.39226475628253D-01 2 17 3 7 0.48293872093475D+00 0.50087726758100D-01 3 17 3 7 0.47413405231885D+01 -0.29166084374155D-01 1 18 3 7 -0.44484082043136D+00 -0.39226475628253D-01 2 18 3 7 0.48293872093496D+00 0.50087726758098D-01 3 18 3 7 0.47413405231887D+01 -0.29166084374153D-01 1 19 3 7 -0.30154452868179D+01 0.61764351561418D-02 2 19 3 7 0.39939332590606D+01 -0.54859697995845D-02 3 19 3 7 -0.29639836161839D+00 0.16795988062121D-01 1 20 3 7 -0.30154452868179D+01 0.61764351561413D-02 2 20 3 7 0.39939332590606D+01 -0.54859697995825D-02 3 20 3 7 -0.29639836161845D+00 0.16795988062121D-01 1 1 1 8 -0.34119545832177D+01 0.24534919728117D-01 2 1 1 8 -0.60931119429412D+00 -0.62667131860602D-02 3 1 1 8 0.58627756627624D+00 0.10593882194419D-01 1 2 1 8 0.34119545832178D+01 -0.24534919728129D-01 2 2 1 8 0.60931119429413D+00 0.62667131860604D-02 3 2 1 8 -0.58627756627625D+00 -0.10593882194418D-01 1 3 1 8 -0.55811917905538D+00 -0.88032337559075D-02 2 3 1 8 0.18400242893230D+00 -0.96791005009861D-03 3 3 1 8 0.78662503091535D-02 -0.31381182230548D-02 1 4 1 8 0.55811917905537D+00 0.88032337559083D-02 2 4 1 8 -0.18400242893229D+00 0.96791005009860D-03 3 4 1 8 -0.78662503091468D-02 0.31381182230555D-02 1 5 1 8 -0.29842419140116D-14 0.20738425384214D-08 2 5 1 8 0.89105395026049D+00 -0.31128250375007D-08 3 5 1 8 -0.11584755732354D+01 -0.81578008764159D-08 1 6 1 8 -0.59218717249681D-14 -0.25835601485383D-14 2 6 1 8 0.21842079578728D-14 -0.18835480714282D-15 3 6 1 8 -0.11989457939777D-15 0.33716473831139D-15 1 7 1 8 -0.23455477709814D-13 -0.27733383209635D-14 2 7 1 8 0.16575477310091D-15 0.15242600558486D-16 3 7 1 8 0.63342753531196D-14 -0.23272156852883D-16 1 8 1 8 0.17103127485998D+02 0.00000000000000D+00 2 8 1 8 -0.11964608912775D+01 0.85435484783889D-07 3 8 1 8 0.66152489403949D+00 -0.39296266395809D-07 1 9 1 8 0.66260619793234D-01 -0.19008188054173D-02 2 9 1 8 -0.20231996251956D+00 0.74936408584539D-03 3 9 1 8 0.10833421476976D+01 0.24669330446017D-01 1 10 1 8 -0.66260619793210D-01 0.19008188054161D-02 2 10 1 8 0.20231996251959D+00 -0.74936408584594D-03 3 10 1 8 -0.10833421476976D+01 -0.24669330446018D-01 1 11 1 8 -0.14348998472423D+01 0.99561485241658D+00 2 11 1 8 0.89837415147404D-01 0.28434571662258D-01 3 11 1 8 -0.43958843349067D+00 -0.38432929013885D+00 1 12 1 8 0.14348998472424D+01 -0.99561485241657D+00 2 12 1 8 -0.89837415147541D-01 -0.28434571662259D-01 3 12 1 8 0.43958843349068D+00 0.38432929013884D+00 1 13 1 8 -0.42653587354496D+00 0.40733070771101D-01 2 13 1 8 -0.57101547054755D+00 0.86049765744083D-01 3 13 1 8 -0.31176258682281D+00 0.24129461132843D-01 1 14 1 8 0.42653587354495D+00 -0.40733070771101D-01 2 14 1 8 0.57101547054755D+00 -0.86049765744083D-01 3 14 1 8 0.31176258682278D+00 -0.24129461132842D-01 1 15 1 8 -0.10161148680487D+00 -0.12921154873967D-01 2 15 1 8 -0.68146394043984D+00 -0.19992458410041D-01 3 15 1 8 -0.89708384060992D+00 0.45108112857928D-01 1 16 1 8 0.10161148680499D+00 0.12921154873963D-01 2 16 1 8 0.68146394044037D+00 0.19992458410020D-01 3 16 1 8 0.89708384060991D+00 -0.45108112857922D-01 1 17 1 8 0.53668345860630D+00 -0.28185231299410D-01 2 17 1 8 -0.44045047321920D+00 0.31562444327087D-01 3 17 1 8 0.43515068697145D+00 -0.16001986766968D-01 1 18 1 8 -0.53668345860631D+00 0.28185231299410D-01 2 18 1 8 0.44045047321919D+00 -0.31562444327087D-01 3 18 1 8 -0.43515068697146D+00 0.16001986766969D-01 1 19 1 8 -0.13845730161113D+01 0.72380285350870D-02 2 19 1 8 -0.47626471351764D+00 -0.15005981134197D-01 3 19 1 8 0.65731579623174D+00 -0.56732508242439D-01 1 20 1 8 0.13845730161116D+01 -0.72380285351077D-02 2 20 1 8 0.47626471351752D+00 0.15005981134219D-01 3 20 1 8 -0.65731579623210D+00 0.56732508242447D-01 1 1 2 8 -0.69558746439051D-01 0.33519815380908D-02 2 1 2 8 0.33480134856160D+01 0.12065918392822D-01 3 1 2 8 0.86899923548525D+00 0.12757658958081D-01 1 2 2 8 0.69558746439058D-01 -0.33519815380906D-02 2 2 2 8 -0.33480134856161D+01 -0.12065918392819D-01 3 2 2 8 -0.86899923548536D+00 -0.12757658958081D-01 1 3 2 8 0.19958313727998D+00 0.86442319679257D-02 2 3 2 8 0.57686310444302D+00 0.14826965851514D-01 3 3 2 8 0.67961455079363D+01 -0.15399510733551D-01 1 4 2 8 -0.19958313727997D+00 -0.86442319679257D-02 2 4 2 8 -0.57686310444304D+00 -0.14826965851524D-01 3 4 2 8 -0.67961455079363D+01 0.15399510733549D-01 1 5 2 8 0.89105691456755D+00 0.36445128936373D-08 2 5 2 8 0.62349256668420D-14 0.13037060676157D-08 3 5 2 8 0.95967947517878D+01 -0.22470642305522D-08 1 6 2 8 0.21893368764751D-14 -0.18835480714282D-15 2 6 2 8 0.48095979102454D-13 -0.66084816315254D-14 3 6 2 8 0.44283015971067D-13 0.93652744686248D-15 1 7 2 8 0.16575477309767D-15 0.15242600558486D-16 2 7 2 8 -0.82452558718524D-13 -0.18200673636163D-14 3 7 2 8 -0.39295435406978D-13 -0.25695478992455D-14 1 8 2 8 -0.11964495053949D+01 -0.92801755418816D-07 2 8 2 8 0.27171439032595D+02 0.00000000000000D+00 3 8 2 8 0.30621762849953D+01 -0.29683733849656D-06 1 9 2 8 -0.10715354635020D+00 0.14813378605735D-01 2 9 2 8 -0.31159283523971D+00 -0.78900338346499D-02 3 9 2 8 -0.71913698842732D+01 -0.19030339771505D+00 1 10 2 8 0.10715354635023D+00 -0.14813378605736D-01 2 10 2 8 0.31159283523968D+00 0.78900338346492D-02 3 10 2 8 0.71913698842733D+01 0.19030339771504D+00 1 11 2 8 0.17280737966028D+00 0.26919297650924D-01 2 11 2 8 -0.26386513098338D+01 0.10039895553932D+01 3 11 2 8 -0.11665557844097D-01 -0.12240381992960D+00 1 12 2 8 -0.17280737966041D+00 -0.26919297650924D-01 2 12 2 8 0.26386513098338D+01 -0.10039895553932D+01 3 12 2 8 0.11665557843166D-01 0.12240381992960D+00 1 13 2 8 -0.10236940830580D+00 0.80797613398193D-01 2 13 2 8 -0.39314106725634D+00 0.10539800877488D+00 3 13 2 8 -0.18790885120284D+01 0.37555646432896D-01 1 14 2 8 0.10236940830580D+00 -0.80797613398192D-01 2 14 2 8 0.39314106725632D+00 -0.10539800877488D+00 3 14 2 8 0.18790885120283D+01 -0.37555646432895D-01 1 15 2 8 0.13720704530739D+01 -0.93931795399980D-02 2 15 2 8 0.52675461638692D+01 -0.14939669842386D-01 3 15 2 8 -0.37668213502738D+00 0.52669567900931D-01 1 16 2 8 -0.13720704530733D+01 0.93931795399765D-02 2 16 2 8 -0.52675461638689D+01 0.14939669842366D-01 3 16 2 8 0.37668213502740D+00 -0.52669567900923D-01 1 17 2 8 0.25621508332100D+00 0.25622006102618D-01 2 17 2 8 0.45311663921924D-01 -0.16202328843040D-01 3 17 2 8 -0.12163822420998D+01 0.57385749439750D-02 1 18 2 8 -0.25621508332101D+00 -0.25622006102618D-01 2 18 2 8 -0.45311663921894D-01 0.16202328843041D-01 3 18 2 8 0.12163822420998D+01 -0.57385749439746D-02 1 19 2 8 0.26678709400264D+01 0.10444277046125D-01 2 19 2 8 -0.50877705951579D+01 -0.39081011523117D-02 3 19 2 8 -0.43996757603033D+00 0.21416164457982D-01 1 20 2 8 -0.26678709400265D+01 -0.10444277046102D-01 2 20 2 8 0.50877705951577D+01 0.39081011523083D-02 3 20 2 8 0.43996757603058D+00 -0.21416164457985D-01 1 1 3 8 -0.26816151616296D+00 -0.51820868099592D-02 2 1 3 8 0.99228147842167D+00 0.69398204166009D-02 3 1 3 8 -0.11086389653690D-01 -0.10217755955318D-01 1 2 3 8 0.26816151616295D+00 0.51820868099601D-02 2 2 3 8 -0.99228147842177D+00 -0.69398204166008D-02 3 2 3 8 0.11086389653526D-01 0.10217755955312D-01 1 3 3 8 -0.39059135541117D+00 0.75688831137664D-03 2 3 3 8 0.67534155778312D+01 -0.12288078113778D-01 3 3 3 8 0.41581645217141D+00 0.46388928904226D-02 1 4 3 8 0.39059135541118D+00 -0.75688831137599D-03 2 4 3 8 -0.67534155778312D+01 0.12288078113777D-01 3 4 3 8 -0.41581645217132D+00 -0.46388928904203D-02 1 5 3 8 0.11584876421650D+01 -0.87376214958480D-08 2 5 3 8 0.95967892222620D+01 0.27820480570544D-08 3 5 3 8 0.18382853548248D-14 0.12714943158531D-07 1 6 3 8 -0.11229406559144D-15 0.33716473831139D-15 2 6 3 8 0.44283015971067D-13 0.93652744686250D-15 3 6 3 8 0.36494161172947D-13 0.49131896751974D-14 1 7 3 8 0.62987471089105D-14 -0.23272156852883D-16 2 7 3 8 -0.39304295494856D-13 -0.25695478992455D-14 3 7 3 8 0.32002142709791D-12 0.96861999945378D-14 1 8 3 8 0.66152888511822D+00 0.71029185551163D-07 2 8 3 8 0.30621819332293D+01 0.33115259129583D-06 3 8 3 8 0.46292281750278D+02 0.00000000000000D+00 1 9 3 8 -0.25055805143921D+00 -0.78027860827727D-02 2 9 3 8 -0.17926419446749D+01 -0.28819059804330D-01 3 9 3 8 -0.16044242939865D+00 0.11914068240677D-01 1 10 3 8 0.25055805143922D+00 0.78027860827717D-02 2 10 3 8 0.17926419446749D+01 0.28819059804323D-01 3 10 3 8 0.16044242939866D+00 -0.11914068240676D-01 1 11 3 8 -0.18172566497774D+01 -0.44826001288329D+00 2 11 3 8 -0.10071192072904D+00 -0.11100264511879D+00 3 11 3 8 -0.79046572296046D+01 -0.23201526240615D+01 1 12 3 8 0.18172566497774D+01 0.44826001288327D+00 2 12 3 8 0.10071192072810D+00 0.11100264511879D+00 3 12 3 8 0.79046572296051D+01 0.23201526240614D+01 1 13 3 8 -0.27364761524283D+01 0.35602897432233D-02 2 13 3 8 -0.46274354307469D+01 0.12249582240391D-01 3 13 3 8 -0.16730730623439D+00 -0.76010911761061D-01 1 14 3 8 0.27364761524283D+01 -0.35602897432221D-02 2 14 3 8 0.46274354307469D+01 -0.12249582240390D-01 3 14 3 8 0.16730730623449D+00 0.76010911761060D-01 1 15 3 8 0.21687698938734D+00 0.45240790056765D-01 2 15 3 8 0.61828817619139D+00 0.66510466617500D-01 3 15 3 8 0.40120124420432D+01 -0.33325999191622D-01 1 16 3 8 -0.21687698938734D+00 -0.45240790056759D-01 2 16 3 8 -0.61828817619136D+00 -0.66510466617492D-01 3 16 3 8 -0.40120124420439D+01 0.33325999191645D-01 1 17 3 8 0.30154452868179D+01 -0.61764351561419D-02 2 17 3 8 -0.39939332590607D+01 0.54859697995838D-02 3 17 3 8 -0.29639836161844D+00 0.16795988062124D-01 1 18 3 8 -0.30154452868180D+01 0.61764351561424D-02 2 18 3 8 0.39939332590607D+01 -0.54859697995835D-02 3 18 3 8 0.29639836161839D+00 -0.16795988062126D-01 1 19 3 8 -0.44484082043139D+00 -0.39226475628245D-01 2 19 3 8 0.48293872093497D+00 0.50087726758094D-01 3 19 3 8 -0.47413405231887D+01 0.29166084374175D-01 1 20 3 8 0.44484082043104D+00 0.39226475628253D-01 2 20 3 8 -0.48293872093473D+00 -0.50087726758097D-01 3 20 3 8 0.47413405231886D+01 -0.29166084374155D-01 1 1 1 9 -0.34655944796514D+00 -0.11086582175471D-07 2 1 1 9 -0.47604566476402D+00 -0.16814582638286D-07 3 1 1 9 0.19715070476029D-14 -0.60985621397511D-16 1 2 1 9 -0.31636351237506D-14 0.65365886362255D-16 2 2 1 9 -0.15278051004100D-14 0.17648994741536D-15 3 2 1 9 0.21247939582640D-01 0.46867258425756D-08 1 3 1 9 -0.11950148942890D+01 -0.18785261918410D-07 2 3 1 9 -0.60939674657545D+00 0.74825804389780D-08 3 3 1 9 0.16347834067064D-15 -0.23664779489892D-15 1 4 1 9 0.64725237817426D-14 0.25955594387181D-15 2 4 1 9 -0.56258126035917D-15 0.13085092419596D-15 3 4 1 9 0.10381392416548D+00 0.11582383299947D-07 1 5 1 9 -0.14348988388955D+01 -0.99561513462343D+00 2 5 1 9 -0.17280793635680D+00 0.26919242379585D-01 3 5 1 9 -0.18172570119107D+01 0.44825942252235D+00 1 6 1 9 -0.14348988388955D+01 -0.99561513462343D+00 2 6 1 9 -0.17280793635681D+00 0.26919242379586D-01 3 6 1 9 0.18172570119107D+01 -0.44825942252235D+00 1 7 1 9 0.66260619793235D-01 0.19008188054178D-02 2 7 1 9 -0.10715354635021D+00 -0.14813378605736D-01 3 7 1 9 0.25055805143921D+00 -0.78027860827727D-02 1 8 1 9 0.66260619793234D-01 0.19008188054174D-02 2 8 1 9 -0.10715354635020D+00 -0.14813378605736D-01 3 8 1 9 -0.25055805143921D+00 0.78027860827728D-02 1 9 1 9 0.89389457666614D+01 0.00000000000000D+00 2 9 1 9 0.92760426250381D+00 0.62814156001575D-07 3 9 1 9 -0.71104791504565D-14 0.13877787807814D-16 1 10 1 9 -0.18917647200250D-14 -0.52771363433998D-16 2 10 1 9 -0.12126476819555D-14 0.56333090476272D-16 3 10 1 9 0.13508528060953D+01 0.27590749943481D-08 1 11 1 9 -0.63796738050855D-17 0.26377051512936D-16 2 11 1 9 0.62232594786795D-15 0.70830019403547D-17 3 11 1 9 0.30724356842664D+00 0.79043045646845D-08 1 12 1 9 0.15694139197542D-14 0.13720629640961D-09 2 12 1 9 -0.59958950146296D+00 -0.48814790053310D-08 3 12 1 9 0.66989865611690D-15 0.23286383938714D-16 1 13 1 9 -0.14676929248685D+01 -0.64741943089073D-09 2 13 1 9 -0.75352350756541D+00 0.12787583375864D-08 3 13 1 9 -0.13911442315853D+01 -0.79836889589643D-08 1 14 1 9 0.83239145370968D-01 -0.19895659670028D-01 2 14 1 9 0.55834777400993D+00 -0.21015462511488D-01 3 14 1 9 -0.12756132421446D+01 -0.11498231829397D-01 1 15 1 9 -0.83239145370964D-01 0.19895659670028D-01 2 15 1 9 -0.55834777400994D+00 0.21015462511487D-01 3 15 1 9 -0.12756132421446D+01 -0.11498231829399D-01 1 16 1 9 -0.14676929248685D+01 -0.64741906928827D-09 2 16 1 9 -0.75352350756541D+00 0.12787582888464D-08 3 16 1 9 0.13911442315853D+01 0.79836885522052D-08 1 17 1 9 -0.67033110219162D+00 -0.13725684560804D-01 2 17 1 9 0.83825489427698D+00 0.29613994108063D-01 3 17 1 9 -0.74448980247682D+00 0.36877640368578D-01 1 18 1 9 0.32727469999195D-01 -0.34537179515790D-06 2 18 1 9 -0.54403671042544D+00 -0.59966147965178D-06 3 18 1 9 -0.95367064821531D+00 0.48363266383435D-07 1 19 1 9 -0.32727469999189D-01 0.34537179591826D-06 2 19 1 9 0.54403671042544D+00 0.59966148028595D-06 3 19 1 9 -0.95367064821530D+00 0.48363264263764D-07 1 20 1 9 -0.67033110219162D+00 -0.13725684560804D-01 2 20 1 9 0.83825489427698D+00 0.29613994108062D-01 3 20 1 9 0.74448980247682D+00 -0.36877640368578D-01 1 1 2 9 0.53616008673611D-01 -0.24772081558803D-07 2 1 2 9 -0.21724496975360D+01 -0.86183536850501D-08 3 1 2 9 -0.14073438967469D-13 0.15125693860538D-14 1 2 2 9 -0.15267433586726D-14 0.17648994741536D-15 2 2 2 9 -0.14713473634173D-14 -0.14785960961616D-15 3 2 2 9 0.87852324247815D+00 0.12183570656076D-07 1 3 2 9 -0.46523303941558D+00 0.15398840518021D-07 2 3 2 9 -0.12368887393920D+01 -0.11244913726051D-07 3 3 2 9 0.28670423730404D-15 0.12757344866727D-15 1 4 2 9 -0.56258126035917D-15 0.13085092419596D-15 2 4 2 9 0.19720602877222D-14 -0.39239851220577D-14 3 4 2 9 -0.86709724151597D-01 -0.41128710667338D-08 1 5 2 9 -0.89837739456405D-01 0.28434528067082D-01 2 5 2 9 -0.26386507453038D+01 -0.10039892930659D+01 3 5 2 9 0.10070949206385D+00 -0.11100268448362D+00 1 6 2 9 -0.89837739456408D-01 0.28434528067082D-01 2 6 2 9 -0.26386507453037D+01 -0.10039892930659D+01 3 6 2 9 -0.10070949206382D+00 0.11100268448362D+00 1 7 2 9 -0.20231996251957D+00 -0.74936408584625D-03 2 7 2 9 -0.31159283523970D+00 0.78900338346501D-02 3 7 2 9 0.17926419446749D+01 -0.28819059804324D-01 1 8 2 9 -0.20231996251956D+00 -0.74936408584606D-03 2 8 2 9 -0.31159283523971D+00 0.78900338346497D-02 3 8 2 9 -0.17926419446749D+01 0.28819059804325D-01 1 9 2 9 0.92760345745922D+00 -0.50582856682839D-07 2 9 2 9 0.72215703335078D+01 0.00000000000000D+00 3 9 2 9 -0.44097027952851D-13 -0.69388939039072D-17 1 10 2 9 -0.12126476818521D-14 0.57200452214261D-16 2 10 2 9 0.12885191711117D-14 -0.25055175789946D-14 3 10 2 9 -0.65174774839858D+00 0.19994422993294D-07 1 11 2 9 0.62232594786795D-15 0.70830019403546D-17 2 11 2 9 -0.94844534218409D-15 0.67223848181586D-16 3 11 2 9 0.20126935342470D+01 0.12010642885858D-10 1 12 2 9 -0.59958950146296D+00 0.48814815471560D-08 2 12 2 9 0.27230410807053D-14 -0.67106664689754D-08 3 12 2 9 0.98998923482838D-14 -0.12492435220505D-14 1 13 2 9 -0.59663969054869D+00 -0.10325910261949D-07 2 13 2 9 0.44257123415122D+00 -0.31163242477939D-08 3 13 2 9 -0.11544331629168D+01 -0.12440778900798D-07 1 14 2 9 0.30023471278905D+00 -0.41327194931040D-02 2 14 2 9 -0.21488626510910D-01 0.15164309944358D-02 3 14 2 9 -0.15292517314635D+01 -0.55659318564008D-03 1 15 2 9 -0.30023471278905D+00 0.41327194931030D-02 2 15 2 9 0.21488626510903D-01 -0.15164309944371D-02 3 15 2 9 -0.15292517314635D+01 -0.55659318564346D-03 1 16 2 9 -0.59663969054869D+00 -0.10325910310689D-07 2 16 2 9 0.44257123415120D+00 -0.31163247947210D-08 3 16 2 9 0.11544331629168D+01 0.12440780203737D-07 1 17 2 9 0.98026860942437D+00 0.39454287820012D-01 2 17 2 9 -0.22537600443644D+00 -0.41867266062296D-01 3 17 2 9 0.19277728803763D+01 -0.51534844201749D-01 1 18 2 9 -0.19375862305741D+00 0.33747397525107D-06 2 18 2 9 0.99984334761587D-01 -0.18695458634476D-06 3 18 2 9 0.19757613553938D+01 0.66017240271822D-06 1 19 2 9 0.19375862305741D+00 -0.33747397462210D-06 2 19 2 9 -0.99984334761571D-01 0.18695458551962D-06 3 19 2 9 0.19757613553939D+01 0.66017240835203D-06 1 20 2 9 0.98026860942437D+00 0.39454287820012D-01 2 20 2 9 -0.22537600443643D+00 -0.41867266062295D-01 3 20 2 9 -0.19277728803763D+01 0.51534844201750D-01 1 1 3 9 0.19715070492573D-14 -0.63154025742482D-16 2 1 3 9 -0.14073438967469D-13 0.15125693860538D-14 3 1 3 9 -0.12782420581770D+01 -0.58937995555889D-07 1 2 3 9 0.33766389153620D+00 0.10623609630858D-08 2 2 3 9 0.26303757206776D+01 -0.18228243090913D-07 3 2 3 9 0.14581776438464D-14 -0.22400689348726D-15 1 3 3 9 0.16347834067064D-15 -0.23664779489892D-15 2 3 3 9 0.28670423730404D-15 0.12757344866727D-15 3 3 3 9 -0.37027410533118D+01 -0.12589759285420D-06 1 4 3 9 -0.63017924966180D-01 -0.13109017245930D-07 2 4 3 9 -0.25794895146193D+00 -0.11773231496637D-07 3 4 3 9 0.20029413871686D-13 -0.26623959152347D-14 1 5 3 9 -0.43958873293661D+00 0.38432970855454D+00 2 5 3 9 0.11665392487426D-01 -0.12240299583630D+00 3 5 3 9 -0.79046526102779D+01 0.23201542406778D+01 1 6 3 9 0.43958873293667D+00 -0.38432970855454D+00 2 6 3 9 -0.11665392487412D-01 0.12240299583630D+00 3 6 3 9 -0.79046526102779D+01 0.23201542406778D+01 1 7 3 9 -0.10833421476976D+01 0.24669330446017D-01 2 7 3 9 0.71913698842732D+01 -0.19030339771504D+00 3 7 3 9 -0.16044242939864D+00 -0.11914068240676D-01 1 8 3 9 0.10833421476976D+01 -0.24669330446017D-01 2 8 3 9 -0.71913698842732D+01 0.19030339771504D+00 3 8 3 9 -0.16044242939865D+00 -0.11914068240677D-01 1 9 3 9 -0.71104791504565D-14 -0.13877787807814D-16 2 9 3 9 -0.44097027959468D-13 -0.69388939039073D-17 3 9 3 9 0.45267194511340D+02 0.00000000000000D+00 1 10 3 9 0.13508431465700D+01 -0.29446731313828D-08 2 10 3 9 -0.65173464590688D+00 -0.20552899130127D-07 3 10 3 9 0.39293171863021D-13 -0.15858447654387D-14 1 11 3 9 -0.30724356842664D+00 0.79043045646845D-08 2 11 3 9 0.20126935342470D+01 -0.12010997690411D-10 3 11 3 9 0.67992302545457D-15 -0.11544381297632D-15 1 12 3 9 0.66989865611690D-15 0.23286383938714D-16 2 12 3 9 0.98998923482838D-14 -0.12492435220505D-14 3 12 3 9 -0.15417212537662D-13 0.47876741439004D-07 1 13 3 9 -0.34100348313250D+01 0.13632692380396D-07 2 13 3 9 -0.31797023650156D+01 0.15699518449923D-07 3 13 3 9 -0.80226528455018D+00 -0.28878417615441D-07 1 14 3 9 -0.28011454254677D+01 -0.42123524428052D-01 2 14 3 9 -0.38203171519071D+01 -0.74341640913301D-01 3 14 3 9 0.23437487584050D+01 0.58255878771836D-01 1 15 3 9 -0.28011454254677D+01 -0.42123524428055D-01 2 15 3 9 -0.38203171519071D+01 -0.74341640913304D-01 3 15 3 9 -0.23437487584050D+01 -0.58255878771843D-01 1 16 3 9 0.34100348313250D+01 -0.13632692780217D-07 2 16 3 9 0.31797023650156D+01 -0.15699517145249D-07 3 16 3 9 -0.80226528455018D+00 -0.28878418469609D-07 1 17 3 9 -0.28887231537357D+01 0.11049317929218D+00 2 17 3 9 0.38475374507551D+01 -0.17615986978702D+00 3 17 3 9 -0.73952045000310D+00 0.94971861344591D-01 1 18 3 9 -0.24672764490829D+01 0.81474365807393D-06 2 18 3 9 0.45233035133574D+01 -0.86012076973160D-06 3 18 3 9 0.29944073876141D+01 -0.20178476504652D-06 1 19 3 9 -0.24672764490829D+01 0.81474365595426D-06 2 19 3 9 0.45233035133575D+01 -0.86012076409779D-06 3 19 3 9 -0.29944073876141D+01 0.20178475915078D-06 1 20 3 9 0.28887231537357D+01 -0.11049317929218D+00 2 20 3 9 -0.38475374507551D+01 0.17615986978702D+00 3 20 3 9 -0.73952045000309D+00 0.94971861344588D-01 1 1 1 10 -0.28523351763842D-14 -0.76920041112006D-16 2 1 1 10 -0.14396083189590D-14 0.30432064542246D-15 3 1 1 10 0.21247939582633D-01 0.46867255583688D-08 1 2 1 10 -0.34655944796501D+00 -0.11086581163014D-07 2 2 1 10 -0.47604566476397D+00 -0.16814580585693D-07 3 2 1 10 0.10423214785660D-14 -0.32498179471364D-16 1 3 1 10 0.52322647135963D-14 0.69368443056041D-15 2 3 1 10 0.20698592035674D-14 -0.23478247875564D-16 3 3 1 10 0.10381392416552D+00 0.11582382541287D-07 1 4 1 10 -0.11950148942890D+01 -0.18785261752927D-07 2 4 1 10 -0.60939674657534D+00 0.74825804567487D-08 3 4 1 10 0.75081765364939D-15 -0.13180075199547D-15 1 5 1 10 0.14348988388952D+01 0.99561513462342D+00 2 5 1 10 0.17280793635678D+00 -0.26919242379586D-01 3 5 1 10 0.18172570119106D+01 -0.44825942252233D+00 1 6 1 10 -0.14348988388953D+01 -0.99561513462343D+00 2 6 1 10 -0.17280793635679D+00 0.26919242379585D-01 3 6 1 10 0.18172570119105D+01 -0.44825942252235D+00 1 7 1 10 0.66260619793209D-01 0.19008188054164D-02 2 7 1 10 -0.10715354635020D+00 -0.14813378605735D-01 3 7 1 10 0.25055805143922D+00 -0.78027860827716D-02 1 8 1 10 -0.66260619793210D-01 -0.19008188054162D-02 2 8 1 10 0.10715354635023D+00 0.14813378605737D-01 3 8 1 10 0.25055805143922D+00 -0.78027860827718D-02 1 9 1 10 -0.18917647200250D-14 0.80526939049627D-16 2 9 1 10 -0.12126476819555D-14 -0.56333090476273D-16 3 9 1 10 0.13508528060953D+01 0.27590756138721D-08 1 10 1 10 0.89389457666607D+01 0.00000000000000D+00 2 10 1 10 0.92760426250377D+00 0.62814156001575D-07 3 10 1 10 0.13499806800156D-12 0.13877787807814D-16 1 11 1 10 -0.38706472161034D-13 0.13720780940143D-09 2 11 1 10 -0.59958950146291D+00 -0.48814815564345D-08 3 11 1 10 0.80344833860761D-15 0.13038698929407D-16 1 12 1 10 -0.13535345700593D-16 0.66311226489008D-16 2 12 1 10 0.12389266097267D-15 0.54418750452795D-17 3 12 1 10 0.30724356842664D+00 0.79043045641124D-08 1 13 1 10 0.83239145370991D-01 -0.19895659670029D-01 2 13 1 10 0.55834777400995D+00 -0.21015462511486D-01 3 13 1 10 -0.12756132421447D+01 -0.11498231829402D-01 1 14 1 10 -0.14676929248685D+01 -0.64741930427182D-09 2 14 1 10 -0.75352350756544D+00 0.12787583745433D-08 3 14 1 10 -0.13911442315853D+01 -0.79836891481860D-08 1 15 1 10 -0.14676929248685D+01 -0.64741931357428D-09 2 15 1 10 -0.75352350756543D+00 0.12787581853045D-08 3 15 1 10 0.13911442315853D+01 0.79836890390647D-08 1 16 1 10 -0.83239145370988D-01 0.19895659670029D-01 2 16 1 10 -0.55834777400994D+00 0.21015462511487D-01 3 16 1 10 -0.12756132421447D+01 -0.11498231829400D-01 1 17 1 10 0.32727469999218D-01 -0.34537179675659D-06 2 17 1 10 -0.54403671042545D+00 -0.59966148118629D-06 3 17 1 10 -0.95367064821533D+00 0.48363262433128D-07 1 18 1 10 -0.67033110219160D+00 -0.13725684560804D-01 2 18 1 10 0.83825489427701D+00 0.29613994108063D-01 3 18 1 10 -0.74448980247686D+00 0.36877640368579D-01 1 19 1 10 -0.67033110219159D+00 -0.13725684560804D-01 2 19 1 10 0.83825489427700D+00 0.29613994108063D-01 3 19 1 10 0.74448980247685D+00 -0.36877640368579D-01 1 20 1 10 -0.32727469999228D-01 0.34537179587671D-06 2 20 1 10 0.54403671042544D+00 0.59966148040423D-06 3 20 1 10 -0.95367064821532D+00 0.48363264236199D-07 1 1 2 10 -0.14385465772217D-14 0.30432064542246D-15 2 1 2 10 0.70226490399803D-15 -0.15424656650652D-15 3 1 2 10 0.87852324247809D+00 0.12183567861399D-07 1 2 2 10 0.53616008673661D-01 -0.24772079506210D-07 2 2 2 10 -0.21724496975363D+01 -0.86183619040646D-08 3 2 2 10 0.23364814344297D-13 -0.13736569185865D-15 1 3 2 10 0.20698592035674D-14 -0.23478247875564D-16 2 3 2 10 -0.17364779066401D-13 -0.26422545367606D-14 3 3 2 10 -0.86709724151600D-01 -0.41128696414103D-08 1 4 2 10 -0.46523303941547D+00 0.15398840535791D-07 2 4 2 10 -0.12368887393921D+01 -0.11244913477704D-07 3 4 2 10 -0.11890949818827D-14 0.66731582791945D-15 1 5 2 10 0.89837739456383D-01 -0.28434528067082D-01 2 5 2 10 0.26386507453034D+01 0.10039892930659D+01 3 5 2 10 -0.10070949206404D+00 0.11100268448361D+00 1 6 2 10 -0.89837739456393D-01 0.28434528067082D-01 2 6 2 10 -0.26386507453037D+01 -0.10039892930659D+01 3 6 2 10 -0.10070949206400D+00 0.11100268448362D+00 1 7 2 10 -0.20231996251956D+00 -0.74936408584502D-03 2 7 2 10 -0.31159283523968D+00 0.78900338346486D-02 3 7 2 10 0.17926419446749D+01 -0.28819059804326D-01 1 8 2 10 0.20231996251959D+00 0.74936408584661D-03 2 8 2 10 0.31159283523968D+00 -0.78900338346490D-02 3 8 2 10 0.17926419446749D+01 -0.28819059804319D-01 1 9 2 10 -0.12126476819555D-14 -0.55465728738284D-16 2 9 2 10 0.12885191711117D-14 0.25332731546102D-14 3 9 2 10 -0.65174774839858D+00 0.19994421866276D-07 1 10 2 10 0.92760345745918D+00 -0.50582856682839D-07 2 10 2 10 0.72215703335075D+01 0.00000000000000D+00 3 10 2 10 -0.22780745880051D-13 -0.69388939039073D-17 1 11 2 10 -0.59958950146291D+00 0.48814789960525D-08 2 11 2 10 -0.86138674562993D-14 -0.67106627171386D-08 3 11 2 10 -0.79080947171976D-14 0.29404122656251D-14 1 12 2 10 0.12389266097267D-15 0.54418750452795D-17 2 12 2 10 0.11637658077567D-14 -0.69698166350441D-16 3 12 2 10 0.20126935342470D+01 0.12010724492627D-10 1 13 2 10 0.30023471278907D+00 -0.41327194931016D-02 2 13 2 10 -0.21488626510935D-01 0.15164309944363D-02 3 13 2 10 -0.15292517314635D+01 -0.55659318564795D-03 1 14 2 10 -0.59663969054873D+00 -0.10325910224992D-07 2 14 2 10 0.44257123415119D+00 -0.31163250683616D-08 3 14 2 10 -0.11544331629168D+01 -0.12440779737482D-07 1 15 2 10 -0.59663969054871D+00 -0.10325910414231D-07 2 15 2 10 0.44257123415119D+00 -0.31163261562355D-08 3 15 2 10 0.11544331629168D+01 0.12440779935014D-07 1 16 2 10 -0.30023471278906D+00 0.41327194931029D-02 2 16 2 10 0.21488626510923D-01 -0.15164309944375D-02 3 16 2 10 -0.15292517314634D+01 -0.55659318564419D-03 1 17 2 10 -0.19375862305742D+00 0.33747397372003D-06 2 17 2 10 0.99984334761579D-01 -0.18695458210116D-06 3 17 2 10 0.19757613553938D+01 0.66017241219996D-06 1 18 2 10 0.98026860942441D+00 0.39454287820012D-01 2 18 2 10 -0.22537600443644D+00 -0.41867266062296D-01 3 18 2 10 0.19277728803764D+01 -0.51534844201750D-01 1 19 2 10 0.98026860942439D+00 0.39454287820012D-01 2 19 2 10 -0.22537600443645D+00 -0.41867266062295D-01 3 19 2 10 -0.19277728803764D+01 0.51534844201751D-01 1 20 2 10 0.19375862305742D+00 -0.33747397450208D-06 2 20 2 10 -0.99984334761581D-01 0.18695458585405D-06 3 20 2 10 0.19757613553938D+01 0.66017240762928D-06 1 1 3 10 0.33766389153619D+00 0.10623606788790D-08 2 1 3 10 0.26303757206776D+01 -0.18228245885590D-07 3 1 3 10 0.47360697445233D-14 -0.80575063714527D-16 1 2 3 10 0.10423214802204D-14 -0.34666583816335D-16 2 2 3 10 0.23364814344297D-13 -0.13736569185865D-15 3 2 3 10 -0.12782420581768D+01 -0.58937988398056D-07 1 3 3 10 -0.63017924966139D-01 -0.13109018004590D-07 2 3 3 10 -0.25794895146193D+00 -0.11773230071313D-07 3 3 3 10 0.30813859392647D-13 0.29281187335941D-15 1 4 3 10 0.75081765364939D-15 -0.13180075199546D-15 2 4 3 10 -0.11890949818827D-14 0.66731582791945D-15 3 4 3 10 -0.37027410533119D+01 -0.12589759289543D-06 1 5 3 10 0.43958873293660D+00 -0.38432970855453D+00 2 5 3 10 -0.11665392487622D-01 0.12240299583630D+00 3 5 3 10 0.79046526102786D+01 -0.23201542406777D+01 1 6 3 10 0.43958873293644D+00 -0.38432970855454D+00 2 6 3 10 -0.11665392487590D-01 0.12240299583630D+00 3 6 3 10 -0.79046526102783D+01 0.23201542406778D+01 1 7 3 10 -0.10833421476976D+01 0.24669330446018D-01 2 7 3 10 0.71913698842732D+01 -0.19030339771504D+00 3 7 3 10 -0.16044242939865D+00 -0.11914068240678D-01 1 8 3 10 -0.10833421476976D+01 0.24669330446018D-01 2 8 3 10 0.71913698842733D+01 -0.19030339771504D+00 3 8 3 10 0.16044242939866D+00 0.11914068240676D-01 1 9 3 10 0.13508431465700D+01 -0.29446725118588D-08 2 9 3 10 -0.65173464590688D+00 -0.20552900257145D-07 3 9 3 10 0.39293171863021D-13 0.16968670679013D-14 1 10 3 10 0.13499806800156D-12 -0.13877787807814D-16 2 10 3 10 -0.22780745886668D-13 -0.69388939039072D-17 3 10 3 10 0.45267194511340D+02 0.00000000000000D+00 1 11 3 10 0.80344833860761D-15 0.13038698929407D-16 2 11 3 10 -0.79080947171976D-14 0.29404122656251D-14 3 11 3 10 0.89818713737092D-13 0.47876737341026D-07 1 12 3 10 -0.30724356842664D+00 0.79043045641124D-08 2 12 3 10 0.20126935342470D+01 -0.12010916083642D-10 3 12 3 10 0.40810380726222D-14 -0.20489763534403D-16 1 13 3 10 -0.28011454254677D+01 -0.42123524428058D-01 2 13 3 10 -0.38203171519071D+01 -0.74341640913309D-01 3 13 3 10 0.23437487584050D+01 0.58255878771849D-01 1 14 3 10 -0.34100348313250D+01 0.13632692191175D-07 2 14 3 10 -0.31797023650157D+01 0.15699517613239D-07 3 14 3 10 -0.80226528455020D+00 -0.28878419411931D-07 1 15 3 10 0.34100348313250D+01 -0.13632692293357D-07 2 15 3 10 0.31797023650157D+01 -0.15699517413972D-07 3 15 3 10 -0.80226528455022D+00 -0.28878418581327D-07 1 16 3 10 -0.28011454254677D+01 -0.42123524428055D-01 2 16 3 10 -0.38203171519071D+01 -0.74341640913305D-01 3 16 3 10 -0.23437487584050D+01 -0.58255878771844D-01 1 17 3 10 -0.24672764490830D+01 0.81474365414444D-06 2 17 3 10 0.45233035133574D+01 -0.86012076024986D-06 3 17 3 10 0.29944073876140D+01 -0.20178475207602D-06 1 18 3 10 -0.28887231537357D+01 0.11049317929218D+00 2 18 3 10 0.38475374507552D+01 -0.17615986978702D+00 3 18 3 10 -0.73952045000310D+00 0.94971861344592D-01 1 19 3 10 0.28887231537357D+01 -0.11049317929218D+00 2 19 3 10 -0.38475374507552D+01 0.17615986978702D+00 3 19 3 10 -0.73952045000315D+00 0.94971861344592D-01 1 20 3 10 -0.24672764490830D+01 0.81474365591975D-06 2 20 3 10 0.45233035133574D+01 -0.86012076482054D-06 3 20 3 10 -0.29944073876140D+01 0.20178475747808D-06 1 1 1 11 0.64589903821403D-14 0.19258816618414D-14 2 1 1 11 -0.13259624381804D-14 -0.90962563803894D-16 3 1 1 11 -0.10381392416551D+00 -0.11582382677622D-07 1 2 1 11 0.11950148942890D+01 0.18785238670539D-07 2 2 1 11 -0.60939674657544D+00 0.74825831976890D-08 3 2 1 11 -0.15335580028914D-14 0.20480793753418D-15 1 3 1 11 0.16364465052166D-14 0.96884868636642D-16 2 3 1 11 -0.33019655841950D-14 -0.12908736386201D-15 3 3 1 11 0.21247939582636D-01 0.46867257177949D-08 1 4 1 11 -0.34655944796485D+00 -0.11086580830084D-07 2 4 1 11 0.47604566476413D+00 0.16814580756358D-07 3 4 1 11 -0.23766816617479D-14 -0.14199229438620D-15 1 5 1 11 -0.66260619793180D-01 -0.19008188054166D-02 2 5 1 11 -0.10715354635021D+00 -0.14813378605736D-01 3 5 1 11 0.25055805143925D+00 -0.78027860827716D-02 1 6 1 11 0.66260619793175D-01 0.19008188054167D-02 2 6 1 11 0.10715354635022D+00 0.14813378605736D-01 3 6 1 11 0.25055805143924D+00 -0.78027860827719D-02 1 7 1 11 0.14348988388952D+01 0.99561513462342D+00 2 7 1 11 -0.17280793635668D+00 0.26919242379586D-01 3 7 1 11 -0.18172570119106D+01 0.44825942252233D+00 1 8 1 11 -0.14348988388953D+01 -0.99561513462343D+00 2 8 1 11 0.17280793635670D+00 -0.26919242379585D-01 3 8 1 11 -0.18172570119104D+01 0.44825942252235D+00 1 9 1 11 -0.63796738050855D-17 -0.26377051512936D-16 2 9 1 11 0.62232594786795D-15 -0.70830019403546D-17 3 9 1 11 -0.30724356842664D+00 -0.79043045646845D-08 1 10 1 11 -0.38706472161034D-13 -0.13720780940143D-09 2 10 1 11 -0.59958950146291D+00 -0.48814789960525D-08 3 10 1 11 0.80344833860761D-15 -0.13038698929407D-16 1 11 1 11 0.89389457666607D+01 0.00000000000000D+00 2 11 1 11 -0.92760426250369D+00 -0.62814156001575D-07 3 11 1 11 -0.12790274422967D-12 0.13877787807814D-16 1 12 1 11 0.39461882718425D-14 0.81979653632243D-16 2 12 1 11 -0.17105996173488D-15 -0.38817040588757D-16 3 12 1 11 0.13508528060953D+01 0.27590749573086D-08 1 13 1 11 0.32727469999186D-01 -0.34537179697229D-06 2 13 1 11 0.54403671042547D+00 0.59966148145246D-06 3 13 1 11 0.95367064821537D+00 -0.48363262323459D-07 1 14 1 11 0.67033110219158D+00 0.13725684560803D-01 2 14 1 11 0.83825489427701D+00 0.29613994108061D-01 3 14 1 11 -0.74448980247683D+00 0.36877640368581D-01 1 15 1 11 0.67033110219157D+00 0.13725684560803D-01 2 15 1 11 0.83825489427701D+00 0.29613994108060D-01 3 15 1 11 0.74448980247684D+00 -0.36877640368581D-01 1 16 1 11 -0.32727469999204D-01 0.34537179644653D-06 2 16 1 11 -0.54403671042545D+00 -0.59966148022534D-06 3 16 1 11 0.95367064821538D+00 -0.48363264297997D-07 1 17 1 11 -0.83239145370989D-01 0.19895659670028D-01 2 17 1 11 0.55834777400995D+00 -0.21015462511487D-01 3 17 1 11 -0.12756132421446D+01 -0.11498231829399D-01 1 18 1 11 -0.14676929248685D+01 -0.64741929004986D-09 2 18 1 11 0.75352350756542D+00 -0.12787583812130D-08 3 18 1 11 0.13911442315853D+01 0.79836891017999D-08 1 19 1 11 -0.14676929248685D+01 -0.64741942190583D-09 2 19 1 11 0.75352350756541D+00 -0.12787581185708D-08 3 19 1 11 -0.13911442315853D+01 -0.79836889955511D-08 1 20 1 11 0.83239145370987D-01 -0.19895659670029D-01 2 20 1 11 -0.55834777400993D+00 0.21015462511489D-01 3 20 1 11 -0.12756132421446D+01 -0.11498231829397D-01 1 1 2 11 -0.13259624379736D-14 -0.90962563803894D-16 2 1 2 11 -0.15658494438417D-14 -0.43004396343367D-14 3 1 2 11 -0.86709724151753D-01 -0.41128706196451D-08 1 2 2 11 -0.46523303941556D+00 0.15398843276732D-07 2 2 2 11 0.12368887393921D+01 0.11244919877852D-07 3 2 2 11 0.81120952228998D-14 0.13703891844895D-14 1 3 2 11 -0.33009038430781D-14 -0.12908736386201D-15 2 3 2 11 -0.67624358188686D-15 0.57609950110114D-16 3 3 2 11 -0.87852324247811D+00 -0.12183569312868D-07 1 4 2 11 -0.53616008673504D-01 0.24772079676875D-07 2 4 2 11 -0.21724496975368D+01 -0.86183644057267D-08 3 4 2 11 0.31916482173574D-14 0.59358477815908D-14 1 5 2 11 -0.20231996251957D+00 -0.74936408584601D-03 2 5 2 11 0.31159283523964D+00 -0.78900338346490D-02 3 5 2 11 -0.17926419446748D+01 0.28819059804321D-01 1 6 2 11 0.20231996251958D+00 0.74936408584640D-03 2 6 2 11 -0.31159283523963D+00 0.78900338346494D-02 3 6 2 11 -0.17926419446749D+01 0.28819059804323D-01 1 7 2 11 -0.89837739456284D-01 0.28434528067083D-01 2 7 2 11 0.26386507453034D+01 0.10039892930659D+01 3 7 2 11 -0.10070949206468D+00 0.11100268448362D+00 1 8 2 11 0.89837739456300D-01 -0.28434528067082D-01 2 8 2 11 -0.26386507453037D+01 -0.10039892930659D+01 3 8 2 11 -0.10070949206463D+00 0.11100268448362D+00 1 9 2 11 0.62232594786795D-15 -0.70830019403545D-17 2 9 2 11 -0.94844534218409D-15 -0.67223848181586D-16 3 9 2 11 0.20126935342470D+01 0.12010997690411D-10 1 10 2 11 -0.59958950146291D+00 0.48814815564345D-08 2 10 2 11 -0.86138674562993D-14 0.67106627171386D-08 3 10 2 11 -0.79080947171976D-14 -0.29404122656251D-14 1 11 2 11 -0.92760345745911D+00 0.50582856682839D-07 2 11 2 11 0.72215703335078D+01 0.00000000000000D+00 3 11 2 11 -0.44097027959468D-13 0.69388939039073D-17 1 12 2 11 -0.17105996173488D-15 -0.38817040588757D-16 2 12 2 11 0.19659537411577D-13 -0.24214929886824D-14 3 12 2 11 0.65174774839862D+00 -0.19994422282308D-07 1 13 2 11 0.19375862305744D+00 -0.33747397344865D-06 2 13 2 11 0.99984334761523D-01 -0.18695458406710D-06 3 13 2 11 0.19757613553939D+01 0.66017241155944D-06 1 14 2 11 0.98026860942441D+00 0.39454287820010D-01 2 14 2 11 0.22537600443647D+00 0.41867266062295D-01 3 14 2 11 -0.19277728803764D+01 0.51534844201754D-01 1 15 2 11 0.98026860942440D+00 0.39454287820010D-01 2 15 2 11 0.22537600443648D+00 0.41867266062297D-01 3 15 2 11 0.19277728803764D+01 -0.51534844201752D-01 1 16 2 11 -0.19375862305742D+00 0.33747397468445D-06 2 16 2 11 -0.99984334761522D-01 0.18695458605793D-06 3 16 2 11 0.19757613553938D+01 0.66017240747954D-06 1 17 2 11 0.30023471278907D+00 -0.41327194931027D-02 2 17 2 11 0.21488626510905D-01 -0.15164309944360D-02 3 17 2 11 0.15292517314635D+01 0.55659318564343D-03 1 18 2 11 0.59663969054871D+00 0.10325910218323D-07 2 18 2 11 0.44257123415129D+00 -0.31163259901642D-08 3 18 2 11 -0.11544331629168D+01 -0.12440779367531D-07 1 19 2 11 0.59663969054869D+00 0.10325910480965D-07 2 19 2 11 0.44257123415125D+00 -0.31163240445749D-08 3 19 2 11 0.11544331629168D+01 0.12440779788992D-07 1 20 2 11 -0.30023471278905D+00 0.41327194931042D-02 2 20 2 11 -0.21488626510868D-01 0.15164309944365D-02 3 20 2 11 0.15292517314634D+01 0.55659318564023D-03 1 1 3 11 0.63017924966148D-01 0.13109017868255D-07 2 1 3 11 -0.25794895146209D+00 -0.11773231049548D-07 3 1 3 11 0.15119053361585D-13 0.62676994131194D-15 1 2 3 11 -0.15335580028914D-14 0.20480793753418D-15 2 2 3 11 0.81120952228998D-14 0.13703891844895D-14 3 2 3 11 0.37027410533120D+01 0.12589760590738D-06 1 3 3 11 0.33766389153619D+00 0.10623608383051D-08 2 3 3 11 -0.26303757206776D+01 0.18228244434121D-07 3 3 3 11 -0.34207389922651D-14 -0.34346855293386D-15 1 4 3 11 -0.23766816600936D-14 -0.14416069873118D-15 2 4 3 11 0.31916482173574D-14 0.59358477815908D-14 3 4 3 11 -0.12782420581763D+01 -0.58937989639703D-07 1 5 3 11 -0.10833421476976D+01 0.24669330446018D-01 2 5 3 11 -0.71913698842732D+01 0.19030339771504D+00 3 5 3 11 0.16044242939860D+00 0.11914068240677D-01 1 6 3 11 -0.10833421476976D+01 0.24669330446018D-01 2 6 3 11 -0.71913698842732D+01 0.19030339771504D+00 3 6 3 11 -0.16044242939859D+00 -0.11914068240678D-01 1 7 3 11 -0.43958873293661D+00 0.38432970855453D+00 2 7 3 11 -0.11665392488275D-01 0.12240299583630D+00 3 7 3 11 0.79046526102786D+01 -0.23201542406777D+01 1 8 3 11 -0.43958873293640D+00 0.38432970855454D+00 2 8 3 11 -0.11665392488219D-01 0.12240299583630D+00 3 8 3 11 -0.79046526102779D+01 0.23201542406778D+01 1 9 3 11 0.30724356842664D+00 -0.79043045646845D-08 2 9 3 11 0.20126935342470D+01 -0.12010642885858D-10 3 9 3 11 0.67992302545457D-15 0.11544381297632D-15 1 10 3 11 0.80344833860761D-15 -0.13038698929407D-16 2 10 3 11 -0.79080947171976D-14 -0.29404122656251D-14 3 10 3 11 0.89818713737092D-13 -0.47876737341026D-07 1 11 3 11 -0.12790274422967D-12 -0.13877787807814D-16 2 11 3 11 -0.44097027952851D-13 0.69388939039073D-17 3 11 3 11 0.45267194511341D+02 0.00000000000000D+00 1 12 3 11 0.13508431465700D+01 -0.29446731684235D-08 2 12 3 11 0.65173464590692D+00 0.20552899841111D-07 3 12 3 11 -0.97980595884241D-14 -0.32451930675943D-14 1 13 3 11 0.24672764490830D+01 -0.81474365400701D-06 2 13 3 11 0.45233035133575D+01 -0.86012076085915D-06 3 13 3 11 0.29944073876142D+01 -0.20178475163281D-06 1 14 3 11 -0.28887231537357D+01 0.11049317929218D+00 2 14 3 11 -0.38475374507552D+01 0.17615986978702D+00 3 14 3 11 0.73952045000310D+00 -0.94971861344593D-01 1 15 3 11 0.28887231537357D+01 -0.11049317929218D+00 2 15 3 11 0.38475374507552D+01 -0.17615986978702D+00 3 15 3 11 0.73952045000316D+00 -0.94971861344591D-01 1 16 3 11 0.24672764490830D+01 -0.81474365600931D-06 2 16 3 11 0.45233035133574D+01 -0.86012076497028D-06 3 16 3 11 -0.29944073876142D+01 0.20178475928392D-06 1 17 3 11 -0.28011454254677D+01 -0.42123524428055D-01 2 17 3 11 0.38203171519071D+01 0.74341640913304D-01 3 17 3 11 -0.23437487584049D+01 -0.58255878771844D-01 1 18 3 11 0.34100348313251D+01 -0.13632692230622D-07 2 18 3 11 -0.31797023650156D+01 0.15699517981455D-07 3 18 3 11 -0.80226528455018D+00 -0.28878418698190D-07 1 19 3 11 -0.34100348313250D+01 0.13632692343810D-07 2 19 3 11 0.31797023650156D+01 -0.15699517561729D-07 3 19 3 11 -0.80226528455022D+00 -0.28878418074680D-07 1 20 3 11 -0.28011454254677D+01 -0.42123524428052D-01 2 20 3 11 0.38203171519071D+01 0.74341640913301D-01 3 20 3 11 0.23437487584049D+01 0.58255878771840D-01 1 1 1 12 0.11950148942892D+01 0.18785284889324D-07 2 1 1 12 -0.60939674657526D+00 0.74825776906182D-08 3 1 1 12 0.10064345225366D-14 -0.98794097085265D-16 1 2 1 12 0.70985113073084D-14 -0.15579476266956D-14 2 2 1 12 0.11494264874139D-14 -0.96409830206399D-16 3 2 1 12 -0.10381392416551D+00 -0.11582383295871D-07 1 3 1 12 -0.34655944796498D+00 -0.11086583299824D-07 2 3 1 12 0.47604566476400D+00 0.16814582569228D-07 3 3 1 12 -0.42986351798784D-15 0.54906030274831D-16 1 4 1 12 0.20126327357192D-14 -0.59933812700298D-16 2 4 1 12 -0.17579841704114D-14 0.96679726316260D-16 3 4 1 12 0.21247939582642D-01 0.46867259083654D-08 1 5 1 12 0.66260619793231D-01 0.19008188054178D-02 2 5 1 12 0.10715354635022D+00 0.14813378605736D-01 3 5 1 12 -0.25055805143922D+00 0.78027860827726D-02 1 6 1 12 0.66260619793234D-01 0.19008188054179D-02 2 6 1 12 0.10715354635022D+00 0.14813378605736D-01 3 6 1 12 0.25055805143922D+00 -0.78027860827727D-02 1 7 1 12 0.14348988388953D+01 0.99561513462342D+00 2 7 1 12 -0.17280793635683D+00 0.26919242379586D-01 3 7 1 12 -0.18172570119104D+01 0.44825942252233D+00 1 8 1 12 0.14348988388953D+01 0.99561513462342D+00 2 8 1 12 -0.17280793635684D+00 0.26919242379586D-01 3 8 1 12 0.18172570119105D+01 -0.44825942252233D+00 1 9 1 12 0.15694139197542D-14 -0.13720629640961D-09 2 9 1 12 -0.59958950146296D+00 -0.48814815471560D-08 3 9 1 12 0.66989865611690D-15 -0.23286383938714D-16 1 10 1 12 -0.13535345700593D-16 -0.66311226489008D-16 2 10 1 12 0.12389266097267D-15 -0.54418750452796D-17 3 10 1 12 -0.30724356842664D+00 -0.79043045641124D-08 1 11 1 12 0.39461882718425D-14 -0.54224078016614D-16 2 11 1 12 -0.17105996163148D-15 0.37949678850769D-16 3 11 1 12 0.13508528060953D+01 0.27590756509128D-08 1 12 1 12 0.89389457666612D+01 0.00000000000000D+00 2 12 1 12 -0.92760426250373D+00 -0.62814156001575D-07 3 12 1 12 -0.50517928555009D-17 0.13877787807815D-16 1 13 1 12 0.67033110219161D+00 0.13725684560805D-01 2 13 1 12 0.83825489427701D+00 0.29613994108065D-01 3 13 1 12 -0.74448980247686D+00 0.36877640368576D-01 1 14 1 12 0.32727469999204D-01 -0.34537179493932D-06 2 14 1 12 0.54403671042544D+00 0.59966147936552D-06 3 14 1 12 0.95367064821533D+00 -0.48363266296809D-07 1 15 1 12 -0.32727469999204D-01 0.34537179598314D-06 2 15 1 12 -0.54403671042545D+00 -0.59966148065271D-06 3 15 1 12 0.95367064821533D+00 -0.48363264339982D-07 1 16 1 12 0.67033110219161D+00 0.13725684560805D-01 2 16 1 12 0.83825489427702D+00 0.29613994108065D-01 3 16 1 12 0.74448980247686D+00 -0.36877640368575D-01 1 17 1 12 -0.14676929248685D+01 -0.64741989091708D-09 2 17 1 12 0.75352350756542D+00 -0.12787583644282D-08 3 17 1 12 0.13911442315853D+01 0.79836890157912D-08 1 18 1 12 -0.83239145370984D-01 0.19895659670028D-01 2 18 1 12 0.55834777400994D+00 -0.21015462511488D-01 3 18 1 12 -0.12756132421447D+01 -0.11498231829399D-01 1 19 1 12 0.83239145370986D-01 -0.19895659670029D-01 2 19 1 12 -0.55834777400994D+00 0.21015462511486D-01 3 19 1 12 -0.12756132421446D+01 -0.11498231829403D-01 1 20 1 12 -0.14676929248685D+01 -0.64741947241077D-09 2 20 1 12 0.75352350756542D+00 -0.12787583257065D-08 3 20 1 12 -0.13911442315853D+01 -0.79836889193146D-08 1 1 2 12 -0.46523303941539D+00 0.15398837769661D-07 2 1 2 12 0.12368887393920D+01 0.11244907752492D-07 3 1 2 12 0.38476324321452D-15 -0.52893186208015D-16 1 2 2 12 0.11494264876207D-14 -0.96409830206399D-16 2 2 2 12 -0.41532836700164D-14 0.74256017354325D-14 3 2 2 12 -0.86709724151587D-01 -0.41128712692572D-08 1 3 2 12 -0.53616008673632D-01 0.24772081489745D-07 2 3 2 12 -0.21724496975364D+01 -0.86183542400267D-08 3 3 2 12 -0.28587241037126D-14 -0.42195733223013D-14 1 4 2 12 -0.17569224290876D-14 0.96679726316260D-16 2 4 2 12 -0.14684742672215D-14 -0.23122495208358D-16 3 4 2 12 -0.87852324247811D+00 -0.12183569273537D-07 1 5 2 12 0.20231996251958D+00 0.74936408584597D-03 2 5 2 12 -0.31159283523971D+00 0.78900338346508D-02 3 5 2 12 0.17926419446749D+01 -0.28819059804324D-01 1 6 2 12 0.20231996251958D+00 0.74936408584580D-03 2 6 2 12 -0.31159283523972D+00 0.78900338346512D-02 3 6 2 12 -0.17926419446749D+01 0.28819059804325D-01 1 7 2 12 -0.89837739456436D-01 0.28434528067083D-01 2 7 2 12 0.26386507453037D+01 0.10039892930659D+01 3 7 2 12 -0.10070949206370D+00 0.11100268448362D+00 1 8 2 12 -0.89837739456437D-01 0.28434528067083D-01 2 8 2 12 0.26386507453037D+01 0.10039892930659D+01 3 8 2 12 0.10070949206370D+00 -0.11100268448362D+00 1 9 2 12 -0.59958950146296D+00 0.48814790053310D-08 2 9 2 12 0.27230410807053D-14 0.67106664689754D-08 3 9 2 12 0.98998923482838D-14 0.12492435220505D-14 1 10 2 12 0.12389266097267D-15 -0.54418750452795D-17 2 10 2 12 0.11637658077567D-14 0.69698166350441D-16 3 10 2 12 0.20126935342470D+01 0.12010916083642D-10 1 11 2 12 -0.17105996173488D-15 0.37949678850769D-16 2 11 2 12 0.19659537411577D-13 0.24492485642981D-14 3 11 2 12 0.65174774839862D+00 -0.19994422577261D-07 1 12 2 12 -0.92760345745915D+00 0.50582856682839D-07 2 12 2 12 0.72215703335073D+01 0.00000000000000D+00 3 12 2 12 -0.22780745886665D-13 0.69388939039072D-17 1 13 2 12 0.98026860942441D+00 0.39454287820014D-01 2 13 2 12 0.22537600443644D+00 0.41867266062297D-01 3 13 2 12 -0.19277728803763D+01 0.51534844201745D-01 1 14 2 12 0.19375862305742D+00 -0.33747397553559D-06 2 14 2 12 0.99984334761555D-01 -0.18695458689278D-06 3 14 2 12 0.19757613553938D+01 0.66017240244816D-06 1 15 2 12 -0.19375862305742D+00 0.33747397425708D-06 2 15 2 12 -0.99984334761572D-01 0.18695458672464D-06 3 15 2 12 0.19757613553939D+01 0.66017240822943D-06 1 16 2 12 0.98026860942441D+00 0.39454287820014D-01 2 16 2 12 0.22537600443644D+00 0.41867266062296D-01 3 16 2 12 0.19277728803764D+01 -0.51534844201745D-01 1 17 2 12 0.59663969054871D+00 0.10325910235107D-07 2 17 2 12 0.44257123415124D+00 -0.31163249491945D-08 3 17 2 12 -0.11544331629168D+01 -0.12440779687185D-07 1 18 2 12 0.30023471278905D+00 -0.41327194931031D-02 2 18 2 12 0.21488626510934D-01 -0.15164309944359D-02 3 18 2 12 0.15292517314634D+01 0.55659318564473D-03 1 19 2 12 -0.30023471278906D+00 0.41327194931015D-02 2 19 2 12 -0.21488626510914D-01 0.15164309944376D-02 3 19 2 12 0.15292517314634D+01 0.55659318564765D-03 1 20 2 12 0.59663969054871D+00 0.10325910273829D-07 2 20 2 12 0.44257123415120D+00 -0.31163246015733D-08 3 20 2 12 0.11544331629168D+01 0.12440779842372D-07 1 1 3 12 0.10064345225366D-14 -0.98794097085266D-16 2 1 3 12 0.38476324321452D-15 -0.52893186208015D-16 3 1 3 12 0.37027410533118D+01 0.12589757952881D-06 1 2 3 12 0.63017924966153D-01 0.13109017250006D-07 2 2 3 12 -0.25794895146192D+00 -0.11773231699160D-07 3 2 3 12 -0.79974437964016D-14 -0.62639722887399D-15 1 3 3 12 -0.42986351633347D-15 0.52737625929860D-16 2 3 3 12 -0.28587241037126D-14 -0.42195733223013D-14 3 3 3 12 -0.12782420581767D+01 -0.58937992442389D-07 1 4 3 12 0.33766389153620D+00 0.10623610288756D-08 2 4 3 12 -0.26303757206776D+01 0.18228244473452D-07 3 4 3 12 -0.79172190961627D-14 -0.17075117947562D-15 1 5 3 12 0.10833421476976D+01 -0.24669330446017D-01 2 5 3 12 0.71913698842732D+01 -0.19030339771504D+00 3 5 3 12 -0.16044242939865D+00 -0.11914068240677D-01 1 6 3 12 -0.10833421476976D+01 0.24669330446017D-01 2 6 3 12 -0.71913698842732D+01 0.19030339771504D+00 3 6 3 12 -0.16044242939867D+00 -0.11914068240676D-01 1 7 3 12 -0.43958873293641D+00 0.38432970855453D+00 2 7 3 12 -0.11665392487291D-01 0.12240299583630D+00 3 7 3 12 0.79046526102783D+01 -0.23201542406777D+01 1 8 3 12 0.43958873293641D+00 -0.38432970855453D+00 2 8 3 12 0.11665392487288D-01 -0.12240299583630D+00 3 8 3 12 0.79046526102783D+01 -0.23201542406777D+01 1 9 3 12 0.66989865611690D-15 -0.23286383938714D-16 2 9 3 12 0.98998923482838D-14 0.12492435220505D-14 3 9 3 12 -0.15417212537662D-13 -0.47876741439004D-07 1 10 3 12 0.30724356842664D+00 -0.79043045641124D-08 2 10 3 12 0.20126935342470D+01 -0.12010724492627D-10 3 10 3 12 0.40810380726222D-14 0.20489763534403D-16 1 11 3 12 0.13508431465700D+01 -0.29446724748193D-08 2 11 3 12 0.65173464590692D+00 0.20552899546159D-07 3 11 3 12 -0.97980595884241D-14 0.33562153700568D-14 1 12 3 12 -0.50517928554994D-17 -0.13877787807815D-16 2 12 3 12 -0.22780745880048D-13 0.69388939039073D-17 3 12 3 12 0.45267194511341D+02 0.00000000000000D+00 1 13 3 12 -0.28887231537357D+01 0.11049317929217D+00 2 13 3 12 -0.38475374507552D+01 0.17615986978701D+00 3 13 3 12 0.73952045000310D+00 -0.94971861344589D-01 1 14 3 12 0.24672764490830D+01 -0.81474365799424D-06 2 14 3 12 0.45233035133574D+01 -0.86012076999819D-06 3 14 3 12 0.29944073876141D+01 -0.20178476411696D-06 1 15 3 12 0.24672764490830D+01 -0.81474365603047D-06 2 15 3 12 0.45233035133575D+01 -0.86012076419263D-06 3 15 3 12 -0.29944073876141D+01 0.20178475799596D-06 1 16 3 12 0.28887231537357D+01 -0.11049317929217D+00 2 16 3 12 0.38475374507552D+01 -0.17615986978702D+00 3 16 3 12 0.73952045000311D+00 -0.94971861344589D-01 1 17 3 12 0.34100348313250D+01 -0.13632692316631D-07 2 17 3 12 -0.31797023650157D+01 0.15699517661801D-07 3 17 3 12 -0.80226528455020D+00 -0.28878418651262D-07 1 18 3 12 -0.28011454254677D+01 -0.42123524428055D-01 2 18 3 12 0.38203171519071D+01 0.74341640913306D-01 3 18 3 12 -0.23437487584050D+01 -0.58255878771844D-01 1 19 3 12 -0.28011454254677D+01 -0.42123524428058D-01 2 19 3 12 0.38203171519071D+01 0.74341640913309D-01 3 19 3 12 0.23437487584050D+01 0.58255878771848D-01 1 20 3 12 -0.34100348313250D+01 0.13632692420046D-07 2 20 3 12 0.31797023650157D+01 -0.15699517508349D-07 3 20 3 12 -0.80226528455021D+00 -0.28878417445769D-07 1 1 1 13 -0.18060885107789D+00 0.11778815498407D-06 2 1 1 13 -0.72301354005635D+00 -0.72587142141249D-07 3 1 1 13 -0.14815028338488D+00 -0.18314629844646D-07 1 2 1 13 0.34159599944584D-01 0.10186584683517D-01 2 2 1 13 -0.50608893451166D+00 0.25217175319866D-02 3 2 1 13 0.12198240512232D+00 -0.15071331504371D-02 1 3 1 13 -0.43486473279454D+00 0.15350506746488D-01 2 3 1 13 -0.16761329463301D-01 -0.31249629992596D-01 3 3 1 13 0.11152602876191D+01 0.62582020916283D-02 1 4 1 13 0.92518036334154D-02 0.30638199655596D-07 2 4 1 13 0.80259503795466D+00 -0.99245321699271D-07 3 4 1 13 -0.35195673198029D+00 -0.59913875928694D-07 1 5 1 13 -0.13845699646769D+01 -0.72384269306941D-02 2 5 1 13 -0.26678717282475D+01 0.10447588286235D-01 3 5 1 13 -0.44483828644679D+00 0.39228738516759D-01 1 6 1 13 -0.53668345860631D+00 -0.28185231299411D-01 2 6 1 13 0.25621508332100D+00 -0.25622006102618D-01 3 6 1 13 0.30154452868180D+01 0.61764351561429D-02 1 7 1 13 0.10161148680499D+00 -0.12921154873962D-01 2 7 1 13 -0.13720704530733D+01 -0.93931795399651D-02 3 7 1 13 0.21687698938736D+00 -0.45240790056755D-01 1 8 1 13 -0.42653643115826D+00 -0.40732564614947D-01 2 8 1 13 -0.10237005265681D+00 -0.80797304429651D-01 3 8 1 13 -0.27364772025514D+01 -0.35599509164354D-02 1 9 1 13 -0.14676938359579D+01 0.53627212790624D-06 2 9 1 13 -0.59663993014509D+00 -0.69414797576984D-06 3 9 1 13 -0.34100493917735D+01 -0.13728680027413D-05 1 10 1 13 0.83238608982227D-01 0.59687000398189D-01 2 10 1 13 0.30023390271234D+00 0.12398159382866D-01 3 10 1 13 -0.28011525411382D+01 0.12637057955213D+00 1 11 1 13 0.32727469999186D-01 0.34537179747189D-06 2 11 1 13 0.19375862305744D+00 0.33747397297334D-06 3 11 1 13 0.24672764490830D+01 0.81474365324373D-06 1 12 1 13 0.67033110219161D+00 -0.13725684560806D-01 2 12 1 13 0.98026860942441D+00 -0.39454287820015D-01 3 12 1 13 -0.28887231537357D+01 -0.11049317929217D+00 1 13 1 13 0.13149817390300D+02 0.00000000000000D+00 2 13 1 13 0.69426528609109D+01 0.20550907331479D+00 3 13 1 13 -0.12192480104861D+01 -0.15981767360659D+00 1 14 1 13 0.97974114254989D+00 -0.18266885601904D-02 2 14 1 13 -0.22712929095630D+00 -0.26549202704897D-02 3 14 1 13 -0.78365840750489D+00 -0.13606025531406D-01 1 15 1 13 0.11978246338924D-14 0.30219137692492D-01 2 15 1 13 -0.80071830988698D-01 -0.38348271525882D-02 3 15 1 13 -0.66023830363373D+00 0.20917464521660D-01 1 16 1 13 0.16224381971234D+00 -0.24836270070312D-15 2 16 1 13 -0.35636845037218D-01 0.12544612862741D-08 3 16 1 13 0.40741232101580D-01 0.12643178915269D-06 1 17 1 13 -0.16935223534622D-14 0.65408225279596D-02 2 17 1 13 -0.92274773342067D+00 -0.50983329631380D-02 3 17 1 13 -0.30400543782107D+00 0.27279424757350D-01 1 18 1 13 0.60682061506544D+01 -0.14024934078309D-13 2 18 1 13 -0.18812291655311D+01 0.76904784201163D-07 3 18 1 13 0.29234546368569D-02 0.83167620883891D-07 1 19 1 13 -0.27779041561395D-14 -0.14248825411419D-01 2 19 1 13 -0.31440136644699D-01 0.33867480518988D-01 3 19 1 13 0.43612370464150D-01 -0.24830039566379D-02 1 20 1 13 0.19603351542170D-14 -0.49131390844874D-07 2 20 1 13 -0.43399967089214D-01 0.36377534542912D-02 3 20 1 13 -0.34013761498442D+00 -0.29127273390724D-02 1 1 2 13 -0.31573643564814D+00 -0.78755441598462D-07 2 1 2 13 -0.13059176915072D+01 -0.55909801769548D-06 3 1 2 13 -0.12016467324020D+01 -0.66071606544603D-06 1 2 2 13 -0.29645719455466D+00 0.10397496925165D-01 2 2 2 13 -0.42669990022297D+00 0.40911720073868D-02 3 2 2 13 0.14104596669027D+01 0.24786916402170D-03 1 3 2 13 0.34479890278870D+00 -0.54361281411069D-02 2 3 2 13 -0.17851870533803D+01 -0.22602251736466D-02 3 3 2 13 0.13647920929405D+00 0.13824023979019D-01 1 4 2 13 0.30490190754153D+00 -0.68056515857598D-07 2 4 2 13 0.10669534109937D+01 -0.20708554993139D-06 3 4 2 13 0.13109063117039D+01 0.47398380955818D-07 1 5 2 13 0.47626649773436D+00 -0.15005135265684D-01 2 5 2 13 -0.50877729273305D+01 0.39091583880358D-02 3 5 2 13 -0.48293397746189D+00 0.50088873825505D-01 1 6 2 13 -0.44045047321920D+00 -0.31562444327087D-01 2 6 2 13 -0.45311663921885D-01 -0.16202328843040D-01 3 6 2 13 0.39939332590607D+01 0.54859697995852D-02 1 7 2 13 0.68146394044034D+00 -0.19992458410008D-01 2 7 2 13 -0.52675461638689D+01 -0.14939669842359D-01 3 7 2 13 0.61828817619142D+00 -0.66510466617488D-01 1 8 2 13 -0.57101763754834D+00 -0.86049775603675D-01 2 8 2 13 -0.39314070199047D+00 -0.10539739545061D+00 3 8 2 13 -0.46274463292544D+01 -0.12250041505251D-01 1 9 2 13 -0.75352302634896D+00 0.25526941976658D-06 2 9 2 13 0.44257479394549D+00 -0.31536862000972D-06 3 9 2 13 -0.31797146926205D+01 -0.81543201320499D-06 1 10 2 13 0.55834732066972D+00 0.63046389702132D-01 2 10 2 13 -0.21488779706603D-01 -0.45492857508528D-02 3 10 2 13 -0.38203216284890D+01 0.22302494991981D+00 1 11 2 13 0.54403671042547D+00 -0.59966148191043D-06 2 11 2 13 0.99984334761523D-01 0.18695458468813D-06 3 11 2 13 0.45233035133575D+01 0.86012075788931D-06 1 12 2 13 0.83825489427701D+00 -0.29613994108066D-01 2 12 2 13 0.22537600443644D+00 -0.41867266062297D-01 3 12 2 13 -0.38475374507552D+01 -0.17615986978701D+00 1 13 2 13 0.69426571478982D+01 -0.20550963496243D+00 2 13 2 13 0.16540543133682D+02 0.00000000000000D+00 3 13 2 13 0.20506088072319D+01 0.20032682093087D+00 1 14 2 13 -0.22712898881450D+00 -0.26542770768413D-02 2 14 2 13 -0.63003020552730D+00 -0.72209940761316D-03 3 14 2 13 -0.10849401454823D+01 -0.12216080443963D-01 1 15 2 13 0.80071830988700D-01 -0.38348271525882D-02 2 15 2 13 -0.40712558647147D-15 -0.21789018231944D-01 3 15 2 13 -0.14699393025031D+01 0.30327434888119D-01 1 16 2 13 -0.35636845037218D-01 -0.12544613583682D-08 2 16 2 13 0.28873768072398D+00 -0.12095121251624D-14 3 16 2 13 -0.19324351108276D+00 -0.45017726289680D-07 1 17 2 13 -0.92274773342066D+00 0.50983329631423D-02 2 17 2 13 0.28338515165622D-13 -0.18910615735654D-01 3 17 2 13 -0.30061611266247D-01 0.74174299812190D-01 1 18 2 13 0.18812291655311D+01 0.76904784445542D-07 2 18 2 13 -0.30894398169472D+01 0.47286817484766D-14 3 18 2 13 0.34828097813268D+00 -0.37678409729239D-06 1 19 2 13 -0.31440993033376D-01 -0.33867627316431D-01 2 19 2 13 -0.39859085097935D-14 0.17281658324453D-01 3 19 2 13 0.18729564246326D+00 -0.87260515821044D-02 1 20 2 13 -0.43400177186253D-01 0.36381076052581D-02 2 20 2 13 0.89686045629277D-14 -0.25620558039252D-06 3 20 2 13 -0.11204977375783D+01 0.92699308904841D-02 1 1 3 13 0.52399840543396D+00 0.94125318968557D-06 2 1 3 13 -0.79397099005575D+00 0.22384955690698D-06 3 1 3 13 -0.31623867245851D+00 -0.84332937636896D-06 1 2 3 13 -0.32589235607619D+00 -0.53961947241596D-03 2 2 3 13 0.98454495694056D+00 0.63353830294865D-02 3 2 3 13 0.45332216840792D+00 0.33781122828638D-02 1 3 3 13 0.56626506089943D+00 0.48887486834200D-02 2 3 3 13 -0.40625835904004D+00 -0.84648125232138D-02 3 3 3 13 -0.24683163743508D+01 -0.24138185634086D-01 1 4 3 13 -0.81823224224843D+00 -0.30844531107131D-06 2 4 3 13 0.92567424803798D+00 0.81584878502837D-07 3 4 3 13 -0.40516331287107D+00 -0.30872768920502D-06 1 5 3 13 0.65729793861610D+00 0.56729719069150D-01 2 5 3 13 0.43995953810398D+00 0.21412943871371D-01 3 5 3 13 -0.47413359179875D+01 -0.29166180687229D-01 1 6 3 13 0.43515068697146D+00 0.16001986766970D-01 2 6 3 13 0.12163822420998D+01 0.57385749439763D-02 3 6 3 13 0.29639836161845D+00 0.16795988062123D-01 1 7 3 13 -0.89708384060989D+00 -0.45108112857918D-01 2 7 3 13 -0.37668213502734D+00 -0.52669567900920D-01 3 7 3 13 -0.40120124420439D+01 -0.33325999191658D-01 1 8 3 13 -0.31176128987343D+00 -0.24129534220527D-01 2 8 3 13 -0.18790884315294D+01 -0.37556306773517D-01 3 8 3 13 -0.16731051450895D+00 0.76010268556754D-01 1 9 3 13 -0.13911435770838D+01 0.59213082741108D-06 2 9 3 13 -0.11544339529138D+01 0.11863208086167D-05 3 9 3 13 -0.80225609774917D+00 0.66510954070663D-06 1 10 3 13 -0.12756130326614D+01 0.34494705371224D-01 2 10 3 13 -0.15292499234972D+01 0.16697700502267D-02 3 10 3 13 0.23437484698202D+01 -0.17476761537554D+00 1 11 3 13 0.95367064821537D+00 0.48363261469975D-07 2 11 3 13 0.19757613553939D+01 -0.66017241468888D-06 3 11 3 13 0.29944073876142D+01 0.20178474963441D-06 1 12 3 13 -0.74448980247686D+00 -0.36877640368574D-01 2 12 3 13 -0.19277728803763D+01 -0.51534844201742D-01 3 12 3 13 0.73952045000310D+00 0.94971861344589D-01 1 13 3 13 -0.12192282832178D+01 0.15981597695191D+00 2 13 3 13 0.20506336458695D+01 -0.20032798601149D+00 3 13 3 13 0.15429838433929D+02 0.00000000000000D+00 1 14 3 13 -0.78365893399544D+00 -0.13608913465564D-01 2 14 3 13 -0.10849379490595D+01 -0.12217998512349D-01 3 14 3 13 -0.37395346539821D+00 -0.14330319628261D-02 1 15 3 13 -0.66023830363373D+00 -0.20917464521661D-01 2 15 3 13 -0.14699393025031D+01 -0.30327434888119D-01 3 15 3 13 -0.80232255418624D-15 0.20130405233753D-01 1 16 3 13 -0.40741232101579D-01 0.12643178915096D-06 2 16 3 13 0.19324351108276D+00 -0.45017726291414D-07 3 16 3 13 -0.10368719777310D+01 -0.28425445952859D-14 1 17 3 13 -0.30400543782107D+00 -0.27279424757350D-01 2 17 3 13 0.30061611266250D-01 0.74174299812190D-01 3 17 3 13 -0.17372324645001D-13 -0.21347222096564D-02 1 18 3 13 -0.29234546368605D-02 0.83167620897552D-07 2 18 3 13 0.34828097813268D+00 0.37678409447862D-06 3 18 3 13 -0.11227810170086D+01 0.67677989533768D-14 1 19 3 13 -0.43612744495605D-01 -0.24829134260823D-02 2 19 3 13 0.18729653077669D+00 0.87261315418295D-02 3 19 3 13 -0.53216374096568D-14 0.86356341490434D-02 1 20 3 13 0.34013846158742D+00 0.29145182007415D-02 2 20 3 13 -0.11204992093732D+01 0.92684176117340D-02 3 20 3 13 0.13587309403008D-13 -0.69201872636558D-07 1 1 1 14 0.34159599944569D-01 0.10186584683515D-01 2 1 1 14 -0.50608893451166D+00 0.25217175319921D-02 3 1 1 14 0.12198240512238D+00 -0.15071331504289D-02 1 2 1 14 -0.18060885107796D+00 0.11778815488321D-06 2 2 1 14 -0.72301354005635D+00 -0.72587142226826D-07 3 2 1 14 -0.14815028338498D+00 -0.18314630014236D-07 1 3 1 14 0.92518036333728D-02 0.30638199855187D-07 2 3 1 14 0.80259503795468D+00 -0.99245325454969D-07 3 3 1 14 -0.35195673198039D+00 -0.59913862424637D-07 1 4 1 14 -0.43486473279451D+00 0.15350506746489D-01 2 4 1 14 -0.16761329463272D-01 -0.31249629992596D-01 3 4 1 14 0.11152602876192D+01 0.62582020916281D-02 1 5 1 14 0.13845699646768D+01 0.72384269307146D-02 2 5 1 14 0.26678717282473D+01 -0.10447588286213D-01 3 5 1 14 0.44483828644711D+00 -0.39228738516769D-01 1 6 1 14 -0.53668345860630D+00 -0.28185231299410D-01 2 6 1 14 0.25621508332101D+00 -0.25622006102617D-01 3 6 1 14 0.30154452868180D+01 0.61764351561422D-02 1 7 1 14 0.10161148680487D+00 -0.12921154873970D-01 2 7 1 14 -0.13720704530738D+01 -0.93931795400103D-02 3 7 1 14 0.21687698938730D+00 -0.45240790056769D-01 1 8 1 14 0.42653643115825D+00 0.40732564614947D-01 2 8 1 14 0.10237005265681D+00 0.80797304429651D-01 3 8 1 14 0.27364772025514D+01 0.35599509164341D-02 1 9 1 14 0.83238608982205D-01 0.59687000398189D-01 2 9 1 14 0.30023390271232D+00 0.12398159382869D-01 3 9 1 14 -0.28011525411381D+01 0.12637057955212D+00 1 10 1 14 -0.14676938359579D+01 0.53627212777962D-06 2 10 1 14 -0.59663993014513D+00 -0.69414797580679D-06 3 10 1 14 -0.34100493917736D+01 -0.13728680025520D-05 1 11 1 14 0.67033110219158D+00 -0.13725684560804D-01 2 11 1 14 0.98026860942441D+00 -0.39454287820011D-01 3 11 1 14 -0.28887231537357D+01 -0.11049317929218D+00 1 12 1 14 0.32727469999204D-01 0.34537179543892D-06 2 12 1 14 0.19375862305742D+00 0.33747397506028D-06 3 12 1 14 0.24672764490830D+01 0.81474365723096D-06 1 13 1 14 0.97974114254989D+00 -0.18266885601892D-02 2 13 1 14 -0.22712929095630D+00 -0.26549202704935D-02 3 13 1 14 -0.78365840750489D+00 -0.13606025531406D-01 1 14 1 14 0.13149817390300D+02 0.00000000000000D+00 2 14 1 14 0.69426528609113D+01 0.20550907331479D+00 3 14 1 14 -0.12192480104857D+01 -0.15981767360659D+00 1 15 1 14 0.16224381971232D+00 -0.15885114162366D-14 2 15 1 14 -0.35636845037223D-01 0.12544613536055D-08 3 15 1 14 0.40741232101577D-01 0.12643178916625D-06 1 16 1 14 -0.73704516468511D-15 0.30219137692492D-01 2 16 1 14 -0.80071830988700D-01 -0.38348271525878D-02 3 16 1 14 -0.66023830363373D+00 0.20917464521660D-01 1 17 1 14 0.60682061506544D+01 0.54960124181611D-14 2 17 1 14 -0.18812291655310D+01 0.76904784191025D-07 3 17 1 14 0.29234546368705D-02 0.83167620921612D-07 1 18 1 14 -0.42124782053607D-14 0.65408225279573D-02 2 18 1 14 -0.92274773342068D+00 -0.50983329631403D-02 3 18 1 14 -0.30400543782107D+00 0.27279424757350D-01 1 19 1 14 0.16722551646527D-14 -0.49131391012793D-07 2 19 1 14 -0.43399967089215D-01 0.36377534542910D-02 3 19 1 14 -0.34013761498442D+00 -0.29127273390720D-02 1 20 1 14 0.30460218137475D-15 -0.14248825411419D-01 2 20 1 14 -0.31440136644699D-01 0.33867480518988D-01 3 20 1 14 0.43612370464157D-01 -0.24830039566380D-02 1 1 2 14 -0.29645719455466D+00 0.10397496925171D-01 2 1 2 14 -0.42669990022289D+00 0.40911720073827D-02 3 1 2 14 0.14104596669028D+01 0.24786916400984D-03 1 2 2 14 -0.31573643564814D+00 -0.78755441684038D-07 2 2 2 14 -0.13059176915070D+01 -0.55909801850160D-06 3 2 2 14 -0.12016467324020D+01 -0.66071606520783D-06 1 3 2 14 0.30490190754155D+00 -0.68056519613296D-07 2 3 2 14 0.10669534109937D+01 -0.20708555399422D-06 3 3 2 14 0.13109063117039D+01 0.47398370056786D-07 1 4 2 14 0.34479890278873D+00 -0.54361281411068D-02 2 4 2 14 -0.17851870533804D+01 -0.22602251736405D-02 3 4 2 14 0.13647920929377D+00 0.13824023979018D-01 1 5 2 14 -0.47626649773460D+00 0.15005135265706D-01 2 5 2 14 0.50877729273307D+01 -0.39091583880327D-02 3 5 2 14 0.48293397746212D+00 -0.50088873825510D-01 1 6 2 14 -0.44045047321919D+00 -0.31562444327087D-01 2 6 2 14 -0.45311663921933D-01 -0.16202328843039D-01 3 6 2 14 0.39939332590606D+01 0.54859697995840D-02 1 7 2 14 0.68146394043985D+00 -0.19992458410053D-01 2 7 2 14 -0.52675461638691D+01 -0.14939669842403D-01 3 7 2 14 0.61828817619137D+00 -0.66510466617511D-01 1 8 2 14 0.57101763754834D+00 0.86049775603675D-01 2 8 2 14 0.39314070199045D+00 0.10539739545060D+00 3 8 2 14 0.46274463292544D+01 0.12250041505250D-01 1 9 2 14 0.55834732066970D+00 0.63046389702134D-01 2 9 2 14 -0.21488779706578D-01 -0.45492857508523D-02 3 9 2 14 -0.38203216284890D+01 0.22302494991980D+00 1 10 2 14 -0.75352302634899D+00 0.25526941972962D-06 2 10 2 14 0.44257479394547D+00 -0.31536861918915D-06 3 10 2 14 -0.31797146926206D+01 -0.81543201236831D-06 1 11 2 14 0.83825489427701D+00 -0.29613994108062D-01 2 11 2 14 0.22537600443647D+00 -0.41867266062294D-01 3 11 2 14 -0.38475374507552D+01 -0.17615986978702D+00 1 12 2 14 0.54403671042544D+00 -0.59966147982349D-06 2 12 2 14 0.99984334761555D-01 0.18695458751381D-06 3 12 2 14 0.45233035133574D+01 0.86012076702834D-06 1 13 2 14 -0.22712898881450D+00 -0.26542770768451D-02 2 13 2 14 -0.63003020552730D+00 -0.72209940761284D-03 3 13 2 14 -0.10849401454823D+01 -0.12216080443967D-01 1 14 2 14 0.69426571478986D+01 -0.20550963496243D+00 2 14 2 14 0.16540543133682D+02 0.00000000000000D+00 3 14 2 14 0.20506088072323D+01 0.20032682093087D+00 1 15 2 14 -0.35636845037223D-01 -0.12544612910368D-08 2 15 2 14 0.28873768072395D+00 -0.40061024841141D-14 3 15 2 14 -0.19324351108277D+00 -0.45017724987160D-07 1 16 2 14 0.80071830988698D-01 -0.38348271525878D-02 2 16 2 14 -0.25399405211092D-14 -0.21789018231943D-01 3 16 2 14 -0.14699393025031D+01 0.30327434888119D-01 1 17 2 14 0.18812291655311D+01 0.76904784435404D-07 2 17 2 14 -0.30894398169472D+01 0.59904266775343D-16 3 17 2 14 0.34828097813267D+00 -0.37678409496965D-06 1 18 2 14 -0.92274773342068D+00 0.50983329631400D-02 2 18 2 14 -0.75542206886296D-13 -0.18910615735645D-01 3 18 2 14 -0.30061611266267D-01 0.74174299812195D-01 1 19 2 14 -0.43400177186255D-01 0.36381076052580D-02 2 19 2 14 -0.34959339848509D-14 -0.25620557990984D-06 3 19 2 14 -0.11204977375783D+01 0.92699308904830D-02 1 20 2 14 -0.31440993033377D-01 -0.33867627316431D-01 2 20 2 14 -0.26647172695652D-13 0.17281658324452D-01 3 20 2 14 0.18729564246324D+00 -0.87260515821024D-02 1 1 3 14 -0.32589235607614D+00 -0.53961947240777D-03 2 1 3 14 0.98454495694062D+00 0.63353830294747D-02 3 1 3 14 0.45332216840792D+00 0.33781122828518D-02 1 2 3 14 0.52399840543386D+00 0.94125318951598D-06 2 2 3 14 -0.79397099005576D+00 0.22384955714518D-06 3 2 3 14 -0.31623867245849D+00 -0.84332937597714D-06 1 3 3 14 -0.81823224224853D+00 -0.30844529756899D-06 2 3 3 14 0.92567424803796D+00 0.81584867603806D-07 3 3 3 14 -0.40516331287114D+00 -0.30872766025512D-06 1 4 3 14 0.56626506089947D+00 0.48887486834199D-02 2 4 3 14 -0.40625835904033D+00 -0.84648125232145D-02 3 4 3 14 -0.24683163743508D+01 -0.24138185634083D-01 1 5 3 14 -0.65729793861579D+00 -0.56729719069160D-01 2 5 3 14 -0.43995953810376D+00 -0.21412943871377D-01 3 5 3 14 0.47413359179878D+01 0.29166180687206D-01 1 6 3 14 0.43515068697147D+00 0.16001986766969D-01 2 6 3 14 0.12163822420997D+01 0.57385749439751D-02 3 6 3 14 0.29639836161834D+00 0.16795988062125D-01 1 7 3 14 -0.89708384060995D+00 -0.45108112857932D-01 2 7 3 14 -0.37668213502739D+00 -0.52669567900943D-01 3 7 3 14 -0.40120124420432D+01 -0.33325999191616D-01 1 8 3 14 0.31176128987341D+00 0.24129534220526D-01 2 8 3 14 0.18790884315294D+01 0.37556306773516D-01 3 8 3 14 0.16731051450905D+00 -0.76010268556753D-01 1 9 3 14 -0.12756130326613D+01 0.34494705371218D-01 2 9 3 14 -0.15292499234972D+01 0.16697700502188D-02 3 9 3 14 0.23437484698202D+01 -0.17476761537553D+00 1 10 3 14 -0.13911435770839D+01 0.59213082760030D-06 2 10 3 14 -0.11544339529139D+01 0.11863208094534D-05 3 10 3 14 -0.80225609774919D+00 0.66510954250312D-06 1 11 3 14 -0.74448980247683D+00 -0.36877640368580D-01 2 11 3 14 -0.19277728803764D+01 -0.51534844201751D-01 3 11 3 14 0.73952045000310D+00 0.94971861344593D-01 1 12 3 14 0.95367064821533D+00 0.48363265443325D-07 2 12 3 14 0.19757613553938D+01 -0.66017240557761D-06 3 12 3 14 0.29944073876141D+01 0.20178476211856D-06 1 13 3 14 -0.78365893399544D+00 -0.13608913465564D-01 2 13 3 14 -0.10849379490595D+01 -0.12217998512353D-01 3 13 3 14 -0.37395346539821D+00 -0.14330319628276D-02 1 14 3 14 -0.12192282832174D+01 0.15981597695191D+00 2 14 3 14 0.20506336458699D+01 -0.20032798601149D+00 3 14 3 14 0.15429838433929D+02 0.00000000000000D+00 1 15 3 14 -0.40741232101582D-01 0.12643178916452D-06 2 15 3 14 0.19324351108274D+00 -0.45017724988895D-07 3 15 3 14 -0.10368719777310D+01 0.23401404832572D-14 1 16 3 14 -0.66023830363373D+00 -0.20917464521660D-01 2 16 3 14 -0.14699393025031D+01 -0.30327434888120D-01 3 16 3 14 -0.78808122161663D-14 0.20130405233753D-01 1 17 3 14 -0.29234546368469D-02 0.83167620935273D-07 2 17 3 14 0.34828097813267D+00 0.37678409680222D-06 3 17 3 14 -0.11227810170085D+01 -0.21918674599543D-16 1 18 3 14 -0.30400543782107D+00 -0.27279424757350D-01 2 18 3 14 0.30061611266230D-01 0.74174299812195D-01 3 18 3 14 -0.32656457629424D-13 -0.21347222096600D-02 1 19 3 14 0.34013846158742D+00 0.29145182007419D-02 2 19 3 14 -0.11204992093733D+01 0.92684176117328D-02 3 19 3 14 0.10086432938211D-13 -0.69201871423545D-07 1 20 3 14 -0.43612744495598D-01 -0.24829134260823D-02 2 20 3 14 0.18729653077667D+00 0.87261315418315D-02 3 20 3 14 -0.37518137193011D-13 0.86356341490456D-02 1 1 1 15 -0.34159599944575D-01 -0.10186584683516D-01 2 1 1 15 0.50608893451165D+00 -0.25217175319903D-02 3 1 1 15 0.12198240512237D+00 -0.15071331504308D-02 1 2 1 15 -0.18060885107793D+00 0.11778815483594D-06 2 2 1 15 -0.72301354005638D+00 -0.72587142907135D-07 3 2 1 15 0.14815028338494D+00 0.18314630434978D-07 1 3 1 15 -0.92518036333797D-02 -0.30638199750964D-07 2 3 1 15 -0.80259503795468D+00 0.99245323722725D-07 3 3 1 15 -0.35195673198040D+00 -0.59913869294776D-07 1 4 1 15 -0.43486473279450D+00 0.15350506746489D-01 2 4 1 15 -0.16761329463365D-01 -0.31249629992596D-01 3 4 1 15 -0.11152602876191D+01 -0.62582020916284D-02 1 5 1 15 0.53668345860630D+00 0.28185231299410D-01 2 5 1 15 -0.25621508332100D+00 0.25622006102618D-01 3 5 1 15 0.30154452868179D+01 0.61764351561418D-02 1 6 1 15 -0.13845699646767D+01 -0.72384269306937D-02 2 6 1 15 -0.26678717282473D+01 0.10447588286235D-01 3 6 1 15 0.44483828644711D+00 -0.39228738516759D-01 1 7 1 15 -0.42653643115826D+00 -0.40732564614947D-01 2 7 1 15 -0.10237005265682D+00 -0.80797304429652D-01 3 7 1 15 0.27364772025514D+01 0.35599509164336D-02 1 8 1 15 -0.10161148680487D+00 0.12921154873966D-01 2 8 1 15 0.13720704530739D+01 0.93931795399871D-02 3 8 1 15 0.21687698938734D+00 -0.45240790056762D-01 1 9 1 15 -0.83238608982201D-01 -0.59687000398188D-01 2 9 1 15 -0.30023390271233D+00 -0.12398159382868D-01 3 9 1 15 -0.28011525411381D+01 0.12637057955212D+00 1 10 1 15 -0.14676938359579D+01 0.53627212778892D-06 2 10 1 15 -0.59663993014511D+00 -0.69414797561756D-06 3 10 1 15 0.34100493917736D+01 0.13728680026542D-05 1 11 1 15 0.67033110219157D+00 -0.13725684560804D-01 2 11 1 15 0.98026860942440D+00 -0.39454287820011D-01 3 11 1 15 0.28887231537357D+01 0.11049317929218D+00 1 12 1 15 -0.32727469999204D-01 -0.34537179648274D-06 2 12 1 15 -0.19375862305742D+00 -0.33747397377829D-06 3 12 1 15 0.24672764490830D+01 0.81474365528107D-06 1 13 1 15 0.11978246338924D-14 -0.30219137692492D-01 2 13 1 15 0.80071830988700D-01 0.38348271525882D-02 3 13 1 15 -0.66023830363373D+00 0.20917464521661D-01 1 14 1 15 0.16224381971232D+00 0.15885114162366D-14 2 14 1 15 -0.35636845037223D-01 0.12544612910368D-08 3 14 1 15 -0.40741232101582D-01 -0.12643178916452D-06 1 15 1 15 0.13149817390301D+02 0.00000000000000D+00 2 15 1 15 0.69426528609114D+01 0.20550907331479D+00 3 15 1 15 0.12192480104857D+01 0.15981767360659D+00 1 16 1 15 -0.97974114254990D+00 0.18266885601904D-02 2 16 1 15 0.22712929095631D+00 0.26549202704920D-02 3 16 1 15 -0.78365840750489D+00 -0.13606025531406D-01 1 17 1 15 -0.53176707826981D-14 0.14248825411419D-01 2 17 1 15 0.31440136644696D-01 -0.33867480518988D-01 3 17 1 15 0.43612370464159D-01 -0.24830039566379D-02 1 18 1 15 0.68197670028744D-15 -0.49131391063911D-07 2 18 1 15 -0.43399967089214D-01 0.36377534542911D-02 3 18 1 15 0.34013761498442D+00 0.29127273390720D-02 1 19 1 15 0.17827261276152D-14 0.65408225279571D-02 2 19 1 15 -0.92274773342067D+00 -0.50983329631403D-02 3 19 1 15 0.30400543782107D+00 -0.27279424757350D-01 1 20 1 15 -0.60682061506544D+01 0.42009439397963D-14 2 20 1 15 0.18812291655310D+01 -0.76904784159249D-07 3 20 1 15 0.29234546368725D-02 0.83167620888504D-07 1 1 2 15 0.29645719455465D+00 -0.10397496925169D-01 2 1 2 15 0.42669990022291D+00 -0.40911720073840D-02 3 1 2 15 0.14104596669028D+01 0.24786916401329D-03 1 2 2 15 -0.31573643564817D+00 -0.78755442364348D-07 2 2 2 15 -0.13059176915070D+01 -0.55909801824736D-06 3 2 2 15 0.12016467324020D+01 0.66071606314256D-06 1 3 2 15 -0.30490190754155D+00 0.68056517886256D-07 2 3 2 15 -0.10669534109937D+01 0.20708555362728D-06 3 3 2 15 0.13109063117039D+01 0.47398377815005D-07 1 4 2 15 0.34479890278865D+00 -0.54361281411070D-02 2 4 2 15 -0.17851870533803D+01 -0.22602251736407D-02 3 4 2 15 -0.13647920929397D+00 -0.13824023979016D-01 1 5 2 15 0.44045047321920D+00 0.31562444327087D-01 2 5 2 15 0.45311663921894D-01 0.16202328843039D-01 3 5 2 15 0.39939332590606D+01 0.54859697995831D-02 1 6 2 15 0.47626649773463D+00 -0.15005135265684D-01 2 6 2 15 -0.50877729273306D+01 0.39091583880385D-02 3 6 2 15 0.48293397746209D+00 -0.50088873825508D-01 1 7 2 15 -0.57101763754834D+00 -0.86049775603676D-01 2 7 2 15 -0.39314070199044D+00 -0.10539739545061D+00 3 7 2 15 0.46274463292544D+01 0.12250041505248D-01 1 8 2 15 -0.68146394043984D+00 0.19992458410030D-01 2 8 2 15 0.52675461638692D+01 0.14939669842381D-01 3 8 2 15 0.61828817619139D+00 -0.66510466617495D-01 1 9 2 15 -0.55834732066971D+00 -0.63046389702133D-01 2 9 2 15 0.21488779706571D-01 0.45492857508536D-02 3 9 2 15 -0.38203216284890D+01 0.22302494991981D+00 1 10 2 15 -0.75352302634897D+00 0.25526941991886D-06 2 10 2 15 0.44257479394546D+00 -0.31536861810648D-06 3 10 2 15 0.31797146926206D+01 0.81543201218292D-06 1 11 2 15 0.83825489427701D+00 -0.29613994108061D-01 2 11 2 15 0.22537600443648D+00 -0.41867266062296D-01 3 11 2 15 0.38475374507552D+01 0.17615986978702D+00 1 12 2 15 -0.54403671042545D+00 0.59966148111067D-06 2 12 2 15 -0.99984334761572D-01 -0.18695458734221D-06 3 12 2 15 0.45233035133575D+01 0.86012076122278D-06 1 13 2 15 -0.80071830988698D-01 0.38348271525882D-02 2 13 2 15 -0.40712558647147D-15 0.21789018231944D-01 3 13 2 15 -0.14699393025031D+01 0.30327434888119D-01 1 14 2 15 -0.35636845037223D-01 -0.12544613536055D-08 2 14 2 15 0.28873768072395D+00 0.40061024841141D-14 3 14 2 15 0.19324351108274D+00 0.45017724988895D-07 1 15 2 15 0.69426571478987D+01 -0.20550963496243D+00 2 15 2 15 0.16540543133682D+02 0.00000000000000D+00 3 15 2 15 -0.20506088072322D+01 -0.20032682093087D+00 1 16 2 15 0.22712898881450D+00 0.26542770768436D-02 2 16 2 15 0.63003020552730D+00 0.72209940761420D-03 3 16 2 15 -0.10849401454823D+01 -0.12216080443969D-01 1 17 2 15 0.31440993033373D-01 0.33867627316431D-01 2 17 2 15 -0.17437536929815D-14 -0.17281658324453D-01 3 17 2 15 0.18729564246326D+00 -0.87260515821037D-02 1 18 2 15 -0.43400177186254D-01 0.36381076052580D-02 2 18 2 15 0.76020554147980D-14 -0.25620558023154D-06 3 18 2 15 0.11204977375783D+01 -0.92699308904829D-02 1 19 2 15 -0.92274773342067D+00 0.50983329631399D-02 2 19 2 15 -0.59554996602244D-13 -0.18910615735641D-01 3 19 2 15 0.30061611266246D-01 -0.74174299812196D-01 1 20 2 15 -0.18812291655311D+01 -0.76904784403628D-07 2 20 2 15 0.30894398169472D+01 -0.23564139661080D-14 3 20 2 15 0.34828097813268D+00 -0.37678409626249D-06 1 1 3 15 -0.32589235607614D+00 -0.53961947240970D-03 2 1 3 15 0.98454495694062D+00 0.63353830294781D-02 3 1 3 15 -0.45332216840789D+00 -0.33781122828543D-02 1 2 3 15 -0.52399840543390D+00 -0.94125318909524D-06 2 2 3 15 0.79397099005575D+00 -0.22384955921045D-06 3 2 3 15 -0.31623867245852D+00 -0.84332937428645D-06 1 3 3 15 -0.81823224224852D+00 -0.30844530443479D-06 2 3 3 15 0.92567424803800D+00 0.81584875360290D-07 3 3 3 15 0.40516331287115D+00 0.30872767565670D-06 1 4 3 15 -0.56626506089939D+00 -0.48887486834202D-02 2 4 3 15 0.40625835904012D+00 0.84648125232170D-02 3 4 3 15 -0.24683163743508D+01 -0.24138185634085D-01 1 5 3 15 0.43515068697145D+00 0.16001986766968D-01 2 5 3 15 0.12163822420998D+01 0.57385749439743D-02 3 5 3 15 -0.29639836161840D+00 -0.16795988062122D-01 1 6 3 15 -0.65729793861580D+00 -0.56729719069150D-01 2 6 3 15 -0.43995953810379D+00 -0.21412943871374D-01 3 6 3 15 -0.47413359179877D+01 -0.29166180687228D-01 1 7 3 15 0.31176128987341D+00 0.24129534220525D-01 2 7 3 15 0.18790884315294D+01 0.37556306773514D-01 3 7 3 15 -0.16731051450903D+00 0.76010268556750D-01 1 8 3 15 -0.89708384060991D+00 -0.45108112857925D-01 2 8 3 15 -0.37668213502737D+00 -0.52669567900926D-01 3 8 3 15 0.40120124420432D+01 0.33325999191637D-01 1 9 3 15 -0.12756130326613D+01 0.34494705371221D-01 2 9 3 15 -0.15292499234972D+01 0.16697700502222D-02 3 9 3 15 -0.23437484698202D+01 0.17476761537553D+00 1 10 3 15 0.13911435770839D+01 -0.59213082749465D-06 2 10 3 15 0.11544339529139D+01 -0.11863208096527D-05 3 10 3 15 -0.80225609774921D+00 0.66510954167946D-06 1 11 3 15 0.74448980247683D+00 0.36877640368580D-01 2 11 3 15 0.19277728803764D+01 0.51534844201749D-01 3 11 3 15 0.73952045000316D+00 0.94971861344591D-01 1 12 3 15 0.95367064821533D+00 0.48363263486498D-07 2 12 3 15 0.19757613553939D+01 -0.66017241135887D-06 3 12 3 15 -0.29944073876141D+01 -0.20178475599756D-06 1 13 3 15 -0.66023830363373D+00 -0.20917464521660D-01 2 13 3 15 -0.14699393025031D+01 -0.30327434888119D-01 3 13 3 15 -0.80232255418624D-15 -0.20130405233753D-01 1 14 3 15 0.40741232101577D-01 -0.12643178916625D-06 2 14 3 15 -0.19324351108277D+00 0.45017724987160D-07 3 14 3 15 -0.10368719777310D+01 -0.23401404832572D-14 1 15 3 15 0.12192282832174D+01 -0.15981597695191D+00 2 15 3 15 -0.20506336458697D+01 0.20032798601149D+00 3 15 3 15 0.15429838433929D+02 0.00000000000000D+00 1 16 3 15 -0.78365893399544D+00 -0.13608913465564D-01 2 16 3 15 -0.10849379490595D+01 -0.12217998512355D-01 3 16 3 15 0.37395346539822D+00 0.14330319628258D-02 1 17 3 15 -0.43612744495596D-01 -0.24829134260823D-02 2 17 3 15 0.18729653077669D+00 0.87261315418303D-02 3 17 3 15 0.84368018127566D-14 -0.86356341490425D-02 1 18 3 15 -0.34013846158742D+00 -0.29145182007419D-02 2 18 3 15 0.11204992093733D+01 -0.92684176117328D-02 3 18 3 15 0.25086097142570D-13 -0.69201871119871D-07 1 19 3 15 0.30400543782107D+00 0.27279424757350D-01 2 19 3 15 -0.30061611266251D-01 -0.74174299812196D-01 3 19 3 15 -0.36653259882800D-13 -0.21347222096603D-02 1 20 3 15 -0.29234546368449D-02 0.83167620902599D-07 2 20 3 15 0.34828097813268D+00 0.37678409551025D-06 3 20 3 15 0.11227810170086D+01 -0.43722825963659D-14 1 1 1 16 -0.18060885107789D+00 0.11778815568507D-06 2 1 1 16 -0.72301354005635D+00 -0.72587142236119D-07 3 1 1 16 0.14815028338488D+00 0.18314629745106D-07 1 2 1 16 -0.34159599944587D-01 -0.10186584683517D-01 2 2 1 16 0.50608893451168D+00 -0.25217175319883D-02 3 2 1 16 0.12198240512233D+00 -0.15071331504353D-02 1 3 1 16 -0.43486473279454D+00 0.15350506746488D-01 2 3 1 16 -0.16761329463314D-01 -0.31249629992596D-01 3 3 1 16 -0.11152602876191D+01 -0.62582020916285D-02 1 4 1 16 -0.92518036334092D-02 -0.30638199696969D-07 2 4 1 16 -0.80259503795470D+00 0.99245323481764D-07 3 4 1 16 -0.35195673198042D+00 -0.59913869122081D-07 1 5 1 16 -0.53668345860631D+00 -0.28185231299410D-01 2 5 1 16 0.25621508332101D+00 -0.25622006102616D-01 3 5 1 16 -0.30154452868179D+01 -0.61764351561425D-02 1 6 1 16 -0.13845699646769D+01 -0.72384269306937D-02 2 6 1 16 -0.26678717282475D+01 0.10447588286236D-01 3 6 1 16 0.44483828644680D+00 -0.39228738516761D-01 1 7 1 16 -0.42653643115827D+00 -0.40732564614947D-01 2 7 1 16 -0.10237005265681D+00 -0.80797304429651D-01 3 7 1 16 0.27364772025514D+01 0.35599509164350D-02 1 8 1 16 0.10161148680499D+00 -0.12921154873962D-01 2 8 1 16 -0.13720704530733D+01 -0.93931795399656D-02 3 8 1 16 -0.21687698938734D+00 0.45240790056756D-01 1 9 1 16 -0.14676938359579D+01 0.53627212754463D-06 2 9 1 16 -0.59663993014509D+00 -0.69414797572110D-06 3 9 1 16 0.34100493917736D+01 0.13728680031411D-05 1 10 1 16 -0.83238608982224D-01 -0.59687000398189D-01 2 10 1 16 -0.30023390271233D+00 -0.12398159382868D-01 3 10 1 16 -0.28011525411381D+01 0.12637057955212D+00 1 11 1 16 -0.32727469999204D-01 -0.34537179694613D-06 2 11 1 16 -0.19375862305742D+00 -0.33747397420566D-06 3 11 1 16 0.24672764490830D+01 0.81474365523215D-06 1 12 1 16 0.67033110219161D+00 -0.13725684560806D-01 2 12 1 16 0.98026860942441D+00 -0.39454287820015D-01 3 12 1 16 0.28887231537357D+01 0.11049317929217D+00 1 13 1 16 0.16224381971234D+00 0.24836270070312D-15 2 13 1 16 -0.35636845037218D-01 0.12544613583682D-08 3 13 1 16 -0.40741232101579D-01 -0.12643178915096D-06 1 14 1 16 -0.73704516468511D-15 -0.30219137692492D-01 2 14 1 16 0.80071830988698D-01 0.38348271525878D-02 3 14 1 16 -0.66023830363373D+00 0.20917464521660D-01 1 15 1 16 -0.97974114254990D+00 0.18266885601893D-02 2 15 1 16 0.22712929095631D+00 0.26549202704912D-02 3 15 1 16 -0.78365840750489D+00 -0.13606025531406D-01 1 16 1 16 0.13149817390301D+02 0.00000000000000D+00 2 16 1 16 0.69426528609110D+01 0.20550907331479D+00 3 16 1 16 0.12192480104861D+01 0.15981767360659D+00 1 17 1 16 -0.22871347096673D-14 -0.49131390892369D-07 2 17 1 16 -0.43399967089216D-01 0.36377534542913D-02 3 17 1 16 0.34013761498442D+00 0.29127273390722D-02 1 18 1 16 0.42165008989989D-14 0.14248825411418D-01 2 18 1 16 0.31440136644700D-01 -0.33867480518988D-01 3 18 1 16 0.43612370464152D-01 -0.24830039566380D-02 1 19 1 16 -0.60682061506544D+01 0.42512351294691D-14 2 19 1 16 0.18812291655311D+01 -0.76904784193059D-07 3 19 1 16 0.29234546368589D-02 0.83167620885199D-07 1 20 1 16 -0.36919237977875D-14 0.65408225279594D-02 2 20 1 16 -0.92274773342067D+00 -0.50983329631380D-02 3 20 1 16 0.30400543782107D+00 -0.27279424757350D-01 1 1 2 16 -0.31573643564814D+00 -0.78755441693331D-07 2 1 2 16 -0.13059176915071D+01 -0.55909801371387D-06 3 1 2 16 0.12016467324020D+01 0.66071606430652D-06 1 2 2 16 0.29645719455467D+00 -0.10397496925167D-01 2 2 2 16 0.42669990022294D+00 -0.40911720073864D-02 3 2 2 16 0.14104596669028D+01 0.24786916401899D-03 1 3 2 16 0.34479890278870D+00 -0.54361281411072D-02 2 3 2 16 -0.17851870533803D+01 -0.22602251736416D-02 3 3 2 16 -0.13647920929385D+00 -0.13824023979018D-01 1 4 2 16 -0.30490190754157D+00 0.68056517638356D-07 2 4 2 16 -0.10669534109937D+01 0.20708555297149D-06 3 4 2 16 0.13109063117040D+01 0.47398373750581D-07 1 5 2 16 -0.44045047321919D+00 -0.31562444327086D-01 2 5 2 16 -0.45311663921905D-01 -0.16202328843040D-01 3 5 2 16 -0.39939332590606D+01 -0.54859697995835D-02 1 6 2 16 0.47626649773436D+00 -0.15005135265683D-01 2 6 2 16 -0.50877729273304D+01 0.39091583880356D-02 3 6 2 16 0.48293397746189D+00 -0.50088873825504D-01 1 7 2 16 -0.57101763754834D+00 -0.86049775603675D-01 2 7 2 16 -0.39314070199046D+00 -0.10539739545061D+00 3 7 2 16 0.46274463292544D+01 0.12250041505250D-01 1 8 2 16 0.68146394044037D+00 -0.19992458410009D-01 2 8 2 16 -0.52675461638689D+01 -0.14939669842361D-01 3 8 2 16 -0.61828817619136D+00 0.66510466617487D-01 1 9 2 16 -0.75352302634896D+00 0.25526941981532D-06 2 9 2 16 0.44257479394548D+00 -0.31536861946800D-06 3 9 2 16 0.31797146926205D+01 0.81543201191419D-06 1 10 2 16 -0.55834732066971D+00 -0.63046389702133D-01 2 10 2 16 0.21488779706591D-01 0.45492857508540D-02 3 10 2 16 -0.38203216284890D+01 0.22302494991981D+00 1 11 2 16 -0.54403671042545D+00 0.59966148068330D-06 2 11 2 16 -0.99984334761522D-01 -0.18695458668244D-06 3 11 2 16 0.45233035133574D+01 0.86012076200043D-06 1 12 2 16 0.83825489427702D+00 -0.29613994108066D-01 2 12 2 16 0.22537600443644D+00 -0.41867266062296D-01 3 12 2 16 0.38475374507552D+01 0.17615986978701D+00 1 13 2 16 -0.35636845037218D-01 -0.12544612862741D-08 2 13 2 16 0.28873768072398D+00 0.12095121251624D-14 3 13 2 16 0.19324351108276D+00 0.45017726291414D-07 1 14 2 16 -0.80071830988700D-01 0.38348271525878D-02 2 14 2 16 -0.25399405211092D-14 0.21789018231943D-01 3 14 2 16 -0.14699393025031D+01 0.30327434888120D-01 1 15 2 16 0.22712898881450D+00 0.26542770768428D-02 2 15 2 16 0.63003020552730D+00 0.72209940761181D-03 3 15 2 16 -0.10849401454823D+01 -0.12216080443961D-01 1 16 2 16 0.69426571478983D+01 -0.20550963496243D+00 2 16 2 16 0.16540543133682D+02 0.00000000000000D+00 3 16 2 16 -0.20506088072320D+01 -0.20032682093087D+00 1 17 2 16 -0.43400177186256D-01 0.36381076052582D-02 2 17 2 16 0.62231835136807D-14 -0.25620558083393D-06 3 17 2 16 0.11204977375783D+01 -0.92699308904839D-02 1 18 2 16 0.31440993033378D-01 0.33867627316431D-01 2 18 2 16 0.12598952815604D-14 -0.17281658324452D-01 3 18 2 16 0.18729564246327D+00 -0.87260515821037D-02 1 19 2 16 -0.18812291655311D+01 -0.76904784437438D-07 2 19 2 16 0.30894398169471D+01 -0.22765382387926D-14 3 19 2 16 0.34828097813269D+00 -0.37678409641905D-06 1 20 2 16 -0.92274773342067D+00 0.50983329631423D-02 2 20 2 16 0.36332120519406D-13 -0.18910615735655D-01 3 20 2 16 0.30061611266252D-01 -0.74174299812194D-01 1 1 3 16 -0.52399840543395D+00 -0.94125318978511D-06 2 1 3 16 0.79397099005569D+00 -0.22384955804649D-06 3 1 3 16 -0.31623867245851D+00 -0.84332937041159D-06 1 2 3 16 -0.32589235607617D+00 -0.53961947241423D-03 2 2 3 16 0.98454495694063D+00 0.63353830294838D-02 3 2 3 16 -0.45332216840794D+00 -0.33781122828616D-02 1 3 3 16 -0.56626506089940D+00 -0.48887486834203D-02 2 3 3 16 0.40625835904024D+00 0.84648125232146D-02 3 3 3 16 -0.24683163743508D+01 -0.24138185634084D-01 1 4 3 16 -0.81823224224853D+00 -0.30844530426557D-06 2 4 3 16 0.92567424803804D+00 0.81584871299335D-07 3 4 3 16 0.40516331287124D+00 0.30872767202694D-06 1 5 3 16 -0.43515068697145D+00 -0.16001986766969D-01 2 5 3 16 -0.12163822420998D+01 -0.57385749439746D-02 3 5 3 16 0.29639836161842D+00 0.16795988062126D-01 1 6 3 16 -0.65729793861611D+00 -0.56729719069151D-01 2 6 3 16 -0.43995953810398D+00 -0.21412943871370D-01 3 6 3 16 -0.47413359179876D+01 -0.29166180687227D-01 1 7 3 16 0.31176128987343D+00 0.24129534220527D-01 2 7 3 16 0.18790884315294D+01 0.37556306773516D-01 3 7 3 16 -0.16731051450894D+00 0.76010268556756D-01 1 8 3 16 0.89708384060991D+00 0.45108112857919D-01 2 8 3 16 0.37668213502740D+00 0.52669567900918D-01 3 8 3 16 -0.40120124420439D+01 -0.33325999191660D-01 1 9 3 16 0.13911435770839D+01 -0.59213082700779D-06 2 9 3 16 0.11544339529138D+01 -0.11863208099214D-05 3 9 3 16 -0.80225609774916D+00 0.66510954156774D-06 1 10 3 16 -0.12756130326613D+01 0.34494705371221D-01 2 10 3 16 -0.15292499234972D+01 0.16697700502230D-02 3 10 3 16 -0.23437484698202D+01 0.17476761537554D+00 1 11 3 16 0.95367064821538D+00 0.48363263444513D-07 2 11 3 16 0.19757613553938D+01 -0.66017241060898D-06 3 11 3 16 -0.29944073876142D+01 -0.20178475728552D-06 1 12 3 16 0.74448980247686D+00 0.36877640368574D-01 2 12 3 16 0.19277728803764D+01 0.51534844201743D-01 3 12 3 16 0.73952045000311D+00 0.94971861344589D-01 1 13 3 16 0.40741232101580D-01 -0.12643178915269D-06 2 13 3 16 -0.19324351108276D+00 0.45017726289680D-07 3 13 3 16 -0.10368719777310D+01 0.28425445952859D-14 1 14 3 16 -0.66023830363373D+00 -0.20917464521660D-01 2 14 3 16 -0.14699393025031D+01 -0.30327434888119D-01 3 14 3 16 -0.78808122161663D-14 -0.20130405233753D-01 1 15 3 16 -0.78365893399544D+00 -0.13608913465564D-01 2 15 3 16 -0.10849379490595D+01 -0.12217998512347D-01 3 15 3 16 0.37395346539822D+00 0.14330319628279D-02 1 16 3 16 0.12192282832178D+01 -0.15981597695191D+00 2 16 3 16 -0.20506336458696D+01 0.20032798601149D+00 3 16 3 16 0.15429838433929D+02 0.00000000000000D+00 1 17 3 16 -0.34013846158742D+00 -0.29145182007417D-02 2 17 3 16 0.11204992093733D+01 -0.92684176117338D-02 3 17 3 16 0.10351083137188D-13 -0.69201872443662D-07 1 18 3 16 -0.43612744495603D-01 -0.24829134260823D-02 2 18 3 16 0.18729653077671D+00 0.87261315418302D-02 3 18 3 16 -0.73200388539820D-14 -0.86356341490457D-02 1 19 3 16 -0.29234546368585D-02 0.83167620899294D-07 2 19 3 16 0.34828097813269D+00 0.37678409535282D-06 3 19 3 16 0.11227810170085D+01 0.25534391409692D-15 1 20 3 16 0.30400543782107D+00 0.27279424757350D-01 2 20 3 16 -0.30061611266245D-01 -0.74174299812194D-01 3 20 3 16 -0.93787186559419D-14 -0.21347222096605D-02 1 1 1 17 0.43486473279458D+00 -0.15350506746489D-01 2 1 1 17 -0.16761329463244D-01 -0.31249629992591D-01 3 1 1 17 0.11152602876194D+01 0.62582020916374D-02 1 2 1 17 0.92518036333994D-02 0.30638199694113D-07 2 2 1 17 -0.80259503795466D+00 0.99245321884704D-07 3 2 1 17 0.35195673198032D+00 0.59913875758156D-07 1 3 1 17 -0.18060885107794D+00 0.11778815522253D-06 2 3 1 17 0.72301354005636D+00 0.72587142471045D-07 3 3 1 17 0.14815028338498D+00 0.18314629794580D-07 1 4 1 17 -0.34159599944601D-01 -0.10186584683517D-01 2 4 1 17 -0.50608893451168D+00 0.25217175319879D-02 3 4 1 17 0.12198240512229D+00 -0.15071331504353D-02 1 5 1 17 0.10161148680498D+00 -0.12921154873962D-01 2 5 1 17 0.13720704530734D+01 0.93931795399652D-02 3 5 1 17 -0.21687698938736D+00 0.45240790056755D-01 1 6 1 17 -0.42653643115825D+00 -0.40732564614947D-01 2 6 1 17 0.10237005265682D+00 0.80797304429651D-01 3 6 1 17 0.27364772025514D+01 0.35599509164355D-02 1 7 1 17 0.13845699646770D+01 0.72384269307143D-02 2 7 1 17 -0.26678717282476D+01 0.10447588286213D-01 3 7 1 17 -0.44483828644672D+00 0.39228738516769D-01 1 8 1 17 0.53668345860630D+00 0.28185231299410D-01 2 8 1 17 0.25621508332100D+00 -0.25622006102618D-01 3 8 1 17 0.30154452868179D+01 0.61764351561419D-02 1 9 1 17 -0.67033110219162D+00 0.13725684560805D-01 2 9 1 17 0.98026860942437D+00 -0.39454287820013D-01 3 9 1 17 -0.28887231537357D+01 -0.11049317929217D+00 1 10 1 17 0.32727469999218D-01 0.34537179725619D-06 2 10 1 17 -0.19375862305742D+00 -0.33747397324124D-06 3 10 1 17 -0.24672764490830D+01 -0.81474365336728D-06 1 11 1 17 -0.83238608982226D-01 -0.59687000398189D-01 2 11 1 17 0.30023390271234D+00 0.12398159382868D-01 3 11 1 17 -0.28011525411381D+01 0.12637057955212D+00 1 12 1 17 -0.14676938359579D+01 0.53627212836626D-06 2 12 1 17 0.59663993014510D+00 0.69414797579668D-06 3 12 1 17 0.34100493917736D+01 0.13728680026775D-05 1 13 1 17 -0.16927227543600D-14 -0.65408225279596D-02 2 13 1 17 -0.92274773342066D+00 -0.50983329631403D-02 3 13 1 17 -0.30400543782107D+00 0.27279424757350D-01 1 14 1 17 0.60682061506544D+01 -0.13814445166339D-13 2 14 1 17 0.18812291655311D+01 -0.76904784190808D-07 3 14 1 17 -0.29234546368469D-02 -0.83167620921395D-07 1 15 1 17 -0.53176707826981D-14 -0.14248825411419D-01 2 15 1 17 0.31440136644696D-01 -0.33867480518988D-01 3 15 1 17 -0.43612370464143D-01 0.24830039566379D-02 1 16 1 17 -0.22871347096673D-14 0.49131390892369D-07 2 16 1 17 -0.43399967089216D-01 0.36377534542907D-02 3 16 1 17 -0.34013761498442D+00 -0.29127273390722D-02 1 17 1 17 0.13149817390301D+02 0.00000000000000D+00 2 17 1 17 -0.69426528609109D+01 -0.20550907331479D+00 3 17 1 17 0.12192480104862D+01 0.15981767360659D+00 1 18 1 17 -0.97974114254991D+00 0.18266885601896D-02 2 18 1 17 -0.22712929095630D+00 -0.26549202704913D-02 3 18 1 17 -0.78365840750489D+00 -0.13606025531406D-01 1 19 1 17 0.28754209331204D-14 -0.30219137692492D-01 2 19 1 17 -0.80071830988698D-01 -0.38348271525881D-02 3 19 1 17 -0.66023830363373D+00 0.20917464521661D-01 1 20 1 17 0.16224381971233D+00 0.43789100713492D-15 2 20 1 17 0.35636845037221D-01 -0.12544613440478D-08 3 20 1 17 -0.40741232101581D-01 -0.12643178917469D-06 1 1 2 17 0.34479890278878D+00 -0.54361281411015D-02 2 1 2 17 0.17851870533801D+01 0.22602251736435D-02 3 1 2 17 -0.13647920929397D+00 -0.13824023979004D-01 1 2 2 17 -0.30490190754152D+00 0.68056516041297D-07 2 2 2 17 0.10669534109937D+01 -0.20708555026117D-06 3 2 2 17 0.13109063117039D+01 0.47398380924590D-07 1 3 2 17 0.31573643564816D+00 0.78755441928258D-07 2 3 2 17 -0.13059176915070D+01 -0.55909801714508D-06 3 3 2 17 -0.12016467324020D+01 -0.66071606515594D-06 1 4 2 17 -0.29645719455467D+00 0.10397496925166D-01 2 4 2 17 0.42669990022295D+00 -0.40911720073868D-02 3 4 2 17 -0.14104596669028D+01 -0.24786916401744D-03 1 5 2 17 -0.68146394044034D+00 0.19992458410008D-01 2 5 2 17 -0.52675461638689D+01 -0.14939669842361D-01 3 5 2 17 0.61828817619141D+00 -0.66510466617486D-01 1 6 2 17 0.57101763754834D+00 0.86049775603675D-01 2 6 2 17 -0.39314070199044D+00 -0.10539739545061D+00 3 6 2 17 -0.46274463292544D+01 -0.12250041505251D-01 1 7 2 17 0.47626649773431D+00 -0.15005135265706D-01 2 7 2 17 0.50877729273304D+01 -0.39091583880322D-02 3 7 2 17 0.48293397746186D+00 -0.50088873825513D-01 1 8 2 17 -0.44045047321920D+00 -0.31562444327087D-01 2 8 2 17 0.45311663921924D-01 0.16202328843040D-01 3 8 2 17 -0.39939332590607D+01 -0.54859697995838D-02 1 9 2 17 0.83825489427698D+00 -0.29613994108064D-01 2 9 2 17 -0.22537600443644D+00 0.41867266062296D-01 3 9 2 17 0.38475374507551D+01 0.17615986978702D+00 1 10 2 17 -0.54403671042545D+00 0.59966148164426D-06 2 10 2 17 0.99984334761579D-01 0.18695458272566D-06 3 10 2 17 0.45233035133574D+01 0.86012075725226D-06 1 11 2 17 0.55834732066972D+00 0.63046389702133D-01 2 11 2 17 0.21488779706571D-01 0.45492857508524D-02 3 11 2 17 0.38203216284890D+01 -0.22302494991981D+00 1 12 2 17 0.75352302634897D+00 -0.25526941973974D-06 2 12 2 17 0.44257479394551D+00 -0.31536861931352D-06 3 12 2 17 -0.31797146926205D+01 -0.81543201243075D-06 1 13 2 17 -0.92274773342066D+00 0.50983329631400D-02 2 13 2 17 0.28336197683478D-13 0.18910615735654D-01 3 13 2 17 0.30061611266250D-01 -0.74174299812190D-01 1 14 2 17 -0.18812291655310D+01 -0.76904784435621D-07 2 14 2 17 -0.30894398169472D+01 0.52146274940176D-14 3 14 2 17 0.34828097813267D+00 -0.37678409771035D-06 1 15 2 17 0.31440993033373D-01 0.33867627316431D-01 2 15 2 17 -0.17437536929815D-14 0.17281658324453D-01 3 15 2 17 0.18729564246326D+00 -0.87260515821026D-02 1 16 2 17 -0.43400177186256D-01 0.36381076052576D-02 2 16 2 17 0.62231835136807D-14 0.25620558083393D-06 3 16 2 17 0.11204977375783D+01 -0.92699308904830D-02 1 17 2 17 -0.69426571478982D+01 0.20550963496243D+00 2 17 2 17 0.16540543133681D+02 0.00000000000000D+00 3 17 2 17 0.20506088072319D+01 0.20032682093087D+00 1 18 2 17 -0.22712898881450D+00 -0.26542770768429D-02 2 18 2 17 0.63003020552732D+00 0.72209940761189D-03 3 18 2 17 0.10849401454823D+01 0.12216080443962D-01 1 19 2 17 0.80071830988701D-01 -0.38348271525881D-02 2 19 2 17 0.11475469251514D-14 0.21789018231943D-01 3 19 2 17 0.14699393025031D+01 -0.30327434888120D-01 1 20 2 17 0.35636845037221D-01 0.12544613005945D-08 2 20 2 17 0.28873768072398D+00 -0.11477125585121D-14 3 20 2 17 -0.19324351108275D+00 -0.45017725814897D-07 1 1 3 17 0.56626506089967D+00 0.48887486834291D-02 2 1 3 17 0.40625835904015D+00 0.84648125232288D-02 3 1 3 17 0.24683163743510D+01 0.24138185634093D-01 1 2 3 17 0.81823224224843D+00 0.30844531089644D-06 2 2 3 17 0.92567424803794D+00 0.81584878475079D-07 3 2 3 17 -0.40516331287108D+00 -0.30872768524387D-06 1 3 3 17 -0.52399840543386D+00 -0.94125318973564D-06 2 3 3 17 -0.79397099005573D+00 0.22384955719707D-06 3 3 3 17 -0.31623867245855D+00 -0.84332937399110D-06 1 4 3 17 -0.32589235607621D+00 -0.53961947241423D-03 2 4 3 17 -0.98454495694060D+00 -0.63353830294823D-02 3 4 3 17 -0.45332216840798D+00 -0.33781122828617D-02 1 5 3 17 0.89708384060989D+00 0.45108112857918D-01 2 5 3 17 -0.37668213502734D+00 -0.52669567900917D-01 3 5 3 17 -0.40120124420439D+01 -0.33325999191661D-01 1 6 3 17 0.31176128987342D+00 0.24129534220527D-01 2 6 3 17 -0.18790884315294D+01 -0.37556306773517D-01 3 6 3 17 -0.16731051450893D+00 0.76010268556752D-01 1 7 3 17 0.65729793861619D+00 0.56729719069159D-01 2 7 3 17 -0.43995953810401D+00 -0.21412943871380D-01 3 7 3 17 0.47413359179873D+01 0.29166180687207D-01 1 8 3 17 0.43515068697145D+00 0.16001986766968D-01 2 8 3 17 -0.12163822420998D+01 -0.57385749439750D-02 3 8 3 17 -0.29639836161844D+00 -0.16795988062124D-01 1 9 3 17 -0.74448980247681D+00 -0.36877640368577D-01 2 9 3 17 0.19277728803763D+01 0.51534844201746D-01 3 9 3 17 -0.73952045000310D+00 -0.94971861344591D-01 1 10 3 17 -0.95367064821533D+00 -0.48363261579644D-07 2 10 3 17 0.19757613553938D+01 -0.66017241532940D-06 3 10 3 17 0.29944073876140D+01 0.20178475007761D-06 1 11 3 17 -0.12756130326613D+01 0.34494705371221D-01 2 11 3 17 0.15292499234972D+01 -0.16697700502222D-02 3 11 3 17 -0.23437484698202D+01 0.17476761537554D+00 1 12 3 17 0.13911435770839D+01 -0.59213082747138D-06 2 12 3 17 -0.11544339529139D+01 0.11863208094048D-05 3 12 3 17 -0.80225609774919D+00 0.66510954174939D-06 1 13 3 17 -0.30400543782107D+00 -0.27279424757350D-01 2 13 3 17 -0.30061611266247D-01 -0.74174299812190D-01 3 13 3 17 -0.17372585531149D-13 0.21347222096564D-02 1 14 3 17 0.29234546368705D-02 -0.83167620935490D-07 2 14 3 17 0.34828097813267D+00 0.37678409406152D-06 3 14 3 17 -0.11227810170085D+01 0.73253213488964D-14 1 15 3 17 0.43612744495612D-01 0.24829134260823D-02 2 15 3 17 0.18729653077669D+00 0.87261315418313D-02 3 15 3 17 0.84368018127566D-14 0.86356341490425D-02 1 16 3 17 0.34013846158742D+00 0.29145182007417D-02 2 16 3 17 0.11204992093733D+01 -0.92684176117329D-02 3 16 3 17 0.10351083137188D-13 0.69201872443662D-07 1 17 3 17 0.12192282832179D+01 -0.15981597695191D+00 2 17 3 17 0.20506336458695D+01 -0.20032798601149D+00 3 17 3 17 0.15429838433929D+02 0.00000000000000D+00 1 18 3 17 -0.78365893399544D+00 -0.13608913465564D-01 2 18 3 17 0.10849379490595D+01 0.12217998512348D-01 3 18 3 17 0.37395346539824D+00 0.14330319628269D-02 1 19 3 17 -0.66023830363373D+00 -0.20917464521660D-01 2 19 3 17 0.14699393025031D+01 0.30327434888119D-01 3 19 3 17 -0.14259849023293D-15 -0.20130405233753D-01 1 20 3 17 0.40741232101578D-01 -0.12643178917642D-06 2 20 3 17 0.19324351108276D+00 -0.45017725813162D-07 3 20 3 17 -0.10368719777310D+01 -0.50695058562776D-15 1 1 1 18 0.92518036333799D-02 0.30638200021204D-07 2 1 1 18 -0.80259503795468D+00 0.99245325663730D-07 3 1 1 18 0.35195673198046D+00 0.59913862342212D-07 1 2 1 18 0.43486473279453D+00 -0.15350506746488D-01 2 2 1 18 -0.16761329463294D-01 -0.31249629992602D-01 3 2 1 18 0.11152602876192D+01 0.62582020916189D-02 1 3 1 18 -0.34159599944594D-01 -0.10186584683516D-01 2 3 1 18 -0.50608893451168D+00 0.25217175319901D-02 3 3 1 18 0.12198240512231D+00 -0.15071331504309D-02 1 4 1 18 -0.18060885107794D+00 0.11778815491958D-06 2 4 1 18 0.72301354005631D+00 0.72587142600265D-07 3 4 1 18 0.14815028338500D+00 0.18314629919725D-07 1 5 1 18 -0.10161148680494D+00 0.12921154873966D-01 2 5 1 18 -0.13720704530736D+01 -0.93931795399872D-02 3 5 1 18 0.21687698938740D+00 -0.45240790056762D-01 1 6 1 18 -0.42653643115826D+00 -0.40732564614947D-01 2 6 1 18 0.10237005265681D+00 0.80797304429651D-01 3 6 1 18 0.27364772025514D+01 0.35599509164351D-02 1 7 1 18 0.13845699646769D+01 0.72384269307146D-02 2 7 1 18 -0.26678717282474D+01 0.10447588286212D-01 3 7 1 18 -0.44483828644706D+00 0.39228738516769D-01 1 8 1 18 -0.53668345860631D+00 -0.28185231299410D-01 2 8 1 18 -0.25621508332101D+00 0.25622006102618D-01 3 8 1 18 -0.30154452868180D+01 -0.61764351561424D-02 1 9 1 18 0.32727469999195D-01 0.34537179565750D-06 2 9 1 18 -0.19375862305741D+00 -0.33747397477922D-06 3 9 1 18 -0.24672764490829D+01 -0.81474365732453D-06 1 10 1 18 -0.67033110219160D+00 0.13725684560805D-01 2 10 1 18 0.98026860942440D+00 -0.39454287820013D-01 3 10 1 18 -0.28887231537357D+01 -0.11049317929217D+00 1 11 1 18 -0.14676938359580D+01 0.53627212776540D-06 2 11 1 18 0.59663993014510D+00 0.69414797581346D-06 3 11 1 18 0.34100493917736D+01 0.13728680025915D-05 1 12 1 18 -0.83238608982220D-01 -0.59687000398189D-01 2 12 1 18 0.30023390271233D+00 0.12398159382868D-01 3 12 1 18 -0.28011525411382D+01 0.12637057955212D+00 1 13 1 18 0.60682061506544D+01 0.57056339683931D-14 2 13 1 18 0.18812291655311D+01 -0.76904784200946D-07 3 13 1 18 -0.29234546368605D-02 -0.83167620883674D-07 1 14 1 18 -0.42116786062585D-14 -0.65408225279573D-02 2 14 1 18 -0.92274773342068D+00 -0.50983329631380D-02 3 14 1 18 -0.30400543782107D+00 0.27279424757350D-01 1 15 1 18 0.68197670028744D-15 0.49131391063911D-07 2 15 1 18 -0.43399967089214D-01 0.36377534542909D-02 3 15 1 18 -0.34013761498442D+00 -0.29127273390720D-02 1 16 1 18 0.42165008989989D-14 -0.14248825411418D-01 2 16 1 18 0.31440136644700D-01 -0.33867480518988D-01 3 16 1 18 -0.43612370464149D-01 0.24830039566380D-02 1 17 1 18 -0.97974114254991D+00 0.18266885601901D-02 2 17 1 18 -0.22712929095630D+00 -0.26549202704919D-02 3 17 1 18 -0.78365840750489D+00 -0.13606025531406D-01 1 18 1 18 0.13149817390301D+02 0.00000000000000D+00 2 18 1 18 -0.69426528609112D+01 -0.20550907331479D+00 3 18 1 18 0.12192480104859D+01 0.15981767360659D+00 1 19 1 18 0.16224381971233D+00 -0.58836121633032D-16 2 19 1 18 0.35636845037221D-01 -0.12544613644024D-08 3 19 1 18 -0.40741232101581D-01 -0.12643178917624D-06 1 20 1 18 0.31532492148395D-14 -0.30219137692492D-01 2 20 1 18 -0.80071830988697D-01 -0.38348271525883D-02 3 20 1 18 -0.66023830363373D+00 0.20917464521660D-01 1 1 2 18 -0.30490190754154D+00 0.68056519823792D-07 2 1 2 18 0.10669534109938D+01 -0.20708555513325D-06 3 1 2 18 0.13109063117039D+01 0.47398371213707D-07 1 2 2 18 0.34479890278874D+00 -0.54361281411131D-02 2 2 2 18 0.17851870533802D+01 0.22602251736406D-02 3 2 2 18 -0.13647920929388D+00 -0.13824023979031D-01 1 3 2 18 -0.29645719455468D+00 0.10397496925169D-01 2 3 2 18 0.42669990022297D+00 -0.40911720073824D-02 3 3 2 18 -0.14104596669028D+01 -0.24786916401401D-03 1 4 2 18 0.31573643564810D+00 0.78755442057477D-07 2 4 2 18 -0.13059176915070D+01 -0.55909801829090D-06 3 4 2 18 -0.12016467324019D+01 -0.66071606309402D-06 1 5 2 18 0.68146394044011D+00 -0.19992458410030D-01 2 5 2 18 0.52675461638691D+01 0.14939669842383D-01 3 5 2 18 -0.61828817619144D+00 0.66510466617497D-01 1 6 2 18 0.57101763754834D+00 0.86049775603675D-01 2 6 2 18 -0.39314070199044D+00 -0.10539739545061D+00 3 6 2 18 -0.46274463292544D+01 -0.12250041505250D-01 1 7 2 18 0.47626649773449D+00 -0.15005135265706D-01 2 7 2 18 0.50877729273305D+01 -0.39091583880342D-02 3 7 2 18 0.48293397746207D+00 -0.50088873825512D-01 1 8 2 18 0.44045047321919D+00 0.31562444327087D-01 2 8 2 18 -0.45311663921894D-01 -0.16202328843041D-01 3 8 2 18 0.39939332590607D+01 0.54859697995835D-02 1 9 2 18 -0.54403671042544D+00 0.59966148010975D-06 2 9 2 18 0.99984334761587D-01 0.18695458696233D-06 3 9 2 18 0.45233035133574D+01 0.86012076673400D-06 1 10 2 18 0.83825489427701D+00 -0.29613994108064D-01 2 10 2 18 -0.22537600443644D+00 0.41867266062296D-01 3 10 2 18 0.38475374507552D+01 0.17615986978702D+00 1 11 2 18 0.75352302634897D+00 -0.25526941972295D-06 2 11 2 18 0.44257479394557D+00 -0.31536861827255D-06 3 11 2 18 -0.31797146926205D+01 -0.81543201275040D-06 1 12 2 18 0.55834732066971D+00 0.63046389702133D-01 2 12 2 18 0.21488779706599D-01 0.45492857508524D-02 3 12 2 18 0.38203216284890D+01 -0.22302494991981D+00 1 13 2 18 -0.18812291655311D+01 -0.76904784445759D-07 2 13 2 18 -0.30894398169472D+01 0.54585001231639D-15 3 13 2 18 0.34828097813268D+00 -0.37678409538674D-06 1 14 2 18 -0.92274773342068D+00 0.50983329631422D-02 2 14 2 18 -0.75544524368440D-13 0.18910615735645D-01 3 14 2 18 0.30061611266230D-01 -0.74174299812195D-01 1 15 2 18 -0.43400177186254D-01 0.36381076052578D-02 2 15 2 18 0.76020554147980D-14 0.25620558023154D-06 3 15 2 18 0.11204977375783D+01 -0.92699308904840D-02 1 16 2 18 0.31440993033378D-01 0.33867627316431D-01 2 16 2 18 0.12598952815604D-14 0.17281658324452D-01 3 16 2 18 0.18729564246327D+00 -0.87260515821026D-02 1 17 2 18 -0.22712898881450D+00 -0.26542770768435D-02 2 17 2 18 0.63003020552732D+00 0.72209940761412D-03 3 17 2 18 0.10849401454823D+01 0.12216080443968D-01 1 18 2 18 -0.69426571478985D+01 0.20550963496243D+00 2 18 2 18 0.16540543133682D+02 0.00000000000000D+00 3 18 2 18 0.20506088072320D+01 0.20032682093087D+00 1 19 2 18 0.35636845037221D-01 0.12544612802399D-08 2 19 2 18 0.28873768072398D+00 -0.11340161208849D-14 3 19 2 18 -0.19324351108275D+00 -0.45017723971090D-07 1 20 2 18 0.80071830988701D-01 -0.38348271525883D-02 2 20 2 18 0.69340430962327D-15 0.21789018231944D-01 3 20 2 18 0.14699393025030D+01 -0.30327434888119D-01 1 1 3 18 0.81823224224857D+00 0.30844529748223D-06 2 1 3 18 0.92567424803793D+00 0.81584868760726D-07 3 1 3 18 -0.40516331287124D+00 -0.30872765706028D-06 1 2 3 18 0.56626506089950D+00 0.48887486834106D-02 2 2 3 18 0.40625835904024D+00 0.84648125232017D-02 3 2 3 18 0.24683163743508D+01 0.24138185634072D-01 1 3 3 18 -0.32589235607620D+00 -0.53961947240979D-03 2 3 3 18 -0.98454495694060D+00 -0.63353830294789D-02 3 3 3 18 -0.45332216840795D+00 -0.33781122828539D-02 1 4 3 18 -0.52399840543384D+00 -0.94125318961050D-06 2 4 3 18 -0.79397099005565D+00 0.22384955925899D-06 3 4 3 18 -0.31623867245853D+00 -0.84332937843261D-06 1 5 3 18 -0.89708384060985D+00 -0.45108112857925D-01 2 5 3 18 0.37668213502732D+00 0.52669567900929D-01 3 5 3 18 0.40120124420436D+01 0.33325999191638D-01 1 6 3 18 0.31176128987342D+00 0.24129534220527D-01 2 6 3 18 -0.18790884315294D+01 -0.37556306773516D-01 3 6 3 18 -0.16731051450904D+00 0.76010268556755D-01 1 7 3 18 0.65729793861585D+00 0.56729719069159D-01 2 7 3 18 -0.43995953810380D+00 -0.21412943871378D-01 3 7 3 18 0.47413359179876D+01 0.29166180687205D-01 1 8 3 18 -0.43515068697146D+00 -0.16001986766969D-01 2 8 3 18 0.12163822420998D+01 0.57385749439746D-02 3 8 3 18 0.29639836161839D+00 0.16795988062126D-01 1 9 3 18 -0.95367064821531D+00 -0.48363265529951D-07 2 9 3 18 0.19757613553938D+01 -0.66017240584766D-06 3 9 3 18 0.29944073876141D+01 0.20178476304812D-06 1 10 3 18 -0.74448980247686D+00 -0.36877640368577D-01 2 10 3 18 0.19277728803764D+01 0.51534844201747D-01 3 10 3 18 -0.73952045000310D+00 -0.94971861344592D-01 1 11 3 18 0.13911435770839D+01 -0.59213082755739D-06 2 11 3 18 -0.11544339529138D+01 0.11863208090852D-05 3 11 3 18 -0.80225609774917D+00 0.66510954179632D-06 1 12 3 18 -0.12756130326613D+01 0.34494705371221D-01 2 12 3 18 0.15292499234972D+01 -0.16697700502235D-02 3 12 3 18 -0.23437484698202D+01 0.17476761537554D+00 1 13 3 18 0.29234546368569D-02 -0.83167620897769D-07 2 13 3 18 0.34828097813268D+00 0.37678409638599D-06 3 13 3 18 -0.11227810170086D+01 0.53560372092002D-15 1 14 3 18 -0.30400543782107D+00 -0.27279424757350D-01 2 14 3 18 -0.30061611266267D-01 -0.74174299812195D-01 3 14 3 18 -0.32656718515572D-13 0.21347222096600D-02 1 15 3 18 0.34013846158742D+00 0.29145182007419D-02 2 15 3 18 0.11204992093733D+01 -0.92684176117339D-02 3 15 3 18 0.25086097142570D-13 0.69201871119871D-07 1 16 3 18 0.43612744495606D-01 0.24829134260823D-02 2 16 3 18 0.18729653077671D+00 0.87261315418314D-02 3 16 3 18 -0.73200388539820D-14 0.86356341490457D-02 1 17 3 18 -0.78365893399544D+00 -0.13608913465564D-01 2 17 3 18 0.10849379490595D+01 0.12217998512354D-01 3 17 3 18 0.37395346539824D+00 0.14330319628268D-02 1 18 3 18 0.12192282832176D+01 -0.15981597695191D+00 2 18 3 18 0.20506336458696D+01 -0.20032798601149D+00 3 18 3 18 0.15429838433929D+02 0.00000000000000D+00 1 19 3 18 0.40741232101578D-01 -0.12643178917798D-06 2 19 3 18 0.19324351108277D+00 -0.45017723969355D-07 3 19 3 18 -0.10368719777310D+01 0.21270824916749D-14 1 20 3 18 -0.66023830363373D+00 -0.20917464521661D-01 2 20 3 18 0.14699393025030D+01 0.30327434888120D-01 3 20 3 18 0.61441780420912D-14 -0.20130405233754D-01 1 1 1 19 -0.92518036333788D-02 -0.30638199284225D-07 2 1 1 19 0.80259503795468D+00 -0.99245323813558D-07 3 1 1 19 0.35195673198045D+00 0.59913868885384D-07 1 2 1 19 0.43486473279452D+00 -0.15350506746488D-01 2 2 1 19 -0.16761329463336D-01 -0.31249629992602D-01 3 2 1 19 -0.11152602876192D+01 -0.62582020916189D-02 1 3 1 19 0.34159599944593D-01 0.10186584683516D-01 2 3 1 19 0.50608893451168D+00 -0.25217175319895D-02 3 3 1 19 0.12198240512230D+00 -0.15071331504330D-02 1 4 1 19 -0.18060885107792D+00 0.11778815493566D-06 2 4 1 19 0.72301354005636D+00 0.72587142698633D-07 3 4 1 19 -0.14815028338497D+00 -0.18314630074189D-07 1 5 1 19 0.42653643115826D+00 0.40732564614947D-01 2 5 1 19 -0.10237005265681D+00 -0.80797304429652D-01 3 5 1 19 0.27364772025514D+01 0.35599509164343D-02 1 6 1 19 0.10161148680495D+00 -0.12921154873962D-01 2 6 1 19 0.13720704530737D+01 0.93931795399646D-02 3 6 1 19 0.21687698938742D+00 -0.45240790056756D-01 1 7 1 19 0.53668345860631D+00 0.28185231299411D-01 2 7 1 19 0.25621508332100D+00 -0.25622006102618D-01 3 7 1 19 -0.30154452868179D+01 -0.61764351561418D-02 1 8 1 19 -0.13845699646768D+01 -0.72384269306939D-02 2 8 1 19 0.26678717282475D+01 -0.10447588286235D-01 3 8 1 19 -0.44483828644708D+00 0.39228738516760D-01 1 9 1 19 -0.32727469999189D-01 -0.34537179641786D-06 2 9 1 19 0.19375862305741D+00 0.33747397414678D-06 3 9 1 19 -0.24672764490829D+01 -0.81474365519098D-06 1 10 1 19 -0.67033110219159D+00 0.13725684560805D-01 2 10 1 19 0.98026860942439D+00 -0.39454287820013D-01 3 10 1 19 0.28887231537357D+01 0.11049317929217D+00 1 11 1 19 -0.14676938359579D+01 0.53627212789725D-06 2 11 1 19 0.59663993014509D+00 0.69414797555082D-06 3 11 1 19 -0.34100493917736D+01 -0.13728680027047D-05 1 12 1 19 0.83238608982223D-01 0.59687000398189D-01 2 12 1 19 -0.30023390271233D+00 -0.12398159382866D-01 3 12 1 19 -0.28011525411381D+01 0.12637057955213D+00 1 13 1 19 -0.27779041561395D-14 0.14248825411419D-01 2 13 1 19 -0.31440136644699D-01 0.33867480518988D-01 3 13 1 19 -0.43612370464151D-01 0.24830039566379D-02 1 14 1 19 0.16722551646527D-14 0.49131391012793D-07 2 14 1 19 -0.43399967089215D-01 0.36377534542909D-02 3 14 1 19 0.34013761498442D+00 0.29127273390720D-02 1 15 1 19 0.17835257267174D-14 -0.65408225279571D-02 2 15 1 19 -0.92274773342068D+00 -0.50983329631379D-02 3 15 1 19 0.30400543782107D+00 -0.27279424757350D-01 1 16 1 19 -0.60682061506544D+01 0.40671976187086D-14 2 16 1 19 -0.18812291655311D+01 0.76904784192842D-07 3 16 1 19 -0.29234546368585D-02 -0.83167620885416D-07 1 17 1 19 0.28754209331204D-14 0.30219137692492D-01 2 17 1 19 0.80071830988701D-01 0.38348271525881D-02 3 17 1 19 -0.66023830363373D+00 0.20917464521660D-01 1 18 1 19 0.16224381971233D+00 0.58836121633032D-16 2 18 1 19 0.35636845037221D-01 -0.12544612802399D-08 3 18 1 19 0.40741232101578D-01 0.12643178917798D-06 1 19 1 19 0.13149817390301D+02 0.00000000000000D+00 2 19 1 19 -0.69426528609112D+01 -0.20550907331479D+00 3 19 1 19 -0.12192480104860D+01 -0.15981767360659D+00 1 20 1 19 0.97974114254992D+00 -0.18266885601918D-02 2 20 1 19 0.22712929095632D+00 0.26549202704905D-02 3 20 1 19 -0.78365840750488D+00 -0.13606025531407D-01 1 1 2 19 0.30490190754154D+00 -0.68056517977089D-07 2 1 2 19 -0.10669534109938D+01 0.20708555150975D-06 3 1 2 19 0.13109063117039D+01 0.47398375054110D-07 1 2 2 19 0.34479890278867D+00 -0.54361281411128D-02 2 2 2 19 0.17851870533802D+01 0.22602251736390D-02 3 2 2 19 0.13647920929400D+00 0.13824023979031D-01 1 3 2 19 0.29645719455468D+00 -0.10397496925168D-01 2 3 2 19 -0.42669990022294D+00 0.40911720073836D-02 3 3 2 19 -0.14104596669028D+01 -0.24786916401684D-03 1 4 2 19 0.31573643564815D+00 0.78755442155845D-07 2 4 2 19 -0.13059176915071D+01 -0.55909801791248D-06 3 4 2 19 0.12016467324020D+01 0.66071606444975D-06 1 5 2 19 -0.57101763754834D+00 -0.86049775603676D-01 2 5 2 19 0.39314070199043D+00 0.10539739545061D+00 3 5 2 19 -0.46274463292544D+01 -0.12250041505249D-01 1 6 2 19 -0.68146394044004D+00 0.19992458410007D-01 2 6 2 19 -0.52675461638692D+01 -0.14939669842362D-01 3 6 2 19 -0.61828817619151D+00 0.66510466617486D-01 1 7 2 19 -0.44045047321920D+00 -0.31562444327087D-01 2 7 2 19 0.45311663921905D-01 0.16202328843040D-01 3 7 2 19 0.39939332590606D+01 0.54859697995845D-02 1 8 2 19 -0.47626649773444D+00 0.15005135265684D-01 2 8 2 19 -0.50877729273305D+01 0.39091583880366D-02 3 8 2 19 0.48293397746209D+00 -0.50088873825508D-01 1 9 2 19 0.54403671042544D+00 -0.59966148074392D-06 2 9 2 19 -0.99984334761571D-01 -0.18695458614065D-06 3 9 2 19 0.45233035133575D+01 0.86012076112794D-06 1 10 2 19 0.83825489427700D+00 -0.29613994108064D-01 2 10 2 19 -0.22537600443645D+00 0.41867266062295D-01 3 10 2 19 -0.38475374507552D+01 -0.17615986978702D+00 1 11 2 19 0.75352302634896D+00 -0.25526941998559D-06 2 11 2 19 0.44257479394552D+00 -0.31536862021294D-06 3 11 2 19 0.31797146926205D+01 0.81543201231680D-06 1 12 2 19 -0.55834732066971D+00 -0.63046389702132D-01 2 12 2 19 -0.21488779706582D-01 -0.45492857508541D-02 3 12 2 19 0.38203216284890D+01 -0.22302494991981D+00 1 13 2 19 -0.31440993033376D-01 -0.33867627316431D-01 2 13 2 19 -0.39859085097935D-14 -0.17281658324453D-01 3 13 2 19 0.18729564246326D+00 -0.87260515821019D-02 1 14 2 19 -0.43400177186255D-01 0.36381076052579D-02 2 14 2 19 -0.34959339848509D-14 0.25620557990984D-06 3 14 2 19 -0.11204977375783D+01 0.92699308904839D-02 1 15 2 19 -0.92274773342067D+00 0.50983329631423D-02 2 15 2 19 -0.59557312390321D-13 0.18910615735641D-01 3 15 2 19 -0.30061611266251D-01 0.74174299812196D-01 1 16 2 19 0.18812291655311D+01 0.76904784437655D-07 2 16 2 19 0.30894398169471D+01 -0.29979833576050D-14 3 16 2 19 0.34828097813269D+00 -0.37678409625921D-06 1 17 2 19 -0.80071830988698D-01 0.38348271525881D-02 2 17 2 19 0.11475469251514D-14 -0.21789018231943D-01 3 17 2 19 0.14699393025031D+01 -0.30327434888119D-01 1 18 2 19 0.35636845037221D-01 0.12544613644024D-08 2 18 2 19 0.28873768072398D+00 0.11340161208849D-14 3 18 2 19 0.19324351108277D+00 0.45017723969355D-07 1 19 2 19 -0.69426571478985D+01 0.20550963496243D+00 2 19 2 19 0.16540543133682D+02 0.00000000000000D+00 3 19 2 19 -0.20506088072320D+01 -0.20032682093087D+00 1 20 2 19 0.22712898881451D+00 0.26542770768421D-02 2 20 2 19 -0.63003020552731D+00 -0.72209940761336D-03 3 20 2 19 0.10849401454823D+01 0.12216080443966D-01 1 1 3 19 0.81823224224859D+00 0.30844530402627D-06 2 1 3 19 0.92567424803794D+00 0.81584872601130D-07 3 1 3 19 0.40516331287125D+00 0.30872767449097D-06 1 2 3 19 -0.56626506089947D+00 -0.48887486834107D-02 2 2 3 19 -0.40625835904010D+00 -0.84648125232020D-02 3 2 3 19 0.24683163743509D+01 0.24138185634074D-01 1 3 3 19 -0.32589235607622D+00 -0.53961947241188D-03 2 3 3 19 -0.98454495694062D+00 -0.63353830294817D-02 3 3 3 19 0.45332216840797D+00 0.33781122828567D-02 1 4 3 19 0.52399840543387D+00 0.94125318945603D-06 2 4 3 19 0.79397099005575D+00 -0.22384955790326D-06 3 4 3 19 -0.31623867245860D+00 -0.84332937766254D-06 1 5 3 19 0.31176128987342D+00 0.24129534220526D-01 2 5 3 19 -0.18790884315294D+01 -0.37556306773515D-01 3 5 3 19 0.16731051450898D+00 -0.76010268556752D-01 1 6 3 19 -0.89708384060983D+00 -0.45108112857919D-01 2 6 3 19 0.37668213502725D+00 0.52669567900918D-01 3 6 3 19 -0.40120124420436D+01 -0.33325999191659D-01 1 7 3 19 -0.43515068697145D+00 -0.16001986766968D-01 2 7 3 19 0.12163822420998D+01 0.57385749439757D-02 3 7 3 19 -0.29639836161839D+00 -0.16795988062121D-01 1 8 3 19 0.65729793861583D+00 0.56729719069151D-01 2 8 3 19 -0.43995953810379D+00 -0.21412943871374D-01 3 8 3 19 -0.47413359179875D+01 -0.29166180687227D-01 1 9 3 19 -0.95367064821530D+00 -0.48363263410280D-07 2 9 3 19 0.19757613553939D+01 -0.66017241148147D-06 3 9 3 19 -0.29944073876141D+01 -0.20178475715238D-06 1 10 3 19 0.74448980247685D+00 0.36877640368577D-01 2 10 3 19 -0.19277728803764D+01 -0.51534844201748D-01 3 10 3 19 -0.73952045000315D+00 -0.94971861344592D-01 1 11 3 19 -0.13911435770839D+01 0.59213082744767D-06 2 11 3 19 0.11544339529138D+01 -0.11863208095049D-05 3 11 3 19 -0.80225609774920D+00 0.66510954116587D-06 1 12 3 19 -0.12756130326613D+01 0.34494705371224D-01 2 12 3 19 0.15292499234972D+01 -0.16697700502264D-02 3 12 3 19 0.23437484698202D+01 -0.17476761537554D+00 1 13 3 19 0.43612744495604D-01 0.24829134260823D-02 2 13 3 19 0.18729653077669D+00 0.87261315418321D-02 3 13 3 19 -0.53216374096568D-14 -0.86356341490434D-02 1 14 3 19 -0.34013846158742D+00 -0.29145182007419D-02 2 14 3 19 -0.11204992093733D+01 0.92684176117338D-02 3 14 3 19 0.10086432938211D-13 0.69201871423545D-07 1 15 3 19 0.30400543782107D+00 0.27279424757350D-01 2 15 3 19 0.30061611266246D-01 0.74174299812196D-01 3 15 3 19 -0.36653521615981D-13 0.21347222096603D-02 1 16 3 19 0.29234546368589D-02 -0.83167620899077D-07 2 16 3 19 0.34828097813269D+00 0.37678409551179D-06 3 16 3 19 0.11227810170085D+01 -0.75593971096973D-14 1 17 3 19 -0.66023830363373D+00 -0.20917464521661D-01 2 17 3 19 0.14699393025031D+01 0.30327434888120D-01 3 17 3 19 -0.14259849023293D-15 0.20130405233753D-01 1 18 3 19 -0.40741232101581D-01 0.12643178917624D-06 2 18 3 19 -0.19324351108275D+00 0.45017723971090D-07 3 18 3 19 -0.10368719777310D+01 -0.21270824916749D-14 1 19 3 19 -0.12192282832176D+01 0.15981597695191D+00 2 19 3 19 -0.20506336458695D+01 0.20032798601149D+00 3 19 3 19 0.15429838433929D+02 0.00000000000000D+00 1 20 3 19 -0.78365893399543D+00 -0.13608913465564D-01 2 20 3 19 0.10849379490595D+01 0.12217998512352D-01 3 20 3 19 -0.37395346539826D+00 -0.14330319628263D-02 1 1 1 20 0.43486473279457D+00 -0.15350506746488D-01 2 1 1 20 -0.16761329463243D-01 -0.31249629992591D-01 3 1 1 20 -0.11152602876193D+01 -0.62582020916367D-02 1 2 1 20 -0.92518036334017D-02 -0.30638199337122D-07 2 2 1 20 0.80259503795470D+00 -0.99245323504493D-07 3 2 1 20 0.35195673198040D+00 0.59913869158788D-07 1 3 1 20 -0.18060885107792D+00 0.11778815525214D-06 2 3 1 20 0.72301354005637D+00 0.72587141989616D-07 3 3 1 20 -0.14815028338498D+00 -0.18314630510653D-07 1 4 1 20 0.34159599944591D-01 0.10186584683516D-01 2 4 1 20 0.50608893451168D+00 -0.25217175319899D-02 3 4 1 20 0.12198240512231D+00 -0.15071331504331D-02 1 5 1 20 -0.42653643115827D+00 -0.40732564614947D-01 2 5 1 20 0.10237005265681D+00 0.80797304429651D-01 3 5 1 20 -0.27364772025514D+01 -0.35599509164345D-02 1 6 1 20 0.10161148680499D+00 -0.12921154873962D-01 2 6 1 20 0.13720704530733D+01 0.93931795399654D-02 3 6 1 20 0.21687698938734D+00 -0.45240790056755D-01 1 7 1 20 0.53668345860631D+00 0.28185231299410D-01 2 7 1 20 0.25621508332101D+00 -0.25622006102618D-01 3 7 1 20 -0.30154452868179D+01 -0.61764351561413D-02 1 8 1 20 0.13845699646771D+01 0.72384269307147D-02 2 8 1 20 -0.26678717282476D+01 0.10447588286213D-01 3 8 1 20 0.44483828644672D+00 -0.39228738516769D-01 1 9 1 20 -0.67033110219162D+00 0.13725684560805D-01 2 9 1 20 0.98026860942437D+00 -0.39454287820013D-01 3 9 1 20 0.28887231537357D+01 0.11049317929217D+00 1 10 1 20 -0.32727469999228D-01 -0.34537179637631D-06 2 10 1 20 0.19375862305742D+00 0.33747397402677D-06 3 10 1 20 -0.24672764490830D+01 -0.81474365515647D-06 1 11 1 20 0.83238608982223D-01 0.59687000398189D-01 2 11 1 20 -0.30023390271232D+00 -0.12398159382869D-01 3 11 1 20 -0.28011525411381D+01 0.12637057955212D+00 1 12 1 20 -0.14676938359579D+01 0.53627212794776D-06 2 12 1 20 0.59663993014510D+00 0.69414797575796D-06 3 12 1 20 -0.34100493917736D+01 -0.13728680027809D-05 1 13 1 20 0.19603351542170D-14 0.49131390844874D-07 2 13 1 20 -0.43399967089214D-01 0.36377534542908D-02 3 13 1 20 0.34013761498442D+00 0.29127273390724D-02 1 14 1 20 0.30460218137475D-15 0.14248825411419D-01 2 14 1 20 -0.31440136644699D-01 0.33867480518988D-01 3 14 1 20 -0.43612370464145D-01 0.24830039566380D-02 1 15 1 20 -0.60682061506544D+01 0.41183561701195D-14 2 15 1 20 -0.18812291655311D+01 0.76904784159032D-07 3 15 1 20 -0.29234546368449D-02 -0.83167620888721D-07 1 16 1 20 -0.36911241986853D-14 -0.65408225279594D-02 2 16 1 20 -0.92274773342067D+00 -0.50983329631403D-02 3 16 1 20 0.30400543782107D+00 -0.27279424757350D-01 1 17 1 20 0.16224381971233D+00 -0.43789100713492D-15 2 17 1 20 0.35636845037221D-01 -0.12544613005945D-08 3 17 1 20 0.40741232101578D-01 0.12643178917642D-06 1 18 1 20 0.31532492148395D-14 0.30219137692492D-01 2 18 1 20 0.80071830988701D-01 0.38348271525883D-02 3 18 1 20 -0.66023830363373D+00 0.20917464521661D-01 1 19 1 20 0.97974114254992D+00 -0.18266885601879D-02 2 19 1 20 0.22712929095632D+00 0.26549202704927D-02 3 19 1 20 -0.78365840750488D+00 -0.13606025531406D-01 1 20 1 20 0.13149817390301D+02 0.00000000000000D+00 2 20 1 20 -0.69426528609109D+01 -0.20550907331479D+00 3 20 1 20 -0.12192480104862D+01 -0.15981767360659D+00 1 1 2 20 0.34479890278876D+00 -0.54361281411016D-02 2 1 2 20 0.17851870533801D+01 0.22602251736433D-02 3 1 2 20 0.13647920929385D+00 0.13824023979003D-01 1 2 2 20 0.30490190754157D+00 -0.68056517666289D-07 2 2 2 20 -0.10669534109937D+01 0.20708555195190D-06 3 2 2 20 0.13109063117039D+01 0.47398375109540D-07 1 3 2 20 0.31573643564817D+00 0.78755441446828D-07 2 3 2 20 -0.13059176915071D+01 -0.55909801624961D-06 3 3 2 20 0.12016467324020D+01 0.66071606395398D-06 1 4 2 20 0.29645719455468D+00 -0.10397496925168D-01 2 4 2 20 -0.42669990022294D+00 0.40911720073847D-02 3 4 2 20 -0.14104596669028D+01 -0.24786916401714D-03 1 5 2 20 0.57101763754834D+00 0.86049775603675D-01 2 5 2 20 -0.39314070199046D+00 -0.10539739545061D+00 3 5 2 20 0.46274463292544D+01 0.12250041505252D-01 1 6 2 20 -0.68146394044037D+00 0.19992458410008D-01 2 6 2 20 -0.52675461638689D+01 -0.14939669842361D-01 3 6 2 20 -0.61828817619138D+00 0.66510466617482D-01 1 7 2 20 -0.44045047321919D+00 -0.31562444327087D-01 2 7 2 20 0.45311663921887D-01 0.16202328843042D-01 3 7 2 20 0.39939332590606D+01 0.54859697995825D-02 1 8 2 20 0.47626649773431D+00 -0.15005135265706D-01 2 8 2 20 0.50877729273303D+01 -0.39091583880332D-02 3 8 2 20 -0.48293397746185D+00 0.50088873825511D-01 1 9 2 20 0.83825489427698D+00 -0.29613994108063D-01 2 9 2 20 -0.22537600443643D+00 0.41867266062295D-01 3 9 2 20 -0.38475374507551D+01 -0.17615986978702D+00 1 10 2 20 0.54403671042544D+00 -0.59966148086220D-06 2 10 2 20 -0.99984334761581D-01 -0.18695458647508D-06 3 10 2 20 0.45233035133574D+01 0.86012076185069D-06 1 11 2 20 -0.55834732066970D+00 -0.63046389702135D-01 2 11 2 20 -0.21488779706536D-01 -0.45492857508530D-02 3 11 2 20 0.38203216284890D+01 -0.22302494991980D+00 1 12 2 20 0.75352302634897D+00 -0.25526941977846D-06 2 12 2 20 0.44257479394548D+00 -0.31536861965594D-06 3 12 2 20 0.31797146926206D+01 0.81543201226342D-06 1 13 2 20 -0.43400177186253D-01 0.36381076052577D-02 2 13 2 20 0.89686045629277D-14 0.25620558039252D-06 3 13 2 20 -0.11204977375783D+01 0.92699308904828D-02 1 14 2 20 -0.31440993033377D-01 -0.33867627316431D-01 2 14 2 20 -0.26647172695652D-13 -0.17281658324452D-01 3 14 2 20 0.18729564246324D+00 -0.87260515821039D-02 1 15 2 20 0.18812291655310D+01 0.76904784403845D-07 2 15 2 20 0.30894398169472D+01 -0.29181076302896D-14 3 15 2 20 0.34828097813268D+00 -0.37678409641664D-06 1 16 2 20 -0.92274773342067D+00 0.50983329631400D-02 2 16 2 20 0.36329804731328D-13 0.18910615735655D-01 3 16 2 20 -0.30061611266245D-01 0.74174299812194D-01 1 17 2 20 0.35636845037221D-01 0.12544613440478D-08 2 17 2 20 0.28873768072398D+00 0.11477125585121D-14 3 17 2 20 0.19324351108276D+00 0.45017725813162D-07 1 18 2 20 -0.80071830988697D-01 0.38348271525883D-02 2 18 2 20 0.69340430962327D-15 -0.21789018231944D-01 3 18 2 20 0.14699393025030D+01 -0.30327434888120D-01 1 19 2 20 0.22712898881451D+00 0.26542770768443D-02 2 19 2 20 -0.63003020552731D+00 -0.72209940761265D-03 3 19 2 20 0.10849401454823D+01 0.12216080443964D-01 1 20 2 20 -0.69426571478982D+01 0.20550963496243D+00 2 20 2 20 0.16540543133681D+02 0.00000000000000D+00 3 20 2 20 -0.20506088072321D+01 -0.20032682093087D+00 1 1 3 20 -0.56626506089964D+00 -0.48887486834285D-02 2 1 3 20 -0.40625835904024D+00 -0.84648125232295D-02 3 1 3 20 0.24683163743510D+01 0.24138185634092D-01 1 2 3 20 0.81823224224854D+00 0.30844530430314D-06 2 2 3 20 0.92567424803803D+00 0.81584872658294D-07 3 2 3 20 0.40516331287122D+00 0.30872767432246D-06 1 3 3 20 0.52399840543386D+00 0.94125318901957D-06 2 3 3 20 0.79397099005579D+00 -0.22384955839903D-06 3 3 3 20 -0.31623867245856D+00 -0.84332937552216D-06 1 4 3 20 -0.32589235607620D+00 -0.53961947241195D-03 2 4 3 20 -0.98454495694062D+00 -0.63353830294820D-02 3 4 3 20 0.45332216840794D+00 0.33781122828569D-02 1 5 3 20 -0.31176128987343D+00 -0.24129534220526D-01 2 5 3 20 0.18790884315294D+01 0.37556306773517D-01 3 5 3 20 -0.16731051450894D+00 0.76010268556757D-01 1 6 3 20 -0.89708384060991D+00 -0.45108112857919D-01 2 6 3 20 0.37668213502738D+00 0.52669567900914D-01 3 6 3 20 -0.40120124420440D+01 -0.33325999191660D-01 1 7 3 20 -0.43515068697144D+00 -0.16001986766968D-01 2 7 3 20 0.12163822420998D+01 0.57385749439736D-02 3 7 3 20 -0.29639836161845D+00 -0.16795988062121D-01 1 8 3 20 -0.65729793861618D+00 -0.56729719069159D-01 2 8 3 20 0.43995953810403D+00 0.21412943871378D-01 3 8 3 20 0.47413359179874D+01 0.29166180687207D-01 1 9 3 20 0.74448980247682D+00 0.36877640368577D-01 2 9 3 20 -0.19277728803763D+01 -0.51534844201747D-01 3 9 3 20 -0.73952045000309D+00 -0.94971861344588D-01 1 10 3 20 -0.95367064821532D+00 -0.48363263382715D-07 2 10 3 20 0.19757613553938D+01 -0.66017241075872D-06 3 10 3 20 -0.29944073876140D+01 -0.20178475547967D-06 1 11 3 20 -0.12756130326613D+01 0.34494705371218D-01 2 11 3 20 0.15292499234972D+01 -0.16697700502190D-02 3 11 3 20 0.23437484698201D+01 -0.17476761537553D+00 1 12 3 20 -0.13911435770839D+01 0.59213082737143D-06 2 12 3 20 0.11544339529139D+01 -0.11863208095583D-05 3 12 3 20 -0.80225609774919D+00 0.66510954053696D-06 1 13 3 20 -0.34013846158742D+00 -0.29145182007415D-02 2 13 3 20 -0.11204992093732D+01 0.92684176117327D-02 3 13 3 20 0.13587309403008D-13 0.69201872636558D-07 1 14 3 20 0.43612744495610D-01 0.24829134260823D-02 2 14 3 20 0.18729653077667D+00 0.87261315418301D-02 3 14 3 20 -0.37518137193011D-13 -0.86356341490456D-02 1 15 3 20 0.29234546368725D-02 -0.83167620902382D-07 2 15 3 20 0.34828097813268D+00 0.37678409535523D-06 3 15 3 20 0.11227810170086D+01 -0.29317705992345D-14 1 16 3 20 0.30400543782107D+00 0.27279424757350D-01 2 16 3 20 0.30061611266252D-01 0.74174299812194D-01 3 16 3 20 -0.93789803891226D-14 0.21347222096605D-02 1 17 3 20 -0.40741232101581D-01 0.12643178917469D-06 2 17 3 20 -0.19324351108275D+00 0.45017725814897D-07 3 17 3 20 -0.10368719777310D+01 0.50695058562776D-15 1 18 3 20 -0.66023830363373D+00 -0.20917464521660D-01 2 18 3 20 0.14699393025030D+01 0.30327434888119D-01 3 18 3 20 0.61441780420912D-14 0.20130405233754D-01 1 19 3 20 -0.78365893399543D+00 -0.13608913465564D-01 2 19 3 20 0.10849379490595D+01 0.12217998512351D-01 3 19 3 20 -0.37395346539826D+00 -0.14330319628274D-02 1 20 3 20 -0.12192282832179D+01 0.15981597695191D+00 2 20 3 20 -0.20506336458697D+01 0.20032798601149D+00 3 20 3 20 0.15429838433928D+02 0.00000000000000D+00
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 5.00000000E-01 5.00000000E-01 1.0 1 1 1 1 0.89988262692113D+01 0.00000000000000D+00 2 1 1 1 0.13273567434368D+01 0.57199711370141D-06 3 1 1 1 -0.43068421978871D-13 0.00000000000000D+00 1 2 1 1 0.15192993816476D-13 -0.48677212514569D-14 2 2 1 1 0.15982460963386D-13 0.62344082924050D-15 3 2 1 1 0.57918343930094D-01 0.65253877336862D-08 1 3 1 1 0.46702592785630D-14 -0.86032290001362D-08 2 3 1 1 -0.23064140651240D+01 -0.55454090203115D-08 3 3 1 1 -0.34668326382139D-14 0.39310418732198D-16 1 4 1 1 -0.84217037468504D-14 0.60931377461179D-15 2 4 1 1 0.37509449824175D-14 -0.19504706850149D-15 3 4 1 1 -0.30083899582474D+00 -0.25433258668932D-08 1 5 1 1 0.60636549210166D+00 -0.42085538741850D-02 2 5 1 1 0.31761822919589D+00 -0.21355621797700D-02 3 5 1 1 0.39711644530348D+00 0.29270099808045D-02 1 6 1 1 0.60636549210170D+00 -0.42085538741836D-02 2 6 1 1 0.31761822919590D+00 -0.21355621797699D-02 3 6 1 1 -0.39711644530348D+00 -0.29270099808049D-02 1 7 1 1 -0.12845923974808D+00 -0.31058073606039D-01 2 7 1 1 0.35116554270211D+00 0.64737058921261D-03 3 7 1 1 0.64874695791644D+01 -0.95073242474050D-02 1 8 1 1 -0.12845923974806D+00 -0.31058073606039D-01 2 8 1 1 0.35116554270211D+00 0.64737058921425D-03 3 8 1 1 -0.64874695791644D+01 0.95073242474067D-02 1 9 1 1 -0.36319127869882D+00 0.12333021066653D-07 2 9 1 1 0.12577957172345D+00 0.21635480022470D-07 3 9 1 1 0.63178138756494D-14 0.19065299584286D-15 1 10 1 1 0.13537165724066D-14 0.20115044373706D-15 2 10 1 1 0.50497906954923D-14 -0.17954357147441D-15 3 10 1 1 -0.35225490033342D+00 0.31162646733630D-08 1 11 1 1 -0.17828020597083D-14 -0.59725279318935D-16 2 11 1 1 -0.30986602126738D-15 0.15990210447902D-16 3 11 1 1 0.24095667808050D+01 -0.12254095036523D-07 1 12 1 1 0.32584030570683D+01 -0.57307604220800D-08 2 12 1 1 -0.12134762704438D+00 -0.35866681802991D-08 3 12 1 1 -0.47748309577196D-14 0.19471133486508D-15 1 13 1 1 0.84163095559425D+00 0.23254878629976D-08 2 13 1 1 0.95320618894116D+00 -0.52200324591699D-08 3 13 1 1 -0.84564277358091D+00 -0.20158172505994D-07 1 14 1 1 -0.40053332053902D+00 -0.13838444397699D-01 2 14 1 1 -0.78714711650421D+00 -0.15604524917161D-01 3 14 1 1 -0.70042568642642D+00 -0.14423150740342D-02 1 15 1 1 0.40053332053902D+00 0.13838444397698D-01 2 15 1 1 0.78714711650424D+00 0.15604524917164D-01 3 15 1 1 -0.70042568642646D+00 -0.14423150740322D-02 1 16 1 1 0.84163095559426D+00 0.23254889846113D-08 2 16 1 1 0.95320618894116D+00 -0.52200316621642D-08 3 16 1 1 0.84564277358097D+00 0.20158171705550D-07 1 17 1 1 -0.11682226319502D+01 -0.87286015242564D-02 2 17 1 1 0.14641252210917D+00 -0.16744411954459D-01 3 17 1 1 -0.23054956166593D+00 0.15504920857026D-02 1 18 1 1 0.53789782066794D+00 0.15056872959353D-06 2 18 1 1 -0.68712473251339D+00 -0.19760182082258D-06 3 18 1 1 0.11902835930204D+01 0.22901719213410D-06 1 19 1 1 -0.53789782066791D+00 -0.15056873131803D-06 2 19 1 1 0.68712473251340D+00 0.19760181900191D-06 3 19 1 1 0.11902835930204D+01 0.22901718511439D-06 1 20 1 1 -0.11682226319502D+01 -0.87286015242546D-02 2 20 1 1 0.14641252210914D+00 -0.16744411954459D-01 3 20 1 1 0.23054956166592D+00 -0.15504920857018D-02 1 1 2 1 0.13273531362024D+01 0.62595422724576D-06 2 1 2 1 0.88562707050896D+01 0.00000000000000D+00 3 1 2 1 -0.25718077050176D-13 -0.11102230246252D-15 1 2 2 1 0.15982460963386D-13 0.62344082924050D-15 2 2 2 1 0.86299860371912D-14 0.50594949675394D-14 3 2 2 1 -0.39775958539700D+00 -0.58974324149907D-09 1 3 2 1 -0.23064140651239D+01 0.55454252750456D-08 2 3 2 1 0.10597629981962D-13 -0.84115977597669D-08 3 3 2 1 0.30416398452973D-16 0.16677837658653D-15 1 4 2 1 0.37509449815903D-14 -0.19504706850149D-15 2 4 2 1 -0.96847634162176D-14 0.56202573797586D-15 3 4 2 1 0.49705989637781D-01 -0.66113756789006D-08 1 5 2 1 0.11893782534885D+00 -0.96931299378288D-03 2 5 2 1 -0.75557409289752D+00 0.13834039556009D-01 3 5 2 1 0.63824951117218D+01 0.16443904434713D-01 1 6 2 1 0.11893782534886D+00 -0.96931299378279D-03 2 6 2 1 -0.75557409289750D+00 0.13834039556007D-01 3 6 2 1 -0.63824951117217D+01 -0.16443904434712D-01 1 7 2 1 0.54241979068730D+00 0.53702044046859D-02 2 7 2 1 -0.64023917450728D+00 0.82649819979753D-02 3 7 2 1 0.15622400674681D-02 0.32920533895527D-02 1 8 2 1 0.54241979068730D+00 0.53702044046876D-02 2 8 2 1 -0.64023917450727D+00 0.82649819979741D-02 3 8 2 1 -0.15622400674623D-02 -0.32920533895525D-02 1 9 2 1 -0.23107319893686D+00 0.41078804338895D-08 2 9 2 1 -0.20831002667813D+01 0.95482930354304D-08 3 9 2 1 0.56658033344280D-14 0.24650863928752D-14 1 10 2 1 0.50502524839585D-14 -0.17910989060541D-15 2 10 2 1 0.34013611601607D-14 0.38481120534800D-16 3 10 2 1 -0.23291021470691D+01 -0.20432359689184D-07 1 11 2 1 -0.30986602204286D-15 0.16423891316896D-16 2 11 2 1 -0.27123883299397D-14 0.24082624468052D-15 3 11 2 1 0.20828577590339D+00 -0.70889439862756D-08 1 12 2 1 -0.16810517670985D+00 -0.53107829509350D-08 2 12 2 1 0.34031489089165D+00 0.26520271124117D-08 3 12 2 1 0.70036480997908D-15 -0.53230201486339D-15 1 13 2 1 0.80557933044719D+00 -0.55138757901857D-08 2 13 2 1 0.88299059641767D+00 0.69515488723976D-08 3 13 2 1 0.67932742941592D+00 0.17790193892941D-07 1 14 2 1 -0.78632530987330D+00 -0.63106206074891D-02 2 14 2 1 -0.29452192971427D+00 -0.42432835830072D-02 3 14 2 1 0.78834034603551D+00 -0.20194645910240D-02 1 15 2 1 0.78632530987332D+00 0.63106206074919D-02 2 15 2 1 0.29452192971427D+00 0.42432835830072D-02 3 15 2 1 0.78834034603552D+00 -0.20194645910286D-02 1 16 2 1 0.80557933044719D+00 -0.55138749897105D-08 2 16 2 1 0.88299059641765D+00 0.69515500061396D-08 3 16 2 1 -0.67932742941597D+00 -0.17790190676979D-07 1 17 2 1 0.51689538388875D-01 -0.33029634723405D-01 2 17 2 1 -0.15713437869597D+01 0.18478138079790D-02 3 17 2 1 -0.52264722169611D+00 0.33296080090905D-02 1 18 2 1 -0.71678759202771D+00 -0.58517304308561D-07 2 18 2 1 0.64763245546005D+00 -0.26415742414275D-06 3 18 2 1 0.10013965666997D+01 0.45336947240118D-06 1 19 2 1 0.71678759202771D+00 0.58517302486157D-07 2 19 2 1 -0.64763245546005D+00 0.26415742757879D-06 3 19 2 1 0.10013965666997D+01 0.45336946655671D-06 1 20 2 1 0.51689538388818D-01 -0.33029634723406D-01 2 20 2 1 -0.15713437869597D+01 0.18478138079828D-02 3 20 2 1 0.52264722169611D+00 -0.33296080090898D-02 1 1 3 1 -0.43068421978871D-13 0.11102230246252D-15 2 1 3 1 -0.25718077063411D-13 0.11102230246252D-15 3 1 3 1 0.14389037999128D+02 0.00000000000000D+00 1 2 3 1 0.57917839242202D-01 -0.10843310414748D-07 2 2 3 1 -0.39775755527541D+00 -0.36263432274629D-09 3 2 3 1 -0.54172065598362D-13 0.82070130361909D-14 1 3 3 1 -0.34668326382139D-14 0.39310418732198D-16 2 3 3 1 0.30416398297877D-16 0.16677837658653D-15 3 3 3 1 0.14146049734213D-13 -0.18682927754594D-08 1 4 3 1 -0.30083899582474D+00 0.25433274085678D-08 2 4 3 1 -0.49705989637847D-01 -0.66113756789006D-08 3 4 3 1 0.95246547552954D-15 -0.10974041967094D-14 1 5 3 1 -0.20820342969383D+00 -0.15159211048925D-02 2 5 3 1 0.55231091070683D+01 0.11281895321223D-01 3 5 3 1 -0.54803933629177D+00 0.21211865159825D-02 1 6 3 1 0.20820342969383D+00 0.15159211048921D-02 2 6 3 1 -0.55231091070683D+01 -0.11281895321222D-01 3 6 3 1 -0.54803933629174D+00 0.21211865159821D-02 1 7 3 1 0.51831940275149D+01 -0.10292072185768D-01 2 7 3 1 -0.31208497403830D+00 0.17471032892683D-02 3 7 3 1 0.11343374882711D+01 -0.26622721372256D-02 1 8 3 1 -0.51831940275149D+01 0.10292072185770D-01 2 8 3 1 0.31208497403831D+00 -0.17471032892681D-02 3 8 3 1 0.11343374882711D+01 -0.26622721372263D-02 1 9 3 1 0.63178138768902D-14 0.19065299584286D-15 2 9 3 1 0.56658033352552D-14 0.24650863928752D-14 3 9 3 1 -0.10931789013953D+01 0.25724904889348D-07 1 10 3 1 0.95301266759511D-01 0.74374275013123D-08 2 10 3 1 -0.58080560419071D+00 0.75773551276391D-08 3 10 3 1 -0.31620623244517D-16 0.24200207883688D-15 1 11 3 1 0.62248111267650D+00 -0.17489672209200D-07 2 11 3 1 -0.85025806103171D-01 0.69288400202447D-08 3 11 3 1 0.14136811392578D-14 0.11793863256881D-14 1 12 3 1 -0.47748309577196D-14 0.19471133486508D-15 2 12 3 1 0.70036481018587D-15 -0.53230201486339D-15 3 12 3 1 0.60405779955809D+00 -0.64228702190344D-07 1 13 3 1 -0.44828247296916D+00 0.14105206728128D-07 2 13 3 1 0.73874301785765D+00 -0.15679500367278D-07 3 13 3 1 0.33564101453543D-02 0.14151722417617D-07 1 14 3 1 -0.61948808567300D+00 0.29798087047795D-02 2 14 3 1 0.55375110754942D+00 0.17221670951169D-03 3 14 3 1 0.38453250910952D+00 -0.49275599810510D-02 1 15 3 1 -0.61948808567303D+00 0.29798087047815D-02 2 15 3 1 0.55375110754941D+00 0.17221670950711D-03 3 15 3 1 -0.38453250910952D+00 0.49275599810541D-02 1 16 3 1 0.44828247296922D+00 -0.14105207529440D-07 2 16 3 1 -0.73874301785768D+00 0.15679503583240D-07 3 16 3 1 0.33564101453405D-02 0.14151723292812D-07 1 17 3 1 -0.67078264993156D+00 -0.97105436486160D-02 2 17 3 1 -0.33257813959708D+00 -0.17228537221859D-02 3 17 3 1 -0.20724822922072D+01 0.20038783343433D-01 1 18 3 1 0.11674946922127D+01 0.43632838127262D-07 2 18 3 1 0.76341655697845D+00 -0.17317798991693D-06 3 18 3 1 -0.48038748013563D+00 0.91572769342554D-07 1 19 3 1 0.11674946922127D+01 0.43632831098885D-07 2 19 3 1 0.76341655697846D+00 -0.17317799575967D-06 3 19 3 1 0.48038748013563D+00 -0.91572779890746D-07 1 20 3 1 0.67078264993154D+00 0.97105436486168D-02 2 20 3 1 0.33257813959707D+00 0.17228537221866D-02 3 20 3 1 -0.20724822922071D+01 0.20038783343432D-01 1 1 1 2 0.15192993816476D-13 0.48677212514569D-14 2 1 1 2 0.15982460963179D-13 -0.62344082924050D-15 3 1 1 2 0.57918343930094D-01 0.65253902783935D-08 1 2 1 2 0.89988262692113D+01 0.00000000000000D+00 2 2 1 2 0.13273567434365D+01 0.57199711370141D-06 3 2 1 2 -0.43585783326501D-15 0.00000000000000D+00 1 3 1 2 -0.18732603275892D-13 -0.23202038525921D-15 2 3 1 2 0.46508719796282D-14 -0.49218185312848D-14 3 3 1 2 0.30083899582480D+00 0.25433245686665D-08 1 4 1 2 0.90137007279726D-14 0.86032294152567D-08 2 4 1 2 0.23064140651240D+01 0.55454176369348D-08 3 4 1 2 -0.26928553683031D-14 -0.86528150883346D-17 1 5 1 2 -0.60636549210176D+00 0.42085538741875D-02 2 5 1 2 -0.31761822919589D+00 0.21355621797708D-02 3 5 1 2 -0.39711644530348D+00 -0.29270099808040D-02 1 6 1 2 0.60636549210172D+00 -0.42085538741890D-02 2 6 1 2 0.31761822919589D+00 -0.21355621797706D-02 3 6 1 2 -0.39711644530349D+00 -0.29270099808041D-02 1 7 1 2 0.12845923974807D+00 0.31058073606030D-01 2 7 1 2 -0.35116554270219D+00 -0.64737058921585D-03 3 7 1 2 -0.64874695791646D+01 0.95073242473706D-02 1 8 1 2 -0.12845923974809D+00 -0.31058073606030D-01 2 8 1 2 0.35116554270214D+00 0.64737058921581D-03 3 8 1 2 -0.64874695791645D+01 0.95073242473880D-02 1 9 1 2 -0.25214391312679D-14 0.12017961680446D-15 2 9 1 2 -0.29248275621372D-14 -0.22831089565256D-15 3 9 1 2 0.35225490033343D+00 -0.31162647320705D-08 1 10 1 2 0.36319127869871D+00 -0.12333015424325D-07 2 10 1 2 -0.12577957172350D+00 -0.21635482440920D-07 3 10 1 2 0.10526430140842D-13 -0.19718202498179D-15 1 11 1 2 -0.32584030570682D+01 0.57307611276395D-08 2 11 1 2 0.12134762704473D+00 0.35866750583571D-08 3 11 1 2 -0.10397420186220D-13 -0.54421581279289D-15 1 12 1 2 -0.50652920629815D-14 0.42729999972076D-15 2 12 1 2 -0.97728491936796D-15 0.17761103799651D-16 3 12 1 2 -0.24095667808050D+01 0.12254097175244D-07 1 13 1 2 0.40053332053903D+00 0.13838444397698D-01 2 13 1 2 0.78714711650424D+00 0.15604524917160D-01 3 13 1 2 0.70042568642651D+00 0.14423150740259D-02 1 14 1 2 -0.84163095559429D+00 -0.23254921161044D-08 2 14 1 2 -0.95320618894115D+00 0.52200349890592D-08 3 14 1 2 0.84564277358080D+00 0.20158164953771D-07 1 15 1 2 -0.84163095559427D+00 -0.23254906245490D-08 2 15 1 2 -0.95320618894123D+00 0.52200351072999D-08 3 15 1 2 -0.84564277358086D+00 -0.20158164616394D-07 1 16 1 2 -0.40053332053905D+00 -0.13838444397698D-01 2 16 1 2 -0.78714711650426D+00 -0.15604524917162D-01 3 16 1 2 0.70042568642651D+00 0.14423150740283D-02 1 17 1 2 -0.53789782066793D+00 -0.15056872837776D-06 2 17 1 2 0.68712473251339D+00 0.19760182072979D-06 3 17 1 2 -0.11902835930202D+01 -0.22901718374176D-06 1 18 1 2 0.11682226319502D+01 0.87286015242566D-02 2 18 1 2 -0.14641252210913D+00 0.16744411954476D-01 3 18 1 2 0.23054956166575D+00 -0.15504920856737D-02 1 19 1 2 0.11682226319502D+01 0.87286015242522D-02 2 19 1 2 -0.14641252210920D+00 0.16744411954475D-01 3 19 1 2 -0.23054956166567D+00 0.15504920856734D-02 1 20 1 2 0.53789782066794D+00 0.15056873215730D-06 2 20 1 2 -0.68712473251343D+00 -0.19760182115988D-06 3 20 1 2 -0.11902835930204D+01 -0.22901719115413D-06 1 1 2 2 0.15982460963179D-13 -0.62387451010949D-15 2 1 2 2 0.86299860371912D-14 -0.50594949675394D-14 3 1 2 2 -0.39775958539700D+00 -0.58975032745798D-09 1 2 2 2 0.13273531362021D+01 0.62595422724576D-06 2 2 2 2 0.88562707050896D+01 0.00000000000000D+00 3 2 2 2 -0.32823504387098D-13 -0.11102230246252D-15 1 3 2 2 0.46508719796282D-14 -0.49218185312848D-14 2 3 2 2 -0.17203632074073D-13 0.44557195178410D-16 3 3 2 2 -0.49705989637830D-01 0.66113760525626D-08 1 4 2 2 0.23064140651239D+01 -0.55454166584224D-08 2 4 2 2 0.40819247904109D-15 0.84115986420941D-08 3 4 2 2 -0.31227801883431D-14 -0.11809761428951D-15 1 5 2 2 -0.11893782534884D+00 0.96931299378361D-03 2 5 2 2 0.75557409289757D+00 -0.13834039556015D-01 3 5 2 2 -0.63824951117218D+01 -0.16443904434734D-01 1 6 2 2 0.11893782534885D+00 -0.96931299378343D-03 2 6 2 2 -0.75557409289761D+00 0.13834039556016D-01 3 6 2 2 -0.63824951117217D+01 -0.16443904434721D-01 1 7 2 2 -0.54241979068738D+00 -0.53702044046891D-02 2 7 2 2 0.64023917450731D+00 -0.82649819979715D-02 3 7 2 2 -0.15622400674730D-02 -0.32920533895532D-02 1 8 2 2 0.54241979068732D+00 0.53702044046891D-02 2 8 2 2 -0.64023917450733D+00 0.82649819979716D-02 3 8 2 2 -0.15622400674646D-02 -0.32920533895540D-02 1 9 2 2 -0.29252893506034D-14 -0.22787721478357D-15 2 9 2 2 -0.96649876172774D-15 -0.87450052083188D-17 3 9 2 2 0.23291021470691D+01 0.20432356020204D-07 1 10 2 2 0.23107319893681D+00 -0.41078828523401D-08 2 10 2 2 0.20831002667817D+01 -0.95483137574991D-08 3 10 2 2 -0.57509962589507D-14 0.12149795519521D-14 1 11 2 2 0.16810517671020D+00 0.53107898289929D-08 2 11 2 2 -0.34031489089181D+00 -0.26520262845100D-08 3 11 2 2 -0.16118901091945D-13 0.47025411971469D-15 1 12 2 2 -0.97728491898022D-15 0.17327422930657D-16 2 12 2 2 -0.19995120863543D-14 -0.77370575854863D-15 3 12 2 2 -0.20828577590335D+00 0.70889438007580D-08 1 13 2 2 0.78632530987332D+00 0.63106206074885D-02 2 13 2 2 0.29452192971431D+00 0.42432835830089D-02 3 13 2 2 -0.78834034603550D+00 0.20194645910337D-02 1 14 2 2 -0.80557933044718D+00 0.55138783166056D-08 2 14 2 2 -0.88299059641760D+00 -0.69515502024974D-08 3 14 2 2 -0.67932742941599D+00 -0.17790185232221D-07 1 15 2 2 -0.80557933044726D+00 0.55138784383157D-08 2 15 2 2 -0.88299059641757D+00 -0.69515499789129D-08 3 15 2 2 0.67932742941603D+00 0.17790184107787D-07 1 16 2 2 -0.78632530987335D+00 -0.63106206074897D-02 2 16 2 2 -0.29452192971432D+00 -0.42432835830073D-02 3 16 2 2 -0.78834034603552D+00 0.20194645910300D-02 1 17 2 2 0.71678759202770D+00 0.58517304212302D-07 2 17 2 2 -0.64763245545998D+00 0.26415742617594D-06 3 17 2 2 -0.10013965666997D+01 -0.45336946596720D-06 1 18 2 2 -0.51689538388833D-01 0.33029634723423D-01 2 18 2 2 0.15713437869598D+01 -0.18478138079715D-02 3 18 2 2 0.52264722169620D+00 -0.33296080090522D-02 1 19 2 2 -0.51689538388874D-01 0.33029634723422D-01 2 19 2 2 0.15713437869598D+01 -0.18478138079722D-02 3 19 2 2 -0.52264722169609D+00 0.33296080090524D-02 1 20 2 2 -0.71678759202774D+00 -0.58517304635453D-07 2 20 2 2 0.64763245545997D+00 -0.26415742363578D-06 3 20 2 2 -0.10013965666998D+01 -0.45336947146516D-06 1 1 3 2 0.57917839242203D-01 -0.10843307870041D-07 2 1 3 2 -0.39775755527540D+00 -0.36264140870519D-09 3 1 3 2 -0.54172065598362D-13 -0.82061456744529D-14 1 2 3 2 -0.43585783326501D-15 0.11102230246252D-15 2 2 3 2 -0.32823504400332D-13 0.11102230246252D-15 3 2 3 2 0.14389037999124D+02 0.00000000000000D+00 1 3 3 2 0.30083899582480D+00 -0.25433287067945D-08 2 3 3 2 0.49705989637798D-01 0.66113760525626D-08 3 3 3 2 -0.44038973548284D-14 0.74036821324534D-15 1 4 3 2 -0.26928553685099D-14 -0.86528150883346D-17 2 4 3 2 -0.31227801883948D-14 -0.11809761428951D-15 3 4 3 2 -0.75518178058157D-14 0.18682922494414D-08 1 5 3 2 0.20820342969382D+00 0.15159211048930D-02 2 5 3 2 -0.55231091070683D+01 -0.11281895321243D-01 3 5 3 2 0.54803933629178D+00 -0.21211865159802D-02 1 6 3 2 0.20820342969382D+00 0.15159211048929D-02 2 6 3 2 -0.55231091070684D+01 -0.11281895321231D-01 3 6 3 2 -0.54803933629186D+00 0.21211865159861D-02 1 7 3 2 -0.51831940275151D+01 0.10292072185734D-01 2 7 3 2 0.31208497403830D+00 -0.17471032892688D-02 3 7 3 2 -0.11343374882711D+01 0.26622721372188D-02 1 8 3 2 -0.51831940275150D+01 0.10292072185752D-01 2 8 3 2 0.31208497403831D+00 -0.17471032892695D-02 3 8 3 2 0.11343374882710D+01 -0.26622721372186D-02 1 9 3 2 -0.95301266759500D-01 -0.74374275600193D-08 2 9 3 2 0.58080560419071D+00 -0.75773587966198D-08 3 9 3 2 -0.44924977857795D-14 0.16939627208785D-15 1 10 3 2 0.10526430141669D-13 -0.19718202498179D-15 2 10 3 2 -0.57509962589507D-14 0.12149795519521D-14 3 10 3 2 0.10931789013951D+01 -0.25724892118569D-07 1 11 3 2 -0.10397420186220D-13 -0.54421581279289D-15 2 11 3 2 -0.16118901093599D-13 0.47025411971469D-15 3 11 3 2 -0.60405779955822D+00 0.64228704333827D-07 1 12 3 2 -0.62248111267651D+00 0.17489674347921D-07 2 12 3 2 0.85025806103203D-01 -0.69288402057623D-08 3 12 3 2 -0.67227259076164D-14 0.10306094075811D-14 1 13 3 2 0.61948808567309D+00 -0.29798087047878D-02 2 13 3 2 -0.55375110754942D+00 -0.17221670950196D-03 3 13 3 2 -0.38453250910957D+00 0.49275599810586D-02 1 14 3 2 0.44828247296905D+00 -0.14105214282087D-07 2 14 3 2 -0.73874301785772D+00 0.15679509028214D-07 3 14 3 2 -0.33564101453791D-02 -0.14151727061544D-07 1 15 3 2 -0.44828247296910D+00 0.14105214619463D-07 2 15 3 2 0.73874301785773D+00 -0.15679510151781D-07 3 15 3 2 -0.33564101454151D-02 -0.14151728050126D-07 1 16 3 2 0.61948808567308D+00 -0.29798087047854D-02 2 16 3 2 -0.55375110754941D+00 -0.17221670950566D-03 3 16 3 2 0.38453250910954D+00 -0.49275599810562D-02 1 17 3 2 -0.11674946922125D+01 -0.43632829729717D-07 2 17 3 2 -0.76341655697846D+00 0.17317799635091D-06 3 17 3 2 0.48038748013542D+00 -0.91572783024913D-07 1 18 3 2 0.67078264993137D+00 0.97105436486449D-02 2 18 3 2 0.33257813959716D+00 0.17228537222243D-02 3 18 3 2 0.20724822922069D+01 -0.20038783343407D-01 1 19 3 2 -0.67078264993130D+00 -0.97105436486452D-02 2 19 3 2 -0.33257813959705D+00 -0.17228537222240D-02 3 19 3 2 0.20724822922070D+01 -0.20038783343402D-01 1 20 3 2 -0.11674946922127D+01 -0.43632837140354D-07 2 20 3 2 -0.76341655697859D+00 0.17317799085122D-06 3 20 3 2 -0.48038748013562D+00 0.91572769107181D-07 1 1 1 3 0.46702592785630D-14 0.86032290001362D-08 2 1 1 3 -0.23064140651239D+01 -0.55454252750456D-08 3 1 1 3 -0.34668326382139D-14 -0.39310418732198D-16 1 2 1 3 -0.18732603275892D-13 0.23202038525921D-15 2 2 1 3 0.46508719796282D-14 0.49218185312848D-14 3 2 1 3 0.30083899582480D+00 0.25433287067945D-08 1 3 1 3 0.89988262692132D+01 0.00000000000000D+00 2 3 1 3 -0.13273567434366D+01 -0.57199711370141D-06 3 3 1 3 -0.14646712548467D-13 0.00000000000000D+00 1 4 1 3 0.39508966695178D-15 0.10937067912906D-15 2 4 1 3 0.18393350970129D-13 -0.80070850172229D-15 3 4 1 3 0.57918343930123D-01 0.65253887049006D-08 1 5 1 3 -0.12845923974808D+00 -0.31058073606028D-01 2 5 1 3 -0.35116554270225D+00 -0.64737058921405D-03 3 5 1 3 -0.64874695791644D+01 0.95073242473856D-02 1 6 1 3 -0.12845923974808D+00 -0.31058073606029D-01 2 6 1 3 -0.35116554270227D+00 -0.64737058921389D-03 3 6 1 3 0.64874695791644D+01 -0.95073242473852D-02 1 7 1 3 -0.60636549210179D+00 0.42085538741861D-02 2 7 1 3 0.31761822919590D+00 -0.21355621797717D-02 3 7 1 3 0.39711644530349D+00 0.29270099808059D-02 1 8 1 3 -0.60636549210180D+00 0.42085538741864D-02 2 8 1 3 0.31761822919589D+00 -0.21355621797708D-02 3 8 1 3 -0.39711644530348D+00 -0.29270099808040D-02 1 9 1 3 -0.32584030570684D+01 0.57307607877652D-08 2 9 1 3 -0.12134762704465D+00 -0.35866752816293D-08 3 9 1 3 -0.27656612838313D-14 0.18027834189074D-14 1 10 1 3 0.11600158213856D-14 -0.42437301130913D-15 2 10 1 3 -0.30178665471587D-14 0.35229805518497D-16 3 10 1 3 0.24095667808050D+01 -0.12254095514761D-07 1 11 1 3 0.10145342220908D-14 -0.57008449146097D-16 2 11 1 3 -0.31995455075150D-15 -0.25696549922840D-15 3 11 1 3 0.35225490033342D+00 -0.31162646877419D-08 1 12 1 3 -0.36319127869864D+00 0.12333020924791D-07 2 12 1 3 -0.12577957172349D+00 -0.21635479667530D-07 3 12 1 3 0.59555050364148D-14 -0.44082679891976D-15 1 13 1 3 -0.11682226319502D+01 -0.87286015242552D-02 2 13 1 3 -0.14641252210917D+00 0.16744411954469D-01 3 13 1 3 0.23054956166565D+00 -0.15504920856832D-02 1 14 1 3 0.53789782066792D+00 0.15056873101702D-06 2 14 1 3 0.68712473251340D+00 0.19760182036410D-06 3 14 1 3 -0.11902835930203D+01 -0.22901719124196D-06 1 15 1 3 -0.53789782066790D+00 -0.15056872969311D-06 2 15 1 3 -0.68712473251340D+00 -0.19760181935291D-06 3 15 1 3 -0.11902835930203D+01 -0.22901718426497D-06 1 16 1 3 -0.11682226319502D+01 -0.87286015242531D-02 2 16 1 3 -0.14641252210917D+00 0.16744411954469D-01 3 16 1 3 -0.23054956166566D+00 0.15504920856827D-02 1 17 1 3 -0.84163095559426D+00 -0.23254905061435D-08 2 17 1 3 0.95320618894116D+00 -0.52200371790593D-08 3 17 1 3 -0.84564277358080D+00 -0.20158161443437D-07 1 18 1 3 0.40053332053903D+00 0.13838444397699D-01 2 18 1 3 -0.78714711650425D+00 -0.15604524917163D-01 3 18 1 3 -0.70042568642654D+00 -0.14423150740316D-02 1 19 1 3 -0.40053332053904D+00 -0.13838444397698D-01 2 19 1 3 0.78714711650424D+00 0.15604524917161D-01 3 19 1 3 -0.70042568642656D+00 -0.14423150740289D-02 1 20 1 3 -0.84163095559427D+00 -0.23254906347100D-08 2 20 1 3 0.95320618894116D+00 -0.52200376757550D-08 3 20 1 3 0.84564277358086D+00 0.20158163115362D-07 1 1 2 3 -0.23064140651240D+01 0.55454090203115D-08 2 1 2 3 0.10597629981962D-13 0.84115977597669D-08 3 1 2 3 0.30416398297877D-16 -0.16677837658653D-15 1 2 2 3 0.46508719796282D-14 0.49218185312848D-14 2 2 2 3 -0.17203632074073D-13 -0.44557195178410D-16 3 2 2 3 0.49705989637798D-01 -0.66113760525626D-08 1 3 2 3 -0.13273531362022D+01 -0.62595422724576D-06 2 3 2 3 0.88562707050896D+01 0.00000000000000D+00 3 3 2 3 -0.54139786486362D-13 0.11102230246252D-15 1 4 2 3 0.18393350970129D-13 -0.80070850172229D-15 2 4 2 3 0.19813987991235D-14 -0.39339590217474D-14 3 4 2 3 0.39775958539714D+00 0.58974441568274D-09 1 5 2 3 -0.54241979068744D+00 -0.53702044046873D-02 2 5 2 3 -0.64023917450729D+00 0.82649819979702D-02 3 5 2 3 0.15622400674703D-02 0.32920533895534D-02 1 6 2 3 -0.54241979068746D+00 -0.53702044046872D-02 2 6 2 3 -0.64023917450729D+00 0.82649819979715D-02 3 6 2 3 -0.15622400674705D-02 -0.32920533895540D-02 1 7 2 3 0.11893782534886D+00 -0.96931299378451D-03 2 7 2 3 0.75557409289757D+00 -0.13834039556007D-01 3 7 2 3 -0.63824951117218D+01 -0.16443904434729D-01 1 8 2 3 0.11893782534884D+00 -0.96931299378367D-03 2 8 2 3 0.75557409289757D+00 -0.13834039556007D-01 3 8 2 3 0.63824951117217D+01 0.16443904434722D-01 1 9 2 3 -0.16810517671010D+00 -0.53107900522651D-08 2 9 2 3 -0.34031489089158D+00 -0.26520266553721D-08 3 9 2 3 -0.71641022323978D-14 0.38479223234889D-15 1 10 2 3 -0.30178665471328D-14 0.35663486387491D-16 2 10 2 3 -0.31483030034309D-14 0.12007403077388D-14 3 10 2 3 -0.20828577590334D+00 0.70889437655056D-08 1 11 2 3 -0.32041633921770D-15 -0.25674865879390D-15 2 11 2 3 0.28234253004611D-14 -0.31206449022738D-15 3 11 2 3 -0.23291021470691D+01 -0.20432357053226D-07 1 12 2 3 0.23107319893682D+00 -0.41078800789499D-08 2 12 2 3 -0.20831002667817D+01 0.95482911356725D-08 3 12 2 3 0.62440521796126D-14 -0.12671932145849D-14 1 13 2 3 -0.51689538388847D-01 0.33029634723416D-01 2 13 2 3 -0.15713437869598D+01 0.18478138079752D-02 3 13 2 3 -0.52264722169603D+00 0.33296080090624D-02 1 14 2 3 0.71678759202771D+00 0.58517303846614D-07 2 14 2 3 0.64763245545997D+00 -0.26415742531930D-06 3 14 2 3 0.10013965666997D+01 0.45336947171217D-06 1 15 2 3 -0.71678759202772D+00 -0.58517302833690D-07 2 15 2 3 -0.64763245546001D+00 0.26415742586450D-06 3 15 2 3 0.10013965666997D+01 0.45336946581010D-06 1 16 2 3 -0.51689538388860D-01 0.33029634723416D-01 2 16 2 3 -0.15713437869598D+01 0.18478138079774D-02 3 16 2 3 0.52264722169606D+00 -0.33296080090638D-02 1 17 2 3 0.80557933044719D+00 -0.55138805100751D-08 2 17 2 3 -0.88299059641760D+00 -0.69515502463558D-08 3 17 2 3 -0.67932742941596D+00 -0.17790184857577D-07 1 18 2 3 -0.78632530987333D+00 -0.63106206074914D-02 2 18 2 3 0.29452192971430D+00 0.42432835830063D-02 3 18 2 3 -0.78834034603555D+00 0.20194645910283D-02 1 19 2 3 0.78632530987332D+00 0.63106206074896D-02 2 19 2 3 -0.29452192971430D+00 -0.42432835830071D-02 3 19 2 3 -0.78834034603555D+00 0.20194645910308D-02 1 20 2 3 0.80557933044719D+00 -0.55138810033014D-08 2 20 2 3 -0.88299059641759D+00 -0.69515502514526D-08 3 20 2 3 0.67932742941595D+00 0.17790185498332D-07 1 1 3 3 -0.34668326382139D-14 -0.39310418732198D-16 2 1 3 3 0.30416398452973D-16 -0.16677837658653D-15 3 1 3 3 0.14146049734213D-13 0.18682927754594D-08 1 2 3 3 0.30083899582480D+00 -0.25433245686665D-08 2 2 3 3 -0.49705989637830D-01 -0.66113760525626D-08 3 2 3 3 -0.44038973548284D-14 -0.74036821324534D-15 1 3 3 3 -0.14646712548467D-13 0.11102230246252D-15 2 3 3 3 -0.54139786473127D-13 -0.11102230246252D-15 3 3 3 3 0.14389037999124D+02 0.00000000000000D+00 1 4 3 3 0.57917839242231D-01 -0.10843309443534D-07 2 4 3 3 0.39775755527554D+00 0.36263549693020D-09 3 4 3 3 0.60808611339555D-13 -0.35533773825318D-14 1 5 3 3 -0.51831940275149D+01 0.10292072185749D-01 2 5 3 3 -0.31208497403830D+00 0.17471032892690D-02 3 5 3 3 0.11343374882711D+01 -0.26622721372176D-02 1 6 3 3 0.51831940275149D+01 -0.10292072185749D-01 2 6 3 3 0.31208497403830D+00 -0.17471032892696D-02 3 6 3 3 0.11343374882711D+01 -0.26622721372193D-02 1 7 3 3 -0.20820342969382D+00 -0.15159211048911D-02 2 7 3 3 -0.55231091070684D+01 -0.11281895321239D-01 3 7 3 3 0.54803933629193D+00 -0.21211865159758D-02 1 8 3 3 0.20820342969383D+00 0.15159211048930D-02 2 8 3 3 0.55231091070682D+01 0.11281895321232D-01 3 8 3 3 0.54803933629192D+00 -0.21211865159790D-02 1 9 3 3 -0.27656612838313D-14 0.18027834189074D-14 2 9 3 3 -0.71641022308469D-14 0.38479223234889D-15 3 9 3 3 -0.60405779955785D+00 0.64228704276942D-07 1 10 3 3 0.62248111267653D+00 -0.17489672687438D-07 2 10 3 3 0.85025806103215D-01 -0.69288402410147D-08 3 10 3 3 0.19668657751882D-13 -0.73797189618399D-15 1 11 3 3 -0.95301266759512D-01 -0.74374275156901D-08 2 11 3 3 -0.58080560419071D+00 0.75773577635974D-08 3 11 3 3 -0.57189181531533D-15 0.13312542867367D-15 1 12 3 3 0.59555050376556D-14 -0.44082679891976D-15 2 12 3 3 0.62440521787854D-14 -0.12671932145849D-14 3 12 3 3 -0.10931789013949D+01 0.25724904355623D-07 1 13 3 3 0.67078264993127D+00 0.97105436486353D-02 2 13 3 3 -0.33257813959699D+00 -0.17228537222140D-02 3 13 3 3 -0.20724822922069D+01 0.20038783343409D-01 1 14 3 3 -0.11674946922126D+01 -0.43632837235123D-07 2 14 3 3 0.76341655697853D+00 -0.17317799060420D-06 3 14 3 3 -0.48038748013547D+00 0.91572767260852D-07 1 15 3 3 -0.11674946922126D+01 -0.43632830251192D-07 2 15 3 3 0.76341655697850D+00 -0.17317799650627D-06 3 15 3 3 0.48038748013545D+00 -0.91572781718537D-07 1 16 3 3 -0.67078264993127D+00 -0.97105436486358D-02 2 16 3 3 0.33257813959702D+00 0.17228537222126D-02 3 16 3 3 -0.20724822922069D+01 0.20038783343413D-01 1 17 3 3 -0.44828247296905D+00 0.14105217792420D-07 2 17 3 3 -0.73874301785766D+00 0.15679509401992D-07 3 17 3 3 -0.33564101454147D-02 -0.14151728731816D-07 1 18 3 3 -0.61948808567311D+00 0.29798087047821D-02 2 18 3 3 -0.55375110754944D+00 -0.17221670950738D-03 3 18 3 3 -0.38453250910959D+00 0.49275599810538D-02 1 19 3 3 -0.61948808567314D+00 0.29798087047849D-02 2 19 3 3 -0.55375110754946D+00 -0.17221670950489D-03 3 19 3 3 0.38453250910959D+00 -0.49275599810567D-02 1 20 3 3 0.44828247296910D+00 -0.14105216120495D-07 2 20 3 3 0.73874301785768D+00 -0.15679508762104D-07 3 20 3 3 -0.33564101454360D-02 -0.14151725723690D-07 1 1 1 4 -0.84217037468504D-14 -0.60931377461179D-15 2 1 1 4 0.37509449815903D-14 0.19504706850149D-15 3 1 1 4 -0.30083899582474D+00 -0.25433274085678D-08 1 2 1 4 0.90137007279726D-14 -0.86032294152567D-08 2 2 1 4 0.23064140651239D+01 0.55454166584224D-08 3 2 1 4 -0.26928553685099D-14 0.86528150883346D-17 1 3 1 4 0.39508966695178D-15 -0.10937067912906D-15 2 3 1 4 0.18393350969922D-13 0.80070850172229D-15 3 3 1 4 0.57918343930123D-01 0.65253893071790D-08 1 4 1 4 0.89988262692095D+01 0.00000000000000D+00 2 4 1 4 -0.13273567434368D+01 -0.57199711370141D-06 3 4 1 4 -0.21752139906068D-13 0.00000000000000D+00 1 5 1 4 -0.12845923974807D+00 -0.31058073606039D-01 2 5 1 4 -0.35116554270222D+00 -0.64737058921436D-03 3 5 1 4 -0.64874695791645D+01 0.95073242473755D-02 1 6 1 4 0.12845923974803D+00 0.31058073606040D-01 2 6 1 4 0.35116554270218D+00 0.64737058921142D-03 3 6 1 4 -0.64874695791645D+01 0.95073242473901D-02 1 7 1 4 -0.60636549210177D+00 0.42085538741881D-02 2 7 1 4 0.31761822919586D+00 -0.21355621797713D-02 3 7 1 4 0.39711644530348D+00 0.29270099808035D-02 1 8 1 4 0.60636549210177D+00 -0.42085538741882D-02 2 8 1 4 -0.31761822919587D+00 0.21355621797708D-02 3 8 1 4 0.39711644530351D+00 0.29270099808033D-02 1 9 1 4 0.66341307944375D-15 0.11306148127993D-14 2 9 1 4 0.14628089106379D-15 0.98896520881532D-16 3 9 1 4 0.24095667808050D+01 -0.12254097973133D-07 1 10 1 4 -0.32584030570681D+01 0.57307490643955D-08 2 10 1 4 -0.12134762704457D+00 -0.35866746138403D-08 3 10 1 4 -0.76588931218202D-14 0.21367787582820D-14 1 11 1 4 -0.36319127869847D+00 0.12333017523606D-07 2 11 1 4 -0.12577957172338D+00 -0.21635477584590D-07 3 11 1 4 0.43662574646064D-14 -0.25949176583137D-15 1 12 1 4 0.16687580108175D-15 0.17015639707964D-15 2 12 1 4 -0.93511827139831D-16 0.16406625760116D-15 3 12 1 4 0.35225490033343D+00 -0.31162647516471D-08 1 13 1 4 0.53789782066795D+00 0.15056872998975D-06 2 13 1 4 0.68712473251339D+00 0.19760181757580D-06 3 13 1 4 -0.11902835930202D+01 -0.22901717773786D-06 1 14 1 4 -0.11682226319502D+01 -0.87286015242525D-02 2 14 1 4 -0.14641252210914D+00 0.16744411954469D-01 3 14 1 4 0.23054956166567D+00 -0.15504920856825D-02 1 15 1 4 -0.11682226319502D+01 -0.87286015242529D-02 2 15 1 4 -0.14641252210923D+00 0.16744411954470D-01 3 15 1 4 -0.23054956166560D+00 0.15504920856827D-02 1 16 1 4 -0.53789782066794D+00 -0.15056873000731D-06 2 16 1 4 -0.68712473251342D+00 -0.19760181900455D-06 3 16 1 4 -0.11902835930204D+01 -0.22901718360464D-06 1 17 1 4 0.40053332053903D+00 0.13838444397700D-01 2 17 1 4 -0.78714711650424D+00 -0.15604524917160D-01 3 17 1 4 -0.70042568642656D+00 -0.14423150740260D-02 1 18 1 4 -0.84163095559426D+00 -0.23254903118641D-08 2 18 1 4 0.95320618894115D+00 -0.52200364414836D-08 3 18 1 4 -0.84564277358080D+00 -0.20158163254409D-07 1 19 1 4 -0.84163095559426D+00 -0.23254889379662D-08 2 19 1 4 0.95320618894122D+00 -0.52200384312939D-08 3 19 1 4 0.84564277358080D+00 0.20158163858429D-07 1 20 1 4 -0.40053332053905D+00 -0.13838444397699D-01 2 20 1 4 0.78714711650424D+00 0.15604524917162D-01 3 20 1 4 -0.70042568642655D+00 -0.14423150740286D-02 1 1 2 4 0.37509449824175D-14 0.19504706850149D-15 2 1 2 4 -0.96847634162176D-14 -0.56202573797586D-15 3 1 2 4 -0.49705989637847D-01 0.66113756789006D-08 1 2 2 4 0.23064140651240D+01 -0.55454176369348D-08 2 2 2 4 0.40819247904109D-15 -0.84115986420941D-08 3 2 2 4 -0.31227801883948D-14 0.11809761428951D-15 1 3 2 4 0.18393350970129D-13 0.80114218259128D-15 2 3 2 4 0.19813987991235D-14 0.39339590217474D-14 3 3 2 4 0.39775958539713D+00 0.58974915327406D-09 1 4 2 4 -0.13273531362024D+01 -0.62595422724576D-06 2 4 2 4 0.88562707050896D+01 0.00000000000000D+00 3 4 2 4 0.84416046986849D-13 0.11102230246252D-15 1 5 2 4 -0.54241979068741D+00 -0.53702044046877D-02 2 5 2 4 -0.64023917450735D+00 0.82649819979739D-02 3 5 2 4 0.15622400674690D-02 0.32920533895533D-02 1 6 2 4 0.54241979068737D+00 0.53702044046847D-02 2 6 2 4 0.64023917450738D+00 -0.82649819979747D-02 3 6 2 4 0.15622400675107D-02 0.32920533895520D-02 1 7 2 4 0.11893782534881D+00 -0.96931299378419D-03 2 7 2 4 0.75557409289759D+00 -0.13834039556015D-01 3 7 2 4 -0.63824951117218D+01 -0.16443904434732D-01 1 8 2 4 -0.11893782534883D+00 0.96931299378367D-03 2 8 2 4 -0.75557409289760D+00 0.13834039556017D-01 3 8 2 4 -0.63824951117219D+01 -0.16443904434722D-01 1 9 2 4 0.14628089021076D-15 0.99330201750526D-16 2 9 2 4 -0.44953773554259D-15 -0.43600963756203D-15 3 9 2 4 -0.20828577590334D+00 0.70889447383977D-08 1 10 2 4 -0.16810517671002D+00 -0.53107893844761D-08 2 10 2 4 -0.34031489089178D+00 -0.26520239264280D-08 3 10 2 4 -0.16168999099309D-13 -0.51672277693328D-15 1 11 2 4 0.23107319893694D+00 -0.41078779960102D-08 2 11 2 4 -0.20831002667822D+01 0.95483033112240D-08 3 11 2 4 -0.41364293949525D-14 -0.11142951942893D-14 1 12 2 4 -0.93973616433220D-16 0.16384941716666D-15 2 12 2 4 -0.20731419212092D-14 0.99591608894770D-16 3 12 2 4 -0.23291021470691D+01 -0.20432357456232D-07 1 13 2 4 0.71678759202770D+00 0.58517301058313D-07 2 13 2 4 0.64763245545999D+00 -0.26415742691033D-06 3 13 2 4 0.10013965666997D+01 0.45336946108269D-06 1 14 2 4 -0.51689538388819D-01 0.33029634723416D-01 2 14 2 4 -0.15713437869599D+01 0.18478138079759D-02 3 14 2 4 -0.52264722169623D+00 0.33296080090628D-02 1 15 2 4 -0.51689538388918D-01 0.33029634723417D-01 2 15 2 4 -0.15713437869598D+01 0.18478138079751D-02 3 15 2 4 0.52264722169600D+00 -0.33296080090649D-02 1 16 2 4 -0.71678759202774D+00 -0.58517302485334D-07 2 16 2 4 -0.64763245545998D+00 0.26415742471216D-06 3 16 2 4 0.10013965666998D+01 0.45336946539538D-06 1 17 2 4 -0.78632530987332D+00 -0.63106206074882D-02 2 17 2 4 0.29452192971431D+00 0.42432835830083D-02 3 17 2 4 -0.78834034603555D+00 0.20194645910335D-02 1 18 2 4 0.80557933044718D+00 -0.55138797724993D-08 2 18 2 4 -0.88299059641759D+00 -0.69515510685043D-08 3 18 2 4 -0.67932742941595D+00 -0.17790183742072D-07 1 19 2 4 0.80557933044725D+00 -0.55138817588402D-08 2 19 2 4 -0.88299059641759D+00 -0.69515486911474D-08 3 19 2 4 0.67932742941595D+00 0.17790184620736D-07 1 20 2 4 0.78632530987332D+00 0.63106206074898D-02 2 20 2 4 -0.29452192971431D+00 -0.42432835830084D-02 3 20 2 4 -0.78834034603554D+00 0.20194645910306D-02 1 1 3 4 -0.30083899582474D+00 0.25433258668932D-08 2 1 3 4 0.49705989637781D-01 0.66113756789006D-08 3 1 3 4 0.95246547552954D-15 0.10974041967094D-14 1 2 3 4 -0.26928553683031D-14 0.86528150883346D-17 2 2 3 4 -0.31227801883431D-14 0.11809761428951D-15 3 2 3 4 -0.75518178058157D-14 -0.18682922494414D-08 1 3 3 4 0.57917839242231D-01 -0.10843308841255D-07 2 3 3 4 0.39775755527553D+00 0.36264023452153D-09 3 3 3 4 0.60808611339555D-13 0.35542447442698D-14 1 4 3 4 -0.21752139906068D-13 0.11102230246252D-15 2 4 3 4 0.84416047000084D-13 -0.11102230246252D-15 3 4 3 4 0.14389037999128D+02 0.00000000000000D+00 1 5 3 4 -0.51831940275150D+01 0.10292072185739D-01 2 5 3 4 -0.31208497403830D+00 0.17471032892688D-02 3 5 3 4 0.11343374882711D+01 -0.26622721372251D-02 1 6 3 4 -0.51831940275150D+01 0.10292072185754D-01 2 6 3 4 -0.31208497403826D+00 0.17471032892676D-02 3 6 3 4 -0.11343374882711D+01 0.26622721372258D-02 1 7 3 4 -0.20820342969383D+00 -0.15159211048935D-02 2 7 3 4 -0.55231091070684D+01 -0.11281895321242D-01 3 7 3 4 0.54803933629182D+00 -0.21211865159801D-02 1 8 3 4 -0.20820342969380D+00 -0.15159211048938D-02 2 8 3 4 -0.55231091070684D+01 -0.11281895321231D-01 3 8 3 4 -0.54803933629184D+00 0.21211865159889D-02 1 9 3 4 0.62248111267655D+00 -0.17489675145810D-07 2 9 3 4 0.85025806103214D-01 -0.69288392681226D-08 3 9 3 4 0.12604995452372D-13 0.27857197307976D-15 1 10 3 4 -0.76588931218202D-14 0.21367787582820D-14 2 10 3 4 -0.16168999097759D-13 -0.51672277693328D-15 3 10 3 4 -0.60405779955819D+00 0.64228709824588D-07 1 11 3 4 0.43662574658472D-14 -0.25949176583137D-15 2 11 3 4 -0.41364293957797D-14 -0.11142951942893D-14 3 11 3 4 -0.10931789013945D+01 0.25724899474402D-07 1 12 3 4 -0.95301266759503D-01 -0.74374275795954D-08 2 12 3 4 -0.58080560419071D+00 0.75773573605916D-08 3 12 3 4 -0.51386592848428D-14 -0.54371850440767D-15 1 13 3 4 -0.11674946922125D+01 -0.43632823729293D-07 2 13 3 4 0.76341655697848D+00 -0.17317800123369D-06 3 13 3 4 -0.48038748013540D+00 0.91572795593992D-07 1 14 3 4 0.67078264993130D+00 0.97105436486361D-02 2 14 3 4 -0.33257813959719D+00 -0.17228537222137D-02 3 14 3 4 -0.20724822922069D+01 0.20038783343413D-01 1 15 3 4 -0.67078264993122D+00 -0.97105436486359D-02 2 15 3 4 0.33257813959696D+00 0.17228537222115D-02 3 15 3 4 -0.20724822922070D+01 0.20038783343413D-01 1 16 3 4 -0.11674946922127D+01 -0.43632829590863D-07 2 16 3 4 0.76341655697857D+00 -0.17317799692099D-06 3 16 3 4 0.48038748013557D+00 -0.91572778596471D-07 1 17 3 4 -0.61948808567312D+00 0.29798087047877D-02 2 17 3 4 -0.55375110754944D+00 -0.17221670950218D-03 3 17 3 4 -0.38453250910962D+00 0.49275599810606D-02 1 18 3 4 -0.44828247296905D+00 0.14105215981449D-07 2 18 3 4 -0.73874301785765D+00 0.15679510517497D-07 3 18 3 4 -0.33564101453898D-02 -0.14151726932444D-07 1 19 3 4 0.44828247296905D+00 -0.14105215377428D-07 2 19 3 4 0.73874301785768D+00 -0.15679509639700D-07 3 19 3 4 -0.33564101454608D-02 -0.14151727871679D-07 1 20 3 4 -0.61948808567313D+00 0.29798087047851D-02 2 20 3 4 -0.55375110754945D+00 -0.17221670950507D-03 3 20 3 4 0.38453250910956D+00 -0.49275599810572D-02 1 1 1 5 0.60636551621812D+00 0.42095317191380D-02 2 1 1 5 0.11894022890390D+00 0.96930997542201D-03 3 1 1 5 -0.20819969203351D+00 0.15159655689713D-02 1 2 1 5 -0.60636551621821D+00 -0.42095317191405D-02 2 2 1 5 -0.11894022890389D+00 -0.96930997542274D-03 3 2 1 5 0.20819969203350D+00 -0.15159655689718D-02 1 3 1 5 -0.12845923974808D+00 0.31058073606028D-01 2 3 1 5 -0.54241979068744D+00 0.53702044046873D-02 3 3 1 5 -0.51831940275149D+01 -0.10292072185749D-01 1 4 1 5 -0.12845923974807D+00 0.31058073606039D-01 2 4 1 5 -0.54241979068741D+00 0.53702044046877D-02 3 4 1 5 -0.51831940275150D+01 -0.10292072185739D-01 1 5 1 5 0.19027134190200D+02 0.00000000000000D+00 2 5 1 5 0.30753761818168D+00 -0.74012829356996D-07 3 5 1 5 0.45371277977979D+00 -0.35371939424504D-07 1 6 1 5 -0.32248785592821D-13 0.48875304511267D-14 2 6 1 5 -0.17339621696987D-17 -0.30157590229668D-15 3 6 1 5 0.12053389640668D-16 -0.43419127025743D-15 1 7 1 5 0.11132788525000D-14 0.15636020787401D-07 2 7 1 5 0.16208870450129D+02 -0.98250669669654D-08 3 7 1 5 0.64753973119029D+00 -0.61664301696245D-08 1 8 1 5 0.15730591690863D-14 -0.66689751793403D-15 2 8 1 5 -0.21412463753204D-13 0.55849218967476D-14 3 8 1 5 -0.95228856170406D-14 0.15753361692787D-14 1 9 1 5 -0.19782115549746D+01 0.99537882222306D+00 2 9 1 5 -0.31073905560866D-01 -0.38354546409530D-01 3 9 1 5 -0.44791339485187D+00 -0.42603074850767D+00 1 10 1 5 -0.19782115549742D+01 0.99537882222304D+00 2 10 1 5 -0.31073905560850D-01 -0.38354546409531D-01 3 10 1 5 -0.44791339485181D+00 -0.42603074850764D+00 1 11 1 5 -0.15694076038798D-01 -0.13221546769269D-02 2 11 1 5 0.18037524406213D+01 -0.28879279260673D-01 3 11 1 5 0.22085019921775D+00 0.10947011099951D-01 1 12 1 5 -0.15694076038809D-01 -0.13221546769275D-02 2 12 1 5 0.18037524406213D+01 -0.28879279260677D-01 3 12 1 5 0.22085019921787D+00 0.10947011099948D-01 1 13 1 5 0.23532788230268D+01 -0.12586756204578D-01 2 13 1 5 -0.21831659676343D+01 -0.12385695827256D-01 3 13 1 5 -0.80775327761424D+00 0.34945945467448D-01 1 14 1 5 0.23532788230266D+01 -0.12586756204574D-01 2 14 1 5 -0.21831659676344D+01 -0.12385695827256D-01 3 14 1 5 -0.80775327761390D+00 0.34945945467447D-01 1 15 1 5 0.58641202826265D+00 -0.42434203301507D-01 2 15 1 5 0.21890341311868D+00 -0.57975041970885D-01 3 15 1 5 0.62705904656789D+00 -0.82421881349822D-02 1 16 1 5 0.58641202826265D+00 -0.42434203301504D-01 2 16 1 5 0.21890341311867D+00 -0.57975041970881D-01 3 16 1 5 0.62705904656785D+00 -0.82421881349822D-02 1 17 1 5 0.10920925903866D+01 -0.14296338312368D-01 2 17 1 5 0.12478087830558D+01 0.19355587853713D-01 3 17 1 5 -0.87225283577179D+00 0.27747237711741D-01 1 18 1 5 0.10920925903866D+01 -0.14296338312367D-01 2 18 1 5 0.12478087830557D+01 0.19355587853713D-01 3 18 1 5 -0.87225283577176D+00 0.27747237711743D-01 1 19 1 5 0.52646948241185D+00 -0.75686226288419D-01 2 19 1 5 -0.50224696865235D+00 0.13530080062111D+00 3 19 1 5 0.45745023807932D+00 -0.32196623948945D-02 1 20 1 5 0.52646948241186D+00 -0.75686226288418D-01 2 20 1 5 -0.50224696865234D+00 0.13530080062111D+00 3 20 1 5 0.45745023807933D+00 -0.32196623948945D-02 1 1 2 5 0.31761732982056D+00 0.21358255272828D-02 2 1 2 5 -0.75556884958285D+00 -0.13834127344733D-01 3 1 2 5 0.55231085890309D+01 -0.11281703814692D-01 1 2 2 5 -0.31761732982056D+00 -0.21358255272835D-02 2 2 2 5 0.75556884958291D+00 0.13834127344740D-01 3 2 2 5 -0.55231085890309D+01 0.11281703814712D-01 1 3 2 5 -0.35116554270225D+00 0.64737058921405D-03 2 3 2 5 -0.64023917450729D+00 -0.82649819979702D-02 3 3 2 5 -0.31208497403830D+00 -0.17471032892690D-02 1 4 2 5 -0.35116554270222D+00 0.64737058921436D-03 2 4 2 5 -0.64023917450735D+00 -0.82649819979739D-02 3 4 2 5 -0.31208497403830D+00 -0.17471032892688D-02 1 5 2 5 0.30752539862599D+00 0.81079078392965D-07 2 5 2 5 0.19683273113958D+02 0.00000000000000D+00 3 5 2 5 -0.30944148028657D+01 0.28242977947907D-06 1 6 2 5 -0.17339621696988D-17 -0.30157590229668D-15 2 6 2 5 -0.33507079156895D-13 0.14798893697998D-14 3 6 2 5 0.29513552597578D-13 0.28236472969137D-14 1 7 2 5 0.16208870450128D+02 0.98250669669654D-08 2 7 2 5 0.12973915826369D-14 0.26281384395133D-08 3 7 2 5 0.46418172350165D+01 0.80319572380900D-08 1 8 2 5 -0.21412463768404D-13 0.55849218967476D-14 2 8 2 5 0.87040345036330D-15 -0.92197021192326D-15 3 8 2 5 0.37367214760019D-13 -0.36395055630933D-15 1 9 2 5 -0.50065337459860D-01 -0.17349167944217D-01 2 9 2 5 -0.17685234267218D+01 0.10193543494744D+01 3 9 2 5 0.14909656126439D+00 0.10887332677128D+00 1 10 2 5 -0.50065337459844D-01 -0.17349167944218D-01 2 10 2 5 -0.17685234267215D+01 0.10193543494744D+01 3 10 2 5 0.14909656126457D+00 0.10887332677127D+00 1 11 2 5 0.17859320330234D+01 -0.31186136530778D-01 2 11 2 5 -0.84555701093814D-01 -0.25288103443480D-02 3 11 2 5 0.52322751257994D+00 0.60280200069056D-02 1 12 2 5 0.17859320330234D+01 -0.31186136530782D-01 2 12 2 5 -0.84555701093823D-01 -0.25288103443482D-02 3 12 2 5 0.52322751257994D+00 0.60280200069026D-02 1 13 2 5 -0.98619610502719D+00 0.16032274549996D-01 2 13 2 5 0.12926748939159D+01 0.71915817217372D-02 3 13 2 5 -0.13596919767851D+01 0.17043412153380D-01 1 14 2 5 -0.98619610502730D+00 0.16032274549996D-01 2 14 2 5 0.12926748939160D+01 0.71915817217376D-02 3 14 2 5 -0.13596919767849D+01 0.17043412153382D-01 1 15 2 5 -0.23857555948404D+00 -0.34463920729138D-01 2 15 2 5 -0.54144292836912D-01 -0.28275102359186D-01 3 15 2 5 0.41659732056843D+00 -0.49748253466809D-02 1 16 2 5 -0.23857555948405D+00 -0.34463920729134D-01 2 16 2 5 -0.54144292836905D-01 -0.28275102359183D-01 3 16 2 5 0.41659732056846D+00 -0.49748253466809D-02 1 17 2 5 0.24452075078458D+01 0.47573476840694D-03 2 17 2 5 0.23168943120457D+01 -0.71500529342295D-02 3 17 2 5 0.12362503312941D+01 -0.45313182285101D-01 1 18 2 5 0.24452075078458D+01 0.47573476840657D-03 2 18 2 5 0.23168943120459D+01 -0.71500529342310D-02 3 18 2 5 0.12362503312940D+01 -0.45313182285097D-01 1 19 2 5 -0.30236673461977D-01 0.15440326016474D+00 2 19 2 5 0.30976009217220D+00 -0.15408707822108D+00 3 19 2 5 -0.61507911902728D+00 0.19381019719641D-01 1 20 2 5 -0.30236673461971D-01 0.15440326016474D+00 2 20 2 5 0.30976009217220D+00 -0.15408707822108D+00 3 20 2 5 -0.61507911902729D+00 0.19381019719641D-01 1 1 3 5 0.39711712290637D+00 -0.29264258522131D-02 2 1 3 5 0.63824956855525D+01 -0.16444631122563D-01 3 1 3 5 -0.54803902129656D+00 -0.21208851119820D-02 1 2 3 5 -0.39711712290638D+00 0.29264258522126D-02 2 2 3 5 -0.63824956855525D+01 0.16444631122584D-01 3 2 3 5 0.54803902129657D+00 0.21208851119797D-02 1 3 3 5 -0.64874695791644D+01 -0.95073242473856D-02 2 3 3 5 0.15622400674703D-02 -0.32920533895534D-02 3 3 3 5 0.11343374882711D+01 0.26622721372176D-02 1 4 3 5 -0.64874695791645D+01 -0.95073242473755D-02 2 4 3 5 0.15622400674691D-02 -0.32920533895533D-02 3 4 3 5 0.11343374882711D+01 0.26622721372251D-02 1 5 3 5 0.45371300483266D+00 0.69864355616582D-07 2 5 3 5 -0.30944350059557D+01 -0.31495966972823D-06 3 5 3 5 0.44789469878655D+02 0.00000000000000D+00 1 6 3 5 -0.25104371217081D-16 -0.43419127025743D-15 2 6 3 5 0.29522989639384D-13 0.28236472969137D-14 3 6 3 5 0.35424995986130D-12 -0.72734192880008D-14 1 7 3 5 0.64753973119029D+00 0.61664301696245D-08 2 7 3 5 -0.46418172350165D+01 0.80319572380900D-08 3 7 3 5 0.18061441934713D-14 0.53154083300592D-07 1 8 3 5 -0.95247588935535D-14 0.15753361692787D-14 2 8 3 5 0.37367214657655D-13 -0.36395055630933D-15 3 8 3 5 0.79401323448466D-14 -0.12266668101839D-14 1 9 3 5 -0.13600813990370D+01 -0.45730387005027D+00 2 9 3 5 0.19974278796883D+00 0.11413765786575D+00 3 9 3 5 -0.73433638552647D+01 -0.22752171886107D+01 1 10 3 5 -0.13600813990369D+01 -0.45730387005024D+00 2 10 3 5 0.19974278796902D+00 0.11413765786575D+00 3 10 3 5 -0.73433638552655D+01 -0.22752171886106D+01 1 11 3 5 0.35171366375816D-01 -0.13677493424677D-02 2 11 3 5 0.23734332837183D+00 0.91697917313622D-02 3 11 3 5 -0.18506734839479D+00 -0.26211647208999D-02 1 12 3 5 0.35171366375936D-01 -0.13677493424704D-02 2 12 3 5 0.23734332837183D+00 0.91697917313592D-02 3 12 3 5 -0.18506734839480D+00 -0.26211647208988D-02 1 13 3 5 0.18762999119308D+00 0.35430677569610D-01 2 13 3 5 0.37979198883359D+00 0.42470736443640D-01 3 13 3 5 0.39092827247254D+01 -0.28121610040765D-01 1 14 3 5 0.18762999119343D+00 0.35430677569609D-01 2 14 3 5 0.37979198883383D+00 0.42470736443641D-01 3 14 3 5 0.39092827247255D+01 -0.28121610040766D-01 1 15 3 5 0.34007399469184D+01 0.13686640135059D-02 2 15 3 5 0.27496806876738D+01 0.76488031477961D-02 3 15 3 5 0.17035920554806D+00 0.30749743633631D-01 1 16 3 5 0.34007399469183D+01 0.13686640135059D-02 2 16 3 5 0.27496806876738D+01 0.76488031477961D-02 3 16 3 5 0.17035920554807D+00 0.30749743633632D-01 1 17 3 5 0.18828771588215D+00 0.36654271339291D-01 2 17 3 5 -0.70566199330311D+00 -0.54515837216359D-01 3 17 3 5 0.36602739406624D+01 -0.34764508930423D-01 1 18 3 5 0.18828771588218D+00 0.36654271339293D-01 2 18 3 5 -0.70566199330319D+00 -0.54515837216355D-01 3 18 3 5 0.36602739406620D+01 -0.34764508930421D-01 1 19 3 5 0.27521151676478D+01 0.27750050042516D-01 2 19 3 5 -0.35041292863927D+01 -0.52900794309324D-02 3 19 3 5 0.61613537883457D+00 0.13064958162860D+00 1 20 3 5 0.27521151676479D+01 0.27750050042516D-01 2 20 3 5 -0.35041292863927D+01 -0.52900794309330D-02 3 20 3 5 0.61613537883453D+00 0.13064958162860D+00 1 1 1 6 0.60636551621815D+00 0.42095317191366D-02 2 1 1 6 0.11894022890391D+00 0.96930997542192D-03 3 1 1 6 0.20819969203351D+00 -0.15159655689709D-02 1 2 1 6 0.60636551621817D+00 0.42095317191420D-02 2 2 1 6 0.11894022890390D+00 0.96930997542256D-03 3 2 1 6 0.20819969203350D+00 -0.15159655689717D-02 1 3 1 6 -0.12845923974808D+00 0.31058073606029D-01 2 3 1 6 -0.54241979068746D+00 0.53702044046872D-02 3 3 1 6 0.51831940275149D+01 0.10292072185749D-01 1 4 1 6 0.12845923974803D+00 -0.31058073606040D-01 2 4 1 6 0.54241979068737D+00 -0.53702044046847D-02 3 4 1 6 -0.51831940275150D+01 -0.10292072185754D-01 1 5 1 6 -0.32248785592821D-13 -0.48875304511267D-14 2 5 1 6 -0.17339621696987D-17 0.30157590229668D-15 3 5 1 6 -0.25104371217081D-16 0.43419127025743D-15 1 6 1 6 0.19027134190201D+02 0.00000000000000D+00 2 6 1 6 0.30753761818174D+00 -0.74012829356996D-07 3 6 1 6 -0.45371277977957D+00 0.35371939424504D-07 1 7 1 6 -0.94854346316708D-15 0.66689751793403D-15 2 7 1 6 -0.24362339827570D-13 -0.55849218967476D-14 3 7 1 6 0.28507687900743D-13 -0.15753361692787D-14 1 8 1 6 0.11132789390426D-14 0.15636020787401D-07 2 8 1 6 0.16208870450129D+02 -0.98250669669654D-08 3 8 1 6 -0.64753973119029D+00 0.61664301696245D-08 1 9 1 6 -0.19782115549745D+01 0.99537882222306D+00 2 9 1 6 -0.31073905560878D-01 -0.38354546409529D-01 3 9 1 6 0.44791339485187D+00 0.42603074850767D+00 1 10 1 6 0.19782115549743D+01 -0.99537882222305D+00 2 10 1 6 0.31073905560862D-01 0.38354546409529D-01 3 10 1 6 -0.44791339485164D+00 -0.42603074850766D+00 1 11 1 6 0.15694076038805D-01 0.13221546769272D-02 2 11 1 6 -0.18037524406214D+01 0.28879279260676D-01 3 11 1 6 0.22085019921775D+00 0.10947011099952D-01 1 12 1 6 -0.15694076038802D-01 -0.13221546769270D-02 2 12 1 6 0.18037524406213D+01 -0.28879279260678D-01 3 12 1 6 -0.22085019921788D+00 -0.10947011099947D-01 1 13 1 6 0.58641202826265D+00 -0.42434203301506D-01 2 13 1 6 0.21890341311867D+00 -0.57975041970885D-01 3 13 1 6 -0.62705904656787D+00 0.82421881349827D-02 1 14 1 6 -0.58641202826266D+00 0.42434203301505D-01 2 14 1 6 -0.21890341311867D+00 0.57975041970886D-01 3 14 1 6 0.62705904656790D+00 -0.82421881349837D-02 1 15 1 6 -0.23532788230266D+01 0.12586756204556D-01 2 15 1 6 0.21831659676344D+01 0.12385695827233D-01 3 15 1 6 -0.80775327761389D+00 0.34945945467440D-01 1 16 1 6 0.23532788230267D+01 -0.12586756204575D-01 2 16 1 6 -0.21831659676343D+01 -0.12385695827254D-01 3 16 1 6 0.80775327761426D+00 -0.34945945467452D-01 1 17 1 6 0.52646948241185D+00 -0.75686226288418D-01 2 17 1 6 -0.50224696865234D+00 0.13530080062111D+00 3 17 1 6 -0.45745023807931D+00 0.32196623948933D-02 1 18 1 6 -0.52646948241185D+00 0.75686226288419D-01 2 18 1 6 0.50224696865235D+00 -0.13530080062111D+00 3 18 1 6 0.45745023807929D+00 -0.32196623948949D-02 1 19 1 6 -0.10920925903866D+01 0.14296338312363D-01 2 19 1 6 -0.12478087830556D+01 -0.19355587853690D-01 3 19 1 6 -0.87225283577175D+00 0.27747237711738D-01 1 20 1 6 0.10920925903866D+01 -0.14296338312367D-01 2 20 1 6 0.12478087830559D+01 0.19355587853713D-01 3 20 1 6 0.87225283577179D+00 -0.27747237711741D-01 1 1 2 6 0.31761732982057D+00 0.21358255272827D-02 2 1 2 6 -0.75556884958284D+00 -0.13834127344731D-01 3 1 2 6 -0.55231085890308D+01 0.11281703814691D-01 1 2 2 6 0.31761732982056D+00 0.21358255272833D-02 2 2 2 6 -0.75556884958294D+00 -0.13834127344740D-01 3 2 2 6 -0.55231085890309D+01 0.11281703814700D-01 1 3 2 6 -0.35116554270227D+00 0.64737058921389D-03 2 3 2 6 -0.64023917450729D+00 -0.82649819979715D-02 3 3 2 6 0.31208497403830D+00 0.17471032892696D-02 1 4 2 6 0.35116554270218D+00 -0.64737058921142D-03 2 4 2 6 0.64023917450738D+00 0.82649819979747D-02 3 4 2 6 -0.31208497403826D+00 -0.17471032892676D-02 1 5 2 6 -0.17339621696987D-17 0.30157590229668D-15 2 5 2 6 -0.33507079156895D-13 -0.14798893697998D-14 3 5 2 6 0.29522989639384D-13 -0.28236472969137D-14 1 6 2 6 0.30752539862604D+00 0.81079078392965D-07 2 6 2 6 0.19683273113958D+02 0.00000000000000D+00 3 6 2 6 0.30944148028657D+01 -0.28242977947907D-06 1 7 2 6 -0.24362339842769D-13 -0.55849218967476D-14 2 7 2 6 -0.87039957773632D-15 0.92197021192326D-15 3 7 2 6 -0.18132602766713D-13 0.36395055630933D-15 1 8 2 6 0.16208870450129D+02 0.98250669669654D-08 2 8 2 6 0.12973915900802D-14 0.26281384395133D-08 3 8 2 6 -0.46418172350165D+01 -0.80319572380900D-08 1 9 2 6 -0.50065337459872D-01 -0.17349167944217D-01 2 9 2 6 -0.17685234267219D+01 0.10193543494744D+01 3 9 2 6 -0.14909656126438D+00 -0.10887332677128D+00 1 10 2 6 0.50065337459856D-01 0.17349167944217D-01 2 10 2 6 0.17685234267216D+01 -0.10193543494744D+01 3 10 2 6 0.14909656126455D+00 0.10887332677127D+00 1 11 2 6 -0.17859320330234D+01 0.31186136530782D-01 2 11 2 6 0.84555701093823D-01 0.25288103443481D-02 3 11 2 6 0.52322751257993D+00 0.60280200069043D-02 1 12 2 6 0.17859320330234D+01 -0.31186136530783D-01 2 12 2 6 -0.84555701093815D-01 -0.25288103443486D-02 3 12 2 6 -0.52322751257994D+00 -0.60280200069043D-02 1 13 2 6 -0.23857555948405D+00 -0.34463920729137D-01 2 13 2 6 -0.54144292836908D-01 -0.28275102359184D-01 3 13 2 6 -0.41659732056845D+00 0.49748253466812D-02 1 14 2 6 0.23857555948405D+00 0.34463920729138D-01 2 14 2 6 0.54144292836902D-01 0.28275102359185D-01 3 14 2 6 0.41659732056842D+00 -0.49748253466811D-02 1 15 2 6 0.98619610502726D+00 -0.16032274550019D-01 2 15 2 6 -0.12926748939160D+01 -0.71915817217418D-02 3 15 2 6 -0.13596919767849D+01 0.17043412153371D-01 1 16 2 6 -0.98619610502720D+00 0.16032274549997D-01 2 16 2 6 0.12926748939159D+01 0.71915817217365D-02 3 16 2 6 0.13596919767851D+01 -0.17043412153381D-01 1 17 2 6 -0.30236673461975D-01 0.15440326016474D+00 2 17 2 6 0.30976009217220D+00 -0.15408707822108D+00 3 17 2 6 0.61507911902729D+00 -0.19381019719641D-01 1 18 2 6 0.30236673461980D-01 -0.15440326016474D+00 2 18 2 6 -0.30976009217220D+00 0.15408707822108D+00 3 18 2 6 -0.61507911902729D+00 0.19381019719642D-01 1 19 2 6 -0.24452075078457D+01 -0.47573476838330D-03 2 19 2 6 -0.23168943120459D+01 0.71500529342127D-02 3 19 2 6 0.12362503312940D+01 -0.45313182285086D-01 1 20 2 6 0.24452075078460D+01 0.47573476840705D-03 2 20 2 6 0.23168943120457D+01 -0.71500529342287D-02 3 20 2 6 -0.12362503312941D+01 0.45313182285097D-01 1 1 3 6 -0.39711712290637D+00 0.29264258522135D-02 2 1 3 6 -0.63824956855524D+01 0.16444631122562D-01 3 1 3 6 -0.54803902129652D+00 -0.21208851119816D-02 1 2 3 6 -0.39711712290638D+00 0.29264258522127D-02 2 2 3 6 -0.63824956855525D+01 0.16444631122571D-01 3 2 3 6 -0.54803902129664D+00 -0.21208851119856D-02 1 3 3 6 0.64874695791644D+01 0.95073242473852D-02 2 3 3 6 -0.15622400674705D-02 0.32920533895540D-02 3 3 3 6 0.11343374882711D+01 0.26622721372193D-02 1 4 3 6 -0.64874695791645D+01 -0.95073242473901D-02 2 4 3 6 0.15622400675107D-02 -0.32920533895520D-02 3 4 3 6 -0.11343374882711D+01 -0.26622721372258D-02 1 5 3 6 0.12053389640668D-16 0.43419127025743D-15 2 5 3 6 0.29513552597578D-13 -0.28236472969137D-14 3 5 3 6 0.35424995986130D-12 0.72734192880008D-14 1 6 3 6 -0.45371300483244D+00 -0.69864355616582D-07 2 6 3 6 0.30944350059557D+01 0.31495966972823D-06 3 6 3 6 0.44789469878657D+02 0.00000000000000D+00 1 7 3 6 0.28509561177256D-13 -0.15753361692787D-14 2 7 3 6 -0.18132602664349D-13 0.36395055630933D-15 3 7 3 6 -0.79401477610375D-14 0.12266668101839D-14 1 8 3 6 -0.64753973119029D+00 -0.61664301696245D-08 2 8 3 6 0.46418172350165D+01 -0.80319572380900D-08 3 8 3 6 0.18061443442228D-14 0.53154083300592D-07 1 9 3 6 0.13600813990370D+01 0.45730387005027D+00 2 9 3 6 -0.19974278796882D+00 -0.11413765786575D+00 3 9 3 6 -0.73433638552646D+01 -0.22752171886107D+01 1 10 3 6 -0.13600813990368D+01 -0.45730387005025D+00 2 10 3 6 0.19974278796899D+00 0.11413765786575D+00 3 10 3 6 0.73433638552652D+01 0.22752171886107D+01 1 11 3 6 0.35171366375819D-01 -0.13677493424667D-02 2 11 3 6 0.23734332837183D+00 0.91697917313609D-02 3 11 3 6 0.18506734839481D+00 0.26211647208981D-02 1 12 3 6 -0.35171366375948D-01 0.13677493424713D-02 2 12 3 6 -0.23734332837184D+00 -0.91697917313608D-02 3 12 3 6 -0.18506734839478D+00 -0.26211647208995D-02 1 13 3 6 -0.34007399469184D+01 -0.13686640135054D-02 2 13 3 6 -0.27496806876738D+01 -0.76488031477958D-02 3 13 3 6 0.17035920554805D+00 0.30749743633631D-01 1 14 3 6 0.34007399469184D+01 0.13686640135043D-02 2 14 3 6 0.27496806876738D+01 0.76488031477959D-02 3 14 3 6 -0.17035920554810D+00 -0.30749743633634D-01 1 15 3 6 0.18762999119345D+00 0.35430677569602D-01 2 15 3 6 0.37979198883381D+00 0.42470736443631D-01 3 15 3 6 -0.39092827247255D+01 0.28121610040790D-01 1 16 3 6 -0.18762999119308D+00 -0.35430677569613D-01 2 16 3 6 -0.37979198883358D+00 -0.42470736443640D-01 3 16 3 6 0.39092827247254D+01 -0.28121610040766D-01 1 17 3 6 -0.27521151676478D+01 -0.27750050042517D-01 2 17 3 6 0.35041292863927D+01 0.52900794309322D-02 3 17 3 6 0.61613537883451D+00 0.13064958162860D+00 1 18 3 6 0.27521151676478D+01 0.27750050042516D-01 2 18 3 6 -0.35041292863927D+01 -0.52900794309315D-02 3 18 3 6 -0.61613537883461D+00 -0.13064958162860D+00 1 19 3 6 0.18828771588219D+00 0.36654271339288D-01 2 19 3 6 -0.70566199330318D+00 -0.54515837216344D-01 3 19 3 6 -0.36602739406620D+01 0.34764508930442D-01 1 20 3 6 -0.18828771588214D+00 -0.36654271339292D-01 2 20 3 6 0.70566199330312D+00 0.54515837216355D-01 3 20 3 6 0.36602739406624D+01 -0.34764508930421D-01 1 1 1 7 -0.12845923974808D+00 0.31058073606039D-01 2 1 1 7 0.54241979068730D+00 -0.53702044046859D-02 3 1 1 7 0.51831940275149D+01 0.10292072185768D-01 1 2 1 7 0.12845923974807D+00 -0.31058073606030D-01 2 2 1 7 -0.54241979068738D+00 0.53702044046891D-02 3 2 1 7 -0.51831940275151D+01 -0.10292072185734D-01 1 3 1 7 -0.60636551621824D+00 -0.42095317191391D-02 2 3 1 7 0.11894022890391D+00 0.96930997542364D-03 3 3 1 7 -0.20819969203350D+00 0.15159655689699D-02 1 4 1 7 -0.60636551621822D+00 -0.42095317191411D-02 2 4 1 7 0.11894022890386D+00 0.96930997542332D-03 3 4 1 7 -0.20819969203351D+00 0.15159655689723D-02 1 5 1 7 0.11132788525000D-14 -0.15636020787401D-07 2 5 1 7 0.16208870450129D+02 -0.98250669669654D-08 3 5 1 7 0.64753973119029D+00 -0.61664301696245D-08 1 6 1 7 -0.94854346316708D-15 -0.66689751793403D-15 2 6 1 7 -0.24362339842769D-13 0.55849218967476D-14 3 6 1 7 0.28509561177256D-13 0.15753361692787D-14 1 7 1 7 0.19027134190201D+02 0.00000000000000D+00 2 7 1 7 -0.30753761818163D+00 0.74012829356996D-07 3 7 1 7 -0.45371277977941D+00 0.35371939424504D-07 1 8 1 7 -0.33247986314984D-13 0.48875304511267D-14 2 8 1 7 -0.16488930845526D-14 -0.30157590229668D-15 3 8 1 7 0.20099422673590D-13 -0.43419127025743D-15 1 9 1 7 -0.15694076038795D-01 -0.13221546769269D-02 2 9 1 7 -0.18037524406214D+01 0.28879279260677D-01 3 9 1 7 -0.22085019921787D+00 -0.10947011099948D-01 1 10 1 7 -0.15694076038802D-01 -0.13221546769271D-02 2 10 1 7 -0.18037524406213D+01 0.28879279260672D-01 3 10 1 7 -0.22085019921786D+00 -0.10947011099951D-01 1 11 1 7 0.19782115549742D+01 -0.99537882222305D+00 2 11 1 7 -0.31073905560737D-01 -0.38354546409529D-01 3 11 1 7 -0.44791339485178D+00 -0.42603074850766D+00 1 12 1 7 0.19782115549745D+01 -0.99537882222305D+00 2 12 1 7 -0.31073905560914D-01 -0.38354546409530D-01 3 12 1 7 -0.44791339485158D+00 -0.42603074850766D+00 1 13 1 7 -0.10920925903866D+01 0.14296338312364D-01 2 13 1 7 0.12478087830558D+01 0.19355587853690D-01 3 13 1 7 -0.87225283577179D+00 0.27747237711739D-01 1 14 1 7 -0.10920925903867D+01 0.14296338312371D-01 2 14 1 7 0.12478087830555D+01 0.19355587853736D-01 3 14 1 7 -0.87225283577185D+00 0.27747237711750D-01 1 15 1 7 -0.52646948241184D+00 0.75686226288418D-01 2 15 1 7 -0.50224696865235D+00 0.13530080062111D+00 3 15 1 7 0.45745023807929D+00 -0.32196623948928D-02 1 16 1 7 -0.52646948241186D+00 0.75686226288417D-01 2 16 1 7 -0.50224696865234D+00 0.13530080062111D+00 3 16 1 7 0.45745023807932D+00 -0.32196623948942D-02 1 17 1 7 0.23532788230269D+01 -0.12586756204574D-01 2 17 1 7 0.21831659676342D+01 0.12385695827255D-01 3 17 1 7 0.80775327761430D+00 -0.34945945467451D-01 1 18 1 7 0.23532788230267D+01 -0.12586756204577D-01 2 18 1 7 0.21831659676343D+01 0.12385695827255D-01 3 18 1 7 0.80775327761397D+00 -0.34945945467446D-01 1 19 1 7 0.58641202826266D+00 -0.42434203301506D-01 2 19 1 7 -0.21890341311866D+00 0.57975041970885D-01 3 19 1 7 -0.62705904656788D+00 0.82421881349830D-02 1 20 1 7 0.58641202826266D+00 -0.42434203301506D-01 2 20 1 7 -0.21890341311866D+00 0.57975041970885D-01 3 20 1 7 -0.62705904656786D+00 0.82421881349814D-02 1 1 2 7 0.35116554270211D+00 -0.64737058921261D-03 2 1 2 7 -0.64023917450728D+00 -0.82649819979753D-02 3 1 2 7 -0.31208497403830D+00 -0.17471032892683D-02 1 2 2 7 -0.35116554270219D+00 0.64737058921585D-03 2 2 2 7 0.64023917450731D+00 0.82649819979715D-02 3 2 2 7 0.31208497403830D+00 0.17471032892688D-02 1 3 2 7 0.31761732982057D+00 0.21358255272844D-02 2 3 2 7 0.75556884958291D+00 0.13834127344731D-01 3 3 2 7 -0.55231085890309D+01 0.11281703814708D-01 1 4 2 7 0.31761732982052D+00 0.21358255272841D-02 2 4 2 7 0.75556884958293D+00 0.13834127344739D-01 3 4 2 7 -0.55231085890309D+01 0.11281703814711D-01 1 5 2 7 0.16208870450129D+02 0.98250669669654D-08 2 5 2 7 0.12973915826369D-14 -0.26281384395133D-08 3 5 2 7 -0.46418172350165D+01 -0.80319572380900D-08 1 6 2 7 -0.24362339827570D-13 0.55849218967476D-14 2 6 2 7 -0.87039957773632D-15 -0.92197021192326D-15 3 6 2 7 -0.18132602664349D-13 -0.36395055630933D-15 1 7 2 7 -0.30752539862594D+00 -0.81079078392965D-07 2 7 2 7 0.19683273113958D+02 0.00000000000000D+00 3 7 2 7 -0.30944148028666D+01 0.28242977947907D-06 1 8 2 7 -0.16488930845526D-14 -0.30157590229668D-15 2 8 2 7 -0.36504681323383D-13 0.14798893697998D-14 3 8 2 7 -0.91118003185219D-14 0.28236472969137D-14 1 9 2 7 -0.17859320330234D+01 0.31186136530782D-01 2 9 2 7 -0.84555701093814D-01 -0.25288103443491D-02 3 9 2 7 0.52322751257988D+00 0.60280200069035D-02 1 10 2 7 -0.17859320330234D+01 0.31186136530778D-01 2 10 2 7 -0.84555701093817D-01 -0.25288103443480D-02 3 10 2 7 0.52322751257991D+00 0.60280200069039D-02 1 11 2 7 -0.50065337459730D-01 -0.17349167944217D-01 2 11 2 7 0.17685234267216D+01 -0.10193543494744D+01 3 11 2 7 -0.14909656126522D+00 -0.10887332677127D+00 1 12 2 7 -0.50065337459908D-01 -0.17349167944218D-01 2 12 2 7 0.17685234267217D+01 -0.10193543494744D+01 3 12 2 7 -0.14909656126426D+00 -0.10887332677127D+00 1 13 2 7 0.24452075078459D+01 0.47573476838335D-03 2 13 2 7 -0.23168943120457D+01 0.71500529342097D-02 3 13 2 7 -0.12362503312941D+01 0.45313182285088D-01 1 14 2 7 0.24452075078455D+01 0.47573476842986D-03 2 14 2 7 -0.23168943120459D+01 0.71500529342511D-02 3 14 2 7 -0.12362503312941D+01 0.45313182285108D-01 1 15 2 7 -0.30236673461978D-01 0.15440326016474D+00 2 15 2 7 -0.30976009217220D+00 0.15408707822108D+00 3 15 2 7 0.61507911902727D+00 -0.19381019719640D-01 1 16 2 7 -0.30236673461967D-01 0.15440326016474D+00 2 16 2 7 -0.30976009217220D+00 0.15408707822109D+00 3 16 2 7 0.61507911902731D+00 -0.19381019719641D-01 1 17 2 7 0.98619610502712D+00 -0.16032274549996D-01 2 17 2 7 0.12926748939158D+01 0.71915817217363D-02 3 17 2 7 -0.13596919767851D+01 0.17043412153381D-01 1 18 2 7 0.98619610502718D+00 -0.16032274549996D-01 2 18 2 7 0.12926748939160D+01 0.71915817217381D-02 3 18 2 7 -0.13596919767849D+01 0.17043412153381D-01 1 19 2 7 0.23857555948406D+00 0.34463920729138D-01 2 19 2 7 -0.54144292836902D-01 -0.28275102359183D-01 3 19 2 7 0.41659732056845D+00 -0.49748253466811D-02 1 20 2 7 0.23857555948406D+00 0.34463920729137D-01 2 20 2 7 -0.54144292836906D-01 -0.28275102359184D-01 3 20 2 7 0.41659732056846D+00 -0.49748253466805D-02 1 1 3 7 0.64874695791644D+01 0.95073242474050D-02 2 1 3 7 0.15622400674681D-02 -0.32920533895527D-02 3 1 3 7 0.11343374882711D+01 0.26622721372256D-02 1 2 3 7 -0.64874695791646D+01 -0.95073242473706D-02 2 2 3 7 -0.15622400674730D-02 0.32920533895532D-02 3 2 3 7 -0.11343374882711D+01 -0.26622721372188D-02 1 3 3 7 0.39711712290638D+00 -0.29264258522145D-02 2 3 3 7 -0.63824956855525D+01 0.16444631122579D-01 3 3 3 7 0.54803902129672D+00 0.21208851119753D-02 1 4 3 7 0.39711712290637D+00 -0.29264258522122D-02 2 4 3 7 -0.63824956855525D+01 0.16444631122582D-01 3 4 3 7 0.54803902129660D+00 0.21208851119797D-02 1 5 3 7 0.64753973119029D+00 0.61664301696245D-08 2 5 3 7 0.46418172350165D+01 -0.80319572380900D-08 3 5 3 7 0.18061441934713D-14 -0.53154083300592D-07 1 6 3 7 0.28507687900743D-13 0.15753361692787D-14 2 6 3 7 -0.18132602766713D-13 -0.36395055630933D-15 3 6 3 7 -0.79401477610375D-14 -0.12266668101839D-14 1 7 3 7 -0.45371300483228D+00 -0.69864355616582D-07 2 7 3 7 -0.30944350059566D+01 -0.31495966972823D-06 3 7 3 7 0.44789469878656D+02 0.00000000000000D+00 1 8 3 7 0.20136580434448D-13 -0.43419127025743D-15 2 8 3 7 -0.91023632767160D-14 0.28236472969137D-14 3 8 3 7 0.33826274830670D-12 -0.72734192880008D-14 1 9 3 7 -0.35171366375937D-01 0.13677493424700D-02 2 9 3 7 0.23734332837177D+00 0.91697917313601D-02 3 9 3 7 -0.18506734839479D+00 -0.26211647208991D-02 1 10 3 7 -0.35171366375926D-01 0.13677493424670D-02 2 10 3 7 0.23734332837181D+00 0.91697917313604D-02 3 10 3 7 -0.18506734839478D+00 -0.26211647208987D-02 1 11 3 7 -0.13600813990369D+01 -0.45730387005025D+00 2 11 3 7 -0.19974278796966D+00 -0.11413765786575D+00 3 11 3 7 0.73433638552655D+01 0.22752171886107D+01 1 12 3 7 -0.13600813990367D+01 -0.45730387005025D+00 2 12 3 7 -0.19974278796870D+00 -0.11413765786575D+00 3 12 3 7 0.73433638552652D+01 0.22752171886107D+01 1 13 3 7 0.18828771588214D+00 0.36654271339289D-01 2 13 3 7 0.70566199330311D+00 0.54515837216346D-01 3 13 3 7 -0.36602739406624D+01 0.34764508930443D-01 1 14 3 7 0.18828771588208D+00 0.36654271339300D-01 2 14 3 7 0.70566199330310D+00 0.54515837216366D-01 3 14 3 7 -0.36602739406617D+01 0.34764508930398D-01 1 15 3 7 0.27521151676478D+01 0.27750050042518D-01 2 15 3 7 0.35041292863927D+01 0.52900794309332D-02 3 15 3 7 -0.61613537883458D+00 -0.13064958162860D+00 1 16 3 7 0.27521151676478D+01 0.27750050042516D-01 2 16 3 7 0.35041292863927D+01 0.52900794309324D-02 3 16 3 7 -0.61613537883453D+00 -0.13064958162860D+00 1 17 3 7 -0.18762999119303D+00 -0.35430677569613D-01 2 17 3 7 0.37979198883357D+00 0.42470736443640D-01 3 17 3 7 0.39092827247253D+01 -0.28121610040766D-01 1 18 3 7 -0.18762999119337D+00 -0.35430677569607D-01 2 18 3 7 0.37979198883378D+00 0.42470736443640D-01 3 18 3 7 0.39092827247254D+01 -0.28121610040767D-01 1 19 3 7 -0.34007399469184D+01 -0.13686640135050D-02 2 19 3 7 0.27496806876738D+01 0.76488031477959D-02 3 19 3 7 0.17035920554807D+00 0.30749743633631D-01 1 20 3 7 -0.34007399469184D+01 -0.13686640135066D-02 2 20 3 7 0.27496806876738D+01 0.76488031477965D-02 3 20 3 7 0.17035920554806D+00 0.30749743633633D-01 1 1 1 8 -0.12845923974806D+00 0.31058073606039D-01 2 1 1 8 0.54241979068730D+00 -0.53702044046876D-02 3 1 1 8 -0.51831940275149D+01 -0.10292072185770D-01 1 2 1 8 -0.12845923974809D+00 0.31058073606030D-01 2 2 1 8 0.54241979068732D+00 -0.53702044046891D-02 3 2 1 8 -0.51831940275150D+01 -0.10292072185752D-01 1 3 1 8 -0.60636551621825D+00 -0.42095317191394D-02 2 3 1 8 0.11894022890389D+00 0.96930997542280D-03 3 3 1 8 0.20819969203350D+00 -0.15159655689718D-02 1 4 1 8 0.60636551621822D+00 0.42095317191412D-02 2 4 1 8 -0.11894022890388D+00 -0.96930997542280D-03 3 4 1 8 -0.20819969203347D+00 0.15159655689726D-02 1 5 1 8 0.15730591690863D-14 0.66689751793403D-15 2 5 1 8 -0.21412463768404D-13 -0.55849218967476D-14 3 5 1 8 -0.95247588935535D-14 -0.15753361692787D-14 1 6 1 8 0.11132789390426D-14 -0.15636020787401D-07 2 6 1 8 0.16208870450129D+02 -0.98250669669654D-08 3 6 1 8 -0.64753973119029D+00 0.61664301696245D-08 1 7 1 8 -0.33247986314984D-13 -0.48875304511267D-14 2 7 1 8 -0.16488930845526D-14 0.30157590229668D-15 3 7 1 8 0.20136580434448D-13 0.43419127025743D-15 1 8 1 8 0.19027134190200D+02 0.00000000000000D+00 2 8 1 8 -0.30753761818154D+00 0.74012829356996D-07 3 8 1 8 0.45371277977920D+00 -0.35371939424504D-07 1 9 1 8 -0.15694076038802D-01 -0.13221546769271D-02 2 9 1 8 -0.18037524406213D+01 0.28879279260676D-01 3 9 1 8 0.22085019921788D+00 0.10947011099948D-01 1 10 1 8 0.15694076038808D-01 0.13221546769279D-02 2 10 1 8 0.18037524406213D+01 -0.28879279260675D-01 3 10 1 8 -0.22085019921786D+00 -0.10947011099950D-01 1 11 1 8 -0.19782115549743D+01 0.99537882222306D+00 2 11 1 8 0.31073905560763D-01 0.38354546409530D-01 3 11 1 8 -0.44791339485157D+00 -0.42603074850767D+00 1 12 1 8 0.19782115549744D+01 -0.99537882222305D+00 2 12 1 8 -0.31073905560897D-01 -0.38354546409530D-01 3 12 1 8 0.44791339485162D+00 0.42603074850766D+00 1 13 1 8 -0.52646948241185D+00 0.75686226288418D-01 2 13 1 8 -0.50224696865235D+00 0.13530080062111D+00 3 13 1 8 -0.45745023807930D+00 0.32196623948955D-02 1 14 1 8 0.52646948241186D+00 -0.75686226288420D-01 2 14 1 8 0.50224696865234D+00 -0.13530080062111D+00 3 14 1 8 0.45745023807929D+00 -0.32196623948941D-02 1 15 1 8 0.10920925903867D+01 -0.14296338312367D-01 2 15 1 8 -0.12478087830553D+01 -0.19355587853712D-01 3 15 1 8 -0.87225283577185D+00 0.27747237711741D-01 1 16 1 8 -0.10920925903866D+01 0.14296338312364D-01 2 16 1 8 0.12478087830560D+01 0.19355587853689D-01 3 16 1 8 0.87225283577179D+00 -0.27747237711737D-01 1 17 1 8 0.58641202826267D+00 -0.42434203301504D-01 2 17 1 8 -0.21890341311865D+00 0.57975041970884D-01 3 17 1 8 0.62705904656785D+00 -0.82421881349820D-02 1 18 1 8 -0.58641202826266D+00 0.42434203301506D-01 2 18 1 8 0.21890341311866D+00 -0.57975041970884D-01 3 18 1 8 -0.62705904656789D+00 0.82421881349834D-02 1 19 1 8 -0.23532788230267D+01 0.12586756204559D-01 2 19 1 8 -0.21831659676343D+01 -0.12385695827231D-01 3 19 1 8 0.80775327761395D+00 -0.34945945467438D-01 1 20 1 8 0.23532788230269D+01 -0.12586756204573D-01 2 20 1 8 0.21831659676342D+01 0.12385695827256D-01 3 20 1 8 -0.80775327761432D+00 0.34945945467457D-01 1 1 2 8 0.35116554270211D+00 -0.64737058921425D-03 2 1 2 8 -0.64023917450727D+00 -0.82649819979741D-02 3 1 2 8 0.31208497403831D+00 0.17471032892681D-02 1 2 2 8 0.35116554270214D+00 -0.64737058921581D-03 2 2 2 8 -0.64023917450733D+00 -0.82649819979716D-02 3 2 2 8 0.31208497403831D+00 0.17471032892695D-02 1 3 2 8 0.31761732982055D+00 0.21358255272836D-02 2 3 2 8 0.75556884958290D+00 0.13834127344732D-01 3 3 2 8 0.55231085890308D+01 -0.11281703814701D-01 1 4 2 8 -0.31761732982054D+00 -0.21358255272836D-02 2 4 2 8 -0.75556884958293D+00 -0.13834127344741D-01 3 4 2 8 -0.55231085890309D+01 0.11281703814700D-01 1 5 2 8 -0.21412463753204D-13 -0.55849218967476D-14 2 5 2 8 0.87040345036330D-15 0.92197021192326D-15 3 5 2 8 0.37367214657655D-13 0.36395055630933D-15 1 6 2 8 0.16208870450129D+02 0.98250669669654D-08 2 6 2 8 0.12973915900802D-14 -0.26281384395133D-08 3 6 2 8 0.46418172350165D+01 0.80319572380900D-08 1 7 2 8 -0.16488930845526D-14 0.30157590229668D-15 2 7 2 8 -0.36504681323383D-13 -0.14798893697998D-14 3 7 2 8 -0.91023632767160D-14 -0.28236472969137D-14 1 8 2 8 -0.30752539862585D+00 -0.81079078392965D-07 2 8 2 8 0.19683273113957D+02 0.00000000000000D+00 3 8 2 8 0.30944148028666D+01 -0.28242977947907D-06 1 9 2 8 -0.17859320330234D+01 0.31186136530781D-01 2 9 2 8 -0.84555701093820D-01 -0.25288103443496D-02 3 9 2 8 -0.52322751257987D+00 -0.60280200069037D-02 1 10 2 8 0.17859320330234D+01 -0.31186136530780D-01 2 10 2 8 0.84555701093822D-01 0.25288103443475D-02 3 10 2 8 0.52322751257992D+00 0.60280200069036D-02 1 11 2 8 0.50065337459758D-01 0.17349167944217D-01 2 11 2 8 -0.17685234267217D+01 0.10193543494744D+01 3 11 2 8 -0.14909656126516D+00 -0.10887332677128D+00 1 12 2 8 -0.50065337459891D-01 -0.17349167944218D-01 2 12 2 8 0.17685234267218D+01 -0.10193543494744D+01 3 12 2 8 0.14909656126426D+00 0.10887332677127D+00 1 13 2 8 -0.30236673461979D-01 0.15440326016474D+00 2 13 2 8 -0.30976009217220D+00 0.15408707822108D+00 3 13 2 8 -0.61507911902731D+00 0.19381019719642D-01 1 14 2 8 0.30236673461970D-01 -0.15440326016474D+00 2 14 2 8 0.30976009217221D+00 -0.15408707822108D+00 3 14 2 8 0.61507911902726D+00 -0.19381019719641D-01 1 15 2 8 -0.24452075078454D+01 -0.47573476840611D-03 2 15 2 8 0.23168943120459D+01 -0.71500529342317D-02 3 15 2 8 -0.12362503312941D+01 0.45313182285097D-01 1 16 2 8 0.24452075078460D+01 0.47573476838233D-03 2 16 2 8 -0.23168943120456D+01 0.71500529342100D-02 3 16 2 8 0.12362503312941D+01 -0.45313182285089D-01 1 17 2 8 0.23857555948407D+00 0.34463920729137D-01 2 17 2 8 -0.54144292836895D-01 -0.28275102359187D-01 3 17 2 8 -0.41659732056845D+00 0.49748253466809D-02 1 18 2 8 -0.23857555948405D+00 -0.34463920729137D-01 2 18 2 8 0.54144292836906D-01 0.28275102359186D-01 3 18 2 8 0.41659732056841D+00 -0.49748253466815D-02 1 19 2 8 -0.98619610502718D+00 0.16032274550020D-01 2 19 2 8 -0.12926748939160D+01 -0.71915817217422D-02 3 19 2 8 -0.13596919767849D+01 0.17043412153374D-01 1 20 2 8 0.98619610502713D+00 -0.16032274549995D-01 2 20 2 8 0.12926748939158D+01 0.71915817217365D-02 3 20 2 8 0.13596919767851D+01 -0.17043412153380D-01 1 1 3 8 -0.64874695791644D+01 -0.95073242474067D-02 2 1 3 8 -0.15622400674623D-02 0.32920533895525D-02 3 1 3 8 0.11343374882711D+01 0.26622721372263D-02 1 2 3 8 -0.64874695791645D+01 -0.95073242473880D-02 2 2 3 8 -0.15622400674645D-02 0.32920533895540D-02 3 2 3 8 0.11343374882710D+01 0.26622721372186D-02 1 3 3 8 -0.39711712290638D+00 0.29264258522126D-02 2 3 3 8 0.63824956855524D+01 -0.16444631122572D-01 3 3 3 8 0.54803902129671D+00 0.21208851119785D-02 1 4 3 8 0.39711712290641D+00 -0.29264258522119D-02 2 4 3 8 -0.63824956855526D+01 0.16444631122572D-01 3 4 3 8 -0.54803902129663D+00 -0.21208851119884D-02 1 5 3 8 -0.95228856170406D-14 -0.15753361692787D-14 2 5 3 8 0.37367214760019D-13 0.36395055630933D-15 3 5 3 8 0.79401323448466D-14 0.12266668101839D-14 1 6 3 8 -0.64753973119029D+00 -0.61664301696245D-08 2 6 3 8 -0.46418172350165D+01 0.80319572380900D-08 3 6 3 8 0.18061443442228D-14 -0.53154083300592D-07 1 7 3 8 0.20099422673590D-13 0.43419127025743D-15 2 7 3 8 -0.91118003185219D-14 -0.28236472969137D-14 3 7 3 8 0.33826274830670D-12 0.72734192880008D-14 1 8 3 8 0.45371300483207D+00 0.69864355616582D-07 2 8 3 8 0.30944350059566D+01 0.31495966972823D-06 3 8 3 8 0.44789469878655D+02 0.00000000000000D+00 1 9 3 8 0.35171366375939D-01 -0.13677493424705D-02 2 9 3 8 -0.23734332837176D+00 -0.91697917313603D-02 3 9 3 8 -0.18506734839479D+00 -0.26211647208987D-02 1 10 3 8 -0.35171366375926D-01 0.13677493424686D-02 2 10 3 8 0.23734332837181D+00 0.91697917313602D-02 3 10 3 8 0.18506734839480D+00 0.26211647208984D-02 1 11 3 8 -0.13600813990367D+01 -0.45730387005027D+00 2 11 3 8 -0.19974278796959D+00 -0.11413765786576D+00 3 11 3 8 -0.73433638552651D+01 -0.22752171886107D+01 1 12 3 8 0.13600813990367D+01 0.45730387005025D+00 2 12 3 8 0.19974278796870D+00 0.11413765786575D+00 3 12 3 8 0.73433638552650D+01 0.22752171886107D+01 1 13 3 8 -0.27521151676478D+01 -0.27750050042515D-01 2 13 3 8 -0.35041292863927D+01 -0.52900794309315D-02 3 13 3 8 -0.61613537883451D+00 -0.13064958162860D+00 1 14 3 8 0.27521151676478D+01 0.27750050042516D-01 2 14 3 8 0.35041292863927D+01 0.52900794309327D-02 3 14 3 8 0.61613537883462D+00 0.13064958162860D+00 1 15 3 8 0.18828771588209D+00 0.36654271339291D-01 2 15 3 8 0.70566199330309D+00 0.54515837216355D-01 3 15 3 8 0.36602739406617D+01 -0.34764508930420D-01 1 16 3 8 -0.18828771588215D+00 -0.36654271339287D-01 2 16 3 8 -0.70566199330313D+00 -0.54515837216347D-01 3 16 3 8 -0.36602739406623D+01 0.34764508930443D-01 1 17 3 8 0.34007399469183D+01 0.13686640135061D-02 2 17 3 8 -0.27496806876738D+01 -0.76488031477961D-02 3 17 3 8 0.17035920554806D+00 0.30749743633630D-01 1 18 3 8 -0.34007399469184D+01 -0.13686640135047D-02 2 18 3 8 0.27496806876738D+01 0.76488031477955D-02 3 18 3 8 -0.17035920554809D+00 -0.30749743633634D-01 1 19 3 8 -0.18762999119339D+00 -0.35430677569600D-01 2 19 3 8 0.37979198883378D+00 0.42470736443634D-01 3 19 3 8 -0.39092827247254D+01 0.28121610040788D-01 1 20 3 8 0.18762999119301D+00 0.35430677569619D-01 2 20 3 8 -0.37979198883359D+00 -0.42470736443639D-01 3 20 3 8 0.39092827247252D+01 -0.28121610040766D-01 1 1 1 9 -0.36318833812228D+00 -0.94495937074548D-08 2 1 1 9 -0.23107696383781D+00 -0.17109108100466D-07 3 1 1 9 0.63178138744087D-14 -0.19065299584286D-15 1 2 1 9 -0.25214391312679D-14 -0.12017961680446D-15 2 2 1 9 -0.29252893506034D-14 0.22787721478357D-15 3 2 1 9 -0.95301266759500D-01 0.74374275600193D-08 1 3 1 9 -0.32584030570684D+01 -0.57307607877652D-08 2 3 1 9 -0.16810517671010D+00 0.53107900522651D-08 3 3 1 9 -0.27656612838313D-14 -0.18027834189074D-14 1 4 1 9 0.66341307944375D-15 -0.11306148127993D-14 2 4 1 9 0.14628089021076D-15 -0.99330201750526D-16 3 4 1 9 0.62248111267655D+00 0.17489675145810D-07 1 5 1 9 -0.19782106028327D+01 -0.99537915799096D+00 2 5 1 9 -0.50065306767879D-01 0.17348956263854D-01 3 5 1 9 -0.13600813684464D+01 0.45730351148437D+00 1 6 1 9 -0.19782106028326D+01 -0.99537915799096D+00 2 6 1 9 -0.50065306767892D-01 0.17348956263854D-01 3 6 1 9 0.13600813684464D+01 -0.45730351148437D+00 1 7 1 9 -0.15694076038795D-01 0.13221546769269D-02 2 7 1 9 -0.17859320330234D+01 -0.31186136530787D-01 3 7 1 9 -0.35171366375937D-01 -0.13677493424705D-02 1 8 1 9 -0.15694076038802D-01 0.13221546769271D-02 2 8 1 9 -0.17859320330234D+01 -0.31186136530786D-01 3 8 1 9 0.35171366375939D-01 0.13677493424710D-02 1 9 1 9 0.93053731732252D+01 0.00000000000000D+00 2 9 1 9 0.89352286251643D+00 0.59498164033963D-07 3 9 1 9 -0.72623361775764D-14 -0.13877787807815D-16 1 10 1 9 0.73097511957349D-14 -0.22969847810520D-15 2 10 1 9 0.43260172593134D-14 -0.13329960894692D-15 3 10 1 9 -0.16925289538691D+01 -0.59669323867108D-08 1 11 1 9 -0.84751511049850D-15 -0.25691333200634D-15 2 11 1 9 0.21842492047650D-14 -0.69305009116211D-15 3 11 1 9 -0.11668559819571D+00 0.10012733224281D-07 1 12 1 9 -0.26402084870250D-14 0.21188208009900D-08 2 12 1 9 -0.10001355854719D+01 0.49878640005432D-09 3 12 1 9 -0.74407407068130D-15 0.13062323080682D-16 1 13 1 9 0.11157897667569D+01 0.25277139044722D-08 2 13 1 9 0.14170006352116D+01 0.42946828525094D-09 3 13 1 9 0.21235589146700D+01 0.16407900600642D-07 1 14 1 9 -0.77315874204462D-02 -0.21801613299445D-01 2 14 1 9 0.67229056626952D+00 -0.24972201796319D-01 3 14 1 9 -0.11949146428922D+01 -0.59731020981950D-02 1 15 1 9 0.77315874204520D-02 0.21801613299445D-01 2 15 1 9 -0.67229056626952D+00 0.24972201796319D-01 3 15 1 9 -0.11949146428922D+01 -0.59731020981985D-02 1 16 1 9 0.11157897667569D+01 0.25277134308476D-08 2 16 1 9 0.14170006352115D+01 0.42946805401249D-09 3 16 1 9 -0.21235589146700D+01 -0.16407900557298D-07 1 17 1 9 0.42909725326250D+00 0.96571024830956D-02 2 17 1 9 -0.12523540326113D+01 -0.34949201832719D-01 3 17 1 9 0.13654668846558D+01 -0.25767336813667D-01 1 18 1 9 -0.21269098163499D+00 -0.33975177568551D-06 2 18 1 9 -0.50301179776289D+00 -0.30339873608871D-06 3 18 1 9 -0.89382868931026D+00 -0.11804576096703D-06 1 19 1 9 0.21269098163498D+00 0.33975177645604D-06 2 19 1 9 0.50301179776288D+00 0.30339873722364D-06 3 19 1 9 -0.89382868931026D+00 -0.11804576268530D-06 1 20 1 9 0.42909725326250D+00 0.96571024830946D-02 2 20 1 9 -0.12523540326113D+01 -0.34949201832719D-01 3 20 1 9 -0.13654668846558D+01 0.25767336813666D-01 1 1 2 9 0.12577706755930D+00 -0.28746979315923D-07 2 1 2 9 -0.20830955006502D+01 -0.66085075473843D-08 3 1 2 9 0.56658033336008D-14 -0.24650863928752D-14 1 2 2 9 -0.29248275621372D-14 0.22831089565256D-15 2 2 2 9 -0.96649876172774D-15 0.87450052083188D-17 3 2 2 9 0.58080560419071D+00 0.75773587966198D-08 1 3 2 9 -0.12134762704465D+00 0.35866752816293D-08 2 3 2 9 -0.34031489089158D+00 0.26520266553721D-08 3 3 2 9 -0.71641022308469D-14 -0.38479223234889D-15 1 4 2 9 0.14628089106379D-15 -0.98896520881532D-16 2 4 2 9 -0.44953773554259D-15 0.43600963756203D-15 3 4 2 9 0.85025806103214D-01 0.69288392681226D-08 1 5 2 9 -0.31074701061590D-01 0.38354275583803D-01 2 5 2 9 -0.17685229911125D+01 -0.10193541917155D+01 3 5 2 9 0.19973998276556D+00 -0.11413784244335D+00 1 6 2 9 -0.31074701061602D-01 0.38354275583803D-01 2 6 2 9 -0.17685229911126D+01 -0.10193541917155D+01 3 6 2 9 -0.19973998276555D+00 0.11413784244335D+00 1 7 2 9 -0.18037524406214D+01 -0.28879279260682D-01 2 7 2 9 -0.84555701093814D-01 0.25288103443490D-02 3 7 2 9 0.23734332837177D+00 -0.91697917313581D-02 1 8 2 9 -0.18037524406213D+01 -0.28879279260681D-01 2 8 2 9 -0.84555701093820D-01 0.25288103443495D-02 3 8 2 9 -0.23734332837176D+00 0.91697917313583D-02 1 9 2 9 0.89352203019921D+00 -0.48014760468160D-07 2 9 2 9 0.70106209229280D+01 0.00000000000000D+00 3 9 2 9 -0.41659256486041D-13 0.69388939039072D-17 1 10 2 9 0.43260172592100D-14 -0.13329960894692D-15 2 10 2 9 0.90821098363861D-14 -0.35375322299214D-15 3 10 2 9 0.58922710040616D+00 -0.23141651196626D-07 1 11 2 9 0.21842492047650D-14 -0.68611119725821D-15 2 11 2 9 -0.10116375859811D-14 0.23117678935264D-16 3 11 2 9 0.17309372500500D+00 -0.60513692531432D-08 1 12 2 9 -0.10001355854719D+01 -0.49878235384649D-09 2 12 2 9 0.71749607000800D-14 -0.55067990870986D-08 3 12 2 9 0.26843684335461D-14 -0.15416343832432D-15 1 13 2 9 0.97020792468271D+00 0.46176710850607D-08 2 13 2 9 0.14148404989987D+00 0.20079078022758D-08 3 13 2 9 0.11137098308737D+01 0.17714798689374D-07 1 14 2 9 0.66226712589214D+00 -0.83349099763254D-02 2 14 2 9 0.32247316378205D+00 -0.38361917021950D-02 3 14 2 9 -0.13480231488826D+01 -0.28462468700723D-03 1 15 2 9 -0.66226712589214D+00 0.83349099763253D-02 2 15 2 9 -0.32247316378205D+00 0.38361917021959D-02 3 15 2 9 -0.13480231488826D+01 -0.28462468701100D-03 1 16 2 9 0.97020792468269D+00 0.46176708677000D-08 2 16 2 9 0.14148404989988D+00 0.20079082305635D-08 3 16 2 9 -0.11137098308737D+01 -0.17714799480879D-07 1 17 2 9 -0.14405737890597D+01 -0.39946960163866D-01 2 17 2 9 0.57632070221865D+00 0.41313829727513D-01 3 17 2 9 -0.17119795773384D+01 0.42289856139815D-01 1 18 2 9 -0.62889356407283D+00 -0.71669097220802D-07 2 18 2 9 0.43731681324673D+00 0.34735605032727D-07 3 18 2 9 0.17398153256030D+01 0.62230760221946D-06 1 19 2 9 0.62889356407282D+00 0.71669098341853D-07 2 19 2 9 -0.43731681324672D+00 -0.34735605536267D-07 3 19 2 9 0.17398153256030D+01 0.62230760599395D-06 1 20 2 9 -0.14405737890597D+01 -0.39946960163866D-01 2 20 2 9 0.57632070221865D+00 0.41313829727513D-01 3 20 2 9 0.17119795773384D+01 -0.42289856139816D-01 1 1 3 9 0.63178138759596D-14 -0.19065299584286D-15 2 1 3 9 0.56658033344280D-14 -0.24650863928752D-14 3 1 3 9 -0.10931715241664D+01 -0.57205833012990D-07 1 2 3 9 0.35225490033343D+00 0.31162647320705D-08 2 2 3 9 0.23291021470691D+01 -0.20432356020204D-07 3 2 3 9 -0.44924977857795D-14 -0.16939627208785D-15 1 3 3 9 -0.27656612838313D-14 -0.18027834189074D-14 2 3 3 9 -0.71641022323978D-14 -0.38479223234889D-15 3 3 3 9 -0.60405779955785D+00 -0.64228704276942D-07 1 4 3 9 0.24095667808050D+01 0.12254097973133D-07 2 4 3 9 -0.20828577590334D+00 -0.70889447383977D-08 3 4 3 9 0.12604995452372D-13 -0.27857197307976D-15 1 5 3 9 -0.44791349326354D+00 0.42603123174461D+00 2 5 3 9 0.14909695659257D+00 -0.10887274783794D+00 3 5 3 9 -0.73433595725218D+01 0.22752192694038D+01 1 6 3 9 0.44791349326354D+00 -0.42603123174461D+00 2 6 3 9 -0.14909695659257D+00 0.10887274783794D+00 3 6 3 9 -0.73433595725218D+01 0.22752192694038D+01 1 7 3 9 -0.22085019921787D+00 0.10947011099948D-01 2 7 3 9 0.52322751257988D+00 -0.60280200069015D-02 3 7 3 9 -0.18506734839479D+00 0.26211647208991D-02 1 8 3 9 0.22085019921788D+00 -0.10947011099947D-01 2 8 3 9 -0.52322751257987D+00 0.60280200069017D-02 3 8 3 9 -0.18506734839479D+00 0.26211647208988D-02 1 9 3 9 -0.72623361775764D-14 0.13877787807814D-16 2 9 3 9 -0.41659256482732D-13 -0.69388939039072D-17 3 9 3 9 0.44845742012430D+02 0.00000000000000D+00 1 10 3 9 -0.16925184514148D+01 0.60192966949196D-08 2 10 3 9 0.58921368200757D+00 0.23659482855761D-07 3 10 3 9 -0.16058374749949D-13 0.20703410221400D-14 1 11 3 9 -0.11668559819571D+00 -0.10012732809545D-07 2 11 3 9 -0.17309372500494D+00 -0.60513692531432D-08 3 11 3 9 -0.60957451185652D-14 -0.19165167979061D-15 1 12 3 9 -0.74407407068130D-15 0.13062323080682D-16 2 12 3 9 0.26843684335461D-14 -0.15416343832432D-15 3 12 3 9 -0.81938119853487D-14 -0.10706378528153D-07 1 13 3 9 0.36935108977887D+01 -0.12012453254696D-07 2 13 3 9 0.26510183079313D+01 -0.23169385185214D-07 3 13 3 9 0.97947852423047D+00 0.29725112901047D-07 1 14 3 9 -0.30034300605759D+01 -0.36267130947548D-01 2 14 3 9 -0.30802567047354D+01 -0.52727102560344D-01 3 14 3 9 0.26428751368363D+01 0.66691042739209D-01 1 15 3 9 -0.30034300605759D+01 -0.36267130947551D-01 2 15 3 9 -0.30802567047354D+01 -0.52727102560348D-01 3 15 3 9 -0.26428751368363D+01 -0.66691042739215D-01 1 16 3 9 -0.36935108977887D+01 0.12012453287631D-07 2 16 3 9 -0.26510183079313D+01 0.23169384388505D-07 3 16 3 9 0.97947852423047D+00 0.29725112441798D-07 1 17 3 9 0.28203925227030D+01 -0.10126640308881D+00 2 17 3 9 -0.32400070915946D+01 0.11623328030853D+00 3 17 3 9 0.72545834190351D+00 -0.89816573984339D-01 1 18 3 9 -0.25394093574743D+01 0.76542898688204D-06 2 18 3 9 0.38820587360795D+01 -0.11441304133232D-05 3 18 3 9 0.31426422397135D+01 -0.84733985634938D-06 1 19 3 9 -0.25394093574743D+01 0.76542898516377D-06 2 19 3 9 0.38820587360795D+01 -0.11441304095418D-05 3 19 3 9 -0.31426422397135D+01 0.84733985216814D-06 1 20 3 9 -0.28203925227030D+01 0.10126640308881D+00 2 20 3 9 0.32400070915946D+01 -0.11623328030853D+00 3 20 3 9 0.72545834190351D+00 -0.89816573984340D-01 1 1 1 10 0.13537165724066D-14 -0.20115044373706D-15 2 1 1 10 0.50502524839585D-14 0.17910989060541D-15 3 1 1 10 0.95301266759511D-01 -0.74374275013123D-08 1 2 1 10 0.36318833812217D+00 0.94495880651270D-08 2 2 1 10 0.23107696383776D+00 0.17109110518916D-07 3 2 1 10 0.10526430139188D-13 0.19718202498179D-15 1 3 1 10 0.11600158213856D-14 0.42437301130913D-15 2 3 1 10 -0.30178665471328D-14 -0.35663486387491D-16 3 3 1 10 0.62248111267653D+00 0.17489672687438D-07 1 4 1 10 -0.32584030570681D+01 -0.57307490643955D-08 2 4 1 10 -0.16810517671002D+00 0.53107893844761D-08 3 4 1 10 -0.76588931218202D-14 -0.21367787582820D-14 1 5 1 10 -0.19782106028323D+01 -0.99537915799094D+00 2 5 1 10 -0.50065306767863D-01 0.17348956263855D-01 3 5 1 10 -0.13600813684463D+01 0.45730351148433D+00 1 6 1 10 0.19782106028324D+01 0.99537915799095D+00 2 6 1 10 0.50065306767876D-01 -0.17348956263854D-01 3 6 1 10 -0.13600813684462D+01 0.45730351148435D+00 1 7 1 10 -0.15694076038802D-01 0.13221546769271D-02 2 7 1 10 -0.17859320330234D+01 -0.31186136530783D-01 3 7 1 10 -0.35171366375926D-01 -0.13677493424675D-02 1 8 1 10 0.15694076038808D-01 -0.13221546769279D-02 2 8 1 10 0.17859320330234D+01 0.31186136530786D-01 3 8 1 10 -0.35171366375926D-01 -0.13677493424691D-02 1 9 1 10 0.73097511957349D-14 0.25745405372083D-15 2 9 1 10 0.43260172593134D-14 0.13329960894692D-15 3 9 1 10 -0.16925289538691D+01 -0.59669340387362D-08 1 10 1 10 0.93053731732246D+01 0.00000000000000D+00 2 10 1 10 0.89352286251640D+00 0.59498164033963D-07 3 10 1 10 0.13484621097444D-12 -0.13877787807814D-16 1 11 1 10 -0.20489902216293D-14 0.21188218781653D-08 2 11 1 10 -0.10001355854719D+01 0.49878220263899D-09 3 11 1 10 -0.49716747006820D-14 0.17370011026438D-16 1 12 1 10 -0.48488590421900D-14 0.16387418721345D-15 2 12 1 10 -0.68692734359969D-14 -0.15589030009310D-14 3 12 1 10 -0.11668559819568D+00 0.10012732628166D-07 1 13 1 10 -0.77315874204409D-02 -0.21801613299445D-01 2 13 1 10 0.67229056626952D+00 -0.24972201796318D-01 3 13 1 10 -0.11949146428923D+01 -0.59731020982015D-02 1 14 1 10 0.11157897667569D+01 0.25277186452484D-08 2 14 1 10 0.14170006352116D+01 0.42947269835182D-09 3 14 1 10 0.21235589146700D+01 0.16407909306247D-07 1 15 1 10 0.11157897667569D+01 0.25277188529486D-08 2 15 1 10 0.14170006352116D+01 0.42947260582424D-09 3 15 1 10 -0.21235589146700D+01 -0.16407910792132D-07 1 16 1 10 0.77315874204356D-02 0.21801613299445D-01 2 16 1 10 -0.67229056626951D+00 0.24972201796318D-01 3 16 1 10 -0.11949146428923D+01 -0.59731020981987D-02 1 17 1 10 -0.21269098163497D+00 -0.33975177737911D-06 2 17 1 10 -0.50301179776291D+00 -0.30339873814802D-06 3 17 1 10 -0.89382868931027D+00 -0.11804576454025D-06 1 18 1 10 0.42909725326248D+00 0.96571024830970D-02 2 18 1 10 -0.12523540326113D+01 -0.34949201832727D-01 3 18 1 10 0.13654668846558D+01 -0.25767336813662D-01 1 19 1 10 0.42909725326249D+00 0.96571024830977D-02 2 19 1 10 -0.12523540326113D+01 -0.34949201832725D-01 3 19 1 10 -0.13654668846558D+01 0.25767336813661D-01 1 20 1 10 0.21269098163496D+00 0.33975177709061D-06 2 20 1 10 0.50301179776289D+00 0.30339873723816D-06 3 20 1 10 -0.89382868931025D+00 -0.11804576309100D-06 1 1 2 10 0.50497906954923D-14 0.17954357147441D-15 2 1 2 10 0.34013611601607D-14 -0.38481120534800D-16 3 1 2 10 -0.58080560419071D+00 -0.75773551276391D-08 1 2 2 10 -0.12577706755935D+00 0.28746981734373D-07 2 2 2 10 0.20830955006505D+01 0.66085282694530D-08 3 2 2 10 -0.57509962589507D-14 -0.12149795519521D-14 1 3 2 10 -0.30178665471587D-14 -0.35229805518497D-16 2 3 2 10 -0.31483030034309D-14 -0.12007403077388D-14 3 3 2 10 0.85025806103215D-01 0.69288402410147D-08 1 4 2 10 -0.12134762704457D+00 0.35866746138403D-08 2 4 2 10 -0.34031489089178D+00 0.26520239264280D-08 3 4 2 10 -0.16168999097759D-13 0.51672277693328D-15 1 5 2 10 -0.31074701061574D-01 0.38354275583804D-01 2 5 2 10 -0.17685229911122D+01 -0.10193541917154D+01 3 5 2 10 0.19973998276575D+00 -0.11413784244334D+00 1 6 2 10 0.31074701061586D-01 -0.38354275583803D-01 2 6 2 10 0.17685229911123D+01 0.10193541917154D+01 3 6 2 10 0.19973998276572D+00 -0.11413784244334D+00 1 7 2 10 -0.18037524406213D+01 -0.28879279260677D-01 2 7 2 10 -0.84555701093817D-01 0.25288103443480D-02 3 7 2 10 0.23734332837181D+00 -0.91697917313584D-02 1 8 2 10 0.18037524406213D+01 0.28879279260680D-01 2 8 2 10 0.84555701093822D-01 -0.25288103443475D-02 3 8 2 10 0.23734332837181D+00 -0.91697917313582D-02 1 9 2 10 0.43260172592100D-14 0.13329960894692D-15 2 9 2 10 0.90821098363861D-14 0.35375322299214D-15 3 9 2 10 0.58922710040616D+00 -0.23141649132135D-07 1 10 2 10 0.89352203019918D+00 -0.48014760468160D-07 2 10 2 10 0.70106209229277D+01 0.00000000000000D+00 3 10 2 10 -0.20342974413241D-13 0.69388939039072D-17 1 11 2 10 -0.10001355854719D+01 -0.49878655126182D-09 2 11 2 10 -0.32016118329501D-13 -0.55067964663990D-08 3 11 2 10 -0.20856999889054D-14 -0.18137035744773D-15 1 12 2 10 -0.68692734359969D-14 -0.15519641070271D-14 2 12 2 10 -0.50877814280339D-14 -0.21364918170224D-15 3 12 2 10 0.17309372500498D+00 -0.60513697367375D-08 1 13 2 10 0.66226712589215D+00 -0.83349099763241D-02 2 13 2 10 0.32247316378203D+00 -0.38361917021953D-02 3 13 2 10 -0.13480231488826D+01 -0.28462468701454D-03 1 14 2 10 0.97020792468272D+00 0.46176755120393D-08 2 14 2 10 0.14148404989988D+00 0.20079073401367D-08 3 14 2 10 0.11137098308738D+01 0.17714804173974D-07 1 15 2 10 0.97020792468271D+00 0.46176754125729D-08 2 15 2 10 0.14148404989987D+00 0.20079075552339D-08 3 15 2 10 -0.11137098308738D+01 -0.17714804258325D-07 1 16 2 10 -0.66226712589213D+00 0.83349099763242D-02 2 16 2 10 -0.32247316378204D+00 0.38361917021955D-02 3 16 2 10 -0.13480231488826D+01 -0.28462468701041D-03 1 17 2 10 -0.62889356407285D+00 -0.71669099269694D-07 2 17 2 10 0.43731681324673D+00 0.34735606487607D-07 3 17 2 10 0.17398153256030D+01 0.62230761045326D-06 1 18 2 10 -0.14405737890598D+01 -0.39946960163874D-01 2 18 2 10 0.57632070221865D+00 0.41313829727515D-01 3 18 2 10 -0.17119795773385D+01 0.42289856139807D-01 1 19 2 10 -0.14405737890597D+01 -0.39946960163872D-01 2 19 2 10 0.57632070221865D+00 0.41313829727515D-01 3 19 2 10 0.17119795773385D+01 -0.42289856139808D-01 1 20 2 10 0.62889356407283D+00 0.71669098363309D-07 2 20 2 10 -0.43731681324674D+00 -0.34735605567471D-07 3 20 2 10 0.17398153256030D+01 0.62230760596232D-06 1 1 3 10 -0.35225490033342D+00 -0.31162646733630D-08 2 1 3 10 -0.23291021470691D+01 0.20432359689184D-07 3 1 3 10 -0.31620623244517D-16 -0.24200207883688D-15 1 2 3 10 0.10526430140635D-13 0.19718202498179D-15 2 2 3 10 -0.57509962597779D-14 -0.12149795519521D-14 3 2 3 10 0.10931715241662D+01 0.57205820242211D-07 1 3 3 10 0.24095667808050D+01 0.12254095514761D-07 2 3 3 10 -0.20828577590334D+00 -0.70889437655056D-08 3 3 3 10 0.19668657751882D-13 0.73797189618399D-15 1 4 3 10 -0.76588931218202D-14 -0.21367787582820D-14 2 4 3 10 -0.16168999099309D-13 0.51672277693328D-15 3 4 3 10 -0.60405779955819D+00 -0.64228709824588D-07 1 5 3 10 -0.44791349326348D+00 0.42603123174457D+00 2 5 3 10 0.14909695659276D+00 -0.10887274783793D+00 3 5 3 10 -0.73433595725227D+01 0.22752192694037D+01 1 6 3 10 -0.44791349326330D+00 0.42603123174459D+00 2 6 3 10 0.14909695659273D+00 -0.10887274783794D+00 3 6 3 10 0.73433595725224D+01 -0.22752192694037D+01 1 7 3 10 -0.22085019921786D+00 0.10947011099951D-01 2 7 3 10 0.52322751257991D+00 -0.60280200069018D-02 3 7 3 10 -0.18506734839478D+00 0.26211647208988D-02 1 8 3 10 -0.22085019921786D+00 0.10947011099949D-01 2 8 3 10 0.52322751257992D+00 -0.60280200069016D-02 3 8 3 10 0.18506734839480D+00 -0.26211647208984D-02 1 9 3 10 -0.16925184514148D+01 0.60192950428942D-08 2 9 3 10 0.58921368200757D+00 0.23659484920251D-07 3 9 3 10 -0.16058374749949D-13 -0.20703410221400D-14 1 10 3 10 0.13484621097444D-12 0.13877787807814D-16 2 10 3 10 -0.20342974409932D-13 -0.69388939039072D-17 3 10 3 10 0.44845742012432D+02 0.00000000000000D+00 1 11 3 10 -0.49716747006820D-14 0.17370011026438D-16 2 11 3 10 -0.20856999889054D-14 -0.18137035744773D-15 3 11 3 10 0.74027711148809D-13 -0.10706380503396D-07 1 12 3 10 -0.11668559819568D+00 -0.10012733405660D-07 2 12 3 10 -0.17309372500496D+00 -0.60513697367375D-08 3 12 3 10 0.15857649876524D-14 -0.27227468447073D-16 1 13 3 10 -0.30034300605759D+01 -0.36267130947554D-01 2 13 3 10 -0.30802567047354D+01 -0.52727102560352D-01 3 13 3 10 0.26428751368363D+01 0.66691042739219D-01 1 14 3 10 0.36935108977887D+01 -0.12012444535213D-07 2 14 3 10 0.26510183079314D+01 -0.23169379700614D-07 3 14 3 10 0.97947852423049D+00 0.29725117028117D-07 1 15 3 10 -0.36935108977887D+01 0.12012443052797D-07 2 15 3 10 -0.26510183079313D+01 0.23169379611059D-07 3 15 3 10 0.97947852423052D+00 0.29725117255925D-07 1 16 3 10 -0.30034300605759D+01 -0.36267130947552D-01 2 16 3 10 -0.30802567047354D+01 -0.52727102560348D-01 3 16 3 10 -0.26428751368363D+01 -0.66691042739215D-01 1 17 3 10 -0.25394093574743D+01 0.76542898332270D-06 2 17 3 10 0.38820587360794D+01 -0.11441304050894D-05 3 17 3 10 0.31426422397134D+01 -0.84733984471700D-06 1 18 3 10 0.28203925227030D+01 -0.10126640308881D+00 2 18 3 10 -0.32400070915947D+01 0.11623328030852D+00 3 18 3 10 0.72545834190352D+00 -0.89816573984336D-01 1 19 3 10 -0.28203925227030D+01 0.10126640308881D+00 2 19 3 10 0.32400070915947D+01 -0.11623328030853D+00 3 19 3 10 0.72545834190357D+00 -0.89816573984336D-01 1 20 3 10 -0.25394093574743D+01 0.76542898475807D-06 2 20 3 10 0.38820587360794D+01 -0.11441304095873D-05 3 20 3 10 -0.31426422397134D+01 0.84733985151537D-06 1 1 1 11 -0.17828020597083D-14 0.59725279318935D-16 2 1 1 11 -0.30986602204286D-15 -0.16423891316896D-16 3 1 1 11 0.62248111267650D+00 0.17489672209200D-07 1 2 1 11 -0.32584030570682D+01 -0.57307611276395D-08 2 2 1 11 0.16810517671020D+00 -0.53107898289929D-08 3 2 1 11 -0.10397420186220D-13 0.54421581279289D-15 1 3 1 11 0.10145342220908D-14 0.57008449146097D-16 2 3 1 11 -0.32041633921770D-15 0.25674865879390D-15 3 3 1 11 -0.95301266759512D-01 0.74374275156901D-08 1 4 1 11 -0.36318833812193D+00 -0.94495901644079D-08 2 4 1 11 0.23107696383789D+00 0.17109105662586D-07 3 4 1 11 0.43662574633656D-14 0.25949176583137D-15 1 5 1 11 -0.15694076038798D-01 0.13221546769269D-02 2 5 1 11 0.17859320330234D+01 0.31186136530783D-01 3 5 1 11 0.35171366375815D-01 0.13677493424682D-02 1 6 1 11 0.15694076038805D-01 -0.13221546769272D-02 2 6 1 11 -0.17859320330234D+01 -0.31186136530787D-01 3 6 1 11 0.35171366375819D-01 0.13677493424672D-02 1 7 1 11 0.19782106028323D+01 0.99537915799095D+00 2 7 1 11 -0.50065306767749D-01 0.17348956263854D-01 3 7 1 11 -0.13600813684463D+01 0.45730351148435D+00 1 8 1 11 -0.19782106028324D+01 -0.99537915799096D+00 2 8 1 11 0.50065306767777D-01 -0.17348956263854D-01 3 8 1 11 -0.13600813684461D+01 0.45730351148437D+00 1 9 1 11 -0.84751511049850D-15 0.25691333200634D-15 2 9 1 11 0.21842492047650D-14 0.68611119725821D-15 3 9 1 11 -0.11668559819571D+00 0.10012732809545D-07 1 10 1 11 -0.20489902216293D-14 -0.21188218781653D-08 2 10 1 11 -0.10001355854719D+01 0.49878655126182D-09 3 10 1 11 -0.49716747006820D-14 -0.17370011026438D-16 1 11 1 11 0.93053731732241D+01 0.00000000000000D+00 2 11 1 11 -0.89352286251632D+00 -0.59498164033963D-07 3 11 1 11 -0.12805460125679D-12 -0.13877787807814D-16 1 12 1 11 -0.28163514855991D-14 0.14564470152522D-14 2 12 1 11 0.39887432378772D-15 -0.52856441944538D-15 3 12 1 11 0.16925289538691D+01 0.59669329373631D-08 1 13 1 11 -0.21269098163499D+00 -0.33975177877160D-06 2 13 1 11 0.50301179776292D+00 0.30339873799210D-06 3 13 1 11 0.89382868931035D+00 0.11804576473768D-06 1 14 1 11 0.42909725326248D+00 0.96571024830953D-02 2 14 1 11 0.12523540326113D+01 0.34949201832721D-01 3 14 1 11 -0.13654668846558D+01 0.25767336813666D-01 1 15 1 11 0.42909725326248D+00 0.96571024830954D-02 2 15 1 11 0.12523540326113D+01 0.34949201832721D-01 3 15 1 11 0.13654668846558D+01 -0.25767336813666D-01 1 16 1 11 0.21269098163499D+00 0.33975177656861D-06 2 16 1 11 -0.50301179776291D+00 -0.30339873751713D-06 3 16 1 11 0.89382868931034D+00 0.11804576245433D-06 1 17 1 11 0.77315874204267D-02 0.21801613299444D-01 2 17 1 11 0.67229056626954D+00 -0.24972201796320D-01 3 17 1 11 -0.11949146428922D+01 -0.59731020981983D-02 1 18 1 11 -0.11157897667569D+01 -0.25277147028709D-08 2 18 1 11 0.14170006352115D+01 0.42947069362020D-09 3 18 1 11 0.21235589146701D+01 0.16407905929600D-07 1 19 1 11 -0.11157897667569D+01 -0.25277145860750D-08 2 19 1 11 0.14170006352115D+01 0.42947079537728D-09 3 19 1 11 -0.21235589146700D+01 -0.16407905217750D-07 1 20 1 11 -0.77315874204338D-02 -0.21801613299445D-01 2 20 1 11 -0.67229056626952D+00 0.24972201796320D-01 3 20 1 11 -0.11949146428922D+01 -0.59731020981949D-02 1 1 2 11 -0.30986602126738D-15 -0.15990210447902D-16 2 1 2 11 -0.27123883299397D-14 -0.24082624468052D-15 3 1 2 11 -0.85025806103171D-01 -0.69288400202447D-08 1 2 2 11 0.12134762704473D+00 -0.35866750583571D-08 2 2 2 11 -0.34031489089181D+00 0.26520262845100D-08 3 2 2 11 -0.16118901093599D-13 -0.47025411971469D-15 1 3 2 11 -0.31995455075150D-15 0.25696549922840D-15 2 3 2 11 0.28234253004611D-14 0.31206449022738D-15 3 3 2 11 -0.58080560419071D+00 -0.75773577635974D-08 1 4 2 11 -0.12577706755922D+00 0.28746976878043D-07 2 4 2 11 -0.20830955006510D+01 -0.66085178231779D-08 3 4 2 11 -0.41364293941253D-14 0.11142951942893D-14 1 5 2 11 0.18037524406213D+01 0.28879279260678D-01 2 5 2 11 -0.84555701093814D-01 0.25288103443479D-02 3 5 2 11 0.23734332837183D+00 -0.91697917313602D-02 1 6 2 11 -0.18037524406214D+01 -0.28879279260681D-01 2 6 2 11 0.84555701093823D-01 -0.25288103443481D-02 3 6 2 11 0.23734332837183D+00 -0.91697917313589D-02 1 7 2 11 -0.31074701061461D-01 0.38354275583803D-01 2 7 2 11 0.17685229911123D+01 0.10193541917154D+01 3 7 2 11 -0.19973998276639D+00 0.11413784244335D+00 1 8 2 11 0.31074701061487D-01 -0.38354275583803D-01 2 8 2 11 -0.17685229911125D+01 -0.10193541917155D+01 3 8 2 11 -0.19973998276632D+00 0.11413784244335D+00 1 9 2 11 0.21842492047650D-14 0.69305009116211D-15 2 9 2 11 -0.10116375859811D-14 -0.23117678935264D-16 3 9 2 11 -0.17309372500494D+00 0.60513692531432D-08 1 10 2 11 -0.10001355854719D+01 -0.49878220263899D-09 2 10 2 11 -0.32016118329501D-13 0.55067964663990D-08 3 10 2 11 -0.20856999889054D-14 0.18137035744773D-15 1 11 2 11 -0.89352203019910D+00 0.48014760468160D-07 2 11 2 11 0.70106209229284D+01 0.00000000000000D+00 3 11 2 11 -0.41659256486041D-13 -0.69388939039072D-17 1 12 2 11 0.39887432368433D-15 -0.52856441944538D-15 2 12 2 11 -0.12423440313690D-14 0.99625349505878D-15 3 12 2 11 0.58922710040619D+00 -0.23141649435574D-07 1 13 2 11 0.62889356407285D+00 0.71669099113775D-07 2 13 2 11 0.43731681324671D+00 0.34735606259393D-07 3 13 2 11 0.17398153256030D+01 0.62230761017130D-06 1 14 2 11 0.14405737890598D+01 0.39946960163868D-01 2 14 2 11 0.57632070221866D+00 0.41313829727513D-01 3 14 2 11 -0.17119795773385D+01 0.42289856139815D-01 1 15 2 11 0.14405737890598D+01 0.39946960163867D-01 2 15 2 11 0.57632070221867D+00 0.41313829727512D-01 3 15 2 11 0.17119795773385D+01 -0.42289856139815D-01 1 16 2 11 -0.62889356407284D+00 -0.71669098645752D-07 2 16 2 11 -0.43731681324670D+00 -0.34735606558278D-07 3 16 2 11 0.17398153256030D+01 0.62230760607334D-06 1 17 2 11 0.66226712589217D+00 -0.83349099763265D-02 2 17 2 11 -0.32247316378207D+00 0.38361917021961D-02 3 17 2 11 0.13480231488826D+01 0.28462468701063D-03 1 18 2 11 0.97020792468268D+00 0.46176734899605D-08 2 18 2 11 -0.14148404989982D+00 -0.20079078217193D-08 3 18 2 11 -0.11137098308738D+01 -0.17714800926686D-07 1 19 2 11 0.97020792468266D+00 0.46176735951870D-08 2 19 2 11 -0.14148404989982D+00 -0.20079077149430D-08 3 19 2 11 0.11137098308738D+01 0.17714801803729D-07 1 20 2 11 -0.66226712589214D+00 0.83349099763258D-02 2 20 2 11 0.32247316378207D+00 -0.38361917021955D-02 3 20 2 11 0.13480231488825D+01 0.28462468700746D-03 1 1 3 11 0.24095667808050D+01 0.12254095036523D-07 2 1 3 11 0.20828577590339D+00 0.70889439862756D-08 3 1 3 11 0.14136811392578D-14 -0.11793863256881D-14 1 2 3 11 -0.10397420186220D-13 0.54421581279289D-15 2 2 3 11 -0.16118901091945D-13 -0.47025411971469D-15 3 2 3 11 -0.60405779955822D+00 -0.64228704333827D-07 1 3 3 11 0.35225490033342D+00 0.31162646877419D-08 2 3 3 11 -0.23291021470691D+01 0.20432357053226D-07 3 3 3 11 -0.57189181531533D-15 -0.13312542867367D-15 1 4 3 11 0.43662574649166D-14 0.25949176583137D-15 2 4 3 11 -0.41364293945389D-14 0.11142951942893D-14 3 4 3 11 -0.10931715241657D+01 -0.57205827598045D-07 1 5 3 11 0.22085019921775D+00 -0.10947011099950D-01 2 5 3 11 0.52322751257994D+00 -0.60280200069036D-02 3 5 3 11 -0.18506734839479D+00 0.26211647209000D-02 1 6 3 11 0.22085019921775D+00 -0.10947011099951D-01 2 6 3 11 0.52322751257993D+00 -0.60280200069022D-02 3 6 3 11 0.18506734839481D+00 -0.26211647208981D-02 1 7 3 11 -0.44791349326344D+00 0.42603123174459D+00 2 7 3 11 -0.14909695659340D+00 0.10887274783794D+00 3 7 3 11 0.73433595725227D+01 -0.22752192694037D+01 1 8 3 11 -0.44791349326324D+00 0.42603123174461D+00 2 8 3 11 -0.14909695659334D+00 0.10887274783794D+00 3 8 3 11 -0.73433595725222D+01 0.22752192694038D+01 1 9 3 11 -0.11668559819571D+00 -0.10012733224281D-07 2 9 3 11 0.17309372500500D+00 0.60513692531432D-08 3 9 3 11 -0.60957451185652D-14 0.19165167979061D-15 1 10 3 11 -0.49716747006820D-14 -0.17370011026438D-16 2 10 3 11 -0.20856999889054D-14 0.18137035744773D-15 3 10 3 11 0.74027711148809D-13 0.10706380503396D-07 1 11 3 11 -0.12805460125679D-12 0.13877787807814D-16 2 11 3 11 -0.41659256489350D-13 0.69388939039072D-17 3 11 3 11 0.44845742012432D+02 0.00000000000000D+00 1 12 3 11 0.16925184514147D+01 -0.60192961442698D-08 2 12 3 11 0.58921368200761D+00 0.23659484616810D-07 3 12 3 11 -0.31349325296016D-13 -0.12992285608608D-14 1 13 3 11 0.25394093574744D+01 -0.76542898310445D-06 2 13 3 11 0.38820587360795D+01 -0.11441304053749D-05 3 13 3 11 0.31426422397136D+01 -0.84733984463758D-06 1 14 3 11 -0.28203925227029D+01 0.10126640308881D+00 2 14 3 11 -0.32400070915947D+01 0.11623328030853D+00 3 14 3 11 0.72545834190350D+00 -0.89816573984338D-01 1 15 3 11 0.28203925227029D+01 -0.10126640308881D+00 2 15 3 11 0.32400070915947D+01 -0.11623328030853D+00 3 15 3 11 0.72545834190357D+00 -0.89816573984340D-01 1 16 3 11 0.25394093574744D+01 -0.76542898541556D-06 2 16 3 11 0.38820587360795D+01 -0.11441304094850D-05 3 16 3 11 -0.31426422397136D+01 0.84733985111677D-06 1 17 3 11 -0.30034300605759D+01 -0.36267130947551D-01 2 17 3 11 0.30802567047354D+01 0.52727102560348D-01 3 17 3 11 -0.26428751368362D+01 -0.66691042739215D-01 1 18 3 11 0.36935108977887D+01 -0.12012447897982D-07 2 18 3 11 -0.26510183079313D+01 0.23169382947903D-07 3 18 3 11 -0.97947852423050D+00 -0.29725113920092D-07 1 19 3 11 -0.36935108977887D+01 0.12012448634118D-07 2 19 3 11 0.26510183079313D+01 -0.23169382067390D-07 3 19 3 11 -0.97947852423053D+00 -0.29725114355217D-07 1 20 3 11 -0.30034300605759D+01 -0.36267130947548D-01 2 20 3 11 0.30802567047353D+01 0.52727102560345D-01 3 20 3 11 0.26428751368362D+01 0.66691042739207D-01 1 1 1 12 0.32584030570683D+01 0.57307604220800D-08 2 1 1 12 -0.16810517670985D+00 0.53107829509350D-08 3 1 1 12 -0.47748309577196D-14 -0.19471133486508D-15 1 2 1 12 -0.50652920629815D-14 -0.42729999972076D-15 2 2 1 12 -0.97728491898022D-15 -0.17327422930657D-16 3 2 1 12 -0.62248111267651D+00 -0.17489674347921D-07 1 3 1 12 -0.36318833812210D+00 -0.94495935655930D-08 2 3 1 12 0.23107696383777D+00 0.17109107745526D-07 3 3 1 12 0.59555050351740D-14 0.44082679891976D-15 1 4 1 12 0.16687580108175D-15 -0.17015639707964D-15 2 4 1 12 -0.93973616433220D-16 -0.16384941716666D-15 3 4 1 12 -0.95301266759503D-01 0.74374275795954D-08 1 5 1 12 -0.15694076038809D-01 0.13221546769275D-02 2 5 1 12 0.17859320330234D+01 0.31186136530788D-01 3 5 1 12 0.35171366375936D-01 0.13677493424709D-02 1 6 1 12 -0.15694076038802D-01 0.13221546769269D-02 2 6 1 12 0.17859320330234D+01 0.31186136530788D-01 3 6 1 12 -0.35171366375948D-01 -0.13677493424719D-02 1 7 1 12 0.19782106028326D+01 0.99537915799095D+00 2 7 1 12 -0.50065306767927D-01 0.17348956263855D-01 3 7 1 12 -0.13600813684461D+01 0.45730351148435D+00 1 8 1 12 0.19782106028325D+01 0.99537915799095D+00 2 8 1 12 -0.50065306767910D-01 0.17348956263855D-01 3 8 1 12 0.13600813684461D+01 -0.45730351148435D+00 1 9 1 12 -0.26402084870250D-14 -0.21188208009900D-08 2 9 1 12 -0.10001355854719D+01 0.49878235384649D-09 3 9 1 12 -0.74407407068130D-15 -0.13062323080682D-16 1 10 1 12 -0.48488590421900D-14 -0.16387418721345D-15 2 10 1 12 -0.68692734359969D-14 0.15519641070271D-14 3 10 1 12 -0.11668559819568D+00 0.10012733405660D-07 1 11 1 12 -0.28163514855991D-14 -0.14842025908678D-14 2 11 1 12 0.39887432358093D-15 0.52856441944538D-15 3 11 1 12 0.16925289538691D+01 0.59669334880864D-08 1 12 1 12 0.93053731732250D+01 0.00000000000000D+00 2 12 1 12 -0.89352286251636D+00 -0.59498164033963D-07 3 12 1 12 -0.15690881997540D-15 -0.13877787807814D-16 1 13 1 12 0.42909725326249D+00 0.96571024830975D-02 2 13 1 12 0.12523540326113D+01 0.34949201832725D-01 3 13 1 12 -0.13654668846558D+01 0.25767336813660D-01 1 14 1 12 -0.21269098163499D+00 -0.33975177569596D-06 2 14 1 12 0.50301179776291D+00 0.30339873645872D-06 3 14 1 12 0.89382868931029D+00 0.11804576031907D-06 1 15 1 12 0.21269098163497D+00 0.33975177618910D-06 2 15 1 12 -0.50301179776291D+00 -0.30339873747450D-06 3 15 1 12 0.89382868931030D+00 0.11804576304639D-06 1 16 1 12 0.42909725326249D+00 0.96571024830967D-02 2 16 1 12 0.12523540326113D+01 0.34949201832725D-01 3 16 1 12 0.13654668846558D+01 -0.25767336813661D-01 1 17 1 12 -0.11157897667569D+01 -0.25277165009866D-08 2 17 1 12 0.14170006352115D+01 0.42947020597067D-09 3 17 1 12 0.21235589146700D+01 0.16407905757238D-07 1 18 1 12 0.77315874204360D-02 0.21801613299445D-01 2 18 1 12 0.67229056626953D+00 -0.24972201796319D-01 3 18 1 12 -0.11949146428922D+01 -0.59731020981998D-02 1 19 1 12 -0.77315874204356D-02 -0.21801613299446D-01 2 19 1 12 -0.67229056626953D+00 0.24972201796317D-01 3 19 1 12 -0.11949146428923D+01 -0.59731020982022D-02 1 20 1 12 -0.11157897667569D+01 -0.25277162596527D-08 2 20 1 12 0.14170006352115D+01 0.42947052229147D-09 3 20 1 12 -0.21235589146700D+01 -0.16407904153926D-07 1 1 2 12 -0.12134762704438D+00 0.35866681802991D-08 2 1 2 12 0.34031489089165D+00 -0.26520271124117D-08 3 1 2 12 0.70036481018587D-15 0.53230201486339D-15 1 2 2 12 -0.97728491936796D-15 -0.17761103799651D-16 2 2 2 12 -0.19995120863543D-14 0.77370575854863D-15 3 2 2 12 0.85025806103203D-01 0.69288402057623D-08 1 3 2 12 -0.12577706755933D+00 0.28746978960983D-07 2 3 2 12 -0.20830955006505D+01 -0.66085056476265D-08 3 3 2 12 0.62440521804398D-14 0.12671932145849D-14 1 4 2 12 -0.93511827139831D-16 -0.16406625760116D-15 2 4 2 12 -0.20731419212092D-14 -0.99591608894770D-16 3 4 2 12 -0.58080560419071D+00 -0.75773573605916D-08 1 5 2 12 0.18037524406213D+01 0.28879279260682D-01 2 5 2 12 -0.84555701093823D-01 0.25288103443482D-02 3 5 2 12 0.23734332837184D+00 -0.91697917313572D-02 1 6 2 12 0.18037524406213D+01 0.28879279260683D-01 2 6 2 12 -0.84555701093815D-01 0.25288103443486D-02 3 6 2 12 -0.23734332837184D+00 0.91697917313588D-02 1 7 2 12 -0.31074701061638D-01 0.38354275583804D-01 2 7 2 12 0.17685229911124D+01 0.10193541917154D+01 3 7 2 12 -0.19973998276543D+00 0.11413784244334D+00 1 8 2 12 -0.31074701061621D-01 0.38354275583804D-01 2 8 2 12 0.17685229911125D+01 0.10193541917154D+01 3 8 2 12 0.19973998276543D+00 -0.11413784244335D+00 1 9 2 12 -0.10001355854719D+01 -0.49878640005432D-09 2 9 2 12 0.71749607000800D-14 0.55067990870986D-08 3 9 2 12 0.26843684335461D-14 0.15416343832432D-15 1 10 2 12 -0.68692734359969D-14 0.15589030009310D-14 2 10 2 12 -0.50877814280339D-14 0.21364918170224D-15 3 10 2 12 -0.17309372500496D+00 0.60513697367375D-08 1 11 2 12 0.39887432358093D-15 0.52856441944538D-15 2 11 2 12 -0.12423440313690D-14 -0.99625349505878D-15 3 11 2 12 0.58922710040619D+00 -0.23141650893184D-07 1 12 2 12 -0.89352203019914D+00 0.48014760468160D-07 2 12 2 12 0.70106209229282D+01 0.00000000000000D+00 3 12 2 12 -0.20342974413238D-13 -0.69388939039072D-17 1 13 2 12 0.14405737890597D+01 0.39946960163872D-01 2 13 2 12 0.57632070221865D+00 0.41313829727515D-01 3 13 2 12 -0.17119795773385D+01 0.42289856139809D-01 1 14 2 12 0.62889356407284D+00 0.71669097576929D-07 2 14 2 12 0.43731681324671D+00 0.34735605729654D-07 3 14 2 12 0.17398153256030D+01 0.62230760129215D-06 1 15 2 12 -0.62889356407284D+00 -0.71669098596181D-07 2 15 2 12 -0.43731681324672D+00 -0.34735606296797D-07 3 15 2 12 0.17398153256030D+01 0.62230760608684D-06 1 16 2 12 0.14405737890598D+01 0.39946960163872D-01 2 16 2 12 0.57632070221865D+00 0.41313829727515D-01 3 16 2 12 0.17119795773385D+01 -0.42289856139808D-01 1 17 2 12 0.97020792468270D+00 0.46176730231276D-08 2 17 2 12 -0.14148404989985D+00 -0.20079073144440D-08 3 17 2 12 -0.11137098308738D+01 -0.17714801817204D-07 1 18 2 12 0.66226712589216D+00 -0.83349099763251D-02 2 18 2 12 -0.32247316378203D+00 0.38361917021957D-02 3 18 2 12 0.13480231488826D+01 0.28462468701071D-03 1 19 2 12 -0.66226712589216D+00 0.83349099763231D-02 2 19 2 12 0.32247316378204D+00 -0.38361917021968D-02 3 19 2 12 0.13480231488826D+01 0.28462468701402D-03 1 20 2 12 0.97020792468269D+00 0.46176733151623D-08 2 20 2 12 -0.14148404989986D+00 -0.20079076962051D-08 3 20 2 12 0.11137098308738D+01 0.17714801617835D-07 1 1 3 12 -0.47748309577196D-14 -0.19471133486508D-15 2 1 3 12 0.70036480997908D-15 0.53230201486339D-15 3 1 3 12 0.60405779955809D+00 0.64228702190344D-07 1 2 3 12 -0.24095667808050D+01 -0.12254097175244D-07 2 2 3 12 -0.20828577590335D+00 -0.70889438007580D-08 3 2 3 12 -0.67227259076164D-14 -0.10306094075811D-14 1 3 3 12 0.59555050367250D-14 0.44082679891976D-15 2 3 3 12 0.62440521808534D-14 0.12671932145849D-14 3 3 3 12 -0.10931715241661D+01 -0.57205832479265D-07 1 4 3 12 0.35225490033343D+00 0.31162647516471D-08 2 4 3 12 -0.23291021470691D+01 0.20432357456232D-07 3 4 3 12 -0.51386592848428D-14 0.54371850440767D-15 1 5 3 12 0.22085019921787D+00 -0.10947011099948D-01 2 5 3 12 0.52322751257994D+00 -0.60280200069005D-02 3 5 3 12 -0.18506734839480D+00 0.26211647208988D-02 1 6 3 12 -0.22085019921788D+00 0.10947011099947D-01 2 6 3 12 -0.52322751257994D+00 0.60280200069022D-02 3 6 3 12 -0.18506734839478D+00 0.26211647208995D-02 1 7 3 12 -0.44791349326324D+00 0.42603123174459D+00 2 7 3 12 -0.14909695659244D+00 0.10887274783794D+00 3 7 3 12 0.73433595725223D+01 -0.22752192694037D+01 1 8 3 12 0.44791349326330D+00 -0.42603123174459D+00 2 8 3 12 0.14909695659244D+00 -0.10887274783794D+00 3 8 3 12 0.73433595725222D+01 -0.22752192694038D+01 1 9 3 12 -0.74407407068130D-15 -0.13062323080682D-16 2 9 3 12 0.26843684335461D-14 0.15416343832432D-15 3 9 3 12 -0.81938119853487D-14 0.10706378528153D-07 1 10 3 12 -0.11668559819568D+00 -0.10012732628166D-07 2 10 3 12 0.17309372500498D+00 0.60513697367375D-08 3 10 3 12 0.15857649876524D-14 0.27227468447073D-16 1 11 3 12 0.16925184514147D+01 -0.60192955935465D-08 2 11 3 12 0.58921368200760D+00 0.23659483159199D-07 3 11 3 12 -0.31349325296016D-13 0.12992285608608D-14 1 12 3 12 -0.15690881997540D-15 0.13877787807814D-16 2 12 3 12 -0.20342974416547D-13 0.69388939039072D-17 3 12 3 12 0.44845742012432D+02 0.00000000000000D+00 1 13 3 12 -0.28203925227030D+01 0.10126640308881D+00 2 13 3 12 -0.32400070915947D+01 0.11623328030853D+00 3 13 3 12 0.72545834190353D+00 -0.89816573984337D-01 1 14 3 12 0.25394093574743D+01 -0.76542898754387D-06 2 14 3 12 0.38820587360795D+01 -0.11441304142540D-05 3 14 3 12 0.31426422397135D+01 -0.84733985886086D-06 1 15 3 12 0.25394093574743D+01 -0.76542898480267D-06 2 15 3 12 0.38820587360795D+01 -0.11441304094437D-05 3 15 3 12 -0.31426422397135D+01 0.84733985130013D-06 1 16 3 12 0.28203925227030D+01 -0.10126640308881D+00 2 16 3 12 0.32400070915947D+01 -0.11623328030853D+00 3 16 3 12 0.72545834190353D+00 -0.89816573984337D-01 1 17 3 12 0.36935108977887D+01 -0.12012448111978D-07 2 17 3 12 -0.26510183079313D+01 0.23169382053915D-07 3 17 3 12 -0.97947852423049D+00 -0.29725114227723D-07 1 18 3 12 -0.30034300605759D+01 -0.36267130947553D-01 2 18 3 12 0.30802567047354D+01 0.52727102560348D-01 3 18 3 12 -0.26428751368363D+01 -0.66691042739213D-01 1 19 3 12 -0.30034300605759D+01 -0.36267130947555D-01 2 19 3 12 0.30802567047354D+01 0.52727102560351D-01 3 19 3 12 0.26428751368363D+01 0.66691042739218D-01 1 20 3 12 -0.36935108977887D+01 0.12012449697942D-07 2 20 3 12 0.26510183079313D+01 -0.23169382256753D-07 3 20 3 12 -0.97947852423049D+00 -0.29725113989583D-07 1 1 1 13 0.84163057818194D+00 -0.74880249827272D-06 2 1 1 13 0.80558111162734D+00 -0.49477641986588D-06 3 1 1 13 -0.44828122852288D+00 -0.14721994177189D-06 1 2 1 13 0.40053332053903D+00 -0.13838444397699D-01 2 2 1 13 0.78632530987332D+00 -0.63106206074909D-02 3 2 1 13 0.61948808567309D+00 0.29798087047853D-02 1 3 1 13 -0.11682226319502D+01 0.87286015242552D-02 2 3 1 13 -0.51689538388847D-01 -0.33029634723416D-01 3 3 1 13 0.67078264993127D+00 -0.97105436486353D-02 1 4 1 13 0.53789782066795D+00 -0.15056872998975D-06 2 4 1 13 0.71678759202770D+00 -0.58517301058313D-07 3 4 1 13 -0.11674946922125D+01 0.43632823729293D-07 1 5 1 13 0.23532829639727D+01 0.12588627472331D-01 2 5 1 13 -0.98619645269343D+00 -0.16035416249388D-01 3 5 1 13 0.18763038654272D+00 -0.35432183064907D-01 1 6 1 13 0.58641202826265D+00 0.42434203301506D-01 2 6 1 13 -0.23857555948405D+00 0.34463920729137D-01 3 6 1 13 -0.34007399469184D+01 0.13686640135054D-02 1 7 1 13 -0.10920925903866D+01 -0.14296338312364D-01 2 7 1 13 0.24452075078459D+01 -0.47573476837057D-03 3 7 1 13 0.18828771588215D+00 -0.36654271339286D-01 1 8 1 13 -0.52646987880336D+00 -0.75686465898101D-01 2 8 1 13 -0.30234462751216D-01 -0.15440299694563D+00 3 8 1 13 -0.27521155929143D+01 0.27750239130723D-01 1 9 1 13 0.11157902312848D+01 -0.13787637782921D-05 2 9 1 13 0.97020788419845D+00 0.86399124633208D-07 3 9 1 13 0.36935237640409D+01 0.89646542039726D-06 1 10 1 13 -0.77312347167400D-02 0.65404867931901D-01 2 10 1 13 0.66226670866071D+00 0.25004731472478D-01 3 10 1 13 -0.30034371241651D+01 0.10880137817197D+00 1 11 1 13 -0.21269098163499D+00 0.33975177965631D-06 2 11 1 13 0.62889356407285D+00 -0.71669099738275D-07 3 11 1 13 0.25394093574744D+01 0.76542898212607D-06 1 12 1 13 0.42909725326249D+00 -0.96571024830971D-02 2 12 1 13 0.14405737890597D+01 -0.39946960163875D-01 3 12 1 13 -0.28203925227030D+01 -0.10126640308880D+00 1 13 1 13 0.13898122635327D+02 0.00000000000000D+00 2 13 1 13 0.64220335112201D+01 0.18823880084437D+00 3 13 1 13 -0.12557350990269D+01 -0.16706243204776D+00 1 14 1 13 -0.38758753471713D+01 -0.17637703836529D-02 2 14 1 13 -0.44020035000303D+01 0.32984240193006D-02 3 14 1 13 0.18227334375484D+00 -0.19277344790830D-02 1 15 1 13 0.13711483276091D-14 -0.78881406176688D-01 2 15 1 13 0.59774075657538D-01 -0.91889221273374D-01 3 15 1 13 0.33094596257339D+00 0.23244209361993D-02 1 16 1 13 0.24484108676583D+00 0.13766969250412D-15 2 16 1 13 -0.59365354065440D-01 -0.48959010330448D-06 3 16 1 13 0.77639775635174D-01 0.82538685518589D-07 1 17 1 13 -0.90826955720951D-14 0.72400695201136D-02 2 17 1 13 -0.10951670448984D+01 -0.10518327720640D-02 3 17 1 13 -0.30181734532867D+00 -0.91617708047416D-02 1 18 1 13 -0.24784053886372D-14 0.62373851351272D-06 2 18 1 13 0.11571846304922D+01 -0.58739072002615D-06 3 18 1 13 0.17941074822631D+01 -0.10478331382584D-05 1 19 1 13 0.60746088713778D-01 -0.18602070466545D-06 2 19 1 13 0.21267822786135D-01 -0.62947218400915D-02 3 19 1 13 0.66628016534021D+00 -0.31173506039869D-02 1 20 1 13 -0.23777598108147D-14 0.20694161292244D-06 2 20 1 13 -0.72759334883857D-01 0.55423410951158D-02 3 20 1 13 -0.27389608057286D+00 -0.52918730905634D-02 1 1 2 13 0.95320318876926D+00 -0.36389309725829D-06 2 1 2 13 0.88299137538422D+00 -0.28187504022152D-06 3 1 2 13 0.73874028938631D+00 0.83830993452919D-07 1 2 2 13 0.78714711650424D+00 -0.15604524917163D-01 2 2 2 13 0.29452192971431D+00 -0.42432835830091D-02 3 2 2 13 -0.55375110754941D+00 0.17221670950511D-03 1 3 2 13 -0.14641252210917D+00 -0.16744411954469D-01 2 3 2 13 -0.15713437869598D+01 -0.18478138079752D-02 3 3 2 13 -0.33257813959699D+00 0.17228537222140D-02 1 4 2 13 0.68712473251339D+00 -0.19760181757580D-06 2 4 2 13 0.64763245545999D+00 0.26415742691033D-06 3 4 2 13 0.76341655697848D+00 0.17317800123369D-06 1 5 2 13 -0.21831596540526D+01 0.12385679687658D-01 2 5 2 13 0.12926774104379D+01 -0.71916339247599D-02 3 5 2 13 0.37979157642162D+00 -0.42470155283097D-01 1 6 2 13 0.21890341311867D+00 0.57975041970885D-01 2 6 2 13 -0.54144292836908D-01 0.28275102359184D-01 3 6 2 13 -0.27496806876738D+01 0.76488031477958D-02 1 7 2 13 0.12478087830558D+01 -0.19355587853677D-01 2 7 2 13 -0.23168943120457D+01 -0.71500529342032D-02 3 7 2 13 0.70566199330311D+00 -0.54515837216341D-01 1 8 2 13 -0.50224851509074D+00 -0.13530109371527D+00 2 8 2 13 -0.30975812792411D+00 -0.15408726080424D+00 3 8 2 13 -0.35041370877415D+01 0.52902086903695D-02 1 9 2 13 0.14170005718491D+01 -0.45216337893826D-06 2 9 2 13 0.14147966551016D+00 -0.31064300017601D-06 3 9 2 13 0.26510297703737D+01 0.63581639256050D-06 1 10 2 13 0.67229068221357D+00 0.74916605308275D-01 2 10 2 13 0.32247399400846D+00 0.11508575079096D-01 3 10 2 13 -0.30802612353887D+01 0.15818131896180D+00 1 11 2 13 0.50301179776292D+00 -0.30339873862007D-06 2 11 2 13 0.43731681324671D+00 -0.34735605919387D-07 3 11 2 13 0.38820587360795D+01 0.11441304028491D-05 1 12 2 13 0.12523540326113D+01 -0.34949201832728D-01 2 12 2 13 0.57632070221865D+00 -0.41313829727515D-01 3 12 2 13 -0.32400070915947D+01 -0.11623328030852D+00 1 13 2 13 0.64220402558005D+01 -0.18823887449866D+00 2 13 2 13 0.15298044818349D+02 0.00000000000000D+00 3 13 2 13 0.19826211583794D+01 0.19948869321804D+00 1 14 2 13 -0.44020031284309D+01 0.32989355973466D-02 2 14 2 13 -0.41216323764819D+01 0.60781501885002D-02 3 14 2 13 -0.20867294665193D+00 -0.89193357668949D-03 1 15 2 13 -0.59774075657531D-01 -0.91889221273374D-01 2 15 2 13 0.16395634524868D-14 -0.10716488379770D+00 3 15 2 13 -0.34606075502576D+00 0.36465383468236D-02 1 16 2 13 -0.59365354065440D-01 0.48959010311776D-06 2 16 2 13 0.14475652471389D+00 0.56866074846531D-15 3 16 2 13 -0.82639870750695D-01 0.13401808593550D-06 1 17 2 13 -0.10951670448984D+01 0.10518327720693D-02 2 17 2 13 0.32821219444026D-13 -0.17783925419816D-01 3 17 2 13 0.19338028945543D-01 0.41669660085314D-01 1 18 2 13 0.11571846304922D+01 0.58739071820368D-06 2 18 2 13 0.62975255369375D-15 0.97932800343585D-09 3 18 2 13 0.46580936432626D+00 -0.85640432239606D-06 1 19 2 13 -0.21268002343369D-01 -0.62951649308071D-02 2 19 2 13 0.17866896526107D-01 0.33254049878907D-06 3 19 2 13 0.37430864985463D+00 0.54614196068627D-02 1 20 2 13 -0.72760036737826D-01 0.55433092606054D-02 2 20 2 13 0.31471085951350D-15 -0.50448504462324D-06 3 20 2 13 -0.80043183253722D+00 0.52000824587476D-02 1 1 3 13 -0.84564392342542D+00 -0.13861386408502D-06 2 1 3 13 0.67932441581483D+00 0.11489524642200D-07 3 1 3 13 0.33565238386224D-02 -0.28322019321675D-06 1 2 3 13 0.70042568642651D+00 -0.14423150740284D-02 2 2 3 13 -0.78834034603550D+00 -0.20194645910306D-02 3 2 3 13 -0.38453250910957D+00 -0.49275599810572D-02 1 3 3 13 0.23054956166565D+00 0.15504920856832D-02 2 3 3 13 -0.52264722169603D+00 -0.33296080090624D-02 3 3 3 13 -0.20724822922069D+01 -0.20038783343409D-01 1 4 3 13 -0.11902835930202D+01 0.22901717773786D-06 2 4 3 13 0.10013965666997D+01 -0.45336946108269D-06 3 4 3 13 -0.48038748013540D+00 -0.91572795593992D-07 1 5 3 13 -0.80773945037108D+00 -0.34943424899298D-01 2 5 3 13 -0.13596895178969D+01 -0.17040815752442D-01 3 5 3 13 0.39092799049792D+01 0.28119940517958D-01 1 6 3 13 -0.62705904656787D+00 -0.82421881349827D-02 2 6 3 13 -0.41659732056845D+00 -0.49748253466812D-02 3 6 3 13 0.17035920554805D+00 -0.30749743633631D-01 1 7 3 13 -0.87225283577179D+00 -0.27747237711736D-01 2 7 3 13 -0.12362503312941D+01 -0.45313182285084D-01 3 7 3 13 -0.36602739406624D+01 -0.34764508930455D-01 1 8 3 13 -0.45745096942818D+00 -0.32192453776110D-02 2 8 3 13 -0.61507586914084D+00 -0.19382285042191D-01 3 8 3 13 -0.61614090844328D+00 0.13064924968600D+00 1 9 3 13 0.21235578482967D+01 -0.87549349180726D-06 2 9 3 13 0.11137091419462D+01 -0.98587183813382D-06 3 9 3 13 0.97946356471333D+00 -0.30786077892746D-06 1 10 3 13 -0.11949136020981D+01 0.17919309964119D-01 2 10 3 13 -0.13480213827396D+01 0.85386752395975D-03 3 10 3 13 0.26428759172736D+01 -0.20007309666097D+00 1 11 3 13 0.89382868931035D+00 -0.11804576582708D-06 2 11 3 13 0.17398153256030D+01 -0.62230761282889D-06 3 11 3 13 0.31426422397136D+01 0.84733984241713D-06 1 12 3 13 -0.13654668846558D+01 -0.25767336813657D-01 2 12 3 13 -0.17119795773385D+01 -0.42289856139805D-01 3 12 3 13 0.72545834190353D+00 0.89816573984336D-01 1 13 3 13 -0.12557128577609D+01 0.16706222771616D+00 2 13 3 13 0.19826484447408D+01 -0.19948817466567D+00 3 13 3 13 0.15144686983050D+02 0.00000000000000D+00 1 14 3 13 0.18227524897193D+00 -0.19268627743443D-02 2 14 3 13 -0.20867042954993D+00 -0.89241513345041D-03 3 14 3 13 -0.10300521199797D+01 -0.95008581194220D-02 1 15 3 13 0.33094596257339D+00 -0.23244209361992D-02 2 15 3 13 -0.34606075502576D+00 -0.36465383468230D-02 3 15 3 13 0.53767974454164D-14 0.56333672833067D-01 1 16 3 13 -0.77639775635162D-01 0.82538685517722D-07 2 16 3 13 0.82639870750708D-01 0.13401808593376D-06 3 16 3 13 -0.89098768490708D+00 -0.40689412751646D-15 1 17 3 13 -0.30181734532867D+00 0.91617708047416D-02 2 17 3 13 -0.19338028945535D-01 0.41669660085314D-01 3 17 3 13 -0.17542926212631D-13 -0.67656815809709D-02 1 18 3 13 0.17941074822631D+01 0.10478331306708D-05 2 18 3 13 -0.46580936432627D+00 -0.85640432239596D-06 3 18 3 13 0.63301076517089D-14 0.59573347628659D-06 1 19 3 13 0.66628175574442D+00 0.31164528908424D-02 2 19 3 13 -0.37430983841762D+00 0.54623506006127D-02 3 19 3 13 0.17632798563093D+00 -0.60543745030559D-07 1 20 3 13 0.27389758526281D+00 0.52922061447545D-02 2 20 3 13 -0.80043388900749D+00 0.51985952631489D-02 3 20 3 13 -0.83808148981135D-15 0.38876850218849D-07 1 1 1 14 -0.40053332053902D+00 0.13838444397700D-01 2 1 1 14 -0.78632530987330D+00 0.63106206074915D-02 3 1 1 14 -0.61948808567300D+00 -0.29798087047770D-02 1 2 1 14 -0.84163057818198D+00 0.74880250252583D-06 2 2 1 14 -0.80558111162732D+00 0.49477641733946D-06 3 2 1 14 0.44828122852276D+00 0.14721994932585D-06 1 3 1 14 0.53789782066792D+00 -0.15056873101702D-06 2 3 1 14 0.71678759202771D+00 -0.58517303846614D-07 3 3 1 14 -0.11674946922126D+01 0.43632837235123D-07 1 4 1 14 -0.11682226319502D+01 0.87286015242525D-02 2 4 1 14 -0.51689538388819D-01 -0.33029634723416D-01 3 4 1 14 0.67078264993130D+00 -0.97105436486361D-02 1 5 1 14 0.23532829639725D+01 0.12588627472328D-01 2 5 1 14 -0.98619645269352D+00 -0.16035416249388D-01 3 5 1 14 0.18763038654307D+00 -0.35432183064906D-01 1 6 1 14 -0.58641202826266D+00 -0.42434203301505D-01 2 6 1 14 0.23857555948405D+00 -0.34463920729138D-01 3 6 1 14 0.34007399469184D+01 -0.13686640135043D-02 1 7 1 14 -0.10920925903867D+01 -0.14296338312371D-01 2 7 1 14 0.24452075078455D+01 -0.47573476841708D-03 3 7 1 14 0.18828771588209D+00 -0.36654271339297D-01 1 8 1 14 0.52646987880337D+00 0.75686465898102D-01 2 8 1 14 0.30234462751206D-01 0.15440299694563D+00 3 8 1 14 0.27521155929143D+01 -0.27750239130724D-01 1 9 1 14 -0.77312347167453D-02 0.65404867931901D-01 2 9 1 14 0.66226670866071D+00 0.25004731472479D-01 3 9 1 14 -0.30034371241651D+01 0.10880137817197D+00 1 10 1 14 0.11157902312848D+01 -0.13787637830329D-05 2 10 1 14 0.97020788419846D+00 0.86399120213168D-07 3 10 1 14 0.36935237640409D+01 0.89646541173329D-06 1 11 1 14 0.42909725326248D+00 -0.96571024830949D-02 2 11 1 14 0.14405737890598D+01 -0.39946960163872D-01 3 11 1 14 -0.28203925227029D+01 -0.10126640308881D+00 1 12 1 14 -0.21269098163499D+00 0.33975177658067D-06 2 12 1 14 0.62889356407284D+00 -0.71669098201429D-07 3 12 1 14 0.25394093574743D+01 0.76542898655161D-06 1 13 1 14 -0.38758753471713D+01 -0.17637703836516D-02 2 13 1 14 -0.44020035000303D+01 0.32984240192954D-02 3 13 1 14 0.18227334375484D+00 -0.19277344790825D-02 1 14 1 14 0.13898122635327D+02 0.00000000000000D+00 2 14 1 14 0.64220335112206D+01 0.18823880084437D+00 3 14 1 14 -0.12557350990266D+01 -0.16706243204776D+00 1 15 1 14 0.24484108676583D+00 -0.96618101766286D-16 2 15 1 14 -0.59365354065453D-01 -0.48959010329204D-06 3 15 1 14 0.77639775635155D-01 0.82538685703381D-07 1 16 1 14 -0.10023014882025D-13 -0.78881406176688D-01 2 16 1 14 0.59774075657525D-01 -0.91889221273374D-01 3 16 1 14 0.33094596257338D+00 0.23244209362001D-02 1 17 1 14 0.10475874952516D-13 0.62373852356664D-06 2 17 1 14 0.11571846304922D+01 -0.58739071840010D-06 3 17 1 14 0.17941074822631D+01 -0.10478331329119D-05 1 18 1 14 -0.10813780586547D-13 0.72400695201119D-02 2 18 1 14 -0.10951670448984D+01 -0.10518327720666D-02 3 18 1 14 -0.30181734532868D+00 -0.91617708047417D-02 1 19 1 14 -0.17772984948064D-14 0.20694161311322D-06 2 19 1 14 -0.72759334883859D-01 0.55423410951156D-02 3 19 1 14 -0.27389608057286D+00 -0.52918730905633D-02 1 20 1 14 0.60746088713779D-01 -0.18602070473752D-06 2 20 1 14 0.21267822786137D-01 -0.62947218400913D-02 3 20 1 14 0.66628016534021D+00 -0.31173506039870D-02 1 1 2 14 -0.78714711650421D+00 0.15604524917163D-01 2 1 2 14 -0.29452192971427D+00 0.42432835830074D-02 3 1 2 14 0.55375110754942D+00 -0.17221670951485D-03 1 2 2 14 -0.95320318876925D+00 0.36389309472840D-06 2 2 2 14 -0.88299137538415D+00 0.28187504155162D-06 3 2 2 14 -0.73874028938638D+00 -0.83831002114072D-07 1 3 2 14 0.68712473251340D+00 -0.19760182036410D-06 2 3 2 14 0.64763245545997D+00 0.26415742531930D-06 3 3 2 14 0.76341655697853D+00 0.17317799060420D-06 1 4 2 14 -0.14641252210914D+00 -0.16744411954469D-01 2 4 2 14 -0.15713437869599D+01 -0.18478138079759D-02 3 4 2 14 -0.33257813959719D+00 0.17228537222137D-02 1 5 2 14 -0.21831596540527D+01 0.12385679687658D-01 2 5 2 14 0.12926774104381D+01 -0.71916339247603D-02 3 5 2 14 0.37979157642187D+00 -0.42470155283099D-01 1 6 2 14 -0.21890341311867D+00 -0.57975041970886D-01 2 6 2 14 0.54144292836902D-01 -0.28275102359185D-01 3 6 2 14 0.27496806876738D+01 -0.76488031477959D-02 1 7 2 14 0.12478087830555D+01 -0.19355587853724D-01 2 7 2 14 -0.23168943120459D+01 -0.71500529342446D-02 3 7 2 14 0.70566199330310D+00 -0.54515837216361D-01 1 8 2 14 0.50224851509073D+00 0.13530109371527D+00 2 8 2 14 0.30975812792412D+00 0.15408726080424D+00 3 8 2 14 0.35041370877414D+01 -0.52902086903707D-02 1 9 2 14 0.67229068221357D+00 0.74916605308276D-01 2 9 2 14 0.32247399400848D+00 0.11508575079096D-01 3 9 2 14 -0.30802612353887D+01 0.15818131896180D+00 1 10 2 14 0.14170005718491D+01 -0.45216338335136D-06 2 10 2 14 0.14147966551017D+00 -0.31064299971561D-06 3 10 2 14 0.26510297703738D+01 0.63581638707590D-06 1 11 2 14 0.12523540326113D+01 -0.34949201832725D-01 2 11 2 14 0.57632070221866D+00 -0.41313829727513D-01 3 11 2 14 -0.32400070915947D+01 -0.11623328030853D+00 1 12 2 14 0.50301179776291D+00 -0.30339873709363D-06 2 12 2 14 0.43731681324671D+00 -0.34735605389648D-07 3 12 2 14 0.38820587360795D+01 0.11441304117283D-05 1 13 2 14 -0.44020031284309D+01 0.32989355973415D-02 2 13 2 14 -0.41216323764819D+01 0.60781501885003D-02 3 13 2 14 -0.20867294665193D+00 -0.89193357669200D-03 1 14 2 14 0.64220402558010D+01 -0.18823887449866D+00 2 14 2 14 0.15298044818349D+02 0.00000000000000D+00 3 14 2 14 0.19826211583798D+01 0.19948869321804D+00 1 15 2 14 -0.59365354065453D-01 0.48959010313021D-06 2 15 2 14 0.14475652471388D+00 -0.32646432922661D-15 3 15 2 14 -0.82639870750706D-01 0.13401808650108D-06 1 16 2 14 -0.59774075657543D-01 -0.91889221273374D-01 2 16 2 14 -0.10378546201465D-13 -0.10716488379770D+00 3 16 2 14 -0.34606075502578D+00 0.36465383468228D-02 1 17 2 14 0.11571846304922D+01 0.58739071982972D-06 2 17 2 14 -0.16602196325731D-13 0.97932574481653D-09 3 17 2 14 0.46580936432626D+00 -0.85640432152366D-06 1 18 2 14 -0.10951670448984D+01 0.10518327720667D-02 2 18 2 14 -0.46222029839791D-13 -0.17783925419804D-01 3 18 2 14 0.19338028945534D-01 0.41669660085317D-01 1 19 2 14 -0.72760036737828D-01 0.55433092606052D-02 2 19 2 14 -0.30902658937396D-14 -0.50448504418972D-06 3 19 2 14 -0.80043183253721D+00 0.52000824587464D-02 1 20 2 14 -0.21268002343366D-01 -0.62951649308069D-02 2 20 2 14 0.17866896526108D-01 0.33254049886263D-06 3 20 2 14 0.37430864985463D+00 0.54614196068629D-02 1 1 3 14 -0.70042568642642D+00 0.14423150740368D-02 2 1 3 14 0.78834034603551D+00 0.20194645910208D-02 3 1 3 14 0.38453250910952D+00 0.49275599810497D-02 1 2 3 14 0.84564392342531D+00 0.13861387163724D-06 2 2 3 14 -0.67932441581490D+00 -0.11489533302920D-07 3 2 3 14 -0.33565238386473D-02 0.28322019786068D-06 1 3 3 14 -0.11902835930203D+01 0.22901719124196D-06 2 3 3 14 0.10013965666997D+01 -0.45336947171217D-06 3 3 3 14 -0.48038748013547D+00 -0.91572767260852D-07 1 4 3 14 0.23054956166567D+00 0.15504920856825D-02 2 4 3 14 -0.52264722169623D+00 -0.33296080090628D-02 3 4 3 14 -0.20724822922069D+01 -0.20038783343413D-01 1 5 3 14 -0.80773945037074D+00 -0.34943424899297D-01 2 5 3 14 -0.13596895178966D+01 -0.17040815752444D-01 3 5 3 14 0.39092799049792D+01 0.28119940517959D-01 1 6 3 14 0.62705904656790D+00 0.82421881349837D-02 2 6 3 14 0.41659732056842D+00 0.49748253466811D-02 3 6 3 14 -0.17035920554810D+00 0.30749743633634D-01 1 7 3 14 -0.87225283577185D+00 -0.27747237711747D-01 2 7 3 14 -0.12362503312941D+01 -0.45313182285103D-01 3 7 3 14 -0.36602739406617D+01 -0.34764508930410D-01 1 8 3 14 0.45745096942817D+00 0.32192453776096D-02 2 8 3 14 0.61507586914080D+00 0.19382285042190D-01 3 8 3 14 0.61614090844339D+00 -0.13064924968600D+00 1 9 3 14 -0.11949136020980D+01 0.17919309964113D-01 2 9 3 14 -0.13480213827396D+01 0.85386752395244D-03 3 9 3 14 0.26428759172736D+01 -0.20007309666096D+00 1 10 3 14 0.21235578482967D+01 -0.87549350049899D-06 2 10 3 14 0.11137091419463D+01 -0.98587184361842D-06 3 10 3 14 0.97946356471336D+00 -0.30786078308229D-06 1 11 3 14 -0.13654668846558D+01 -0.25767336813663D-01 2 11 3 14 -0.17119795773385D+01 -0.42289856139811D-01 3 11 3 14 0.72545834190350D+00 0.89816573984338D-01 1 12 3 14 0.89382868931029D+00 -0.11804576140848D-06 2 12 3 14 0.17398153256030D+01 -0.62230760394975D-06 3 12 3 14 0.31426422397135D+01 0.84733985664041D-06 1 13 3 14 0.18227524897193D+00 -0.19268627743438D-02 2 13 3 14 -0.20867042954993D+00 -0.89241513345291D-03 3 13 3 14 -0.10300521199797D+01 -0.95008581194234D-02 1 14 3 14 -0.12557128577605D+01 0.16706222771616D+00 2 14 3 14 0.19826484447412D+01 -0.19948817466567D+00 3 14 3 14 0.15144686983050D+02 0.00000000000000D+00 1 15 3 14 -0.77639775635181D-01 0.82538685702514D-07 2 15 3 14 0.82639870750698D-01 0.13401808649935D-06 3 15 3 14 -0.89098768490708D+00 0.33826156355276D-15 1 16 3 14 0.33094596257338D+00 -0.23244209361984D-02 2 16 3 14 -0.34606075502578D+00 -0.36465383468237D-02 3 16 3 14 -0.64579016519435D-14 0.56333672833066D-01 1 17 3 14 0.17941074822631D+01 0.10478331360172D-05 2 17 3 14 -0.46580936432627D+00 -0.85640432152377D-06 3 17 3 14 -0.22313873777965D-13 0.59573347229459D-06 1 18 3 14 -0.30181734532868D+00 0.91617708047416D-02 2 18 3 14 -0.19338028945544D-01 0.41669660085317D-01 3 18 3 14 0.66180716691482D-15 -0.67656815809749D-02 1 19 3 14 0.27389758526281D+00 0.52922061447546D-02 2 19 3 14 -0.80043388900748D+00 0.51985952631477D-02 3 19 3 14 0.27024081020516D-14 0.38876851161739D-07 1 20 3 14 0.66628175574442D+00 0.31164528908423D-02 2 20 3 14 -0.37430983841762D+00 0.54623506006128D-02 3 20 3 14 0.17632798563092D+00 -0.60543745006406D-07 1 1 1 15 0.40053332053902D+00 -0.13838444397699D-01 2 1 1 15 0.78632530987332D+00 -0.63106206074943D-02 3 1 1 15 -0.61948808567303D+00 -0.29798087047790D-02 1 2 1 15 -0.84163057818196D+00 0.74880250103427D-06 2 2 1 15 -0.80558111162741D+00 0.49477641721949D-06 3 2 1 15 -0.44828122852282D+00 -0.14721994966496D-06 1 3 1 15 -0.53789782066790D+00 0.15056872969311D-06 2 3 1 15 -0.71678759202772D+00 0.58517302833690D-07 3 3 1 15 -0.11674946922126D+01 0.43632830251192D-07 1 4 1 15 -0.11682226319502D+01 0.87286015242529D-02 2 4 1 15 -0.51689538388918D-01 -0.33029634723417D-01 3 4 1 15 -0.67078264993122D+00 0.97105436486359D-02 1 5 1 15 0.58641202826265D+00 0.42434203301507D-01 2 5 1 15 -0.23857555948404D+00 0.34463920729138D-01 3 5 1 15 0.34007399469184D+01 -0.13686640135059D-02 1 6 1 15 -0.23532829639725D+01 -0.12588627472310D-01 2 6 1 15 0.98619645269352D+00 0.16035416249411D-01 3 6 1 15 0.18763038654310D+00 -0.35432183064900D-01 1 7 1 15 -0.52646987880336D+00 -0.75686465898100D-01 2 7 1 15 -0.30234462751214D-01 -0.15440299694563D+00 3 7 1 15 0.27521155929143D+01 -0.27750239130725D-01 1 8 1 15 0.10920925903867D+01 0.14296338312368D-01 2 8 1 15 -0.24452075078454D+01 0.47573476839333D-03 3 8 1 15 0.18828771588209D+00 -0.36654271339288D-01 1 9 1 15 0.77312347167529D-02 -0.65404867931901D-01 2 9 1 15 -0.66226670866071D+00 -0.25004731472479D-01 3 9 1 15 -0.30034371241651D+01 0.10880137817197D+00 1 10 1 15 0.11157902312848D+01 -0.13787637832406D-05 2 10 1 15 0.97020788419845D+00 0.86399120309165D-07 3 10 1 15 -0.36935237640409D+01 -0.89646541022312D-06 1 11 1 15 0.42909725326248D+00 -0.96571024830950D-02 2 11 1 15 0.14405737890598D+01 -0.39946960163871D-01 3 11 1 15 0.28203925227029D+01 0.10126640308881D+00 1 12 1 15 0.21269098163497D+00 -0.33975177707034D-06 2 12 1 15 -0.62889356407284D+00 0.71669099220682D-07 3 12 1 15 0.25394093574743D+01 0.76542898381735D-06 1 13 1 15 0.13711483276091D-14 0.78881406176688D-01 2 13 1 15 -0.59774075657531D-01 0.91889221273374D-01 3 13 1 15 0.33094596257339D+00 0.23244209361992D-02 1 14 1 15 0.24484108676583D+00 0.96618101766286D-16 2 14 1 15 -0.59365354065453D-01 -0.48959010313021D-06 3 14 1 15 -0.77639775635181D-01 -0.82538685702514D-07 1 15 1 15 0.13898122635327D+02 0.00000000000000D+00 2 15 1 15 0.64220335112207D+01 0.18823880084437D+00 3 15 1 15 0.12557350990265D+01 0.16706243204776D+00 1 16 1 15 0.38758753471713D+01 0.17637703836518D-02 2 16 1 15 0.44020035000303D+01 -0.32984240192981D-02 3 16 1 15 0.18227334375484D+00 -0.19277344790829D-02 1 17 1 15 -0.60746088713778D-01 0.18602070476374D-06 2 17 1 15 -0.21267822786136D-01 0.62947218400918D-02 3 17 1 15 0.66628016534021D+00 -0.31173506039872D-02 1 18 1 15 0.10932815519766D-14 0.20694161299029D-06 2 18 1 15 -0.72759334883853D-01 0.55423410951160D-02 3 18 1 15 0.27389608057286D+00 0.52918730905630D-02 1 19 1 15 -0.68169764273467D-14 0.72400695201127D-02 2 19 1 15 -0.10951670448984D+01 -0.10518327720668D-02 3 19 1 15 0.30181734532868D+00 0.91617708047415D-02 1 20 1 15 -0.18469641454947D-13 -0.62373852328222D-06 2 20 1 15 -0.11571846304922D+01 0.58739072102725D-06 3 20 1 15 0.17941074822631D+01 -0.10478331362840D-05 1 1 2 15 0.78714711650424D+00 -0.15604524917166D-01 2 1 2 15 0.29452192971427D+00 -0.42432835830075D-02 3 1 2 15 0.55375110754941D+00 -0.17221670951026D-03 1 2 2 15 -0.95320318876932D+00 0.36389309460843D-06 2 2 2 15 -0.88299137538412D+00 0.28187504132717D-06 3 2 2 15 0.73874028938639D+00 0.83831003237747D-07 1 3 2 15 -0.68712473251340D+00 0.19760181935291D-06 2 3 2 15 -0.64763245546001D+00 -0.26415742586450D-06 3 3 2 15 0.76341655697850D+00 0.17317799650627D-06 1 4 2 15 -0.14641252210923D+00 -0.16744411954470D-01 2 4 2 15 -0.15713437869598D+01 -0.18478138079751D-02 3 4 2 15 0.33257813959696D+00 -0.17228537222115D-02 1 5 2 15 0.21890341311868D+00 0.57975041970885D-01 2 5 2 15 -0.54144292836912D-01 0.28275102359186D-01 3 5 2 15 0.27496806876738D+01 -0.76488031477961D-02 1 6 2 15 0.21831596540527D+01 -0.12385679687635D-01 2 6 2 15 -0.12926774104381D+01 0.71916339247645D-02 3 6 2 15 0.37979157642184D+00 -0.42470155283088D-01 1 7 2 15 -0.50224851509074D+00 -0.13530109371527D+00 2 7 2 15 -0.30975812792411D+00 -0.15408726080424D+00 3 7 2 15 0.35041370877414D+01 -0.52902086903712D-02 1 8 2 15 -0.12478087830553D+01 0.19355587853700D-01 2 8 2 15 0.23168943120459D+01 0.71500529342252D-02 3 8 2 15 0.70566199330308D+00 -0.54515837216350D-01 1 9 2 15 -0.67229068221357D+00 -0.74916605308276D-01 2 9 2 15 -0.32247399400848D+00 -0.11508575079097D-01 3 9 2 15 -0.30802612353887D+01 0.15818131896180D+00 1 10 2 15 0.14170005718491D+01 -0.45216338326577D-06 2 10 2 15 0.14147966551016D+00 -0.31064299992723D-06 3 10 2 15 -0.26510297703738D+01 -0.63581638698635D-06 1 11 2 15 0.12523540326113D+01 -0.34949201832724D-01 2 11 2 15 0.57632070221867D+00 -0.41313829727512D-01 3 11 2 15 0.32400070915947D+01 0.11623328030853D+00 1 12 2 15 -0.50301179776291D+00 0.30339873810594D-06 2 12 2 15 -0.43731681324672D+00 0.34735605956791D-07 3 12 2 15 0.38820587360795D+01 0.11441304069180D-05 1 13 2 15 0.59774075657538D-01 0.91889221273374D-01 2 13 2 15 0.16395634524868D-14 0.10716488379770D+00 3 13 2 15 -0.34606075502576D+00 0.36465383468230D-02 1 14 2 15 -0.59365354065453D-01 0.48959010329204D-06 2 14 2 15 0.14475652471388D+00 0.32646432922661D-15 3 14 2 15 0.82639870750698D-01 -0.13401808649935D-06 1 15 2 15 0.64220402558011D+01 -0.18823887449866D+00 2 15 2 15 0.15298044818349D+02 0.00000000000000D+00 3 15 2 15 -0.19826211583796D+01 -0.19948869321804D+00 1 16 2 15 0.44020031284309D+01 -0.32989355973441D-02 2 16 2 15 0.41216323764819D+01 -0.60781501884999D-02 3 16 2 15 -0.20867294665193D+00 -0.89193357669127D-03 1 17 2 15 0.21268002343368D-01 0.62951649308073D-02 2 17 2 15 -0.17866896526108D-01 -0.33254049883502D-06 3 17 2 15 0.37430864985463D+00 0.54614196068629D-02 1 18 2 15 -0.72760036737823D-01 0.55433092606056D-02 2 18 2 15 -0.14444914252437D-14 -0.50448504404923D-06 3 18 2 15 0.80043183253720D+00 -0.52000824587466D-02 1 19 2 15 -0.10951670448984D+01 0.10518327720665D-02 2 19 2 15 -0.38228424062489D-13 -0.17783925419803D-01 3 19 2 15 -0.19338028945541D-01 -0.41669660085316D-01 1 20 2 15 -0.11571846304922D+01 -0.58739071720258D-06 2 20 2 15 0.66101362520663D-14 -0.97932568458709D-09 3 20 2 15 0.46580936432626D+00 -0.85640432112245D-06 1 1 3 15 -0.70042568642646D+00 0.14423150740348D-02 2 1 3 15 0.78834034603552D+00 0.20194645910254D-02 3 1 3 15 -0.38453250910952D+00 -0.49275599810527D-02 1 2 3 15 -0.84564392342538D+00 -0.13861387197548D-06 2 2 3 15 0.67932441581492D+00 0.11489534427354D-07 3 2 3 15 -0.33565238386832D-02 0.28322019885013D-06 1 3 3 15 -0.11902835930203D+01 0.22901718426497D-06 2 3 3 15 0.10013965666997D+01 -0.45336946581010D-06 3 3 3 15 0.48038748013545D+00 0.91572781718537D-07 1 4 3 15 -0.23054956166560D+00 -0.15504920856827D-02 2 4 3 15 0.52264722169600D+00 0.33296080090649D-02 3 4 3 15 -0.20724822922070D+01 -0.20038783343413D-01 1 5 3 15 0.62705904656789D+00 0.82421881349822D-02 2 5 3 15 0.41659732056843D+00 0.49748253466809D-02 3 5 3 15 0.17035920554806D+00 -0.30749743633631D-01 1 6 3 15 -0.80773945037071D+00 -0.34943424899290D-01 2 6 3 15 -0.13596895178966D+01 -0.17040815752433D-01 3 6 3 15 -0.39092799049792D+01 -0.28119940517982D-01 1 7 3 15 0.45745096942818D+00 0.32192453776084D-02 2 7 3 15 0.61507586914081D+00 0.19382285042189D-01 3 7 3 15 -0.61614090844335D+00 0.13064924968600D+00 1 8 3 15 -0.87225283577185D+00 -0.27747237711738D-01 2 8 3 15 -0.12362503312941D+01 -0.45313182285092D-01 3 8 3 15 0.36602739406617D+01 0.34764508930433D-01 1 9 3 15 -0.11949136020980D+01 0.17919309964116D-01 2 9 3 15 -0.13480213827395D+01 0.85386752395620D-03 3 9 3 15 -0.26428759172736D+01 0.20007309666097D+00 1 10 3 15 -0.21235578482967D+01 0.87549350199181D-06 2 10 3 15 -0.11137091419462D+01 0.98587184370450D-06 3 10 3 15 0.97946356471338D+00 -0.30786078332397D-06 1 11 3 15 0.13654668846558D+01 0.25767336813663D-01 2 11 3 15 0.17119795773385D+01 0.42289856139811D-01 3 11 3 15 0.72545834190357D+00 0.89816573984339D-01 1 12 3 15 0.89382868931030D+00 -0.11804576413580D-06 2 12 3 15 0.17398153256030D+01 -0.62230760874444D-06 3 12 3 15 -0.31426422397135D+01 -0.84733984907968D-06 1 13 3 15 0.33094596257339D+00 -0.23244209361993D-02 2 13 3 15 -0.34606075502576D+00 -0.36465383468236D-02 3 13 3 15 0.53767974454164D-14 -0.56333672833067D-01 1 14 3 15 0.77639775635155D-01 -0.82538685703381D-07 2 14 3 15 -0.82639870750706D-01 -0.13401808650108D-06 3 14 3 15 -0.89098768490708D+00 -0.33826156355276D-15 1 15 3 15 0.12557128577605D+01 -0.16706222771616D+00 2 15 3 15 -0.19826484447410D+01 0.19948817466567D+00 3 15 3 15 0.15144686983050D+02 0.00000000000000D+00 1 16 3 15 0.18227524897193D+00 -0.19268627743442D-02 2 16 3 15 -0.20867042954992D+00 -0.89241513345218D-03 3 16 3 15 0.10300521199797D+01 0.95008581194228D-02 1 17 3 15 0.66628175574442D+00 0.31164528908422D-02 2 17 3 15 -0.37430983841762D+00 0.54623506006128D-02 3 17 3 15 -0.17632798563093D+00 0.60543745035762D-07 1 18 3 15 -0.27389758526281D+00 -0.52922061447548D-02 2 18 3 15 0.80043388900747D+00 -0.51985952631479D-02 3 18 3 15 -0.22032038672733D-14 0.38876851283610D-07 1 19 3 15 0.30181734532868D+00 -0.91617708047418D-02 2 19 3 15 0.19338028945537D-01 -0.41669660085316D-01 3 19 3 15 -0.33349955099775D-14 -0.67656815809761D-02 1 20 3 15 0.17941074822631D+01 0.10478331326451D-05 2 20 3 15 -0.46580936432626D+00 -0.85640432112256D-06 3 20 3 15 0.22313420425123D-13 -0.59573347221974D-06 1 1 1 16 0.84163057818195D+00 -0.74880249939434D-06 2 1 1 16 0.80558111162734D+00 -0.49477642066809D-06 3 1 1 16 0.44828122852294D+00 0.14721994257494D-06 1 2 1 16 -0.40053332053905D+00 0.13838444397699D-01 2 2 1 16 -0.78632530987335D+00 0.63106206074921D-02 3 2 1 16 0.61948808567308D+00 0.29798087047829D-02 1 3 1 16 -0.11682226319502D+01 0.87286015242531D-02 2 3 1 16 -0.51689538388860D-01 -0.33029634723416D-01 3 3 1 16 -0.67078264993127D+00 0.97105436486358D-02 1 4 1 16 -0.53789782066794D+00 0.15056873000731D-06 2 4 1 16 -0.71678759202774D+00 0.58517302485334D-07 3 4 1 16 -0.11674946922127D+01 0.43632829590863D-07 1 5 1 16 0.58641202826265D+00 0.42434203301504D-01 2 5 1 16 -0.23857555948405D+00 0.34463920729134D-01 3 5 1 16 0.34007399469183D+01 -0.13686640135059D-02 1 6 1 16 0.23532829639727D+01 0.12588627472329D-01 2 6 1 16 -0.98619645269343D+00 -0.16035416249390D-01 3 6 1 16 -0.18763038654274D+00 0.35432183064911D-01 1 7 1 16 -0.52646987880337D+00 -0.75686465898100D-01 2 7 1 16 -0.30234462751203D-01 -0.15440299694563D+00 3 7 1 16 0.27521155929143D+01 -0.27750239130724D-01 1 8 1 16 -0.10920925903866D+01 -0.14296338312365D-01 2 8 1 16 0.24452075078460D+01 -0.47573476836955D-03 3 8 1 16 -0.18828771588215D+00 0.36654271339284D-01 1 9 1 16 0.11157902312848D+01 -0.13787637778185D-05 2 9 1 16 0.97020788419843D+00 0.86399124854038D-07 3 9 1 16 -0.36935237640409D+01 -0.89646542045796D-06 1 10 1 16 0.77312347167364D-02 -0.65404867931901D-01 2 10 1 16 -0.66226670866070D+00 -0.25004731472478D-01 3 10 1 16 -0.30034371241651D+01 0.10880137817197D+00 1 11 1 16 0.21269098163499D+00 -0.33975177745679D-06 2 11 1 16 -0.62889356407284D+00 0.71669099270252D-07 3 11 1 16 0.25394093574744D+01 0.76542898441635D-06 1 12 1 16 0.42909725326249D+00 -0.96571024830963D-02 2 12 1 16 0.14405737890598D+01 -0.39946960163876D-01 3 12 1 16 0.28203925227030D+01 0.10126640308881D+00 1 13 1 16 0.24484108676583D+00 -0.13766969250412D-15 2 13 1 16 -0.59365354065440D-01 -0.48959010311776D-06 3 13 1 16 -0.77639775635162D-01 -0.82538685517722D-07 1 14 1 16 -0.10023014882025D-13 0.78881406176688D-01 2 14 1 16 -0.59774075657543D-01 0.91889221273374D-01 3 14 1 16 0.33094596257338D+00 0.23244209361984D-02 1 15 1 16 0.38758753471713D+01 0.17637703836527D-02 2 15 1 16 0.44020035000303D+01 -0.32984240192979D-02 3 15 1 16 0.18227334375484D+00 -0.19277344790826D-02 1 16 1 16 0.13898122635327D+02 0.00000000000000D+00 2 16 1 16 0.64220335112203D+01 0.18823880084437D+00 3 16 1 16 0.12557350990269D+01 0.16706243204776D+00 1 17 1 16 -0.31336678235530D-14 0.20694161288124D-06 2 17 1 16 -0.72759334883859D-01 0.55423410951157D-02 3 17 1 16 0.27389608057286D+00 0.52918730905638D-02 1 18 1 16 -0.60746088713776D-01 0.18602070469021D-06 2 18 1 16 -0.21267822786133D-01 0.62947218400917D-02 3 18 1 16 0.66628016534021D+00 -0.31173506039871D-02 1 19 1 16 -0.55152235282014D-14 -0.62373851381735D-06 2 19 1 16 -0.11571846304922D+01 0.58739071817854D-06 3 19 1 16 0.17941074822631D+01 -0.10478331326468D-05 1 20 1 16 -0.15077899481554D-13 0.72400695201143D-02 2 20 1 16 -0.10951670448984D+01 -0.10518327720640D-02 3 20 1 16 0.30181734532867D+00 0.91617708047425D-02 1 1 2 16 0.95320318876925D+00 -0.36389309805530D-06 2 1 2 16 0.88299137538419D+00 -0.28187504135440D-06 3 1 2 16 -0.73874028938633D+00 -0.83830996668989D-07 1 2 2 16 -0.78714711650426D+00 0.15604524917164D-01 2 2 2 16 -0.29452192971432D+00 0.42432835830076D-02 3 2 2 16 -0.55375110754941D+00 0.17221670950881D-03 1 3 2 16 -0.14641252210917D+00 -0.16744411954469D-01 2 3 2 16 -0.15713437869598D+01 -0.18478138079774D-02 3 3 2 16 0.33257813959702D+00 -0.17228537222126D-02 1 4 2 16 -0.68712473251342D+00 0.19760181900455D-06 2 4 2 16 -0.64763245545998D+00 -0.26415742471216D-06 3 4 2 16 0.76341655697857D+00 0.17317799692099D-06 1 5 2 16 0.21890341311867D+00 0.57975041970881D-01 2 5 2 16 -0.54144292836905D-01 0.28275102359183D-01 3 5 2 16 0.27496806876738D+01 -0.76488031477961D-02 1 6 2 16 -0.21831596540526D+01 0.12385679687657D-01 2 6 2 16 0.12926774104380D+01 -0.71916339247592D-02 3 6 2 16 -0.37979157642162D+00 0.42470155283098D-01 1 7 2 16 -0.50224851509073D+00 -0.13530109371527D+00 2 7 2 16 -0.30975812792412D+00 -0.15408726080424D+00 3 7 2 16 0.35041370877415D+01 -0.52902086903703D-02 1 8 2 16 0.12478087830559D+01 -0.19355587853676D-01 2 8 2 16 -0.23168943120456D+01 -0.71500529342034D-02 3 8 2 16 -0.70566199330313D+00 0.54515837216342D-01 1 9 2 16 0.14170005718490D+01 -0.45216337870702D-06 2 9 2 16 0.14147966551017D+00 -0.31064300060256D-06 3 9 2 16 -0.26510297703737D+01 -0.63581639176379D-06 1 10 2 16 -0.67229068221356D+00 -0.74916605308275D-01 2 10 2 16 -0.32247399400847D+00 -0.11508575079097D-01 3 10 2 16 -0.30802612353887D+01 0.15818131896180D+00 1 11 2 16 -0.50301179776291D+00 0.30339873814857D-06 2 11 2 16 -0.43731681324670D+00 0.34735606218272D-07 3 11 2 16 0.38820587360795D+01 0.11441304069592D-05 1 12 2 16 0.12523540326113D+01 -0.34949201832729D-01 2 12 2 16 0.57632070221865D+00 -0.41313829727515D-01 3 12 2 16 0.32400070915947D+01 0.11623328030852D+00 1 13 2 16 -0.59365354065440D-01 0.48959010330448D-06 2 13 2 16 0.14475652471389D+00 -0.56866074846531D-15 3 13 2 16 0.82639870750708D-01 -0.13401808593376D-06 1 14 2 16 0.59774075657525D-01 0.91889221273374D-01 2 14 2 16 -0.10378546201465D-13 0.10716488379770D+00 3 14 2 16 -0.34606075502578D+00 0.36465383468237D-02 1 15 2 16 0.44020031284309D+01 -0.32989355973440D-02 2 15 2 16 0.41216323764819D+01 -0.60781501885007D-02 3 15 2 16 -0.20867294665193D+00 -0.89193357669022D-03 1 16 2 16 0.64220402558007D+01 -0.18823887449866D+00 2 16 2 16 0.15298044818349D+02 0.00000000000000D+00 3 16 2 16 -0.19826211583795D+01 -0.19948869321804D+00 1 17 2 16 -0.72760036737829D-01 0.55433092606053D-02 2 17 2 16 -0.27152408547816D-14 -0.50448504453965D-06 3 17 2 16 0.80043183253721D+00 -0.52000824587479D-02 1 18 2 16 0.21268002343370D-01 0.62951649308073D-02 2 18 2 16 -0.17866896526106D-01 -0.33254049870311D-06 3 18 2 16 0.37430864985463D+00 0.54614196068627D-02 1 19 2 16 -0.11571846304922D+01 -0.58739072005129D-06 2 19 2 16 -0.26281668423282D-14 -0.97932786171287D-09 3 19 2 16 0.46580936432627D+00 -0.85640432221441D-06 1 20 2 16 -0.10951670448984D+01 0.10518327720693D-02 2 20 2 16 0.24827613666725D-13 -0.17783925419816D-01 3 20 2 16 -0.19338028945542D-01 -0.41669660085317D-01 1 1 3 16 0.84564392342549D+00 0.13861386488459D-06 2 1 3 16 -0.67932441581486D+00 -0.11489527858162D-07 3 1 3 16 0.33565238386086D-02 -0.28322019409108D-06 1 2 3 16 0.70042568642651D+00 -0.14423150740308D-02 2 2 3 16 -0.78834034603552D+00 -0.20194645910269D-02 3 2 3 16 0.38453250910954D+00 0.49275599810549D-02 1 3 3 16 -0.23054956166566D+00 -0.15504920856827D-02 2 3 3 16 0.52264722169606D+00 0.33296080090638D-02 3 3 3 16 -0.20724822922069D+01 -0.20038783343413D-01 1 4 3 16 -0.11902835930204D+01 0.22901718360464D-06 2 4 3 16 0.10013965666998D+01 -0.45336946539538D-06 3 4 3 16 0.48038748013557D+00 0.91572778596471D-07 1 5 3 16 0.62705904656785D+00 0.82421881349822D-02 2 5 3 16 0.41659732056846D+00 0.49748253466809D-02 3 5 3 16 0.17035920554807D+00 -0.30749743633632D-01 1 6 3 16 0.80773945037109D+00 0.34943424899301D-01 2 6 3 16 0.13596895178969D+01 0.17040815752443D-01 3 6 3 16 0.39092799049791D+01 0.28119940517959D-01 1 7 3 16 0.45745096942820D+00 0.32192453776097D-02 2 7 3 16 0.61507586914084D+00 0.19382285042190D-01 3 7 3 16 -0.61614090844329D+00 0.13064924968600D+00 1 8 3 16 0.87225283577179D+00 0.27747237711734D-01 2 8 3 16 0.12362503312941D+01 0.45313182285084D-01 3 8 3 16 -0.36602739406623D+01 -0.34764508930456D-01 1 9 3 16 -0.21235578482967D+01 0.87549349175698D-06 2 9 3 16 -0.11137091419462D+01 0.98587183892706D-06 3 9 3 16 0.97946356471333D+00 -0.30786077848209D-06 1 10 3 16 -0.11949136020981D+01 0.17919309964117D-01 2 10 3 16 -0.13480213827395D+01 0.85386752395561D-03 3 10 3 16 -0.26428759172736D+01 0.20007309666097D+00 1 11 3 16 0.89382868931034D+00 -0.11804576354374D-06 2 11 3 16 0.17398153256030D+01 -0.62230760873094D-06 3 11 3 16 -0.31426422397136D+01 -0.84733984889632D-06 1 12 3 16 0.13654668846558D+01 0.25767336813658D-01 2 12 3 16 0.17119795773385D+01 0.42289856139805D-01 3 12 3 16 0.72545834190353D+00 0.89816573984337D-01 1 13 3 16 0.77639775635174D-01 -0.82538685518589D-07 2 13 3 16 -0.82639870750695D-01 -0.13401808593550D-06 3 13 3 16 -0.89098768490708D+00 0.40689412751646D-15 1 14 3 16 0.33094596257338D+00 -0.23244209362001D-02 2 14 3 16 -0.34606075502578D+00 -0.36465383468228D-02 3 14 3 16 -0.64579016519435D-14 -0.56333672833066D-01 1 15 3 16 0.18227524897193D+00 -0.19268627743439D-02 2 15 3 16 -0.20867042954992D+00 -0.89241513345114D-03 3 15 3 16 0.10300521199797D+01 0.95008581194227D-02 1 16 3 16 0.12557128577609D+01 -0.16706222771616D+00 2 16 3 16 -0.19826484447409D+01 0.19948817466567D+00 3 16 3 16 0.15144686983050D+02 0.00000000000000D+00 1 17 3 16 -0.27389758526281D+00 -0.52922061447541D-02 2 17 3 16 0.80043388900748D+00 -0.51985952631491D-02 3 17 3 16 0.48308853856366D-14 0.38876850566222D-07 1 18 3 16 0.66628175574442D+00 0.31164528908423D-02 2 18 3 16 -0.37430983841762D+00 0.54623506006126D-02 3 18 3 16 -0.17632798563093D+00 0.60543745054602D-07 1 19 3 16 0.17941074822631D+01 0.10478331362823D-05 2 19 3 16 -0.46580936432626D+00 -0.85640432221430D-06 3 19 3 16 -0.43318283787349D-14 -0.59573347608598D-06 1 20 3 16 0.30181734532867D+00 -0.91617708047407D-02 2 20 3 16 0.19338028945536D-01 -0.41669660085317D-01 3 20 3 16 -0.17542926847906D-13 -0.67656815809712D-02 1 1 1 17 -0.11682226319502D+01 0.87286015242564D-02 2 1 1 17 0.51689538388875D-01 0.33029634723405D-01 3 1 1 17 -0.67078264993156D+00 0.97105436486160D-02 1 2 1 17 -0.53789782066793D+00 0.15056872837776D-06 2 2 1 17 0.71678759202770D+00 -0.58517304212302D-07 3 2 1 17 -0.11674946922125D+01 0.43632829729717D-07 1 3 1 17 -0.84163057818195D+00 0.74880250091587D-06 2 3 1 17 0.80558111162734D+00 -0.49477641514773D-06 3 3 1 17 -0.44828122852276D+00 -0.14721995283792D-06 1 4 1 17 0.40053332053903D+00 -0.13838444397700D-01 2 4 1 17 -0.78632530987332D+00 0.63106206074906D-02 3 4 1 17 -0.61948808567312D+00 -0.29798087047852D-02 1 5 1 17 0.10920925903866D+01 0.14296338312369D-01 2 5 1 17 0.24452075078458D+01 -0.47573476839416D-03 3 5 1 17 0.18828771588215D+00 -0.36654271339288D-01 1 6 1 17 0.52646987880336D+00 0.75686465898100D-01 2 6 1 17 -0.30234462751211D-01 -0.15440299694563D+00 3 6 1 17 -0.27521155929143D+01 0.27750239130725D-01 1 7 1 17 0.23532829639728D+01 0.12588627472327D-01 2 7 1 17 0.98619645269335D+00 0.16035416249389D-01 3 7 1 17 -0.18763038654269D+00 0.35432183064910D-01 1 8 1 17 0.58641202826267D+00 0.42434203301504D-01 2 8 1 17 0.23857555948407D+00 -0.34463920729137D-01 3 8 1 17 0.34007399469183D+01 -0.13686640135061D-02 1 9 1 17 0.42909725326250D+00 -0.96571024830951D-02 2 9 1 17 -0.14405737890597D+01 0.39946960163869D-01 3 9 1 17 0.28203925227030D+01 0.10126640308881D+00 1 10 1 17 -0.21269098163497D+00 0.33975177826729D-06 2 10 1 17 -0.62889356407285D+00 0.71669099894195D-07 3 10 1 17 -0.25394093574743D+01 -0.76542898233738D-06 1 11 1 17 0.77312347167258D-02 -0.65404867931901D-01 2 11 1 17 0.66226670866073D+00 0.25004731472480D-01 3 11 1 17 -0.30034371241651D+01 0.10880137817197D+00 1 12 1 17 -0.11157902312848D+01 0.13787637808886D-05 2 12 1 17 0.97020788419844D+00 0.86399122705549D-07 3 12 1 17 0.36935237640409D+01 0.89646541528230D-06 1 13 1 17 -0.90818078815664D-14 -0.72400695201136D-02 2 13 1 17 -0.10951670448984D+01 -0.10518327720667D-02 3 13 1 17 -0.30181734532867D+00 -0.91617708047417D-02 1 14 1 17 0.10475874952516D-13 -0.62373852356664D-06 2 14 1 17 0.11571846304922D+01 -0.58739071982972D-06 3 14 1 17 0.17941074822631D+01 -0.10478331360172D-05 1 15 1 17 -0.60746088713778D-01 0.18602070470298D-06 2 15 1 17 0.21267822786138D-01 -0.62947218400918D-02 3 15 1 17 0.66628016534021D+00 -0.31173506039870D-02 1 16 1 17 -0.31336678235530D-14 -0.20694161288124D-06 2 16 1 17 -0.72759334883859D-01 0.55423410951157D-02 3 16 1 17 -0.27389608057287D+00 -0.52918730905638D-02 1 17 1 17 0.13898122635327D+02 0.00000000000000D+00 2 17 1 17 -0.64220335112201D+01 -0.18823880084437D+00 3 17 1 17 0.12557350990270D+01 0.16706243204776D+00 1 18 1 17 -0.38758753471713D+01 -0.17637703836513D-02 2 18 1 17 0.44020035000303D+01 -0.32984240192962D-02 3 18 1 17 -0.18227334375484D+00 0.19277344790820D-02 1 19 1 17 0.40854724985373D-14 -0.78881406176687D-01 2 19 1 17 -0.59774075657532D-01 0.91889221273374D-01 3 19 1 17 -0.33094596257341D+00 -0.23244209361988D-02 1 20 1 17 0.24484108676582D+00 -0.76590336316981D-15 2 20 1 17 0.59365354065442D-01 0.48959010349519D-06 3 20 1 17 -0.77639775635171D-01 -0.82538685647329D-07 1 1 2 17 0.14641252210917D+00 0.16744411954459D-01 2 1 2 17 -0.15713437869597D+01 -0.18478138079790D-02 3 1 2 17 -0.33257813959708D+00 0.17228537221859D-02 1 2 2 17 0.68712473251339D+00 -0.19760182072979D-06 2 2 2 17 -0.64763245545998D+00 -0.26415742617594D-06 3 2 2 17 -0.76341655697846D+00 -0.17317799635091D-06 1 3 2 17 0.95320318876925D+00 -0.36389309253667D-06 2 3 2 17 -0.88299137538415D+00 0.28187504159461D-06 3 3 2 17 -0.73874028938632D+00 -0.83831002487958D-07 1 4 2 17 -0.78714711650424D+00 0.15604524917162D-01 2 4 2 17 0.29452192971431D+00 -0.42432835830086D-02 3 4 2 17 -0.55375110754944D+00 0.17221670950533D-03 1 5 2 17 0.12478087830558D+01 -0.19355587853701D-01 2 5 2 17 0.23168943120457D+01 0.71500529342230D-02 3 5 2 17 -0.70566199330310D+00 0.54515837216354D-01 1 6 2 17 -0.50224851509074D+00 -0.13530109371527D+00 2 6 2 17 0.30975812792412D+00 0.15408726080424D+00 3 6 2 17 0.35041370877415D+01 -0.52902086903702D-02 1 7 2 17 0.21831596540525D+01 -0.12385679687658D-01 2 7 2 17 0.12926774104379D+01 -0.71916339247590D-02 3 7 2 17 0.37979157642162D+00 -0.42470155283098D-01 1 8 2 17 -0.21890341311865D+00 -0.57975041970884D-01 2 8 2 17 -0.54144292836895D-01 0.28275102359187D-01 3 8 2 17 -0.27496806876738D+01 0.76488031477961D-02 1 9 2 17 -0.12523540326113D+01 0.34949201832723D-01 2 9 2 17 0.57632070221865D+00 -0.41313829727513D-01 3 9 2 17 -0.32400070915946D+01 -0.11623328030853D+00 1 10 2 17 -0.50301179776291D+00 0.30339873878639D-06 2 10 2 17 0.43731681324673D+00 -0.34735606154540D-07 3 10 2 17 0.38820587360794D+01 0.11441304025637D-05 1 11 2 17 0.67229068221359D+00 0.74916605308277D-01 2 11 2 17 -0.32247399400850D+00 -0.11508575079097D-01 3 11 2 17 0.30802612353887D+01 -0.15818131896180D+00 1 12 2 17 0.14170005718491D+01 -0.45216338086592D-06 2 12 2 17 -0.14147966551014D+00 0.31064299968818D-06 3 12 2 17 -0.26510297703738D+01 -0.63581638942920D-06 1 13 2 17 -0.10951670448984D+01 0.10518327720666D-02 2 13 2 17 0.32819040875285D-13 0.17783925419816D-01 3 13 2 17 -0.19338028945535D-01 -0.41669660085314D-01 1 14 2 17 0.11571846304922D+01 0.58739071840010D-06 2 14 2 17 -0.16602196325731D-13 -0.97932574481653D-09 3 14 2 17 -0.46580936432627D+00 0.85640432152377D-06 1 15 2 17 -0.21268002343366D-01 -0.62951649308073D-02 2 15 2 17 -0.17866896526108D-01 -0.33254049873201D-06 3 15 2 17 -0.37430864985463D+00 -0.54614196068629D-02 1 16 2 17 -0.72760036737829D-01 0.55433092606053D-02 2 16 2 17 -0.27152408547816D-14 0.50448504453965D-06 3 16 2 17 0.80043183253721D+00 -0.52000824587466D-02 1 17 2 17 -0.64220402558005D+01 0.18823887449866D+00 2 17 2 17 0.15298044818348D+02 0.00000000000000D+00 3 17 2 17 0.19826211583794D+01 0.19948869321804D+00 1 18 2 17 0.44020031284309D+01 -0.32989355973423D-02 2 18 2 17 -0.41216323764819D+01 0.60781501885011D-02 3 18 2 17 -0.20867294665193D+00 -0.89193357669183D-03 1 19 2 17 0.59774075657537D-01 0.91889221273374D-01 2 19 2 17 0.40518362336481D-14 -0.10716488379770D+00 3 19 2 17 -0.34606075502577D+00 0.36465383468230D-02 1 20 2 17 0.59365354065442D-01 -0.48959010292706D-06 2 20 2 17 0.14475652471388D+00 -0.16643923824197D-15 3 20 2 17 -0.82639870750701D-01 0.13401808571479D-06 1 1 3 17 -0.23054956166593D+00 -0.15504920857026D-02 2 1 3 17 -0.52264722169611D+00 -0.33296080090905D-02 3 1 3 17 -0.20724822922072D+01 -0.20038783343433D-01 1 2 3 17 -0.11902835930202D+01 0.22901718374176D-06 2 2 3 17 -0.10013965666997D+01 0.45336946596720D-06 3 2 3 17 0.48038748013542D+00 0.91572783024913D-07 1 3 3 17 -0.84564392342532D+00 -0.13861387514844D-06 2 3 3 17 -0.67932441581485D+00 -0.11489533677564D-07 3 3 3 17 -0.33565238386828D-02 0.28322019953182D-06 1 4 3 17 -0.70042568642656D+00 0.14423150740285D-02 2 4 3 17 -0.78834034603555D+00 -0.20194645910303D-02 3 4 3 17 -0.38453250910962D+00 -0.49275599810592D-02 1 5 3 17 -0.87225283577179D+00 -0.27747237711738D-01 2 5 3 17 0.12362503312941D+01 0.45313182285096D-01 3 5 3 17 0.36602739406624D+01 0.34764508930436D-01 1 6 3 17 -0.45745096942820D+00 -0.32192453776088D-02 2 6 3 17 0.61507586914082D+00 0.19382285042190D-01 3 6 3 17 0.61614090844328D+00 -0.13064924968600D+00 1 7 3 17 0.80773945037114D+00 0.34943424899301D-01 2 7 3 17 -0.13596895178969D+01 -0.17040815752443D-01 3 7 3 17 0.39092799049790D+01 0.28119940517959D-01 1 8 3 17 0.62705904656785D+00 0.82421881349820D-02 2 8 3 17 -0.41659732056845D+00 -0.49748253466809D-02 3 8 3 17 0.17035920554806D+00 -0.30749743633630D-01 1 9 3 17 0.13654668846558D+01 0.25767336813664D-01 2 9 3 17 -0.17119795773384D+01 -0.42289856139811D-01 3 9 3 17 0.72545834190351D+00 0.89816573984339D-01 1 10 3 17 -0.89382868931027D+00 0.11804576562965D-06 2 10 3 17 0.17398153256030D+01 -0.62230761311086D-06 3 10 3 17 0.31426422397134D+01 0.84733984249655D-06 1 11 3 17 -0.11949136020981D+01 0.17919309964116D-01 2 11 3 17 0.13480213827396D+01 -0.85386752395584D-03 3 11 3 17 -0.26428759172736D+01 0.20007309666097D+00 1 12 3 17 0.21235578482967D+01 -0.87549349696039D-06 2 12 3 17 -0.11137091419462D+01 0.98587184125818D-06 3 12 3 17 -0.97946356471335D+00 0.30786078026108D-06 1 13 3 17 -0.30181734532867D+00 0.91617708047416D-02 2 13 3 17 0.19338028945543D-01 -0.41669660085314D-01 3 13 3 17 -0.17543755034370D-13 0.67656815809709D-02 1 14 3 17 0.17941074822631D+01 0.10478331329119D-05 2 14 3 17 0.46580936432626D+00 0.85640432152366D-06 3 14 3 17 -0.22313873777965D-13 -0.59573347229459D-06 1 15 3 17 0.66628175574442D+00 0.31164528908424D-02 2 15 3 17 0.37430983841762D+00 -0.54623506006128D-02 3 15 3 17 -0.17632798563093D+00 0.60543745072252D-07 1 16 3 17 0.27389758526280D+00 0.52922061447541D-02 2 16 3 17 0.80043388900748D+00 -0.51985952631479D-02 3 16 3 17 0.48308853856366D-14 -0.38876850566222D-07 1 17 3 17 0.12557128577610D+01 -0.16706222771616D+00 2 17 3 17 0.19826484447408D+01 -0.19948817466567D+00 3 17 3 17 0.15144686983050D+02 0.00000000000000D+00 1 18 3 17 -0.18227524897193D+00 0.19268627743433D-02 2 18 3 17 -0.20867042954992D+00 -0.89241513345275D-03 3 18 3 17 -0.10300521199797D+01 -0.95008581194234D-02 1 19 3 17 -0.33094596257340D+00 0.23244209361997D-02 2 19 3 17 -0.34606075502577D+00 -0.36465383468236D-02 3 19 3 17 0.69007383525579D-14 0.56333672833066D-01 1 20 3 17 0.77639775635164D-01 -0.82538685648196D-07 2 20 3 17 0.82639870750702D-01 0.13401808571652D-06 3 20 3 17 -0.89098768490708D+00 -0.90190908579682D-15 1 1 1 18 0.53789782066794D+00 -0.15056872959353D-06 2 1 1 18 -0.71678759202771D+00 0.58517304308561D-07 3 1 1 18 0.11674946922127D+01 -0.43632838127262D-07 1 2 1 18 0.11682226319502D+01 -0.87286015242566D-02 2 2 1 18 -0.51689538388833D-01 -0.33029634723423D-01 3 2 1 18 0.67078264993137D+00 -0.97105436486449D-02 1 3 1 18 0.40053332053903D+00 -0.13838444397699D-01 2 3 1 18 -0.78632530987333D+00 0.63106206074938D-02 3 3 1 18 -0.61948808567311D+00 -0.29798087047796D-02 1 4 1 18 -0.84163057818195D+00 0.74880250072159D-06 2 4 1 18 0.80558111162732D+00 -0.49477641588530D-06 3 4 1 18 -0.44828122852276D+00 -0.14721995102695D-06 1 5 1 18 0.10920925903866D+01 0.14296338312368D-01 2 5 1 18 0.24452075078458D+01 -0.47573476839379D-03 3 5 1 18 0.18828771588218D+00 -0.36654271339290D-01 1 6 1 18 -0.52646987880336D+00 -0.75686465898101D-01 2 6 1 18 0.30234462751217D-01 0.15440299694563D+00 3 6 1 18 0.27521155929143D+01 -0.27750239130723D-01 1 7 1 18 0.23532829639726D+01 0.12588627472331D-01 2 7 1 18 0.98619645269343D+00 0.16035416249388D-01 3 7 1 18 -0.18763038654301D+00 0.35432183064905D-01 1 8 1 18 -0.58641202826266D+00 -0.42434203301506D-01 2 8 1 18 -0.23857555948405D+00 0.34463920729137D-01 3 8 1 18 -0.34007399469184D+01 0.13686640135047D-02 1 9 1 18 -0.21269098163499D+00 0.33975177656675D-06 2 9 1 18 -0.62889356407283D+00 0.71669097845303D-07 3 9 1 18 -0.25394093574743D+01 -0.76542898589672D-06 1 10 1 18 0.42909725326248D+00 -0.96571024830966D-02 2 10 1 18 -0.14405737890598D+01 0.39946960163877D-01 3 10 1 18 0.28203925227030D+01 0.10126640308881D+00 1 11 1 18 -0.11157902312848D+01 0.13787637790905D-05 2 11 1 18 0.97020788419841D+00 0.86399122238716D-07 3 11 1 18 0.36935237640410D+01 0.89646541506831D-06 1 12 1 18 0.77312347167351D-02 -0.65404867931901D-01 2 12 1 18 0.66226670866072D+00 0.25004731472479D-01 3 12 1 18 -0.30034371241651D+01 0.10880137817197D+00 1 13 1 18 -0.24784053886372D-14 -0.62373851351272D-06 2 13 1 18 0.11571846304922D+01 -0.58739071820368D-06 3 13 1 18 0.17941074822631D+01 -0.10478331306708D-05 1 14 1 18 -0.10812892896018D-13 -0.72400695201119D-02 2 14 1 18 -0.10951670448984D+01 -0.10518327720641D-02 3 14 1 18 -0.30181734532868D+00 -0.91617708047416D-02 1 15 1 18 0.10932815519766D-14 -0.20694161299029D-06 2 15 1 18 -0.72759334883853D-01 0.55423410951155D-02 3 15 1 18 -0.27389608057287D+00 -0.52918730905630D-02 1 16 1 18 -0.60746088713776D-01 0.18602070477651D-06 2 16 1 18 0.21267822786140D-01 -0.62947218400917D-02 3 16 1 18 0.66628016534021D+00 -0.31173506039870D-02 1 17 1 18 -0.38758753471713D+01 -0.17637703836533D-02 2 17 1 18 0.44020035000303D+01 -0.32984240192998D-02 3 17 1 18 -0.18227334375484D+00 0.19277344790835D-02 1 18 1 18 0.13898122635327D+02 0.00000000000000D+00 2 18 1 18 -0.64220335112204D+01 -0.18823880084437D+00 3 18 1 18 0.12557350990268D+01 0.16706243204776D+00 1 19 1 18 0.24484108676584D+00 0.37757309022704D-15 2 19 1 18 0.59365354065444D-01 0.48959010346579D-06 3 19 1 18 -0.77639775635177D-01 -0.82538685869471D-07 1 20 1 18 -0.33055517794708D-14 -0.78881406176688D-01 2 20 1 18 -0.59774075657535D-01 0.91889221273374D-01 3 20 1 18 -0.33094596257340D+00 -0.23244209361997D-02 1 1 2 18 -0.68712473251339D+00 0.19760182082258D-06 2 1 2 18 0.64763245546005D+00 0.26415742414275D-06 3 1 2 18 0.76341655697845D+00 0.17317798991693D-06 1 2 2 18 -0.14641252210913D+00 -0.16744411954476D-01 2 2 2 18 0.15713437869598D+01 0.18478138079715D-02 3 2 2 18 0.33257813959716D+00 -0.17228537222243D-02 1 3 2 18 -0.78714711650425D+00 0.15604524917166D-01 2 3 2 18 0.29452192971430D+00 -0.42432835830066D-02 3 3 2 18 -0.55375110754944D+00 0.17221670951054D-03 1 4 2 18 0.95320318876923D+00 -0.36389309327424D-06 2 4 2 18 -0.88299137538413D+00 0.28187504241676D-06 3 4 2 18 -0.73874028938631D+00 -0.83831003603463D-07 1 5 2 18 0.12478087830557D+01 -0.19355587853700D-01 2 5 2 18 0.23168943120459D+01 0.71500529342244D-02 3 5 2 18 -0.70566199330318D+00 0.54515837216350D-01 1 6 2 18 0.50224851509074D+00 0.13530109371527D+00 2 6 2 18 -0.30975812792412D+00 -0.15408726080424D+00 3 6 2 18 -0.35041370877415D+01 0.52902086903695D-02 1 7 2 18 0.21831596540526D+01 -0.12385679687658D-01 2 7 2 18 0.12926774104380D+01 -0.71916339247607D-02 3 7 2 18 0.37979157642182D+00 -0.42470155283098D-01 1 8 2 18 0.21890341311866D+00 0.57975041970884D-01 2 8 2 18 0.54144292836906D-01 -0.28275102359186D-01 3 8 2 18 0.27496806876738D+01 -0.76488031477955D-02 1 9 2 18 -0.50301179776289D+00 0.30339873672709D-06 2 9 2 18 0.43731681324673D+00 -0.34735604699660D-07 3 9 2 18 0.38820587360795D+01 0.11441304107975D-05 1 10 2 18 -0.12523540326113D+01 0.34949201832730D-01 2 10 2 18 0.57632070221865D+00 -0.41313829727514D-01 3 10 2 18 -0.32400070915947D+01 -0.11623328030852D+00 1 11 2 18 0.14170005718490D+01 -0.45216338134663D-06 2 11 2 18 -0.14147966551011D+00 0.31064300019545D-06 3 11 2 18 -0.26510297703738D+01 -0.63581639032319D-06 1 12 2 18 0.67229068221358D+00 0.74916605308276D-01 2 12 2 18 -0.32247399400846D+00 -0.11508575079097D-01 3 12 2 18 0.30802612353887D+01 -0.15818131896180D+00 1 13 2 18 0.11571846304922D+01 0.58739072002615D-06 2 13 2 18 0.62975255369375D-15 -0.97932800343585D-09 3 13 2 18 -0.46580936432627D+00 0.85640432239596D-06 1 14 2 18 -0.10951670448984D+01 0.10518327720692D-02 2 14 2 18 -0.46224208408531D-13 0.17783925419804D-01 3 14 2 18 -0.19338028945544D-01 -0.41669660085317D-01 1 15 2 18 -0.72760036737823D-01 0.55433092606051D-02 2 15 2 18 -0.14444914252437D-14 0.50448504404923D-06 3 15 2 18 0.80043183253720D+00 -0.52000824587479D-02 1 16 2 18 -0.21268002343364D-01 -0.62951649308073D-02 2 16 2 18 -0.17866896526106D-01 -0.33254049886392D-06 3 16 2 18 -0.37430864985462D+00 -0.54614196068627D-02 1 17 2 18 0.44020031284309D+01 -0.32989355973458D-02 2 17 2 18 -0.41216323764819D+01 0.60781501884994D-02 3 17 2 18 -0.20867294665193D+00 -0.89193357668966D-03 1 18 2 18 -0.64220402558008D+01 0.18823887449866D+00 2 18 2 18 0.15298044818349D+02 0.00000000000000D+00 3 18 2 18 0.19826211583795D+01 0.19948869321804D+00 1 19 2 18 0.59365354065444D-01 -0.48959010295646D-06 2 19 2 18 0.14475652471388D+00 -0.77634587485358D-16 3 19 2 18 -0.82639870750703D-01 0.13401808662665D-06 1 20 2 18 0.59774075657533D-01 0.91889221273374D-01 2 20 2 18 -0.32049451927928D-14 -0.10716488379770D+00 3 20 2 18 -0.34606075502576D+00 0.36465383468235D-02 1 1 3 18 0.11902835930204D+01 -0.22901719213410D-06 2 1 3 18 0.10013965666997D+01 -0.45336947240118D-06 3 1 3 18 -0.48038748013563D+00 -0.91572769342554D-07 1 2 3 18 0.23054956166575D+00 0.15504920856737D-02 2 2 3 18 0.52264722169620D+00 0.33296080090522D-02 3 2 3 18 0.20724822922069D+01 0.20038783343407D-01 1 3 3 18 -0.70042568642654D+00 0.14423150740342D-02 2 3 3 18 -0.78834034603555D+00 -0.20194645910251D-02 3 3 3 18 -0.38453250910959D+00 -0.49275599810524D-02 1 4 3 18 -0.84564392342532D+00 -0.13861387333747D-06 2 4 3 18 -0.67932441581483D+00 -0.11489534793069D-07 3 4 3 18 -0.33565238386579D-02 0.28322019773244D-06 1 5 3 18 -0.87225283577176D+00 -0.27747237711740D-01 2 5 3 18 0.12362503312940D+01 0.45313182285093D-01 3 5 3 18 0.36602739406620D+01 0.34764508930433D-01 1 6 3 18 0.45745096942818D+00 0.32192453776105D-02 2 6 3 18 -0.61507586914082D+00 -0.19382285042191D-01 3 6 3 18 -0.61614090844337D+00 0.13064924968600D+00 1 7 3 18 0.80773945037081D+00 0.34943424899295D-01 2 7 3 18 -0.13596895178967D+01 -0.17040815752443D-01 3 7 3 18 0.39092799049791D+01 0.28119940517960D-01 1 8 3 18 -0.62705904656789D+00 -0.82421881349834D-02 2 8 3 18 0.41659732056841D+00 0.49748253466815D-02 3 8 3 18 -0.17035920554809D+00 0.30749743633634D-01 1 9 3 18 -0.89382868931026D+00 0.11804576205644D-06 2 9 3 18 0.17398153256030D+01 -0.62230760487706D-06 3 9 3 18 0.31426422397135D+01 0.84733985412894D-06 1 10 3 18 0.13654668846558D+01 0.25767336813658D-01 2 10 3 18 -0.17119795773385D+01 -0.42289856139803D-01 3 10 3 18 0.72545834190352D+00 0.89816573984335D-01 1 11 3 18 0.21235578482968D+01 -0.87549349713275D-06 2 11 3 18 -0.11137091419462D+01 0.98587184036766D-06 3 11 3 18 -0.97946356471336D+00 0.30786077996732D-06 1 12 3 18 -0.11949136020980D+01 0.17919309964118D-01 2 12 3 18 0.13480213827395D+01 -0.85386752395592D-03 3 12 3 18 -0.26428759172736D+01 0.20007309666097D+00 1 13 3 18 0.17941074822631D+01 0.10478331382584D-05 2 13 3 18 0.46580936432626D+00 0.85640432239606D-06 3 13 3 18 0.63301076517089D-14 -0.59573347628659D-06 1 14 3 18 -0.30181734532868D+00 0.91617708047416D-02 2 14 3 18 0.19338028945534D-01 -0.41669660085317D-01 3 14 3 18 0.66097834517594D-15 0.67656815809749D-02 1 15 3 18 0.27389758526281D+00 0.52922061447548D-02 2 15 3 18 0.80043388900747D+00 -0.51985952631492D-02 3 15 3 18 -0.22032038672733D-14 -0.38876851283610D-07 1 16 3 18 0.66628175574441D+00 0.31164528908424D-02 2 16 3 18 0.37430983841762D+00 -0.54623506006126D-02 3 16 3 18 -0.17632798563093D+00 0.60543745053412D-07 1 17 3 18 -0.18227524897193D+00 0.19268627743447D-02 2 17 3 18 -0.20867042954992D+00 -0.89241513345057D-03 3 17 3 18 -0.10300521199797D+01 -0.95008581194221D-02 1 18 3 18 0.12557128577607D+01 -0.16706222771616D+00 2 18 3 18 0.19826484447409D+01 -0.19948817466567D+00 3 18 3 18 0.15144686983050D+02 0.00000000000000D+00 1 19 3 18 0.77639775635159D-01 -0.82538685870338D-07 2 19 3 18 0.82639870750700D-01 0.13401808662839D-06 3 19 3 18 -0.89098768490708D+00 -0.68960000107702D-15 1 20 3 18 -0.33094596257340D+00 0.23244209361988D-02 2 20 3 18 -0.34606075502576D+00 -0.36465383468231D-02 3 20 3 18 -0.14364337953480D-13 0.56333672833066D-01 1 1 1 19 -0.53789782066791D+00 0.15056873131803D-06 2 1 1 19 0.71678759202771D+00 -0.58517302486157D-07 3 1 1 19 0.11674946922127D+01 -0.43632831098885D-07 1 2 1 19 0.11682226319502D+01 -0.87286015242522D-02 2 2 1 19 -0.51689538388875D-01 -0.33029634723422D-01 3 2 1 19 -0.67078264993130D+00 0.97105436486452D-02 1 3 1 19 -0.40053332053904D+00 0.13838444397698D-01 2 3 1 19 0.78632530987332D+00 -0.63106206074919D-02 3 3 1 19 -0.61948808567314D+00 -0.29798087047823D-02 1 4 1 19 -0.84163057818195D+00 0.74880249934769D-06 2 4 1 19 0.80558111162739D+00 -0.49477641389723D-06 3 4 1 19 0.44828122852277D+00 0.14721995042119D-06 1 5 1 19 0.52646987880336D+00 0.75686465898101D-01 2 5 1 19 -0.30234462751213D-01 -0.15440299694563D+00 3 5 1 19 0.27521155929143D+01 -0.27750239130724D-01 1 6 1 19 -0.10920925903866D+01 -0.14296338312364D-01 2 6 1 19 -0.24452075078457D+01 0.47573476837053D-03 3 6 1 19 0.18828771588219D+00 -0.36654271339285D-01 1 7 1 19 0.58641202826266D+00 0.42434203301506D-01 2 7 1 19 0.23857555948405D+00 -0.34463920729138D-01 3 7 1 19 -0.34007399469184D+01 0.13686640135050D-02 1 8 1 19 -0.23532829639726D+01 -0.12588627472313D-01 2 8 1 19 -0.98619645269341D+00 -0.16035416249412D-01 3 8 1 19 -0.18763038654303D+00 0.35432183064897D-01 1 9 1 19 0.21269098163498D+00 -0.33975177734075D-06 2 9 1 19 0.62889356407282D+00 -0.71669098966353D-07 3 9 1 19 -0.25394093574743D+01 -0.76542898417845D-06 1 10 1 19 0.42909725326249D+00 -0.96571024830972D-02 2 10 1 19 -0.14405737890597D+01 0.39946960163875D-01 3 10 1 19 -0.28203925227030D+01 -0.10126640308880D+00 1 11 1 19 -0.11157902312848D+01 0.13787637789737D-05 2 11 1 19 0.97020788419840D+00 0.86399122116142D-07 3 11 1 19 -0.36935237640410D+01 -0.89646541583220D-06 1 12 1 19 -0.77312347167364D-02 0.65404867931902D-01 2 12 1 19 -0.66226670866072D+00 -0.25004731472477D-01 3 12 1 19 -0.30034371241651D+01 0.10880137817197D+00 1 13 1 19 0.60746088713778D-01 -0.18602070480126D-06 2 13 1 19 -0.21267822786138D-01 0.62947218400915D-02 3 13 1 19 0.66628016534021D+00 -0.31173506039872D-02 1 14 1 19 -0.17772984948064D-14 -0.20694161311322D-06 2 14 1 19 -0.72759334883859D-01 0.55423410951158D-02 3 14 1 19 0.27389608057287D+00 0.52918730905633D-02 1 15 1 19 -0.68160904308839D-14 -0.72400695201127D-02 2 15 1 19 -0.10951670448984D+01 -0.10518327720639D-02 3 15 1 19 0.30181734532868D+00 0.91617708047418D-02 1 16 1 19 -0.55152235282014D-14 0.62373851381735D-06 2 16 1 19 -0.11571846304922D+01 0.58739072005129D-06 3 16 1 19 0.17941074822631D+01 -0.10478331362823D-05 1 17 1 19 0.40854724985373D-14 0.78881406176687D-01 2 17 1 19 0.59774075657537D-01 -0.91889221273374D-01 3 17 1 19 -0.33094596257340D+00 -0.23244209361997D-02 1 18 1 19 0.24484108676584D+00 -0.37757309022704D-15 2 18 1 19 0.59365354065444D-01 0.48959010295646D-06 3 18 1 19 0.77639775635159D-01 0.82538685870338D-07 1 19 1 19 0.13898122635327D+02 0.00000000000000D+00 2 19 1 19 -0.64220335112204D+01 -0.18823880084437D+00 3 19 1 19 -0.12557350990268D+01 -0.16706243204776D+00 1 20 1 19 0.38758753471713D+01 0.17637703836534D-02 2 20 1 19 -0.44020035000303D+01 0.32984240193023D-02 3 20 1 19 -0.18227334375486D+00 0.19277344790839D-02 1 1 2 19 0.68712473251340D+00 -0.19760181900191D-06 2 1 2 19 -0.64763245546005D+00 -0.26415742757879D-06 3 1 2 19 0.76341655697846D+00 0.17317799575967D-06 1 2 2 19 -0.14641252210920D+00 -0.16744411954475D-01 2 2 2 19 0.15713437869598D+01 0.18478138079722D-02 3 2 2 19 -0.33257813959704D+00 0.17228537222240D-02 1 3 2 19 0.78714711650424D+00 -0.15604524917164D-01 2 3 2 19 -0.29452192971430D+00 0.42432835830074D-02 3 3 2 19 -0.55375110754946D+00 0.17221670950804D-03 1 4 2 19 0.95320318876932D+00 -0.36389309128617D-06 2 4 2 19 -0.88299137538413D+00 0.28187504004027D-06 3 4 2 19 0.73874028938633D+00 0.83831002725557D-07 1 5 2 19 -0.50224851509074D+00 -0.13530109371527D+00 2 5 2 19 0.30975812792411D+00 0.15408726080423D+00 3 5 2 19 -0.35041370877414D+01 0.52902086903704D-02 1 6 2 19 -0.12478087830556D+01 0.19355587853677D-01 2 6 2 19 -0.23168943120459D+01 -0.71500529342062D-02 3 6 2 19 -0.70566199330317D+00 0.54515837216339D-01 1 7 2 19 -0.21890341311866D+00 -0.57975041970885D-01 2 7 2 19 -0.54144292836902D-01 0.28275102359183D-01 3 7 2 19 0.27496806876738D+01 -0.76488031477959D-02 1 8 2 19 -0.21831596540526D+01 0.12385679687634D-01 2 8 2 19 -0.12926774104380D+01 0.71916339247649D-02 3 8 2 19 0.37979157642182D+00 -0.42470155283092D-01 1 9 2 19 0.50301179776288D+00 -0.30339873785508D-06 2 9 2 19 -0.43731681324672D+00 0.34735605196261D-07 3 9 2 19 0.38820587360795D+01 0.11441304070161D-05 1 10 2 19 -0.12523540326113D+01 0.34949201832728D-01 2 10 2 19 0.57632070221865D+00 -0.41313829727514D-01 3 10 2 19 0.32400070915947D+01 0.11623328030852D+00 1 11 2 19 0.14170005718490D+01 -0.45216338144145D-06 2 11 2 19 -0.14147966551011D+00 0.31064300008694D-06 3 11 2 19 0.26510297703737D+01 0.63581638944268D-06 1 12 2 19 -0.67229068221358D+00 -0.74916605308274D-01 2 12 2 19 0.32247399400848D+00 0.11508575079098D-01 3 12 2 19 0.30802612353887D+01 -0.15818131896180D+00 1 13 2 19 0.21268002343365D-01 0.62951649308071D-02 2 13 2 19 0.17866896526107D-01 0.33254049877796D-06 3 13 2 19 -0.37430864985463D+00 -0.54614196068627D-02 1 14 2 19 -0.72760036737828D-01 0.55433092606054D-02 2 14 2 19 -0.30902658937396D-14 0.50448504418972D-06 3 14 2 19 -0.80043183253721D+00 0.52000824587481D-02 1 15 2 19 -0.10951670448984D+01 0.10518327720694D-02 2 15 2 19 -0.38230602631230D-13 0.17783925419803D-01 3 15 2 19 0.19338028945537D-01 0.41669660085316D-01 1 16 2 19 -0.11571846304922D+01 -0.58739071817854D-06 2 16 2 19 -0.26281668423282D-14 0.97932786171287D-09 3 16 2 19 -0.46580936432626D+00 0.85640432221430D-06 1 17 2 19 -0.59774075657532D-01 -0.91889221273374D-01 2 17 2 19 0.40518362336481D-14 0.10716488379770D+00 3 17 2 19 -0.34606075502577D+00 0.36465383468236D-02 1 18 2 19 0.59365354065444D-01 -0.48959010346579D-06 2 18 2 19 0.14475652471388D+00 0.77634587485358D-16 3 18 2 19 0.82639870750700D-01 -0.13401808662839D-06 1 19 2 19 -0.64220402558008D+01 0.18823887449866D+00 2 19 2 19 0.15298044818349D+02 0.00000000000000D+00 3 19 2 19 -0.19826211583794D+01 -0.19948869321804D+00 1 20 2 19 -0.44020031284309D+01 0.32989355973483D-02 2 20 2 19 0.41216323764819D+01 -0.60781501884988D-02 3 20 2 19 -0.20867294665193D+00 -0.89193357668905D-03 1 1 3 19 0.11902835930204D+01 -0.22901718511439D-06 2 1 3 19 0.10013965666997D+01 -0.45336946655671D-06 3 1 3 19 0.48038748013563D+00 0.91572779890746D-07 1 2 3 19 -0.23054956166567D+00 -0.15504920856734D-02 2 2 3 19 -0.52264722169608D+00 -0.33296080090524D-02 3 2 3 19 0.20724822922070D+01 0.20038783343402D-01 1 3 3 19 -0.70042568642656D+00 0.14423150740314D-02 2 3 3 19 -0.78834034603555D+00 -0.20194645910276D-02 3 3 3 19 0.38453250910959D+00 0.49275599810554D-02 1 4 3 19 0.84564392342531D+00 0.13861387273258D-06 2 4 3 19 0.67932441581486D+00 0.11489533914405D-07 3 4 3 19 -0.33565238387290D-02 0.28322019867081D-06 1 5 3 19 0.45745096942820D+00 0.32192453776100D-02 2 5 3 19 -0.61507586914081D+00 -0.19382285042190D-01 3 5 3 19 0.61614090844334D+00 -0.13064924968600D+00 1 6 3 19 -0.87225283577175D+00 -0.27747237711735D-01 2 6 3 19 0.12362503312940D+01 0.45313182285081D-01 3 6 3 19 -0.36602739406620D+01 -0.34764508930455D-01 1 7 3 19 -0.62705904656788D+00 -0.82421881349830D-02 2 7 3 19 0.41659732056845D+00 0.49748253466811D-02 3 7 3 19 0.17035920554807D+00 -0.30749743633631D-01 1 8 3 19 0.80773945037079D+00 0.34943424899288D-01 2 8 3 19 -0.13596895178967D+01 -0.17040815752437D-01 3 8 3 19 -0.39092799049791D+01 -0.28119940517980D-01 1 9 3 19 -0.89382868931026D+00 0.11804576377470D-06 2 9 3 19 0.17398153256030D+01 -0.62230760865154D-06 3 9 3 19 -0.31426422397135D+01 -0.84733984994769D-06 1 10 3 19 -0.13654668846558D+01 -0.25767336813658D-01 2 10 3 19 0.17119795773385D+01 0.42289856139805D-01 3 10 3 19 0.72545834190357D+00 0.89816573984335D-01 1 11 3 19 -0.21235578482968D+01 0.87549349641743D-06 2 11 3 19 0.11137091419462D+01 -0.98587184124817D-06 3 11 3 19 -0.97946356471339D+00 0.30786078040245D-06 1 12 3 19 -0.11949136020981D+01 0.17919309964120D-01 2 12 3 19 0.13480213827395D+01 -0.85386752395923D-03 3 12 3 19 0.26428759172736D+01 -0.20007309666097D+00 1 13 3 19 0.66628175574442D+00 0.31164528908422D-02 2 13 3 19 0.37430983841762D+00 -0.54623506006127D-02 3 13 3 19 0.17632798563093D+00 -0.60543745077455D-07 1 14 3 19 -0.27389758526280D+00 -0.52922061447546D-02 2 14 3 19 -0.80043388900748D+00 0.51985952631494D-02 3 14 3 19 0.27024081020516D-14 -0.38876851161739D-07 1 15 3 19 0.30181734532868D+00 -0.91617708047414D-02 2 15 3 19 -0.19338028945541D-01 0.41669660085316D-01 3 15 3 19 -0.33358239081999D-14 0.67656815809761D-02 1 16 3 19 0.17941074822631D+01 0.10478331326468D-05 2 16 3 19 0.46580936432627D+00 0.85640432221441D-06 3 16 3 19 -0.43318283787349D-14 0.59573347608598D-06 1 17 3 19 -0.33094596257341D+00 0.23244209361988D-02 2 17 3 19 -0.34606075502577D+00 -0.36465383468230D-02 3 17 3 19 0.69007383525579D-14 -0.56333672833066D-01 1 18 3 19 -0.77639775635177D-01 0.82538685869471D-07 2 18 3 19 -0.82639870750703D-01 -0.13401808662665D-06 3 18 3 19 -0.89098768490708D+00 0.68960000107702D-15 1 19 3 19 -0.12557128577608D+01 0.16706222771616D+00 2 19 3 19 -0.19826484447408D+01 0.19948817466567D+00 3 19 3 19 0.15144686983049D+02 0.00000000000000D+00 1 20 3 19 -0.18227524897195D+00 0.19268627743452D-02 2 20 3 19 -0.20867042954992D+00 -0.89241513344996D-03 3 20 3 19 0.10300521199797D+01 0.95008581194214D-02 1 1 1 20 -0.11682226319502D+01 0.87286015242546D-02 2 1 1 20 0.51689538388818D-01 0.33029634723406D-01 3 1 1 20 0.67078264993154D+00 -0.97105436486168D-02 1 2 1 20 0.53789782066794D+00 -0.15056873215730D-06 2 2 1 20 -0.71678759202774D+00 0.58517304635453D-07 3 2 1 20 -0.11674946922127D+01 0.43632837140354D-07 1 3 1 20 -0.84163057818196D+00 0.74880250104443D-06 2 3 1 20 0.80558111162734D+00 -0.49477641465277D-06 3 3 1 20 0.44828122852282D+00 0.14721995116426D-06 1 4 1 20 -0.40053332053905D+00 0.13838444397699D-01 2 4 1 20 0.78632530987332D+00 -0.63106206074922D-02 3 4 1 20 -0.61948808567313D+00 -0.29798087047826D-02 1 5 1 20 0.52646987880337D+00 0.75686465898100D-01 2 5 1 20 -0.30234462751208D-01 -0.15440299694563D+00 3 5 1 20 0.27521155929143D+01 -0.27750239130724D-01 1 6 1 20 0.10920925903866D+01 0.14296338312368D-01 2 6 1 20 0.24452075078460D+01 -0.47573476839427D-03 3 6 1 20 -0.18828771588214D+00 0.36654271339289D-01 1 7 1 20 0.58641202826266D+00 0.42434203301506D-01 2 7 1 20 0.23857555948406D+00 -0.34463920729137D-01 3 7 1 20 -0.34007399469184D+01 0.13686640135066D-02 1 8 1 20 0.23532829639729D+01 0.12588627472327D-01 2 8 1 20 0.98619645269335D+00 0.16035416249388D-01 3 8 1 20 0.18763038654266D+00 -0.35432183064916D-01 1 9 1 20 0.42909725326250D+00 -0.96571024830942D-02 2 9 1 20 -0.14405737890597D+01 0.39946960163870D-01 3 9 1 20 -0.28203925227030D+01 -0.10126640308881D+00 1 10 1 20 0.21269098163496D+00 -0.33975177797532D-06 2 10 1 20 0.62889356407283D+00 -0.71669098987809D-07 3 10 1 20 -0.25394093574743D+01 -0.76542898377274D-06 1 11 1 20 -0.77312347167346D-02 0.65404867931901D-01 2 11 1 20 -0.66226670866071D+00 -0.25004731472480D-01 3 11 1 20 -0.30034371241650D+01 0.10880137817197D+00 1 12 1 20 -0.11157902312848D+01 0.13787637806473D-05 2 12 1 20 0.97020788419843D+00 0.86399122403106D-07 3 12 1 20 -0.36935237640409D+01 -0.89646541689602D-06 1 13 1 20 -0.23777598108147D-14 -0.20694161292244D-06 2 13 1 20 -0.72759334883857D-01 0.55423410951156D-02 3 13 1 20 0.27389608057287D+00 0.52918730905634D-02 1 14 1 20 0.60746088713779D-01 -0.18602070472920D-06 2 14 1 20 -0.21267822786136D-01 0.62947218400913D-02 3 14 1 20 0.66628016534021D+00 -0.31173506039871D-02 1 15 1 20 -0.18469641454947D-13 0.62373852328222D-06 2 15 1 20 -0.11571846304922D+01 0.58739071720258D-06 3 15 1 20 0.17941074822631D+01 -0.10478331326451D-05 1 16 1 20 -0.15077013485092D-13 -0.72400695201143D-02 2 16 1 20 -0.10951670448984D+01 -0.10518327720667D-02 3 16 1 20 0.30181734532867D+00 0.91617708047408D-02 1 17 1 20 0.24484108676582D+00 0.76590336316981D-15 2 17 1 20 0.59365354065442D-01 0.48959010292706D-06 3 17 1 20 0.77639775635164D-01 0.82538685648196D-07 1 18 1 20 -0.33055517794708D-14 0.78881406176688D-01 2 18 1 20 0.59774075657533D-01 -0.91889221273374D-01 3 18 1 20 -0.33094596257340D+00 -0.23244209361988D-02 1 19 1 20 0.38758753471713D+01 0.17637703836511D-02 2 19 1 20 -0.44020035000303D+01 0.32984240192937D-02 3 19 1 20 -0.18227334375486D+00 0.19277344790815D-02 1 20 1 20 0.13898122635327D+02 0.00000000000000D+00 2 20 1 20 -0.64220335112201D+01 -0.18823880084437D+00 3 20 1 20 -0.12557350990271D+01 -0.16706243204776D+00 1 1 2 20 0.14641252210914D+00 0.16744411954459D-01 2 1 2 20 -0.15713437869597D+01 -0.18478138079828D-02 3 1 2 20 0.33257813959707D+00 -0.17228537221866D-02 1 2 2 20 -0.68712473251343D+00 0.19760182115988D-06 2 2 2 20 0.64763245545997D+00 0.26415742363578D-06 3 2 2 20 -0.76341655697859D+00 -0.17317799085122D-06 1 3 2 20 0.95320318876926D+00 -0.36389309204171D-06 2 3 2 20 -0.88299137538414D+00 0.28187504160058D-06 3 3 2 20 0.73874028938633D+00 0.83831001847962D-07 1 4 2 20 0.78714711650424D+00 -0.15604524917164D-01 2 4 2 20 -0.29452192971431D+00 0.42432835830086D-02 3 4 2 20 -0.55375110754945D+00 0.17221670950822D-03 1 5 2 20 -0.50224851509074D+00 -0.13530109371527D+00 2 5 2 20 0.30975812792412D+00 0.15408726080424D+00 3 5 2 20 -0.35041370877415D+01 0.52902086903709D-02 1 6 2 20 0.12478087830559D+01 -0.19355587853701D-01 2 6 2 20 0.23168943120457D+01 0.71500529342222D-02 3 6 2 20 0.70566199330312D+00 -0.54515837216350D-01 1 7 2 20 -0.21890341311866D+00 -0.57975041970885D-01 2 7 2 20 -0.54144292836906D-01 0.28275102359184D-01 3 7 2 20 0.27496806876738D+01 -0.76488031477965D-02 1 8 2 20 0.21831596540525D+01 -0.12385679687659D-01 2 8 2 20 0.12926774104379D+01 -0.71916339247592D-02 3 8 2 20 -0.37979157642162D+00 0.42470155283097D-01 1 9 2 20 -0.12523540326113D+01 0.34949201832723D-01 2 9 2 20 0.57632070221865D+00 -0.41313829727513D-01 3 9 2 20 0.32400070915946D+01 0.11623328030853D+00 1 10 2 20 0.50301179776289D+00 -0.30339873786960D-06 2 10 2 20 -0.43731681324674D+00 0.34735605227466D-07 3 10 2 20 0.38820587360794D+01 0.11441304070616D-05 1 11 2 20 -0.67229068221357D+00 -0.74916605308277D-01 2 11 2 20 0.32247399400851D+00 0.11508575079097D-01 3 11 2 20 0.30802612353886D+01 -0.15818131896180D+00 1 12 2 20 0.14170005718490D+01 -0.45216338116836D-06 2 12 2 20 -0.14147966551015D+00 0.31064300006821D-06 3 12 2 20 0.26510297703738D+01 0.63581638963204D-06 1 13 2 20 -0.72760036737826D-01 0.55433092606053D-02 2 13 2 20 0.31471085951350D-15 0.50448504462324D-06 3 13 2 20 -0.80043183253722D+00 0.52000824587469D-02 1 14 2 20 0.21268002343368D-01 0.62951649308069D-02 2 14 2 20 0.17866896526108D-01 0.33254049870440D-06 3 14 2 20 -0.37430864985462D+00 -0.54614196068629D-02 1 15 2 20 -0.11571846304922D+01 -0.58739072102725D-06 2 15 2 20 0.66101362520663D-14 0.97932568458709D-09 3 15 2 20 -0.46580936432626D+00 0.85640432112256D-06 1 16 2 20 -0.10951670448984D+01 0.10518327720666D-02 2 16 2 20 0.24825435097984D-13 0.17783925419816D-01 3 16 2 20 0.19338028945536D-01 0.41669660085317D-01 1 17 2 20 0.59365354065442D-01 -0.48959010349519D-06 2 17 2 20 0.14475652471388D+00 0.16643923824197D-15 3 17 2 20 0.82639870750702D-01 -0.13401808571652D-06 1 18 2 20 -0.59774075657535D-01 -0.91889221273374D-01 2 18 2 20 -0.32049451927928D-14 0.10716488379770D+00 3 18 2 20 -0.34606075502576D+00 0.36465383468231D-02 1 19 2 20 -0.44020031284309D+01 0.32989355973398D-02 2 19 2 20 0.41216323764819D+01 -0.60781501885017D-02 3 19 2 20 -0.20867294665193D+00 -0.89193357669244D-03 1 20 2 20 -0.64220402558005D+01 0.18823887449866D+00 2 20 2 20 0.15298044818348D+02 0.00000000000000D+00 3 20 2 20 -0.19826211583796D+01 -0.19948869321804D+00 1 1 3 20 0.23054956166592D+00 0.15504920857018D-02 2 1 3 20 0.52264722169611D+00 0.33296080090898D-02 3 1 3 20 -0.20724822922071D+01 -0.20038783343432D-01 1 2 3 20 -0.11902835930204D+01 0.22901719115413D-06 2 2 3 20 -0.10013965666998D+01 0.45336947146516D-06 3 2 3 20 -0.48038748013562D+00 -0.91572769107181D-07 1 3 3 20 0.84564392342537D+00 0.13861387347565D-06 2 3 3 20 0.67932441581486D+00 0.11489533036809D-07 3 3 3 20 -0.33565238387041D-02 0.28322019652282D-06 1 4 3 20 -0.70042568642655D+00 0.14423150740312D-02 2 4 3 20 -0.78834034603554D+00 -0.20194645910274D-02 3 4 3 20 0.38453250910956D+00 0.49275599810559D-02 1 5 3 20 0.45745096942822D+00 0.32192453776100D-02 2 5 3 20 -0.61507586914082D+00 -0.19382285042190D-01 3 5 3 20 0.61614090844330D+00 -0.13064924968600D+00 1 6 3 20 0.87225283577179D+00 0.27747237711738D-01 2 6 3 20 -0.12362503312941D+01 -0.45313182285093D-01 3 6 3 20 0.36602739406624D+01 0.34764508930433D-01 1 7 3 20 -0.62705904656786D+00 -0.82421881349814D-02 2 7 3 20 0.41659732056846D+00 0.49748253466805D-02 3 7 3 20 0.17035920554806D+00 -0.30749743633633D-01 1 8 3 20 -0.80773945037116D+00 -0.34943424899307D-01 2 8 3 20 0.13596895178969D+01 0.17040815752442D-01 3 8 3 20 0.39092799049790D+01 0.28119940517958D-01 1 9 3 20 -0.13654668846558D+01 -0.25767336813663D-01 2 9 3 20 0.17119795773384D+01 0.42289856139812D-01 3 9 3 20 0.72545834190351D+00 0.89816573984339D-01 1 10 3 20 -0.89382868931025D+00 0.11804576418041D-06 2 10 3 20 0.17398153256030D+01 -0.62230760861991D-06 3 10 3 20 -0.31426422397134D+01 -0.84733984929492D-06 1 11 3 20 -0.11949136020980D+01 0.17919309964113D-01 2 11 3 20 0.13480213827395D+01 -0.85386752395266D-03 3 11 3 20 0.26428759172735D+01 -0.20007309666096D+00 1 12 3 20 -0.21235578482967D+01 0.87549349535361D-06 2 12 3 20 0.11137091419462D+01 -0.98587184105534D-06 3 12 3 20 -0.97946356471335D+00 0.30786078003681D-06 1 13 3 20 -0.27389758526281D+00 -0.52922061447545D-02 2 13 3 20 -0.80043388900749D+00 0.51985952631482D-02 3 13 3 20 -0.83808148981135D-15 -0.38876850218849D-07 1 14 3 20 0.66628175574442D+00 0.31164528908423D-02 2 14 3 20 0.37430983841763D+00 -0.54623506006128D-02 3 14 3 20 0.17632798563092D+00 -0.60543745101608D-07 1 15 3 20 0.17941074822631D+01 0.10478331362840D-05 2 15 3 20 0.46580936432626D+00 0.85640432112245D-06 3 15 3 20 0.22313420425123D-13 0.59573347221974D-06 1 16 3 20 0.30181734532867D+00 -0.91617708047425D-02 2 16 3 20 -0.19338028945542D-01 0.41669660085317D-01 3 16 3 20 -0.17543755246128D-13 0.67656815809712D-02 1 17 3 20 -0.77639775635171D-01 0.82538685647329D-07 2 17 3 20 -0.82639870750701D-01 -0.13401808571479D-06 3 17 3 20 -0.89098768490708D+00 0.90190908579682D-15 1 18 3 20 -0.33094596257340D+00 0.23244209361997D-02 2 18 3 20 -0.34606075502576D+00 -0.36465383468235D-02 3 18 3 20 -0.14364337953480D-13 -0.56333672833066D-01 1 19 3 20 -0.18227524897195D+00 0.19268627743428D-02 2 19 3 20 -0.20867042954993D+00 -0.89241513345336D-03 3 19 3 20 0.10300521199797D+01 0.95008581194241D-02 1 20 3 20 -0.12557128577610D+01 0.16706222771616D+00 2 20 3 20 -0.19826484447410D+01 0.19948817466567D+00 3 20 3 20 0.15144686983049D+02 0.00000000000000D+00
List of bloks and their characteristics
Total energy - # elements : 1
1st derivatives - # elements : 66
2nd derivatives (non-stat.) - # elements : 4401 qpt 0.00000000E+00 0.00000000E+00 0.00000000E+00 1.0
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 0.00000000E+00 0.00000000E+00 1.0
2nd derivatives (non-stat.) - # elements : 3600 qpt 0.00000000E+00 5.00000000E-01 0.00000000E+00 1.0
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 5.00000000E-01 0.00000000E+00 1.0
2nd derivatives (non-stat.) - # elements : 3600 qpt 0.00000000E+00 0.00000000E+00 5.00000000E-01 1.0
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 0.00000000E+00 5.00000000E-01 1.0
2nd derivatives (non-stat.) - # elements : 3600 qpt 0.00000000E+00 5.00000000E-01 5.00000000E-01 1.0
2nd derivatives (non-stat.) - # elements : 3600 qpt 5.00000000E-01 5.00000000E-01 5.00000000E-01 1.0
Before starting, you might to consider working in a different subdirectory than for the other lessons. Why not create “Work_latticeModel”?
The file ~abinit/tests/tutomultibinit/Input/tmulti1_1.files lists the file names and root names. You can copy it in the Work_latticeModel directory and look at this file content, you should see:
tutomulti1_1.abi tutomulti1_1.abo tmulti1_DDB
As mentioned in the guide of MULTIBINIT:
- “tutomulti1_1.abi” is the main input file
- “tutomulti1_1.abo” is the main output
- “tmulti1_DDB” is the DDB which contains the system definition and the list of the energy derivatives
It is now time to copy the file ~abinit/tests/tutomultibinit/Input/tmulti1_DDB and ~abinit/tests/tutomultibinit/Input/tmulti1_DDB in your Work_latticeModel directory. You should read carefully the input file:
#--------------------------------------------------------------- #Print the model into XML file: #--------------------------------------------------------------- prt_model = 1 #--------------------------------------------------------------- #Generation of the short-range interaction #--------------------------------------------------------------- ngqpt = 2 2 2 # Mesh of Q-points in the DDB #--------------------------------------------------------------- #Generation of the dipole-dipole interation #--------------------------------------------------------------- dipdip = 0 ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = multibinit #%% input_ddb = tmulti1_DDB #%% [files] #%% files_to_test = #%% tmulti1_1.abo, tolnlines = 0, tolabs = 0.0, tolrel = 0.0, fld_options = -easy; #%% tmulti1_1_model.xml, tolnlines = 0, tolabs = 0.0, tolrel = 0.0, fld_options = -easy; #%% [paral_info] #%% max_nprocs = 1 #%% [extra_info] #%% authors = A. MARTIN #%% keywords = Effective potential, multibinit #%% description = #%% read ddb and generate effective potential #%% topics = LatticeModel #%%<END TEST_INFO>
You should now run (it would take less than a second):
multibinit < tmulti1_1.files > tmulti1_1_stdout
The resulting output file, tmulti1_1.abo, should be similar to the one below.
.Version 9.3.1 of MULTIBINIT .(MPI version, prepared for a x86_64_linux_gnu9.3 computer)
.Copyright (C) 1998-2021 ABINIT group . MULTIBINIT comes with ABSOLUTELY NO WARRANTY. It is free software, and you are welcome to redistribute it under certain conditions (GNU General Public License, see ~abinit/COPYING or http://www.gnu.org/copyleft/gpl.txt).
ABINIT is a project of the Universite Catholique de Louvain, Corning Inc. and other collaborators, see ~abinit/doc/developers/contributors.txt . Please read https://docs.abinit.org/theory/acknowledgments for suggested acknowledgments of the ABINIT effort. For more information, see https://www.abinit.org .
.Starting date : Tue 10 Nov 2020. - ( at 22h19 )
- nproc = 1
================================================================================
Read the information in the reference structure in -/home/buildbot/ABINIT/alps_gnu_9.3_openmpi/trunk_rel2dev/tests/tutomultibinit/Input/tmulti1_DDB to initialize the multibinit input
================================================================================
-outvars_multibinit: echo values of input variables ----------------------
Flags : ifcflag 1 prt_model 1 strcpli -1 Miscellaneous information : asr 2 Interatomic Force Constants Inputs : dipdip 0 ifcana 0 ifcout 2000000 natifc 20 atifc 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Description of grid 1 : brav 1 ngqpt 2 2 2 nqshft 1 q1shft 0.00000000E+00 0.00000000E+00 0.00000000E+00 First list of wavevector (reduced coord.) : nph1l 1 qph1l 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.000E+00
================================================================================
Read the DDB information of the reference system and perform some checks
Real(R)+Recip(G) space primitive vectors, cartesian coordinates (Bohr,Bohr^-1): R(1)= 9.9768860 0.0000000 0.0000000 G(1)= 0.1002317 0.0000000 0.0000000 R(2)= 0.0000000 10.1890339 0.0000000 G(2)= 0.0000000 0.0981447 0.0000000 R(3)= 0.0000000 0.0000000 14.2034780 G(3)= 0.0000000 0.0000000 0.0704053 Unit cell volume ucvol= 1.4438521E+03 bohr^3 Angles (23,13,12)= 9.00000000E+01 9.00000000E+01 9.00000000E+01 degrees Now the whole DDB is in central memory
================================================================================
Extraction of the energy of the structure (unit: Hartree)
Energy = -5.785439537588E+02
================================================================================
Dielectric Tensor and Effective Charges
anaddb : Zero the imaginary part of the Dynamical Matrix at Gamma, and impose the ASR on the effective charges
The violation of the charge neutrality conditions by the effective charges is as follows : atom electric field displacement direction 1 1 -2.403821 0.000000 1 2 -0.000000 0.000000 1 3 0.000000 0.000000 2 1 0.000000 0.000000 2 2 -1.866807 0.000000 2 3 0.000000 0.000000 3 1 -0.000000 0.000000 3 2 0.000000 0.000000 3 3 -1.422018 0.000000
Effective charge tensors after imposition of the charge neutrality, and eventual restriction to some part : atom displacement 1 1 1.453433E+00 8.057855E-02 -1.665606E-17 1 2 3.625397E-02 1.481414E+00 -2.775558E-18 1 3 5.507747E-18 -1.387779E-18 1.570687E+00 2 1 1.453433E+00 8.057855E-02 -1.665606E-17 2 2 3.625397E-02 1.481414E+00 -2.775558E-18 2 3 5.507747E-18 -1.387779E-18 1.570687E+00 3 1 1.453433E+00 -8.057855E-02 -1.665606E-17 3 2 -3.625397E-02 1.481414E+00 -2.775558E-18 3 3 5.507747E-18 -1.387779E-18 1.570687E+00 4 1 1.453433E+00 -8.057855E-02 -1.665606E-17 4 2 -3.625397E-02 1.481414E+00 -2.775558E-18 4 3 5.507747E-18 -1.387779E-18 1.570687E+00 5 1 7.204839E+00 5.113710E-01 7.438256E-01 5 2 -6.876662E-01 7.319820E+00 -2.248431E-01 5 3 -9.178499E-01 -6.062353E-02 7.272712E+00 6 1 7.204839E+00 5.113710E-01 -7.438256E-01 6 2 -6.876662E-01 7.319820E+00 2.248431E-01 6 3 9.178499E-01 6.062353E-02 7.272712E+00 7 1 7.204839E+00 -5.113710E-01 -7.438256E-01 7 2 6.876662E-01 7.319820E+00 -2.248431E-01 7 3 9.178499E-01 -6.062353E-02 7.272712E+00 8 1 7.204839E+00 -5.113710E-01 7.438256E-01 8 2 6.876662E-01 7.319820E+00 2.248431E-01 8 3 -9.178499E-01 6.062353E-02 7.272712E+00 9 1 -1.939073E+00 -1.649446E-01 -1.665606E-17 9 2 2.208078E-02 -1.754548E+00 -2.775558E-18 9 3 5.507747E-18 -1.387779E-18 -5.118020E+00 10 1 -1.939073E+00 -1.649446E-01 -1.665606E-17 10 2 2.208078E-02 -1.754548E+00 -2.775558E-18 10 3 5.507747E-18 -1.387779E-18 -5.118020E+00 11 1 -1.939073E+00 1.649446E-01 -1.665606E-17 11 2 -2.208078E-02 -1.754548E+00 -2.775558E-18 11 3 5.507747E-18 -1.387779E-18 -5.118020E+00 12 1 -1.939073E+00 1.649446E-01 -1.665606E-17 12 2 -2.208078E-02 -1.754548E+00 -2.775558E-18 12 3 5.507747E-18 -1.387779E-18 -5.118020E+00 13 1 -3.359599E+00 -1.623543E+00 -2.028591E-04 13 2 -1.574037E+00 -3.523343E+00 -9.997223E-02 13 3 2.370312E-03 -7.357064E-02 -1.862689E+00 14 1 -3.359599E+00 -1.623543E+00 -2.028591E-04 14 2 -1.574037E+00 -3.523343E+00 -9.997223E-02 14 3 2.370312E-03 -7.357064E-02 -1.862689E+00 15 1 -3.359599E+00 -1.623543E+00 2.028591E-04 15 2 -1.574037E+00 -3.523343E+00 9.997223E-02 15 3 -2.370312E-03 7.357064E-02 -1.862689E+00 16 1 -3.359599E+00 -1.623543E+00 2.028591E-04 16 2 -1.574037E+00 -3.523343E+00 9.997223E-02 16 3 -2.370312E-03 7.357064E-02 -1.862689E+00 17 1 -3.359599E+00 1.623543E+00 2.028591E-04 17 2 1.574037E+00 -3.523343E+00 -9.997223E-02 17 3 -2.370312E-03 -7.357064E-02 -1.862689E+00 18 1 -3.359599E+00 1.623543E+00 2.028591E-04 18 2 1.574037E+00 -3.523343E+00 -9.997223E-02 18 3 -2.370312E-03 -7.357064E-02 -1.862689E+00 19 1 -3.359599E+00 1.623543E+00 -2.028591E-04 19 2 1.574037E+00 -3.523343E+00 9.997223E-02 19 3 2.370312E-03 7.357064E-02 -1.862689E+00 20 1 -3.359599E+00 1.623543E+00 -2.028591E-04 20 2 1.574037E+00 -3.523343E+00 9.997223E-02 20 3 2.370312E-03 7.357064E-02 -1.862689E+00 Now, the imaginary part of the dynamical matrix is zeroed
================================================================================
Extraction of the stress tensor (unit: GPa) and forces (unit: Ha/bohr)
Cartesian components of forces (hartree/bohr)
1 -0.30800054E-05 -0.10255015E-04 -0.31554436E-29 2 0.30800054E-05 0.10255015E-04 -0.15777218E-29 3 0.30800054E-05 -0.10255015E-04 0.00000000E+00 4 -0.30800054E-05 0.10255015E-04 0.00000000E+00 5 0.00000000E+00 0.00000000E+00 0.00000000E+00 6 0.00000000E+00 0.00000000E+00 0.00000000E+00 7 0.00000000E+00 0.00000000E+00 0.00000000E+00 8 0.00000000E+00 0.00000000E+00 0.00000000E+00 9 -0.19666635E-03 -0.33774783E-03 0.00000000E+00 10 0.19666635E-03 0.33774783E-03 0.00000000E+00 11 -0.19666635E-03 0.33774783E-03 0.00000000E+00 12 0.19666635E-03 -0.33774783E-03 0.00000000E+00 13 0.24085511E-03 -0.36542027E-03 0.13299857E-03 14 -0.24085511E-03 0.36542027E-03 -0.13299857E-03 15 -0.24085511E-03 0.36542027E-03 0.13299857E-03 16 0.24085511E-03 -0.36542027E-03 -0.13299857E-03 17 -0.24085511E-03 -0.36542027E-03 0.13299857E-03 18 0.24085511E-03 0.36542027E-03 -0.13299857E-03 19 0.24085511E-03 0.36542027E-03 0.13299857E-03 20 -0.24085511E-03 -0.36542027E-03 -0.13299857E-03
Cartesian components of stress tensor (hartree/bohr^3) sigma(1 1)= -1.27676002E-07 sigma(3 2)= 0.00000000E+00 sigma(2 2)= -5.42027786E-09 sigma(3 1)= 0.00000000E+00 sigma(3 3)= -3.33970359E-08 sigma(2 1)= 0.00000000E+00
================================================================================
Extraction of the clamped elastic tensor (unit:10^2GPa)
3.9133823 1.3361329 1.1936863 -0.0000000 -0.0000000 -0.0000000 1.3361172 3.8023382 1.1335897 -0.0000000 -0.0000000 -0.0000000 1.1936770 1.1335796 4.0167474 -0.0000000 -0.0000000 -0.0000000 -0.0000000 -0.0000000 0.0000000 1.2884614 -0.0000000 0.0000000 -0.0000000 0.0000000 -0.0000000 -0.0000000 1.2158450 0.0000000 -0.0000000 -0.0000000 -0.0000000 0.0000000 -0.0000000 1.4230204
================================================================================
Calculation of acoustic sum rule
================================================================================
Calculation of the interatomic forces from DDB
Homogeneous q point set in the B.Z.
Grid q points : 8 1) 0.00000000E+00 0.00000000E+00 0.00000000E+00 2) 5.00000000E-01 0.00000000E+00 0.00000000E+00 3) 0.00000000E+00 5.00000000E-01 0.00000000E+00 4) 5.00000000E-01 5.00000000E-01 0.00000000E+00 5) 0.00000000E+00 0.00000000E+00 5.00000000E-01 6) 5.00000000E-01 0.00000000E+00 5.00000000E-01 7) 0.00000000E+00 5.00000000E-01 5.00000000E-01 8) 5.00000000E-01 5.00000000E-01 5.00000000E-01
The interatomic forces have been obtained
================================================================================
Calculation of dynamical matrix for each ph1l points
Phonon at Gamma, with non-analyticity in the direction (cartesian coordinates) 0.00000 0.00000 0.00000 Phonon energies in Hartree : -2.294305E-06 -1.589880E-06 -1.457514E-06 4.403333E-04 4.476135E-04 5.009874E-04 5.081990E-04 6.094765E-04 6.228453E-04 6.841952E-04 7.149261E-04 7.563444E-04 7.823985E-04 8.187584E-04 8.503830E-04 8.756807E-04 9.115740E-04 9.303034E-04 9.451129E-04 9.477895E-04 1.008750E-03 1.073909E-03 1.087361E-03 1.094627E-03 1.194544E-03 1.215171E-03 1.243183E-03 1.299532E-03 1.326571E-03 1.393394E-03 1.420781E-03 1.496467E-03 1.550377E-03 1.629425E-03 1.632909E-03 1.672657E-03 1.693239E-03 1.740117E-03 1.970287E-03 1.976703E-03 2.016032E-03 2.076543E-03 2.094483E-03 2.116629E-03 2.126912E-03 2.233949E-03 2.246967E-03 2.248255E-03 2.250899E-03 2.332700E-03 2.346309E-03 2.378494E-03 2.382681E-03 2.422239E-03 2.441826E-03 2.465514E-03 2.565346E-03 3.445785E-03 3.566167E-03 3.726860E-03 Phonon frequencies in cm-1 : - -5.035417E-01 -3.489383E-01 -3.198875E-01 9.664199E+01 9.823980E+01 - 1.099540E+02 1.115368E+02 1.337646E+02 1.366987E+02 1.501635E+02 - 1.569081E+02 1.659984E+02 1.717166E+02 1.796967E+02 1.866375E+02 - 1.921897E+02 2.000674E+02 2.041780E+02 2.074283E+02 2.080157E+02 - 2.213950E+02 2.356958E+02 2.386481E+02 2.402428E+02 2.621722E+02 - 2.666991E+02 2.728472E+02 2.852143E+02 2.911487E+02 3.058145E+02 - 3.118255E+02 3.284365E+02 3.402684E+02 3.576175E+02 3.583822E+02 - 3.671058E+02 3.716230E+02 3.819116E+02 4.324281E+02 4.338362E+02 - 4.424679E+02 4.557485E+02 4.596859E+02 4.645464E+02 4.668033E+02 - 4.902951E+02 4.931522E+02 4.934350E+02 4.940152E+02 5.119685E+02 - 5.149552E+02 5.220192E+02 5.229380E+02 5.316199E+02 5.359190E+02 - 5.411179E+02 5.630283E+02 7.562623E+02 7.826833E+02 8.179513E+02
================================================================================
Calculation of the internal-strain tensor
Force-response internal strain tensor(Unit:Hartree/bohr)
Atom dir strainxx strainyy strainzz strainyz strainxz strainxy 1 x 0.0941002 -0.0408713 -0.0533039 0.0000000 0.0000000 -0.0609607 1 y -0.0828675 0.1403061 -0.0248158 0.0000000 0.0000000 -0.0169793 1 z 0.0000000 0.0000000 0.0000000 -0.0368215 -0.0711707 -0.0000000 2 x -0.0941002 0.0408713 0.0533039 -0.0000000 -0.0000000 0.0609607 2 y 0.0828675 -0.1403061 0.0248158 -0.0000000 -0.0000000 0.0169793 2 z 0.0000000 0.0000000 0.0000000 0.0368215 0.0711707 -0.0000000 3 x -0.0941002 0.0408713 0.0533039 -0.0000000 -0.0000000 -0.0609607 3 y -0.0828675 0.1403061 -0.0248158 0.0000000 0.0000000 0.0169793 3 z 0.0000000 0.0000000 0.0000000 -0.0368215 0.0711707 0.0000000 4 x 0.0941002 -0.0408713 -0.0533039 0.0000000 0.0000000 0.0609607 4 y 0.0828675 -0.1403061 0.0248158 -0.0000000 -0.0000000 -0.0169793 4 z 0.0000000 0.0000000 0.0000000 0.0368215 -0.0711707 0.0000000 5 x -0.0000000 0.0000000 0.0000000 0.0000000 -0.0000000 0.0000000 5 y 0.0000000 0.0000000 0.0000000 -0.0000000 0.0000000 -0.0000000 5 z -0.0000000 -0.0000000 -0.0000000 0.0000000 0.0000000 0.0000000 6 x -0.0000000 0.0000000 0.0000000 -0.0000000 -0.0000000 0.0000000 6 y 0.0000000 0.0000000 0.0000000 -0.0000000 -0.0000000 -0.0000000 6 z -0.0000000 -0.0000000 -0.0000000 0.0000000 -0.0000000 -0.0000000 7 x -0.0000000 -0.0000000 -0.0000000 -0.0000000 -0.0000000 0.0000000 7 y 0.0000000 0.0000000 0.0000000 -0.0000000 -0.0000000 -0.0000000 7 z -0.0000000 -0.0000000 -0.0000000 0.0000000 -0.0000000 -0.0000000 8 x 0.0000000 -0.0000000 -0.0000000 0.0000000 -0.0000000 0.0000000 8 y 0.0000000 0.0000000 0.0000000 -0.0000000 -0.0000000 -0.0000000 8 z -0.0000000 -0.0000000 -0.0000000 0.0000000 -0.0000000 0.0000000 9 x 0.0165308 -0.0318013 -0.1284522 -0.0000000 -0.0000000 0.0027962 9 y 0.0090276 -0.0682327 0.0203506 0.0000000 0.0000000 -0.0401272 9 z -0.0000000 -0.0000000 -0.0000000 0.0337670 -0.0716536 -0.0000000 10 x -0.0165308 0.0318013 0.1284522 0.0000000 0.0000000 -0.0027962 10 y -0.0090276 0.0682327 -0.0203506 -0.0000000 -0.0000000 0.0401272 10 z -0.0000000 -0.0000000 -0.0000000 -0.0337670 0.0716536 -0.0000000 11 x 0.0165308 -0.0318013 -0.1284522 -0.0000000 -0.0000000 -0.0027962 11 y -0.0090276 0.0682327 -0.0203506 -0.0000000 -0.0000000 -0.0401272 11 z -0.0000000 -0.0000000 -0.0000000 -0.0337670 -0.0716536 0.0000000 12 x -0.0165308 0.0318013 0.1284522 0.0000000 0.0000000 0.0027962 12 y 0.0090276 -0.0682327 0.0203506 0.0000000 0.0000000 0.0401272 12 z -0.0000000 -0.0000000 -0.0000000 0.0337670 0.0716536 0.0000000 13 x 0.1036986 0.0028863 -0.0013285 -0.0294432 -0.0159880 0.0323406 13 y 0.0023604 -0.0644718 0.0033325 -0.0085421 -0.0319129 -0.0243703 13 z -0.0364388 -0.0301746 -0.0242418 0.0104449 0.0047313 -0.0546885 14 x -0.1036986 -0.0028863 0.0013285 0.0294432 0.0159880 -0.0323406 14 y -0.0023604 0.0644718 -0.0033325 0.0085421 0.0319129 0.0243703 14 z 0.0364388 0.0301746 0.0242418 -0.0104449 -0.0047313 0.0546885 15 x -0.1036986 -0.0028863 0.0013285 -0.0294432 -0.0159880 -0.0323406 15 y -0.0023604 0.0644718 -0.0033325 -0.0085421 -0.0319129 0.0243703 15 z -0.0364388 -0.0301746 -0.0242418 -0.0104449 -0.0047313 -0.0546885 16 x 0.1036986 0.0028863 -0.0013285 0.0294432 0.0159880 0.0323406 16 y 0.0023604 -0.0644718 0.0033325 0.0085421 0.0319129 -0.0243703 16 z 0.0364388 0.0301746 0.0242418 0.0104449 0.0047313 0.0546885 17 x -0.1036986 -0.0028863 0.0013285 0.0294432 -0.0159880 0.0323406 17 y 0.0023604 -0.0644718 0.0033325 -0.0085421 0.0319129 0.0243703 17 z -0.0364388 -0.0301746 -0.0242418 0.0104449 -0.0047313 0.0546885 18 x 0.1036986 0.0028863 -0.0013285 -0.0294432 0.0159880 -0.0323406 18 y -0.0023604 0.0644718 -0.0033325 0.0085421 -0.0319129 -0.0243703 18 z 0.0364388 0.0301746 0.0242418 -0.0104449 0.0047313 -0.0546885 19 x 0.1036986 0.0028863 -0.0013285 0.0294432 -0.0159880 -0.0323406 19 y -0.0023604 0.0644718 -0.0033325 -0.0085421 0.0319129 -0.0243703 19 z -0.0364388 -0.0301746 -0.0242418 -0.0104449 0.0047313 0.0546885 20 x -0.1036986 -0.0028863 0.0013285 -0.0294432 0.0159880 0.0323406 20 y 0.0023604 -0.0644718 0.0033325 0.0085421 -0.0319129 0.0243703 20 z 0.0364388 0.0301746 0.0242418 0.0104449 -0.0047313 -0.0546885
Bound for ifc SR:
x=[ -1 1], y=[ -1 1] and z=[ -1 1]
================================================================================
Impose acoustic sum rule on total ifc
================================================================================
================================================================================
There is no file for the coefficients from polynomial fitting
================================================================================
Generation of the xml file for the model in tmulti1_1_model.xml
================================================================================
- - Proc. 0 individual time (sec): cpu= 0.3 wall= 0.3
================================================================================
+Total cpu time 0.336 and wall time 0.337 sec
multibinit : the run completed succesfully.
The run you performed was aimed at reading the DDB file, generating the short range interatomic force constants and extract all the other informations related to the harmonic part of the model. You can find inside the output file, the Born effective charges, the clamped-ion elastic tensor and the internal strain coupling parameters. Take some time to open and read the tmulti1_1.abo file. If the DDB file is complete, the generation of the XML file requires only few input variables:
- prt_model = 1 \Longrightarrow the generation of the XML file is activated, takes the time to read the possible options for prt_model.
- ngqpt = 2 2 2 \Longrightarrow specified the q-point mesh included in the tmulti1_DDB file
- dipdip = 0 \Longrightarrow it disables the computation of the dipole-dipole interaction: we don’‘t need to compute it to generate the XML file, MULTIBINIT will be able to regenerate the dipole-dipole interaction in a next run. We remind you that the default for this option is 1 and in the most part of your runs you will not use this option.
After this run, you should see in your directory tmulti1_1_model.xml, you can take some time to open and read this file. As you can see, it contains all the informations about the system definition (lattice parameters, atomic positions) and the data for the harmonic part of the potential.
Your XML file is now ready and you can use it as input for MULTIBINIT. To do that, copy now in your work directory the file ~abinit/tests/tutomultibinit/Input/tmulti1_2.files; you should see inside it:
tutomulti1_2.abi tutomulti1_2.abo tmulti1_1_model.xml
Here, the DDB file is replaced by the XML file. Do not forget to copy the ~abinit/tests/tutomultibinit/Input/tutomulti1_2.abi in your directory before you run:
multibinit < tmulti1_2.files > tmulti1_2_stdout
In tutomulti1_2.abi, prt_model is still set to one so multibinit will write again the model XML file, which is useless at this stage, being a copy of the one read as input. Set this input variable to 0 and, in this case, MULTIBINIT will just read (and not write) the XML file.
With the two last examples, we have shown that MULTIBINIT is able to read either a DDB file or a XML as inputs for the system definition and the harmonic part of the potential.
We can now run our first dynamics: you can copy the files ~abinit/tests/tutomultibinit/Input/tutomulti1_3.* in your work directly and have a look them.
#-------------------------------------------------------------- #molecular dynamics #-------------------------------------------------------------- dynamics = 13 # 13 = NPT simulation. ncell = 4 4 4 # Size of the supercell for the simulation ntime = 1000 # Number of step in the simulation. temperature = 50 # Temperature of the simulation (default = 325K). optcell = 2 # Relaxation of the cell ############################################################## # This section is used only for regression testing of ABINIT # ############################################################## #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = multibinit #%% system_xml = tmulti1_2_model.xml #%% [files] #%% files_to_test = #%% tmulti1_3.abo, tolnlines = 0, tolabs = 0.0, tolrel = 0.0, fld_options = -medium; #%% [paral_info] #%% max_nprocs = 1 #%% [extra_info] #%% authors = A. MARTIN #%% keywords = Effective potential, multibinit #%% description = #%% read xml file and run a molecular dynamics #%% topics = LatticeModel #%%<END TEST_INFO>
The simulation starts from the DDB to correctly account for the dipole-dipole interactions. You can visualize your dynamics with the agate software:
agate tmulti1_3.abo_HIST.nc
Also try to use the effective potential from the xml file instead, in which the dipole-dipole interactions were not corrected. What do you see when you visualize the track?
This MULTIBINIT tutorial is now finished.